Biomimetic cilia arrays generate simultaneous pumping and mixing regimes

Abstract

Living systems employ cilia to control and to sense the flow of fluids for many purposes, such as pumping, locomotion, feeding, and tissue morphogenesis. Beyond their use in biology, functional arrays of artificial cilia have been envisaged as a potential biomimetic strategy for inducing fluid flow and mixing in lab-on-a-chip devices. Here we report on fluid transport produced by magnetically actuated arrays of biomimetic cilia whose size approaches that of their biological counterparts, a scale at which advection and diffusion compete to determine mass transport. Our biomimetic cilia recreate the beat shape of embryonic nodal cilia, simultaneously generating two sharply segregated regimes of fluid flow: Above the cilia tips their motion causes directed, long-range fluid transport, whereas below the tips we show that the cilia beat generates an enhanced diffusivity capable of producing increased mixing rates. These two distinct types of flow occur simultaneously and are separated in space by less than 5 μm, approximately 20% of the biomimetic cilium length. While this suggests that our system may have applications as a versatile microfluidics device, we also focus on the biological implications of our findings. Our statistical analysis of particle transport identifying an enhanced diffusion regime provides novel evidence for the existence of mixing in ciliated systems, and we demonstrate that the directed transport regime is Poiseuille–Couette flow, the first analytical model consistent with biological measurements of fluid flow in the embryonic node.

The cilium is a biological structure unique in its ability to manipulate and sense its fluid environment (1, 2). Research in the last decade has implicated cilia dysfunction in a wide range of human pathologies (3) and has shown that cilia perform an array of unexpected biological functions (4–6) beyond traditional roles such as the clearance of mucus and pathogens from the airways. For example, embryonic nodal cilia drive a fluid flow that plays a key role in the embryogenesis of vertebrate organisms by generating an asymmetric morphogen concentration (7), and cerebrospinal flows produced by arrays of cilia direct cell traffic in the brain (8). Yet, while the role of directed transport within such systems is being explored, the presence of cilia-generated mixing has only recently engendered speculation (9, 10).

Flagellar mixing has been shown to be essential to the health of some microorganisms (11, 12). More broadly, cilia-induced mixing could alter rates and efficacies of diverse fluid-mediated processes such as biochemical signaling, regulation, chemotaxis, and chemosensation. In addition, the relationship between vortical flows near the cilia and the directed transport they produce is not well understood for ciliated systems, such as the embryonic node where mixing could affect biochemical signaling that has been shown critical to the establishment of vertebrate left-right body asymmetry (13, 14). Furthermore, an understanding of fluidic mixing above a ciliated surface is important for designing efficient methods of drug delivery across the epithelium.

Because cilia and flagella are predominantly used in nature for fluid propulsion at the microscale, engineered mimics of these structures have been widely suggested as an appealing microfluidic technology. Microfluidics is a rapidly developing field with great potential significance, promising a miniaturized “lab-on-a-chip” for biological analysis and the synthesis of chemicals. Achieving this goal will require innovative technologies for the effective manipulation of fluids in microfluidic systems.

A number of methods for the propulsion of fluids with artificial cilia systems have been the subject of recent computational studies (15–19). Experimentally, a variety of systems at different scales have demonstrated cilia-like actuation based on piezo-driven stage motion (20), substrate swelling (21), linked magnetic beads (22), liquid crystal elastomers (23), self-oscillating gels (24), and electron beam deflection (25). Engineered systems that have succeeded in generating pumping and mixing include live “carpets” of flagellated bacteria that have produced either mixing or directed flows depending on the system geometry (26), and electromechanical (27) and polymeric (28) paddles that have generated transport and mixing but fall outside of the size and hydrodynamic range relevant to ciliated biological systems. Recently, Vilfan et al. demonstrated a 3 × 3 array of artificial cilia formed from linked 5-μm magnetic beads and used the same beat pattern we describe below to produce directed transport over the array’s total width of approximately 60 μm (29).

Here we report on the simultaneous production of long-range, directed pumping and enhanced mixing, in spatially segregated regimes, by the magnetic actuation of biomimetic cilia arrays (Movies S1 and S2). We find that the pumping and mixing flow regimes are separated by a sharp 5-μm transition region at the tips of the 25-μm tall, 700-nm diameter cilia (Fig. 1). Our analysis of these two flow regimes are of relevance for computational and biological cilia studies, but also highlight the versatility of our cilia arrays as a microfluidics device. We show that an analytical model, Poiseuille–Couette flow, explains our velocity flow profile and that of the embryonic node. Finally, our quantitative observations and statistical analysis of enhanced diffusion below the cilia tips highlight the potential for fluidic mixing in biological ciliated systems.

Fig. 1.

Scanning electron micrograph of a biomimetic cilia array. Each cilium is 700 nm in diameter and 25 μm in length. To prevent collapse, the sample is critical point dried before imaging.

Biomimicry in an Artificial Cilia System

Our biomimetic cilia arrays are formed from a flexible magnetic nanoparticle-polydimethysiloxane (PDMS) composite material and closely match the size of biological cilia. We previously reported on the template fabrication and magnetic actuation of these arrays (30). With our template fabrication method we produce cilia with heights of 10 or 25 μm and diameters of 200–800 nm, and arrays that typically cover approximately 1 mm² comprising approximately 3,000 individual cilia at an average density of 0.02 cilia/μm². The template fabrication method does not require photolithography or specialized equipment and is thus rapid, inexpensive, and allows for the production of cilia at various heights, diameters, and average densities over an arbitrarily large area.

In the presence of an externally applied magnetic field, our superparamagnetic cilia bend to align with local magnetic field lines due to the large aspect ratio of each cilium. To actuate our cilia arrays we use a variable speed motor rotating a permanent magnet (Fig. 2). In this manner we can mimic the beat patterns of several types of biological cilia and control the beat frequency.

Fig. 2.

Biomimetic cilia experimental setup and magnetic actuation. (A) Embryonic nodal cilia produce directed fluid transport with a tilted conical beat, which produces a net movement of fluid in the transport direction due to the fluid’s interaction with the no-slip boundary. (B) The tilted conical orbit is generated by an offset of the actuating magnet’s rotational axis from the sample. (C) Minimum intensity projection of a sequence of brightfield video frames over one cycle of the tilted conical beat of a single cilium and corresponding fluid transport direction. (D) The tilt direction (along x axis) is determined by the azimuthal position of the magnet relative to the sample, thus determining the transport direction (along y axis). The magnitude of the magnet’s offset controls the tilt angle Θ, and the half-cone angle Ψ is determined by the applied magnetic force. (E) As the cilia beat within an enclosed fluidic cell, they produce directional transport above their tips (as in Fig. 3A), with a recirculation along the upper boundary, whereas below the tips the fluid flow is rapid and nondirectional, and tracers exhibit enhanced mixing relative to diffusion (as in Fig. 3B).

It has been established that primary cilia in the embryonic node are motile (31) and drive fluid transport critical to the determination of the vertebrate left/right body axis (7). This cilia-driven flow advects morphogen-loaded vesicles, on the order of 1 μm in diameter, toward what will develop to become the left side of the embryo. These “nodal vesicular parcels” (NVPs) subsequently rupture to release their morphogen cargo on the left, resulting in a left/right morphogen gradient. In addition, it has been shown that fibroblast growth factor (FGF) is required for proper formation and release of the microvilli-tethered NVPs into the cilia-driven flow (14). Thus, the vertebrate embryonic node forms a complex system that must efficiently advect NVPs to the left while simultaneously ensuring that, upon vesicular rupture, the released morphogens are transported slowly enough (via diffusion or advection) to preserve the concentration gradient.

To produce this “nodal flow” these embryonic nodal cilia execute a so-called “tilted conical beat” that is significantly different than the classical planar beat of airway epithelial cilia. Despite being a time-reversible motion (32), this beat produces directional transport in a low Reynolds number, inertialess environment due to the fluid’s interaction with the cell floor (Fig. 2A) (13, 33). Because of the tilted axis, as the cilium tip passes near the cell floor, the volume of fluid entrained by the cilium is reduced due to the no-slip boundary condition. A complete cycle, therefore, produces a net flow in the direction of the cilium’s motion when its tip is farthest from the surface. The tilted conical beat is parameterized by a tilt angle Θ and half-cone angle Ψ, as in Fig. 2D.

In this work, we employ this tilted conical beat with biomimetic cilia at up to 35 Hz to generate, within a single system, both directed flow and enhanced mixing of a Newtonian fluid at the spatial length scale and low Reynolds number characteristic of biological systems (Movies S1 and S2). For the following experiments, we have fabricated our biomimetic cilia arrays within an enclosed fluidic cell with a lateral width of 1 mm and height of 225 μm, approximately an order of magnitude larger in each dimension than the mouse node (see Appendix). Based on our cilia beat cycle, the Reynolds number in our system does not exceed 0.025 (see SI Text).

Results

To characterize our cilia-driven fluid flow, we use video tracking of 500-nm fluorescent microspheres as passive tracers. As in the embryonic node, at these scales diffusion can be significant and so mass transport is characterized by the dimensionless ratio of advective to diffusive motion known as the Péclet number. The Péclet number is given by

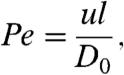[1]

where u and l are characteristic velocity and length scales, respectively, and D₀ is the mass diffusivity, such that advection dominates for Pe > 1 and diffusion dominates for Pe < 1. For our d = 500 nm tracers, the Stokes–Einstein equation D₀ = kT(3πηd)^-1, where kT is the thermal energy scale and η is the viscosity, gives D₀ = 0.9 μm²/s. To estimate a Péclet number for our system we choose a tracer velocity of u = 2 μm/s and the average diameter of the circle traced out by the cilia beat of l = 5 μm, which gives a Péclet number on the order of 10. Thus, while cilia-driven advection is the dominant means of transport, diffusion can still be a significant source of mass transport. In fact, in the embryonic node, recent work with exogenously introduced molecules has shown that chemical gradients are stable only when the molecular weight is above approximately 15 kDa (13). In other words, morphogens must diffuse slowly enough for the cilia-driven flow to induce a Péclet number that is larger than 1.

Tracer motion in our system also exhibits time-scale dependent behavior. At short time scales, the cilia beat produces tracer epicycles that orbit at the frequency of the cilia beat, due to the strong coupling of the cilia beat with the low Reynolds number fluid (34). Because of the no-slip boundary at the cilium surface, tracers in close proximity to cilia should move with speeds comparable to the cilia tip speeds of approximately 700–800 μm/s. Within the plane of the cilia tips, we find that tracers orbit at speeds of about 200 μm/s. At longer time scales, average tracer motion is an order of magnitude slower, and we observe the presence of spatially segregated pumping and mixing regimes.

Pumping Above the Cilia Tips.

Above the tips of the beating cilia, the time-averaged tracer motion is uniform, directed transport (Fig. 3A and Movies S1 and S2). This directed flow is analogous to the flow produced by nodal cilia (13, 35). At low magnification we have observed that this net transport is roughly uniform across the 1-mm width of the fluidic cell (Movie S3). Consistent with in vivo observations of the nodal flow (13, 35) and with computational work (36), the direction of the flow is determined by the direction of the motion of each cilium when its tip is farthest from the specimen floor (Movie S1). We also observe a slow recirculation of fluid along the chamber’s upper boundary due to the enclosed nature of the flow cell. This recirculatory flow has also been reported in the embryonic node (7, 13).

Fig. 3.

Trajectories of 500-nm tracers, with average velocity mapped to color. Cilia actuation simultaneously generates pumping and mixing regimes, with a sharp dividing boundary near the biomimetic cilia tips. Color-mapped velocities are averaged over a 0.25-s time window. (A) Driven tracer motion above the tips (z = 30 μm) is unidirectional transport. (B) Below the tips (z = 15 μm) the flow is nondirectional, heterogeneous, and rapid. (C) Undriven, diffusive motion for comparison with the biomimetic cilia-driven advection. (D) Distributions of the velocities, in the transport direction, for A–C, and least square fits to a skew normal distribution. Distribution widths demonstrate the heterogeneity and nondirectionality of the mixing flow below the biomimetic cilia tips relative to the directed transport above.

Our system offers a large degree of control over the directed fluid transport. The relative positioning of the actuating magnet and the cilia array determines the cilia tilt direction and thus the fluid transport direction (Fig. 2 A and B). By repositioning the magnet we can arbitrarily choose the pumping direction. Further, for a given magnet position the transport direction can be switched 180° by reversing the motor drive. We can also control the flow velocity by adjusting the cilia beat frequency and find a linear relationship between the two (Fig. S1). This flexibility in directionality and velocity of pumping would be a distinct advantage of biomimetic cilia devices in a microfluidics setting.

Cilia-Driven Pumping Is Poiseuille–Couette Flow.

A coarse-grained description of cilia-generated fluid flows is an essential component of large-scale computational modeling of ciliated systems. To construct a velocity flow profile we averaged tracer velocities in the direction of fluid transport at a number of focal planes above and below the biomimetic cilia tips (Fig. 4A). Considering only the portion of the velocity profile above the cilia tips (from z = 25 μm → 225 μm), we find that the directed flow can be explained by Poiseuille–Couette (PC) flow, a linear superposition of shear- and pressure-driven flow in a parallel plate geometry. PC flow is described by a velocity profile

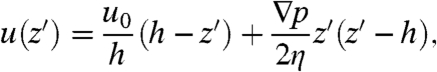[2]

where z^′ = z - 25 μm and the bottom plate at z^′ = 0 (at the cilia tips) slides with velocity u₀ relative to the stationary upper plate at z^′ = h, exerting a shear stress on a fluid of viscosity η under a pressure gradient ∇p. In Fig. 4A the solid curve was obtained as a least-squares fit of the biomimetic cilia-driven velocity profile above the cilia tips to Eq. 2. Thus, the collective motion of thousands of cilia generates a velocity profile that can be coarse-grained as an effective shear stress produced at the cilia tips (Couette flow) and an opposing induced pressure gradient generated by the interaction of the fluid with the closed flow cell boundaries (Poiseuille flow).

Fig. 4.

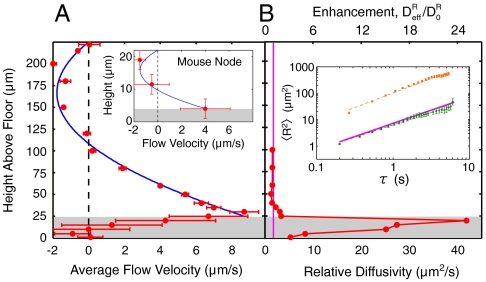
The velocity flow profile and effective relative diffusivity of biomimetic cilia-driven flow. The area below the cilia tips is denoted by the shaded regions. (A) Red points are the tracers’ average velocity, in the transport direction, at various heights above the floor. The solid blue curve is a least-squares fit to the Poiseuille–Couette flow profile of Eq. 2 with fit parameters u₀ = 8.7 μm/s and ∇p = 1.05 Pa/m. The maximum average velocity occurs just above the cilia tips, demonstrating that the collectively driven transport at the tips acts analogously to the velocity u₀ of the sliding plane in PC flow. Because the chamber is enclosed, there is a recirculation of fluid near the upper boundary. (Inset) We fit the PC flow profile to mouse nodal flow velocity data at three heights taken from Okada et al. (13), with parameters u₀ = 4 μm/s and ∇p = 79 Pa/m. The discrepancy in ∇p between the node and our flow cell is likely due to the overall size differences of the two systems (see Appendix). (B) The biomimetic cilia motion induces mixing by producing a maximum relative diffusivity of 42 μm²/s, an enhancement of 25 in relation to the expected relative diffusivity of 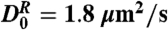(vertical magenta line) from the Stokes–Einstein relation. Above the cilia tips, the relative diffusivity rapidly decays back to the expected value. Horizontal error bars are on the order of the dot size. (Inset) Tracer MSDs and least-squares linear fits to the log of Eq. 5, from above (orange) and below (green) the cilia tips. The solid magenta line is the theoretical MSD with the expected relative diffusivity D₀ and slope of 1.

Previous measurements of fluid flow within the node of a mouse embryo documented the variation of flow away from the plane of the nodal cilia tips (13). In Fig. 4A Inset, we have taken this data from Okada et al. (13) and fit it to the PC flow profile assuming the approximate geometry stated in their work. We can see that Poiseuille–Couette flow is consistent with the flow in our engineered fluid cell and that of the mouse node, suggesting that the three-dimensional nature of the flows in these systems is that of a “driven cavity” (see Appendix) (37). We note that, more recently, Okada et al. performed a numerical simulation of flow in an open pit that is driven by a shear plane, as in Couette flow, in order to confirm the persistence of the recirculatory flow despite their removal of the membranous covering of the nodal cavity (38).

We also note that neither fit to Eq. 2 results in a net zero flux as expected for a two-dimensional, closed system. As pointed out by Liron, this behavior is due to a portion of the return flow that, in three dimensions, is recirculated around the periphery of the system (39). This peripheral recirculation is also evident in the embryonic node in supplemental videos from Okada et al. (13).

Volume Flow Rate.

Another goal in the coarse graining of cilia-driven fluid flows is to be able to predict flow rates and fluid velocities of a system of cilia from knowledge of the beat shape of a single cilium in that system. A result from resistive force theory predicts the volume flow rate for a single cilium based on the parameters of the tilted conical beat,

[3]

where ω is the angular frequency and g = 4/3[1 + 2 ln(2q/a)]^-1 is a geometric factor in which a is the diameter and q is a length parameter of order 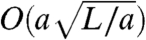(36). In contrast to our experiment in an enclosed flow cell, this result is derived in a semiinfinite space, and so we take this value to be the maximum possible flow rate a single cilium can produce in a system of negligible resistance, or 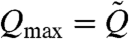. Thus, from the average beat parameters of the cilia driving our velocity profile (see Materials and Methods) we have Q_max = 1.3 ± 0.3 pL/s per cilium.

Experimentally, we can measure the volume flow rate produced by the entire system by noting that for flow in a cell whose width w is larger than its height h (as is the case in both the mouse node and our flow cell) the total volume flow rate can be approximated as

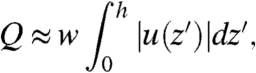[4]

where u(z^′) is the velocity flow profile. Note that we use |u(z^′)| because both the primary flow and the recirculation are attributed to the cilia beat. Performing the integration on the velocity profile of Fig. 4A we get an experimental value of Q^total = 460 ± 50 pL/s.

In order to compare this experimental measurement with the theoretical maximum flow rate per cilium of Q_max = 1.3 pL/s, we would need to know how the flow driven by each cilium in our system contributes to the fluid flow of the entire system. In general, however, this requires knowledge of the interactions between neighboring cilia for which there is no current theory.

From an analogy with classical pumps we can provide limits for the comparison with experiment. In the case of noninteracting cilia, which experimentally would only be realized in a sparse array of cilia, the flow in the system is simply a superposition of each cilium, and thus the N cilia in the array should act like classical pumps that are configured in parallel such that the maximum possible total flow rate would be 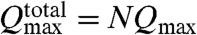, or 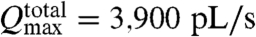. This upper bound is well above the experimental value of 460 pL/s; however, the actual operating point of the model would depend on losses in the system.

In contrast, for strongly interacting cilia we assume that only cilia arrayed across the width of the fluid cell, perpendicular to the transport direction, would behave as classical pumps in parallel. The rest of the cilia, arrayed down the channel, would then act as pumps in series, which would not contribute to 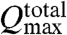. Thus, for n_p cilia arrayed across the width of the cell we have 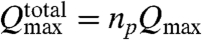. In our experiment we have n_p ≈ 55, giving a lower bound of . In this case, the discrepancy with our experimental measurement implies that cilia arrayed down the length of the channel are still able to make an effective contribution to .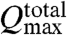

Thus, our experimental value falls within upper and lower bounds considered for non- and strongly interacting cilia. We are optimistic that future experiments performed by varying the number of cilia in an open-ended channel may shed further light on the nature of cilia-cilia interactions.

Enhanced Diffusion Below the Cilia Tips.

Below the cilia tips, the average tracer motion is strikingly different from the directed flow above (Fig. 3B and Movie S2). Here, the fluid motion is dominated by local vortices associated with each beating cilium and tracer trajectories that briefly orbit within then jump to nearby vortices. While similar vortical motion in close proximity to a single cilium has been qualitatively described in experiments (13, 29, 40) and simulations (10, 36), no quantitative analysis of transport phenomena has been undertaken in any ciliated system.

In contrast to the directed transport regime, the flow below the cilia tips shows little overall (time-averaged) directionality, with the standard deviations of the average tracer velocities being at least as large as the mean velocities, except over the 5-μm transition just beneath the cilia tips (Fig. 4A). Tracers exhibit large fluctuations in speed, with the magnitude of individual tracer velocities being largest just below the tips where tracers reach average speeds as high as 30–40 μm/s, as measured over a 0.25-s window.

The nature of this flow regime is suggestive that cilia motion could mix fluids at the microscale. At low Reynolds number, fluids cannot support turbulence and so mixing is often diffusion-limited. Thus, it has been well-documented that mixing can be an obstacle to the efficacy of many microfluidic devices (41). In order to homogenize a fluid over a length l, diffusion requires a time scale t_m = l²D₀. A driven process that generates an enhanced effective diffusivity D_eff will therefore lead to shorter mixing times if the intrinsic diffusivity of the species D₀ is less than D_eff.

To investigate particle transport in this flow regime we analyzed the relative dispersion of tracer pairs with separations given by R(t) = x₂(t) - x₁(t), which has the advantage of suppressing correlated motion of pairs due to uniform advection (42). Mass transport can be characterized by the mean square displacement (MSD) of an ensemble of pair separations, which for motion in two dimensions is given by

[5]

where τ is a lag time, γ is the exponent of the time dependence, and 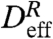is the effective relative diffusivity. The MSD of a diffusive process has a linear time dependence, or γ = 1, while ballistic motion results in γ = 2. By a linear least-squares fit to log[〈R²(τ)〉] vs. log(τ), we find that 〈R²(τ)〉 grows in time with γ ≈ 1 at all heights above the sample floor (Fig. 4B Inset). Thus, despite the dominance of advection in the individual tracer paths as represented by the Péclet number, the temporal evolution of the relative quantity R²(τ) can be characterized as an effective diffusion process with a transport rate given by .

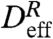Below the tips, the biomimetic cilia motion produces a maximum enhancement of 25 in in relation to the expected relative diffusivity 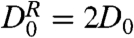(42) of 500 nm tracers (Fig. 4B). This enhancement would produce a commensurate decrease in the mixing time. We note that the relative diffusivity of the directed transport regime above the cilia tips is equal to that expected for the particles’ intrinsic diffusive motion because the uniform transport is suppressed in the relative dispersion calculation. As an additional control, the expected relative diffusivity was accurately obtained for diffusing tracers tracked while the biomimetic cilia were motionless (as in Fig. 3C).

Discussion

Although the directed flow above the cilia in the embryonic node appears to solve the problem of the initial establishment of a long-range chemical gradient, the spatial segregation of directed flow and mixing presents challenges for such a system. The species that is to form a gradient must first reach a region where the directed flow dominates (43), and it must diffuse slowly enough that the flow can efficiently transport the species to the left side of the node. The packaging of signaling molecules into the micron-sized NVPs ensures that the morphogens can be carried across the node at a Péclet number exceeding 1, such that the advective transport dominates. A mechanism whereby the NVPs are dynamically extended into the flow by protruding microvilli allows them to be released at the height of the leftward flow (14). Our results emphasize the importance of such a mechanism and its associated biochemical pathways, which could allow the NVPs to avoid the enhanced mixing generated below the cilia tips.

Once the NVPs are transported across the node, the release of the signaling molecules establishes an initial morphogen gradient. The persistence of this gradient will depend on a competition of cilia-driven advection and the rate of intrinsic particle diffusion, as represented by the Péclet number. For a given flow, the Péclet number is a function of particle size because the rate of intrinsic diffusive transport is inversely related to diameter. Prior to the discovery of the NVPs, size-dependent behavior was observed in which the nodal flow was shown to establish molecular gradients of exogenously introduced proteins with molecular weights above 15 kDa (which corresponds to Pe ≈ 1), whereas for smaller molecules Pe < 1 and so their intrinsic diffusion rapidly homogenized the gradient (13). However, this study was focused on the fate of particles in the flow above the cilia tips, rather than below the tips where chemosensation of a morphogen gradient is likely to occur.

We have demonstrated that particle transport below the tips is more rapid than the flow above, but is nondirectional and scales as an effective diffusion process. A consideration of the average flow speed alone would lead to the conclusion that, below the cilia tips, the Péclet number exceeds 1 even for small molecules. Instead, by comparing the effective diffusivity of the tracers in our experiment with the expected intrinsic diffusivity as a function of particle size, we estimate that the cilia-driven mixing below the tips is only rapid enough to dominate intrinsic diffusivity down to particle sizes of approximately 10 nm (see SI Text). Thus, we would expect that signaling molecules that are used to form the chemical gradient will not experience enhanced mixing below the tips, despite the more rapid speeds than observed in the flow regime above the tips.

In contrast, we note that some processes, such as the FGF-dependent release of the NVPs into the nodal flow (14), could benefit from a more even distribution of signaling species across the nodal floor. In such cases, cilia-driven, size-dependent mixing below the tips could provide a mechanism for enhancing the transport of larger proteins, without affecting the distribution of small molecules due to their more rapid intrinsic diffusivity.

A distinction between our biomimetic system and nodal cilia is the forced synchrony of the cilia beat in our system, whereas nodal cilia are essentially uncoordinated. One clear effect of a synchronized beat in our system is the persistence of the epicyclical tracer motion at heights that are many multiples of the cilia length. In an asynchronous system such epicycles would likely be smoothed out. We note that the effects of each cilium fall off with distance at least as rapidly as 1/r² (10), and so the motion of particles below the cilia tips will be highly dominated by just a few nearby cilia, minimizing effects due to cilia phase differences. In addition, we would expect effects due to synchrony to largely be confined to time scales on par with the cilia beat cycle. As the beat frequency in both our system and the node exceed 10 Hz, and because our main results are derived from average tracer motion over longer time scales, we expect the qualitative differences in fluid flow between the node and our system to be minor.

The ability to design and control biomimetic cilia arrays offers many opportunities to answer fundamental questions in fluid flows generated by dynamic microstructures. Cilia-driven flows in which geometry may play a role, such as the flow of cerebrospinal fluid through the ventricular system of the brain, may be studied. For the lung, questions of the role of mucus viscoelasticity, gravity, and the competition between pumping and draining can be addressed. We have generated coordination reminiscent of the metachronal waves observed in lung epithelia and plan to test the influence of such coordination on directed fluid flows. Additionally, our structures show promise for applications in fluidic sensing, and as an active surface for self-cleaning or antibiofouling, and we expect future material and actuation improvements to offer increased pumping and mixing performance.

Materials and Methods

Fabrication and Sample Preparation.

We previously reported on the fabrication and actuation of our biomimetic cilia arrays (30). To summarize, biomimetic cilia are made from a custom composite material of maghemite nanoparticles dispersed in a widely used silicone elastomer, polydimethylsiloxane (Sylgard 184, Dow Corning). We template this material in the pores of custom polycarbonate track-etched membranes (www.it4ip.be), allowing us to specify the diameter, height, and average density. The composite is heat-cured within the pores of the polycarbonate membrane, in contact with a substrate layer of undoped PDMS, and mounted to a glass coverslip to form a monolithic structure of base and biomimetic cilia array. Once cured, the array is released by dissolution of the polycarbonate membrane with dichloromethane and rinsed with ethanol and aqueous buffer (containing 0.05% Triton-X 100 as a surfactant) before introducing the solution of fluorescent tracers into the fluidic cell. The fluidic cell in our experiments is composed of PDMS on each lateral wall and the sample floor, with a top glass coverslip as the upper boundary. The upper boundary is sealed with Norland Optical Adhesive 81 to eliminate evaporative flows.

Experimental Setup.

Experiments were conducted on a Nikon Diaphot inverted microscope modified to allow imaging in either a reflectance brightfield mode or fluorescence mode. In reflectance we can observe the biomimetic cilia motion in brightfield, allowing positioning of the actuating magnet directly above the fluid chamber to maximize the magnetic forces applied to the array without obstructing the light path.

Video Tracking.

Video tracking above the cilia tips was performed with Video Spot Tracker, a custom automated tracking software developed in-house (freely available at http://cismm.org/downloads/). Because of the rapid speeds and complexity of the flow below the tips, tracers in this regime were tracked with the Manual Tracking plugin in the National Institutes of Health’s ImageJ software. Video was taken with a Pulnix TM6710 camera at 30 or 120 frames per second using a 50×, 0.60 NA magnification objective.

Cilia Beat Parameters.

Average biomimetic cilia beat parameters were determined by tracking the position of the base and the tip of multiple cilia over a beat cycle. If d₁ and d₂ are the projected distance from the base to the nearest and farthest extent of the tip from the base (in the direction of tilt) over a beat cycle, respectively, then Θ = 1/2[sin^-1(d₁/L) + sin^-1(d₂/L)] and Ψ = Θ - sin^-1(d₁/L). For the velocity flow profile experiment in Fig. 3A, Θ = 7.1 ± 0.6° (SEM) and Ψ = 6.3 ± 0.6° (SEM). From a spectral analysis of the tracer epicycle frequency, we measured a cilia beat frequency of ω = 34 Hz.

Appendix

Embryonic Node Geometry.

The shape of the embryonic node varies widely among species. In the mouse it is approximately ellipsoidal, with a height of 20–25 μm and lateral width of about 100 μm (13), about an order of magnitude smaller than our fluidic cell in each dimension. Comparisons of flow patterns among species with various nodal geometries demonstrate that the shape of the node has an insignificant effect on the overall nature of the nodal flow (13).

Driven Cavity Flow.

A well-studied hydrodynamics problem widely used as a test case for numerical simulation techniques is that of the driven cavity. One boundary of a fluid-filled rectangular prism is translated at constant velocity and drives a large vortical flow in the cavity (37). The flow profile has been shown to be approximately constant over much of the width of the cavity in the direction perpendicular to the vortical flow (44). In a low aspect-ratio cavity (w > h), the velocity profile near the center of the cavity is Poiseuille–Couette flow (37, 45). Our velocity profile was measured near the center of the array, several hundreds of microns from any lateral boundaries. Thus, our results suggest that the three-dimensional, time-averaged nature of the flow above the cilia tips in our cell, and possibly that of the node, is that of a driven cavity with the flow at the cilia tips acting as the translating boundary.