FINGER INTERACTION IN A THREE-DIMENSIONAL PRESSING TASK

Abstract

Accurate control of forces produced by the fingers is essential for performing object manipulation. This study examines the indices of finger interaction when accurate time profiles of force are produced in different directions, while using one of the fingers or all four fingers of the hand. We hypothesized that patterns of unintended force production among shear force components may involve features not observed in the earlier studies of vertical force production. In particular, we expected to see unintended forces generated by non-task fingers not in the direction on the instructed force but in the opposite direction as well as substantial force production in directions orthogonal to the instructed direction. We also tested a hypothesis that multi-finger synergies, quantified using the framework of the uncontrolled manifold hypothesis, will help reduce across-trials variance of both total force magnitude and direction. Young, healthy subjects were required to produce accurate ramps of force in five different directions by pressing on force sensors with the fingers of the right (dominant) hand. The index finger induced the smallest unintended forces in non-task fingers. The little finger showed the smallest unintended forces when it was a non-task finger. Task fingers showed substantial force production in directions orthogonal to the intended force direction. During four-finger tasks, individual force vectors typically pointed off the task direction, with these deviations nearly perfectly matched to produce a resultant force in the task direction. Multi-finger synergy indices reflected strong co-variation in the space of finger modes (commands to fingers) that reduced variability of the total force magnitude and direction across trials. The synergy indices increased in magnitude over the first 30% of the trial time and then stayed at a nearly constant level. The synergy index for stabilization of total force magnitude was higher for shear force components as compared to the downward pressing force component. The results suggest complex interactions between enslaving and synergic force adjustments, possibly reflecting the experience with everyday prehensile tasks. For the first time, the data document multi-finger synergies stabilizing both shear force magnitude and force vector direction. These synergies may play a major role in stabilizing the hand action during object manipulation.

INTRODUCTION

In pressing tasks, human fingers produce vectors of force that can vary in both magnitude and direction within a broad range. Until now, most studies of pressing tasks have focused only on normal force production (reviewed in Kilbreath and Gandevia 1994; Li et al. 1998a; Zatsiorsky and Latash 2008) and paid little attention to possible intentional and unintentional shear force production. In particular, studies of normal force production described phenomena of finger interaction such as unintentional force production by uninstructed fingers (enslaving) and lower maximal force produced by fingers in multi-finger tasks as compared to single-finger tasks (force deficit) (Ohtsuki 1981; Kilbreath and Gandevia 1994; Li et al. 1998a; Zatsiorsky et al. 1998, 2000).

Another line of research investigated multi-finger synergies defined as co-varied patterns of commands to fingers across trials that kept total force relatively unchanged (reviewed in Latash and Zatsiorsky 2009). These studies used the framework of the uncontrolled manifold hypothesis (UCM hypothesis, Scholz and Schöner 1999; reviewed in Latash et al. 2007). This hypothesis assumes that the neural controller acts in a space of elemental variables and keeps across-trials variance to a sub-space (UCM) corresponding to a desired value of a performance variable.

The current study has two major objectives: First, to quantify finger interdependence in tasks that require force production in different directions; and second, to explore the existence of multi-finger synergies stabilizing both the magnitude and the direction of the total force vector by co-varying involvement of individual fingers across trials. Within the first objective, we explored unintentional force production for different force directions. Under the term “unintentional force” we imply forces produced by non-task fingers and/or by the task fingers in directions not required by the explicit task, whether due to mechanical, anatomical, or neurophysiological reasons. Unintentional force production includes two components. First, there is enslaving, studied primarily in normal force production tasks (reviewed in Zatsiorsky and Latash 2008). Second, we also studied a novel phenomenon of within-a-finger unintentional force production in non-instructed directions.

Several studies explicitly or implicitly addressed force production by human digits in different directions. Most of these studies explored single-digit force production. In particular, maximal index fingertip force production in all directions was studied by Li et al. (2003). Valero-Cuevas et al. (1998) examined the patterns of muscle activation when subjects produced static forces in five directions (palmar, distal, lateral, dorsal, and medial). Two more studies addressed index finger force production in the flexion-extension plane (Milner and Dhaliwal 2002; Yokogawa and Hara 2002). Valero-Cuevas and his colleagues (2003) also studied the task of compressing a spring with a finger, which imposes restrictions on shear force production.

All these lines of research addressed single-digit tasks and did not consider phenomena of finger interaction. In a study of accurate force production in two different directions, multi-finger synergies stabilizing force direction have been documented: Variance of the resultant force vector was consistently smaller than variances of the individual finger force vectors (Gao et al. 2005). That study, however, considered only two possible directions of force production and did not address phenomena of unintentional force production. Pataky et al. (2007) examined force production in two directions, normal and radial/ulnar, and observed non-zero forces in directions perpendicular to the instructed direction. However, in that study, the fingers pushed against the walls of slots, which prevented motion of the fingers in the radial/ulnar direction, rather than relying on friction as in typical prehensile tasks and in the present study.

It is well known that load-resisting (shear) and grip forces are tightly coupled during object manipulation (Johansson and Westling 1984; Jaric et al. 2005; De Freitas and Jaric 2009). This coupling has been discussed as a consequence of neural strategies, in particular as reflected in synchronization of motor unit action potentials to different muscles and muscle compartments (Santello and Fuglevand 2004). It has also been reported that fingers differ in their roles during typical prehensile tasks, for example the lateral fingers (index and little) play a major role in the generation of the total moment of force on the hand-held object, while the middle finger is primarily involved in resisting the gravitational load (Zatsiorsky et al. 2002). Overall, patterns of unintended force production in three dimensions may be expected to reflect, to a larger degree, synergic finger interactions developed during typical prehensile tasks (for a review see Latash and Zatsiorsky 2009). Therefore, we hypothesized that patterns of unintended force production among shear force components may involve features not observed in the earlier studies of force enslaving during vertical force production. In particular, we expected to see unintended forces not in the direction on the instructed force but in the opposite direction as well as substantial force production in directions orthogonal to the instructed direction. Our second main hypothesis has been based on earlier studies of multi-finger force production (Latash et al. 2002a; Shim et al. 2007; Gao et al. 2005), which suggest that there may be strong multi-finger synergies stabilizing both magnitude and direction of the total force vector in three dimensions.

Methods

Subjects

Eight subjects (four males and four females) volunteered to participate in the study. Their age was 27.5 ± 3.7 years (mean ± standard deviation), height 169.8 ± 4.9 cm, weight 68.0 ± 12.0 kg, hand length from the proximal palmar crease to the tip of the middle finger, 17.8 ± 0.7 cm and hand width, at the level of metacarpal heads, 8.1± 0.7 cm. All subjects were healthy adults, right-handed according to their hand usage during writing and eating, and none of them reported to have any neurological or right upper extremity pathology. None of them reported to be engaged in any activity that may affect hand dexterity (such as being a professional typist or piano player). Prior to study all subjects gave informed consent according to the procedures approved by the Office for Research Protections of the Pennsylvania State University.

Apparatus

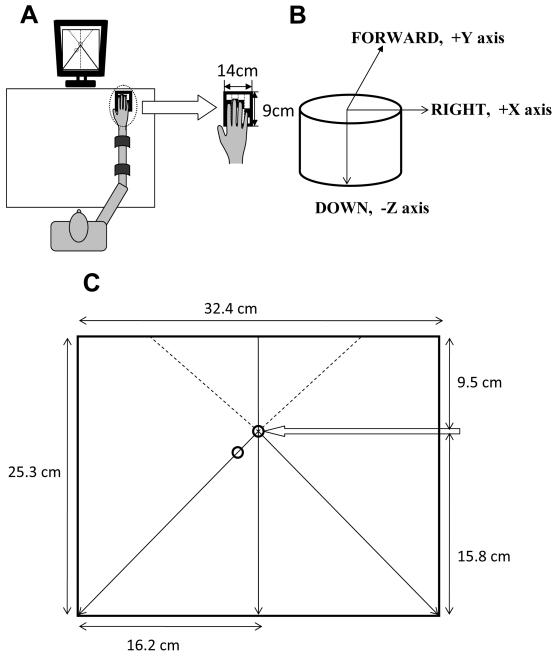
Two setups were used in the experiments. The main part of the experiment used four multi-component force transducers (Nano-17, ATI Industrial Automation, Garner, NC, USA) to measure the three components of the force vector applied to the sensor surface by the tip of each finger of the right hand. The transducers were placed within a frame such that the horizontal distance between the centers of two adjacent transducers was 2 cm. The forward-backward location of the sensors could be adjusted for differences in the lengths of the subjects’ fingers. The sensor surfaces were covered by P-100 sand paper to increase friction. The transducers were oriented such that the force signals along the three orthogonal axes increased upward (Z axis), to the right (X axis), and forward (Y axis) (as shown in Figure 1B).

Figure 1.

A: The experimental setup. B: Orientation of the 6D sensors. C: A schematic of the feedback screen shown to the subject.

The frame with the sensors was placed on the surface of a table. The subjects sat comfortably in front of the table with the right elbow flexed at about 90 degrees, and the right shoulder slightly flexed and abducted (as shown in Figure 1A). A hand rest was placed below the palm to help maintain a comfortable and constant hand configuration. The subjects maintained the same position of the upper extremity throughout the experiment.

The second setup was used in the tests with downward maximal voluntary force production (MVC tests, see the next subsection). Finger forces were measured with a set of unidirectional force sensors (model 208C02; PCB Piezotronics, Inc.) because the multi-component sensors saturated at high forces. Otherwise, the setup used in the MVC tests was similar to the described one (Figure. 1A).

The signals from the sensors were amplified and sampled at 16 bits using a digital-to-analog converter (NI PCI-6225, National Instruments, Austin, TX, USA) at a frequency of 200 Hz. The data were collected on a desktop computer with custom software written in LabView (National Instruments).

Procedure

The experiment consisted of two parts – one-finger pressing tasks and four-finger pressing tasks, which were conducted in two different sessions. Prior to the main part of the experiment, MVCs were recorded for each of the four fingers and for the four fingers acting together, in a random order. In those trials, the subjects had up to 3 s to produce maximal pressing force in the downward direction. Subjects were instructed to “press as hard as possible”. Two MVC trials were performed in a row by each finger and by the four fingers together, and the maximum force produced over the two trials was used in the later calculations. The intervals between the MVC trials were 30 s. The subjects were shown feedback on the screen of the downward force produced by the task finger as a function of time. The order of finger MVC tasks was balanced across subjects.

One-finger accurate ramp force production trials were also performed using 1D sensors to compare the enslaving matrices obtained from 6D sensors with those from 1D sensors. The subjects performed two trials with each finger. The subjects were asked to press with the instructed finger, slowly increasing the force, so as to follow a ramp template shown on the screen. They were asked to keep all other fingers in contact with the sensors. Visual feedback on the pressing force was provided to the subjects as a thick line. The template shown was a horizontal line corresponding to zero force, for three seconds, followed by a diagonal line going up to 22.5% of the subject’s MVC, over the next 5 s.

The main part of the experiment consisted of one- and four-finger tests with accurate force production in five different directions – down, down and right, down and left, down and forward, and down and backward (referred to as D, DR, DL, DF, and DB). The D task was performed under two instructions, to keep the force in the right – left direction zero (referred to as D_RL) and to keep the force in the forward - backward direction zero (referred to as D_FB). In those trials, visual feedback was provided for the force component that the subjects were instructed to keep at zero level. Feedback in the direction not related to the task was not provided. In all trials, the subject was instructed to keep all the fingers in contact with the sensors at all times and not to pay attention to possible force production by non-instructed fingers. An additional one-finger condition was used, pressing down without any feedback on the force along the X or Y axis (referred to as D).

The targets were set at 22.5% MVC for the downward direction, 3.75% MVC for the right-left force directions, and 10% MVC for the forward-backward direction. These values were selected based on a set of pilot trials to allow for comfortable performance of all the tasks and comparable efforts associated with performing the tasks. The feedback was shown to the subjects on the computer screen placed in front of the subjects at a distance of about 65 cm. A schematic of the feedback screen is shown in Figure 1C. One circle (which has an arrow pointing to it in Figure 1C, and was black in the experiment) provided feedback on the current force produced. The subjects were required to apply force such that they cause the location of this circle to match the location of the other circle (which was red in the experiment). The red circle moved with a constant velocity along one of the three lines shown. The target moved along the vertical line for D tasks (D_RL, D_FB and D), along the right slanted line for DR and DF tasks, and along the left slanted line for DL and DB tasks. While the black circle began at the location corresponding to zero force (shown by an arrow in Figure 1C), the red circle began moving from the top of the screen, to give subjects time to prepare. The red circle took 3 s to reach the starting point. The subjects were required to start pressing as soon as the red circle reached the starting point such that the black circle was always on top of the red one, for 5 s. Each circle was 3 mm in diameter.

Feedback gain for movement of the target point along each axis was calculated in percent of MVC per cm. This gain was computed as the percentage of MVC set as target for each direction divided by the length of the line of the screen representing that amount of force. The gain for the three axes was as follows:

• For Z axis: 1.424% of MVC/cm

• For X axis: 0.231% of MVC/cm

• For Y axis: 0.617% of MVC/cm

Before each trial, the subject was instructed in which direction he or she had to press in and along which one of the three lines the cursor would move.

Prior to performing these tasks, the subjects were given sufficient practice time (about 10 min), during which they practiced accurate force production by individual fingers and by all four fingers along each of the force vector directions without a moving target. For the one-finger pressing tasks, there was one practice trial with the moving target followed by three recorded trials for each condition. For these trials, subjects were instructed to “focus only on the task finger” but not to lift any fingers off the sensors at any time. For the four-finger tasks, there were three practice trials with the moving target followed by 15 recorded trials. There were 12-s intervals between the trials. A resting time of 1 minute was provided between sets of trials. None of the subjects complained of pain or fatigue during or after the experiment. Additional rest periods were given when requested.

Data Processing

One-finger pressing tasks were used for calculating enslaving indices and four-finger pressing tasks were used for computing sharing indices and indices of multi-finger synergies (see later). The data were filtered using a two-way 2nd order Butterworth low-pass filter at 2.5 Hz. We tried other (higher) filtering frequencies and found no significant differences in any of the main outcome variables; the 2.5 Hz filter resulted in most consistent within-a-subject data. The data collected at 200 Hz were later resampled into 100 data points for each 5-s trial.

Task Performance

Accuracy of the performance was estimated using the RMS error, which was computed for forces produced in X, Y and Z directions for different tasks.

$$RMS=\frac{1}{F_{Pk}^N}\sqrt{\frac{\sum _{i=1}^N{\left(F_k^i-F_{Pk}^i\right)}^2}{N}}$$

where F_kⁱ is the measured force at sample i along the k axis, F_Pk is the instructed force shown by the moving target, and N the number of samples (100). The RMS was normalized by the maximum instructed force for each condition.

RMS error was also calculated for the direction of force production:

$$RM{S}_{\theta }=\sqrt{\frac{\sum _{i=1}^N{\left({\text{tan}}^{-1}\left(\frac{F_z^i}{F_k^i}\right)-{\text{tan}}^{-1}\left(\frac{F_{Pz}}{F_{Pk}}\right)\right)}^2}{N}}$$

where F_z and F_k are the produced force in the Z and other (X or Y) task direction respectively. RMS error was calculated for each trial and averaged across all trials within a series and then across the subjects for each condition separately.

Enslaving

This index reflects unintentional force production in one-finger tasks either by non-instructed fingers or by the instructed finger in a non-instructed direction. A four-by-four enslaving matrix was computed for each relevant direction (Z and/or either X or Y), for each of the six pressing tasks, resulting in a total of 13 enslaving matrices, E (12 for the six 2D tasks and one for the Down pressing task). Similarly to earlier studies of enslaving, we assumed linear relationships among individual finger forces (Zatsiorsky et al. 1998, 2000; Danion et al. 2003). To obtain entries of the E matrix, the forces produced by non-instructed fingers were regressed on the force produced by the task finger over the whole trial duration:

$$F_{jk}=a_{jk}+b_{jk}{F}_k,$$ (1)

where F_jk is force produced by finger j when k is the task finger and F_k is the force produced by the task finger in a particular direction. Further, the E matrix was computed as:

$$\mathrm{E}=\left[\begin{array}{cccc}\hfill b_{I,I}\hfill & \hfill b_{I,M}\hfill & \hfill b_{I,R}\hfill & \hfill b_{I,L}\hfill \\ \hfill b_{M,I}\hfill & \hfill b_{M,M}\hfill & \hfill b_{M,R}\hfill & \hfill b_{M,L}\hfill \\ \hfill b_{R,I}\hfill & \hfill b_{R,M}\hfill & \hfill b_{R,R}\hfill & \hfill b_{R,L}\hfill \\ \hfill b_{L,I}\hfill & \hfill b_{L,M}\hfill & \hfill b_{L,R}\hfill & \hfill b_{L,L}\hfill \end{array}\right]$$ (2)

where b_j,k is the slope of the regression equation when the force produced by finger j is regressed on force produced by finger k, which is the task finger. We used the best out of the three trials for each condition, where ‘best’ was defined as the one with the highest mean R² (square of correlation coefficient) value.

The enslaving index |E| was calculated as the sum of all non-diagonal entries of the enslaving matrix. Two more indices, E_j and E_i were computed for the Z direction only. E_j is the measure of how each finger enslaves the other fingers in Z direction (the sum of entries over the corresponding column of the enslaving matrix minus 1). E_i is a measure of how a given finger is enslaved by other fingers in Z direction during different pressing conditions (the sum of entries over the corresponding row of the enslaving matrix minus 1).

The enslaving index |E| was also calculated based on the enslaving matrices obtained from single-finger ramp tasks using uni-dimensional sensors, in a similar way. The results for the enslaving matrices were not different from the data obtained from uni-dimensional and 6D sensors. So, in the remaining text we only present 6D sensor data.

Another measure F_UN, was used to characterize unintended force production within each finger across different directions across one-finger pressing tasks. F_UN reflects the amount of force produced by the task finger acting downward (along the Z axis) in a non-instructed direction (X or Y): F_UN = F(non-Z, non-task) / F_Z,task.

F_UN was also calculated using linear regressions. Force produced by the task finger in the non-instructed direction was regressed on force produced by the task finger in the Z direction. F_UNki = a_ki + b_ki F_UNkz , where F_UNki is the force produced by task finger k in non-instructed direction i, F_UNkzis the force produced by the task finger k in Z direction; b_ki is the slope of the regression line. Means and standard deviations of F_UN in the Y direction were computed, across subjects, for each finger individually for three task conditions involving the X axis. It was repeated for F_UN in the X direction for tasks involving Y axis.

Analysis of multi-finger synergies

We quantified multi-finger synergies stabilizing the magnitude of total force and its direction in four-finger trials using the framework of the uncontrolled manifold (UCM) hypothesis (Scholz and Schöner 1999). This analysis quantifies two components of variance in the space of elemental variables (finger modes, see Appendix), one that does not affect a certain value of a performance variable (force magnitude or force direction in our study), and the other that does. We will address these two components as variance within the UCM (V_UCM) and variance orthogonal to the UCM (V_ORT).

V_UCM and V_ORT were computed per degree-of-freedom in the corresponding spaces, for each time sample, across trials for each condition and each subject separately. Details of the computations are presented in the Appendix. Further, an index of synergy, ΔV, was computed reflecting the normalized difference between V_UCM and V_ORT. This index was computed for each of the two main performance variables, the magnitude of the total force and the direction of the total force vector (see the Appendix for the dimensionalities of the corresponding spaces).

Since V_UCM, V_ORT and V_TOT are computed per degree-of-freedom, the index of synergy ΔV for stabilizing force magnitude ranges between 1.334 (all variance is within the UCM) and – 4 (all variance is in orthogonal sub-space). For statistical analysis, the ΔV indexes for Force magnitude stabilization were transformed using Fisher’s z-transformation, modified according to the boundaries of ΔV:

$$z_{\Delta V}=0.5\times lo{g}_{10}\left(\frac{4+\Delta V}{1.334-\Delta V}\right)$$ (3)

The index of synergy ΔV computed for force direction ranges between 1.143 (all variance is within the UCM) and – 8 (all variance is in the orthogonal sub-space). For statistical analysis, the ΔV indexes for Force direction stabilization were transformed using Fisher’s z-transformation, modified according to the boundaries of ΔV:

$$z_{\Delta V}=0.5\times lo{g}_{10}\left(\frac{8+\Delta V}{1.143-\Delta V}\right)$$ (4)

Statistics

Paired t-tests were performed on the enslaving indices obtained from uni-dimensional (used for calculating MVC) and 6D sensors (used for the experiment). To explore the differences in performance between one-finger and four-finger pressing tasks, repeated measures two-way ANOVA was done on the RMS errors of the force vector angle with Fingers (I, M, R, L, IMRL) and Conditions (D_RL, D_FB, DR, DL, DF and DB) as factors. A similar ANOVA was run on the RMS errors of force magnitude in Z direction. In these ANOVAs only the first three trials of the four-finger tasks were included to avoid effects of practice.

To compare the Enslaving index |E| in X direction, we used the Student’s t-test for conditions DR and DL. Similarly, to compare the Enslaving index |E| in Y direction, we used the t-test for conditions DF and DB.

Two-way ANOVA with repeated measures was conducted on Enslaving index |E|, with factors Feedback (none, F_X, F_Y) and Finger (Index, Middle, Ring, Little) to explore the effect of feedback on enslaving in Z direction in D tasks. To explore the trend of E_j across different fingers and conditions, two-way ANOVA with repeated measures was done on Ej (index of how a finger enslaves other fingers), with Finger (I, M, R, L) and Condition (7 levels – D, D_RL, D_FB, DR, DL, DF and DB) as factors. A similar ANOVA was done on E_i.

The index of unintended force production in the non-instructed direction (F_UN) along Y axis was explored with repeated measures ANOVA with factors Finger and Task-direction (three levels of tasks involving X axis, D _RL, DR and DL). A similar ANOVA was done on F_UN along X axis with Finger and Task directions (involving Y axis, D_FB, DF, DB) as factors.

In order to analyze the index of synergy for stabilizing force magnitude, we did two-way ANOVA with repeated measures on the z-transformed ΔV value averaged over the whole time interval of the task, with Condition (6 levels, D_RL, D_FB, DR, DL, DF and DB) and Axis (two relevant axes for each condition – Z and X or Y) as factors. To explore the time profile of the synergy index, a two-way ANOVA was run with repeated measures on the z-transformed ΔV value averaged over every 10% of time interval for each subject, with Condition (6 levels) and Time (10 levels: 10%, 20%, 30%, 40%, 50%, 60%, 70%, 80%, 90% and 100%) as factors. This ANOVA was done separately for the z-transformed ΔV values for the Z axis and for the other relevant axis (X or Y).

A one-way ANOVA with repeated measures was done on the z-transformed ΔV values for stabilizing force direction, with Condition (6 levels, D_RL, D_FB, DR, DL, DF and DB) as the factor. Further, a two-way ANOVA with repeated measures was done on ΔV values (averaged over every 10% of time-interval for each subject and then z-transformed), with Condition (6 levels) and Time (10 levels) as factors.

For all the ANOVAs, the assumption of sphericity was checked using Mauchly’ sphericity test. If sphericity was violated, the degrees of freedom were adjusted as necessary using Greenhouse-Geisser corrections.

Results

Accuracy of Task Performance

The following general features characterized one-finger task performance across all subjects. In one-finger tasks, the subjects produced forces in the task directions by the task finger that, on average, matched closely the target (see Fig. 2A, the solid lines match closely the dashed thin target lines). Non-task fingers typically also produced forces with magnitudes that increased in parallel with the task finger force (this is shown for the normal (z) force for M, R and L fingers in Fig. 2A). This was true for both the downward force component (F_Z) and shear force components (F_Y in Fig. 2A). When the subjects were instructed to produce force in the downward direction, typically non-zero forces were produced along the non-task horizontal axes (e.g., see F_y-I in Fig. 2B).

Figure 2.

A: Force time series of a typical representative trial by the Index finger in the Down Forward (DF) task. The thin dashed lines indicate the desired force profile. Thick solid lines indicate the force produced by task finger in instructed directions. Thick dashed lines indicate the force produced by the non task (enslaved) fingers along Z axis. F_Z_task: Force template in −Z (down) direction. F_Y_task: Force template in +Y (forward) direction. F_Z _I : Index finger force in −Z direction. F_Y_I: Index finger force in +Y (forward) direction. F_Z_M: Middle finger force in −Z direction. F_Z_R: Ring finger force in −Z direction.

B: Force time series of a typical representative trial by the Index finger in the Down task with feedback on the right-left force deviations (D_RL). The thin dashed lines indicate the desired force profile. Thick solid lines indicate the force produced by the subject in the instructed direction and thick dashed line indicates unintended force production (F_UN) along Y axis. F_Z _task: Force template in −Z direction. F_X_task: Force template along X (right-left) axis. F_Z_I : Index finger force in −Z (backward) direction. F_X_I : Index finger force along X (right-left) axis. F_Y_I: Index finger force along Y (forward-backward) axis.

To study how accurately the subjects followed the task direction of force, RMS of force vector angle was computed for both one-finger and four-finger tasks with respect to the task force direction over time. The RMS indices were averaged across trials for each subject, and then averaged across all subjects. The data for different conditions are presented in Table 1. The subjects were significantly more accurate in four-finger tasks as compared to one-finger tasks. Directional errors were higher in the DB (Down-backward) condition as compared to the DL (Down-left), DR (Down-right), D_RL (Down, feedback RL) and D_FB (Down, feedback FB) conditions.

Table 1. RMS error of the force vector angle.

Condition	Four-finger task	One-finger tasks
		Index Finger	Middle Finger	Ring Finger	Little Finger
DLR	2.20 ±2.17	15.58 ± 8.04	8.65 ± 2.33	9.63± 2.74	9.58 ± 4.14
DFB	4.25 ± 2.04	14.80 ± 6.85	9.24 ± 2.04	6.30 ± 0.40	13.77 ± 3.76
DL	3.39 ± 2.92	20.33 ± 9.85	11.55 ± 5.58	14.18± 5.02	11.16 ± 4.91
DR	3.16 ± 1.31	19.58 ± 8.05	14.12 ± 5.10	12.17 ± 2.90	12.61 ± 3.63
DF	5.78 ± 1.78	12.09 ± 3.68	8.70 ± 3.99	10.34 ± 3.66	8.23 ± 2.58
DB	8.60 ± 2.92	21.64 ± 10.50	14.47 ± 5.25	19.09±10.07	15.65 ± 3.39

Means and standard errors across subjects have been presented in degrees.

D_LR : Down – feedback L/R, D_FB: Down – feedback F/B, DL: Down left, DR: Down right, DF: Down forward, DB: Down back.

These findings were confirmed by repeated measures, two-way ANOVA on RMS errors of force vector angle with Fingers (I, M, R, L, IMRL) and Condition (D_RL, D_FB, DR, DL, DF and DB) as factors. Fingers and Condition had significant main effects (F_{[4, 203]}= 7.29, p < 0.001 and F_{[5, 203]} = 2.81, p < 0.05). Tukey comparisons showed that RMS error was less for the four-finger pressing task compared to the one-finger tasks (IMRL < M,R,L,I). The differences among the fingers were not significant. Among conditions, only the DB condition was found to have significantly greater RMS error than the D_RL and DF conditions (p <0.05). The interaction between Finger and Condition was not significant.

There was no significant difference in the RMS error of force magnitude in the Z direction between one-finger and four-finger trials (see Table 2 for the data), which was confirmed by repeated measures ANOVA with Condition (6 levels) and Fingers (5 levels) as factors. There was only a significant main effect of Condition (F_{[2.84, 19.92]} = 4.93, p < 0.05). The RMS error for the DF condition was significant less than for DB, DR and D_RL conditions (p < 0.05).

Table 2. RMS error of force magnitude for the four-finger task.

Condition	RMS FX (×10−3)	RMS FY (×10−3)	RMS FZ (×10−3)
DLR	0.24 ± 0.03	------	1.2 ± 0.08
DFB	-----	0.33 ± 0.08	1.1 ± 0.08
DL	0.43 ± 0.09	------	1.1 ± 0.07
DR	0.52 ± 0.10	------	1.3 ± 0.10
DF	-------	0.66 ± 0.16	1.1 ± 0.08
DB	-------	0.79 ± 0.12	1.3 ± 0.15
RMS error of force magnitude for a one-finger task (Index Finger)
Condition	RMS FX (×10−3)	RMS FY (×10−3)	RMS FZ (×10−3)
DLR	0.31 ± 0.04	------	1.2 ± 0.08
DFB	-----	0.3 ± 0.05	1.1 ± 0.09
DL	0.55 ± 0.30	------	1.1 ± 0.12
DR	0.62 ± 0.29	------	1.1 ± 0.10
DF	-------	0.5 ± 0.07	0.8 ± 0.08
DB	-------	1.1 ± 0.25	1.3 ± 0.21

The forces were divided by the total task magnitude before calculating RMS (so that RMS can be compared across different directions). The data were first averaged across all repetitions for one condition, then averaged across all subjects. Means and standard errors across subjects are presented. D_LR : Down – feedback L/R, D_FB: Down – feedback F/B, DL: Down left, DR: Down right, DF: Down forward, DB: Down back. Only index finger data (from one finger tasks) has been shown for comparison, and this is representative of the data for all one-finger tasks.

Indices of Finger Interaction

Enslaving across fingers

Enslaving across fingers was defined as the involuntary force production by non-task fingers. For each condition, enslaving matrices (E) and indices of enslaving were calculated separately for the forces produced along the three axes (see Methods). To compute entries of the E matrix, the forces produced by non-instructed fingers were regressed on the force produced by the task finger over the whole trial duration. Different columns correspond to different task fingers and different rows correspond to different enslaved fingers.

A typical E matrix along Z-axis for the D_RL task for a typical subject looked as follows:

$$\left[\begin{array}{cccc}\hfill 1.0000\hfill & \hfill 0.6611\hfill & \hfill 0.3240\hfill & \hfill 0.2557\hfill \\ \hfill 0.0249\hfill & \hfill 1.0000\hfill & \hfill 0.8023\hfill & \hfill 0.1049\hfill \\ \hfill 0.0759\hfill & \hfill 0.2760\hfill & \hfill 1.0000\hfill & \hfill 0.2768\hfill \\ \hfill 0.0137\hfill & \hfill 0.2092\hfill & \hfill 0.4896\hfill & \hfill 1.0000\hfill \end{array}\right]$$

It should be noted that this matrix is strongly non-symmetric, i.e. there are large differences between indices of how a finger enslaves another finger and how it is enslaved by that finger.

Enslaving matrices along non-Z axis could have negative entries meaning that non-task fingers produced force in a direction opposite to the force produced by the task finger. Here follows an example of the E matrix along the X-axis for the DL task (a typical subject):

$$\left[\begin{array}{cccc}\hfill 1.0000\hfill & \hfill 0.1184\hfill & \hfill -0.0741\hfill & \hfill -0.1199\hfill \\ \hfill 0.1347\hfill & \hfill 1.0000\hfill & \hfill -0.5434\hfill & \hfill -0.2755\hfill \\ \hfill 0.1282\hfill & \hfill 0.2387\hfill & \hfill 1.0000\hfill & \hfill 0.1481\hfill \\ \hfill 0.0226\hfill & \hfill 0.0960\hfill & \hfill 0.4265\hfill & \hfill 1.0000\hfill \end{array}\right]$$

The numbers of negative entries found in the E matrices across non-D force production tasks, averaged across all the subjects are shown in Table 3.

Table 3. Number of negative entries in enslaving matrices for different non-down tasks.

Condition	Axis	Number of negative entries
DB	Y	4.9± 1.6
DF	Y	1.6 ± 2.1
DL	X	5.1 ± 0.8
DR	X	4.1 ± 2.0

The numbers are averages across all subjects. DL: Down left, DR: Down right, DF: Down forward, DB: Down back.

The enslaving index |E| was calculated as the sum of all non-diagonal entries of the enslaving matrix. Table 4 shows |E| (enslaving index) for different task conditions averaged across all subjects. Enslaving in the X (right-left) direction was found to be asymmetrical whereas enslaving in the Y (forward-backward) direction was nearly symmetrical (Table 4).

Table 4. |E| (enslaving index) for different task conditions.

Condition	|E|X	|E|Y	|E|Z
D	----	----	1.43 ± 0.29
DLR	----	----	2.19 ± 0.61
DFB	----	----	2.65 ± 0.78
DR	4.30 ± 2.30	----	2.47 ± 0.68
DL	0.11 ± 0.29	----	1.68 ± 0.44
DF	----	1.80 ±0.42	2.23 ± 0.57
DB	----	1.22 ± 0.35	1.88 ± 0.42

Averages across all subjects are presented with standard errors.

D_LR : Down – feedback L/R, D_FB: Down – feedback F/B, DL: Down left, DR: Down right, DF: Down forward, DB: Down back.

The |E| index in the X-direction for the DR task was significantly higher than that for the DL task, as supported by a t-test (p < 0.01). In contrast, the |E| index in the Y-direction was not different between the DB and DF conditions (p > 0.4).

|E| in Z-direction did not depend on feedback or instruction about forces in the other direction (X or Y). ANOVA was conducted on |E|, with factors Feedback (none, F_X, F_Y) and Task-finger (I, M, R, L) in Down tasks. There was no significant effect of Feedback and no significant interaction Feedback × Task-finger. However, Task-finger showed a significant effect (F_{[1.6, 11.25]} = 7.09 p < 0.05). In Down tasks (D, D_RL, D_FB), the Ring finger enslaved other fingers in Z direction to a greater extent as compared to the Index and Middle fingers (p < 0.05). Also, the Little finger enslaved other fingers more as compared to the Index finger (p < 0.05).

E_j was used as the measure of how a finger enslaves the other fingers in the Z-direction (it is the sum of entries over a column of the E matrix minus 1). Figure 3 shows that the ability to enslave other fingers was the lowest for the Index finger, followed by the Middle, Ring and Little fingers (I < M < R, L). This was supported by repeated measures ANOVA on E_j, with Finger (I, M, R, L) and Condition (7 levels – D, D_RL, D_FB, DR, DL, DF and DB) as factors. There was a significant effect of Finger (F_[3,189] = 26.10, p < 0.05) without other effects.

Figure 3.

E_j (how a finger enslaves other fingers) values for different conditions.

Values have been averaged across all subjects (with standard error bars). D: Down only, D_RL: Down – feedback on the right-left force changes, D_FB: Down – feedback on the forward-backward force changes, DL: Down left, DR: Down right, DF: Down forward, DB: Down backward.

E_i was used as a measure of how a finger is enslaved by other fingers in Z-direction (it is the sum of entries over a row of the E matrix minus 1). Figure 4 illustrates that the Index, Middle and Ring fingers were enslaved by other fingers stronger than the Little finger was. This was supported by repeated measures ANOVA on E_i, with Finger (I, M, R, L) and Condition (7 levels – D, D_RL, D_FB, DR, DL, DF and DB) as factors. There was a significant effect of Finger (F_[3,189] = 14.11, p < 0.05) without other effects. Tukey comparison revealed that the Little finger was the least enslaved as compared to the Index, Middle and Ring fingers (p < 0.05).

Figure 4.

E_i (How a finger is enslaved by other fingers) values for different conditions.

Values have been averaged across all subjects (with standard error bars). For abbreviations see Figure 3.

Unintended force production by a finger across directions (F_UN)

F_UN was defined as a measure of the amount of force produced by the task finger in a non-instructed direction (X or Y) while pressing downward (along the Z axis). Unintended force along the Y-axis changed with the changes in the task requirements with respect to the X-axis, i.e. whether the task was along +X (right) axis or along −X (left) axis (Figure 5). In contrast, unintended force along X-axis remained the same irrespective of the task requirement changes with respect to Y-axis, i.e. irrespective of whether the task was along +Y (forward) axis or −Y (backward) axis (Figure 6). In order to study if F_UN is a function of task direction and task finger, an ANOVA was run on F_UN with factors Finger and Task-direction. This was done separately to study F_UN along the Y-axis for the three conditions involving the X-axis (D_RL, DL and DR) and to study F_UN along the X-axis for the three conditions involving the Y-axis (D_FB, DF and DB). There was a significant effect of Task-direction on F_UN for the Y-axis. (F_2,77 = 11.74, p < 0.001). The effect of Finger was also significant (F_3,77 = 5.24, p < 0.005). Tukey comparisons showed that F_UN was significantly greater for the DL condition than for the DR and D_RL conditions (p < 0.001) without a difference between DR and D_RL. The Finger × Task-direction interaction was not significant. Thus F_UN along Y axis in increasing order was: D_RL, DR < DL. Also, Tukey comparison revealed that F_UN along Y axis was higher during the Index finger tasks as compared to the Middle, Ring and Little finger tasks (p < 0.05).

Figure 5.

The index of unintended force production F_UN within-a-finger along Y axis for the four fingers, in 3 different pressing tasks involving X axis. Averaged values across subjects with standard error bars are shown. For abbreviations see Figure 3.

Figure 6.

The index of unintended force production F_UN within-a-finger along X axis for the four fingers, in 3 different pressing tasks involving Y axis. Averaged values across subjects with standard error bars are shown. For abbreviations see Figure 3.

In contrast, Task-direction had no significant effect on F_UN for the X-axis. But the Finger × Task-direction interaction was significant. In addition, the main effect of Finger was also significant (F_{[1.2, 8.45]} = 5.14, p < 0.05). Tukey comparisons of the Finger × Task-direction interaction showed that F_UN in the X-direction during DB task was significantly less during the Index finger tasks as compared to the Ring and Little finger tasks. (p < 0.05).

Analysis of Multi-Finger Synergies

In order to analyze multi-finger synergies stabilizing the total force magnitude and force direction, we used the framework of the uncontrolled manifold (UCM) hypothesis. The variance across trials was measured at each time sample and quantified as two components – V_UCM and V_ORT. V_UCM gave a measure of the variance per DOF, which did not have any effect on the performance variable. V_ORT gave a measure of the variance per DOF orthogonal to UCM, which affected the performance variable. A normalized difference between V_UCM and V_ORT, ΔV was used as the index of synergy. Positive ΔV would indicate a synergy stabilizing the performance variable for which ΔV was quantified, while zero or negative ΔV would mean no such synergy.

Across all the task conditions, V_UCM was higher than V_ORT, and ΔV was positive for both magnitude and direction of the force vector (Figure 7 and 8). The grand average of ΔV across all conditions was 0.933 for force force magnitude stabilization and 0.811 for force direction stabilization. Hence, we conclude that strong multi-finger synergies stabilized both force magnitude and direction.

Figure 7.

Time changes of the index of multi-finger synergy (ΔV) stabilizing force magnitude for different task conditions and different force directions. Averages across subjects are shown. For abbreviations see Figure 3.

Figure 8.

Time changes of the index of multi-finger synergy (ΔV) stabilizing force direction for different task conditions involving force production in the right-left direction (A) and in the forward-backward direction (B). Averages across subjects are shown. For abbreviations see Figure 3.

Force magnitude stabilization

The index of synergy (ΔV) showed a dependence on both the task and the axis along which the force magnitude was computed. In addition, the ΔV index increased with time early in the trial duration and then reached a plateau.

Two-way ANOVA with repeated measures on z-transformed ΔV values averaged over the whole time interval was performed with Condition (6 levels, D_RL, D_FB, DR, DL, DF and DB) and Axis (two relevant axes for each condition – Z and X or Y) as factors. There were significant effects of Condition (F_{[5, 77]} = 12.50; p < 0.0001) and of Axis (F_{[1, 77]} = 19.68, p < 0.0001). Tukey comparisons revealed that ΔV was higher for the D_RL task as compared to the DL, D_FB, DF and DB tasks. Also it was higher for the DR as compared to the DL, DF and DB tasks. The synergy index was smaller for force components along Z-axis as compared to force components along the other relevant axis (X or Y) (p < 0.01).

Time changes in ΔV happened mostly over the first 30% of the task interval: The value of ΔV increased from 0.474 (in the 10% time interval) to 0.873 (in the 30% time interval), with small changes afterwards (the values ranging from 0.93 to 1.11). However, ΔV remained significantly greater than zero throughout the task, right from the task initiation. A two-way ANOVA with repeated measures on z-transformed ΔV values with Condition (6 levels) and Time (10 levels) as factors was run for ΔV values computed for forces along Z-axis. Condition showed a significant effect (F_{[5, 413]} = 17.78, p < 0.001 for Condition) without a significant Condition × Time interaction. Tukey’s comparisons showed that ΔV was greater for the D_RL than for the DB and DF tasks and it was greater for the DR and D_FB as compared to the DL, DB and DF tasks (p < 0.01).

For ANOVA on z-transformed ΔV values along the other relevant axis (X or Y), both Condition and Time had significant main effects (F_[5,413] = 136.39, p < 0.001 for Condition; and F_[3.22,22.55] = 38.12, p < 0.0001 for Time) without a Condition × Time interaction. Tukey comparisons showed the following order for ΔV values: D_RL > DR > DL, D_FB > DB, DF (p < 0.01).

Force Direction Stabilization

While the subjects, on average, produced force in the instructed direction, individual finger force vectors could point at substantial angles from the required direction. This is illustrated in Figure 9 that shows finger force vectors averaged for one trial direction (task D_RL) and then over a set of trials performed by a representative subject. Note the visible deviations of finger force vectors from the required direction (set at 90° in Fig. 9), while total finger force points rather precisely in the task direction. The insert in Fig. 9 shows standard deviations of the force direction computed across trials for the same data set. Note the much smaller standard deviation of the total force vector direction as compared to the standard deviations for the individual finger force directions. Such results were typical of all subjects. This suggests existence of multi-finger synergies stabilizing total force direction, a hypothesis tested using the framework of the UCM hypothesis (see Methods).

Figure 9.

Individual finger force vectors for a typical four-finger trial for the Down with feedback on the X-axis (right-left) force task (D_RL) performed by a representative subject. The arrows show the magnitude and the direction of force. The instructed direction corresponds to 90° angle. The insert graph (left, bottom corner) shows standard deviation of force direction computed for the same data set. We used standard deviations rather than circular statistics because of the relatively small variation in the finger force directions. IMRL: total force produced by all four fingers; I, M, R and L: forces produced by the Index, Middle, Ring and Little fingers.

Though the ΔV values computed for force direction were greater than zero for all tasks, they were significantly greater for the tasks involving force production along the X-axis than for the tasks involving force production along the Y-axis (in addition to Z-axis forces). This was supported by one-way ANOVA with repeated measures done on z-transformed ΔV with Condition (6 levels, D_RL, D_FB, DR, DL, DF and DB) as the factor (main effect, F_[5,35] = 21.47, p < 0.0001). Tukey comparisons revealed that ΔV values for force direction stabilization for D_RL, DL and DR conditions were significantly greater than that for D_FB, DF and DB without differences within each of the two groups of tasks.

The value of ΔV gradually increased at the beginning of the task (from 0.496 in the 10% time interval to 0.828 in the 30% time interval), with small changes afterwards (ΔV ranging from 0.82 to 0.91). A two-way ANOVA with repeated measures on z-transformed ΔV values with Condition (6 levels) and Time (10 levels) as factors showed significant effects of both factors (F_[5,413] = 86.46, p < 0.0001 for Condition; and F_[3.34,23.37] =56.49, p < 0.0001 for Time) without an interaction. The value of ΔV increased significantly from the 10% time interval to the 30% time interval (p < 0.001), but the changes after 30% time interval were not statistically significant.

Discussion

Two main hypotheses were tested in the experiments. The first was that shear force components may show features such as unintended force produced by a non-task finger in the direction opposite to the instructed force and also unintended force in a direction orthogonal to the instructed direction. The second hypothesis was that strong multi-finger synergies would be observed stabilizing both magnitude and direction of the total force vector.

Both of these hypotheses have been supported by the findings. In particular, we observed strong multi-finger synergies stabilizing both magnitude of the total force (as in Latash et al. 2002a; Shim et al. 2005) and direction (as could be expected based on an earlier study by Gao et al. 2005). This study is the first to show simultaneous stabilization of force magnitude and direction. It is also the first to document force magnitude and direction stabilizing synergies for shear forces. Indices of involuntary force production showed more complex patterns as compared to earlier reports on finger interdependence during pressing tasks (Li et al. 1998a; Zatsiorsky et al. 1998, 2000). In particular, intentional force production by a finger parallel to the surface of contact could result in unintentional force production by other fingers in the same or in the opposite direction (cf. Pataky et al. 2007). Further, we discuss implications of these and other findings for issues of finger interaction and stabilization of combined finger action in everyday tasks.

Finger Force Interdependence in Three Dimensions

Limitations in the control of individual fingers has been studied in both movement and force production tasks (Schieber 1991; Kilbreath and Gandevia 1994; Li et al. 1998a, 2004; Zatsiorsky et al. 2000; Shim et al. 2007; Ingram et al. 2008). In all these studies, finger motion or force production in a given direction was accompanied by unintentional motion (or force production) by other digits of the hand. Kinematic and kinetic variables were linked in a study showing that motion of a finger is accompanied by force production by other fingers of the hand if they are acting against a stop (Kim et al. 2006). All the mentioned studies reported regular features of these phenomena addressed as enslaving, enslavement, or lack of individuation. In particular, higher enslaving (lower individuation) was reported for fingers that are anatomical neighbors of the task finger as compared to more distant fingers of the hand. The index finger was reported to be most independent while the ring finger typically showed highest enslaving indices.

These phenomena have been discussed as resulting from two groups of factors (reviewed in Schieber and Santello 2007). The first group includes anatomical links among the fingers provided by connective tissues and multi-digit extrinsic muscles with several compartments (Kilbreath and Gandevia 1994; Leijsne et al. 1993, 2008). The second group involves the neural organization of the control of the hand including the overlapping cortical projections of the digits (Rouiller 1996; Latash et al. 2002b; Reilly and Hammond 2006; Schieber et al 2009).

In our study, enslaving showed more complex patterns for the non-vertical force vector components. In particular, E matrices along the X and Y axes contained a substantial number of negative entries (Table 3). Note that the values in Table 3 are out of 12 non-diagonal entries (the diagonal entries of the 4 × 4 matrices are, by definition, +1). So, the average values of about 5 out of 12 suggest that nearly 50% of the forces produced by the non-task fingers were directed opposite to the force produced by the task finger. These observations cannot be easily explained by peripheral factors such as multi-finger muscles and connective tissue links. They very strongly favor a neural factor playing a dominant role in the finger force interdependence patterns.

Asymmetry of enslaving indices has been reported by Shim et al. (2007) who studied finger force production into flexion and into extension. In particular, Shim and colleagues documented higher enslaving indices in extension tasks. In our experiments, significant asymmetry of the enslaving index (|E|) was seen in the left-right direction but not in the forward-backward direction (Table 4). This result is in contrast to a study by Pataky et al. (2007) who reported no asymmetry in MVC tasks involving radial and ulnar finger deviation efforts. Note, however, that in the experiment by Pataky and colleagues the fingers were placed in rigid slots such that radial-ulnar efforts could be produced without a change in the downward force. In our experiments, this was impossible: The downward pressing force had to be sufficient to allow the production of shear forces given the friction. Besides, we studied sub-maximal force production in contrast to the cited Pataky study.

As mentioned earlier, most studies reported highest enslaving indices for the ring finger and lowest indices for the index finger. This result was also confirmed in the study of maximal ulnar and radial efforts (Pataky et al. 2007). In our study, we analyzed the enslaving matrix in more detail and quantified separately two indices: E_j – how strongly a finger enslaves other fingers and E_i – how strongly a finger is enslaved by other fingers. The results were similar to the ones mentioned in the earlier studies for the former index but not for the latter. Indeed, the index finger induced the least enslaving in other fingers reflected by the smallest E_j, while the ring and the little fingers showed the highest E_j values. However, the finger that was least enslaved by other fingers was the little finger, while the three other fingers showed similar E_i indices. These results suggest that enslaving is a more complex phenomenon than previously thought, and reducing it to a single index may be too crude for meaningful analysis.

The complex pattern of unintentional force production suggest an interaction of at least two factors, enslaving and synergic effects. Both factors are expected to lead to co-varied forces in digits that are and are not instructed to produce force. Synergic effects in multi-digit prehensile tasks have been discussed with respect to stabilization of the combined digit action on the hand-held object (Santello and Soechting 2000; reviewed in Zatsiorsky and Latash 2008; Latash and Zatsiorsky 2009). In our one-finger tasks, we did not ask the subjects to stabilize any variable produced by all the fingers together. However, it is possible that the central nervous system tried to bring such variables as the total shear force and the total moment of force acting on the hand to zero without any explicit instruction (cf. the principle of minimization of secondary moments, Li et al. 1998a, 2000). Synergic effects related to stabilization of the mentioned variables may be hidden in the computed enslaving matrices (contributing, in particular, to the large number of negative entries) and to large force changes produced by the strongest and most independent finger such as the index finger when another finger performed the task. Taken together, our results suggest that both enslaving and synergic effects play a major role in defining patterns of unintentional force production.

Unintended Force Production Orthogonal to the Task Direction

To our knowledge, only one study reported unintentional force components orthogonal to the direction of the required action (Pataky et al. 2007). In that study, downward pressing tasks were associated with force vectors that deviated from the vertical direction, on average, by about 8°. Much larger deviations were observed for force production tasks in the radial-ulnar direction (right-left), by over 20°. These phenomena were seen both in task fingers and in non-task (enslaved) fingers. The authors of that study introduced the notion of “preferred direction” and tried to link it to the anatomical architecture of tendon attachments resulting in certain directions of muscle lines of action (Li et al. 2005).

We would like to emphasize a few features of unintended force production orthogonal to the intended action (F_UN) found in our experiments. Unexpectedly, the index finger, which has been described as most independent and best controlled (Zatsiorsky et al. 2000; Shim et al. 2007; Gorniak et al. 2008), produced the largest F_UN along the Y-axis (forward-backward direction). In contrast, along the X-axis (left-right), the index finger showed the smallest F_UN values. These results cannot be easily mapped on the hand muscle anatomy. Rather, they may be related to everyday function of the human hand, in particular to the different roles of the fingers in prehensile tasks involving holding a load and simultaneously counteracting an external torque (Zatsiorsky et al. 2003a,b). It should be noted however that the constraints of this task, in particular the requirement to keep all fingers on the transducers, and the horizontal placement of the force transducers, may limit its applicability to more ecological situations where these constraints are not found.

Accuracy of Performance and Multi-Finger Synergies

Some of our results on directional force vector errors are expected and some are unexpected. On the one hand, the observations of smaller directional errors in four-finger tasks as compared to one-finger tasks are in line with the earlier publication by Gao et al. (2005) and with a general observation that motor redundancy helps produce more accurate performance (Latash et al. 2001; Sosnoff et al. 2005; reviewed in Latash et al. 2007). On the other hand, we did not find differences among the one-finger tasks. In fact, the index finger that was expected to be most accurate showed, on average, larger directional errors as compared to the other three fingers, although the differences were not statistically significant. Note that Vaillancourt et al. (2002) described a negative correlation between the degree of inter-digit individuation and force variability. Based on these results, we expected the most independent index finger to be most accurate. This was not the case, at least not with respect to directional accuracy.

Analysis of multi-finger synergies performed within the framework of the UCM hypothesis showed very strong synergies in the space of finger modes (Latash et al. 2001; Danion et al. 2003) that stabilized both the magnitude and direction of the total force vector. In other words, variance in the space of finger modes was consistently higher within the sub-space (UCM) compatible with the average across trials magnitude and direction of the force vector as compared to the sub-space that led to changes in these variables.

The observation of strong force amplitude stabilizing synergies is not novel (reviewed in Latash et al. 2007; Latash and Zatsiorsky 2009), although earlier studies addressed only magnitude of the pressing force, normal to the surface of contact. Our observations show that such synergies exist for shear force components too. Indeed, the index of synergy (ΔV) was significantly higher for the shear force components as compared to the normal force component.

To our knowledge, this study is the first to apply the framework of the UCM hypothesis to analysis of force vector direction. The values of ΔV were highly positive across all tasks showing that individual finger force vectors co-varied across trials such that direction of the resultant force vector showed relatively low variance as compared to what could be expected without such co-variation. We found higher synergy indices stabilizing force vector direction in tasks that involved force production in the ulnar-radial (left-right) direction as compared to tasks involving force production in the forward-backward direction. This observation may be a consequence of practicing typical everyday tasks, such as taking a drink from a glass, that require accurate control of the moment of force in the plane of digit contacts. Note that this moment of force gets significant contribution from shear forces in the ulnar-radial direction.

Both synergy indices, computed for force vector magnitude and for force vector direction, showed similar time profiles: They both started with relatively low (although significantly positive!) values, these values increased over the first one-third of movement time and then reached a plateau. These results are similar to earlier reports on time profiles of synergy indices during multi-finger pressing tasks that required accurate ramp force production (Shim et al. 2003, 2005). In earlier studies, such results were interpreted as suggesting that the relative amount of variance parallel to the UCM increases with the total force magnitude. However, this explanation obviously does not work with respect to force vector direction, which remained constant over the trial duration. So, time from the trial initiation may be a more important factor defining the synergy index magnitude as suggested in earlier studies of multi-finger synergies (Shim et al. 2003, 2005).

Implications for Finger Coordination in Prehensile Tasks

The human hand is an amazingly versatile instrument for object manipulation. It is feasible that, during the lifetime, the central nervous system develops control mechanisms that use a handful of parameters to tune the descending signals to adjust hand action to such commonly varied characteristics of external objects as mass, friction, and external torque (Schieber and Santello 2004; Latash et al. 2010). This may be done, in particular, by uniting distributed sets of cortical neurons into functional groups (Poliakov and Schieber 1999; Schieber and Santello 2004). Patterns of peripheral variables recorded in experiments are reflective of both the specific experimental tasks and the pre-existent coupling patterns defined by neural adaptations to common everyday tasks.

In our experiment, despite the non-involvement of the thumb, the observed patterns of finger interaction could be defined by the experience with everyday prehensile tasks. In particular, a recent study has shown that shear finger forces co-vary negatively across trials to stabilize the total shear force applied to the hand-held object (Gorniak et al. 2009). Such synergic mechanism could contribute to the apparent negative enslaving observed in our experiments with shear force production. Earlier, a hypothesis was suggested that the rotational action of the hand could be stabilized by pointing the vectors of individual finger forces at the point of the thumb contact (Li et al. 1998b). This obviously requires the shear forces of the radial fingers to be directed against the shear forces of the ulnar fingers potentially contributing to the apparently negative enslaving indices.

Another major phenomenon typical of object manipulation is the load-grip force coupling documented in many studies (Johansson and Westling 1984; Flanagan and Wing 1993; Gysin et al. 2003; Jaric et al. 2005). This mechanism allows to produce feed-forward grip force adjustments to ensure adequate friction to expected shear force changes during object manipulation. The proportional shear and normal force changes typical of the load-grip force coupling might have contributed to the very high indices of multi-finger synergies stabilizing force vector direction in our experiments. Neural mechanisms responsible for such scaling could be reflected in the documented synchronizarion of motor units across muscles involved in different finger actions (Santello and Fuglevand 2004; Winges et al. 2008; Johnston et al. 2009).

To summarize, our study reports, for the first time, indices of unintentional finger forces during one-finger tasks involving force production in all three dimensions. We also report, for the first time, indices of multi-finger synergies stabilizing force vector magnitude and direction in four-finger accurate force production tasks in three dimensions. The results suggest that synergic force adjustments, likely conditioned by everyday experience with prehensile tasks, play a major role in indices of finger force interaction quantified in experiments.

Figure 10.

Appendix: Computation of the two components of variance

To compute the index of multi-finger synergies stabilizing the force vector magnitude and direction, two components of the across-trials variance were computed in the space of commands to fingers, finger modes. This analysis involved the following steps.

To eliminate the co-variation of finger forces due to enslaving, finger forces were transformed into another set of variables, finger modes (Zatsiorsky et al. 1998; Latash et al. 2001; Danion et al. 2004):

$$d\mathrm{F}=\mathrm{E}d\mathrm{m}$$ (5)

$$d\mathrm{m}={\mathrm{E}}^{-1}d\mathrm{F}$$ (assuming that E is an invertible matrix)

where dFis the change in force produced, E is a 4 × 4 enslaving matrix, and dm is the change in mode magnitudes.

Rather than taking the regular matrix inverse, the pseudoinverse was calculated, using the singular value decomposition:

$$\mathrm{U}\mathrm{S}{\mathrm{V}}^T=\mathrm{E}U\ast \mathrm{S}\ast V^T=\mathrm{E}$$ (6)

The pseudoinverse was then calculated from:

$${\mathrm{E}}^{-1}=\mathrm{V}{\mathrm{S}}^{\ast }{\mathrm{U}}^T$$ (7)

where S* is the reciprocal of the non-zero elements in S. However, small values in elements of S (below 0.01) were set to zero before calculating S*. For most cases, the result was equivalent to taking the regular matrix inverse, but the removal of small values in S prevented very large values of the inverse of the enslaving matrix in a small number (< 10%) of extreme cases.

Before calculating variance, the forces in each direction were normalized with respect to the maximum task force in that direction, i.e., the force magnitude in each direction, which the subject was asked to produce. The components of the task force were always considered for each direction separately.

In our study, two performance variables were considered. The first was the sum of the forces (F_TOT) produced by the four fingers in a given task-relevant direction (Z, and either X or Y): F_TOT,k = F_{I k}+ F_Mk + F_Rk + F_Lk, where F_Ik is the force produced by the index finger in the k direction (X, Y or Z).

The Jacobian defines the transformation between small changes in the individual finger force magnitudes and changes in F_TOT:

$$d{F}_{TOT,k}=\left[\begin{array}{cccc}\hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill \end{array}\right]\left[\begin{array}{c}\hfill d{F}_{Ik}\hfill \\ \hfill d{F}_{Mk}\hfill \\ \hfill d{F}_{Rk}\hfill \\ \hfill d{F}_{Lk}\hfill \end{array}\right]$$ (8)

where dF_jk is the change in force produced by j finger in k direction (X,Y or Z).

$$d{F}_{TOT,k}=\mathrm{J}d\mathrm{F}{\mathit{dF}}_{\mathrm{TOT},k}=\mathit{J}\ast$$ (9)

In the space of finger modes, we can express this relationship as:

$$d{F}_{TOT,k}=\mathrm{J}\mathrm{E}d\mathrm{m}$$ (10)

The UCM was approximated linearly as the null-space of J spanned by basis vectors, e_i from the following equation:

$$0=\mathrm{J}\mathrm{E}{\mathrm{e}}_{i}0=\mathrm{J}\ast \mathrm{E}\ast {\mathrm{e}}_{\mathrm{i}}$$ (11)

We calculated f_∥ as the sum of mean-free mode vectors projected onto the UCM:

$${\mathrm{f}}_{\parallel }=\sum _{i=1}^{n-k}({\mathrm{e}}_i^T\cdot d\mathrm{m}){\mathrm{e}}_i{\mathit{f}}_{\parallel }=\sum _{\mathit{i}=1}^{\mathit{n}-\mathit{k}}({\mathit{e}}_{\mathit{i}}^{\mathit{T}}.\mathit{m}).{\mathit{e}}_{\mathit{i}}$$ (12)

where n=4 is the number of elemental variables and k=1 corresponds to the one-dimensional performance variable. f_⊥f_⊥ is the component of mode vectors perpendicular to the null space:

$${\mathrm{f}}_{\perp }=d\mathrm{m}-{\mathrm{f}}_{\parallel }{\mathit{f}}_{\perp }=\mathit{m}-{\mathit{f}}_{\parallel }$$ (13)

Then the variance per degree-of-freedom (DOF) within the UCM, i.e. V_UCM was computed as follows:

$$V_{UCM}=\frac{{\sum }_{trials}{\mid {\mathrm{f}}_{\parallel }\mid }^2}{\left((n-k)N_{trials}\right)}{\mathit{V}}_{\mathit{UCM}}=\frac{{\sum }_{\mathit{trials}}{\mid f_{\parallel }\mid }^2}{\left((n-k){\mathit{N}}_{\mathit{trials}}\right)}$$ (14)

Similarly, V_ORT, i.e. variance per DOF orthogonal to the UCM was calculated as follows:

$$V_{ORT}=\frac{{\sum }_{trials}{\mid {\mathrm{f}}_{\perp }\mid }^2}{\left(k{N}_{trials}\right)}{V}_{\mathit{ORT}}=\frac{{\sum }_{\mathit{trials}}{\mid {\mathit{f}}_{\perp }\mid }^2}{\left({\mathit{kN}}_{\mathit{trials}}\right)}$$ (15)

Further, to allow comparison across subjects, an index, ΔV was computed as the difference between the variance within UCM and the variance orthogonal to UCM, divided by the total variance (all computed per DOF).

$$\Delta V=\frac{V_{UCM}-V_{ORT}}{V_{TOT}}$$ (16)

ΔV indices were computed separately for each of the two relevant directions for each task (Z and X or Y) and each subject separately. Positive ΔV would indicate a multi-finger synergy stabilizing the performance variable, while zero or negative ΔV would mean no such synergy.

The second performance variable considered was the ratio between the two vector components reflecting the direction of the vector. It was defined as the force in the non-Z task direction k (i.e., X or Y) divided by the force in the Z direction:

$$R=\frac{\sum _{i=1}^4{F}_k^i}{\sum _{i=1}^4{F}_Z^i}$$ (17)

This ratio represents the tangent of the force direction angle. In this analysis, forces were used, rather than modes, to ensure that the units are the same for the numerator and denominator. In this case, the performance variable was R; it depended on eight elemental variables, the eight force components of the four finger force vectors.

For forces in a non-Z direction, the elements of the Jacobian were:

$$\frac{\partial R}{\partial F_k^i}=\frac{1}{\sum _i{F}_Z^i}$$ (18)

The elements of the Jacobian for the forces in Z direction were:

$$\frac{\partial R}{\partial F_z^i}=\frac{-\sum _i{F}_k}{\sum _i{\left(F_Z\right)}^2}$$ (19)

Thus the Jacobian matrix was:

$$\left[\frac{1}{\sum _i{F}_Z^i}\frac{-\sum _i{F}_k}{\sum _i{\left(F_Z\right)}^2}\frac{1}{\sum _i{F}_Z^i}\frac{-\sum _i{F}_k}{\sum _i{\left(F_Z\right)}^2}\frac{1}{\sum _i{F}_Z^i}\frac{-\sum _i{F}_k}{\sum _i{\left(F_Z\right)}^2}\frac{1}{\sum _i{F}_Z^i}\frac{-\sum _i{F}_k}{\sum _i{\left(F_Z\right)}^2}\right]$$ (20)

The remainder of the analysis was equivalent to the procedure described above. Briefly, the null-space of the Jacobian was used to approximate the UCM. For each sample over the 5-s trial, mean-free finger forces were projected onto the UCM and onto the orthogonal complement. Variance was computed within both sub-spaces and normalized per degree-of-freedom (the UCM is 7-dimensional and the orthogonal sub-space in one-dimensional). These indices, V_UCM and V_ORT, were used to compute the index of multi-finger synergy (ΔV) stabilizing force vector direction.