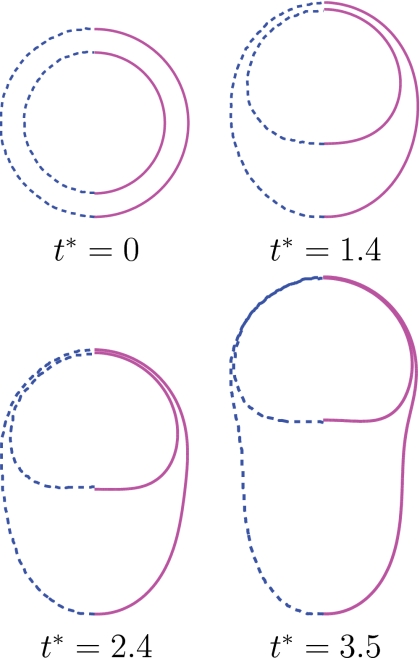Abstract
The impact and spreading of a compound viscous droplet on a flat surface are studied computationally using a front-tracking method as a model for the single cell epitaxy. This is a technology developed to create two-dimensional and three-dimensional tissue constructs cell by cell by printing cell-encapsulating droplets precisely on a substrate using an existing ink-jet printing method. The success of cell printing mainly depends on the cell viability during the printing process, which requires a deeper understanding of the impact dynamics of encapsulated cells onto a solid surface. The present study is a first step in developing a model for deposition of cell-encapsulating droplets. The inner droplet representing the cell, the encapsulating droplet, and the ambient fluid are all assumed to be Newtonian. Simulations are performed for a range of dimensionless parameters to probe the deformation and rate of deformation of the encapsulated cell, which are both hypothesized to be related to cell damage. The deformation of the inner droplet consistently increases: as the Reynolds number increases; as the diameter ratio of the encapsulating droplet to the cell decreases; as the ratio of surface tensions of the air-solution interface to the solution-cell interface increases; as the viscosity ratio of the cell to encapsulating droplet decreases; or as the equilibrium contact angle decreases. It is observed that maximum deformation for a range of Weber numbers has (at least) one local minimum at We=2. Thereafter, the effects of cell deformation on viability are estimated by employing a correlation based on the experimental data of compression of cells between parallel plates. These results provide insight into achieving optimal parameter ranges for maximal cell viability during cell printing.
INTRODUCTION
Impingement of a microdroplet on a flat surface has important applications in engineering such as surface coating, spray cooling, DNA microarrays, and ink-jet printing.1 The impact and spreading of a homogenous one-component (simple) liquid droplet on a flat surface have been studied extensively in the literature from theoretical,2, 3, 4, 5 computational,6, 7, 8, 9, 10 and experimental4, 11, 12, 13 points of view. In spite of a growing interest in generation and manipulation of multicomponent (compound) droplets mainly driven by microfluidic applications14, 15, 16 in recent years, to the best of our knowledge, no work has been done on the impingement of a compound droplet on a solid surface except for the experimental study of Chen et al.15 They formed compound droplets consisting of water as the inner droplet and diesel oil as the encapsulating fluid, and studied the residence time of a compound droplet impinging on a hot surface to understand the heat transfer process in spray combustion.15 The impingement of a compound droplet is of fundamental importance in fluid mechanics. Here, we draw inspiration from the recent experimental cell printing studies where live cell-encapsulating droplets are patterned onto biomaterial coated substrates to engineer three-dimensional tissue constructs17, 18, 19, 20, 21 or to cryopreserve cells.18, 22, 23 The current droplet generation technologies make it possible to generate monodispersed droplets on demand with specified size, such that the droplets can encapsulate only single to few cells and deposit them with spatial control on a substrate.18 This suggests that it would be useful to model the process computationally to predict optimal conditions enhancing cell viability.
Fundamental studies of the dynamics of compound droplets have been done relatively recently compared to the simple droplets24 and there are still fundamental questions that need to be addressed.14, 25 Compound droplets have found important applications in targeted drug delivery,26, 27 food industry,28 waste water management,29 and microfluidics.14 Fluid mechanics of compound droplets have been studied in various geometries and flow conditions. Johnson and Sadhal24 reviewed the translation of compound droplets in quiescent flow. Stone and Leal30 studied the breakup of double emulsion droplets in extensional flows. Bazhlekov et al.31 examined the unsteady motion and deformation of compound droplets rising in an otherwise quiescent fluid due to buoyancy using a finite element method. Smith et al.25 investigated the deformation and breakup of an encapsulated droplet in shear flow using a level-set method and produced a range of morphologies caused by the interaction between the core and outer interfaces. They presented a phase diagram showing the morphologies obtained for a range of capillary numbers and core interfacial tensions. Kawano et al.32 studied deformations of thin liquid spherical shells in a liquid-liquid-gas system both experimentally and computationally. In recent years, the field has been mainly driven by a growing range of applications in microfluidics. Utada et al.14 developed a microcapillary device that generates double emulsions at specified sizes and numbers. This capillary device forms monodisperse double emulsions in one step. Zhou et al.33 computationally studied the formation of compound drops in flow-focusing devices and found that compound drops are formed only in a narrow window of flow and rheological parameters.
Modeling cells as simple Newtonian droplets is not new and has been widely used to study blood cells.34, 35, 36, 37 In these models, the cell is represented by a Newtonian droplet whose viscosity is much higher than that of the ambient fluid. The Newtonian models involve oversimplification as they ignore the complicated internal structure of the cells and lump the effects of the internal structure into the apparent viscosity usually measured by the micropipet aspiration technique.38, 39 A compound droplet has been proposed by Kan et al.40 as a model for leukocyte deformation in an imposed extensional flow and by Marella and Udaykumar41 as a model for leukocyte deformability in micropipet aspiration and recovery phases. In these models, the inner droplet represents the nucleus of the cell while the encapsulating droplet represents the cytoplasm. Kan et al.40 treated both the nucleus and cytoplasm as Newtonian fluids with different material properties. Marella and Udaykumar41 improved this model using a power-law shear thinning fluid for the cytoplasm and an elastic membrane with nonlinear stress-strain curve for the cortical layer.
To the best of our knowledge, only computational modeling of the cell-encapsulating droplet printing has been performed by Wang et al.42 using a smoothed particle hydrodynamics method. They assumed that the receiving substrate is coated by the same liquid as that encapsulating the cell. Therefore, the fluid mechanical problem they considered is fundamentally different from that which we study here.
In the present work, the impact and spreading of a compound droplet are studied computationally using a front-tracking∕finite-difference method43 as a model for the cell-encapsulating droplet printing on a flat solid substrate. In the present model, the cell, the encapsulating liquid, and the surrounding air are assumed to be Newtonian fluids with different material and interfacial properties. The inner droplet is composed of a highly viscous Newtonian fluid representing the cell. This is, of course, an oversimplification, as the cell is not a Newtonian droplet. However, we use this rather simple model to facilitate extensive simulations and defer more complicated non-Newtonian or microstructured models to a future study. It is assumed that the cell-encapsulating droplet partially wets the substrate while the inner droplet is nonwetting. Note that as far as the computational method is concerned, there is no difficulty to allow the inner droplet to wet the substrate but we simply postulate that the cell does not wet or stick to the substrate. The present front-tracking method developed by Unverdi and Tryggvason44 has been recently extended to treat the moving contact lines and successfully applied to model the impact and spreading of a simple droplet by Muradoglu and Tasoglu.45 In this method, the stress singularity at the contact line is removed by moving the contact line, such that the contact angle is equivalent to the dynamic contact angle that is computed at every time step using the correlation given by Kistler.46
To enable commercial implementation of the cell printing technology in the health care industry, approaches need to minimize the cell damage occurring during impact∕collision with the receiving substrate. It is known that cell viability is strongly correlated with cell deformation.47 Lower levels of cell deformation is more likely to enhance survival during the collision. We also hypothesize that the rate of cell deformation is also important in cell viability. Therefore, the goal here is to identify the conditions that yield the smallest cell deformation and deformation rate. For this purpose, effects of relevant nondimensional numbers such as the Reynolds number, the Weber number, the viscosity ratio, the surface tension ratio, the diameter ratio, and the equilibrium contact angle on the cell deformation and deformation rate are investigated. The cell viability is related to the cell deformation using the experimental data obtained from the compression of cells by two parallel plates.47
The paper is organized as follows: The mathematical formulation and numerical model are described in Sec. 2. We present results and discussion in Sec. 3, where some validation tests are also presented to show accuracy of the numerical method. Finally, we present conclusions in Sec. 4.
FORMULATION AND NUMERICAL METHOD
The flow equations are described here in the context of the finite-difference∕front-tracking method. The fluid motion is assumed to be governed by the incompressible Navier–Stokes equations. We solve for the flow inside and outside the droplets in all three phases. Following Unverdi and Tryggvason,44 a single set of governing equations can be written for the entire computational domain, provided that the jumps in material properties such as density and viscosity are correctly accounted for and surface tension is included. In an axisymmetric coordinate system, the Navier–Stokes equations in conservative form are given by
| 1 |
where u and v are the velocity components in the radial and axial directions, p is the pressure, g is the gravitational acceleration, and ρ and μ are the discontinuous density and viscosity fields, respectively. The effect of surface tension is included as a body force shown in the last term on the right hand side, where σ is the surface tension, κ is twice the mean curvature, and n is a unit vector normal to the interface. The surface tension acts only on the interface as indicated by the three-dimensional delta function δ, whose arguments x and xf are the points at which the equation is evaluated and a point at the interface, respectively. The Navier–Stokes equations are supplemented by the incompressibility condition
| (2) |
We also assume that the material properties remain constant following a fluid particle, i.e., Dρ∕Dt=0 and Dμ∕Dt=0, where D∕Dt is the material derivative. The density and viscosity vary discontinuously across the interfaces and are given by
| 3 |
where the subscripts “c,” “d,” and “o” denote properties of the inner droplet, encapsulating droplet, and the ambient fluid, respectively, and I(r,z,t) is the indicator function defined as
| (4) |
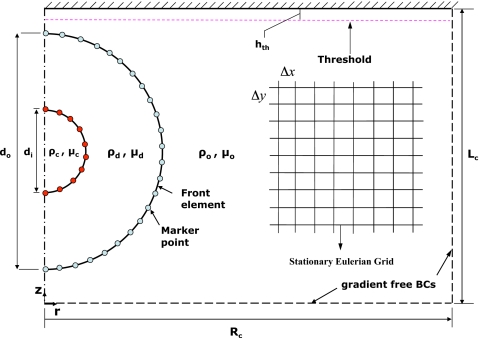
The numerical method is based on the front-tracking∕finite-difference method developed by Unverdi and Tryggvason.44 In this method, a separate Lagrangian grid is used to track the droplet-droplet and droplet-ambient fluid interface. The Lagrangian grid consists of linked marker points (the front) that move with the local flow velocity that is interpolated from the stationary Eulerian grid as sketched in Fig. 1. The piece of the Lagrangian grid between two marker points is called a front element. The Lagrangian grid is used to find the surface tension, which is then distributed onto Eulerian grid points near the interface using Peskin’s48 cosine distribution function and added to the momentum equations as body forces as described by Tryggvason et al.43 At each time step, the indicator function is computed and is used to set the fluid properties inside and outside the droplets. To do this, unit magnitude jumps are distributed in a conservative manner on the Eulerian grid points near the interfaces using the Peskin’s48 cosine distribution function and are then integrated to compute the indicator function everywhere. The computation of the indicator function requires solution of a separable Poisson equation and yields a smooth transition of the indicator function across the interface. The fluid properties are then set as a function of the indicator function according to Eq. 3. The Lagrangian grid is restructured at every time step. This is done by deleting the front elements that are smaller than a specified lower limit and by splitting the front elements that are larger than a specified upper limit, in the same way as described by Tryggvason et al.43 This maintains the front element size to be nearly uniform and comparable to the Eulerian grid size. Restructuring the Lagrangian grid is crucial because it avoids unresolved wiggles due to small elements and lack of resolution due to large elements. The details of the front-tracking method can be found in Unverdi and Tryggvason44 and Tryggvason et al.43
Figure 1.
Schematic illustration of the computational setup.
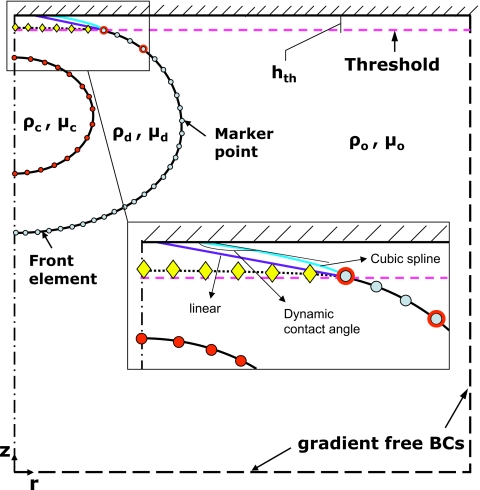
The no-slip boundary condition yields a stress singularity near the contact line. Therefore it requires special treatment. The treatment of the contact line is essentially the same as that of Muradoglu and Tasoglu45 so it is briefly summarized here for the compound droplet case. In the framework of the front-tracking method, the drop interface must be connected to the solid wall explicitly when the droplet approaches sufficiently close to the wall because the interface is tracked explicitly by marker points. For this purpose, we assume that the drop interface connects to the wall when the distance between the drop interface and the solid wall is less than a prespecified threshold value hth as shown in Fig. 2. To achieve this, the interface is continuously monitored during the simulation and the first front element crossing the threshold line is detected. Subsequently, this element is connected to the solid wall such that the contact angle between the wall and droplet is equal to the apparent contact angle θD. In the present work, the apparent contact angle is specified dynamically using Kistler’s correlation12, 46 that relates the apparent contact angle to the capillary number defined as Cacl=μdVcl∕σ, where Vcl is the speed of the contact line. Because Kistler’s correlation is valid for small capillary numbers, following Muradoglu and Tasoglu,45 it is slightly modified as follows:
| (5) |
where is the inverse of the Hoffman’s function fHoff, defined as
| (6) |
In Eq. 6, θe is the equilibrium (static) contact angle and Caclm is defined as Caclm=min(Camax,Cacl) where Camax is the cut-off capillary number introduced to avoid too large or too small values of the apparent contact angle. The apparent contact angle is then determined in the advancing and receding phases as
| (7) |
Following Muradoglu and Tasoglu,45 the contact line velocity is specified as the velocity of the point where the droplet interface crosses the threshold. This definition is found to be very robust. Once the apparent contact angle is determined, the front element crossing the threshold line is connected to the solid wall as follows: First, the distance between the front element that is to be connected and the wall is predicted, assuming that the front element connects to the wall linearly. If this distance is smaller than a prespecified threshold length hth, then the front element is connected to wall by fitting a cubic curve and imposing the dynamic contact angle as sketched in Fig. 2. Otherwise the front element is connected to the wall using a linear function and again imposing the dynamic contact angle on the wall. The threshold length is typically taken as hth=2Δx, where Δx is the Eulerian grid size. Note that we need three points for a cubic fit because one condition is imposed by the apparent contact angle. For this purpose, the first point is selected as the marker point on the front element crossing the interface and the other two are selected such that the distance between the selected marker points is approximately equal to the distance between the first marker point and the wall. Typical marker points used in cubic fit are schematically shown in Fig. 2 as large dots. After the front element on the threshold line is connected to the solid wall, the interface is restructured in a similar way as described by Tryggvason et al.43 In addition to specifying the contact angle dynamically as explained above, the dynamic contact angle is also used to compute the curvature at the center of the front element adjacent to the solid wall. Following Tryggvason et al.,43 the curvature is computed at the center of each front element and is approximated as a difference between the tangent vectors at the end points of the element. The tangent vectors are computed by fitting a cubic polynomial for the internal front elements. In the case of contact line, one marker point of the front element adjacent to the solid wall is placed on the wall so it requires a special treatment. The tangent at this marker point is simply set to the tangent of the dynamic contact angle given by Eq. 7. This procedure is found to be very robust and accurate. The details of the implementation of this slip contact method can be found in Muradoglu and Tasoglu.45
Figure 2.
Schematic illustration of the computational setup for slip contact line method.
The governing equations are solved in their dimensional forms and the results are expressed in terms of relevant dimensionless quantities. Let L and U be the appropriately defined length and velocity scales, respectively, andT=L∕U be the time scale. Then the relevant dimensionless numbers can be summarized as
| 8 |
where Re is the Reynolds number, We is the Weber number, and di and do are the diameters of inner and outer droplets, respectively. The surface tension coefficients of the droplet-droplet interface and the droplet-ambient fluid interface are denoted by σi and σo, respectively.
RESULTS AND DISCUSSION
Validation
The numerical method is first validated in this section. To the best of our knowledge, there is no experimental or computational study about the impact and spreading of a compound droplet on a substrate that we can use for validation of the present numerical method. The accuracy and convergence of the present numerical method have been recently demonstrated by Muradoglu and Tasoglu45 for a simple droplet. Therefore, a comprehensive validation is not repeated here. Instead, emphasis is placed on the validation of the numerical method for the compound droplet case.
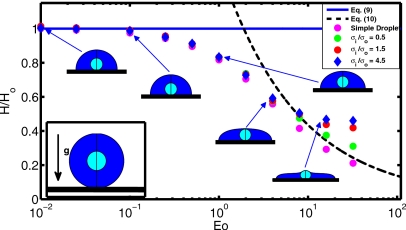
We first consider the relaxation of a compound viscous droplet from a spherical initial condition to its final equilibrium shape. For this test, a concentric spherical compound droplet of the inner radius Ri and the outer radius Ro is initialized near the solid surface, as shown in the inset of Fig. 3, and is allowed to spread until its final static shape is reached for various values of the Eötvös number that represents the ratio of gravitational and surface tension forces. The inner and the encapsulating droplet densities are equal and larger than the surrounding fluid. The viscosities of the inner and encapsulating droplets are also set equal, although viscosity does not have any effect on the final static shape of the droplet. Note that this test case becomes equivalent to the simple droplet case studied by Muradoglu and Tasoglu45 when the ratio of surface tension coefficients is large, i.e., σo∕σi⪢1. The static shape of the droplet generally depends on the equilibrium contact angle θe, the Eötvös number, and the ratio of surface tension coefficients. In the limit of vanishing Eötvös numbers, i.e., Eo⪡1, the equilibrium shape of the droplet is determined by the surface tension force and the encapsulating droplet takes a shape of spherical cap with the maximum height of the droplet Ho, given by45
| (9) |
On the other hand, when Eo⪢1 and σo∕σi⪢1, the compound droplet becomes equivalent to the corresponding simple droplet, the shape of the droplet is controlled mainly by the competition between the gravitational and surface tension forces, and the maximum height of the droplet is proportional to the capillary length,45 i.e.,
| (10) |
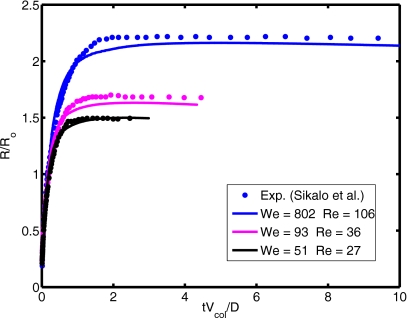
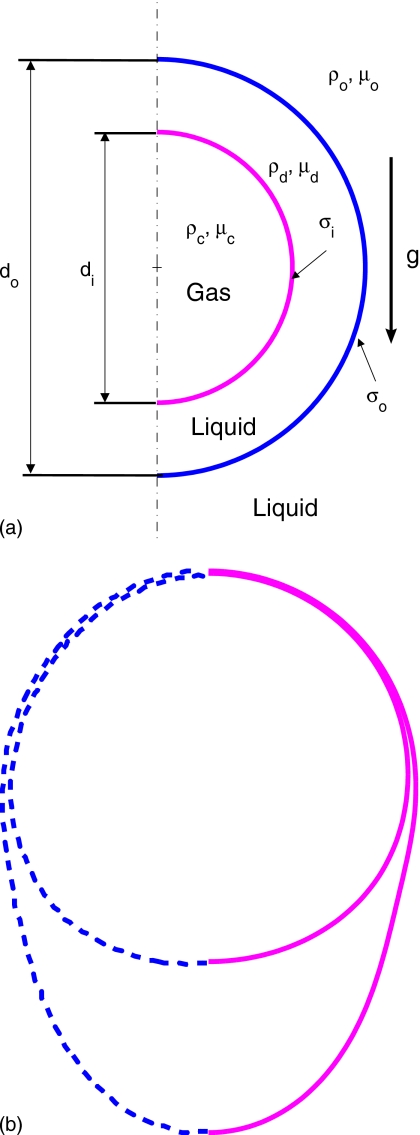
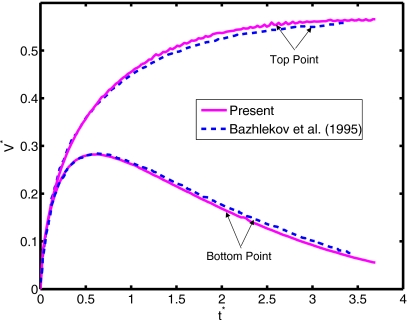
where Ho is given by Eq. 9. Computations are performed for this test case and the results are compared with the asymptotic solutions given by Eqs. 9, 10. For this purpose, the equilibrium contact angle is set to θe=93° and the dynamic angle is used at the contact line. Focus here is placed on the static shape of the droplet. The computational domain extends 6.5 drop radii both in the axial and radial directions and is resolved by a 256×256 uniform Cartesian grid. Figure 3 shows the normalized static droplet height as a function of Eötvös number for the ratio of surface tension coefficients together with the steady shapes of droplet in the range of Eo=0.01 and 64. It is clearly seen that the computed normalized droplet height agrees well with the asymptotic solutions given by Eqs. 9, 10 for Eo⪡1 and Eo⪢1, respectively, when σi∕σo⪡1. For instance, the difference between the asymptotic solution and computational result is less than 0.2% for Eo=0.01 and 10% for Eo=64, respectively. We also note that the difference between the asymptotic solution and computational results decreases monotonically as the Eötvös number increases. For the intermediate values of the Eötvös number, the transition between a spherical cap and a puddle shape occurs. However, the numerical solution deviates significantly from the asymptotic solution for large Eötvös numbers as σi∕σo increases since the inner droplet resists the gravitational forces and causes a bump as shown in Fig. 3. Dynamics of the contact line is of fundamental importance for accurate simulation of impact and spreading of the compound droplet. The treatment of contact line is essentially the same as that of Muradoglu and Tasoglu45 and it has been extensively discussed for simple droplet case. Because there is no experimental or computational study about compound droplet spreading, the treatment of the contact line is tested here for a simple droplet case studied experimentally by Sikalo et al.12 Only one set of results is shown here for completeness in Fig. 4 and readers are referred to Muradoglu and Tasoglu45 for a detailed discussion. In this test case, the impact and spreading of a simple glycerin droplet on a flat wax substrate is considered. The surrounding medium is air. The equilibrium contact angle is set to θe=93°. Simulations are performed for three impact velocities as summarized in Table 1. As can be seen in Fig. 4, there is a good agreement between the computational and experimental results, i.e., the difference between the computational results and the experimental data is less than 10%. Considering the uncertainties in the experimental data and in the correlation used for dynamic contact angle, Fig. 4 indicates the accurate treatment of the contact line. The final validation test deals with buoyancy-driven motion of the compound droplet studied experimentally by Mori49 and computationally using a finite element method by Bazhlekov et al.31 As shown in Fig. 5a, an initially concentric gas-liquid compound droplet (the inner phase is a gas) rises due to buoyancy in an infinite domain. In addition to the dimensionless hydrodynamic parameters given by Eq. 8, the problem also depends on the Eötvös number defined here as Eo=gL2ρo∕σo. Following Bazhlekov et al.,31 the length and velocity scales are defined here as L=Ro (where Ro=do∕2) and . Then the time scale is given byT=L∕U. The flow is assumed to be axisymmetric. The computational domain extends 5 and 15 droplet radii in the radial and axial directions, respectively, and is resolved by 256×768 uniform Cartesian grid. The computational results are first compared with the experimental data of Mori49 in Fig. 5b. For this case, the dimensionless parameters are set to Re=0.016, Eo=2.11, ρd∕ρo=1.29, μd∕μo=0.84, σi∕σo=3.64, di∕do=0.87. As can be seen in Fig. 5b, there is a good agreement between the experimental and computational droplet shapes. We next compare the present computational results with the finite element simulations of Bazhlekov et al.31 For this purpose, the computations are performed for the nondimensional parameters of Re=1.25, Eo=180, ρd∕ρo=1.11, μd∕μo=0.5, σi∕σo=10, di∕do=0.75. The droplet shapes are plotted in Fig. 6 at times t∗=0, 1.4, 2.4, and 3.5 together with the results of Bazhlekov et al.31 This figure shows that there is a qualitatively good agreement between the present results and finite element simulations. The results are then quantified in Fig. 7 where the normalized velocities of the top and bottom points of the compound droplet are plotted as a function of dimensionless time. The velocity of the top point is slightly overpredicted by the present method, but there is overall good agreement with the finite element simulations. Note that Kawano et al.50 reported small-amplitude oscillations of encapsulated liquid interfaces especially just after the compound droplet is generated at the tip of injection nozzle. We have not observed any such oscillations of encapsulated drop interfaces for the cases studied in this section probably due to the fact that the droplet production period is not considered and focus is placed on the steady motion in the present study. We also note that neither Mori49 nor Bazhlekov et al.31 reported any oscillatory behavior of encapsulating drop interfaces.
Figure 3.
The normalized static droplet height vs Eötvös number in the range Eo=0.01 and Eo=64. The solid and dashed lines denote the analytical solutions for the limiting cases of Eo⪡1 and Eo⪢1, respectively. The inset shows the initial conditions for the droplet relaxation test.
Figure 4.
Time evolution of the spread factor of simple glycerin droplet spreading on the wax substrate.
Table 1.
List of cases used for validation.
| Cases | Liquid | Wall | Impact velocity (m∕s) | We | Re | θe (deg) |
|---|---|---|---|---|---|---|
| 1 | Glycerin | Wax | 4.1 | 802 | 106 | 93° |
| 2 | Glycerin | Wax | 1.41 | 93 | 36 | 93° |
| 3 | Glycerin | Wax | 1.04 | 51 | 27 | 93° |
Figure 5.
(a) The sketch for buoyancy-driven compound droplet. (b) Comparison of the compound drop shapes obtained computationally by the present method (right) and experimentally by Mori (left). The dimensionless parameters are Re=0.016, Eo=2.11, ρd∕ρo=1.29, μd∕μo=0.84, σi∕σo=3.64, di∕do=0.87.
Figure 6.
Shape evolution of compound droplet at Re=1.25, Eo=180, ρd∕ρo=1.11, μd∕μo=0.5, σi∕σo=10, di∕do=0.75. The present results (solid lines on the right side) are compared with those of Bazhlekovet al. (dashed lines on the left side).
Figure 7.
The velocities of the top and bottom points of the compound drop at Re=1.25, Eo=180, ρd∕ρo=1.11, μd∕μo=0.5, σi∕σo=10, di∕do=0.75. The present results (solid lines) are compared with the results of Bazhlekov et al. (dashed lines).
Impact and spreading of a compound droplet
After validating the numerical method in Sec. 3A, we now present simulations of compound droplet spreading on a flat substrate. The computational setup is sketched in Fig. 1. Computational domain extends approximately 6 outer drop radii in radial direction and 3 drop radii in axial direction and it is resolved by 512×256 uniform Cartesian grid in all the results presented in this section unless specified otherwise. An extensive grid convergence study of the present numerical method has been performed by Muradoglu and Tasoglu45 for a simple droplet case. Therefore, such a study is not repeated here. However, grid convergence is checked for all the results presented and we ensured that the solutions are grid independent, i.e., the spatial error is below 5%.
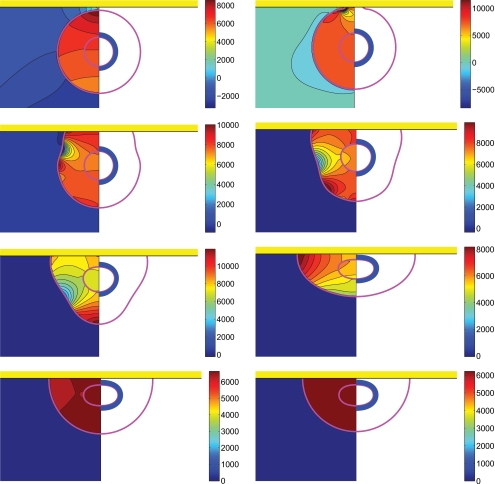
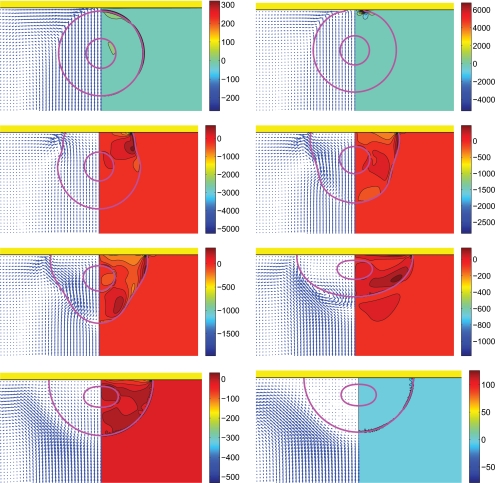
In the experimental study of Demirci and Mostaseno,18 the diameters of the encapsulating droplet and the cell are do=37 μm and di=13 μm (RAJI cell), respectively (do∕di=2.85). The cells are encapsulated in the 8.5% sucrose and 0.3% dextrose solution with density ρd=1030 kg∕m3 and viscosity of μd=1.27×10−3 Pa⋅s. In the simulations, the material properties of the solution encapsulating the cell are set to its physical values. The density of the inner cell is set equal to that of the encapsulating droplet due to a large amount of water content of the cell. There is no known exact value for the viscosity of RAJI cell, or for any cell in general, owing to its microstructured composition, but it can be assumed to be a highly viscous fluid. The viscosity of cell is taken here as an order of magnitude larger than that of the encapsulating droplet mainly due to numerical purposes in spite of the fact that actual apparent viscosity of the cell is much higher. For the same reason, the density of the surrounding air is also set to ρo=51.5 kg∕m3 that is about 40 times larger than its physical value. The material properties used in the simulations are summarized in Table 2 for all three phases. Surface tension at the air-solution interface and the solution-cell interface are 0.076 22 and 0.000 03 N∕m, respectively (σo∕σi=2541). Note that the surface tension at the air-solution interface is based on the experimental data provided by Matubayasi and Nishiyama.51 We assume that the solution remains homogeneous throughout so that the surface tension at the air-solution interface is constant. Based on the experimental data and considerations for numerical stability and convergence, we choose the set of the dimensionless numbers We=0.5, Re=30, do∕di=2.85, σo∕σi=2541, μc∕μd=10, μd∕μo=40, ρc∕ρd=1, ρd∕ρo=20, and θe=90° as the base case. Then, we study the effects of each nondimensional number by systematically varying its value while keeping the other parameters the same as the base case. Note that the density and viscosity ratios between the encapsulating liquid and air are an order of magnitude larger in the experiment. However, it is found that a further increase in the property ratios does not affect the computational results significantly (not shown here). The compound droplet is initially located close to the wall and initiated with a uniform (impact) velocity directed toward the wall. The equilibrium contact angle is chosen as 90° unless stated otherwise. Note that this static contact angle is much larger than the value in the experimental study, i.e., the static contact angle in the experimental work is about 10°. We choose a larger contact angle because it is computationally expensive to resolve the thin liquid layer close to the solid surface for small contact angles. We first present the simulations for the base case. Figure 8 shows snapshots of the collision taken at times t∗=0.000 269, 0.0541, 0.135, 0.216, 0.270, 0.514, 1.027, and 3.843. In this figure, pressure contours are plotted on the left side and the pressure distribution on the cell surface is plotted on the right side of the droplet images. For the same parameters, velocity vectors (left side) and shear stress contours (right side) are plotted in Fig. 9. Shear stress reaches its peak value near the contact line at the beginning of collision and it consistently decreases while the compound droplet is spreading. Even at the beginning of droplet impact, the magnitude of the shear stress is nearly half of the maximum pressure. It is observed that the maximum shear stress occurs at the solution-air interface since all fluid particles within the compound droplet initially have the same velocity while the air is initially quiescent, and thus the velocity gradient is larger at the solution-air interface rather than at the cell-solution interface. Negative shear stress occurs in the vicinity of the contact line where both velocity and pressure gradients are extremely large and there is a stagnation-pointlike flow field. It is emphasized here that it is very likely that the numerical error is also large near the contact line due to large pressure and velocity gradients. The location of maximum pressure changes during the different phases of the collision process. For example, pressure increases near the contact line during the initial impact and spreading period; also just prior to recoil, the maximum pressure is located near the triple point. However, the pressure maximum starts to shift toward the distal point from the wall, where it remains until the recoil phase. Next, we investigate the consequences of variation of the governing dimensionless parameters. In keeping with our emphasis on the inner droplet, we shall define a gross deformation measure as
| (11) |
where Wb and Hb are the maximum droplet dimensions in the radial and axial directions, respectively. Note that t∗∗ (in Figs. 101214161820) is obtained by subtracting the time period between droplet initiation and attachment to the wall from the total elapsed time t and nondimensionalized again with T.
Table 2.
Density and viscosity values of three phases.
| Fluids | Density (kg∕m3) | Viscosity (Pa⋅s) |
|---|---|---|
| Surrounding fluid | 51.5 | 3.175×10−05 |
| Solution encapsulating the cell | 1030 | 1.270×10−03 |
| RAJI cell | 1030 | 1.270×10−02 |
Figure 8.
Evolution of compound droplet impacting on a flat surface [(left half) pressure contours and (right half) pressure distribution on the surface of the cell]. Time evolves from left to right and from top to bottom and the snapshots are taken at times t∗=0.000 269, 0.0541, 0.1351, 0.2162, 0.2703, 0.5135, 1.0270, and 3.8432 (We=0.5, Re=30, do∕di=2.85, σo∕σi=2541, and μc∕μd=10).
Figure 9.
Evolution of compound droplet impacting on a flat surface [(left half) velocity vectors and (right half) shear contours]. Time evolves from left to right and from top to bottom and the snapshots are taken at times t∗=0.000 269, 0.0541, 0.1351, 0.2162, 0.2703, 0.5135, 1.0270, and 3.8432 (We=0.5, Re=30, do∕di=2.85, σo∕σi=2541, and μc∕μd=10).
Figure 10.
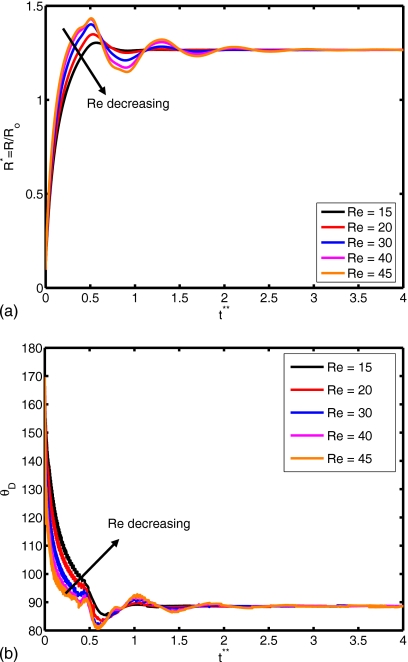
(a) Spread factor and (b) dynamic contact angle vs nondimensional time for Re=15, 20, 30, 40, and 45 (We=0.5, do∕di=2.85, σo∕σi=2541, and μc∕μd=10).
Figure 12.
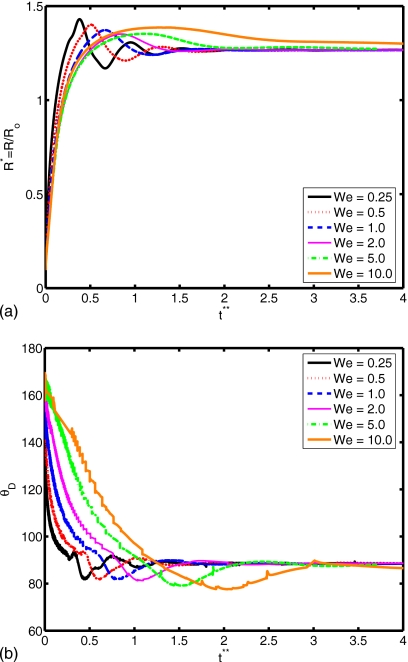
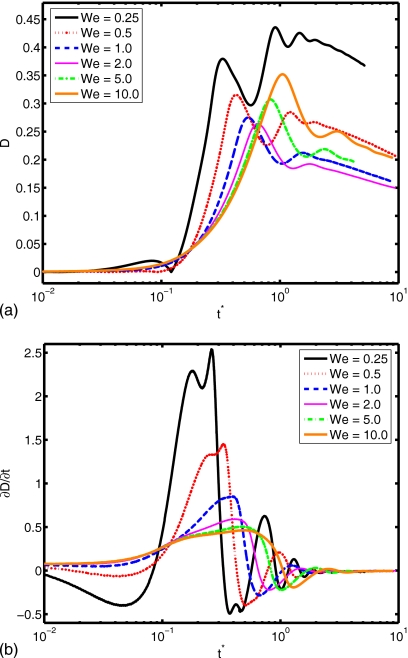
(a) Spread factor and (b) dynamic contact angle vs nondimensional time for We=0.25, 0.5, 1.0, 2.0, 5.0, and 10.0 (Re=30, do∕di=2.85, σo∕σi=2541, and μc∕μd=10).
Figure 14.
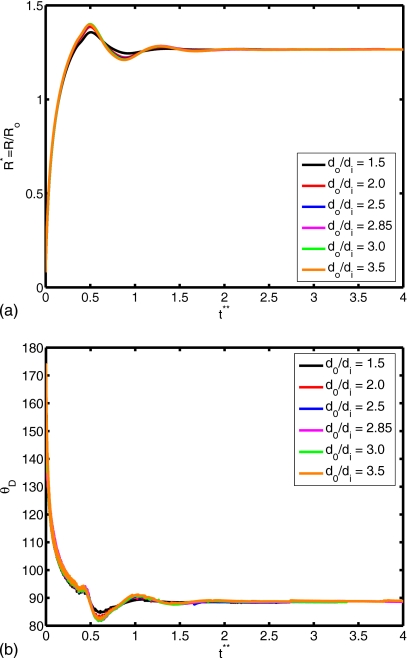
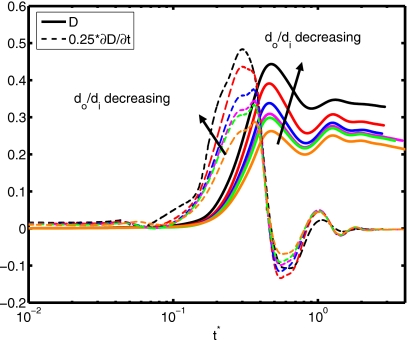
(a) Spread factor and (b) dynamic contact angle vs nondimensional time for do∕di=1.5, 2.0, 2.5, 2.85, 3.0, and 3.5 (We=0.5, Re=30, σo∕σi=2541, and μc∕μd=10).
Figure 16.
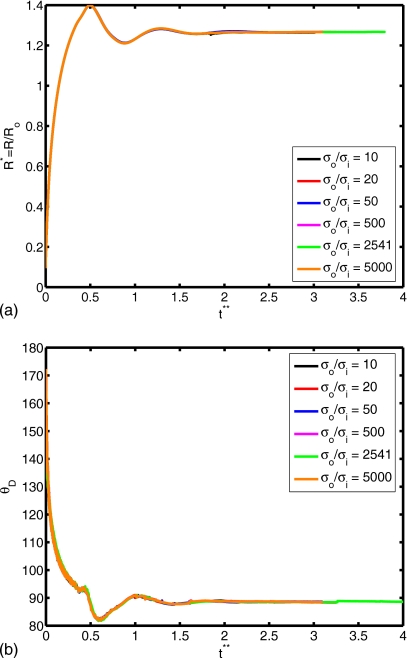
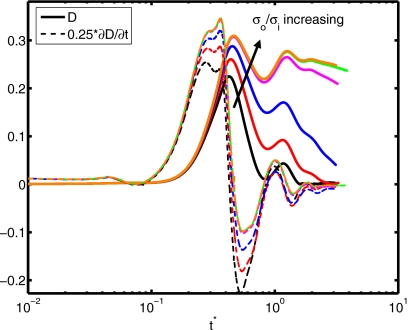
(a) Spread factor and (b) dynamic contact angle vs nondimensional time for σo∕σi=10, 20, 50, 500, 2541, and 5000 (We=0.5, Re=30, do∕di=2.85, and μc∕μd=10).
Figure 18.
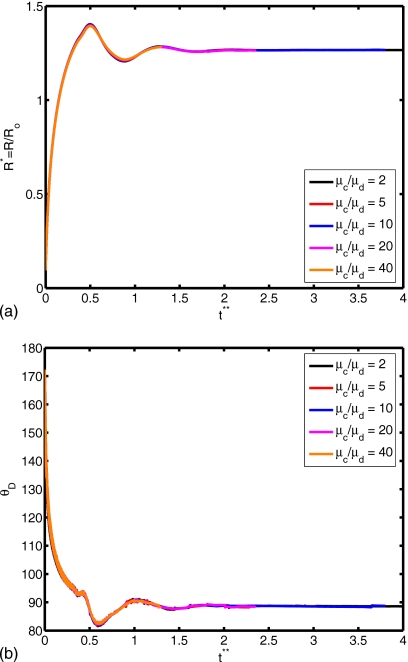
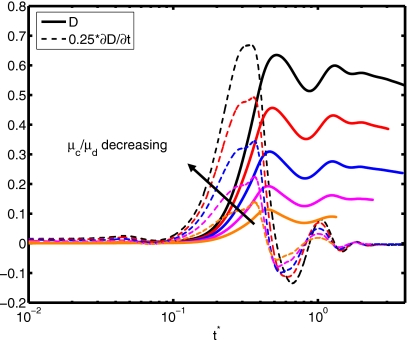
(a) Spread factor and (b) dynamic contact angle vs nondimensional time for μc∕μd=2, 5, 10, 20, and 40 (We=0.5, Re=30, do∕di=2.85, and σo∕σi=2541).
Figure 20.
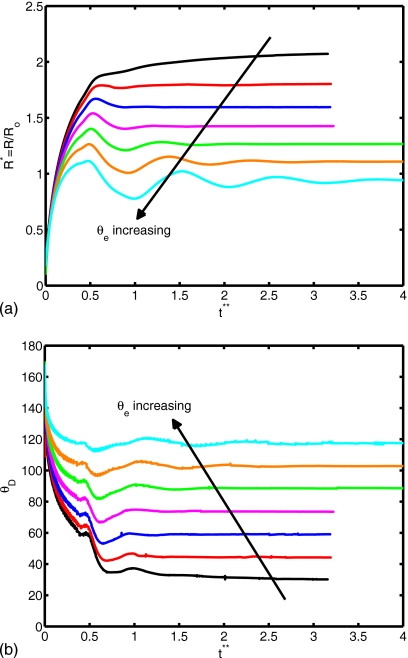
(a) Spread factor and (b) dynamic contact angle vs nondimensional time for θe=30°, 45°, 60°, 75°, 90°, 105°, and 120° (We=0.5, Re=30, do∕di=2.85, σo∕σi=2541, and μc∕μd=10).
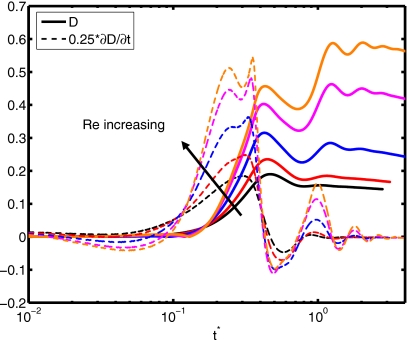
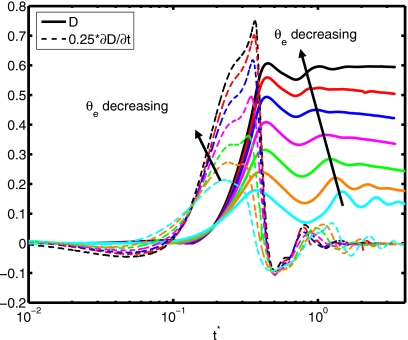
The Reynolds number plays a role in the extent of spreading and in the dynamic contact angle, as shown in Fig. 10. A relative increase in inertial effects leads to a more powerful collision and subsequent cycling between spread and recoil (see Re=45), although all simulations with different Reynolds number converge to the same equilibrium extent of spread. Slowness in spreading for small Re values can also be observed from the evolution of dynamic contact angle in Fig. 10b. The deformation and rate of deformation of the cell are plotted as a function of dimensionless time for Re=15, 20, 30, 40, and 45 in Fig. 11. It is observed that peak cell deformation and rate of deformation increase as Reynolds number increases. Note that cell deformation continues to decrease, even as the cell-encapsulating droplet reaches a steady spread, e.g., at t∗=4.0 for Re=30 in Fig. 8. The simulation is stopped around t∗=4 to limit computational expense. Of course, we expect cell deformation to have vanished at steady state. Next, we examine the effects of the Weber number by varying the Weber number between 0.25 and 10 while keeping the other parameters fixed as in the base case. The results are plotted in Fig. 12 for the extent of spread and the dynamic contact angle. As can be seen from this figure, there is a change in trend around We=2. Maximum spread initially decreases as Weber number increases. Thereafter, it starts to increase with increasing Weber number in a similar way as also observed by Muradoglu and Tasoglu45 for the simple droplet spreading in the range We=10 to 1080. Another observation is that the encapsulating droplet reaches equilibrium conditions faster as Weber number decreases. Deformation and rate of deformation of the cell are plotted in Fig. 13 as a function of dimensionless time for We=0.25, 0.5, 1.0, 2.0, 5.0, and 10.0. A similar trend is also observed in the deformation: it first decreases with We, until We=2, and then it increases with increasing Weber number. On the other hand, the maximum rate of deformation consistently decreases as We increases. It is desirable that the droplet size is sufficiently small so that it contains only a single cell but large enough to provide sufficient protection during the collision. The current printing technologies allow us to control the droplet size precisely within terms of microns. Therefore it is important to examine the effects of the relative droplet size on the viability of the cell. For this purpose, simulations are performed for various values of diameter ratio in the range do∕di=1.5 to 3.5, while keeping the other parameters the same as those in the base case. Figure 14 shows the extent of spread and the dynamic contact angle for various values of the diameter ratio as a function of dimensionless time. Although the dynamics look similar for different values of do∕di, an increase in do∕di leads to a slightly stronger spread and recoil. Deformation and rate of deformation of cell are plotted as a function of dimensionless time for do∕di=1.5, 2.0, 2.5, 2.85, 3.0, and 3.5 in Fig. 15. It is observed that both the deformation and the rate of deformation increase as the ratio of encapsulating droplet diameter to cell diameter decreases.
Figure 11.
Deformation and rate of deformation vs nondimensional time for Re=15, 20, 30, 40, and 45 (We=0.5, do∕di=2.85, σo∕σi=2541, and μc∕μd=10).
Figure 13.
(a) Deformation and (b) rate of deformation vs nondimensional time for We=0.25, 0.5, 1.0, 2.0, 5.0, and 10.0 (Re=30, do∕di=2.85, σo∕σi=2541, and μc∕μd=10).
Figure 15.
Deformation and rate of deformation vs nondimensional time for do∕di=1.5, 2.0, 2.5, 2.85, 3.0, and 3.5 (We=0.5, Re=30, σo∕σi=2541, and μc∕μd=10).
The surface tension is another important parameter in terms of characterizing dynamics of outer droplet, which may affect cell deformation during the printing process. Simulations are performed for the surface tension ratios σo∕σi=10, 20, 50, 500, 2541, and 5000 while keeping the other parameters the same as those in the base case to investigate the effects of the surface tension on the cell viability. The time evolutions of the spread factor and the dynamic contact angle are plotted in Fig. 16. It is interesting to observe that the ratio of surface tension σo∕σi does not have a significant influence on the spread rate and the dynamic contact angle. The deformation and rate of deformation of cell are also plotted Fig. 17 as a function of dimensionless time for σo∕σi=10, 20, 50, 500, 2541, and 5000. It is found that cell deformation and rate of deformation increase as the ratio of surface tension at the air-solution interface to that of the solution-cell interface increases. In contrast, the cell relaxes to its spherical shape faster for smaller values of σo∕σi. Current cell printing techniques used in tissue engineering and biopreservation encapsulate cells in low viscosity solutions such as cell media as well as higher viscosity biomaterials such as collagen and cryoprotectant agents. Therefore, we also investigated the consequences of variation of the viscosity ratio between the cell and the cell-encapsulating droplet for the range μc∕μd=2, 5, 10, 20, and 40 with other parameters constant. In Fig. 18, the extent of spread and the dynamic contact angle are plotted as a function of dimensionless time. It is found that the viscosity ratio μc∕μd does not have any significant influence on the spreading rate and the dynamic contact angle. Cell deformation and rate of deformation are also plotted in Fig. 19 as a function of dimensionless time for μc∕μd=2, 5, 10, 20, and 40. It is observed that cell deformation and rate of deformation increase as viscosity ratio of cell to that of encapsulating droplet decreases. We finally investigate the effects of the equilibrium contact angle. For this purpose, simulations are performed for θe=30°, 45°, 60°, 75°, 90°, 105°, and 120°, while the other parameters are kept the same as those in the base case. Note that static contact angle is dependent on the surface tensions of all involved phases according to Young’s equation. However, the static contact angle can be changed without changing the surface tension at air-liquid interface by simply using different materials (with different surface energy) for the substrate. The extent of spread and the dynamic contact angle are plotted as a function of dimensionless time in Fig. 20. As can be seen, droplets correctly relax to their equilibrium contact angles as the equilibrium conditions are reached. Maximum extent of spread increases as θe decreases. In Fig. 21, deformation and rate of deformation of cell are plotted as a function of dimensionless time for θe=30°, 45°, 60°, 75°, 90°, 105°, and 120°. It is found that the cell deformation and the rate of deformation increase as the equilibrium contact angle decreases. Thus far, the effects of governing nondimensional numbers on the deformation and rate of deformation of the cell have been investigated. Now, we attempt to estimate cell viability during the impact and spreading processes by using the method suggested by Takamatsu et al.47 This method is based on the experimental data obtained from the compression of cells between parallel plates. The model assumes that cells deform symmetrically during the motion of plates. Because the present simulations consistently indicate that the cells deform quite symmetrically (see, for instance, the evolution of cell interface plotted in Fig. 22), we use this method to predict the viability of the cell during the printing process. Takamatsu et al.47 suggest that the viability of an individual cell (η) is given by
| (12) |
where γ=A∕Ao, with A and Ao being the surface areas of the deformed and undeformed cells, respectively. Based on the curve fit to the experimental data, the other parameters in Eq. 12 are specified as γcr=1.5 and Δγ=0.4. The viability of the cells based on the present simulations are summarized in Table 3. Note that only one parameter is varied in each row of Table 3 while all others are set the values in the base case. As can be seen in this table, the cell viability rapidly decreases as θe and μc∕μd decrease. Cell viabilities are near or exceed 90% for the ranges of Re, We, do∕di, and σo∕σi that we studied here. Note that although the minimum static contact angle that we studied (30°) is still larger than the value in the experimental study (10°), viability is decreased to an unacceptable small value, i.e., 26%. However, as we mentioned before, μc∕μd is set to 10 in varying θe case and in other cases except the case in which μc∕μd is varied. Given the fact that cell viscosity is much higher than that of ambient fluid34, 35, 36, 37 and higher μc∕μd leads to higher viability, a simple question arises: What is the combined effect of higher μc∕μd and lower θe on viability? In this study, further computations are not performed because the required computational time is not reasonable with the present method. However, this study provides initial insight of viability trends with respect to several governing nondimensional numbers.
Figure 17.
Deformation and rate of deformation vs nondimensional time for σo∕σi=10, 20, 50, 500, 2541, and 5000 (We=0.5, Re=30, do∕di=2.85, and μc∕μd=10).
Figure 19.
Deformation and rate of deformation vs nondimensional time for μc∕μd=2, 5, 10, 20, and 40 (We=0.5, Re=30, do∕di=2.85, and σo∕σi=2541).
Figure 21.
Deformation and rate of deformation vs nondimensional time for θe=30°, 45°, 60°, 75°, 90°, 105°, and 120° (We=0.5, Re=30, do∕di=2.85, σo∕σi=2541, and μc∕μd=10).
Figure 22.
Evolution of compound droplet (We=0.5, Re=30, do∕di=2.85, σo∕σi=2541, and μc∕μd=10).
Table 3.
Viabilities of cells.
| Re | 15 | 20 | 30 | 40 | 45 | ||
| η | 100.00 | 100.00 | 100.00 | 90.38 | 86.31 | ||
| We | 0.25 | 0.5 | 1 | 2 | 5 | 10 | |
| η | 88.62 | 100.00 | 100.00 | 100.00 | 100.00 | 98.67 | |
| do∕di | 1.5 | 2.0 | 2.5 | 2.85 | 3.0 | 3.5 | |
| η | 88.05 | 92.97 | 97.90 | 100.00 | 100.00 | 100.00 | |
| σo∕σi | 10 | 20 | 50 | 500 | 2541 | 5000 | |
| η | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | |
| μc∕μd | 2 | 5 | 10 | 20 | 40 | ||
| η | 44.07 | 88.43 | 100.00 | 100.00 | 100.00 | ||
| θe | 30° | 45° | 60° | 75° | 90° | 105° | 120° |
| η | 26.15 | 54.81 | 80.77 | 91.84 | 100.00 | 100.00 | 100.00 |
CONCLUSIONS
The impact and spreading of a compound droplet on a smooth flat surface are studied computationally using a finite-difference∕front-tracking method in an axisymmetric setting. The compound droplet is proposed as a model for printing of droplet-encapsulated biological cells.17, 18 The cell is modeled as a highly viscous Newtonian droplet that is encapsulated by a less viscous Newtonian liquid. It is hypothesized that the cell viability is mainly dependent on the cell deformation and its rate. Therefore, the model is used to investigate the optimal conditions that yield minimum deformation and deformation rate. The experimental conditions of Demirci and Montesano18 are taken as the base case and then the effects of nondimensional parameters on the cell viability are investigated by varying each parameter at a time systematically, while keeping the others the same as those in the base case.
Since the numerical method has been already validated comprehensively for a simple droplet impact and spreading on a flat surface, validation tests are performed here to assess the performance of the method for compound droplet. For this purpose, it is first shown that the compound droplet correctly relaxes to its equilibrium shape when it impacts and spreads on a flat surface for a wide range of Eötvös numbers. Then the treatment of the contact line is validated against the experimental data for a simple glycerin droplet spreading on a wax substrate. Finally, the numerical method is applied to simulate the buoyancy-driven motion and the deformation of compound droplet, and results are found to be in a good agreement with the experimental data of Mori49 and also with the finite element simulations of Bazhlekov et al.31
After validating the numerical method, computations are performed to examine the effects of the relevant dimensionless parameters on the dynamics of compound droplet impact and spreading on a flat surface. It is found that maximum spreading of the cell-encapsulating droplet increases as the Reynolds number (Re) increases. As Weber number (We) increases, maximum spread first decreases until We=2, then it increases. The diameter ratio, the viscosity of the cell, and the surface tension at the solution-cell interface are found to have no significant influence on the spreading of the encapsulating droplet in the range we studied here. It is found that the maximum spreading and the equilibrium extent of spread increase as the equilibrium contact angle decreases as expected. The deformation and the rate of deformation of the cell (inner droplet) increase as the Reynolds number and the surface tension ratio of the air-solution interface to the solution-cell interface (σo∕σi) increase. For smaller σo∕σi, the cell relaxes to its equilibrium shape faster. The deformation and the rate of deformation of the cell increases as the diameter ratio of encapsulating droplet to cell (do∕di) and the viscosity ratio of cell to encapsulating droplet (μc∕μd) decreases. It is observed that there is a change in the trend of the peak deformation for different Weber numbers. Maximum deformation first decreases until We=2, then it increases with increasing Weber number. On the other hand, the peak rate of deformation consistently decreases as We increases. Finally, we employ a relation to fit to experimental data of compression of cells between two parallel plates47 to estimate the effects of cell deformation on viability. It is found that the cell viability rapidly decreases as θe and μc∕μd decrease. Cell viability is near or over 90% for the ranges of Re, We, do∕di, and σo∕σi that we studied in this paper. The cell viability is found to decrease rapidly as the equilibrium contact angle decreases below 60°. This can be partly attributed to low viscosity ratio (μc∕μd=10) in varying θe case.
The goal of this paper was to develop a framework for investigating relative importance of governing nondimensional numbers: Re, We, do∕di, σo∕σi, μc∕μd, and θe on cell viability for the problem of deposition of cell-encapsulating droplets. The analysis pointed out along the way that a number of parameters such as μc∕μd and θe should be perturbed simultaneously. We also deferred non-Newtonian or more complicated microstructured cell models to a future study.
ACKNOWLEDGMENTS
We thank Dr. Feng Xu for useful discussions that contributed to this work. S.T. and M.M. are grateful to the Scientific and Technical Research Council of Turkey (TUBITAK) for support of this research through Grant No. 108M238 and the Turkish Academy of Sciences through TUBA-GEBIP program. U.D. was supported by NIH Grant No. R21EB007707.
References
- Yarin A. L., “Drop impact dynamics: Splashing, spreading, receding, bouncing,” Annu. Rev. Fluid Mech. 38, 159 (2006). 10.1146/annurev.fluid.38.050304.092144 [DOI] [Google Scholar]
- Dussan V. E. B. and Davis S. H., “On the motion of a fluid-fluid interface along a solid surface,” J. Fluid Mech. 65, 71 (1974). 10.1017/S0022112074001261 [DOI] [Google Scholar]
- Shikhmurzaev Y. D., “Moving contact lines in liquid-liquid-solid systems,” J. Fluid Mech. 334, 211 (1997). 10.1017/S0022112096004569 [DOI] [Google Scholar]
- Fukai J., Shiiba Y., Yamamoto T., Miyatake O., Poulikakos D., Megaridis C. M., and Zhao Z., “Wetting effects on the spreading of a liquid droplet colliding with a flat surface: Experiment and modeling,” Phys. Fluids 7, 236 (1995). 10.1063/1.868622 [DOI] [Google Scholar]
- Roisman I. V., Rioboo R., and Tropea C., “Normal impact of a liquid drop on a dry surface: Model for spreading and receding,” Proc. R. Soc. London, Ser. A 458, 1411 (2002). 10.1098/rspa.2001.0923 [DOI] [Google Scholar]
- Bussmann M., Mostaghimi J., and Chandra S., “On a three-dimensional volume tracking model of droplet impact,” Phys. Fluids 11, 1406 (1999). 10.1063/1.870005 [DOI] [Google Scholar]
- Manservisi S. and Scardovelli R., “A variational approach to the contact angle dynamics of spreading droplets,” Comput. Fluids 38, 406 (2008). 10.1016/j.compfluid.2008.05.001 [DOI] [Google Scholar]
- Renardy M., Renardy Y., and Li J., “Numerical simulation of moving contact line problem using a volume-of-fluid method,” J. Comput. Phys. 171, 243 (2001). 10.1006/jcph.2001.6785 [DOI] [Google Scholar]
- Pasandideh-Fard M., Qiao Y. M., Chandra S., and Mostaghimi J., “Capillary effects during droplet impact on a solid surface,” Phys. Fluids 8, 650 (1996). 10.1063/1.868850 [DOI] [Google Scholar]
- Spelt P. D. M., “A level-set approach for simulations of flows with multiple moving contact lines with hysteresis,” J. Comput. Phys. 207, 389 (2005). 10.1016/j.jcp.2005.01.016 [DOI] [Google Scholar]
- Chandra S. and Avedisian C. T., “On the collision of a droplet with a solid surface,” Proc. R. Soc. London, Ser. A 432, 13 (1993). [Google Scholar]
- Šikalo Š., Wilhelm H. D., Roisman I. V., Jakirlic S., and Tropea C., “Dynamic contact angle of spreading droplets: Experiments and simulations,” Phys. Fluids 17, 062103 (2005). 10.1063/1.1928828 [DOI] [Google Scholar]
- Mao T., Kuhn D. C. S., and Tran H., “Spread and rebound of liquid droplets upon impact on flat surfaces,” AIChE J. 43, 2169 (1997). 10.1002/aic.690430903 [DOI] [Google Scholar]
- Utada A. S., Lorenceau E., Link D. R., Kaplan P. D., Stone H. A., and Weitz D. A., “Monodisperse double emulsions generated from a microcapillary device,” Science 308, 537 (2005). 10.1126/science.1109164 [DOI] [PubMed] [Google Scholar]
- Chen R. H., Chiu S. L., and Lin T. H., “Resident time of a compound drop impinging on a hot surface,” Appl. Therm. Eng. 27, 2079 (2007). 10.1016/j.applthermaleng.2006.11.014 [DOI] [Google Scholar]
- Shintaku H., Kuwabara T., Kawano S., Suzuki T., Kanno I., and Kotera H., “Micro cell encapsulation and its hydrogel-beads production using microfluidic device,” Microsyst. Technol. 13, 951 (2007). 10.1007/s00542-006-0291-z [DOI] [Google Scholar]
- Nakamura M., Kobayashi A., Takagi F., Watanabe A., Hiruma Y., Ohuchi K., Iwasaki Y., Horie M., and Takatani S., “Biocompatiple inkjet printing technique for designed seeding of individual cells,” Tissue Eng. 11, 1658 (2005). 10.1089/ten.2005.11.1658 [DOI] [PubMed] [Google Scholar]
- Demirci U. and Montesano G., “Single cell epitaxy by acoustic picoliter droplets,” Lab Chip 7, 1139 (2007). 10.1039/b704965j [DOI] [PubMed] [Google Scholar]
- Moon S., Hasan S. K., Song Y. S., Keles H. O., Manzur F., Mikkilineni S., Hong J. W., Nagatomi J., Haeggstrom E., Khademhosseini A., and Demirci U., “Layer by layer three-dimensional tissue epitaxy by cell laden hydrogel droplets,” Tissue Engineering C 16, 157 (2010). 10.1089/ten.tec.2009.0179 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boland T., Tao X., Damon B. J., Manley B., Kesari P., Jalota S., and Bhaduri S., “Drop-on-demand printing of cells and materials for designer tissue constructs,” Mater. Sci. Eng., C 27, 372 (2007). 10.1016/j.msec.2006.05.047 [DOI] [Google Scholar]
- Mironov V., Boland T., Trusk T., Forgacs G., and Markwald R. R., “Organ printing: Computer aided jet-based 3D tissue engineering,” Trends Biotechnol. 21, 157 (2003). 10.1016/S0167-7799(03)00033-7 [DOI] [PubMed] [Google Scholar]
- Demirci U. and Montesano G., “Cell encapsulating droplet vitrification,” Lab Chip 7, 1428 (2007). 10.1039/b705809h [DOI] [PubMed] [Google Scholar]
- Song Y., Adler A., Kayaalp A., Nureddin A., Anchan R., Maas R., and Demirci U., “Vitrification and levitation of a liquid droplet on liquid nitrogen,” Proc. Natl. Acad. Sci. U.S.A. 107, 4596 (2010). 10.1073/pnas.0914059107 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson R. E. and Sadhal S. S., “Fluid mechanics of compound multiphase drops and bubbles,” Annu. Rev. Fluid Mech. 17, 289 (1985). 10.1146/annurev.fl.17.010185.001445 [DOI] [Google Scholar]
- Smith K. A., Ottino J. M., and Olvera de la Cruz M., “Encapsulated drop breakup in shear flow,” Phys. Rev. Lett. 93, 204501 (2004). 10.1103/PhysRevLett.93.204501 [DOI] [PubMed] [Google Scholar]
- Engel R. H., Riggi S. J., and Fahrenbach M. J., “Insulin: Intestinal absorption as water-in-oil-in-water emulsions,” Nature (London) 219, 856 (1968). 10.1038/219856a0 [DOI] [PubMed] [Google Scholar]
- Langer R., “Drug delivery and targeting,” Nature (London) 392, 5 (1998). [PubMed] [Google Scholar]
- Dickinson E., Evison J., Gramshaw J. W., and Schwope D., “Flavor release from a protein-stabilized water-in-oil-in-water emulsion,” Food Hydrocolloids 8, 63 (1994). 10.1016/S0268-005X(09)80145-8 [DOI] [Google Scholar]
- Pal R., “Rheology of double emulsions,” J. Colloid Interface Sci. 307, 509 (2007). 10.1016/j.jcis.2006.12.024 [DOI] [PubMed] [Google Scholar]
- Stone H. A. and Leal L. G., “Breakup of concentric double emulsion droplets in linear flows,” J. Fluid Mech. 211, 123 (1990). 10.1017/S0022112090001525 [DOI] [Google Scholar]
- Bazhlekov I. B., Shopov P. J., and Zapryanov Z. D., “Unsteady motion of type-A compound multiphase drop at moderate Reynolds numbers,” J. Colloid Interface Sci. 169, 1 (1995). 10.1006/jcis.1995.1001 [DOI] [Google Scholar]
- Kawano S., Shirai A., and Nagasaka S., “Deformations of thin liquid spherical shells in liquid-liquid-gas systems,” Phys. Fluids 19, 012105 (2007). 10.1063/1.2429070 [DOI] [Google Scholar]
- Zhou C., Yue O., and Feng J., “Formation of simple and compound drops in microfluidic devices,” Phys. Fluids 18, 092105 (2006). 10.1063/1.2353116 [DOI] [Google Scholar]
- Yeung A. and Evans E., “Cortical shell-liquid core model for passive flow of liquid-like spherical cells into micropipets,” Biophys. J. 56, 139 (1989). 10.1016/S0006-3495(89)82659-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Needham D. and Hochmuth R. M., “Rapid flow of passive neutrophils into 4 μm pipet and measurement of cytoplasmic viscosity,” J. Biomech. Eng. 112, 269 (1990). 10.1115/1.2891184 [DOI] [PubMed] [Google Scholar]
- Tran-Son-Tay R., Needham D., Yeung A., and Hochmuth R. M., “Time-dependent recovery of passive neutrophils after large deformation,” Biophys. J. 60, 856 (1991). 10.1016/S0006-3495(91)82119-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Agresar G., Linderman J. J., Tryggvason G., and Powell K. G., “An adaptive, Cartesian, front-tracking method for the motion, deformation and adhesion of circulating cells,” J. Comput. Phys. 143, 346 (1998). 10.1006/jcph.1998.5967 [DOI] [Google Scholar]
- Evans E. and Yeung A., “Apparent viscosity and cortical tension of blood granulocytes determined by micropipet aspiration,” Biophys. J. 56, 151 (1989). 10.1016/S0006-3495(89)82660-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hochmuth R. M., “Micropipette aspiration of living cells,” J. Biomech. 33, 15 (2000). 10.1016/S0021-9290(99)00175-X [DOI] [PubMed] [Google Scholar]
- Kan H. -C., Udaykumar H. S., Shyy W., and Tran-Son-Tay R., “Hydrodynamics of a compound drop with application to leukocyte modeling,” Phys. Fluids 10, 760 (1998). 10.1063/1.869601 [DOI] [Google Scholar]
- Marella S. V. and Udaykumar H. S., “Computational analysis of the deformability of leukocytes modeled with viscous and elastic structural components,” Phys. Fluids 16, 244 (2004). 10.1063/1.1629691 [DOI] [Google Scholar]
- Wang W., Huang Y., Grujicic M., and Chrisey D. B., “Study of impact-induced mechanical effects in cell direct writing using smooth particle hydrodynamic method,” ASME J. Manuf. Sci. Eng. 130, 021012 (2008). 10.1115/1.2896118 [DOI] [Google Scholar]
- Tryggvason G., Bunner B., Esmaeeli A., Juric D., Al-Rawahi N., Tauber W., Han J., Nas S., and Jan Y. J., “A front-tracking method for the computations of multiphase flow,” J. Comput. Phys. 169, 708 (2001). 10.1006/jcph.2001.6726 [DOI] [Google Scholar]
- Unverdi S. O. and Tryggvason G., “A front-tracking method for viscous incompressible multiphase flows,” J. Comput. Phys. 100, 25 (1992). 10.1016/0021-9991(92)90307-K [DOI] [Google Scholar]
- Muradoglu M. and Tasoglu S., “A front-tracking method for computational modeling of impact and spreading of viscous droplets on solid walls,” Comput. Fluids 39, 615 (2010). 10.1016/j.compfluid.2009.10.009 [DOI] [Google Scholar]
- Kistler S. F., in Wettability, edited by Berg J. C. (Dekker, New York, 1993). [Google Scholar]
- Takamatsu H. and Rubinsky B., “Viability of deformed cells,” Cryobiology 39, 243 (1999). 10.1006/cryo.1999.2207 [DOI] [PubMed] [Google Scholar]
- Peskin C. S., “Numerical analysis of blood flow in the heart,” J. Comput. Phys. 25, 220 (1977). 10.1016/0021-9991(77)90100-0 [DOI] [Google Scholar]
- Mori Y. H., “Configurations of gas-liquid 2-phase bubbles in immiscible liquid media,” Int. J. Multiphase Flow 4, 383 (1978). 10.1016/0301-9322(78)90032-0 [DOI] [Google Scholar]
- Kawano S., Hashimoto H., Ihara A., and Azima T., “Small-amplitude oscillations of encapsulated liquid drop interfaces,” JSME Int. J., Ser. B 40, 33 (1997). [Google Scholar]
- Matubayasi N. and Nishiyama A., “Thermodynamic quantities of surface formation of aqueous electrolyte solutions VI. Comparison with typical nonelectrolytes, sucrose and glucose,” J. Colloid Interface Sci. 298, 910 (2006). 10.1016/j.jcis.2006.01.008 [DOI] [PubMed] [Google Scholar]