Advanced Human Carotid Plaque Progression Correlates Positively with Flow Shear Stress Using Follow-Up Scan Data: An In Vivo MRI Multi-Patient 3D FSI Study

Abstract

Although it has been well-accepted that atherosclerosis initiation and early progression correlate negatively with flow wall shear stresses (FSS), increasing evidence suggests mechanisms governing advanced plaque progression are not well understood. Fourteen patients were scanned 2–4 times at 18 month intervals using a histologically validated multi-contrast magnetic resonance imaging (MRI) protocol to acquire carotid plaque progression data. Thirty-two scan pairs (baseline and follow-up scans) were formed with slices matched for model construction and analysis. 3D fluid-structure interaction (FSI) models were constructed and plaque wall stress (PWS) and flow shear stress (FSS) were obtained from all matching lumen data points (400–1000 per plaque; 100 points per matched slice) to quantify correlations with plaque progression measured by vessel wall thickness increase (WTI). Using FSS and PWS data from follow-up scan, 21 out of 32 scan pairs showed a significant positive correlation between WTI and FSS (positive/negative/no significance ratio = 21/8/3), and 26 out of 32 scan pairs showed a significant negative correlation between WTI and PWS (positive/negative/no significance ratio = 2/26/4). The mean FSS value of lipid core nodes (n=5294) from all 47 plaque models was 63.5 dyn/cm², which was 45% higher than that from all normal vessel nodes (n=27553, p<0.00001)). The results from this intensive FSI study indicate that flow shear stress from follow-up scan correlates positively with advanced plaque progression which is different from what has been observed in plaque initiation and early-stage progression. It should be noted that the correlation results do not automatically lead to any causality conclusions.

1. Introduction

Low and oscillating blood flow shear stresses (LFSS) have been shown to correlate positively with intimal thickening and atherosclerosis initiation (Friedman et al., 1987, 1993; Giddens et al., 1993; Ku et al., 1985; Gibson et al., 1993; Nerem, 1992; Suo and Giddens et al., 2008). However, the LFSS hypothesis cannot explain why intermediate and advanced plaques continue to grow under elevated high shear stress conditions (Tang et al., 2008). Controversy over the LFSS hypothesis have led several groups to search for other mechanisms governing advanced plaque progression such as plaque wall (structure) stresses (PWS) (Joshi et al., 2004; Wentzel et al., 2005). Tang et al. used in vivo magnetic resonance imaging (MRI) patient-tracking data and 2D structural models to quantify correlation between plaque progression measured by vessel wall thickness increase (WTI) between baseline and follow-up scans and structural plaque wall stress. Their results indicated that 18 out of 21 patients showed significant negative correlation between wall thickness increase and plaque wall stress from follow-up scan (Tang et al., 2008). Patient-specific plaque growth functions were also derived based on patient-tracking MRI data and used in computational simulation of plaque progression and good agreement between simulated growth and MRI data was found (error <2%, Tang et al., 2008).

This study uses 3D models with fluid-structure interactions (FSI) based on in vivo MRI data taken from patients at multiple time points. The 3D FSI models were solved and plaque wall stress (PWS) and flow shear stress (FSS) data at lumen wall were obtained to quantify their correlations with plaque progression measured by vessel wall thickness increase (WTI). Location-specific results for vessel wall thickness increase, locations of plaque components (necrotic lipid core, calcification and loose matrix) and their association with flow shear stress from 32 matched baseline and follow-up scan pairs and 47 plaques were reported.

2. Methods

2.1 In vivo Serial MRI Data Acquisition and Segmentation

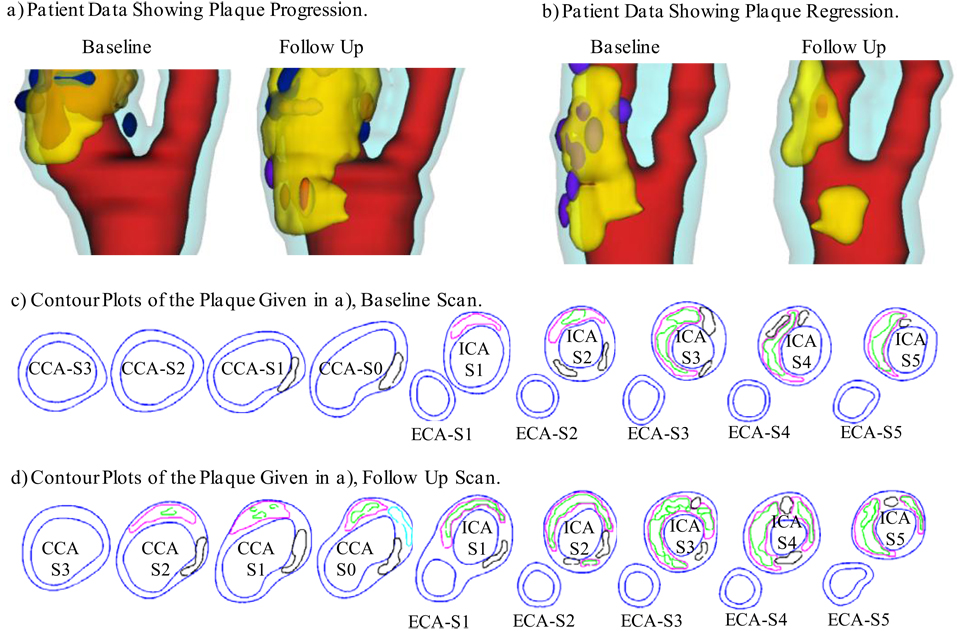
After informed consent, serial MRI data of carotid atherosclerotic plaques from 14 patients (13 male, 1 female; age: 59–81, mean=71.9) were acquired 2–4 times (scan interval: 18 months) by the University of Washington Vascular Imaging Laboratory using protocols approved by the University of Washington Institutional Review Board. MRI scans were conducted on a GE SIGNA 1.5-T whole body scanner using an established protocol (Yuan and Kerwin, 2004). Multi-contrast images in T1, T2, proton density(PD), time-of-flight (TOF), and contrast-enhanced (CE) T1 weighted images of atherosclerotic plaques were generated to characterize plaque tissue composition and luminal and vessel wall morphology (Yuan et al., 2001a, 2001b, 2004). A custom-designed computer package CASCADE (Computer-Aided System for Cardiovascular Disease Evaluation) developed by the Vascular Imaging Laboratory (VIL) at the University of Washington (UW) was used to perform image analysis and segmentation. Upon completion of a review, an extensive report was generated and segmented contour lines for different plaque components for each slice were stored for computational model reconstructions. The slice thickness was 2 mm. Field of view = 160 mm × 160 mm. Matrix size 512 × 512 (the real matrix size was 256×256. Images were machine interpolated to 512×512). After interpolation, the in-plane resolution was 0.31×0.31mm . Thirty-two scan-pairs (called baseline and follow-up scans) were formed for this study, with MRI slices matched for each pair. Figure 1 gives two examples re-constructed from MRI data showing plaque progression and regression.

Figure 1.

3D plaque samples re-constructed from in vivo MR images showing progression and regression. (a): one sample showing plaque growth; (b): one sample showing plaque reduction. Scan time interval: 18 months. Red: lumen; Yellow: lipid; Dark blue: calcification; light blue: outer wall. (c) and (d): Contour plots of the plaque given in a). Black: Calcification; Magenta: lipid core. Some hemorrhage (green) were found inside lipid cores.

2.2. 3D Geometry Re-Construction and Mesh Generation

Under in vivo conditions, arteries are axially stretched and pressurized. Therefore, in vivo MRI plaque geometry needs to be shrunk axially and circumferentially a priori to obtain the no-load starting geometry for computational simulations. The shrinkage in axial direction was 9% so that the vessel would regain its in vivo length with a 10% axial stretch. Circumferential shrinkage for lumen (about 8–12%) and outer wall (about 2–5%) was determined by trial-and-error so that: 1) total mass of the vessel was conserved; 2) the loaded plaque geometry after 10% axial stretch and pressurization had the best match with the original in vivo geometry.

Because advanced plaques have complex irregular geometries and 3D FSI models involve large deformation and large strain, the 3D FSI model may not converge if an automatically generated mesh was used. A geometry-fitting mesh generation technique was developed to generate mesh for these models (Tang et al., 2009). Using this technique, the 3D plaque and fluid domains were divided into hundreds of small “volumes” to curve-fit the irregular plaque geometries. Computational meshes for these volumes were then generated by ADINA (ADINA R & D, Inc., Watertown, MA, USA), a commercial finite element software used to solve these FSI models. Details of the mesh generation process were described in Tang et al. (2009).

2.3 3D Fluid-Structure Interaction Plaque Model and Solution Methods

3D FSI models were constructed for all the 32 pairs (cases) to obtain both flow shear stress (FSS) and plaque wall stress (PWS) fields for correlation analysis. Since the focus of this study was to determine the correlations between mechanical forces (FSS and PWS) and plaque progression, the artery wall in the FSI model was assumed to be uniform, hyperelastic, isotropic, incompressible and homogeneous. This limitation will be further discussed in 4.2. The nonlinear modified Mooney-Rivlin model was used to describe the material properties of the vessel wall (Bathe, 2002; Huang et al., 2001; Tang et al., 2004). The strain energy function was given by,

$$\mathrm{W}={\mathrm{c}}_1({\mathrm{I}}_1-3)+{\mathrm{c}}_2({\mathrm{I}}_2-3)+{\mathrm{D}}_1[\text{exp}({\mathrm{D}}_2({\mathrm{I}}_1-3))-1],$$ (1)

$${\mathrm{I}}_1={\displaystyle \sum C_{ii},{\mathrm{I}}_2=½[{\mathrm{I}}_1^2-{\mathrm{C}}_{\text{ij}}{\mathrm{C}}_{\text{ij}}],}$$ (2)

where I₁ and I₂ are the first and second strain invariants, C =[C_ij] = X^TX is the right Cauchy-Green deformation tensor, X=[X_ij] = [∂x_i/∂a_j], (xi) is the current position, (a_i) is the original position, c_i and D_i are material parameters chosen to match experimental measurements and the current literature (Humphrey, 2002; Kobayashi et al., 2003). Parameter values used for the arterial vessel wall in this model were: c₁=368000 dyn/cm² , c₂=0, D₁ =144000 dyn/cm² , D₂ =2.0.

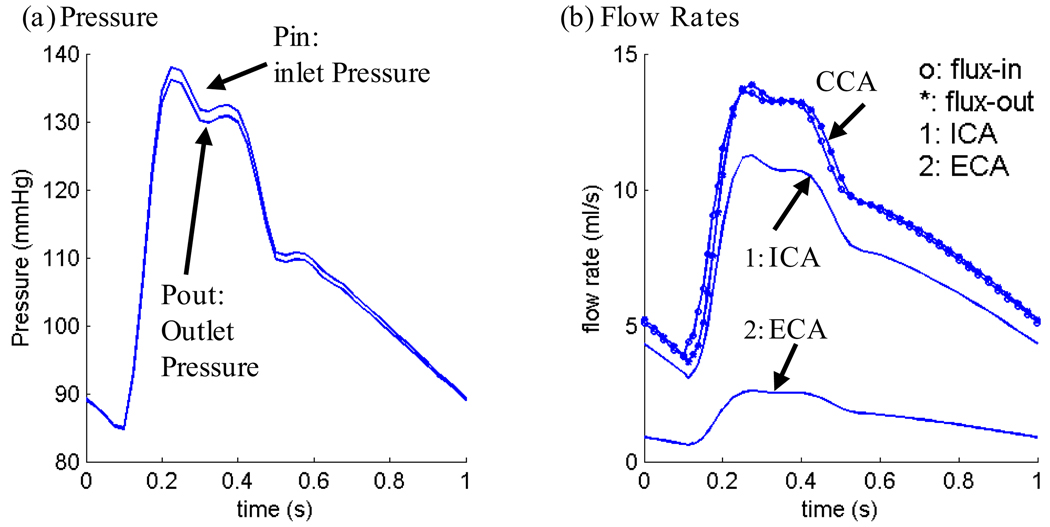
Blood flow was assumed to be laminar, Newtonian, viscous and incompressible. The incompressible Navier-Stokes equations with arbitrary Lagrangian-Eulerian (ALE) formulation were used as the governing equations. A no-slip condition, natural traction equilibrium boundary condition and continuity of displacement were assumed on the interface between solid and fluid. Inlet and outlet were fixed in longitudinal (axial) direction, but allowed to expand/contract with flow otherwise. Patient-specific systolic and diastolic pressure conditions from the last hospital admission were used as the maximum and minimum of the imposed pulsatile pressure waveforms at the inlet and outlet of the artery. Figure 2 gives an example of pressure wave forms specified at the inlet and outlet of a plaque and corresponding flow rates obtained from the FSI model. Details of the FSI model have been described in (Tang, et al. 2004, 2008; Yang et al., 2007) and are omitted here.

Figure 2.

Pressure conditions specified at the inlet (CCA) and outlet (ICA and ECA) of a plaque sample and the corresponding flow rates obtained from the FSI model.

The 3D FSI models were solved by ADINA, using unstructured finite element methods for both fluid and solid domains. Nonlinear incremental iterative procedures were used to handle fluid-structure interactions. The governing finite element equations for both solid and fluid models were solved by Newton-Raphson iteration method. More details of the computational models and solution methods can be found in Tang et al. (2004), Yang et al. (2007) and Bathe (2002). Plaque wall stress and flow shear stress data corresponding to peak systolic pressure were recorded for analysis.

2.4 Plaque Progression Measurements, node type and Data Extraction for Correlation Analysis

For each scan pair, slices from the baseline (Time 1, or T1) and follow-up (Time 2, or T2) scans were matched using the carotid bifurcation as the registration reference (see Fig. 1 (c)–(d) for illustration). Only matched common carotid artery (CCA) and internal carotid artery (ICA) slices were chosen for analysis since external carotid arteries (ECA) are less prone to atherosclerosis. For each matched slice, 100 evenly-spaced points from the lumen were selected and vessel wall thickness, PWS, and FSS from 3D FSI model solutions at each point for Time 1 and Time 2 were obtained for analysis. For the 32 pairs, 400–1000 matched data points for each plaque were obtained for correlation analysis. Plaque progression at each data point was expressed by vessel wall thickness increase (WTI) defined as

$$\text{WTI}=\text{Wall}\text{Thickness}\text{at}\mathrm{T}2-\text{Wall}\text{Thickness}\text{at}\mathrm{T}1.$$ (3)

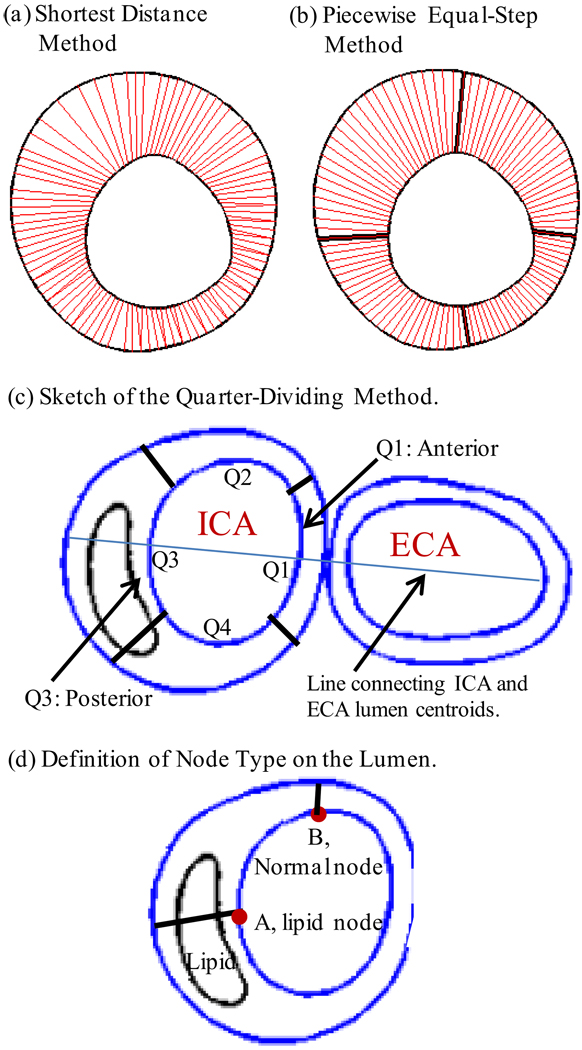
In view of the fact that advanced plaques have irregular geometries, a piecewise equal-step method was introduced to calculate wall thickness at each data point [see Fig. 3 (a)–(b)]. This method is better than the shortest-distance method used in our previous paper (Tang et al., 2008). Each slice was divided into four quadrants Q1-Q4, each quadrant containing 25 lumen points which were part of the 100 selected points. For each quadrant, 25 even-spaced points were chosen on the outer vessel boundary. The corresponding points on the inner and outer boundaries were paired and the distance between the paired points was defined as vessel wall thickness at the given lumen point. This method was sufficient for the cases covered in this paper.

Figure 3.

Schematic drawing demonstrating the Piecewise Equal-Step method for vessel wall thickness and the quarter-dividing method. (a) Shortest distance method: for every selected data point on lumen, a point on the out-boundary with the shortest distance was chosen as the matching point; (b) piecewise equal-step method; (c) sketch of the quarter-dividing method. A line connecting the centers of ICA and ECA lumen area was determined first. Then Q1 was determined so that the intersection of the lumen and the centerline was chosen as a data point and Q1 contains 12 data points on each side of the center line. (d) Definition of node type for a lumen point.

Division of Q1-Q4 was handled so that the quadrants were also used to identify locations of plaque components and location-specific plaque progression. The slice just before bifurcation was labeled CCA-S0. Starting from that slice, the first slice with both ICA and ECA is ICA-S1 (the ECA was used in model construction, however, stress data from the ECA was not used in the analysis). Other ICA slices were numbered sequentially. CCA slices were numbered similarly, with CCA-S1 below CCA-S0. For an ICA slice, the quadrants were divided as shown in Figure 3. All CCA slices were aligned in the direction determined by the ICA-S1. This assured a (Slice, Quadrant) coordinate system for plaque location. For CCA slices, Q1 and Q3 were referred to as the anterior and posterior quadrants, with respect to the carotid bifurcation. FSS and PWS distribution data was extracted from the 32 pairs and 47 plaques, with this location-specific system.

Every selected data point (100/slice) on the lumen was assigned a node type (lipid, calcification, loose matrix, and normal) according to its location and the plaque component it is covering (see Fig. 3 (d)). If the line connecting the lumen point and its corresponding out-boundary point meets a plaque component, the lumen point is assigned to that component type (lipid in Fig. 3 (d)). If the line goes through several components, the first component is used as the node type of the lumen node. If the connecting line does not hit any component, the node is assigned as a normal node. The density of each component for a given region was defined as:

$$\text{Density}\text{of}\text{Component}\mathrm{A}=(\text{Component}\mathrm{A}\text{points})/(\text{Total}\text{points}\text{of}\text{the}\text{given}\text{region}).$$ (4)

Plaque component distribution and their possible association with mechanical forces were quantified using density, slice and quadrant locations.

2.5 Statistical Analysis

Standard statistical linear regression analysis was performed to quantify the correlation between plaque progression measured by WTI and flow shear stress and the correlation between WTI and plaque wall stress. Flow shear stress values associated with plaque components were compared with those from normal wall data points. A t-test (P<0.05) was used to determine if there was a significant difference between the compared data.

3. Results

3.1 Wall Thickness Increase Correlates Positively with FSS and Negatively with PWS Using Time 2 Data

Table 1 summarizes correlation results between WTI and both FSS and PWS at Time 1 and Time 2. Using FSS and PWS data at Time 2, statistically significant positive correlation between WTI and FSS was found in 21 of the 32 cases examined (8 negative, 3 no significance). The 95% confidence interval (CI) for Pearson correlation (PC) coefficient values was (0.012, 0.187). A statistically significant negative correlation between WTI and PWS was found in 26 of the 32 cases (2 positive, 4 no significance). The 95% CI for Pearson correlation (PC) coefficient values was (−0.273, −0.142).

Table 1.

Correlation results from 32 scan pairs showing plaque progression (WTI) has a) positive correlation with FSS from follow-up scan (21 out of 32); b) negative correlation with FSS from baseline scan (15 negative, 10 positive, 7 no significance); c) negative correlation with plaque stress from follow-up scan (26 out of 32); d) positive correlation with plaque stress from baseline scan (18 out of 32).

Case #	# of Data Pts	PWS Baseline		PWS Follow-Up		FSS Baseline		FSS Follow-Up
		r	p	r	p	r	p	r	p
C1	400	−0.060	0.232	−0.301	<0.001	0.057	0.258	0.113	0.024
C2	400	0.192	<0.001	−0.209	<0.001	−0.107	0.033	0.094	0.061
C3	900	0.019	0.564	−0.440	<0.001	0.330	<0.001	0.464	<0.001
C4	400	0.467	<0.001	−0.079	0.116	−0.587	<0.001	−0.204	<0.001
C5	800	0.270	<0.001	−0.108	0.002	0.196	<0.001	0.468	<0.001
C6	800	−0.039	0.274	−0.279	<0.001	−0.404	<0.001	0.149	<0.001
C7	800	0.133	<0.001	−0.179	<0.001	0.124	<0.001	0.145	<0.001
C8	800	0.267	<0.001	−0.133	<0.001	−0.074	0.038	0.249	<0.001
C9	600	0.457	<0.001	0.208	<0.001	−0.223	<0.001	−0.259	<0.001
C10	600	−0.297	<0.001	−0.622	<0.001	0.359	<0.001	0.291	<0.001
C11	700	−0.048	0.208	−0.325	<0.001	−0.090	0.017	−0.154	<0.001
C12	700	−0.024	0.530	−0.228	<0.001	0.073	0.052	0.130	0.001
C13	600	−0.119	0.004	−0.229	<0.001	−0.054	0.188	0.061	0.134
C14	1000	−0.098	0.002	−0.341	<0.001	0.170	<0.001	0.307	<0.001
C15	1000	0.235	<0.001	−0.101	0.001	0.152	<0.001	0.399	<0.001
C16	900	−0.037	0.269	−0.302	<0.001	−0.172	<0.001	−0.108	0.001
C17	800	−0.125	<0.001	−0.386	<0.001	0.061	0.086	0.338	<0.001
C18	800	0.030	0.397	−0.368	<0.001	0.080	0.024	0.199	<0.001
C19	800	−0.017	0.632	−0.228	<0.001	−0.070	0.047	0.261	<0.001
C20	800	0.492	<0.001	0.253	<0.001	−0.576	<0.001	−0.455	<0.001
C21	900	0.097	0.004	−0.080	0.016	0.130	<0.001	0.122	<0.001
C22	900	−0.135	<0.001	−0.241	<0.001	−0.035	0.301	0.081	0.016
C23	700	0.408	<0.001	−0.144	<0.001	−0.234	<0.001	0.325	<0.001
C24	800	0.242	<0.001	−0.402	<0.001	−0.022	0.539	0.163	<0.001
C25	800	0.227	<0.001	−0.374	<0.001	−0.153	<0.001	0.236	<0.001
C26	700	0.107	0.005	−0.221	<0.001	0.056	0.139	0.162	<0.001
C27	700	0.024	0.531	−0.416	<0.001	−0.412	<0.001	−0.062	0.102
C28	900	0.470	<0.001	−0.011	0.741	−0.414	<0.001	−0.245	<0.001
C29	900	0.080	0.017	0.013	0.694	0.188	<0.001	0.144	<0.001
C30	800	0.110	0.002	−0.052	0.140	0.339	<0.001	0.385	<0.001
C31	800	0.127	<0.001	−0.149	<0.001	−0.423	<0.001	−0.361	<0.001
C32	800	0.119	0.001	−0.158	<0.001	−0.527	<0.001	−0.246	<0.001
Positive		18		2		10		21
Negative		5		26		15		8
No Signifi.		9		4		7		3
95% CI		(0.039, 0.184)		(−0.273, −0.142)		(−0.167, 0.025)		(0.012, 0.187)

Table 2 provides mean WT, WTI and FSS values for each case as background information. We emphasize that all data were taken corresponding to peak systolic pressure and “mean values” were average values over all geometrical data points. Since WTI and FSS changes from different nodes may cancel out and lead to small net change, mean absolute values of WTI and difference between FSS(T2) and FSS(T1) were also provided. It is clear that the relative changes of both WT and FSS were not always small. Relative WT changes could be around 20%. And FSS values from T1 to T2 also demonstrated noticeable changes (as high as 50%).

Table 2.

Average plaque wall thickness (unit: mm) and flow shear stress (unit: dyn/cm²) changes for the 32 pairs studies. The follow-up scan of the scan pairs were used for WT.

Case #	# of Data Pts	Mean Wall Thickness Data(mm)				Mean FSS Data(dyn/cm2)
		WT T1	WT T2	WTI	|WTI|	FSS T1	FSS T2	FSS Change	|FSS| Change
C1	400	1.546	1.597	0.051	0.311	38.604	69.287	30.683	30.840
C2	400	1.649	1.637	−0.013	0.188	84.919	86.859	1.941	21.816
C3	900	1.435	1.712	0.277	0.430	51.687	44.387	−7.300	14.716
C4	400	1.349	1.377	0.027	0.293	69.396	63.773	−5.622	27.463
C5	800	1.367	1.385	0.018	0.228	66.349	57.249	−9.100	21.541
C6	800	1.069	1.117	0.048	0.176	59.884	56.499	−3.385	18.320
C7	800	1.117	1.040	−0.077	0.162	56.499	58.419	1.920	10.081
C8	800	1.040	1.057	0.016	0.174	58.419	52.316	−6.103	14.543
C9	600	2.186	2.072	−0.115	0.441	20.289	21.302	1.013	8.967
C10	600	2.072	2.157	0.085	0.374	21.302	21.040	−0.262	9.029
C11	700	1.796	1.761	−0.035	0.400	58.893	71.442	12.550	26.692
C12	700	1.761	1.745	−0.016	0.171	71.442	53.985	−17.457	26.337
C13	600	1.765	1.865	0.100	0.310	62.226	50.084	−12.142	20.922
C14	1000	1.480	1.574	0.094	0.309	28.834	30.532	1.698	9.136
C15	1000	1.574	1.639	0.066	0.348	30.532	29.739	−0.793	11.448
C16	900	1.899	1.817	−0.082	0.380	37.751	42.580	4.830	13.424
C17	800	1.848	2.089	0.241	0.391	43.536	30.057	−13.479	17.951
C18	800	1.723	1.676	−0.046	0.296	20.241	20.020	−0.221	3.949
C19	800	1.676	1.923	0.247	0.343	20.020	18.631	−1.389	5.244
C20	800	1.571	1.397	−0.174	0.223	61.779	46.911	−14.868	20.760
C21	900	1.445	1.500	0.055	0.371	57.319	50.672	−6.647	15.595
C22	900	1.500	1.749	0.249	0.398	50.672	42.038	−8.634	16.357
C23	700	1.536	2.102	0.566	0.664	25.430	30.521	5.091	12.215
C24	800	2.070	1.723	−0.347	0.500	33.588	28.574	−5.014	13.333
C25	800	1.723	1.986	0.263	0.413	28.574	31.007	2.433	13.683
C26	700	1.260	1.461	0.201	0.304	58.000	53.272	−4.729	15.969
C27	700	1.461	1.723	0.263	0.351	53.272	49.751	−3.520	22.779
C28	900	1.725	1.840	0.115	0.246	46.480	37.761	−8.719	15.219
C29	900	1.840	1.948	0.108	0.315	37.761	37.265	−0.496	18.690
C30	800	2.347	2.697	0.350	0.537	67.093	64.090	−3.003	22.032
C31	800	2.697	2.906	0.209	0.479	64.090	80.306	16.216	23.250
C32	800	2.906	3.054	0.148	0.586	80.306	73.237	−7.069	35.337

3.2 Correlation Analysis between WTI and FSS/ PWS Using Time 1 Data

The correlations between WTI and FSS/PWS using Time 1 data were reversed and weaker when compared to results using Time 2 data. Positive, negative and no significance cases between WTI and FSS were 10, 15, and 7 out of 32, respectively. The 95% PC confidence interval was (−0.167, 0.025). Positive, negative and no significance cases between WTI and PWS were 18, 5, and 9 out of 32. The 95% PC confidence interval was (0.039, 0.184).

3.3 Increased Plaque Progression Occurred in the Posterior Quadrants of the ICA, Corresponding to Disturbed Flow Region

Table 3 shows location-specific vessel wall thickness and WTI using the (Slice, Quadrant) location system, averaged for the 32 cases. Averaged WTI over the 32 pairs for Q3 (posterior) was 0.216 mm, which was 390%, 176%, and 484% higher than WTI for Q1 (anterior), Q2, and Q4, respectively. Slice-averaged WTI was 0.231 mm at ICA-S4, highest among all slices. These results indicated that increased plaque progression occurred in disturbed flow regions, i.e., distal to the carotid bifurcation, and in the posterior quadrant. Average FSS values from the 4 quadrants showed little difference. Vessel wall thickness data were provided as baseline information. Table 4 gave Q1-Q4 WT and WTI information for each pair analyzed. Table 5 gives the averaged density information of necrotic core, calcification and loose matrix for the 47 plaques using the (Slice, Quadrant) system.

Table 3.

Average vessel wall thickness (unit: mm), wall thickness increase and flow shear stress (unit: dyn/cm²) of the 32 pairs by quadrants and slices: location-specific data. The follow-up scan of the scan pairs were used for WT and FSS.

Slice Location	# of cases	Q1			Q2			Q3			Q4			Slice Average
		WT	WTI	FSS	WT	WTI	FSS	WT	WTI	FSS	WT	WTI	FSS	WT	WTI	FSS
ICA S5	5	3.00	.040	106.28	2.15	.135	123.40	1.95	.161	80.79	2.42	−.182	84.94	2.38	.038	98.85
ICA S4	16	1.89	.139	64.28	1.78	.261	67.15	2.59	.381	80.12	2.36	.142	72.65	2.16	.231	71.05
ICA S3	26	1.43	.012	59.32	1.43	.098	60.97	2.24	.229	60.59	2.08	.056	53.91	1.79	.099	58.70
ICA S2	30	1.49	.066	51.63	1.54	.108	48.19	2.34	.239	53.07	2.02	.056	48.00	1.85	.117	50.22
ICA S1	32	1.39	.055	48.75	1.69	.098	44.89	2.44	.218	50.28	1.94	.032	48.59	1.86	.101	48.13
CCA S0	32	1.46	.049	52.12	1.70	−.006	39.95	2.48	.182	34.94	1.86	−.021	35.19	1.87	.051	40.55
CCA S1	31	1.41	.037	41.05	1.72	.040	38.36	2.66	.236	34.96	1.96	.046	39.34	1.94	.090	38.43
CCA S2	30	1.30	−.003	40.01	1.56	.101	41.44	2.36	.285	36.65	1.84	.048	42.07	1.76	.108	40.04
CCA S3	21	1.19	.007	34.69	1.32	−.008	32.42	1.65	.129	24.22	1.38	.029	24.70	1.39	.039	29.01
CCA S4	15	1.17	.075	32.23	1.25	.078	33.28	1.40	.092	24.18	1.29	.059	27.92	1.28	.076	29.40
CCA S5	5	1.16	.052	44.41	1.49	.037	27.31	1.63	−.031	9.77	1.24	−.050	27.51	1.38	.002	27.25
Q-Ave	243	1.44	.044	48.50	1.58	.078	46.03	2.28	.216	43.97	1.88	.037	43.89	1.79	.094	45.60

Table 4.

Quadrant-average vessel wall thickness (unit: mm) and wall thickness increase for the 32 pairs: case-by-case morphological data. The follow-up scan of each pair was used for WT.

Cases	# of Slices	Q1		Q2		Q3		Q4		Case Average
		WT	WTI	WT	WTI	WT	WTI	WT	WTI	WT	WTI
C1	4	1.172	−0.042	1.377	−0.231	2.480	0.369	1.361	0.109	1.597	0.051
C2	4	1.109	0.080	1.431	−0.088	2.367	−0.147	1.639	0.105	1.637	−0.013
C3	9	1.149	0.064	1.609	0.330	2.581	0.709	1.508	0.003	1.712	0.277
C4	4	1.043	0.124	1.578	0.289	1.696	−0.320	1.189	0.016	1.377	0.027
C5	8	1.061	−0.096	1.246	0.087	1.652	0.068	1.582	0.015	1.385	0.018
C6	8	1.042	0.006	1.065	0.105	1.306	0.046	1.056	0.035	1.117	0.048
C7	8	0.921	−0.120	1.091	0.029	1.256	−0.052	0.893	−0.164	1.040	−0.077
C8	8	0.931	0.004	0.994	−0.131	1.293	0.069	1.008	0.124	1.057	0.016
C9	6	2.226	0.073	1.748	−0.182	2.018	−0.424	2.294	0.075	2.072	−0.115
C10	6	2.285	0.017	1.697	−0.077	2.311	0.363	2.335	0.039	2.157	0.085
C11	7	1.032	−0.233	1.398	−0.069	2.661	0.450	1.955	−0.286	1.761	−0.035
C12	7	1.057	−0.018	1.313	0.046	2.639	0.044	1.971	−0.137	1.745	−0.016
C13	6	1.118	−0.024	1.300	0.132	2.929	0.418	2.114	−0.125	1.865	0.100
C14	10	1.366	−0.003	1.656	0.287	1.887	0.185	1.385	−0.094	1.574	0.094
C15	10	1.545	0.156	1.607	−0.112	1.789	−0.049	1.617	0.269	1.639	0.066
C16	9	1.273	−0.182	1.544	−0.297	2.409	0.003	2.042	0.148	1.817	−0.082
C17	8	1.476	0.230	1.758	−0.030	3.031	0.537	2.093	0.228	2.089	0.241
C18	8	1.419	−0.050	1.552	−0.119	1.762	−0.117	1.972	0.100	1.676	−0.046
C19	8	1.555	0.127	1.665	0.116	2.233	0.549	2.241	0.196	1.923	0.247
C20	8	0.985	−0.097	1.212	−0.291	1.913	−0.274	1.478	−0.035	1.397	−0.174
C21	9	1.077	0.073	1.457	0.359	2.182	0.224	1.284	−0.438	1.500	0.055
C22	9	1.015	−0.056	1.458	0.006	2.934	0.771	1.587	0.274	1.749	0.249
C23	7	1.658	0.455	2.095	0.451	2.927	0.789	1.727	0.570	2.102	0.566
C24	8	1.085	−0.546	1.713	−0.305	2.749	−0.115	1.346	−0.421	1.723	−0.347
C25	8	1.457	0.370	1.944	0.164	2.970	0.264	1.574	0.255	1.986	0.263
C26	7	1.320	0.275	1.121	0.101	1.758	0.344	1.644	0.084	1.461	0.201
C27	7	1.547	0.169	1.450	0.329	2.050	0.372	1.845	0.181	1.723	0.263
C28	9	1.684	0.244	1.429	0.107	1.811	0.136	2.436	−0.026	1.840	0.115
C29	9	1.639	−0.009	1.903	0.482	1.973	0.083	2.276	−0.124	1.948	0.108
C30	8	2.386	0.320	2.232	0.332	2.940	0.557	3.231	0.191	2.697	0.350
C31	8	2.592	0.095	2.252	0.106	3.104	0.289	3.675	0.344	2.906	0.209
C32	8	2.642	0.047	2.539	0.348	3.582	0.446	3.451	−0.249	3.054	0.148
Q-Ave	243	1.438	0.044	1.584	0.078	2.280	0.216	1.878	0.037	1.795	0.094

Table 5.

Distribution of plaque component density by slices and quadrants averaged using the 47 plaque samples.

Slice	# of Slices	Necrotic Core				Ca				Loose Matrix
		Q1	Q2	Q3	Q4	Q1	Q2	Q3	Q4	Q1	Q2	Q3	Q4
ICA S5	8	0.485	0.170	0.095	0.455	0.015	0.135	0.000	0.000	0.000	0.000	0.000	0.000
ICA S4	24	0.213	0.118	0.388	0.280	0.037	0.162	0.148	0.042	0.000	0.000	0.005	0.042
ICA S3	39	0.116	0.096	0.328	0.284	0.042	0.068	0.055	0.042	0.030	0.016	0.062	0.077
ICA S2	45	0.080	0.108	0.229	0.215	0.064	0.087	0.120	0.116	0.032	0.038	0.078	0.048
ICA S1	47	0.069	0.135	0.304	0.246	0.000	0.101	0.138	0.034	0.011	0.059	0.073	0.028
CCA S0	47	0.012	0.120	0.287	0.178	0.000	0.104	0.128	0.113	0.007	0.007	0.026	0.011
CCA S1	46	0.011	0.126	0.240	0.133	0.001	0.097	0.194	0.143	0.033	0.018	0.059	0.013
CCA S2	44	0.016	0.069	0.223	0.113	0.000	0.043	0.108	0.109	0.018	0.028	0.056	0.046
CCA S3	31	0.000	0.000	0.040	0.053	0.000	0.030	0.059	0.000	0.000	0.003	0.008	0.008
CCA S4	23	0.000	0.010	0.044	0.019	0.000	0.009	0.021	0.014	0.000	0.016	0.016	0.000
CCA S5	9	0.000	0.022	0.036	0.044	0.000	0.000	0.000	0.000	0.000	0.031	0.062	0.000
Average		0.061	0.094	0.232	0.177	0.015	0.079	0.109	0.073	0.016	0.023	0.047	0.030

3.4 Lipid Rich Necrotic Core Regions Were Associated with Higher Flow Shear Stress Values

Mean FSS values for each component type (lipid, calcification, and loose matrix) were obtained for the 47 plaques and compared with the mean values of normal vessel nodes to assess statistically significant differences. Results are summarized in Table 6. Mean FSS values from lipid nodes were statistically significantly higher than those from normal nodes for 30 out of 39 plaques with lipid core inclusions. The mean FSS value of lipid core nodes (n=5294) from all 47 plaques was 63.5 dyn/cm², which was 45% higher than that from all normal vessel nodes (n=27553, p<0.00001). Mean FSS values from all loose matrix nodes (n=1047) was 49.3 dyn/cm², about 12.8% higher than that of the normal nodes. Mean FSS values from all Ca nodes (n=2506) was 45.2 dyn/cm² only 3.4% higher than the normal nodes value.

Table 6.

Mean flow shear stress (FSS) values of lipid core, calcification, loose matrix and normal wall nodes for the 47 plaques studied. P-values are for comparison between the component nodes and normal nodes. n= number of nodes. Unit: dyn/cm².

Case	Total Pts	Lipid			Ca			Loose Matrix			Normal		NWI
		FSS	n	p	FSS	n	p	FSS	n	p	FSS	n
P1	900	54.5	74	.000	35.3	58	.000	0.0	0	.000	70.0	768	0.63
P2	400	74.1	46	.382	66.0	64	.475	0.0	0	.000	69.3	290	0.66
P3	400	80.9	55	.578	0.0	0	.000	101.4	23	.056	84.4	322	0.76
P4	900	86.6	109	.000	21.7	19	.003	81.4	18	.000	46.7	754	0.73
P5	900	53.7	81	.027	0.0	0	.000	0.0	0	.000	43.5	819	0.84
P6	400	96.9	35	.000	0.0	0	.000	97.2	7	.001	66.2	358	0.63
P7	400	65.7	9	.828	0.0	0	.000	0.0	0	.000	63.7	391	0.64
P8	800	102.2	9	.000	92.3	48	.000	82.3	60	.000	62.7	683	0.69
P9	900	121.3	35	.000	102.9	73	.000	39.1	28	.173	47.6	764	0.71
P10	800	0.0	0	.000	77.1	25	.001	55.2	50	.230	59.6	725	0.58
P11	800	0.0	0	.000	58.8	46	.314	70.4	57	.000	55.2	697	0.68
P12	800	0.0	0	.000	73.0	37	.000	101.4	18	.000	56.7	745	0.66
P13	800	0.0	0	.000	89.3	27	.000	118.1	18	.000	49.4	755	0.70
P14	600	48.0	175	.000	53.0	10	.000	6.2	16	.242	7.9	399	0.82
P15	600	40.5	87	.000	48.0	10	.000	14.1	28	.125	17.6	475	0.75
P16	600	45.4	60	.000	56.7	18	.000	18.4	108	.389	16.7	414	0.83
P17	700	91.3	139	.000	31.7	41	.001	0.0	0	.000	52.4	520	0.78
P18	700	91.8	156	.000	31.3	55	.000	0.0	0	.000	69.5	489	0.77
P19	800	77.5	135	.000	32.1	59	.003	0.0	0	.000	48.0	606	0.79
P20	600	55.1	106	.052	11.4	15	.000	88.4	21	.000	48.4	458	0.79
P21	1000	72.7	64	.000	0.0	0	.000	0.0	0	.000	25.8	936	0.72
P22	1000	95.2	47	.000	24.4	14	.691	0.0	0	.000	27.4	939	0.75
P23	1000	99.5	24	.000	118.8	15	.000	0.0	0	.000	26.6	961	0.82
P24	900	65.3	22	.000	40.5	137	.079	0.0	0	.000	36.4	741	0.73
P25	900	55.2	45	.000	45.9	209	.016	23.1	20	.001	41.2	626	0.70
P26	800	48.1	18	.000	34.3	163	.000	0.0	0	.000	28.4	619	0.74
P27	800	29.9	117	.000	28.8	146	.000	11.7	41	.000	16.1	496	0.69
P28	800	25.8	307	.000	26.2	102	.000	0.0	0	.000	13.9	391	0.71
P29	800	23.0	344	.000	24.0	134	.000	14.0	13	.225	11.7	309	0.80
P30	800	112.7	170	.000	0.0	0	.000	0.0	0	.000	48.0	630	0.86
P31	900	80.0	142	.000	68.5	25	.018	58.7	12	.522	52.4	721	0.86
P32	900	61.7	172	.000	88.0	27	.000	0.0	0	.000	46.5	701	0.84
P33	900	56.1	203	.000	60.4	15	.000	0.0	0	.000	37.4	682	0.92
P34	700	0.0	0	.000	29.9	80	.001	0.0	0	.000	24.8	620	0.70
P35	800	0.0	0	.000	28.4	170	.000	0.0	0	.000	35.0	630	0.71
P36	800	0.0	0	.000	25.6	133	.017	0.0	0	.000	29.2	667	0.70
P37	800	0.0	0	.000	32.8	163	.017	0.0	0	.000	30.6	637	0.74
P38	700	54.1	22	.329	26.3	37	.000	0.0	0	.000	60.0	641	0.55
P39	700	46.7	149	.000	53.7	33	.581	20.3	19	.000	56.4	499	0.63
P40	700	83.5	58	.000	21.3	33	.000	26.0	5	.055	48.3	604	0.74
P41	900	88.0	100	.000	0.0	0	.000	24.3	44	.000	42.3	756	0.76
P42	900	45.6	93	.000	21.1	11	.038	55.2	66	.000	35.4	730	0.77
P43	900	48.5	117	.000	0.0	0	.000	0.0	0	.000	35.6	783	0.78
P44	800	63.1	423	.000	55.2	72	.001	44.9	50	.000	81.5	255	0.91
P45	800	65.3	365	.164	106.1	68	.000	46.2	111	.005	58.9	256	0.94
P46	800	78.3	434	.000	101.4	45	.004	54.4	214	.000	131.4	107	0.96
P47	800	71.7	547	.001	65.1	69	.003	0.0	0	.000	80.8	184	0.94
Total	36400	63.5	5294	.000	45.2	2506	.028	49.3	1047	.000	43.7	27553	0.75

4. Discussion

4.1 Correlation and Causality between Wall Thickness Increase and Flow Shear Stress (FSS)

The results from 32 pairs indicate a positive correlation between WTI and FSS using follow-up FSS values. While we believe this is the first time positive correlation between WTI and FSS using multi-patient in vivo MRI plaque progression data and 3D FSI models, the results do not in actuality contradict the current low and oscillating blood flow shear stresses (LFSS) hypothesis for the following reasons: a) the results were from advanced plaques with an averaged 75% stenosis severity by area, while the LFSS hypothesis was for plaque intimal thickening, initiation and early progression; b) the positive correlation between WTI and FSS came from the fact that FSS values at the follow-up scan was used. Using FSS values from the baseline scan created weaker results (positive/negative/no significance ratio was 10/15/7). The number of negative correlation cases (15) was only slightly higher than that of positive correlation cases (10).

It is important to point out that the correlation results do not lead to any causality conclusions. Indeed, it is not clear if the higher FSS was caused by plaque progression which is linked to lumen narrowing or if the higher FSS promoted plaque progression. Different study models need to be designed to investigate causality relations.

4.2. Correlation between Wall Thickness Increase and Plaque Wall Stress: Model Limitations and Justification

Twenty-six cases showed a negative correlation between WTI and PWS, a value stronger than that found from the FSS results. Atherosclerotic plaques grow in all three dimensions. Flow shear stress has an important influence on lumen surface. At the same time, structural forces have influence on the entire plaque, including plaque internal growth. From a mechanical point of view, both fluid and structural forces should be considered as possible mechanisms governing plaque progression.

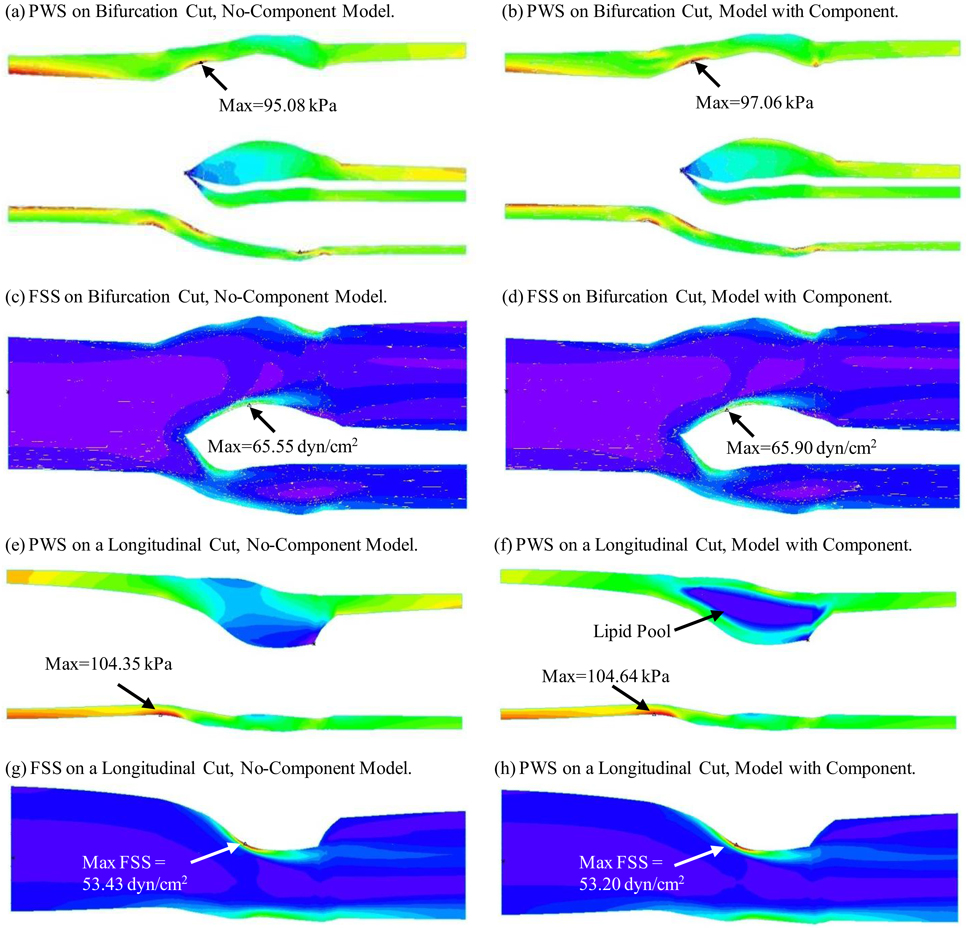
Although the use of a no-component model reduced the model construction effort, it still required two years to build 47 plaque models). The no-component modeling approach needs to be validated and errors need to be assessed. Figure 4 compares FSS and PWS distributions obtained from both the no-component model and the model with components using one cut-surface showing bifurcation and another longitudinal cut-surface showing the lipid core. FSS distributions from both models were almost identical on the two cut-surfaces. The result was not unexpected because the no-component modeling simplification did not change the fluid domain and its effect on the overall plaque deformation and therefore FSS results were minimal (error < 0.5%). PWS distributions from both models did not show much difference on the bifurcation cut surface because that region contained no components. However, a noticeable difference of PWS distributions was found on the longitudinal cut which contained a lipid pool. It is clear that errors introduced by the no-component approach depend heavily on the number of components, component size, and the total “thin-cap” lumen area, the factors most relevant to our calculations. The error for FSS over the 600 data points measured by the L₂-norm was less than 3%. The error for PWS was 15%. Therefore the no-component model provides reasonable FSS predictions, while results based on PWS predictions should be taken with caution. We are currently automating our model construction process and multi-component models will be made to improve accuracy of our predictions.

Figure 4.

Comparison of PWS and FSS distributions on a bifurcation cut surface and a longitudinal cut surface from No-Component Model and model with components showing good agreement for FSS and reasonable agreement for PWS.

Other model limitations include: a) the use of an isotropic material model for the vessel because patient-specific anisotropic material properties were not available in vivo (Holzapfel et al., 2002); b) flow was assumed laminar because the average stenosis severity (by diameter) of the 47 plaques was 50% as given in Table 4 (Ku et al., 1997); and c) arm systole and diastole pressures taken at past scan visit were used to scale the pressure profile used in the simulations since pressure conditions right at the location of the plaque were not available.

4.3 Weak Correlation between FSS and WTI for Advanced Plaques and the Need for Localized Analysis

Although this study reports a clear positive correlation between plaque progression and flow shear stress using follow-up scan, the overall correlation was rather weak. This suggests that more detailed data analysis may be needed to discover localized plaque progression and mechanical stress (FSS and PWS) behaviors that the overall correlation analysis could not reveal. Plaque progression is a multi-faceted process. Other than mechanical factors, plaque tissue type, component size and location, cell activities, blood conditions such as cholesterol level, diabetes, changes caused by medication, and other chemical conditions, inflammation and lumen surface condition may all have impact on plaque progression. Mechanical forces acting on various cells may have considerable effect on plaque progression. Investigations and findings from all the areas, modalities and disciplines should be integrated together to obtain a more thorough understanding of the complicated atherosclerotic progression process.