Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2011 Sep 17.
Published in final edited form as: J Biomech. 2010 Jun 15;43(13):2460–2466. doi: 10.1016/j.jbiomech.2010.05.032

Type and orientation of yielded trabeculae during overloading of trabecular bone along orthogonal directions

Xiutao Shi a, X Sherry Liu b, Xiang Wang, X Edward Guo b, Glen L Niebur a,*
PMCID: PMC2937097  NIHMSID: NIHMS212541  PMID: 20554282

Abstract

Trabecular architecture plays a major role in bone mechanics. Osteoporosis leads to a transition from a plate-like to a more rod-like trabecular morphology, which may contribute to fracture risk beyond that predicted by changes in density. In this study, microstructural finite element analysis results were analyzed using Individual Trabeculae Segmentation (ITS) to identify the type and orientation of trabeculae where tissue yielded during compressive overloads in two orthogonal directions. For both apparent loading conditions, most of the yielded tissue was found in longitudinally oriented plates. However, the primary loading mode of yielded trabeculae was axial compression with superposed bending for on-axis loading in contrast to bending for transverse loading. For either loading direction, most plate-like trabeculae yielded in the same loading mode, regardless of their orientation. In contrast, rods oriented parallel to the loading axis yielded in compression, while rods oblique or perpendicular to the loading axis yielded in combined bending and tension. The predominance of tissue yielding in plates during both on-axis and transverse overloading explains why on-axis overloading is detrimental to the off-axis mechanical properties. At the same time, a large fraction of the tissue in rod-like trabeculae parallel to the loading direction yielded in both on-axis and transverse loading. Hence, rods may be more likely to be damaged and potentially resorbed by damage mediated remodeling.

Keywords: trabecular bone, trabecular type, trabecular orientation, failed trabeculae, transverse overloading

Introduction

Trabecular tissue loss in osteoporotic and aging patients is accompanied by topological changes in microstructure, including the conversion of trabecular plates to rods (Wehrli, 2007). Such changes negatively affect the elastic, yield, and damage behaviors, as trabecular plates play more crucial roles than rods in apparent modulus, apparent yield strength, and microdamage formation (Fang et al., 2010; Liu et al., 2009; Liu et al., 2006). More rod-like morphologies, characterized by an increase in Structure Model Index (SMI), are associated with a decrease in toughness and strength (Garrison et al., 2009) and increased microdamage susceptibility during overloading of bovine tibiae (Wang and Niebur, 2006). SMI is also positively correlated with in vivo microdamage burden in human vertebrae (Arlot et al., 2008). If microdamage stimulates increased remodeling (Burr, 2002) that in turn leads to more rod-like morphologies (Liu et al., 2008; Wehrli, 2007), unstable degradation of the mechanical properties may result.

Trabecular bone is subjected to a variety of loads during activities of daily living, and the orientation of the applied strains with respect to the trabecular orientation plays an important role in trabecular tissue yielding. Thinning of trabeculae and perforation of plates are not uniform in osteoporotic bone, resulting in disproportionate changes in the mechanical properties along the longitudinal and horizontal directions. Trabeculae oriented horizontally tend to be perforated, become thinner, or eventually disappear (Gibson, 2005; Homminga et al., 2004; Kothari et al., 1999; Thomsen et al., 2002), while those oriented longitudinally tend to retain their thickness (Homminga et al., 2004; Thomsen et al., 2002). Such structures are more susceptible to buckling under normal axial compressive loads and damage from unusual or off-axis loading (McDonnell et al., 2007). Computational models have been used to successfully study apparent level yielding (Bevill et al., 2006; Niebur et al., 2000) and tissue level yielding (Kosmopoulos et al., 2008; Nagaraja et al., 2005; Niebur et al., 2002; Shi et al., 2009; Verhulp et al., 2008) in trabecular bone. In bovine trabecular bone, computational simulations indicate less tissue level yielding for transverse loading than on-axis loading (Niebur et al., 2002; Shi et al., 2009). These results are consistent with experiments where an on-axis overload caused a 35% reduction in the elastic modulus of human vertebral trabecular bone along the transverse direction, while transverse overloading caused only a statistically insignificant 10% decrease in the on-axis properties (Badiei et al., 2007).

Understanding the effects of trabecular architecture on the mechanics of trabecular bone under various loading conditions should provide insight into bone quality, which will be useful in the development and evaluation of treatments for osteoporosis. The objective of this study was to identify the trabecular morphologies that are susceptible to tissue level yielding in trabecular bone. Specifically, the aims of this study were to: 1) identify the yielded tissue in trabecular bone samples overloaded in on-axis and transverse compression using microstructural Finite Element Analysis (micro-FEA) models; 2) decompose the samples into individual plate and rod elements that contained yielded tissue using Individual Trabeculae Segmentation (ITS) technique (Liu et al., 2008); 3) categorize the failure modes of individual trabeculae according to the predominant stress states; and 4) compare the failure modes between the two apparent loading modes.

Materials and Methods

Ten cylindrical bovine proximal tibial trabecular bone specimens from a previous study (Wang et al., 2005) were analyzed. The orientation of the specimens was controlled using micro-CT imaging to ensure that the principal trabecular orientation was aligned with the axis of the specimens (Wang et al., 2004). The specimens were scanned at 20 μm isotropic resolution in a micro-CT scanner (μCT-80, Scanco Medical AG, Brüttisellen, Switzerland) and the architecture was quantified using the standard software (μCT Evaluation Program V4.3, Scanco Medical AG, Brüttisellen, Switzerland, Table 1). The threshold for evaluation and subsequent finite element modeling was chosen to match the image volume fraction with that measured by Archimedes' Principle.

Table 1.

Structural parameters of the samples (n = 10)

Parametersa Mean S.D. Range
BV/TVb 0.243 0.044 0.190 – 0.320
BMD (g/cm3) 2.312 0.110 2.060 – 2.428
Tb.Th* (mm) 0.184 0.034 0.133 – 0.235
Tb.Sp* (mm) 0.606 0.080 0.467 – 0.700
SMI 0.568 0.391 −0.131 – 1.078
Conn.D. (1/mm3) 5.410 2.674 2.611 – 11.449
DA 1.828 0.195 1.603 – 2.265
Open in a new tab
a

BV/TV = bone volume fraction; BMD = bone mineral density; Tb.Th* = trabecular thickness; Tb.Sp* = trabecular spacing; SMI = structure model index; Conn.D. = connectivity density; and DA = degree of anisotropy.

b

Measured by Archimedes' Principle.

Microstructural finite element models were created for each specimen by directly converting bone voxels into eight-node finite elements (Hollister et al., 1994). Cuboid regions, approximately 5 × 5 × 6 mm3 in size, were taken from the center of the cylindrical specimens, allowing application of boundary conditions for uniform transverse loading. The images were downsampled to 40 μm isotropic resolution by region-averaging in order to reduce computational time while satisfying the requirements for numerical convergence (Bevill et al., 2006; Bevill and Keaveny, 2009; Charras and Guldberg, 2000; Niebur et al., 1999; Verhulp et al., 2008). The trabecular tissue was modeled as a homogenous isotropic material with a specimen-specific back-calculated tissue modulus. Briefly, a single step linear FEA was performed to calculate the ratio of tissue modulus to apparent modulus for each specimen. The specimen-specific tissue modulus was obtained by multiplying this ratio with the experimentally determined apparent modulus for each specimen (van Rietbergen et al., 1995). A bilinear elastic tissue constitutive model with an asymmetric principal strain yield criterion (Niebur et al., 2000) was applied with compressive and tensile tissue yield strains of 0.83% and 0.41%, respectively (Bayraktar et al., 2004). The Poisson's ratio was set to 0.3. Each sample was analyzed twice, with boundary conditions corresponding to 1.2% on-axis compressive strain and 1.2% transverse compressive strain, respectively. Geometric nonlinearity was not included, but the effects would be small for the dense plate-like samples and low apparent strains used in this study (Bevill et al., 2006).

ITS was used to identify individual plates and rods within each sample (Liu et al., 2008), and the amount of bone tissue in each trabecular type – plate or rod – was quantified. Trabeculae were further classified as longitudinal, oblique, or horizontal based on their orientation with respect to the specimen axis, which was aligned with the principal trabecular orientation (Table 2).

Table 2.

Distribution of bone tissue in samples (Mean ± S.D., n = 10)

Category % (by tissue volume) % (by number of each type)
Platea 80.44 ± 10.36
 Longitudinalb 87.59 ± 3.31 72.30 ± 4.97
 Obliqueb 10.08 ± 2.99 19.80 ± 4.24
 Horizontalb 2.33 ± 0.81 7.90 ± 1.15
Roda 19.55 ± 10.35
 Longitudinal 20.35 ± 3.86 7.36 ± 1.91
 Oblique 32.56 ± 3.74 20.24 ± 4.04
 Horizontal 47.09 ± 2.92 72.39 ± 4.48
Open in a new tab
a

Plate vs. rod distribution was calculated by tissue volume only. Means sum to slightly less than 100%, because there was a small amount of tissue that could not be classified as either plates or rods.

b

Longitudinal: 0–30°; Oblique: 30–60°; Horizontal: 60–90° relative to the axis of the specimens, which was aligned with the principal trabecular orientation. Means sum to 100% within rounding error.

The tissue strains were calculated from the models, and regions that exceeded the yield strains were identified. Due to the porous architecture of trabecular bone, bone tissue can yield due to either compressive or tensile strain under apparent compressive loading. As such, tissue that yielded due to exceeding the compressive or tensile strain limit was detected and segmented separately. The distribution of the yielded tissue within trabecular types and orientations, and the fraction of the total tissue within each trabecular type and orientation combination that yielded were calculated.

Failed trabeculae were identified, and the fraction of each type or orientation of trabeculae that failed was quantified. Most trabeculae contained some yielded tissuedue to the irregular mesh boundary introducing artificial stress concentrations (Guldberg et al., 1998). As such, a threshold of 15% of the tissue within a trabecula was used to identify trabeculae that had failed. A parameter study was conducted to determine the effect of using different thresholds, and the results were not sensitive to this parameter when varied over a range from 5% to 20%. The trabeculae were further categorized as having failed in compression, bending, or tension based on the volume ratio of tissue that yielded in tension to compression being less than 1/4, from 1/4 to 3/4, or greater than 3/4.

Statistical analysis was performed with Student's t-test in Microsoft Excel. The Tukey post-hoc test was used to identify groups with significant differences for ANOVA using JMP 7.0 (SAS Institute Inc., Cary, NC).

Results

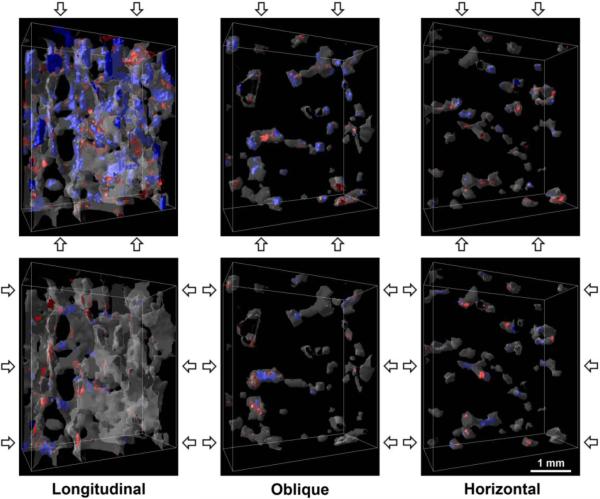
The samples were primarily composed of longitudinally oriented plates. On average, 80 ± 10% (Mean ± S.D.) of the tissue was found in plates, over 70% of which were oriented in the longitudinal direction. In contrast, over 70% of the rods were oriented in the horizontal direction. Longitudinal trabeculae had a greater volume than horizontal trabeculae (Table 2). Visualization software AVS (Advanced Visual Systems Inc., Waltham, MA) was used to verify the rod- and plate-like morphologies of the segmented trabeculae and their orientations (Figs. 1 and 2).

Figure 1.

Figure 1

Open in a new tab

Renderings of the plate and rod trabeculae within a 3.6 × 1.6 × 4.2 mm3 subregion of a representative sample. Blue regions indicate tissue yielded due to compressive strain and red due to tensile strain. The top images are results for on-axis compression to 1.2% apparent strain, and the bottom images for transverse compression, as indicated by the arrows.

Figure 2.

Figure 2

Open in a new tab

Renderings of the longitudinal, oblique, and horizontal trabeculae within a 3.6 × 1.6 × 4.2 mm3 subregion of a representative sample. Blue regions indicate tissue yielded due to compressive strain and red due to tensile strain. The top row of images show the results for on-axis compression to 1.2% apparent strain, and the bottom row for transverse compression, as indicated by the arrows.

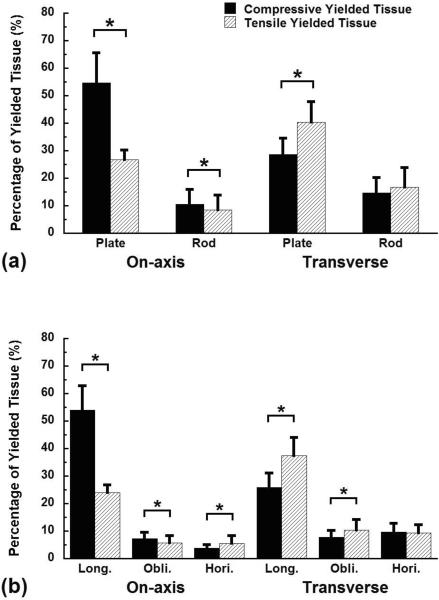
Most of the tissue that yielded was in plates and longitudinally oriented trabeculae for both loading conditions. Plates contained 81 ± 11% of the yielded tissue for on-axis loading, and 69 ± 12% of the yielded tissue was found in plates for transverse loading (Fig. 3a). Similarly, 78 ± 8% of the yielded tissue was found in longitudinal trabeculae for on-axis and 63 ± 10% for transverse loading (Fig. 3b). Combining these data, longitudinally oriented plates were the primary site of yielding, accounting for 73 ± 11% of the total yielded tissue in apparent on-axis compression and 60 ± 12% in apparent transverse compression, respectively.

Figure 3.

Figure 3

Open in a new tab

The distribution of the yielded tissue by trabecular type (a) or orientation (b) for on-axis and transverse compression to 1.2% apparent strain. The columns in each loading mode sum to 100%. Error bars are one standard deviation (n = 10). * indicates p < 0.05.

The apparent loading direction affected whether tissue yielded due to compressive vs. tensile strain. When compressed on-axis, over twice as much tissue yielded due to compressive vs. tensile strain in plates (p < 0.01, Fig. 3a). In contrast, tensile yielding was more common in plates for apparent level transverse compression. Similarly, in rods over 1.3 times as much tissue yielded due to compressive vs. tensile strain for apparent level on-axis compression, while compressive and tensile yielding were equally common for apparent level transverse compression.

When compared by trabecular orientation, the yielding modes differed for the two apparent loading directions. During apparent level on-axis compression, the ratio of tissue that yielded in compression to tension was greater than two in longitudinal trabeculae, but tensile yielding was predominant in horizontal trabeculae (Fig. 3b). In contrast, during transverse compression, tensile yielding dominated in longitudinal trabeculae (p < 0.05), while there was similar amount of tissue yielded in both compression and tension for horizontal trabeculae (p > 0.15).

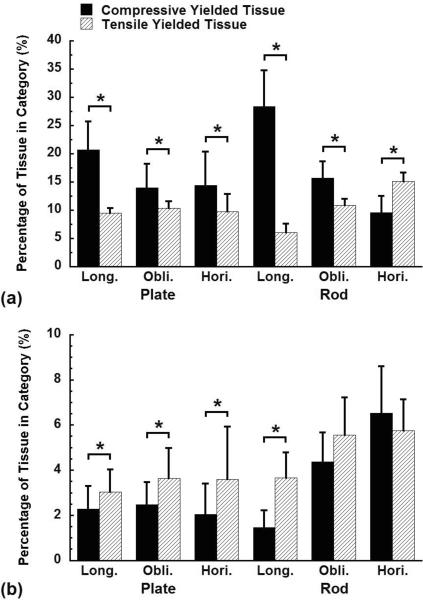
The fraction of tissue that yielded due to compressive vs. tensile strain within each trabecular type depended on apparent loading direction and trabecular orientation. In plates, there was a higher fraction of tissue that yielded due to compressive strain than tensile strain for on-axis loading (Fig. 4a), while tensile yielding dominated for transverse loading (Fig. 4b), regardless of the plate orientation. However, the yielding modes of rods depended on both the loading direction and their orientations. Following on-axis compression, the volume ratio of the yielded tissue that was strained in compression to tension was over four in longitudinal rods, between one and two in oblique rods, and less than one in horizontal rods during on-axis loading (Fig. 4a). This trend was reversed for transverse loading (Fig. 4b).

Figure 4.

Figure 4

Open in a new tab

The fraction of the total tissue within each trabecular type and orientation combination that yielded due to either compressive or tensile strain at 1.2% apparent on-axis (a) or transverse (b) compressive strain. Note the different scales between on-axis and transverse loading. Error bars are one standard deviation (n = 10). * indicates p < 0.05.

In trabeculae oriented parallel to the apparent loading direction, the volume ratio of tissue that yielded due to compressive vs. tensile strain was higher in rods than in plates. During on-axis loading, the ratio was 5.2 ± 2.4 for longitudinal rods, in contrast to 2.2 ± 0.6 for longitudinal plates (p = 0.001, Fig. 4a). During transverse loading, the ratios were 1.2 ± 0.3 for horizontal rods and 0.6 ± 0.3 for horizontal plates, respectively (p = 0.002, Fig. 4b). When considering all yielded tissue, a higher fraction of the total tissue in rods parallel to the loading direction yielded than for similarly oriented plates for both apparent loading modes (p < 0.05).

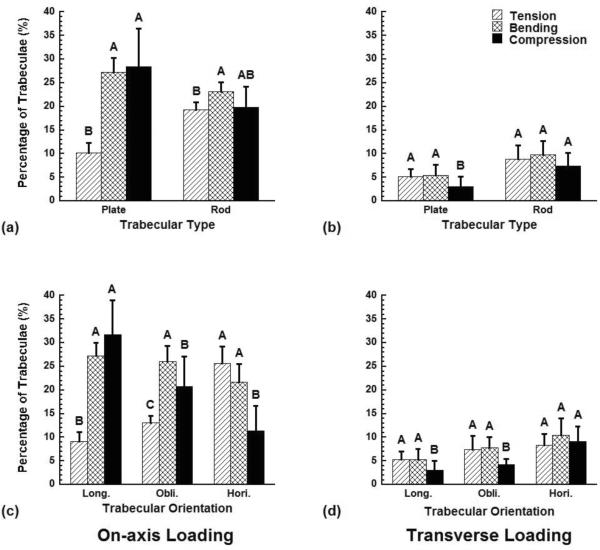
The distribution of the failed trabeculae - those where more than 15% of the tissue yielded - depended on trabecular type and orientation for on-axis loading but not transverse loading (Fig. 5). Following on-axis overloading, the fraction of trabeculae that failed in compression and bending was higher than that in tension in plates and longitudinal trabeculae, while the fraction of trabeculae that failed in bending was the highest in rods and oblique trabeculae (p < 0.05, Fig. 5a, c). The fraction of trabeculae that failed in tension and bending was the highest in horizontal trabeculae (p < 0.05, Fig. 5c). In contrast, during transverse loading, there was no preferred trabecular failure mode, although a slightly smaller fraction of trabeculae failed in compression than in tension or bending for plates, longitudinal and oblique trabeculae (p < 0.05, Fig. 5b, d).

Figure 5.

Figure 5

Open in a new tab

The fraction of the trabeculae within each trabecular type or orientation category that failed in tension, bending, or compression when the samples were compressed to 1.2% on-axis and transverse apparent strain. A trabecula was defined as failed when over 15% of its tissue had yielded. Error bars are one standard deviation (n = 10). Bars marked by the same letter are not significantly different (p < 0.05, ANOVA).

Discussion

Understanding which trabecular microstructures are most susceptible to damage and failure under various loading conditions should provide insight into bone quality and the mechanisms of osteoporosis treatments. Longitudinal plates were the main site of trabecular yielding for both apparent on-axis and transverse compression in dense plate-like architectures, revealing the structural importance of these trabecular elements. However, during on-axis loading, longitudinal plates were axially compressed with superposed bending – as indicated by the predominance of compressive yielding – while during transverse loading, the plates were primarily bent as indicated by more tensile yielding. Bending was the most important failure mode in rods and off-axis trabeculae for both on-axis and transverse loading.

The main strength of this study was the identification of the specific trabecular types and orientations using the ITS technique where yielded tissue was predicted by micro-FEA. The quantity of data and the need to investigate the trends for a population make such methods invaluable for post-processing micro-FEA results. However, there are also important limitations that must be considered when interpreting the results. First, bovine tibial trabecular bone specimens, which are plate-dominated structures, were used in the study, and the results may differ in rod-dominated structures, such as vertebral trabecular bone. Second, the relationships between tissue level yielding and microdamage formation or modulus decreases have not been fully established. As such, further studies of these correlations are needed.

An important limitation of this study is the tissue level constitutive model. This constitutive model results in correct prediction of the apparent level yield behavior (Niebur et al., 2000), and the strain limits in the tissue level constitutive model are consistent with the yield limits measured in cortical bone tissue (Bayraktar et al., 2004; Reilly and Burstein, 1975). While these factors support its validity, there has been no direct correlation of the yielded tissue in the models to either permanent deformation or microdamage in actual samples. There is a correlation between the proportion of the predicted yielded tissue that occurs in longitudinal rods and the measured microcrack density (Shi et al., 2010), but in general tissue level yielding does not correlate with microcrack density. Indeed, while microdamage occurs in regions of higher local stress and strain calculated by linear finite element models (Nagaraja et al., 2005), not all high-stress regions are damaged. As such, the yielded regions do not necessarily represent regions of visible microdamage. Neither permanent deformation nor submicroscopic forms of tissue damage have been quantified and compared to finite element models. As such, the constitutive model is a plausible, but not proven model.

The findings further explain the differences in the morphology of the predicted yielded regions between on-axis and transverse overloading (Shi et al., 2009). Yielded regions are larger and more oriented during on-axis compression, because they occur in plates. In transverse compression, the plates do not have a single yielded region of a single mode, but instead have adjacent tensile and compressive yielded regions. In general, plates provide most of the mechanical support in the trabecular structure, and their yielding modes differ between apparent loading modes but are similar for all trabecular orientations. Recent studies that reached similar conclusions did not explore the yielding modes (Fang et al., 2010; Liu et al., 2009). In contrast, rods of each orientation have different proportions of tensile and compressive yielding. When taking into account the loading orientation, rods parallel and perpendicular to the apparent loading direction always have greater fractions of compressive and tensile yielding, respectively.

The results complement experimental studies of damage and overloading in trabecular bone. The major contribution from longitudinal plates during both on-axis and transverse loading suggests that damage caused by on-axis compression may also affect transverse mechanical properties. This is consistent with the experiments that found on-axis overloading caused a significant decrease in the shear modulus of bovine trabecular bone (Wang et al., 2005), and a 35% reduction in the transverse apparent elastic modulus in human vertebral trabecular bone (Badiei et al., 2007). As such, in vivo microdamage that is associated with normal loading during activities of daily living may be detrimental to the mechanical properties for shear or other abnormal loads (Homminga et al., 2004; Wang and Niebur, 2006).

The results also complement recent work by Bevill et al. (Bevill et al., 2009), which found that human femoral trabecular bone, when loaded off-axis has lower levels of tissue yielding and a higher proportion of tissue that yielded in tension than compression. Our results further confirm the concept of increased bending of the plate-like trabeculae when the apparent level loading is transverse to the principal trabecular orientation.

The results extend our understanding of the relative roles of trabecular plates and rods beyond the elastic range (Liu et al., 2008; Liu et al., 2006) to the yielding stage. Although rods play a role in both on-axis and transverse compressive loading depending on their orientation relative to the loading direction, the greatest volume of yielded tissue occurs in trabecular plates for both loading modes. In osteoporotic and aging trabecular bone, horizontal trabeculae are preferentially thinned and perforated while longitudinal trabeculae maintain their thickness, leading to a more anisotropic structure that has a greater susceptibility to fractures (Homminga et al., 2004; McDonnell et al., 2007; Tanck et al., 2009; Thomsen et al., 2002; van Ruijven et al., 2005). This altered structure has a decreased number of plates along the horizontal direction, and the present results show that rods oriented along the apparent loading axis are more likely to fail than plates. Since yielding in rods is directly correlated to increased microcrack density (Shi et al., 2010), the transition of horizontal trabeculae to a more rod-like morphology in osteoporotic bone may make the whole structure more vulnerable to damage from unusual or off-axis loading.

Supplementary Material

01

Acknowledgments

This study was supported by the National Institutes of Health (AR052008 and AR051376) and by an NSF MRI Grant (DBI-0420980).

Footnotes

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

Conflict of interest statement None of the authors has any financial or personal interests with organizations that may benefit from this work.

References

  1. Arlot ME, Burt-Pichat B, Roux JP, Vashishth D, Bouxsein ML, Delmas PD. Microarchitecture influences microdamage accumulation in human vertebral trabecular bone. Journal of Bone and Mineral Research. 2008;23(10):1613–1618. doi: 10.1359/jbmr.080517. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Badiei A, Bottema MJ, Fazzalari NL. Influence of orthogonal overload on human vertebral trabecular bone mechanical properties. Journal of Bone and Mineral Research. 2007;22(11):1690–1699. doi: 10.1359/jbmr.070706. [DOI] [PubMed] [Google Scholar]
  3. Bayraktar HH, Morgan EF, Niebur GL, Morris GE, Wong EK, Keaveny TM. Comparison of the elastic and yield properties of human femoral trabecular and cortical bone tissue. Journal of Biomechanics. 2004;37(1):27–35. doi: 10.1016/s0021-9290(03)00257-4. [DOI] [PubMed] [Google Scholar]
  4. Bevill G, Eswaran SK, Gupta A, Papadopoulos P, Keaveny TM. Influence of bone volume fraction and architecture on computed large-deformation failure mechanisms in human trabecular bone. Bone. 2006;39(6):1218–1225. doi: 10.1016/j.bone.2006.06.016. [DOI] [PubMed] [Google Scholar]
  5. Bevill G, Farhamand F, Keaveny TM. Heterogeneity of yield strain in low-density versus high-density human trabecular bone. Journal of Biomechanics. 2009;42(13):2165–2170. doi: 10.1016/j.jbiomech.2009.05.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Bevill G, Keaveny TM. Trabecular bone strength predictions using finite element analysis of micro-scale images at limited spatial resolution. Bone. 2009;44(4):579–584. doi: 10.1016/j.bone.2008.11.020. [DOI] [PubMed] [Google Scholar]
  7. Burr DB. Targeted and nontargeted remodeling. Bone. 2002;30(1):2–4. doi: 10.1016/s8756-3282(01)00619-6. [DOI] [PubMed] [Google Scholar]
  8. Charras GT, Guldberg RE. Improving the local solution accuracy of large-scale digital image-based finite element analyses. Journal of Biomechanics. 2000;33(2):255–259. doi: 10.1016/s0021-9290(99)00141-4. [DOI] [PubMed] [Google Scholar]
  9. Fang G, Ji B, Liu XS, Guo XE. Quantification of trabecular bone microdamage using the virtual internal bond model and the individual trabeculae segmentation technique. Computer Methods in Biomechanics and Biomedical Engineering. 2010 doi: 10.1080/10255840903405660. Paper in Press. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Garrison JG, Slaboch CL, Niebur GL. Density and architecture have greater effects on the toughness of trabecular bone than damage. Bone. 2009;44(5):924–929. doi: 10.1016/j.bone.2008.12.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Gibson LJ. Biomechanics of cellular solids. Journal of Biomechanics. 2005;38(3):377–399. doi: 10.1016/j.jbiomech.2004.09.027. [DOI] [PubMed] [Google Scholar]
  12. Guldberg RE, Hollister SJ, Charras GT. The accuracy of digital image-based finite element models. Journal of Biomechanical Engineering. 1998;120(2):289–295. doi: 10.1115/1.2798314. [DOI] [PubMed] [Google Scholar]
  13. Hollister SJ, Brennan JM, Kikuchi N. A homogenization sampling procedure for calculating trabecular bone effective stiffness and tissue level stress. Journal of Biomechanics. 1994;27(4):433–444. doi: 10.1016/0021-9290(94)90019-1. [DOI] [PubMed] [Google Scholar]
  14. Homminga J, Van-Rietbergen B, Lochmuller EM, Weinans H, Eckstein F, Huiskes R. The osteoporotic vertebral structure is well adapted to the loads of daily life, but not to infrequent “Error” Loads. Bone. 2004;34(3):510–516. doi: 10.1016/j.bone.2003.12.001. [DOI] [PubMed] [Google Scholar]
  15. Kosmopoulos V, Schizas C, Keller TS. Modeling the onset and propagation of trabecular bone microdamage during low-cycle fatigue. Journal of Biomechanics. 2008;41(3):515–522. doi: 10.1016/j.jbiomech.2007.10.020. [DOI] [PubMed] [Google Scholar]
  16. Kothari M, Keaveny TM, Lin JC, Newitt DC, Majumdar S. Measurement of intraspecimen variations in vertebral cancellous bone architecture. Bone. 1999;25(2):245–250. doi: 10.1016/s8756-3282(99)00161-1. [DOI] [PubMed] [Google Scholar]
  17. Liu XS, Bevill G, Keaveny TM, Sajda P, Guo XE. Micromechanical analyses of vertebral trabecular bone based on individual trabeculae segmentation of plates and rods. Journal of Biomechanics. 2009;42(3):249–256. doi: 10.1016/j.jbiomech.2008.10.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Liu XS, Huang AH, Zhang XH, Sajda P, Ji B, Guo XE. Dynamic simulation of three dimensional architectural and mechanical alterations in human trabecular bone during menopause. Bone. 2008;43(2):292–301. doi: 10.1016/j.bone.2008.04.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Liu XS, Sajda P, Saha PK, Wehrli FW, Bevill G, Keaveny TM, Guo XE. Complete volumetric decomposition of individual trabecular plates and rods and its morphological correlations with anisotropic elastic moduli in human trabecular bone. Journal of Bone and Mineral Research. 2008;23(2):223–235. doi: 10.1359/JBMR.071009. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Liu XS, Sajda P, Saha PK, Wehrli FW, Guo XE. Quantification of the roles of trabecular microarchitecture and trabecular type in determining the elastic modulus of human trabecular bone. Journal of Bone and Mineral Research. 2006;21(10):1608–1617. doi: 10.1359/jbmr.060716. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. McDonnell P, McHugh PE, O'Mahoney D. Vertebral osteoporosis and trabecular bone quality. Annals of Biomedical Engineering. 2007;35(2):170–189. doi: 10.1007/s10439-006-9239-9. [DOI] [PubMed] [Google Scholar]
  22. Nagaraja S, Couse TL, Guldberg RE. Trabecular bone microdamage and microstructural stresses under uniaxial compression. Journal of Biomechanics. 2005;38(4):707–716. doi: 10.1016/j.jbiomech.2004.05.013. [DOI] [PubMed] [Google Scholar]
  23. Niebur GL, Feldstein MJ, Keaveny TM. Biaxial failure behavior of bovine tibial trabecular bone. Journal of Biomechanical Engineering. 2002;124(6):699–705. doi: 10.1115/1.1517566. [DOI] [PubMed] [Google Scholar]
  24. Niebur GL, Feldstein MJ, Yuen JC, Chen TJ, Keaveny TM. High-resolution finite element models with tissue strength asymmetry accurately predict failure of trabecular bone. Journal of Biomechanics. 2000;33(12):1575–1583. doi: 10.1016/s0021-9290(00)00149-4. [DOI] [PubMed] [Google Scholar]
  25. Niebur GL, Yuen JC, Hsia AC, Keaveny TM. Convergence behavior of high-resolution finite element models of trabecular bone. Journal of Biomechanical Engineering. 1999;121(6):629–635. doi: 10.1115/1.2800865. [DOI] [PubMed] [Google Scholar]
  26. Reilly DT, Burstein AH. The elastic and ultimate properties of compact bone tissue. Journal of Biomechanics. 1975;8(6):393–405. doi: 10.1016/0021-9290(75)90075-5. [DOI] [PubMed] [Google Scholar]
  27. Shi X, Liu XS, Wang X, Guo XE, Niebur GL. Effects of trabecular type and orientation on microdamage susceptibility in trabecular bone. Bone. 2010;46(5):1260–1266. doi: 10.1016/j.bone.2010.02.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Shi X, Wang X, Niebur GL. Effects of loading orientation on the morphology of the predicted yielded regions in trabecular bone. Annals of Biomedical Engineering. 2009;37(2):354–362. doi: 10.1007/s10439-008-9619-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Tanck E, Bakker AD, Kregting S, Cornelissen B, Klein-Nulend J, Van Rietbergen B. Predictive value of femoral head heterogeneity for fracture risk. Bone. 2009;44(4):590–595. doi: 10.1016/j.bone.2008.12.022. [DOI] [PubMed] [Google Scholar]
  30. Thomsen JS, Ebbesen EN, Mosekilde LI. Age-related differences between thinning of horizontal and vertical trabeculae in human lumbar bone as assessed by a new computerized method. Bone. 2002;31(1):136–142. doi: 10.1016/s8756-3282(02)00801-3. [DOI] [PubMed] [Google Scholar]
  31. van Rietbergen B, Weinans H, Huiskes R, Odgaard A. A new method to determine trabecular bone elastic properties and loading using micromechanical finite-element models. Journal of Biomechanics. 1995;28(1):69–81. doi: 10.1016/0021-9290(95)80008-5. [DOI] [PubMed] [Google Scholar]
  32. van Ruijven LJ, Giesen EB, Mulder L, Farella M, van Eijden TM. The effect of bone loss on rod-like and plate-like trabeculae in the cancellous bone of the mandibular condyle. Bone. 2005;36(6):1078–1085. doi: 10.1016/j.bone.2005.02.018. [DOI] [PubMed] [Google Scholar]
  33. Verhulp E, Van Rietbergen B, Muller R, Huiskes R. Micro-finite element simulation of trabecular-bone post-yield behaviour--effects of material model, element size and type. Computer Methods in Biomechanics and Biomedical Engineering. 2008;11(4):389–395. doi: 10.1080/10255840701848756. [DOI] [PubMed] [Google Scholar]
  34. Wang X, Guyette J, Liu X, Roeder RK, Niebur GL. Axial-shear interaction effects on microdamage in bovine tibial trabecular bone. European Journal of Morphology. 2005;42(1–2):61–70. doi: 10.1080/09243860500095570. [DOI] [PubMed] [Google Scholar]
  35. Wang X, Liu X, Niebur GL. Preparation of on-axis cylindrical trabecular bone specimens using micro-ct imaging. Journal of Biomechanical Engineering. 2004;126(1):122–125. doi: 10.1115/1.1645866. [DOI] [PubMed] [Google Scholar]
  36. Wang X, Niebur GL. Microdamage propagation in trabecular bone due to changes in loading mode. Journal of Biomechanics. 2006;39(5):781–790. doi: 10.1016/j.jbiomech.2005.02.007. [DOI] [PubMed] [Google Scholar]
  37. Wehrli FW. Structural and functional assessment of trabecular and cortical bone by micro magnetic resonance imaging. Journal of Magnetic Resonance Imaging. 2007;25(2):390–409. doi: 10.1002/jmri.20807. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

01
NIHMS212541-supplement-01.doc (849KB, doc)

RESOURCES