Abstract
During the last decade, theory and experiments have provided clear evidence that specific helical patterns of charged groups and adsorbed (condensed) counterions on the DNA surface are responsible for many important features of DNA-DNA interactions in hydrated aggregates. The effects of helical structure on DNA-DNA interactions result from a preferential juxtaposition of the negatively charged sugar phosphate backbone with counterions bound within the grooves of the opposing molecule. Analysis of x-ray diffraction experiments confirmed the mutual alignment of parallel molecules in hydrated aggregates required for such juxtaposition. However, it remained unclear how this alignment and molecular interactions might be affected by intrinsic and thermal fluctuations, which cause structural deviations away from an ideal double helical conformation. We previously argued that the torsional flexibility of DNA allows the molecules to adapt their structure to accommodate a more electrostatically favorable alignment between molecules, partially compensating disruptive fluctuation effects. In the present work, we develop a more comprehensive theory, incorporating also stretching and bending fluctuations of DNA. We found the effects of stretching to be qualitatively and quantitatively similar to those of twisting fluctuations. However, this theory predicts more dramatic and surprising effects of bending. Undulations of DNA in hydrated aggregates strongly amplify rather than weaken the helical structure effects. They enhance the structural adaptation, leading to better alignment of neighboring molecules and pushing the geometry of the DNA backbone closer to that of an ideal helix. These predictions are supported by a quantitative comparison of the calculated and measured osmotic pressures in DNA.
I. Introduction
Direct interactions between DNA double helices are necessary for the packaging of DNA in cells1 and viruses2, ejection of DNA by viruses3,4,5, and in the functioning of novel DNA-based ‘smart’ materials6,7. They could also play an important role in genetic recombination8,9,10,11. Because DNA is highly charged, it was presumed from early on that interactions between DNA double helices should be dominated by electrostatics12,13,14. Forces measured between DNA double helices were indeed found to be consistent with electrostatic interactions predicted for worm-like, homogeneously-charged chains, but not in the last 2 nm of surface-to-surface separation15,16. Because the latter distance range is the one most relevant for biology and the one in which the most interesting phenomena are observed, interpretations of these forces are still hotly debated17,18. In a review of different theories and experiments, we argued that the short-range forces between DNA molecules are of electrostatic origin18.
A rigorous theory of electrostatic DNA-DNA interactions must account not only for the net charge of the molecules but also for the helical patterning of fixed molecular charges, preferential binding and the resultant patterning of counterions, and thermal fluctuations and correlations in these charge patterns18,19. These resulting interactions between DNA molecules may be crudely separated into three components. The net charge of the molecule leads to net-charge repulsion, which may be approximated as an interaction between homogeneously charged cylinders. Discrete patterns of phosphate and counterion charges lead to image-charge repulsion from dielectric cores of neighboring molecules, which is severely underestimated and often omitted in homogeneously-charged cylinder approximations20,21. Correlated alignment of positive and negative charges on opposing surfaces results in an attractive electrostatic force. Many DNA counterions preferentially bind in grooves between the negatively charged phosphate strands22, resulting in an “electrostatic zipper” attraction caused by zipper-like alignment of the negatively charged phosphate strands with positively charged grooves on neighboring molecules23. This attraction is particularly salient in cases of biologically important, polyvalent counterions such as spermine and spermidine that exhibit strong preferential binding in the major groove of DNA18,22.
A theory of interactions between ideal, rigid, DNA-like helices predicted that electrostatic zipper attraction and image-charge repulsion may be important for many observed phenomena. For instance, they may contribute to DNA condensation by counterions18,20,23, the B-to-A transition in dense DNA aggregates24, and the formation of the cholesteric phase in more hydrated aggregates25,26,27,28.
However, real DNA molecules are neither ideal nor rigid helices. They twist, stretch, and bend because of sequence-dependent variations in the geometry of base pair stacking29, and because of thermal motions30,31,32. These intrinsic and thermal fluctuations in the double helix structure may affect DNA-DNA interactions, for instance, by disrupting the energetically favorable zipper alignment. Conversely, the interactions may suppress the fluctuations and induce an adaptation of the molecular structure towards a more favorable alignment. Calculations of twisting fluctuations and torsional adaptation have revealed a complex balance of forces, geometry, and motion, which cannot be neglected33,34,35. In particular, the sequence-dependent intrinsic fluctuations may be responsible for sequence homology recognition between intact, double helical molecules10,36,37.
Full understanding of the balance among DNA structure, flexibility, fluctuations and interactions requires a comprehensive statistical-mechanical theory, in which all of these factors are treated on the same footing. So far, only twisting fluctuations were analyzed in this context34,35. We argued that stretching fluctuations should affect interactions between DNA molecules in the same way as twisting, but this was not rigorously proven18. The effects of bending fluctuations on DNA-DNA interactions were explored in the past by others15,38–42 but only within models in which the helical structure of DNA was neglected and the surface charge density was presumed to be uniform.
In the present study, we develop a theory incorporating all of these fluctuations (intrinsic and thermal), helical patterns of discrete surface charges, and structural adaptation of DNA to intermolecular interactions. We demonstrate that the effects of twisting and stretching fluctuations and adaptation are indeed similar and show how they combine (this had been shown previously in Ref. 43 for intrinsic fluctuations only), confirming our previous estimates18. The effect of undulations turns out to be more dramatic and less intuitive. In particular, thermal undulations of DNA may enhance rather than disrupt the long-range alignment of phosphate strands, pushing the molecules toward a more ideal helical conformation rather than the other way around. Moreover, they may amplify the interactions associated with the helical structure of DNA by up to two orders of magnitude. We also find the predictions of the current theory to be quantitatively consistent with the measured osmotic stress isotherms in DNA aggregates.
Although subtle, the underlying physics of the phenomena we consider here is quite clear. However, the comprehensive statistical mechanics of the interplay between fluctuations, helical structure, and DNA-DNA interactions require fairly cumbersome ‘helical’ algebra and field-theoretical methods. Thus, in the main text we review the basic concepts of the theory (Model and Methods), present its most important predictions (Results), and compare them with experimentally measured osmotic stress isotherms of DNA aggregates (Comparison with experiments), and then interpret and summarize our findings (Discussion). All derivations and auxiliary formulae are described in a supplement available online.
II. Model and Methods
II.1. DNA geometry and mechanics
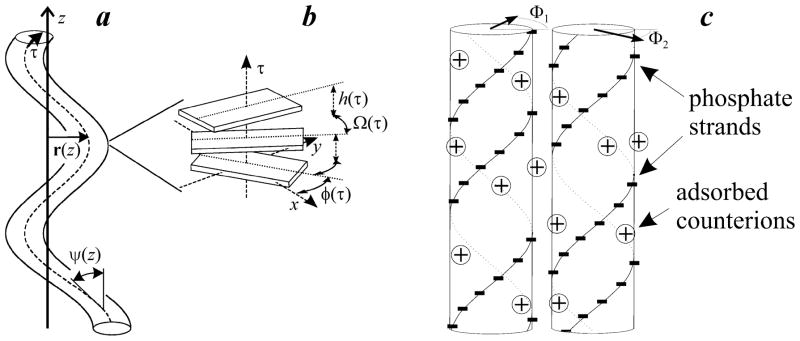
Figure 1 schematically illustrates the definitions for the lateral displacement rμ, axial rise per base pair hμ, and azimuthal orientation of the double helix φμ that are affected by bending, torsional, and stretching fluctuations of each molecule μ in a hexagonal aggregate.
Figure 1.
Schematic illustration of DNA conformation and alignment in an aggregate. (a) Bending fluctuations: r(z) is the displacement of DNA centerline (dashed curve) from its average position selected as the direction of the z-axis, τ (z) is the coordinate along the centerline, ψ (z) is the tilt angle between the centerline and z-axis. (b) Azimuthal orientation φ (τ) of DNA and rise h (τ) and twist Ω (τ) between adjacent base pairs along the centerline. (c) Two DNA molecules in favorable electrostatic juxtaposition with negatively charged phosphate strands on one molecule opposite to positively charged grooves on another.
To describe the elastic energy associated with these fluctuations, we utilize the elastic rod (ER) model44,18
| (1) |
Here τ and <h> are the contour length and average rise per base pair along the DNA centerline, hμ ≡ hμ(τ) and Ωμ ≡ Ωμ(τ) are the actual base pair rise and twist along the centerline, and and are the intrinsic base pair rise and twist at zero stress. The elastic moduli B, Cs, and Ct correspond to bending, stretching and twisting deformations, respectively. Since we are interested in small distortions, we neglect any potential dependence of the elastic moduli on τ. We also assume that the intrinsic curvature of the helix can be neglected compared to thermal fluctuations since the intrinsic bending persistence length32,45 (~ 4000 Å) is much larger than the thermal one (~500 Å). On the other hand, one should note that nucleotide sequences with more than three A-T bases in a row can introduce significant intrinsic curvature46. However, a systematic incorporation of this additional effect would significantly increase the complexity of the analysis with little benefit for facilitating understanding of the underlying physics.
II.2. Helical phase of DNA
The alignment of phosphate strands on opposing molecules μ and ν is described simply by the difference in azimuthal orientations of these molecules φμ(τ) − φν(τ). However, for the purpose of our analysis, it is more convenient to describe each molecule with its helical phase Φμ(τ) defined as43:
| (2) |
where ḡ = 〈Ω〉/〈h〉 is the mean reciprocal pitch of DNA (<Ω> is the average twist between adjoining base pairs). In an ideal, straight helix Ω and h do not depend on τ and Ω = ḡh, so that Φμ(τ) = φμ(0) simply describes the azimuthal orientation of the helix at the selected coordinate origin (τ = 0). In general, Φμ(τ) − φμ(0) defines the deviation of the azimuthal orientation of the molecule at any point τ along its centerline from that of an ideal helix with the same mean reciprocal pitch and the same azimuthal orientation at τ = 0. Mutual alignment of molecules μ and ν may thus be described by the difference in their helical phases,
| (3) |
II.3. Helical coherence
Isolated DNA molecules
The ability of neighboring molecules to retain the alignment of phosphate strands over a long juxtaposition length is determined by fluctuations in their helical phases. Helical phase fluctuations in an isolated DNA molecule over long sequences (τ′−τ ≫ h) may be approximated by simple random walk correlations43,47
| (4) |
where λc is the helical coherence length measured along the centerline of DNA. The helical coherence length defines the length over which the DNA conformation remains close to that of an ideal helix.
Intrinsic helical phase fluctuations are caused by the sequence dependence of both the intrinsic twist angle Ω and axial rise h between adjoining base pairs. From NMR structures of DNA oligonucleotides in solution and x-ray diffraction of hydrated DNA fibers, we estimate the corresponding intrinsic helical coherence length of DNA as43 . Thermal twist and rise fluctuations do not alter the functional form of Eq. (4), but they alter the value of the helical coherence length, as discussed in Results (λc and are related by Eq. (27)). Bending fluctuations (intrinsic or thermal) do not affect λc defined with respect to the curved centerline of the molecule48.
Hexagonal aggregates of DNA
For molecules confined in a hexagonal aggregate, the description of helical phase fluctuations becomes more complex. First, analysis of intermolecular correlations requires all geometric parameters to be defined in a global reference frame. However, provided that displacements rμ of the centerline of each molecule from the straight, mean axis are small, the twist and rise fluctuations, as well as the helical coherence length, in the global reference frame may be approximated by their values along the curved centerline (see online supplement). Hence, hereafter we simply replace the centerline coordinate τ with the z coordinate in the global reference frame (Fig. 1).
Second, if the molecules were infinitely rigid and their structures did not adapt to intermolecular interactions, the maximum juxtaposition length over which they could retain the alignment of the phosphate strands would be ~λc. The helical phases of longer molecules would be completely uncorrelated, resulting in a loss of the attractive contribution to the electrostatic interaction energy, associated with the favorable alignment apposition of negatively charged phosphate strands and positively charged grooves (Fig. 1c). But, because DNA is not infinitely rigid, electrostatic interactions affect the structure and fluctuations of the molecules33,34. The resulting structural adaptation alters the pair correlation function of helical phase fluctuations for each molecule as described in Results.
II.4. Aggregate energy
To calculate how torsional, stretching, and bending fluctuations affect DNA-DNA interactions in a hexagonal aggregate, we approximate the total energy of DNA molecules in the aggregate by49
| (5) |
Here N is the number of molecules in the aggregate; is the elastic rod energy of each molecule μ, given by Eq. (1); is the energy of steric interaction associated with hard-core collisions between molecules μ and ν, described within a model proposed in Refs. 50, 51 (Eqs. (S.1) and (S.2) of the online supplement); and is the electrostatic energy of pair interactions between molecules μ and ν, given by Eqs. (6)–(8) below. The summation of and is performed over all nearest neighbor pairs, assuming that the electrostatic screening length is sufficiently short to prevent significant contributions from interactions between distant pairs. Finally, accounts for the deviation from pair-wise additivity due to nonlinear effects. These effects become important at large interstitial electrostatic potentials in dense aggregates, and are described by Eqs. (14)–(17) below. We select isolated, straight molecules (Rμ−Rν→∞, rμ = 0) as the reference state for the energy (E=0).
Electrostatic pair interaction energy
For small fluctuations and sufficiently slow variations in |rμ − rν| and Φμ − Φν with z, the electrostatic pair interaction energy may be approximated by
| (6) |
where L (≫H) is the length of the helices, kB is Boltzmann’s constant, T is the absolute temperature, and κ−1 is the effective screening length in the aggregate. For an isolated pair of molecules, or at a very large spacing between neighboring molecules in the aggregate, is the Debye screening length. However, with decreasing spacing between neighboring molecules, the effective screening length in the aggregate also decreases (see Eqs. (14) and (15)) 52.
The pair interaction potential u(κ,R,ΔΦ) describes the interaction between two parallel, ideal helices with an interaxial distance R and relative azimuthal orientation ΔΦ. Deviations away from ideal helical geometry affect this interaction energy through the dependence of R and ΔΦ on z. For a more detailed discussion of the limits of this approximation see Ref. 18. One should note that the helical phase, as it appears in Eq. (6), has been defined globally with respect to the z-axis (along the direction of the mean axis of the molecules). The pair interaction potential u(κ,R,ΔΦ)
| (7) |
where δn,m is the Kronecker delta (δn,m=1 at n=m and δn,m=0 at n≠m), is approximated by the sum of the first three helical harmonics (n=0, 1, 2) 53 of direct (un(κ, R)) and image-charge ( ) electrostatic interactions defined below18.
The direct interaction energy – the energy of fixed charges and bound (condensed) counterions on a molecule in the electric field created by its nearest neighbor molecule – is defined by
| (8) |
Here a is the DNA radius, lB is the Bjerrum length (≈ 7 Å at room temperature); 1/lc is the linear density of the fixed charged groups on the molecular surface (lc≈ 1.7 Å for B-DNA); ζn are normalized helical moments of the surface charge density18; Kn(x) is the modified Bessel function of the second kind (sometimes referred to as the Macdonald function); ; and
| (9) |
The image-charge energy – the energy of the water-impermeable dielectric core of a molecule in the electric field created by its nearest neighbor molecule20 – is defined by
| (10) |
where
| (11) |
is the Ω-function introduced in Refs. 20, 23. In(y) and are the modified Bessel functions of the first kind and their derivatives with respect to the argument, respectively.
The helical moments ζn of the surface charge density may be determined from experiments, computer simulations, or theoretical modeling using the recipe discussed in Ref. 18. For the purpose of the present work, however, we use a simpler empirical model that allows us to avoid a priori assumptions about counterion-DNA interactions54. Specifically, we assume that ζn may be approximated with18
| (12) |
where θ, f1, and f2 are empirical parameters; θ is the fraction of the fixed DNA charge neutralized by condensed/adsorbed counterions, f1 and f2 are the fractions of counterions localized in the minor and major grooves, respectively, 1 − f1 − f2 is the fraction of condensed counterions that are delocalized on the DNA surface, and φ̃s ≈ 0.4π is the azimuthal half-width of the narrow groove of DNA.
This model for ζn, which is based on experimental studies of counterion binding, implies weaker interactions of condensed counterions with each other than with DNA bases and phosphates18. Localization of adsorbed counterions in the grooves of DNA (f1, f2) is expected, e.g., for polyvalent biological counterions (spermine, spermidine and basic polypeptides) as well as for some metal ions18,55. A significant delocalized fraction of counterions (1−f1−f2) may be a reasonable approximation for monovalent ions. Point-like multivalent counterions (3+ or higher) may exhibit significant counterion-counterion correlations not captured by Eq. (12), in which case a more complex model for ζn may be required18.
Note that the pair interaction potential (per unit length) between uniformly charged cylinders is nothing more than the zero-harmonic direct interaction and image terms:
| (13) |
It depends only on the distance between the molecules and the effective screening length in the aggregate. In contrast, the amplitude and even the sign of the pair interaction potential between helices depends also on their mutual azimuthal alignment ΔΦ.
Non-additive electrostatic interactions
Because DNA is highly charged, the interstitial electrostatic potential ϕs (at the surface of the Wigner-Seitz cell) in a DNA aggregate may exceed kBT/e, where e is the elementary charge. At such potentials intermolecular interactions may become non-additive, resulting in an additional contribution to the electrostatic interaction energy. A large interstitial potential within the aggregate also increases the concentration of free electrolyte ions inside the aggregate compared to the bulk. This effect may be accounted for by linearizing the Poisson-Boltzmann equation at |qie(ϕ − ϕs)| ≪ kBT rather than at |qieϕ| ≪ kBT. This results in a renormalization of the inverse screening length κ (see Refs. 18, 52). To a first approximation, and κ depend only on the average aggregate density and average surface charge density on each molecule but not on the helical arrangement of surface charges or small distortions. Therefore, to calculate and κ, we use a modification of the cell model for uniformly charged cylinders52. Within this model, κ and ϕs are calculated as the roots of the following system of equations:
| (14) |
| (15) |
where are the concentrations of different ions (labeled by index i) in the electrolyte solution outside the aggregate, qi are the charge numbers for these ions (e.g., qi=2 for a 2+ ion and qi=−1 for a 1− ion), e is the elementary charge, is the Wigner-Seitz cell radius, and R0 = |Rm − Rn| is the average interaxial distance between nearest neighbors in the aggregate.
The value of , which is the difference in electrostatic interaction energies per uniformly charged cylinder calculated within the cell model and that obtained by pair-wise summation, may then be calculated from
| (16) |
where for a 1:1 electrolyte solution
| (17) |
For the derivation of Eqs. (16) and (17), and more detailed explanations, see e.g., Refs. 18, 52. Note that κ and ϕs found from Eqs. (14) and (15) depend on R0 so that the corresponding dependence of ϕs on R′ should be used in Eq. (17).
II.5. Thermal fluctuations
We assume that thermal fluctuations in rμ, hμ, and Ωμ of an individual molecule may be decoupled from intrinsic structural fluctuations associated with sequence-related variations in the base pair step parameters56. In an aggregate, the intrinsic and thermal fluctuations become coupled through intermolecular interactions34. To account for this coupling in both twisting and stretching fluctuations, we utilize the variational approximation described in the online supplement. We neglect the intrinsic bending of DNA, since the intrinsic persistence length of DNA is estimated to be much larger than the thermal one (see the end of Section II.1) 57. We also neglect potential variations in local elastic constants associated with intrinsic distortions 58.
Because depends on Φμ but not on Ωμ and hμ independently, we may analyze only those fluctuation modes that affect rμ and Φμ (see online supplement). We describe the corresponding fluctuations, rμ and δΦμ = Φμ(z) − φμ(0), within a variational approximation59 by utilizing an effective, quadratic fluctuation energy
| (18) |
where (≈ 500 Å, Ref. 32, 45) is the bending persistence length of DNA, and
| (19) |
is the helical persistence length of DNA (since kBT/Ct ≈ kBTḡ2/Cs ≈ 1.4×105 cm−1, Refs. 60, 61, ). The first two terms in Eq. (18) describe the bending, stretching, and torsional energy cost associated with rμ and δΦμ fluctuations (see online supplement). The last two terms model the limitation on the amplitude of the fluctuations due to steric and electrostatic interactions (which depend on rμ and δΦμ, nonlinearly) through the use of effective quadratic potentials. The parameters α and β, which define the latter potentials, are the variational parameters in this model.
The free energy of DNA molecules within this model may be approximated with62
| (20) |
Here Drμ and DδΦμ indicate path integrals over all possible trajectories of rμ(z) and δΦμ(z), and the effective partition function is
| (21) |
The values of α and β are obtained by minimization of F with respect to these parameters.
This model is based on the Gibbs-Bogoliubov inequality59,63, which states that FDNA defined by Eqs. (20) and (21) is larger or equal to the true free energy of the system at any α and β. Statistical averaging based on Zeff with the values of α and β that minimize FDNA may also be used for calculating all pertinent correlation functions and averages. The corresponding calculations are provided in the online supplement.
II.6. Intermolecular interactions and osmotic pressure
We characterize interactions between molecules in a DNA aggregate by calculating the osmotic pressure Π dependence on the interaxial distance R, which has been measured in a number of experimental studies64–66. In a hexagonal aggregate
| (22) |
where Vw is the volume of the solvent inside the aggregate. Important subtleties of the model, which require utilization of ∂FDNA/∂R0 rather than dFDNA/dR0 in this equation49, are discussed in the online supplement.
III. Results
III.1. Undulations
Because of the complexity of DNA structure, many different degrees of freedom contribute to sequence-related (intrinsic) and thermal fluctuations of the DNA conformation29. However, only double helix bending and helical pitch variations, which distort the DNA centerline and result in accumulating distortions away from the ideal helical conformation, are important for intermolecular interactions.
We describe bending of each molecule ν in a hexagonal aggregate by the lateral displacement rν(z) of its centerline from the vertical position (Fig. 1A). In the simplest approximation of uncorrelated undulations, we find51
| (23) |
Here d is the root-mean-square (rms) undulation amplitude (this can be seen by taking |z − z′| → ∞)38,67, and
| (24) |
is the undulation correlation length (or deflection length68). In Eqs. (23) and (24), we neglected the contribution of intrinsic bending of lateral displacements since the corresponding persistence length was estimated32,45 to be much larger than .
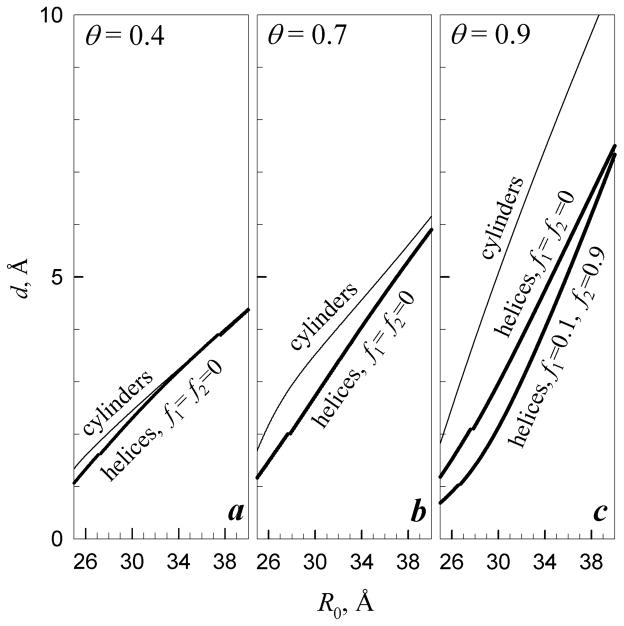
Figure 2 illustrates the dependence of d on the interaxial spacing between the molecules. At θ = 0.4, the undulations of each molecule are confined primarily by the net-charge electrostatic repulsion from its neighbors; and the dependence of d on the average interaxial separation R0 between neighboring molecules is close to that expected for homogeneously charged cylinders51. However, when a larger fraction of the bare DNA charge is compensated by bound counterions, the interaction of the discrete phosphate and counterion charges, along with interactions with the dielectric cores of surrounding molecules18,20 and steric collisions between the molecules51, become the primary limiting factors for the undulation amplitude. A self-consistent model for the calculation of d that accounts for these interactions is described in the online supplement (Eqs. (S.43)–(S.49)). Note that the decrease in the net charge of DNA (e.g., from 30% of the bare charge at θ =0.7 to 10% of the bare charge at θ =0.9) has a relatively minor effect on d at large θ, because the image-charge repulsion between charged helices is nearly independent of θ for molecules in this range of net charges. Even when longer-range interactions become attractive at θ ≥ 0.9, d remains nearly the same because the short-range repulsion prevents the molecules from coming too close to each other (Fig. 2c; f1=0.1, f2=0.9).
Figure 2.
Effect of counterion binding on undulation amplitude. (a) θ = 0.4, (b) θ = 0.7, (c) θ = 0.9. Thin lines show root mean square (rms) displacement d of molecules with homogeneous surface charge density (cylinders). Bold lines show d for molecules with DNA-like density of fixed surface charges (helices) and random (f1=f2 = 0) or preferential counterion binding in the major groove (f1 = 0.1 and f2 = 0.9). Small breaks in the bold lines are associated with phase transitions in mutual alignment of the helices (Fig. 3). The calculations were performed based on Eqs. (S.43)–(S.49) reported in the online supplement with a = 11.2 Å, lc=1.7 Å, λD ≈ 7 Å (0.15 M, 1:1 electrolyte in the bulk solution), lB ≈ 7 Å (ε = 80), , and λc = 105 Å ( and ).
III.2. Helical pitch fluctuations and molecular alignment: Phase transitions
Interactions between DNA molecules depend not only on the interaxial separation but also on the mutual alignment of strands and grooves of nearest neighbor molecules in the aggregate18. The latter, azimuthal alignment may be defined through the helical phase Φ(z) of each molecule (see Eqs. (2), (3), and Fig. 1c). Intrinsic and thermal fluctuations in the helical pitch hinder energetically favorable alignment by altering the helical phase, thereby affecting interactions between neighbors in an aggregate. Conversely, intermolecular interactions affect the helical structure and pitch fluctuations in DNA. As a result, DNA molecules adapt to intermolecular interactions, thereby balancing the interaction energy with the cost of altering the helical pitch fluctuations. We refer to this effect as the structural adaptation of DNA and characterize it by the structural adaptation length33 λh and its renormalized value (see Eq. (30)). The renormalized structural adaptation length in undulating DNA may be calculated from Eqs. (S.43) – (S.49) derived in the online supplement. It defines correlations in helical phase fluctuations along each molecule and the length scale at which the interactions restore the helical coherence of DNA (Section III.3).
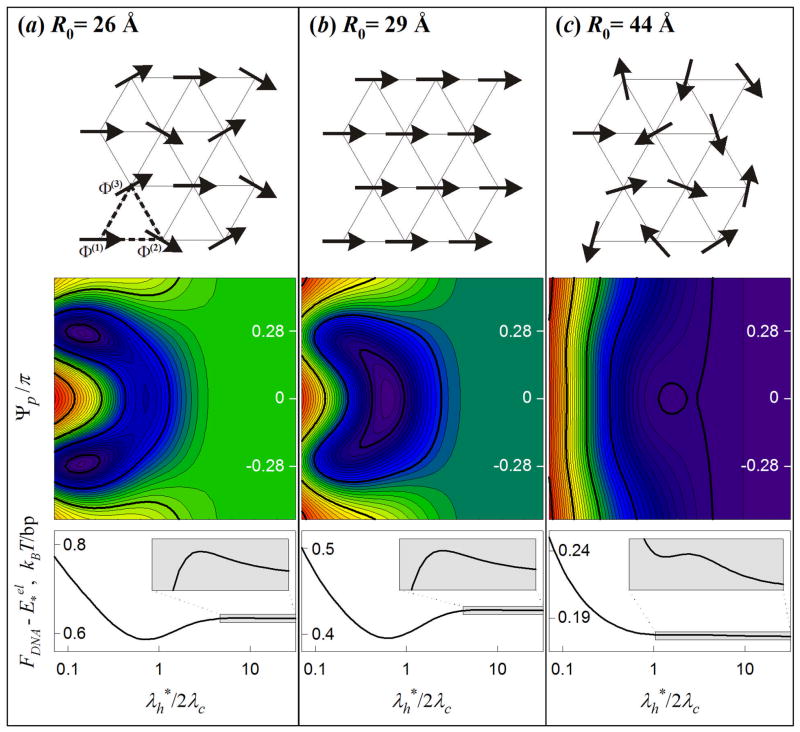
Before we proceed to a more detailed analysis of structural adaptation, in this section we qualitatively describe phases with different mutual alignments of the molecules in the aggregate. The possibility of the existence of several phases with different alignments and helical phase fluctuations in DNA assemblies was first noted in Ref. 20 and later analyzed for straight helices without33 and with34,35 thermal torsional fluctuations. In the present study, we incorporate undulations and stretching of DNA (see online supplement). The present study reveals at least three phases at different average interaxial spacings R0, distinguished by correlations between average helical phases of the nearest neighbor molecules (Φ̄μ) and by the extent of structural adaptation ( ), Fig. 3.
Figure 3.
Phase states of DNA aggregates. (a) Potts state: The molecules have the same set of three different helical phases Φ̄(1), Φ̄(2) and Φ̄(3) (Φ̄(1) -Φ̄(2) = Φ̄(3) -Φ̄(1) = Ψp) within each triangle of the hexagonal lattice (top picture). (b) Ferro state: All molecules have the same helical phase (Ψp =0). (c) Random state: The helical phases are random. Color contour plots illustrate the dependence of the free energy FDNA (in log scale) on Ψp and normalized structural adaptation length ( , Eq. (34)). Bottom graphs show the dependence of FDNA on at Ψp =0; the insets enlarge the boxed, shaded regions. FDNA may have up to three distinct minima: and Ψp ~ ± π/4 is the Potts state [global minimum in (a)]; and Ψp = 0 is the ferro state [global minimum in (b), local minimum in (a) and (c)]; and arbitrary Ψp is the random state [global minimum in (c), local minimum in (a) and (b)]. The calculations were performed at θ = 0.7 and f1=f2=0 with the same values of other parameters as in Fig. 2.
At R0>Rc, intermolecular interactions are too weak for suppressing the amplitude of helical phase fluctuations and is infinite (no structural adaptation), resulting in a phase with no long range order (i.e., 〈cos(Φμ − Φν)〉 = 0, Fig. 3C); we refer to this alignment and phase state of the aggregate as “random”. At R0<Rc, structural adaptation becomes energetically favorable, is finite, and azimuthal orientations of the molecules are correlated over their entire length. Within each triangular elementary cell, the molecules may have different average helical phases, but they are periodically aligned within the lattice, Φ̄μ = Φ̄(1),Φ̄(2),Φ̄(3) and
| (25) |
as shown in Fig. 3A and 3B. At R*<R0<Rc, the most favorable alignment is with Ψp=0 (Fig. 3B); we refer to this alignment and phase state as “ferro”. At R0<R*, Ψp≠0 and depends on R0 (Fig. 3A); we refer to this alignment and phase state as “Potts” 69. Our theory presented in the online supplement suggests first order transitions between these phases. The values of Rc and R* as well as the dependence of Ψp on R0 in the Potts phase are calculated numerically by minimization of the free energy with respect to Ψp and .
Note that previously we focused on the analysis of only the ordered phases and did not address the transition to the random phase33,35,69,70. These studies did not account for undulations, and the corresponding predictions were expected to be less accurate at large R0, at which the latter transition would become relevant. Here we, nevertheless, account for this transition. At the same time, for simplicity, we do not discuss any additional ordered phases that may exist within a narrow region near R0=R* under some circumstances69,70. Also, note that the effects of both phase transitions on the undulation amplitude are weak, because the undulations are limited primarily by image-charge and steric repulsions at large θ and by the net-charge repulsion at small θ. None of these interactions depends on the mutual alignment of the molecules.
III.3. Helical pitch fluctuations and molecular alignment: Structural adaptation
In the random state, only short-range axial correlations in helical phases of neighbor DNA molecules are possible. These correlations arise from the lower energy cost of correlated vs. uncorrelated thermal fluctuations in the helical phase. However, the resulting effects are small and we assume that the helical phase of each molecule in such aggregates is unaffected by the neighbors71. Then, the dependence of the helical phase displacement on |z−z′| is approximately the same as along the centerline of an isolated DNA molecule (Eq. (4)),
| (26) |
where λc is the helical coherence length of DNA,
| (27) |
is the intrinsic helical coherence length43, and the helical persistence length is given by Eq. (19). In the absence of structural adaptation, small undulations have negligible effect on the helical coherence of DNA; see online supplement, Eqs. (S.64)–(S.78). The unlimited accumulation of helical phase displacements at large |z− z′| prevents mutual alignment of neighboring molecules.
In the ferro and Potts states, structural adaptation of DNA limits accumulation of the helical phase displacement as described by the following equation (online supplement)
| (28) |
At |z− z′| ≪ λh, the structural adaptation is negligible and the helical phase displacement may be approximated with Eq. (26). At distances comparable to the structural adaptation length (|z − z′| ~λh), the adaptation becomes significant, limiting accumulation of distortions in the helical phase. At |z − z′| ≫ λh,
| (29) |
where
| (30) |
The values of λh and may be calculated from Eqs. (S.43)–(S.49) of the online supplement. Based on the estimates for and given in Sections II.3 and II.5, respectively, .
Thus, the structural adaptation establishes long-range order in the helical phase without affecting short-range fluctuations. Stronger structural adaptation (smaller λh and ) reduces the deviations of DNA geometry from that of an ideal helix.
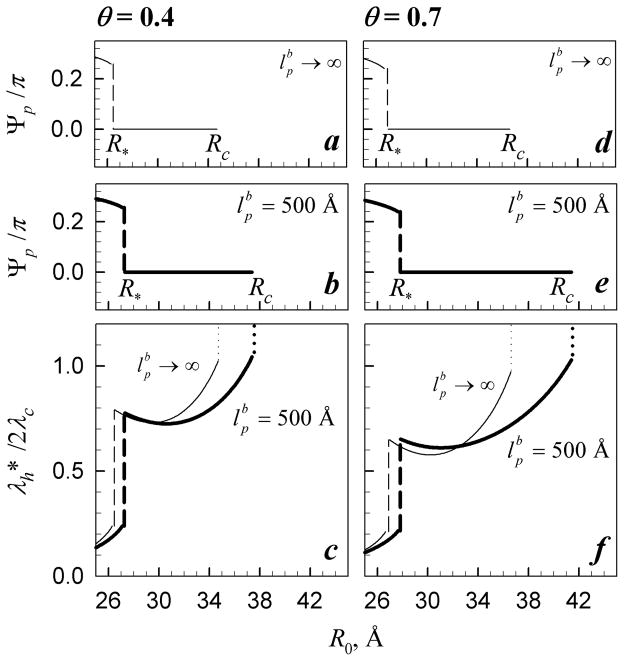
Because structural adaptation of DNA depends on the strength of the interactions among neighboring molecules, λh and depend on θ and R. This dependence is illustrated in Figure 4. The jumps in each curve are due to the phase transitions discussed in Section III.2. Counterintuitively, undulations reduce disruptions of the helical coherence of DNA below the transition and at large distances (R > 37–38 Å), i.e., they push DNA conformation toward that of more ideal helices rather than the other way around. We return to a more detailed discussion of this effect in the next section. At intermediate R, the effect is more complex due to azimuthal frustrations discussed in Refs. 18, 34, 35, 70.
Figure 4.
Effect of undulations on alignment and structural adaptation of DNA molecules. Bold and thin lines show Ψp and calculated with ( ) and without ( ) undulations, respectively. The dashed lines indicate the transition from the Potts (Fig. 3a) to ferro (Fig. 3b) state. The dotted lines in (c) and (f) indicate the transition from the ferro to random (Fig. 3c, ) state. The calculations were performed at f1=f2=0 and θ=0.4 (a–c) and θ=0.7 (d–f) with the same values of all other parameters as in Fig. 2.
III.4. Osmotic pressure
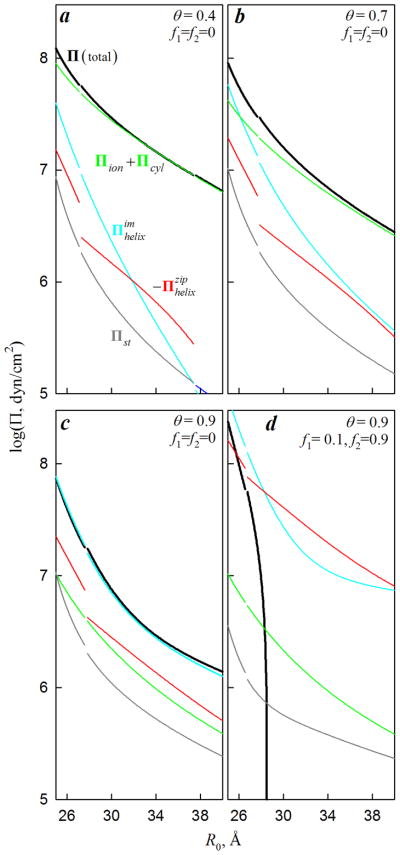
Effects of intrinsic and thermal fluctuations on intermolecular interactions may be understood by analyzing the aggregate osmotic pressure, which may be represented as a sum of five principal components,
| (31) |
Each component of the osmotic pressure is calculated from Eq. (22) as a derivative of the corresponding component of the free energy (Eqs. (5)–(21)) as described in the online supplement (Eqs. (S.38)–(S.57)). The first three components are the same as for worm-like chains with uniform surface charge densities51. The last two components are related to the helical patterning of discrete surface charges. Each component of the osmotic pressure may be approximated by the following expressions.
It follows from Eq. (17),
| (32) |
is the osmotic pressure of free counterions that accumulate inside the aggregate due to nonzero interstitial potential ϕs.
| (33) |
is the “steric” osmotic pressure associated with hard-core collisions between undulating molecules in the aggregate51. General expressions for Πcyl, , and are fairly cumbersome, so that they are presented in the online supplement (Eqs. (S.54)–(S.57)). At small undulations (d ≪ R0 − 2a), however, these components of the osmotic pressure may be approximated with the following simplified expressions:
| (34) |
is the osmotic pressure associated with the electrostatic repulsion among undulating, uniformly-charged wormlike chains51;
| (35) |
is the osmotic pressure associated with image-charge interactions between helically organized surface charges and dielectric cores of nearest neighbor molecules;
| (36) |
is the osmotic pressure associated with electrostatic zipper attraction23 between correlated (aligned in a zipper-like fashion) helical patterns of surface charges on neighboring molecules. Here ucyl(κ,R0) is defined by Eq. (13); un(κ, R0) and are defined by Eqs. (8) and (10), respectively; ∂/∂R0 must be calculated at constant κ (see online supplement); Ψp defined by Eq. (25) characterizes the alignment of the molecules (Fig. 3A,B); and
| (37) |
Note that Πcyl and are always positive (repulsive) and is always negative (attractive). In the random phase state of the aggregate (Fig. 3C), Ψp and σ(nΨp) are not defined, but in the latter case 71 and the osmotic pressure does not depend on Ψp.
Relative contributions of these different components of the osmotic pressure depend on specific conditions (Fig. 5). For infinitely rigid and long, straight molecules, d = 0 and . For DNA, is generally small and can be neglected, but all other components are important in at least some cases. In particular, Πion+Πcyl, associated with the net charge of DNA, is dominant at small θ, which appears to be the case, e.g., in NaCl solutions (see Fig. 7a). and , associated with the helical structure of DNA, are dominant at large θ, which appears to be the case in the presence of counterions that tend to condense DNA (see Fig. 7b).
Figure 5.
Osmotic pressure components in DNA aggregates. Except for the indicated values, all parameters were as in Fig. 2. Thin lines show individual components; bold, black lines show the sum of all components. Breaks in the lines are associated with phase transitions (Figs. 3, 4). The attractive component ( , red line) is shown with the opposite sign. In a, the line for ends at R0 ≈ 38 Å due to the transition to the random state, in which .
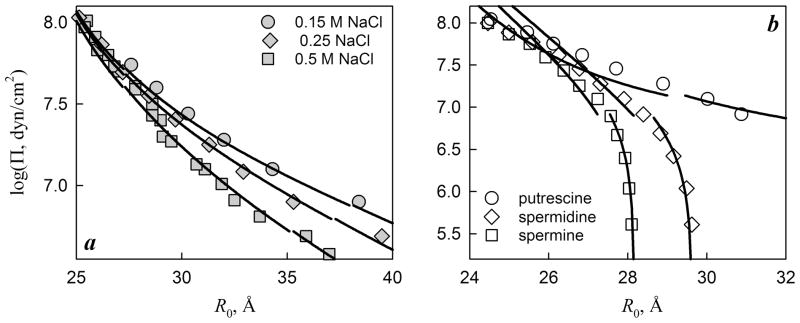
Figure 7.
Measured and fitted osmotic pressures of DNA aggregates in NaCl (a) and polyamine (b) solutions. Data from Refs. 25, 65, 66 were kindly provided by D.C. Rau. Best fits of the NaCl data were achieved at a = 11.2 Å and θ = 0.45, assuming random counterion binding (f1=f2=0); the quality of the fits was not significantly affected by varying f1 and f2. Using the same a and assuming that polyamines preferentially bind in DNA grooves (f1 + f2=1), best fits of the polyamine data were achieved at θ = 0.65, f1 = 0.2, f2 = 0.8 (putrescine); θ = 0.94, f1 = 0.2, f2 = 0.8 (spermidine); and θ = 0.91, f1 = 0.08, f2 = 0.92 (spermine). Preferential binding in the major groove deduced from the fits is consistent with experimental binding studies74. The values of λD and κ were calculated from Eq. (18) based on the actual electrolyte concentrations used in the experiments.
It is clear from Eqs. (34)–(36) that undulations enhance all components of intermolecular interactions by effectively bringing the molecules closer together. This enhancement, illustrated in Fig. 6, is particularly strong for shorter-range image charge ( ) and zipper ( ) interactions, resulting in stronger structural adaptation and a more ideal helical structure of DNA than in the absence of undulations.
Figure 6.

Effect of undulations on different components of the osmotic pressure. Except for the indicated values, all parameters were as in Fig. 2.
IV. Comparison with experiments
Predictions for the osmotic pressure of DNA aggregates are compared with the corresponding experimental measurements in Figure 7. The osmotic pressures measured at different concentrations of NaCl represent a larger group of experimental data for monovalent counterions15,25,64,65. As shown in Fig. 7a, these data are fit well by our theory assuming a = 11.2 Å and θ=0.45. To reduce the number of adjustable parameters, we assumed random binding of Na+ on the DNA surface (f1=f2=0, Eq. (12)) 33,72. For the same reason, we also neglected the potential dependence of θ on R0 since this dependence and its effect on the osmotic pressure are expected to be weak in the relevant range of R0 (in which R0 is larger than the effective screening length inside the aggregates) 52.
Importantly, the fitted value of a is consistent with the expected effective radius of B-DNA (10±2.5 Å), since the centers of phosphate groups lie at ~ 10 Å from the molecular axis and the effective diameter of the phosphate group is73 5–6 Å. The fitted θ is also consistent with the values expected from theoretical models of counterion condensation on DNA at 0.15 M – 0.5 M NaCl concentrations59.
Osmotic pressures measured at small concentrations of polyamines are also well described by our theory at the same value of a = 11.2 Å (Fig. 7b). Polyamines tend to condense DNA and may play an important role as biological counterions66. They are known to bind to DNA much stronger than Na+ and have strong preference for binding in the major groove of DNA 74. As in the case of NaCl, we assumed θ, f1, and f2 to be independent of R0, consistent with strong chemisorption of these ions. This assumption is additionally justified by the experimental observation that the osmotic pressure curves remain the same over a wide range of polyamine concentrations75, indicating full saturation of the binding sites in the whole range of R0. The fitted values of θ, f1, and f2 are in complete agreement with all of these expectations.
Na+-DNA and polyamine-DNA aggregates demonstrate two qualitatively different types of osmotic pressure curves, both of which are described by the same theory simply by accounting for expected differences in counterion binding. We are aware of only two other sets of osmotic pressure curve measurements that exhibit qualitatively different behavior from Na+-DNA and polyamine-DNA aggregates. In Mn2+-DNA and Co(NH3)63+-DNA aggregates65, packing phase transitions were observed with changes in the counterion concentration and temperature. However, because of the strong dependence of the osmotic pressures on the counterion concentration, the fitting of the latter data with θ, f1, and f2 independent of R0 would be unjustified. Therefore, we will consider these more complex cases in a separate publication.
Note that a fraction of experimental data for osmotic stress isotherms is obtained for low aggregate densities at which the structure of the aggregate corresponds to a cholesteric, rather than a columnar, phase. For instance, polyamine-DNA aggregates remain in the hexagonal state over the entire range of R0 shown in Fig. 7b (Ref. 75), but Na+-DNA aggregates exhibit a transition from the hexagonal phase at R0 < 30–35 Å to a cholesteric phase at larger R0 (Ref. 76). Because our theory has been designed for the hexagonal phase, its application to the cholesteric phase is speculative and should be viewed with caution. Nevertheless, the following arguments suggest that such an extrapolation of the osmotic pressure isotherms may not be unreasonable.
Empirically, the measured osmotic pressure isotherms follow the same dependence on the interaxial spacing between nearest neighbors (R0) before and after the expected hexagonal-to-cholesteric transition at R0 = 30–35 Å (Fig. 7A). Fundamentally, local packing and local interactions of nearest neighbors in the cholesteric phase may be expected to be similar to the hexagonal phase when neighbor molecules may be approximated as parallel and positionally confined at the length scale ~ λB. Beyond λB, fluctuations in the interaxial distance are uncorrelated and the molecules may be considered as independent segments of this length. In other words, we expect the hexagonal phase formulas to describe osmotic pressures in the cholesteric phase as long as 2πλB/P ≪ 1, where P is the cholesteric pitch. For instance, within the region of R0 shown in Fig. 7A, we expect P (~1–20 μm) 76 to be at least two orders of magnitude larger than λB (< 100 Å, Eq. (24)), consistent with the continuity of the osmotic pressure isotherms across the expected hexagonal-to-cholesteric transition.
V. Discussion
The two most important conclusions that follow from the results of this study are:
The double helix structure, flexibility, and fluctuations are all important factors in determining mean electrostatic interactions within DNA aggregates. None of these factors can be neglected a priori.
Electrostatic interactions quantitatively account for the measured osmotic pressures in DNA aggregates not only at large but also at small interaxial separations, once the helical structure, flexibility and fluctuations are taken into account.
The relative contributions of the helical structure, flexibility, and different fluctuation modes depend on the aggregate density, the ionic strength, the composition of electrolyte solution, etc. The quantitative description of the interplay between these factors is fairly complex, but the physics underlying this interplay is straightforward.
Structural adaptation of DNA suppresses twisting and stretching fluctuations
Electrostatic interactions between DNA molecules confined in a hexagonal aggregate favor zipper-like alignment and juxtaposition of negatively charged phosphate strands and positively charged grooves on neighboring molecules (Fig. 1c). The ability of DNA molecules to establish and maintain this alignment is determined by two competing tendencies. Intrinsic (sequence-dependent) and thermal twisting and stretching fluctuations may disrupt the alignment. Structural adaptation to a more ideal helical conformation, which yields a more favorable electrostatic interaction energy, may restore the alignment. The structural fluctuations and adaptation are two manifestations of DNA flexibility, which must always be considered together. In this study, we have found that the electrostatic benefit from the structural adaptation generally exceeds the elastic and entropic costs of suppressing the twisting and stretching fluctuations at surface-to-surface separations below 20–25 Å (Figs. 3, 4). Consistently, an alignment of phosphate strands on neighboring molecules was observed experimentally in hydrated fibers up to a 20–25 Å surface separation77 and in DNA packed inside viral capsids2.
Undulations enhance the structural adaptation
The electrostatic interaction responsible for the structural adaptation decays exponentially with a characteristic , which is restricted by the helical pitch of DNA 18,33 (2π/ḡ). The reason why this interaction may suppress the twisting and stretching fluctuations, even at surface separation as large as 20 Å despite the ≤ 5 Å decay length, is that it is enhanced by thermal undulations of DNA.
Indeed, undulations have a dual effect. First, they tilt the molecules, disrupting the zipper alignment. Statistical mechanical calculations have shown here that this effect should be negligible because of the sufficiently large bending rigidity of DNA. Furthermore, undulations reduce the distance of the closest approach between the molecules. Stronger electrostatic forces at smaller intermolecular separations cause stronger structural adaptation of DNA. Therefore, somewhat counterintuitively, undulations help to suppress both twisting and stretching fluctuations, pushing DNA towards a more ideal helical geometry.
Undulations enhance the effect of helical structure on DNA interactions
Enhancement of electrostatic forces by DNA undulations was discussed previously within the homogeneously charged cylinder model38. Crudely, the enhancement results from averaging the exponential electrostatic force ∝ exp[(x− x′)/λ] with the Gaussian probability ∝ exp[− (x2 + x′2)/d2] of the undulations x and x′ of neighboring molecules in their interaxial direction (d is the rms undulation amplitude and λ is the characteristic decay length of the interaction). This leads to an enhancement factor ~ exp(d2/2λ2), which is larger for interactions with shorter decay lengths (see Eqs. (34)–(36) and more accurate expressions in the online supplement).
Because forces associated with the helical organization of charges on the DNA surface have shorter decay lengths, undulations significantly increase their relative contribution to the net interaction. To illustrate this effect, consider a DNA aggregate in physiological saline solution, in which the surfaces of neighboring DNA molecules are separated by 15–20 Å of water. In such an aggregate, the expected amplitude of DNA undulations is d ≈ 4–6 Å (Fig. 2). The three components of electrostatic interactions at this separation are: (i) the repulsion associated with the net charge of the helices, which decays with the characteristic length 6–7 Å; (ii) the electrostatic zipper attraction associated with the juxtaposition of negatively charged phosphate strands and positively charged grooves, which decays with the characteristic length ≈4 Å; and (iii) the image-charge repulsion of helically distributed surface charges from the dielectric cores of neighboring molecules, which decays with the characteristic length18≈2 Å. Using the enhacement factor of exp(d2/2λ2), we find that undulations will enhance the net-charge repulsion ~20–60%, the electrostatic zipper attraction ~60–200%, and the image-charge repulsion ~10–90 times, consistent with the more accurate calculations shown in Fig. 6. This enhancement makes the short-range forces relevant even at 15–20 Å surface-to-surface separation.
Undulation-enhanced electrostatics explains the observed osmotic pressure isotherms
Previous studies showed good agreement between forces calculated for homogeneously charged, undulating cylinders and osmotic pressure isotherms measured for DNA aggregates in NaCl solutions at surface separations larger than ~ 20 Å (Ref. 15). At the same time, the osmotic pressure isotherms at smaller separations or in aggregates condensed by some divalent and polyvalent counterions could not be explained within the same model, raising a question about the origin of the underlying forces65,66. We proposed that these isotherms may result from the effects of the double helical structure of DNA on the electrostatic forces between DNA 18,20,33. The earlier, simplified model of these structure-dependent forces rationalized a number of observed features of these forces, including the exponential decay lengths of measured osmotic pressure isotherms18. However, with the development of the theory it became clear that a more detailed quantitative comparison with experiments requires a more careful analysis of the effects of various intrinsic and thermal fluctuations in the double helix structure.
After accounting for these fluctuations in the present study, we found that undulation-enhanced, structure-dependent electrostatic forces may explain the measured osmotic pressure isotherms not only qualitatively but also quantitatively (Fig. 7). The difference between the osmotic pressure isotherms of DNA aggregates in NaCl and in the presence of polyvalent counterions appears to be associated with stronger binding and preferential localization of the latter in DNA grooves22, as we hypothesized based on the earlier model23. This binding reduces the net-charge repulsion and increases the electrostatic zipper attraction. As a result, the balance of the forces changes from predominantly net-charge and uniform cylinder image-charge repulsions in NaCl to predominantly electrostatic zipper attraction and helix specific image-charge repulsion in counterion-condensed DNA aggregates.
Overall, the simplified theory reviewed in Ref. 18 captures many qualitative features of DNA-DNA interactions. Accounting for additional degrees of freedom, and the corresponding thermal fluctuations, largely changes the quantitative predictions (Fig. 6), improving the agreement with the data (Fig. 7). The present, more comprehensive analysis, however, has yielded one nontrivial qualitative prediction that image repulsion cannot be neglected compared to the zipper attraction at any interaxial separation (Fig. 5). This was not expected in the earlier theory, which predicted a two times shorter characteristic decay length for the image repulsion compared to the zipper attraction18. The same prediction still holds at separations at which the factor of two difference between the decay lengths was observed (R0 from 26 to 30 Å, Fig. 6)66. However, at larger separations, at which the image repulsion was expected to be negligible, undulations enhance the image repulsion much more than the zipper attraction. This dramatically alters the balance between these forces. Intuitively, this effect may be understood as follows. When a significant fraction of the DNA charge is balanced by bound counterions and the zipper attraction is important, the amplitude of the undulations is limited primarily by the short-range image repulsion. Undulations always drive the molecules close enough for them to feel a substantial impact of this repulsion. This new finding may have particularly important implications for chiral interactions between double helices. Chiral image forces between helices may have nontrivial effects on the amplitude and even the sign of the chiral torque. Our earlier calculations of the chiral torque26,27, in which these forces were neglected, may thus need to be revisited.
In conclusion, the agreement of our predictions with data supports the idea that DNA-DNA interactions are predominantly electrostatic and may be described by accounting for the helical organization of surface charges and bound counterions. Nevertheless, given uncertainties inherent in macroscopic-like, continuum description of electrostatics at such distances, we cannot exclude contributions arising from other interactions. For instance, the discrete nature of water may give rise to additional forces, often referred to as hydration forces66. The mean-field model of hydration forces78 is mathematically equivalent to the electrostatic theory, except for unknown values of phenomenological parameters21. Thus, it should lead to qualitatively similar predictions for DNA-DNA interactions21, complicating attempts to distinguish the contributions from electrostatics and hydration18. In principle, the most consistent approach would be ab-initio, all-atom calculations, without model assumptions about interaction potentials, and other approximations built into present simulations. However, such calculations of DNA-DNA interactions are still far beyond the reach of computational technology.
Supplementary Material
Acknowledgments
We acknowledge useful, stimulating discussions with Adrian Parsegian, Rudy Podgornik, Don Rau, and Loren Willams. This was a long-term, five year project, for which we gratefully acknowledge financial support from the Max-Planck Society (DJL); the Alexander von Humboldt Foundation (AW); the Leverhulme Trust, Grant F/0758/AE and EPSRC, Grant EP/H010106/1(AAK); and the Intramural Research Program of NICHD, NIH (SL).
Footnotes
Supporting information available: All derivations and auxiliary formulae are described in a supplementary material. This material is available free of charge via the Internet at http://pubs.acs.org.
References
- 1.Bloomfield VA. Curr Opin Struct Biol. 1996;6:334. doi: 10.1016/s0959-440x(96)80052-2. [DOI] [PubMed] [Google Scholar]
- 2.Leforestier A, Livolant F. Proc Natl Acad Sci USA. 2009;106:9157. doi: 10.1073/pnas.0901240106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Tzlil S, Kindt JT, Gelbart WM, Ben-Shaul A. Biophys J. 2003;84:1616. doi: 10.1016/S0006-3495(03)74971-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Purohit PK, Inamdar MM, Grayson PD, Squires TM, Kondev J, Phillips R. Biophys J. 2005;88:851. doi: 10.1529/biophysj.104.047134. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Gelbart WM, Knobler CM. Phys Today. 2008;61:42. [Google Scholar]
- 6.Seeman NC, Lukeman PS. Rep Prog Phys. 2005;68:237. doi: 10.1088/0034-4885/68/1/R05. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Heath JR, Ratner MA. Phys Today. 2003;56:43. [Google Scholar]
- 8.Zickler D. Chromosoma. 2006;115:158. doi: 10.1007/s00412-006-0048-6. [DOI] [PubMed] [Google Scholar]
- 9.Barzel A, Kupiec M. Nat Rev Genet. 2008;9:27. doi: 10.1038/nrg2224. [DOI] [PubMed] [Google Scholar]
- 10.Baldwin GS, Brooks NJ, Robson RE, Wynveen A, Goldar A, Leikin S, Seddon JM, Kornyshev AA. J Phys Chem B. 2008;112:1060. doi: 10.1021/jp7112297. [DOI] [PubMed] [Google Scholar]
- 11.Danilowicz C, Limouse C, Hatch K, Conover A, Coljee VW, Kleckner N, Prentiss M. Proc Natl Acad Sci USA. 2009;106:13196. doi: 10.1073/pnas.0904729106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Frank-Kamenetskii MD, Anshelevich VV, Lukashin AV. Sov Phys Usp. 1987;151:595. [Google Scholar]
- 13.Jayaram B, Beveridge DL. Annu Rev Biophys Biomol Struct. 1996;25:367. doi: 10.1146/annurev.bb.25.060196.002055. [DOI] [PubMed] [Google Scholar]
- 14.Gelbart WM, Bruinsma RF, Pincus PA, Parsegian VA. Phys Today. 2000;53:38. [Google Scholar]
- 15.Podgornik R, Rau DC, Parsegian VA. Biophys J. 1994;66:962. doi: 10.1016/S0006-3495(94)80877-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Strey HH, Parsegian VA, Podgornik R. Phys Rev E. 1999;59:999. [Google Scholar]
- 17.Strey HH, Podgornik R, Rau DC, Parsegian VA. Curr Opin Struct Biol. 1998;8:309. doi: 10.1016/s0959-440x(98)80063-8. [DOI] [PubMed] [Google Scholar]
- 18.Kornyshev AA, Lee DJ, Leikin S, Wynveen A. Rev Mod Phys. 2007;79:943. [Google Scholar]
- 19.Kanduč M, Dobnikar J, Podgornik R. Soft Matter. 2009;5:868. [Google Scholar]
- 20.Since the interaction of a charge with a dielectric boundary (separating media with different dielectric constants) may be described as it were between the charge and its image(s) across the boundary, this interaction is often referred to as an image force ( Landau LD, Lifshitz EM. Electrodynamics of continuous media. Pergamon Press; Oxford: 1982. ). The force is repulsive when the charge is in a medium with higher dielectric constant and attractive when the charge is in a medium with lower dielectric constant. Image forces have two manifestations in the context of DNA-DNA interactions. First, charges located in water at the surface of one molecule repel from the dielectric core of an opposing molecule. Second, polarization of the dielectric core almost doubles the electric field created in water by a charge located at the core surface, as if the field were created by the charge and its image.
- 21.Kornyshev AA, Leikin S. J Chem Phys. 1997;107:3656. [Google Scholar]
- 22.Hsiao C, Tannenbaum M, Van Deusen H, Hershkovitz E, Perng G, Tannenbaum A, Williams LD. In: Nucleic Acid Metal Ion Interactions. Hud N, editor. RSC; London: 2008. pp. 1–35. [Google Scholar]
- 23.Kornyshev AA, Leikin S. Phys Rev Lett. 1999;82:4138. [Google Scholar]
- 24.Kornyshev AA, Leikin S. Proc Natl Acad Sci USA. 1998;95:13579. doi: 10.1073/pnas.95.23.13579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Podgornik R, Strey HH, Gawrisch K, Rau DC, Rupprecht A, Parsegian VA. Proc Natl Acad Sci USA. 1996;93:4261. doi: 10.1073/pnas.93.9.4261. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Kornyshev AA, Leikin S. Phys Rev E. 2000;62:2576. doi: 10.1103/physreve.62.2576. [DOI] [PubMed] [Google Scholar]
- 27.Kornyshev AA, Leikin S, Malinin SV. Eur Phys J E. 2002;7:83. [Google Scholar]
- 28.Cherstvy AG. J Phys Chem B. 2008;112:12585. doi: 10.1021/jp801220p. [DOI] [PubMed] [Google Scholar]
- 29.Olson WK, Zhurkin VB. Curr Opin Struct Biol. 2000;10:286. doi: 10.1016/s0959-440x(00)00086-5. [DOI] [PubMed] [Google Scholar]
- 30.Odijk T. J Polym Sci, Polym Phys Ed. 1977;15:477. [Google Scholar]
- 31.Skolnick J, Fixman M. Macromolecules. 1977;10:945. [Google Scholar]
- 32.Marko JF, Siggia ED. Macromolecules. 1995;28:8759. [Google Scholar]
- 33.Cherstvy AG, Kornyshev AA, Leikin S. J Phys Chem B. 2004;108:6508. doi: 10.1021/jp0380475. [DOI] [PubMed] [Google Scholar]
- 34.Lee DJ, Wynveen A, Kornyshev AA. Phys Rev E. 2004;70:051913. doi: 10.1103/PhysRevE.70.051913. [DOI] [PubMed] [Google Scholar]
- 35.Lee DJ, Wynveen A. J Phys: Condens Matter. 2006;18:787. doi: 10.1088/0953-8984/22/7/072202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Kornyshev AA, Wynveen A. Proc Natl Acad Sci USA. 2009;106:4683. doi: 10.1073/pnas.0811208106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Lee DJ, Kornyshev AA. J Chem Phys. 2009;131:155104. doi: 10.1063/1.3224123. Erratum: 19901. [DOI] [PubMed] [Google Scholar]
- 38.Odijk T. Biophys Chem. 1993;46:69. [Google Scholar]
- 39.Smith DA. J Phys A: Math Gen. 2001;34:4507. [Google Scholar]
- 40.Podgornik R, Parsegian VA. Macromolecules. 1990;23:2265. [Google Scholar]
- 41.Strey HH, Parsegian VA, Podgornik R. Phys Rev Lett. 1997;78:895. doi: 10.1103/PhysRevLett.84.3105. [DOI] [PubMed] [Google Scholar]
- 42.Selinger JV, Bruinsma RF. Phys Rev A. 1991;43:2922. doi: 10.1103/physreva.43.2922. [DOI] [PubMed] [Google Scholar]
- 43.Wynveen A, Lee DJ, Kornyshev AA, Leikin S. Nucleic Acids Res. 2008;36:5540. doi: 10.1093/nar/gkn514. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Yakushevich LV. Nonlinear Physics of DNA. Wiley; New York: 2004. [Google Scholar]
- 45.Bolshoy A, McNamara P, Harrington RE, Trifonov EN. Proc Natl Acad Sci USA. 1991;88:2312. doi: 10.1073/pnas.88.6.2312. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Koo HS, Wu HM, Crothers DM. Nature. 1986;320:501. doi: 10.1038/320501a0. [DOI] [PubMed] [Google Scholar]
- 47.So far, this approximation has been tested and found valid only for random sequences 43. It is less clear whether the same approximation also applies to genomic DNA, in which long-range correlations in the base pair composition have been reported (Peng, C-K; Buldyrev, C. V., Goldberger, A. L., Havlin, S., Sciortino, F., Simons, M., Stanley, H. E. Nature 1992, 356, 168). Potential effects of such correlations in genomic sequences on DNA-DNA interaxtions are, however, likely to be “washed out” by random juxtaposition of different genomic fragments in fibers.
- 48.Note that roll, tilt and slide between adjacent base pairs also depend on the sequence 29,45. These lead to small bending distortions, but they do not affect to the intrinsic coherence length.
- 49.Note that each term in Eq. (5) is a free energy at fixed conformations and separations between the molecules in the aggregate. We refer to these terms as energies to underscore that they do not account for conformational fluctuations of the molecules. For simplicity, Eq. (5) includes only the energy terms that explicitly depend on the separation and conformation of DNA molecules. Other terms do not have to be explicitly specified in the context of the present theory, but this approach leads to important subtleties in calculation derivatives of the aggregate free energy discussed in the online supplement.
- 50.Helfrich W, Harbich W. Chem Scr. 1985;25:32. [Google Scholar]
- 51.Lee DJ, Leikin S, Wynveen A. J Phys: Condens Matter. 2010;22:072202. doi: 10.1088/0953-8984/22/7/072202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Cherstvy AG, Kornyshev AA, Leikin S. J Phys Chem B. 2002;106:13362. doi: 10.1021/jp0380475. [DOI] [PubMed] [Google Scholar]
- 53.In general, the summation in Eq. (7) should be performed to infinite n, but computations show that for DNA the sum rapidly converges and can usually be truncated after n=2 (Refs. 20, 23, 18). The contribution of at least one of the terms with n≤2 is always much larger than the sum of the terms with n≥3 because Kn(κnR) exponentially decreases with increasing κn (≈ nḡ at large n, Eq. (9)). The reason why the sum cannot be truncated at smaller n is that the amplitudes of terms with n=0 and n=1 may become small for some counterions ( at θ≈ 1 and f1 − f2 ≈ cos(φ̃s)).
- 54.A variety of theoretical models and computer simulations of counterion-DNA interactions have been reviewed, e.g., in ( Sharp KA, Honig B. Curr Opin Struct Biol. 1995;5:323. doi: 10.1016/0959-440x(95)80093-x.Beveridge DL, McConnell KJ. Curr Opin Struct Biol. 2000;10:182. doi: 10.1016/s0959-440x(00)00076-2.Cheatham TE., III Curr Opin Struct Biol. 2004;14:360. doi: 10.1016/j.sbi.2004.05.001.Korolev N, Lyubartsev AP, Nordenskiöld L. Adv Colloid Interface Sci. 2009 doi: 10.1016/j.cis.2009.08.002.). However, many of the theoretical predictions are at odds with each other and experiments, which is not surprising given that counterion binding to DNA is strongly affected by the coordination chemistry of the ions, water and DNA; see, e.g., Ref. (55). Accurate modeling of such coordination chemistry may require a full quantum mechanical description of electron clouds of all relevant atoms. Furthermore, since counterion binding affects interactions and conformation of DNA in hexagonal aggregates, the converse must also be true; local counterion binding may depend on collective effects concerned with the large scale variations in the DNA interactions and conformation. In other words, modeling of counterion-DNA interactions may require ab initio simulations of millions of interacting atoms over very large time intervals and conformational space, which are still far beyond the reach of the available computational technology.
- 55.Hud N, editor. Nucleic Acid Metal Interactions. RSC; London: 2008. [Google Scholar]
- 56.Berman HM, Olson WK, Beveridge DL, Westbrook J, Gelbin A, Demeny T, Hsieh S-H, Srinivasan AR, Schneider B. Biophys J. 1992;63:751. doi: 10.1016/S0006-3495(92)81649-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.For non-interacting molecules the combined persistence length is given by , where is the intrinsic bending persistence length and is the themal bending persistence length. However, if , then . This suggests that intrinsic bending is not important.
- 58.Over large length scales, we expect that such effects will not matter.
- 59.Netz RR, Orland H. Eur Phys J E. 2003;11:301. doi: 10.1140/epje/i2002-10159-0. [DOI] [PubMed] [Google Scholar]
- 60.Wenner JR, Williams MC, Rouzina I, Bloomfield VA. Biophys J. 2002;82:3160. doi: 10.1016/S0006-3495(02)75658-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Crothers DM, Drak J, Kahn JD, Levene SD. Methods Enzymol. 1992;212:3. doi: 10.1016/0076-6879(92)12003-9. [DOI] [PubMed] [Google Scholar]
- 62.Note that this model formally allows unrestricted thermal undulations, resulting in nonphysical overlap between the cores of the molecules. Although the probability of such overlap is low, this feature of the model requires some caution in averaging of the electrostatic energy (see online supplement).
- 63.Bogoliubov NN. Dokl Akad Nauk SSSR. 1958;119:244. [Google Scholar]
- 64.Rau DC, Lee B, Parsegian VA. Proc Natl Acad Sci USA. 1984;81:2621. doi: 10.1073/pnas.81.9.2621. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Rau DC, Parsegian VA. Biophys J. 1992;61:246. doi: 10.1016/S0006-3495(92)81831-3. ibid. 1992, 61, 260. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Todd BA, Parsegian VA, Shirahata A, Thomas TJ, Rau DC. Biophys J. 2008;94:4775. doi: 10.1529/biophysj.107.127332. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Odijk T. Macromolecules. 1983;16:1340. [Google Scholar]
- 68.It is important to make clear that λB is not a characteristic wavelength of undulation fluctuations. With stronger confinement (smaller d) it vanishes because λB characterizes the distance along the z-axis after which bending deviations away from a molecule’s mean centerline can no longer accumulate. The molecule is then deflected back towards its mean center-line. This justifies referring to λB as the deflection length).
- 69.Harreis HM, Kornyshev AA, Likos CN, Löwen H, Sutmann G. Phys Rev Lett. 2002;89:018303. doi: 10.1103/PhysRevLett.89.018303. [DOI] [PubMed] [Google Scholar]
- 70.Wynveen A, Lee DJ, Kornyshev AA. Eur Phys J E. 2005;16:303. doi: 10.1140/epje/i2004-10087-y. [DOI] [PubMed] [Google Scholar]
- 71.We neglect the weak attraction resulting from correlated thermal fluctuations of the helical phase of neighbor molecules 35,70, which is akin to and should be considered together with the zero-frequency van der Waals attraction.
- 72.Even better fits may be achieved by adjusting the Na+ preference for the binding in minor (f1) and major (f2) grooves. However, since the predicted osmotic pressures in NaCl have weak dependence on this preference, utilization of f1 and f2 as adjustable parameters may result in over-fitting the data.
- 73.Saenger W. Principles of Nucleic Acid Structure. Springer; New York: 1983. [Google Scholar]
- 74.Wemmer DE, Srivenugopal KS, Reid BR, Morris DR. J Mol Biol. 1985;185:457. doi: 10.1016/0022-2836(85)90418-8. [DOI] [PubMed] [Google Scholar]
- 75.Yang J, Rau DC. Biophys J. 2005;89:1932. doi: 10.1529/biophysj.105.065060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Livolant F, Leforestier A. Prog Polym Sci. 1996;21:1115. [Google Scholar]
- 77.Kornyshev AA, Lee DJ, Leikin S, Wynveen A, Zimmerman SB. Phys Rev Lett. 2005;95:148102. doi: 10.1103/PhysRevLett.95.148102. [DOI] [PubMed] [Google Scholar]
- 78.Marčelja S, Radic N. Chem Phys Lett. 1976;42:129. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.