Ordered Subset Analysis for Case-Control Studies

Abstract

Genetic heterogeneity, which may manifest on a population level as different frequencies of a specific disease susceptibility allele in different subsets of patients, is a common problem for candidate gene and genome-wide association studies of complex human diseases. The ordered subset analysis (OSA) was originally developed as a method to reduce genetic heterogeneity in the context of family-based linkage studies. Here, we have extended a previously proposed method (OSACC) for applying the OSA methodology to case-control datasets. We have evaluated the type I error and power of different OSACC permutation tests with an extensive simulation study. Case-control datasets were generated under two different models by which continuous clinical or environmental covariates may influence the relationship between susceptibility genotypes and disease risk. Our results demonstrate that OSACC is more powerful under some disease models than the commonly used trend test and a previously proposed joint test of main genetic and gene-environment interaction effects. An additional unique benefit of OSACC is its ability to identify a more informative subset of cases that may be subjected to more detailed molecular analysis, such as DNA sequencing of selected genomic regions to detect functional variants in linkage disequilibrium with the associated polymorphism. The OSACC-identified covariate threshold may also improve the power of an additional dataset to replicate previously reported associations that may only be detectable in a fraction of the original and replication datasets. In summary, we have demonstrated that OSACC is a useful method for improving SNP association signals in genetically heterogeneous datasets.

Introduction

Complex human diseases are characterized by substantial etiologic heterogeneity, which is often unrecognizable by clinical exam. Genetic heterogeneity, which represents one particular aspect of etiologic heterogeneity, frequently complicates genetic association studies. Here, we define genetic heterogeneity as different frequencies of a specific disease susceptibility allele in different subsets of patients. In a case-control comparison of unrelated individuals, heterogeneity with respect to the disease-associated allele may greatly reduce the power of the study. A recent genome-wide association study (GWAS) of asthma provided a compelling example for the advantage of explicitly modeling genetic heterogeneity [Bouzigon et al., 2008]. An in-depth evaluation of a previously implicated asthma susceptibility region supported by both GWAS and candidate gene studies revealed that most of the association evidence was contributed by a subset of patients with early-onset asthma (<5 years of age); within this subset, the association was particularly strong in those who were exposed to environmental tobacco smoke, suggesting that the risk variants in this genomic region may interact with early-life tobacco smoke exposure. Given the ubiquity of heterogeneity in genetic association studies, statistical methods that are able to identify more homogeneous subsets of patients (or families) continue to be of great interest. In the context of next-generation DNA sequencing studies, it is especially important to select the most informative subset of individuals for sequencing, once a promising allelic association between a genotyped marker and a putative disease gene has been identified. While a selection of individuals by marker genotypes or haplotypes is commonly implemented [Haines et al., 2005], additional criteria that may improve the probability of successfully identifying one or more causal variants within the gene (or region) of interest would be extremely helpful.

Our group has previously developed the ordered subset analysis (OSA) methodology as a test of linkage heterogeneity [Hauser et al., 2004] and a test of heterogeneity for family-based association mapping (APL-OSA) [Chung et al., 2008]. Here, we have extended a previously proposed method for applying the OSA method to case-control datasets [Macgregor et al., 2006] and performed an extensive simulation study to compare and contrast different OSA permutation tests. As in our previous work [Schmidt et al., 2008], we have simulated data under complex disease-generating models that include clinical and/or environmental continuous covariates. The specific models investigated here include: (i) Covariate-based genetic heterogeneity; and (ii) gene-environment (G×E) interaction. In the heterogeneity model, distinct susceptibility genes are associated with distinct covariate distributions in two subsets of patients, without direct covariate effects on disease risk. An example for this model is the age at onset distribution of BRCA1 carriers, which has a much lower mean than that of non-carriers. This observation was crucial for the original BRCA1 linkage mapping study, which observed a strong correlation between the average age at onset of breast cancer cases within a family and the family-specific lod score for the genomic region containing BRCA1[Hall et al., 1990]. In the G×E interaction model implemented here, a covariate interacts statistically with a particular susceptibility gene, in the absence of main effects of the gene or covariate. In this case, the covariate has a direct effect on disease risk, but this effect is only observed in carriers of a susceptible genotype. This G×E interaction model may only apply to a subset of patients in the dataset, while the disease risk of other patient subsets is influenced by different susceptibility gene(s) and/or other environmental covariates. Thus, the relevant gene may be missed unless the particular subset of patients is identified. Under both models, sampling variability in the covariate distribution across datasets, coupled with failure to account for the covariate-based genetic heterogeneity, may explain the lack of replication of a previously reported genetic association in a different dataset.

In the following sections, we summarize the relevant previous work and then describe how several different permutation tests may be incorporated into an OSA algorithm for case-control datasets. We have evaluated these tests with an extensive simulation study, using the two disease-generating models described above. Finally, we discuss the effect of population stratification on the type I error of the test statistics, and describe how our methodology may be used to select a subset of cases for more detailed molecular analysis, such as DNA sequencing.

Methods

Ordered Subset Analysis

Conceptually, OSA is related to mixture models [Smith, 1963; Ott, 1983] which allow for the possibility that different subsets of an available dataset may best be modeled by different sets of parameters in a likelihood function or regression model equation. However, the subset membership for any particular sample is unknown a priori. A particular goal may be to select the subset of samples that is maximally informative for the association of primary interest, analogous to the goal of Classification and Regression Trees (CART) [Breiman L et al., 1984]. However, OSA is only concerned with grouping samples (or sampling units, such as families), and does not simultaneously select a subset of variables that are maximally predictive of the outcome variable of primary interest. The original OSA method, referred to as “linkage-OSA”, was developed in the context of a family-based linkage analysis and operates on family-specific nonparametric lod scores [Hauser et al., 2004]. This method has successfully been applied to several complex disease datasets [Jacobson et al., 2008; Allingham et al., 2005; Schmidt et al., 2004; Shah et al., 2006; Elbein et al., 2009]. A similar OSA approach was implemented for family-based association testing, where the family-specific test statistic is a contrast between observed allelic transmissions to affected offspring and expected transmissions under the null hypothesis of no association [Chung et al., 2008].

An adaptation of the OSA algorithm to a case-control dataset, referred to as OSACC, was proposed by McGregor et al. [Macgregor et al., 2006]. Their approach was designed for the situation in which covariate values are only available for cases, not controls (e.g., age at onset of the disease). To test whether the association between single-nucleotide polymorphism (SNP) genotypes and disease status is significantly stronger in a subset of cases, the cases are ordered by ascending (or descending) covariate values, a 2×2 contingency table (allele vs. case-control status) is formed, and an allelic association chi-square statistic is calculated for each subset of cases and all available controls. The case subset with maximum association evidence is identified. As in linkage-OSA, a permutation test is used to assess the significance of the maximized test statistic. To implement this test, the SNP genotypes of cases and controls are permuted and the maximization procedure is repeated to generate an empirical distribution of maximized chi-square statistics. Here, we have extended the previous work in three ways: First, we incorporated covariates measured on controls, as well as cases; second, we implemented multiple different permutation tests in a publicly available software package; third, we evaluated the performance of the different permutation tests under complex disease-generating models with an extensive simulation study. The performance of the OSACC tests was compared to three existing methods for testing an association between a marker and a binary disease phenotype, or to test specifically for G×E interaction: (1) the Cochran-Armitage trend test, which ignores environmental covariates; (2) a previously proposed 2 degree-of-freedom (df) joint test of main genetic effect and G×E interaction [Kraft et al., 2007]; (3) a case-only test of G×E interaction [Piegorsch et al., 1994].

OSACC Algorithm

In the following section, we use the term OSACC1 when only covariate values of cases are considered, as in the previous work [Macgregor et al., 2006], and the term OSACC2 when covariate values of controls are incorporated. OSACC1-risk and OSACC2-risk refer to global tests of association between marker genotype and disease status when allowing for covariate influences. In contrast, OSACC1-hom and OSACC2-hom specifically test whether the strength of association between marker genotype and disease status is significantly different in different parts of the covariate distribution. When a logistic regression model is used to test for association, an overview of the relevant null hypotheses of interest is provided in Table I. This table illustrates that all of the OSACC tests amount to an implicit fitting of two distinct logit models to the entire dataset, but without assuming a pre-specified value of the heterogeneity parameter α. The difference between the “risk” and “hom” tests is that OSACC1-risk and OSACC2-risk test whether the association parameter in the estimated proportion α of the data is different from zero, while OSACC1-hom and OSACC2-hom test for equality of the association parameters in the two subsets defined by α (with estimated proportions α and 1-α, respectively).

Table I.

Null (H₀) and alternative (H₁) hypotheses for the test statistics of interest. α: proportion of individuals in the LD subset, as defined in the text. D, X and G are defined in the text. For the case-only test, G=1 for marker genotypes AA and Aa and G=0 otherwise.

Test	Model	H0	H1
OSACC1-risk	$log(\frac{P(D=1|G,X)}{1-P(D=1|G,X)})={\delta }_0+{\delta }_1^{a}G$ and $log(\frac{P(D=1|G,X)}{1-P(D=1|G,X)})={\delta }_0+{\delta }_1^{1-a}G$	${\delta }_1^a={\delta }_1^{1-a}=0$ ∀ 0 ≤ α ≤ 1	${\delta }_1^a\ne 0$ for some α ∈ (0,1)
OSACC2-risk	$log(\frac{P(D=1|G,X)}{1-P(D=1|G,X)})={\delta }_0+{\delta }_1^{a}G$ and $log(\frac{P(D=1|G,X)}{1-P(D=1|G,X)})={\delta }_0+{\delta }_1^{1-a}G$	${\delta }_1^a={\delta }_1^{1-a}=0$ ∀ 0 ≤ α ≤ 1	${\delta }_1^a\ne 0$ for some α ∈ (0,1)
Trend test	$log(\frac{P(D=1|G,X)}{1-P(D=1|G,X)})={\delta }_0+{\delta }_{1}G$	δ1 = 0	δ1 ≠ 0
Joint 2 df test	$log(\frac{P(D=1|G,X)}{1-P(D=1|G,X)})={\beta }_0+{\beta }_{1}G+{\beta }_{2}X+{\beta }_3(x\ast G)$	β1 = β3 = 0	β1 ≠ 0 or β3 ≠ 0
OSACC1-hom	$log(\frac{P(D=1|G,X)}{1-P(D=1|G,X)})={\delta }_0+{\delta }_1^{a}G$ and $log(\frac{P(D=1|G,X)}{1-P(D=1|G,X)})={\delta }_0+{\delta }_1^{1-a}G$	${\delta }_1^a={\delta }_1^{1-a}$ ∀ 0 ≤ α ≤ 1	${\delta }_1^a\ne {\delta }^{1-\alpha }$ for some α ∈ (0,1)
OSACC2-hom	$log(\frac{P(D=1|G,X)}{1-P(D=1|G,X)})={\delta }_0+{\delta }_1^{a}G$ and $log(\frac{P(D=1|G,X)}{1-P(D=1|G,X)})={\delta }_0+{\delta }_1^{1-a}G$	${\delta }_1^a={\delta }_1^{1-a}$ ∀ 0 ≤ α ≤ 1	${\delta }_1^a\ne {\delta }^{1-\alpha }$ for some α ∈ (0,1)
Case-only test	$log(\frac{P(G=1|D=1)}{1-P(G=1|D=1)})={\gamma }_0+{\gamma }_{3}X$	γ3 = 0	γ3 ≠ 0

Let D, X, and G denote the three variables of interest in a case-control dataset. D=1 for cases and D=0 for controls; X denotes a continuous normally distributed covariate (see Discussion for other types of covariates); G denotes the three possible SNP genotypes AA, Aa and aa. The association of primary interest is between D and G, while X may influence this relationship in various ways. We define a subset of the entire case-control dataset as S={D, X, G}. Let n_D denote the number of individuals with disease status D in S; n_G the number of individuals with genotype G in S; n_D,G the number of individuals with disease status D and genotype G in S; and n the total number of individuals in S. When individuals are sorted by ascending covariate values, the OSACC1 and OSACC2 test statistics are defined as:

$$\begin{array}{l}{T}_{\mathit{\text{OSACC}}1}=\underset{S\in S_{\mathit{\text{OSACC}}1}(x)}{max}\sum _{\text{D}}\sum _G{(n_{\text{D},G}-n\ast \frac{n_{\text{D}}}{n}\ast \frac{n_G}{n})}^2/(n\ast \frac{n_{\text{D}}}{n}\ast \frac{n_G}{n})\\ T_{\mathit{\text{OSACC}}2}=\underset{S\in S_{\mathit{\text{OSACC}}2}(x)}{max}\sum _{\text{D}}\sum _G{(n_{\text{D},G}-n\ast \frac{n_{\text{D}}}{n}\ast \frac{n_G}{n})}^2/(n\ast \frac{n_{\text{D}}}{n}\ast \frac{n_G}{n})\end{array}$$

where

$$\begin{array}{c}{S}_{\mathit{\text{OSACC}}1}(x)=\{(\text{D},X,G):(X\le x\cap D=1)\cup D=0),\\ S_{\mathit{\text{OSACC}}2}(x)=\{(\text{D},X,G):X\le x\}\end{array}$$

The covariate cutoff point x* is unknown a priori and identified by the OSACC algorithm as described below. When sorting individuals by descending covariate values, the subset definitions are:

$$\begin{array}{c}{S}_{\mathit{\text{OSACC}}1}(x)=\{(D,X,G):(X\ge x\cap D=1)\cup D=0),\\ S_{\mathit{\text{OSACC}}2}(x)=\{(D,X,G):X\ge x\}.\end{array}$$

The OSACC algorithm for ascending covariate values can be summarized as follows:

1. Individuals (only cases for OSACC1; cases and controls for OSACC2) are sorted from low to high covariate values.

2. Start with an initial set S of individuals. The default setting for OSACC1 is to initially evaluate the 20 cases with the lowest covariate values and all controls. For OSACC2, the 20 cases and 20 controls with lowest covariate values are analyzed in the first step. Calculate the allelic association chi-square statistic.

3. Add the individual(s) with the next-largest covariate value to the set S. For OSACC1, one case is added; if two or more cases have identical covariate values (ties), they are added together. For OSACC2, the individual added to set S may be a case, a control, or both. As in OSACC1, ties (regardless of case-control status) are added jointly. The allelic association chi-square statistic is re-calculated for the new set S.

4. Repeat step 3 until all individuals have been added into set S. The set S* with the maximum chi-square statistic, and the corresponding covariate cutoff value x*, are then identified. The p-value based on the standard asymptotic distribution of the chi-square statistic is calculated for set S* and denoted p_raw.

5. For OSACC1-risk, permute genotypes of cases and controls, which eliminates any correlation between genotypes and the cases' covariate values and between genotypes and disease status. For OSACC2-risk, permute all three variables of interest (D, X, and G) independently. For OSACC1-hom, permute the covariate values only within the group of cases, which preserves the relationship between genotypes and disease status. For OSACC2-hom, permute the covariate values of cases and controls.

6. Repeat steps 1-4 for each permutation to generate an empirical distribution of maximized chi-square statistics (and hence the minimized p_raw). Under the respective null hypothesis for the four distinct permutation tests (Table I), an empirical p-value is assigned to the identified subset S* as follows: If p_i is the smallest p-value from the i-th permutation, count the number of permutations for which p_i is smaller than p_raw and divide it by the total number of permutations, i.e. $p_{\mathit{\text{emp}}}={\sum }_{i=1}^{K}I(p_i\le p_{\mathit{\text{raw}}})/K$, where K is the total number of permutations and I(x) is the indicator function.

The expected cell count in the 2×2 contingency table for allelic association may be below five, in which case the distribution of the test statistic may not be well approximated by a chi-square distribution. Therefore, the OSACC algorithm applies Fisher's exact test if this situation is encountered at any step, either in the real dataset or in a random permutation. In this case, the subset S* in step 4 is identified as the one generating the smallest p-value for Fisher's exact test.

Evaluation of Power and Type I Error

The goal of our simulation study was to compare the performance of the OSACC permutation tests with three existing methods for testing an association between marker and disease status, or to test specifically for G×E interaction: (1) the trend test, which completely ignores heterogeneity due to clinical or environmental covariates; (2) a flexible joint 2 df test of marginal genetic effects and G×E interaction [Kraft et al., 2007]; and (3) a case-only test of G×E interaction [Piegorsch et al., 1994], which tests for risk heterogeneity across the covariate distribution. While the specific null hypotheses and test statistics for the OSACC permutation tests and the comparison tests are different (Table I), the underlying models can be expressed in very similar forms. The null hypothesis for the OSACC-risk permutation tests and the trend test can be conceptualized as the “no risk” space. The null hypothesis for the 2 df likelihood ratio test (LRT) is similar, but based on a logistic regression model that includes a product term for G×E interaction, as illustrated in Table I and in equation (1) below.

$$log(\frac{P(D=1|G,X)}{1-P(D=1|G,X)})={\beta }_0+{\beta }_{1}G+{\beta }_{2}X+{\beta }_3(X\ast G)$$ (1)

The 2 df LRT is calculated as the ratio of the likelihood function maximized over all model parameters and the likelihood function maximized when β₁ and β₃ are constrained to be zero. The null hypothesis for the OSACC-hom permutation tests can be conceptualized as the “risk homogeneity” space. The null hypothesis for the case-only test, which models the probability of observing the susceptible genotype in cases as a function of their covariate values, is similar to the OSACC-hom permutation tests. However, it evaluates a specific heterogeneity alternative, namely statistical interaction on the multiplicative scale. This interaction induces different levels of association between marker and disease status across the covariate distribution. Under the rare disease assumption, and under independence of G and X in the general population, previous work has shown that the model parameter in the case-only logistic regression model (Table I) is a reasonable approximation of the interaction parameter β₃ in the logistic regression model for the full case-control dataset in equation (1) [Piegorsch et al., 1994; Schmidt and Schaid, 1999].

We used the simulation package SIMLA [Schmidt et al., 2005] to generate case-control datasets (500 cases, 500 controls) under the covariate-based heterogeneity and G×E interaction models. SIMLA uses the logistic regression model in equation (1) as the penetrance function for binary disease outcomes. The intercept β₀ is calculated by the software to satisfy the constraints imposed by the user-specified disease prevalence and all other disease model parameters (marker allele frequency, mode of inheritance, disease odds ratios (ORs)). Our simulation models are summarized in Table II. In the covariate-based heterogeneity model, referred to as “het-model”, β₁ > 0, β₂ = β₃ = 0 in equation (1). In the multiplicative gene-environment (G×E) interaction model, referred to as “G×E-model”, β₁ = β₂ = 0, β₃ > 0 in equation (1). To simulate a heterogeneous dataset, a proportion α of the cases and controls was generated under linkage disequilibrium (LD) between a single genotyped SNP marker and the bi-allelic susceptibility gene, specified as r² (Table II). The proportion α applied equally to cases and controls, and this subset of the dataset will be referred to as the “LD subset”. The proportion (1-α) of the dataset, in which the marker was in complete linkage equilibrium with the disease gene (r²=0), will be referred to as the “no-LD subset”. The disease susceptibility allele frequency was held fixed at 0.3. The desired levels of LD (e.g., r²=1 in the LD subset and r²=0 in the no-LD subset) were simulated by specifying different haplotype frequencies in the two subsets, with each haplotype including the marker and disease locus. Marker genotypes were assumed to be in Hardy-Weinberg equilibrium. Covariates were generated from normal distributions with the means and standard deviations shown in Table II. In the het-model, the covariate is intended to be informative for distinguishing between the LD subset and the no-LD subset; hence, we simulated two distinct normal distributions with different means and the same standard deviation for each subset. In the G×E model, the covariate was simulated from a single normal distribution. All simulation models presented here assumed a log-additive (multiplicative) mode of inheritance. Since the case-only analysis requires a binary response variable, we compared carriers of the susceptibility allele to non-carriers.

Table II.

Simulation models for 500 cases and 500 controls. A log-additive mode of inheritance, disease susceptibility allele frequency of 30% and disease prevalence of 5% are assumed throughout. α: proportion of individuals in the LD subset. OR for het-model: odds ratio per copy of the disease susceptibility allele in the LD subset. OR for G×E model: odds ratio per copy of the susceptibility allele and unit increase of the covariate in the LD subset. μ^α, μ^1−α: covariate mean in the LD subset and no-LD subset, respectively; σ standard deviation of covariate distribution in both subsets. r²: linkage disequilibrium (LD) between genotyped marker and disease susceptibility gene in the LD subset (r²=0 in the no-LD subset).

Model	α	OR	μα	μ1−α	σ	r2
het	0-1	1.0-2.8	20	40	10	0.4-1.0
G×E	0-1	1.0-2.8	25	25	12.5	0.4-1.0

To evaluate the type I error rate of the different OSACC test statistics for a desired significance level of 5%, we generated 5,000 replicates under the null hypothesis of complete linkage equilibrium between the marker and the susceptibility gene in the LD subset, which is equivalent to α=0. To evaluate power, we generated 500 replicates under the different models summarized in Table II. We applied the OSACC algorithm described above to an ascending (het-model) or descending (G×E model) ordering of covariate values. Testing only one covariate order is equivalent to testing a more specific (one-sided) alternative hypothesis, which could be motivated by a previous OSA linkage analysis that is followed up by case-control association mapping. If OSACC is applied with both a descending and ascending ordering of covariate values, the significance level should be adjusted for multiple testing. Our previous development of the APL-OSA method demonstrated that a Bonferroni correction for the two covariate orders is appropriate for maintaining the correct type I error rate [Chung et al., 2008].

Visualization of Simulation Models

In order to visualize the role of the simulated continuous covariate in our two disease-generating models of interest, and to develop intuition for the performance of the test statistics, we used the software SIMLAPLOT [Qin et al., 2007]. For the het-model, Figure 1 shows the probabilities of the three possible marker genotypes conditional on being a case and on having a certain covariate value X=x. At each value of x, the sum of the three conditional probabilities is 1.0. The left panel corresponds to the null hypothesis of no association between marker and disease risk, for which the marker genotype frequencies of cases do not vary across the covariate range and correspond to the expected Hardy-Weinberg equilibrium proportions; the same genotype frequencies would be observed in unrelated controls. The middle panel (α=0.3, OR=2) shows that the allele frequency difference between cases and controls is maximized in the lower covariate range, while cases from the upper covariate range are very similar to controls. Therefore, taking the covariate values into account should increase the power to detect a disease-marker association. The right panel (α=0.7, OR=2) shows that a higher proportion of the “LD subset” leads to an increase in the proportion of cases contained in the lower tail of the covariate distribution. This is expected to reduce the difference in power between methods that do or do not take the covariate into account. In comparison with the het-model, the G×E model generates a more subtle change in genotype frequencies across the covariate range for α=0.3 (Figure 2, middle panel). Here, only the cases from the upper tail of the covariate distribution are informative for the marker-disease association, but much less so. The left panel (null hypothesis) is identical to the one in Figure 1. The right panel illustrates that a similarly strong gradient of change is observed for the het-model and the G×E-model for α=0.7.

Figure 1.

Conditional genotype probabilities for the het-model from Table II (r²=1). The probabilities of each possible marker genotype (aa, Aa, AA), given D=1 (case) and covariate value X=x, are shown. The sum of these probabilities is 1.0 at each value of X.

Figure 2.

Conditional genotype probabilities for the G×E model from Table II (r²=1). The probabilities of each possible marker genotype (aa, Aa, AA), given D=1 (case) and covariate value X=x, are shown. The sum of these probabilities is 1.0 at each value of X.

Results

The results of applying the OSACC algorithm to the case-control datasets simulated under the two disease-generating models (Table II) are described below. The algorithm has been implemented in software that may be downloaded at http://wwwchg.duhs.duke.edu/research/software.html. Details about the software formatting requirements and analysis options are described in a manual that is distributed with the source code and executable. On an AMD ×86 fast processor running Solaris 10, it took approximately 18 minutes to generate and analyze 500 replicates of 500 cases/500 controls each, when 1,000 permutation tests were run on each replicate. A single analysis of a real dataset will, of course, be much faster, and its speed depends primarily on how many permutations are needed to accurately estimate the empirical p-values.

Covariate-Based Genetic Heterogeneity Model

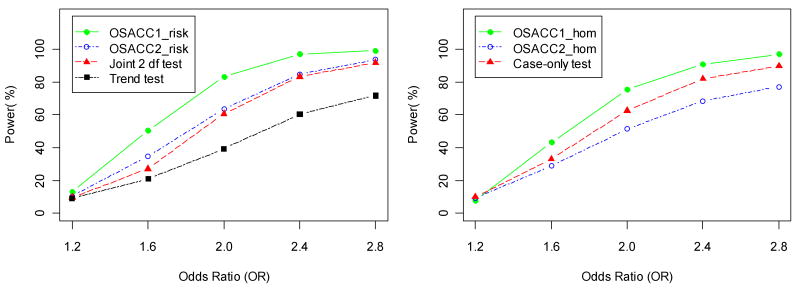
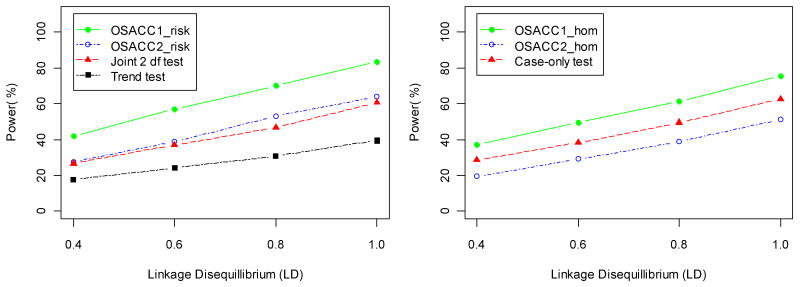
Table III shows power and type I error rates for the simulated het-model with r²=1 in the LD subset, using an ascending covariate order. The first four rows compare the tests of the “no risk” null hypothesis, while the next three rows compare the tests of the “risk homogeneity” null hypothesis. All tests maintained the correct type I error under the respective null hypotheses (first column, α=0). For the het-model, both α=0 and α=1 correspond to the “risk homogeneity” null hypothesis. For 0.1<=α <=0.5, the OSACC1-risk test performed much better than the trend test (e.g., power 83.4% vs. 39.4% at α=0.3), as expected from the SIMLAPLOT visualization (Figure 1). The power difference between OSACC1-risk and the joint 2 df test was smaller (e.g., 83.4% vs. 60.8% at α=0.3). The 2 df joint test, which allows for risk heterogeneity by including a covariate term and G×E interaction term in the regression model, was more powerful than the trend test for α<=0.5. As α approached 1.0, modeling the covariate-based heterogeneity did not improve the power to detect association, relative to the trend test. OSACC2-risk and the 2 df joint test performed very similarly throughout the range of α values. The greater power of OSACC1 is likely due to the fact that all controls are used in the test statistic (rather than a subset, as in OSACC2), which is an advantage as long as there is no substantial variation in their marker allele frequencies across covariate values, e.g., as a result of population stratification (see below). The permutation tests of the “no risk” null hypothesis were more powerful than the tests of the “risk homogeneity” null hypothesis (e.g., 97% power of OSACC1-risk vs. 82% power of OSACC1-hom at α=0.5), which is consistent with previous findings that tests of risk homogeneity tend to have moderate power unless the difference in effect sizes is large [Nam, 1999]. The “risk homogeneity” tests had maximum power at α=0.5, while the “no risk” tests maximized at α=1.0, as expected. The case-only test performed better than OSACC2-hom, but worse than OSACC1-hom. Figure 3 illustrates the change in the power of all seven tests as a function of the main genetic effect (OR ranging from 1.2 to 2.8) for α=0.3, while Figure 4 illustrates the change in power as a function of the LD parameter (r² ranging from 0.4 to 1.0).

Table III.

Estimated type I error and power for the het-model from Table II with OR=2 and r²=1. 5,000 replicates were generated for α=0 (null hypothesis for all tests) and α=1 (null hypothesis for tests of risk homogeneity). 500 replicates were generated for 0.1<=α<=0.9.

	α
	0 (null hypothesis)	0.1	0.3	0.5	0.7	0.9	1.0
OSACC1-risk	0.050	0.326	0.834	0.970	0.988	0.998	1.0
OSACC2-risk	0.051	0.186	0.638	0.916	0.986	0.998	1.0
Joint 2df	0.051	0.138	0.608	0.910	0.982	0.998	1.0
Trend test	0.051	0.11	0.384	0.83	0.986	0.998	1.0
OSACC1-hom	0.051	0.322	0.754	0.820	0.734	0.328	0.050
OSACC2-hom	0.051	0.182	0.514	0.590	0.494	0.244	0.046
Case-only test	0.048	0.196	0.626	0.752	0.618	0.238	0.046

Figure 3.

Power (at significance level 0.05) of the risk tests (left panel) and homogeneity tests (right panel) for the het-model from Table II as a function of the assumed odds ratio (OR) per copy of the disease susceptibility allele in the LD subset, for α= 0.3 and r²=1.

Figure 4.

Power (at significance level 0.05) of the risk tests (left panel) and homogeneity tests (right panel) for the het-model from Table II as a function of the assumed linkage disequilibrium (r²) between marker and disease allele in the LD subset, for α= 0.3 and OR=2.

Gene-Environment Interaction Model

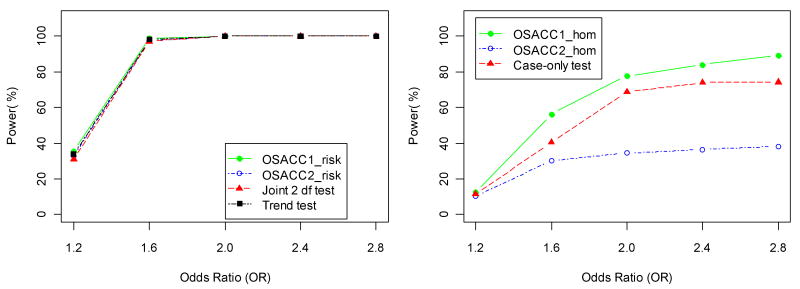
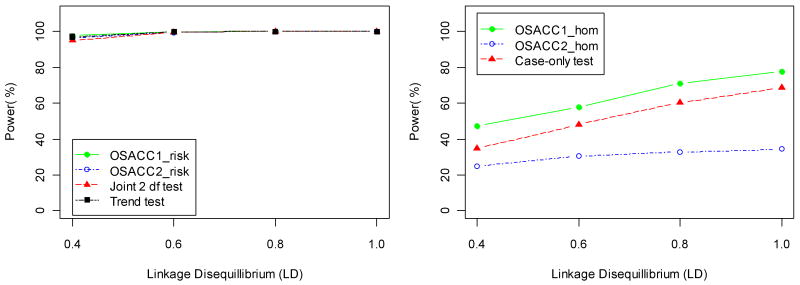
Table IV shows power and type I error rates for the simulated G×E model (with r²=1 in the LD subset and absence of main effects). In this case, the continuous covariate confers an increased disease risk only to carriers of the susceptibility allele. This induces an increasing marginal association between disease status and marker genotypes with increasing covariate values, as illustrated by SIMLAPLOT (Figure 2), and hence, a descending covariate ordering is appropriate. Under the G×E model, all tests maintained the correct type I error under the respective null hypotheses. Note that only α=0 corresponds to the “risk homogeneity” null hypothesis. When α=1, the presence of interaction induces the greatest change in genotype frequencies across covariate values (Figure 2), and hence the three homogeneity tests (OSACC1-hom, OSACC2-hom, case-only test) had maximum power. The power of the homogeneity tests was generally low (<54%) for low values of α (0.1<=α <=0.5), as expected from Figure 2. OSACC1-risk performed better than OSACC2-risk, but the power difference was much smaller than under the het-model and the trend test was essentially equivalent to OSACC1-risk (e.g., at α=0.3, power 78.8% for OSACC1-risk vs. 69.4% for OSACC2-risk vs. 76.4% for the trend test). OSACC2-risk performed similarly to the joint 2 df test across all α values, with both tests having lower power than the trend test at α=0.3, in contrast to the het-model. For larger values of α (≥0.5), all tests of the “no risk” null hypothesis had close to 100% power. For α=0.7, Figure 5 illustrates the change in power of all seven tests as a function of the G×E interaction effect (OR ranging from 1.2 to 2.8). Figure 6 illustrates the change in power as a function of the LD parameter (r² ranging from 0.4 to 1.0). These figures show that it can be valuable to apply the OSACC homogeneity tests even when the OSACC risk tests do not perform better than the standard trend test and the joint 2 df test. We note that the results summarized in Tables III and IV were qualitatively similar under non-multiplicative inheritance models (data not shown).

Table IV.

Estimated type I error and power for the G×E model from Table II with OR=2 and r²=1. 5,000 replicates were generated for α=0 (null hypothesis for all tests). 500 replicates were generated for 0.1<=α<=1.0.

	α
	0 (null hypothesis)	0.1	0.3	0.5	0.7	0.9	1.0
OSACC1-risk	0.051	0.176	0.788	0.988	1.0	1.0	1.0
OSACC2-risk	0.052	0.132	0.694	0.986	1.0	1.0	1.0
Joint 2df	0.054	0.142	0.632	0.970	1.0	1.0	1.0
Trend test	0.055	0.152	0.764	0.986	1.0	1.0	1.0
OSACC1-hom	0.046	0.064	0.244	0.538	0.776	0.888	0.936
OSACC2-hom	0.046	0.056	0.144	0.248	0.344	0.400	0.459
Case-only test	0.049	0.054	0.138	0.370	0.686	0.858	0.945

Figure 5.

Power (at significance level 0.05) of the risk tests (left panel) and homogeneity tests (right panel) for the G×E model from Table II as a function of the assumed odds ratio (OR) per copy of the susceptibility allele and unit increase of the covariate in the LD subset, for α= 0.7 and r²=1.

Figure 6.

Power (at significance level 0.05) of the risk tests (left panel) and homogeneity tests (right panel) for the G×E model from Table II as a function of the assumed linkage disequilibrium (r²) between marker and disease allele in the LD subset, for α= 0.7 and OR=2.

Population Stratification

To evaluate the behavior of the OSACC statistics under population stratification, we simulated two sub-populations with extreme differences in both their covariate distribution and the frequency (p) of the disease-associated marker allele (p=0.3 and μ=20 in sub-population 1 vs. p=0.6 and μ=40 in sub-population 2). When different proportions of cases and controls were sampled from the two subpopulations (20% vs. 60%), all of the risk and homogeneity tests had inflated type I error rates under the het-model. This is expected since the type of population stratification we simulated induced a strong correlation between marker allele frequencies and covariate values (gene-environment correlation) in the absence of association between marker and disease. One way to overcome the effect of population stratification is to frequency-match the cases and controls with respect to the two subpopulations. This approach worked well to control the type I error rate of the OSACC2-risk, joint 2 df and trend test; however, OSACC1-risk continued to have an inflated type I error rate (0.82 for the above example) even under frequency-matching, since a subset of cases was compared to the entire group of “stratified” controls. Two of the homogeneity tests (OSACC1-hom and the case-only test) also continued to have inflated type I error rates under the het-model, even when cases and controls were frequency-matched. Under the G×E interaction model, which is based on a single covariate distribution, all of the risk tests maintained the correct type I error when cases and controls were frequency-matched. The homogeneity tests maintained correct type I error rates regardless of the presence or absence of frequency-matching. While OSACC2 procedures showed some robustness to population stratification, overall, these results demonstrate that procedures to evaluate and correct for population stratification in case-control datasets are still required in order to correctly interpret the results of the OSACC permutation tests.

Study Design for Sequencing Studies

One of the unique benefits of OSACC is the identification of covariate-defined subsets of individuals. Therefore, we evaluated the ability of the OSACC algorithm to identify cases from the “correct” LD subset. We restricted this evaluation to the OSACC1-risk and OSACC1-hom permutation tests since they were more powerful than the corresponding OSACC2 tests under the simulation models considered here. Table V shows the proportion of cases from the simulated LD subset, out of all cases who had marker genotype AA and were included in the OSACC-identified subset, but only if the empirical p-value of the permutation test for the simulated replicate was <=0.05. For comparison, Table V also shows the proportion of cases from the simulated LD subset, out of all cases who had marker genotype AA, if the trend test was significant at the 5% level for the simulated replicate. For the het-model with 0.1<=α<=0.7, the OSACC-identified subset of cases always included a substantially higher proportion of cases from the “correct” LD subset than the entire set of cases; the absolute difference ranged from 58.0% (α=0.1) to 13.6% (α=0.7) (Table V). OSACC1-hom provided a very small improvement over OSACC1-risk. In contrast to the het-model, the proportion of cases from the “correct” LD subset was not substantially higher in the OSACC-identified subset of cases when the G×E model was used to generate the data (Table V). These results demonstrate that OSACC may be very useful for identifying the subset of cases in the current dataset that is most informative for molecular follow-up studies, such as DNA sequencing of gene(s) that harbor variants in LD with the associated polymorphism. While we did not explore whether the OSACC-identified covariate threshold enhanced the expected allele frequency difference between cases and controls in an additional independent case-control dataset, this is likely to be the case as long as at least some fraction of the disease risk in the new dataset is due to the same underlying mechanism. Therefore, the application of OSACC may improve the power to replicate a previously identified association in additional datasets.

Table V.

Proportion of cases from the LD subset, based upon selection of cases by marker genotype AA and membership in the OSACC-identified subset (for replicates with permutation-based p-value<=0.05; first two columns) vs. selection by marker genotype AA alone (for replicates with trend test p-value<=0.05; third column). Het-model and G×E model as described in Table II.

	Het-model (OR=2 and r2=1)			G×E model (OR=2 and r2=1)
α	OSACC1-risk	OSACC1-hom	Trend test	OSACC1-risk	OSACC1-hom	Trend test
0.1	0.743	0.775	0.163	0.256	0.284	0.214
0.3	0.862	0.880	0.444	0.552	0.581	0.510
0.5	0.913	0.926	0.645	0.737	0.744	0.712
0.7	0.945	0.955	0.809	0.868	0.870	0.852
0.9	0.974	0.990	0.941	0.961	0.961	0.956

Discussion

Our results show that OSACC1-risk provides superior power to identify a disease-associated gene in the presence of covariate-based heterogeneity, compared to both the trend test and the previously proposed joint 2 df test. Perhaps more importantly, OSACC is able to identify a subset of patients that is genetically more homogeneous and enriched for one particular susceptibility allele that influences a complex human phenotype. Consistent with our previous work [Schmidt et al., 2008], we found that OSACC works particularly well in the het-model when the subset of interest makes up a moderate proportion (approximately 15-30%) of the available dataset. When it is much smaller, the increase in homogeneity is outweighed by the decrease in sample size [Leal and Ott, 2000]; when it is much larger, methods that ignore the covariate-based heterogeneity (e.g., the Cochran-Armitage trend test) have similar or better power to detect the susceptibility allele of interest, although they fail to provide the additional information about the subset of cases with an enriched allele frequency. With the increasing importance of downstream applications, such as next-generation DNA sequencing of targeted regions in a relatively small number of individuals [Li and Leal, 2009], the identification of such a subset may be just as important as the “gene discovery” itself. It may also be possible to use measures of sequence similarity as an OSA covariate to help zoom in on the causal variant, the expectation being that cases who share a common susceptibility allele are likely to have a more similar sequence surrounding this allele than cases who do not carry this particular allele. The reduction of genetic heterogeneity is also of utmost importance in the context of personalized genomic medicine. For inherently complex diseases, patient heterogeneity is believed to be a major reason for the failure of clinical trials to identify effective treatment modalities [Beghi et al., 2007]. For these reasons, we believe that OSACC makes an important contribution to the area of study design. This has been demonstrated in a recent candidate gene study of cardiovascular disease, which applied the age-of-onset threshold identified by linkage-OSA to an independent case-control association study and found substantially stronger association evidence in the corresponding subset of cases with early disease onset (<38 years of age) [Shah et al., 2009a].

Under the assumption of gene-environment independence, and under population homogeneity, our results demonstrate that methods which evaluate covariate information from cases only (OSACC1) can be substantially more powerful than those that incorporate covariate values of controls (OSACC2), both in terms of detecting a marker-disease association (OSACC1-risk) and of rejecting the null hypothesis of risk homogeneity (OSACC1-hom). This is likely due to reduced variability in the effect size estimates when a larger number of “homogeneous” controls are used for comparison, rather than a smaller subset of controls whose covariate values are matched to cases. The disadvantage of OSACC1-risk is its greatly inflated type I error in the presence of population stratification, even when cases and controls are frequency-matched. For this reason, a significant OSACC1-risk result should initially be interpreted with caution in practical applications. It may reflect an underlying heterogeneity model, but could also be due to population stratification. If available, genome-wide marker data should be used to confirm that cases and controls represent the same genetically homogeneous source population. If they do not, OSACC1-risk should be applied separately to genetically more homogeneous strata of individuals, as identified by clustering or principal components-based methods [Purcell et al., 2007; Price et al., 2006]. If genome-wide data are not available, it should be tested whether allele frequencies at the marker of interest change as a function of common confounders, such as age, sex, and race/ethnicity, and if the covariate distribution is bimodal. If the covariate used for OSACC1-risk can also be measured in controls, and if a similar result is obtained with OSACC2-risk, this supports a genuine association, rather than type I error due to population stratification. However, inconsistent results may also be due to the reduced power of OSACC2-risk to detect an underlying heterogeneity model. Under the G×E interaction model, the OSACC-risk tests do not provide a substantial improvement in power over the trend test. However, as illustrated in Figures 5 and 6, it may still be valuable to apply a homogeneity test like OSACC1-hom to a disease-related covariate of interest. This test has slightly higher power than the case-only test of G×E interaction, and may reveal important changes in the effect size of the disease-associated variant across the covariate distribution. Such changes could be completely missed when only the trend test is applied.

While we focused our attention on simulation models in which the genotype OR that applies to the entire dataset can be expressed as a weighted average of subset-specific ORs, there are other possible disease-generating mechanisms that involve a continuous covariate. For example, in a quantitative trait locus (QTL) model, correlation between genotypes and covariate (trait) values in both cases and controls is induced by a mixture distribution whose weights correspond to QTL genotype frequencies. The covariate values themselves may have an effect on disease risk, and hence the QTL genotypes can be interpreted as “indirect” susceptibility genotypes. One of the best real data examples of this model is the FTO gene (OMIM 610966). It was shown to be a QTL for body mass index (BMI), but was originally detected as a susceptibility gene for type 2 diabetes (T2D), due to the increased T2D risk associated with an increased BMI [Frayling et al., 2007]. We have previously shown that the OSA approach applied to a family-based linkage analysis is sensitive to the presence of a QTL, which represents a special case of correlation between genotype and covariate in the general population [Schmidt et al., 2007]. Unlike the G×E interaction model, for which most of the information is provided by cases rather than controls, the controls are just as informative as cases in a QTL model. Additional simulations (data not shown) confirmed that OSACC2 was almost always more powerful than OSACC1 in this situation.

A benefit of the algorithm implemented in our software is that it is completely nonparametric and generates valid results regardless of the nature and distribution of the OSA covariate (continuous, categorical, or binary). This is due to the fact that the actually observed covariate distribution, including any “tied” observations with identical covariate values, is maintained in each permutation. Another benefit is the algorithm's flexibility with respect to the test statistic that is used to evaluate allelic or genotypic association. An alternative to the allelic chi-square statistic we have presented here would be the Wald statistic for the SNP model term in a logistic regression, to facilitate adjustment for other important covariates. Limitations of the currently implemented OSACC method include the evaluation of only one SNP at a time, as opposed to a haplotype-, multi-locus, or gene-based approach, and the evaluation of a single covariate. In principle, the extension to multiple markers is straightforward and would only require a change in the test statistic that is evaluated for each permutation. While the relative merits of single-locus vs. haplotype-based analyses have been debated for some time [Nielsen et al., 2004], a general consensus has not yet emerged. With few exceptions [Allen and Satten, 2009], association analyses at the genome-wide level have tended to apply single-SNP tests with some adjustment for multiple testing. The extension of the OSACC algorithm to multiple covariates is more challenging. There are at least two possible approaches: One could combine multiple covariates, some of which are likely correlated with one another, into a univariate summary measure prior to applying OSACC; this could be achieved by various multivariate data reduction methods [Shah et al., 2009b]. Another approach would involve a selection of the most important “subsetting covariates” as part of the OSACC maximization process; this could be implemented with recursive partitioning techniques.

In summary, the strengths of the OSACC methodology include (i) the greater power of the OSACC1-risk test to identify a disease-associated gene in the presence of covariate-based heterogeneity, compared to both the trend test and the previously proposed joint 2 df test; (ii) the method's nonparametric nature, including its robustness to outliers, due to the ranking procedure that is applied; (iii) the identification of a case subset that is enriched for a particular susceptibility allele. The latter is useful both for molecular follow-up analyses and for improving the power of an independently collected dataset to replicate previously reported associations that may only be detectable in a fraction of the original and replication datasets.