Facile C-H bond cleavage via a proton coupled electron transfer involving a C-H⋯Cu^II interaction

Abstract

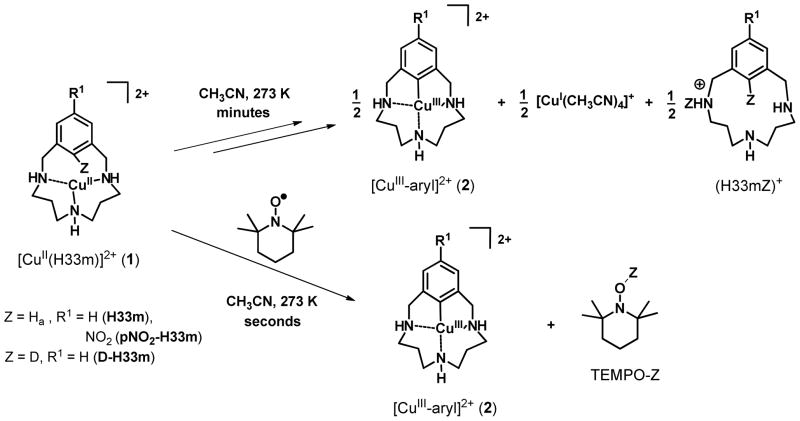
The present study provides mechanistic details of a mild aromatic C-H activation effected by a copper(II) center ligated in a triazamacrocylic ligand, affording equimolar amounts of Cu^III-aryl species and Cu^I as reaction products. At low-temperatures the Cu^II complex 1 forms a 3-center 3-electron C-H⋯Cu^II interaction, identified by pulse-EPR spectroscopy and supported by density functional theory (DFT) calculations. C-H bond cleavage is coupled with copper oxidation, as a Cu^III-aryl product 2 is formed. This reaction proceeds to completion at 273 K within minutes through either a copper disproportionation reaction or, alternatively, an even faster reaction with one-equivalent of TEMPO (2,2,6,6-tetramethylpiperidine-1-oxyl), quantitatively yielding 2. Kinetic studies of both reactions strongly implicate a rate-limiting proton coupled electron transfer (PCET) as the key C-H activation step, a mechanism that does not conform to either the C-H activation mechanism in a Ni^II analogue or to any previously proposed C-H activation mechanisms.

Introduction

Selective activation and functionalization of C-H bonds is a grand challenge of modern chemistry to enhance our ability to convert common hydrocarbon feedstocks to value-added products.^1–4 Activation of ostensibly non-reactive C-H bonds under mild conditions is generally thought to require a metal catalyst operating through a limited number of reaction mechanisms.^5–7 Metal-mediated cleavage of the C-H bond usually proceeds through oxidative addition⁵ or electrophilic metallation,⁶ but other mechanistic proposals such as σ-bond metathesis and σ-complex assisted metathesis (σ-CAM)⁷ have also been proposed. Another attractive pathway involves an initial formation of a weak interaction between a metal (M) and a C-H σ-bond, aptly described as a σ-complex with an agostic C-H⋯M interaction.⁸ The reactivity and selectivity of C-H activation through this mechanism is generally accepted to result from the nature of such σ-complexes, many of which have been structurally and spectroscopically characterized.^9–12 Functionalization of C-H bonds through such an agostic mechanism is possible, albeit generally at elevated temperatures over days and almost exclusively with non-earth-abundant precious second and third row transition metals.^13–19

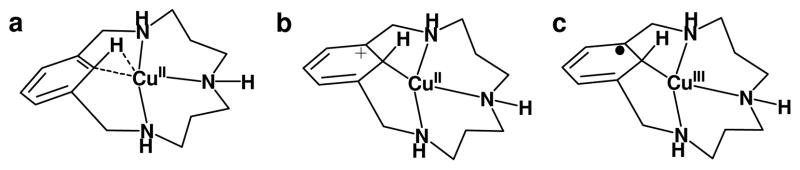
We reported some years ago an intriguing C-H activation reaction effected by Cu^II ligated to triazamacrocyclic ligands that involved a Cu^II disproportionation to afford equimolar amounts of Cu^III-aryl (2) and Cu^I products (Figure 1, top).^20,21 However, the complex kinetic data precluded any simple mechanistic proposal for the rate-limiting step of this reaction. We report here the EPR characterization of the initially formed Cu^II macrocyclic species 1 (using H33m as ligand, Figure 1), which implicate a 3-center 3-electron C-H⋯Cu^II interaction for the C-H group that is activated. The structure of this intermediate species is supported by DFT calculations. Kinetic data obtained by UV-vis monitoring strongly support a mechanism that involves a rate-limiting proton-coupled electron transfer (PCET) step, involving 1 and another Cu^II complex capable of accepting a proton and a electron. This results in a copper disproportionation as Cu^III and Cu^I products are formed. Additional support for this PCET mechanism is the reaction of 1 with TEMPO, affording quantitative formation of the Cu^III-aryl (2) and TEMPO-H (Figure 1). This reaction proceeds even faster than the copper disproportionation reaction. The identification of this unusual C-H activation mechanistic pathway is important to explain the observed facile reactivity under remarkably mild conditions. The resulting Cu^III-aryl product reacts efficiently under mild conditions with nucleophiles such as hydride or nitrogen/oxygen nucleophiles,^22–24 leading to productive functionalization of the aromatic C-H bond, and thereby completing a C-H activation/functionalization cycle. Altogether, this mechanistic understanding provides new insights into the design of new catalysts that effect mild C-H activations via PCET that could be coupled with desired heteroatom functionalization processes.

Figure 1.

Facile C-H activation in the triazamacrocyclic ligands mediated by the reactivity of the C-H⋯Cu^II species in the absence (upper reaction) or with the addition of TEMPO radical (lower reaction).

Experimental Section

Ligands H33m, D-H33m and pNO₂-H33m were synthesized following published procedures^20–22 and characterization of complex 2 was performed accordingly to previous work.²⁰

Synthesis of [Cu^II(H33m)](CF₃SO₃)₂, 1·(CF₃SO₃)₂ and [Cu^II(D-H33m)](CF₃SO₃)₂

Acetonitrile solutions of equimolar amounts of the H33m or the mono-deuterated H33m ligand (D-H33m) and Cu^II(CF₃SO₃)₂ were cooled to 233 K (CH₃CN/liquid-N₂ (LN₂)) and mixed to form a green solution. UV-vis (CH₃CN): λ_max (ε) = 272 (4060), 324 (8500), 425 (960), 640 nm (185 M⁻¹·cm⁻¹). The calculated extinction coefficients assumed a quantitative formation of the 1:1 complex and are not corrected for solvent contraction.

Synthesis of [Ni^II(H33m)(CH₃CN)](ClO₄)₂, 3·(ClO₄)₂

Acetonitrile solutions of equimolar amounts of H33m and Ni^II(ClO₄)₂·6H₂O were mixed at 298 K to give a green solution. UV-vis (CH₃CN): λ_max (ε) = 325 (sh, 180), 385 (sh, 92), 600 nm (27 M⁻¹·cm⁻¹). The calculated extinction coefficients of 3 assumed a quantitative formation of the 1:1 complex and are not corrected for solvent contraction. ¹H-NMR (600 MHz, CD₃CN, 248 K, paramagnetic spectrum): broad signals at 418, 255, 241, 85, 60, 51, 46, 44, 17, −8, −16, −19 ppm. Peaks in the 0–8 ppm range correspond to free ligand (<20%). Similar UV-Vis and ¹H-NMR spectra were obtained for complex, [Ni^II(D-H33m)(CH₃CN)](ClO₄)₂ (Figure S8, Supporting Information).

Synthesis of [Ni^II-aryl](NO₃), 4·(NO₃)

Equimolar amounts of H33m (11.5 mg, 0.049 mmol) and Ni^II(NO₃)₂·6H₂O (14.3 mg, 0.049 mmol) were mixed and stirred in 2 mL of CH₃CN overnight. After filtering, diethyl ether was diffused slowly allowing for the formation of X-ray diffraction quality crystals in a 55% yield (11.3 mg, 0.027 mmol). UV-vis (CH₃CN): λ_max (ε) = 425 (439), 484 nm (sh, 125 M⁻¹·cm⁻¹). ESI-MS (CH₃CN): 290 [Ni^II-aryl]⁺. X-Ray Diffraction details in Table S1, Supporting Information. A similar procedure using Ni^II(ClO₄)₂ yielded 4·(ClO₄). ¹H-NMR (600 MHz, CD₃CN, 298 K): δ = 6.96 (t, 1H), 6.69 (d, 2H), 4,10 (m, 2H), 3.67 (m, 2H), 2.70 (m, 4H), 2.65 (m, 2H), 2.53 (m, 2H), 1,80 (m, 2H), 1,42 (m, 2H). ¹³C-NMR (150 MHz, CD₃CN, 298 K): δ = 124.9, 117.8, 62.9, 50.8, 50.8, 26.8.

Sample preparation for EPR studies

[Cu^II(H33m)](CF₃SO₃)₂, 1·(CF₃SO₃)₂

Equimolar amounts of H33m (8.41 mg, 36 μmol) and Cu^II(CF₃SO₃)₂ were dissolved in butyronitrile (1.5 ml and 0.5 ml respectively) at room temperature. Before mixing, each solution was cooled to 233 K (CH₃CN/LN₂). The resulting intense green solution was stirred for 3 min, after which ca. 120 μl were transferred to a pre-cooled (193 K) X-band EPR sample tube, which was immediately placed into LN₂ yielding a green colored glass. The sample tube was kept frozen throughout the EPR experiments.

[Cu^II(D-H33m)](CF₃SO₃)₂

A similar procedure was followed to prepare the mono-deuterated analogue using D-H33m (9.40 mg, 40 μmol) and Cu^II(CF₃SO₃)₂ (14.50 mg, 40 μmol) in butyronitrile.

EPR spectroscopy details

Continuous wave (cw) EPR measurements at X-band were performed on a Bruker E500 spectrometer equipped with a super-high Q cavity. Experimental conditions: mw frequency, 9.495 GHz; mw power incident to the cavity, 0.2 mW; modulation frequency, 100 kHz; modulation amplitude, 0.1 mT. Sample cooling was achieved using a LN₂ dewar (120 K).

Pulse EPR measurements at X-band (mw frequency 9.748 GHz) were performed on a Bruker E580 spectrometer at 15 K. The field-swept EPR spectrum was recorded via the FID following a pulse length of 500 ns. Davies-ENDOR experiments were carried out with a pulse sequence of π - T - π/2 - τ - π - τ - echo with a π/2 pulse of length 16 ns, a radio frequency pulse of length 10 μs and either a waiting time τ between the pulses of 200 ns or a more selective sequence with a π/2 pulse of length 200 ns and τ of 500 ns.

HYSCORE spectroscopy with the pulse sequence π/2 - τ - π/2 - t₁ - π - t₂ - π/2 - τ - echo were carried out with the following instrumental parameters: t_π/2 = t_π = 16 ns; starting values of the two variable times t₁ and t₂, 96 ns; time increment, Δt = 16 ns (data matrix 400 × 400); in order to eliminate blind-spot artifacts, up to seven spectra were recorded with τ = 100, 118, 136, 160, 178, 240 and 360 ns for [Cu^II(H33m)](CF₃SO₃)₂ and three with τ = 100, 140, 168 ns for [Cu^II(D-H33m)](CF₃SO₃)₂ and summed up. An eight-step phase cycle was used to remove undesired echoes.

The data were processed with the program MATLAB 7.0 (The MathWorks, Natick, MA). The HYSCORE time traces were baseline corrected with a second-order exponential, apodized with a gaussian window and zero filled. After a two-dimensional Fourier transform the absolute-value spectra were calculated. The experimental cw EPR spectra were simulated using the EasySpin package.²⁵ The HYSCORE spectra were simulated with a custom program,²⁶ taking into account peak amplitudes.

Computational details

All geometry optimizations were performed at the B3LYP level,^27–29 with a standard 6–31++G(d,p) basis set³⁰ in the Gaussian03 package.³¹ The geometry optimizations were performed without symmetry constraints and the stationary points found were characterized by analytical frequency calculations. Solvent effects including contributions of non electrostatic terms were estimated in single point calculations on the gas phase optimized structures, based on the polarizable continuous solvation model PCM using CH₃CN as a solvent.³² The solvent effect was introduced by the conductor polarizable calculation model (CPCM).^32–33 The cavity was created via a series of overlapping spheres. Solvent effects were also considered in Time-Dependent DFT (TD-DFT) calculations with the same functional and basis set on 1 and 3. Natural bond orbital (NBO) analysis³⁴ at the same level of theory provided a quantitative picture of the C-H⋯Cu^II interaction in terms of the second order delocalization energy correction (Table S2).³⁵

In addition, local aromaticity changes have been quantified using two probes of local aromaticity based on structure and magnetic properties, respectively. As a structure-based measure of aromaticity, the harmonic oscillator model of aromaticity (HOMA) index (Eq. 1) is used, defined by Kruszewski and Krygowski as:³⁶

$$\mathit{HOMA}=1-\frac{\alpha }{n}\sum _{i=1}^n{(R_{\mathit{opt}}-R_i)}^2$$ (Eq. 1)

where n is the number of bonds considered, and α is an empirical constant (for C-C bonds α = 257.7) fixed to give HOMA = 0 for a nonaromatic model system, and HOMA = 1 for a system with all C-C bonds equal to an optimal value R_opt (1.388 Å), assumed to be achieved for fully aromatic systems. R_i stands for a certain bond length. This index is one of the most effective structural indicators of aromaticity.³⁷ As a magnetic index of aromaticity, the nucleus-independent chemical shift (NICS) proposed by Schleyer and co-workers was used.³⁸ This is one of the most widely employed indicators of aromaticity and it is defined as the negative value of the absolute shielding computed at a ring center or at some other interesting point of the system. A more negative NICS value indicates greater aromaticity. NICS(1) values estimated at 1 Å above the centre of the ring have been also computed.³⁹

Based on the optimized geometry of 1, spin-unrestricted DFT calculations were performed with the Amsterdam Density Functional (ADF 2006.01) package.⁴⁰ The calculation of the hyperfine parameters was performed with the BPW91 functional⁴¹ and an all-electron triple-ζ basis set with double polarization functions (TZ2P) with the scalar relativistic zero-order regular approximation (ZORA) method.⁴²

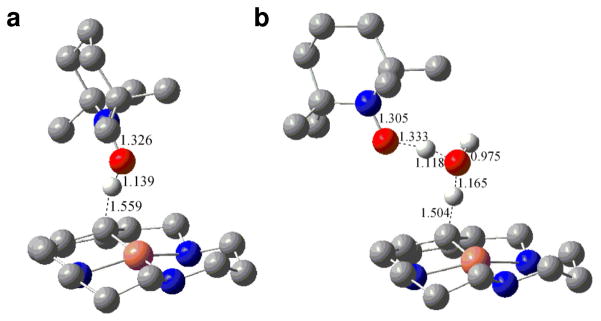
Calculations have been performed on [Cu^II(H33m)]²⁺ (1) and [Ni^II(H33m)(CH₃CN)]²⁺ (3) (Figures 2 and 6, Table S3).³⁵ Compound 1 has a doublet ground state, with the quadruplet state lying 75 kcal mol⁻¹ above in energy. Complex 3 is 6.2 kcal mol⁻¹ more stable in the triplet ground state compared to the lowest-lying singlet excited state, which agrees with the experimental paramagnetic ¹H-NMR spectrum (Figure S8),³⁵ suggesting a non-square planar d⁸-high spin Ni^II species.⁴³ Finally, calculations for the reaction of 1 and TEMPO with and without an interventing water molecule have also been performed (Figure 5).

Figure 2.

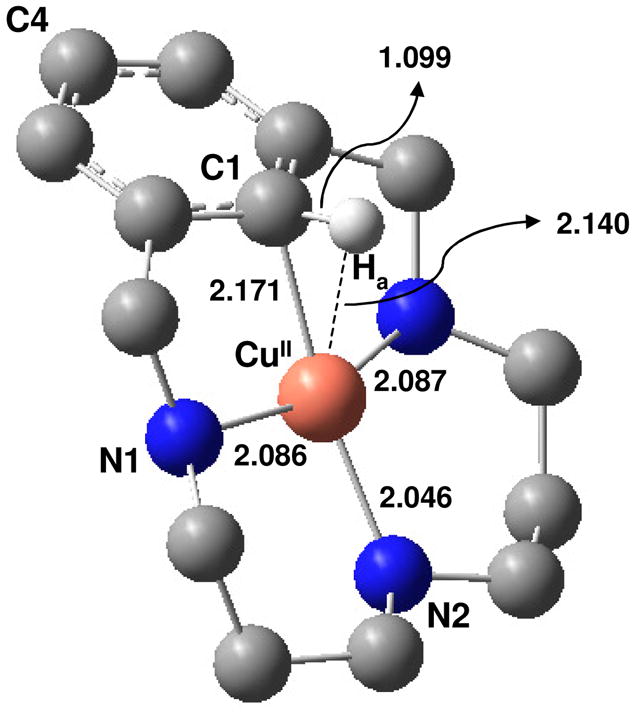
DFT optimized model of 1 with selected bond distances (Å). All hydrogen atoms are excluded except for the H_a involved in the C-H_a ⋯Cu^II interaction.

Figure 6.

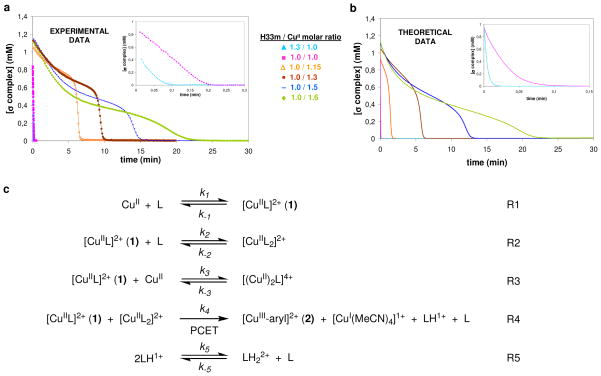
(a) UV-Vis monitoring at 425 nm of the disproportionation reaction of C-H⋯Cu^II species 1 under different H33m:Cu molar ratios at 298 K (inset, decay of 1 for 1.3:1 and 1:1 ratios); (b) Theoretical fit of the data to the 5 step model (k₁ = 1.8·10⁵ M⁻¹s⁻¹, k₋₁ = 7.4·10⁻⁴ M⁻¹s⁻¹, k₂ = 1.8·10⁴ M⁻¹s⁻¹, k₋₂ = 1.9·10⁻⁵ M⁻¹s⁻¹, k₃ = 6.0 M⁻¹s⁻¹, k₋₃ = 9.1·10⁻⁵ M⁻¹s⁻¹, k₄ = 8.0·10³ M⁻¹s⁻¹, k₅ = 8.5·10⁴ M⁻¹s⁻¹ and k₋₅ = 7.3·10⁶ M⁻¹s⁻¹); (c) Proposed model for the C-H activation reaction.

Figure 5.

DFT optimization of transition states for (a) the bimolecular reaction between complex 1 and TEMPO with an energy barrier of 22.9 kcal mol⁻¹, and (b) the same reaction assisted by an interventing water molecule with an energy barrier of 9.0 kcal mol⁻¹.

X-ray diffraction measurements

Crystal structure measurement of complex 4·(NO₃) was performed at 153(2) K on a BRUKER SMART APEX CCD diffractometer using graphite-monochromated Mo Kα radiation (λ = 0.71073 Å) from an X-Ray Tube (Figure 6 and Table S1).³⁵ The measurements were made in the range 2.27 to 31.53° for θ. Full-sphere data collection was carried out with ω and ϕ scans. A total of 22905 reflections were collected of which 4890 [R_int = 0.0566] were unique. The structure was solved by direct methods and refined by full-matrix least-squares methods on F². All non-hydrogen atoms were refined anisotropically. The H-atoms were placed in geometrically optimized positions and forced to ride on the atom to which they are attached. Programs used: data collection, Smart version 5.631 (Bruker AXS 1997–02); data reduction, Saint + version 6.36A (Bruker AXS 2001); absorption correction, SADABS version 2.10 (Bruker AXS 2001). Structure solution and refinement was done using SHELXTL Version 6.14 (Bruker AXS 2000–2003). Cambridge Crystallographic Data Centre (CCDC) deposit number: 726565.

Kinetic simulations

The decay profiles of 1 under different experimental conditions were monitored by UV-vis spectroscopy, and fitted with the KINTECUS program.⁴⁴ The best fitting of the experimental data trends was achieved by first obtaining the best constants for the five-reaction model (Figure 6) for the [H33m]/[Cu^II] molar ratio of 1.0/2.0 ([H33m] = 1.25 mM). Constants k₋₁, k₋₂ and k₋₃ were allowed to vary while the remaining variables were fixed (k₁ = 1.8·10⁺⁵ M⁻¹s⁻¹, k₂ = 1.8·10⁺⁴ M⁻¹s⁻¹, k₃ = 6.0 M⁻¹s⁻¹, k₄ = 8.0·10⁺³ M⁻¹s⁻¹, k₅ = 8.5·10⁺⁴ M⁻¹s⁻¹ and k₋₅ = 7.3·10⁺⁶ M⁻¹s⁻¹). The rate constants that provided the best fit were k₋₁ = 7.4·10⁻⁴ M⁻¹s⁻¹, k₋₂ = 1.9·10⁻⁵ M⁻¹s⁻¹, k₋₃ = 9.1·10⁻⁵ M⁻¹s⁻¹. The calculated decay profiles of 1 for the remaining [H33m]/[Cu^II] molar ratios were obtained without modification of the kinetic constants (Figure 6).

Results and Discussion

Equimolar amounts of Cu^II and the triazamacrocyclic ligand H33m react in acetonitrile at 253 K to form 1 with UV-vis spectroscopic features at 425 and 640 nm (ε = 960 M⁻¹ cm⁻¹, 185 M⁻¹ cm⁻¹, respectively). Upon warming to 273 K, this complex disproportionates, forming equal amounts of 2 and a Cu^I product (Figure 1). The X-ray structure and Cu-K edge X-ray absorption spectrum of 2 indicate a planar, four-coordinate Cu^III center.²⁰ The proclivity of Cu^III and Cu^II to adopt a planar coordination geometry combined with the macrocyclic constraints of the H33m ligand plausibly suggested the existence of a close C-H⋯Cu^II interaction in 1. However, the limited thermal stability of 1 has precluded its crystallographic characterization (t_½ = 100 min, 253 K). A DFT optimized model of 1 predicts a significant tilting of the aromatic ring relative to the planar Cu^II coordination (31°), showing a C-H⋯Cu^II interaction. The key metrical parameters of this model (Figure 2) are comparable Cu⋯C1 and Cu⋯H_a distances (2.17 and 2.14 Å, respectively), an acute C1-H_a⋯Cu^II angle of 77°, an elongated C1-H_a bond compared to the free ligand (1.099 and 1.084 Å, respectively), and nearly equivalent C-C bonds within the benzene ring.^9,45

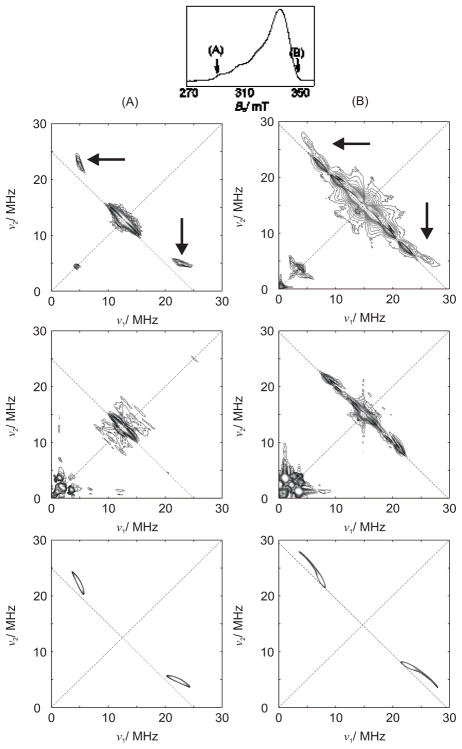
Spectroscopic characterization of the C-H interaction to a paramagnetic metal center such as Cu^II is problematic, as traditional NMR experiments are generally precluded.^17,46 However, direct information on the Cu^II coordination environment in 1 was obtained from Hyperfine Sublevel Correlation (HYSCORE) spectroscopy, a pulsed-EPR experiment,⁴⁷ through regiospecific deuteration of the H_a position. This ligand will be referred to as D-H33m.²² The X-band continuous-wave EPR spectra of the H33m and D-H33m Cu^II complexes are identical and exhibit axial symmetry, consistent with an electronic ground state with an unpaired electron localized in a copper d_x2-y2 orbital. The HYSCORE spectrum shows mainly isotropic hyperfine (hf) interactions positioned at the ¹H Larmor frequency, arising from the surrounding protons. The additional ridge-like patterns, that are displaced significantly from the anti-diagonal in 1 (arrows, Figure 3), are absent in the spectrum of the complex formed with D-H33m. This unambiguously associates these signals with the H_a position. Additionally, in the latter sample, signals in the low-frequency range (2–3 MHz) are observed with a deuterium hf coupling that is consistent with the observed proton hf coupling.

Figure 3.

X-band HYSCORE spectra taken at the observer positions (A) and (B) as indicated in the top figure. First row: 1 formed with H33m. The features that disappear upon mono-deuteration of the ligand are indicated with arrows. Second row: 1 formed with D-H33m. Third row: HYSCORE simulation of the C-H_a interaction of interest.

The HYSCORE parameters for H_a from spectral simulations (A₁ = A₂ = 13 MHz, A₃ = 28.5 MHz, tilt angle (β) of 40–60° between g_|| and A₃) predict a copper to H_a distance of 1.8 – 2.5 Å from the calculated dipolar contribution T = 5.17 MHz. This large range results from assuming either a 100% (pure ionic bonding) or 40% (DFT estimate) localization of the unpaired electron on the copper center. Assuming a mid-range β angle of 50°, the Cu⋯H_a distance is restricted to less than 2.15 Å, very close to that predicted by DFT calculations (2.14 Å).

The experimentally and computationally characterized C-H ⋯Cu^II interaction in 1 is unusual as the accepting orbital on the d⁹ copper center is half-filled, yielding a 3-center 3-electron interaction. A C-H⋯M agostic designation is not formally appropriate as it requires σ donation from a σ_C-H bond orbital to an empty d orbital of the transition metal (3 center-2 electron interaction), with the possibility of back-donation from the metal to the empty σ*_C-H orbital.^8,9 Lacking an unfilled d orbital, this interaction in 1 is probably best described as a σ complex rather than an agostic interaction. Other possible descriptions such as an anagostic type of interaction,⁹ an intermolecular multicenter hetero-acceptor hydrogen bond (IMH),⁴⁴ a Wheland metal arenium intermediate, or a ligand radical species are not consistent with the experimental or calculated data. The tight C-H--Cu^II association measured experimentally and supported by calculations preclude an anagostic designation.⁹ A Natural Bond Orbital (NBO) analysis suggests that the interaction is much too strong to be classified as an IMH; the net σ_C-H to Cu^II second order delocalization energy (Cu^II-d_x2-y2, SOMO in Table S5)³⁵ of 25.5 kcal mol⁻¹ is significantly higher than that for a typical hydrogen bond (1.5 kcal mol⁻¹).⁴⁵ NBO analysis also indicates backdonation from a variety of filled Cu^II orbitals with the proper orientation to the σ*_C-H orbital with a delocalization energy of 2.2 kcal mol⁻¹. A Wheland arenium intermediate involves a significant loss of aromaticity, which is not observed in the optimized structure.^6,48 The absence of expansion of the arene ring⁴⁸ in 1 (d_C-C(average) = 1.404 Å, benzene ring d_C-C(average) = 1.400 Å), and the small decrease of aromaticity of the six-membered ring in 1 compared to H33m ligand (HOMA indexes are 0.963 and 0.909, and NICS(1) indexes are −9.68 ppm and − 7.45 ppm, for H33m and 1, respectively) argue against a metal arenium species or an arene radical species. A ligand radical species is also precluded by the EPR spectrum that clearly indicates a Cu^II center. Indeed, the total spin density observed over the six C atoms of the ring is 0.2 electrons, and the NPA (Natural Population Analysis) charges over C and H atoms of the benzene ring increase by +0.27 with respect to the free ligand, which is in line with a minimum alteration of the aromaticity (Figure 4).⁵⁰ A similar behavior was found for a C-H⋯Rh^I interaction in a pincer-type complex that was described as an agostic interaction.⁵¹ Combined, these results support the designation of 1 as a σ-complex, which to our knowledge is the first example reported for a Cu^II center.^8–9,45

Figure 4.

The C-H⋯Cu interaction in 1 is best described as a C-H⋯Cu^II σ-interaction (a), rather than an arenium species (b) or an aryl-radical-Cu^III species (c).

The C-H activation process may be achieved either by a Cu^II disproportionation reaction or by the addition of one equivalent of TEMPO, a neutral radical species with limited oxidizing abilities.⁵¹ Even though 1 is not detectable by ¹H NMR due to its paramagnetic nature, the diamagnetic products of either reaction are identified readily. A 1:1 ligand:Cu^II(CF₃SO₃)₂ molar ratio in acetonitrile leads to a 1:1 ratio of 2 and the monoprotonated H33m ligand; the Cu^I presumably forms a [Cu^I(MeCN)₄]¹⁺ complex (Figure 1) in which the MeCN ligands exchange with the bulk MeCN solvent. A 1:1:1 ligand:Cu^II(CF₃SO₃)₂:TEMPO molar ratio under similar conditions leads quantitatively to a 1:1 ratio of 2 and TEMPO-H, the latter of which is the one-proton, one-electron reduced form of TEMPO.

The kinetics of both reactions were monitored by the disappearance of the characteristic 425 nm CT band of 1. This CT band results from an aromatic-π to copper d_x2-y2 charge transfer (CT), which traditionally ligated Cu^II complexes do not exhibit. Indeed, time-dependent DFT calculations confirm the nature of this CT band (Table S6).^35,52 In the case of TEMPO, the reaction occurs within seconds at 273 K and 40 minutes at 233 K with a single equivalent. At the lower temperature, the reaction rate is found to be first-order in [TEMPO] and exhibits a kinetic isotope effect (KIE) k_H/k_D of 3.0 for 1 formed with the H33m and D-H33m ligands, respectively. The activation parameters determined (ΔH^‡ = 11.0 ± 0.5 kcal mol⁻¹, ΔS^‡ = −20.4 ± 2.0 cal K⁻¹ mol⁻¹) for the reaction are consistent with a bimolecular association as a rate-limiting step.³⁵ The insensitivity of the reaction rate to changes in the ionic strength of the solution suggests a rate-limiting step involving at least a single uncharged species.³⁵ As TEMPO is only a mild oxidant,⁵³ a bimolecular, rate-limiting PCET step is consistent with this data, in which removal of the inner aromatic C-H proton by the TEMPO radical is coupled directly to the copper oxidation. PCET from heteroatom N-H or O-H bonds of ligands directly coordinated to redox-active metal centers are well documented.^54,55 The addition of a one-electron oxidant such as ferrocenium cation under the same conditions as for TEMPO did not promote degradation of the 425 nm CT band of 1 (Figure S6f).³⁵ To gain further mechanistic insights into this reaction, DFT calculations were run to probe possible transition states (TS) to account for the product formation (Figure 5). The direct reaction of 1 with TEMPO afforded a TS with an energy barrier of 22.9 kcal mol⁻¹, far above the experimental enthalpy of 11 kcal mol⁻¹. A TS more in line with the experimental barrier is found by including an intervening water molecule that serves as a relay; the calculated barrier is 9 kcal mol⁻¹. Apparently, the steric clash of the methyl groups of TEMPO with complex 1 leads to a much higher barrier.⁵⁶ Experimentally, the addition of small amounts of water (ca. 0.2 % v/v) to the reaction solution causes significantly faster decays, in agreement with computational results (Figure S6g).³⁵

The copper disproportionation reaction is much more complicated, as evidenced by its extreme sensitivity to the ligand:Cu^II molar ratio. Ligand in excess of a 1:1 ratio greatly accelerates the disappearance of 1, while excess Cu^II leads to slower, biphasic decays (Figure 6a). The decay of 1 with a 1.3:1 H33m:Cu^II ratio (i.e. excess ligand) is fitted reasonably with a single exponential, as is the decay of 1 formed with D-H33m, yielding a KIE of 2.6 at 286 K. This complicated behavior can be modeled adequately with a 5-step mechanism in which the C-H bond cleavage must be rate-limiting (Figure 6b–c).⁴⁴ Certainly, additional steps provide better fits, but no 4-step mechanism could be obtained that adequately reproduced the biphasic behavior.

The first step involves the formation of the σ C-H complex (1, R1) that reacts subsequently with another equivalent of ligand ([Cu^IIL₂]²⁺, R2, fast) or of copper ([(Cu^II)₂L]⁴⁺, R3, slow). The starting conditions very much impact the copper speciation among these three copper-containing complexes. A rate-limiting bimolecular step between 1 and [Cu^IIL₂]²⁺ is postulated as a PCET reaction (R4), in which C-H bond cleavage involves simultaneous copper(II) oxidation and copper(II) reduction to form [Cu^III-aryl]²⁺, [Cu^I(MeCN)₄]¹⁺, LH¹⁺ and free L products. A facile equilibrium between the mono and diprotonated forms of the ligand (R5) allows additional unprotonated ligand to enter into the reaction.⁵⁷ The third equilibrium (R3) involving copper is necessary in the model to reproduce the biphasic behavior under excess copper conditions.

This mechanistic model predicts that under excess ligand conditions, facile decay of 1 results from an increased concentration of [Cu^IIL₂]²⁺, which is maintained at a low yet nearly constant concentration relative to 1. This allows for the single exponential disappearance of 1 under excess ligand conditions. Such single exponential behavior also occurs by the addition of several equivalents of a trialkylamine base. A 50% yield of the Cu^III-aryl product based on copper is predicted and is measured experimentally. Under conditions of excess copper, the decay of 1 is biphasic. The initial burst in the first phase yields product due to a rapid initial formation of a small amount of [Cu^IIL₂]²⁺; the slower portion of the first phase tracks the formation of [(Cu^II)₂L]⁴⁺. The second phase begins as the concentration of free Cu^II becomes small, allowing the free ligand, which is released upon product formation (R4), to form additional [Cu^IIL₂]²⁺. Positive feedback is created and rapid product formation occurs. Under these conditions, the [Cu^III-aryl]²⁺ yield is predicted and is found to be less than 50% based on the ligand concentration, as the [(Cu^II)₂L]⁴⁺ species does not release significant amounts of copper in the time of the experiment.

The key step in this postulated mechanism is a rate-limiting C-H bond cleavage that involves two different Cu^II species, both of which are dicationic (R4). The linear dependence of log(k_obs) versus (ionic strength)^1/2 under excess ligand conditions³⁵ is inconsistent with any mechanism in which the rate-limiting bimolecular step involves a neutral species, such as a simple base-assisted deprotonation. For instance, a bimolecular disproportionation of 1 to yield [Cu^III(H33m)]³⁺ and [Cu^IL]⁺ is not supported by the data, as the rate limiting step would be a base-assisted deprotonation mechanism with a second order dependence on 1 under all conditions. A sequential two-step mechanism with an initial fast outer-sphere electron-transfer from 1 to [Cu^IIL₂]²⁺ followed by a rate-limiting proton transfer between the resulting [Cu^III(H33m)]³⁺ and a charged base is plausible. However, the faster decay observed with the harder to oxidize [Cu^II(pNO₂-H33m)]²⁺ complex is difficult to reconcile,²¹ especially considering the absence of a potent oxidant. Finally, the kinetic profiles are unaffected under an O₂ atmosphere, which argues against any radical mediated mechanism.

The related paramagnetic, d⁸ Ni^II complex [Ni^II(H33m)(MeCN)]²⁺, 3, also activates the C-H bond in a single exponential process, but the characteristics of this reaction are significantly different; the reaction is at least 10³ slower with a k_H/k_D KIE of 12 at 298 K, is not accelerated by added base or TEMPO, and forms a Ni^II-aryl, 4, not a Ni^III-aryl species, as the final product (Figure 7).³⁵ The DFT optimized structure of 3 show metrical parameters comparable to those of 1. A classical 3-centre 2-electron agostic description is appropriate for 3, with the empty d_x2-y2 orbital as the acceptor. The reaction mechanism to obtain 4 is currently unknown as it does not conform to a base-assisted deprotonation,⁵⁸ and oxidative addition to form a Ni^IV hydride does not have any chemical precedent.

Figure 7.

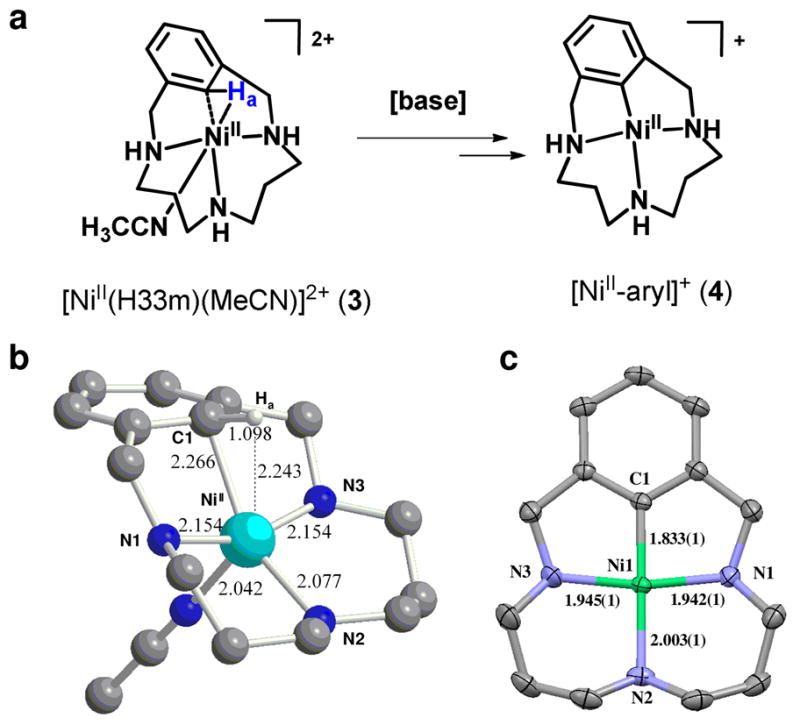
a) C-H bond cleavage in [Ni^II(H33m)(MeCN)]²⁺, 3, to afford [Ni^II-aryl]⁺ complex, 4. b) DFT optimized geometry (B3LYP, 6–31++G(d,p)) of the triplet species 3 (selected bond distances in Å). c) X-ray structure of complex 4·(NO₃) (the ellipsoid representation is at 50% probability; hydrogen atoms and nitrate counteranion are omitted for clarity).

Conclusions

In summary, we have reported a detailed study that covers the key mechanistic aspects of a mild C-H activation process conducted by a triazamacrocyclic Cu^II complex. Low temperature spectroscopic characterization of the intermediate [Cu^II(H33m)]²⁺, 1, suggests an aromatic C-H bond in close proximity to the Cu^II center. A non-conventional σ interaction due to the half filled d_x2-y2 copper accepting orbital is suggested by DFT analysis. Importantly, pulse EPR methods in combination with DFT calculations provide great insights into paramagnetic metal-hydrocarbon interactions when more conventional NMR studies are precluded. The reactivity of 1 has been explored by kinetic UV-vis measurements with the help of isotopic-substitution experiments, both in the absence or presence of TEMPO, suggesting a mechanism controlled by a rate-limiting PCET step. The Ni^II analogue complex 3, shows different kinetic behavior to afford the [Ni^II-aryl]⁺ complex 4 as product, with no changes in the nickel oxidation state. The dramatic differences in the C-H activation steps of the Cu^II and Ni^II complexes formed with the macrocyclic H33m ligand strongly support different C-H activation mechanisms within comparable structures. In the copper case, the accessibility of the +3 oxidation state and the stability of the square-planar [Cu^III-aryl]²⁺ species are presumably key attributes that allow a PCET mechanism, which is absent in the Ni case. Moreover, TEMPO radical does not react with 3 but its reaction with 1 involves the removal of the aryl-hydrogen atom thereby oxidizing the copper center. Given that the O-H bond dissociation energy (BDE) of TEMPO-H is only 72 kcal mol⁻¹,⁵⁴ the C-H⋯Cu^II interaction must significantly weaken this C-H BDE. The recognition of this C-H bond activation via a PCET pathway suggests new routes for designing new metal catalysts that may lead to more effective and selective C-H functionalization reactions under mild conditions.^59–60