Addressing Accuracy and Precision Issues in iTRAQ Quantitation

Abstract

iTRAQ (isobaric tags for relative or absolute quantitation) is a mass spectrometry technology that allows quantitative comparison of protein abundance by measuring peak intensities of reporter ions released from iTRAQ-tagged peptides by fragmentation during MS/MS. However, current data analysis techniques for iTRAQ struggle to report reliable relative protein abundance estimates and suffer with problems of precision and accuracy. The precision of the data is affected by variance heterogeneity: low signal data have higher relative variability; however, low abundance peptides dominate data sets. Accuracy is compromised as ratios are compressed toward 1, leading to underestimation of the ratio. This study investigated both issues and proposed a methodology that combines the peptide measurements to give a robust protein estimate even when the data for the protein are sparse or at low intensity. Our data indicated that ratio compression arises from contamination during precursor ion selection, which occurs at a consistent proportion within an experiment and thus results in a linear relationship between expected and observed ratios. We proposed that a correction factor can be calculated from spiked proteins at known ratios. Then we demonstrated that variance heterogeneity is present in iTRAQ data sets irrespective of the analytical packages, LC-MS/MS instrumentation, and iTRAQ labeling kit (4-plex or 8-plex) used. We proposed using an additive-multiplicative error model for peak intensities in MS/MS quantitation and demonstrated that a variance-stabilizing normalization is able to address the error structure and stabilize the variance across the entire intensity range. The resulting uniform variance structure simplifies the downstream analysis. Heterogeneity of variance consistent with an additive-multiplicative model has been reported in other MS-based quantitation including fields outside of proteomics; consequently the variance-stabilizing normalization methodology has the potential to increase the capabilities of MS in quantitation across diverse areas of biology and chemistry.

Different techniques are being used and developed in the field of proteomics to allow quantitative comparison of samples between one state and another. These can be divided into gel- (1–4) or mass spectrometry-based (5–8) techniques. Comparative studies have found that each technique has strengths and weaknesses and plays a complementary role in proteomics (9, 10). There is significant interest in stable isotope labeling strategies of proteins or peptides as with every measurement there is the potential to use an internal reference allowing relative quantitation comparison, which significantly increases sensitivity of detection of change in abundance. Isobaric labeling techniques such as tandem mass tags (11, 12) or isobaric tags for relative or absolute quantitation (iTRAQ)¹ (13, 14) allow multiplexing of four, six and eight separately labeled samples within one experiment. In contrast to most other quantitative proteomics methods where precursor ion intensities are measured, here the measurement and ensuing quantitation of iTRAQ reporter ions occurs after fragmentation of the precursor ion. Differentially labeled peptides are selected in MS as a single mass precursor ion as the size difference of the tags is equalized by a balance group. The reporter ions are only liberated in MS/MS after the reporter ion and balance groups fragment from the labeled peptides during CID. iTRAQ has been applied to a wide range of biological applications from bacteria under nitrate stress (15) to mouse models of cerebellar dysfunction (16).

For the majority of MS-based quantitation methods (including MS/MS-based methods like iTRAQ), the measurements are made at the peptide level and then combined to compute a summarized value for the protein from which they arose. An advantage is that the protein can be identified and quantified from data of multiple peptides often with multiple values per distinct peptide, thereby enhancing confidence in both identity and the abundance. However, the question arises of how to summarize the peptide readings to obtain an estimate of the protein ratio. This will involve some sort of averaging, and we need to consider the distribution of the data, in particular the following three aspects. (i) Are the data centered around a single mode (which would be related to the true protein quantitation), or are there phenomena that make them multimodal? (ii) Are the data approximately symmetric (non-skewed) around the mode? (iii) Are there outliers? In the case of multimodality, it is recommended that an effort be made to separate the various phenomena into their separate variables and to dissect the multimodality. Li et al. (17) developed ASAP ratio for ICAT data that includes a complex data combination strategy. Peptide abundance ratios are calculated by combining data from multiple fractions across MS runs and then averaging across peptides to give an abundance ratio for each parent protein. GPS Explorer, a software package developed for iTRAQ, assumes normality in the peptide ratio for a protein once an outlier filter is applied (18). The iTRAQ package ProQuant assumes that peptide ratio data for a protein follow a log-normal distribution (19). Averaging can be via mean (20), weighted average (21, 22), or weighted correlation (23). Some of these methods try to take into account the varying precision of the peptide measurements. There are many different ideas of how to process peptide data, but as yet no systematic study has been completed to guide analysis and ensure the methods being utilized are appropriate.

The quality of a quantitation method can be considered in terms of precision, which refers to how well repeated measurements agree with each other, and accuracy, which refers to how much they on average deviate from the true value. Both of these types of variability are inherent to the measurement process. Precision is affected by random errors, non-reproducible and unpredictable fluctuations around the true value. (In)accuracy, by contrast, is caused by systematic biases that go consistently in the same direction. In iTRAQ, systematic biases can arise because of inconsistencies in iTRAQ labeling efficiency and protein digestion (22). Typically, ratiometric normalization has been used to address this tag bias where all peptide ratios are multiplied by a global normalization factor determined to center the ratio distribution on 1 (19, 22). Even after such normalization, concerns have been raised that iTRAQ has imperfect accuracy with ratios shrunken toward 1, and this underestimation has been reported across multiple MS platforms (23–27). It has been suggested that this underestimation arises from co-eluting peptides with similar m/z values, which are co-selected during ion selection and co-fragmented during CID (23, 27). As the majority of these will be at a 1:1 ratio across the reporter ion tags (as required for normalization in iTRAQ experiments), they will contribute a background value equally to each of the iTRAQ reporter ion signals and diminish the computed ratios.

With regard to random errors, iTRAQ data are seen to exhibit heterogeneity of variance; that is the variance of the signal depends on its mean. In particular, the coefficient of variation (CV) is higher in data from low intensity peaks than in data from high intensity peaks (16, 22, 23). This has also been observed in other MS-based quantitation techniques when quantifying from the MS signal (28–30). Different approaches have been proposed to model the variance heterogeneity. Pavelka et al. (31) used a power law global error model in conjunction with quantitation data derived from spectral counts. Other authors have proposed that the higher CV at low signal arises from the majority of MS instrumentation measuring ion counts as whole numbers (32). Anderle et al. (28) described a two-component error model in which Poisson statistics of ion counts measured as whole numbers dominate at the low intensity end of the dynamic range and multiplicative effects dominate at the high intensity end and demonstrated its fit to label-free LC-MS quantitation data. Previously, in the 1990s, Rocke and Lorenzato (29) proposed a two-component additive-multiplicative error model in an environmental toxin monitoring study utilizing gas chromatography MS.

How can the variance heterogeneity be addressed in the data analysis? Some of the current approaches include outlier removal (18, 25), weighted means (21, 22), inclusion filters (16, 22), logarithmic transformation (19), and weighted correlation analysis (23). Outlier removal methods, for example using Dixon's test, assume a normal distribution for which there is little empirical basis. The inclusion filter method, where low intensity data are excluded, reduces the protein coverage considerably if the heterogeneity is to be significantly reduced. The weighted mean method results in higher intensity readings contributing more to the weighted mean than readings from low intensity readings. Filtering, outlier removal, and weighted methods are of limited use for peptides for which only a few low intensity readings were made; however, such cases typically dominate the data sets. Even with a logarithmic transformation, heterogeneity has been reported for iTRAQ data (16, 19, 22). Current methods struggle to address the issue and to maintain sensitivity.

Here we investigate the data analysis issues that relate to precision and accuracy in quantitation and propose a robust methodology that is designed to make use of all data without ad hoc filtering rules. The additive-multiplicative model mentioned above motivates the so-called generalized logarithm transformation, a transformation that addresses heterogeneity of variance by approximately stabilizing the variance of the transformed signal across its whole dynamic range (33). Huber et al. (33) provided an open source software package, variance-stabilizing normalization (VSN), that determines the data-dependent transformation parameters. Here we report that the application of this transformation is beneficial for the analysis of iTRAQ data. We investigated the error structure of iTRAQ quantitation data using different peak identification and quantitation packages, LC-MS/MS data collection systems, and both the 4-plex and 8-plex iTRAQ systems. The usefulness of the VSN transformation to address heterogeneity of variance was demonstrated. Furthermore, we considered the correlations between multiple, peptide-level readings for the same protein and proposed a method to summarize them to a protein abundance estimate. We considered same-same comparisons to assess the magnitude of experimental variability and then used a set of complex biological samples whose biology has been well characterized to assess the power of the method to detect true differential abundance. We assessed the accuracy of the system with a four-protein mixture at known ratios spanning a -fold change expression range of 1–4. From this, we proposed a methodology to address the accuracy issues of iTRAQ.

EXPERIMENTAL PROCEDURES

Table I summarizes the data sets used in this analysis. Detailed experimental procedural information is available in supplemental Experimental Design document. To evaluate experimental variability in the iTRAQ system, we prepared same-same data sets for which an aliquot of the same sample was labeled by each of the available isobaric tags and then combined prior to peptide separation and quantitation. Same-same data sets were collected for different sample types, quantitation systems, MS/MS systems, and for both the 4- and 8-plex labeling systems. To investigate iTRAQ accuracy, an experiment was prepared with a background of proteins at an unchanging level but with the addition of four spiked proteins of known ratios (Table II). Two of the proteins were present at 1:1 to allow data normalization to adjust for tag differences. To examine the approach on a complex biological system with biological differences, iTRAQ data were collected from yeast grown under various nutritionally limiting conditions.

Table I. Summary of various data sets used within this study.

Study type	Sample type (data set name)	iTRAQ system	LC-MS/MS system	Quantitation system
Same-same	Erwinia (Erwinia B)	4-Plex	QSTAR	i-Tracker
				Mascot
	Erwinia (Erwinia C)	4-Plex	QSTAR	i-Tracker
				Mascot
	Erwinia	4-Plex	OrbitrapXL	Mascot
	Phosphorylase B	8-Plex	QSTAR	Mascot
			OrbitrapXL	Mascot
Known ratio	Proteins at known ratios	4-Plex	QSTAR	i-Tracker
			Premier
Biologically unknown	Yeast grown under nutritionally limiting conditions	4-Plex	QSTAR	i-Tracker

Table II. Breakdown of proteins included in known ratio preparation and level of these proteins for each TRAQ reporter tag.

Protein	114	115	116	117
BSA	1	2	3	4
Cytochrome c	1	1	1	1
Enolase	4	3	2	1
Phosphorylase b	1	1	1	1

RESULTS

Raw Data Analysis

Data Sampling Characteristics of iTRAQ

Examining the peptide-level data highlights an unbalanced peptide sampling; some peptides are sampled many times, whereas the majority of peptides are only sampled once or twice (supplemental Fig. 1). At the protein level, this leads to some proteins having only one reading, whereas others have hundreds. The majority of these peptide readings are low volume, and hence to maximize the sensitivity of the study it is desirable to keep these peptides for the data analysis (supplemental Fig. 2). The volume distribution arises as sampling of peptides is not random but rather occurs as a result of a data-dependent selection process in the MS for the high intensity peaks beyond any exclusion list/dynamic exclusion process applied. This limits iTRAQ to relative level comparison only (i.e. comparing ratios).

Fragmentation Behavior

To assess biases and variability in fragmentation, we examined the ratio between reporter ion maximum intensity and the 145-Da peak maximum intensity in the phosphorylase b data set, whose high sampling depth allowed analysis at the peptide level. The 145-Da peak arises from incomplete fragmentation and is composed of the balance group attached to the 114–117-Da reporter group. The mass of 145 Da is common to all four 4-plex tags. We considered the top 31 sampled peptides (which comprise 50% of the data set). The data were filtered by removing peptide readings if they contained missing reporter ion values or if two or more of the reporter ion peak maximum intensities were below 15 counts. First, we found fragmentation efficiency to be peptide-dependent; this is shown by the different ratios for different peptides between the reporter ion and the 145-Da peak intensities (supplemental Fig. 8). Second, fragmentation efficiency was consistent across tags within an experiment run (data not shown); this is unsurprising because with the iTRAQ system fragmentation of the four reporter ion occurs simultaneously. These results provide further support for preferring relative level comparisons over raw measurements.

Heterogeneity of Variance: Variance-Mean Dependence

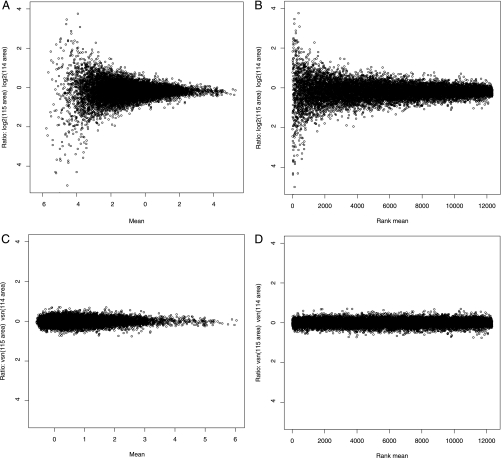
The previous sections used the standard i-Tracker filtering method. To understand the variance behavior fully, all quantified peptides were included in the analyses from this point on. Ratio-intensity (RI) plots were used to assess the distribution of ratios as a function of average signal strength (Fig. 1). Although Fig. 1, A and B, show that the center of the distribution of log ratios has no significant intensity-dependent systematic bias in agreement with the findings of Hu et al. (16), the width of the distribution is significantly larger at low intensities than at high intensities. This heterogeneity of variance has been seen previously in iTRAQ data collected with a 4700 Proteomics Analyzer (Applied Biosystems) and analyzed with GPS Explorer (Applied Biosystems) (16) and independently with data collected with a QSTAR when analyzed with ProQuant v1.1 (21).

Fig. 1.

RI plots for log ratio of 115 to 114 reporter ions against average reporter ion signal in the Erwinia same-same data set B. These plots are used to assess the distribution of ratios as a function of signal strength. In A and B, the y axis shows the logarithm (base 2) of the ratios; in A, the x axis is proportional to the mean, and in B, the x axis is proportional to the rank of the mean. Choosing the rank of the mean for the abscissa distributes the data points evenly along the x axis and helps with the visual assessment of distribution width; when the x axis is simply the mean, the uneven distribution of the data along the x axis range can confound the visual assessment. In C and D, VSN ratios (or generalized log ratios; see “Variance-stabilizing Transformation”) are shown on the y axis; in C, the x axis shows the mean, and in D, the x axis shows the rank of the mean. For the display of A and B (logarithm transformation), data were filtered to remove zero and negative values, whereas all data are shown in C and D (VSN transformation).

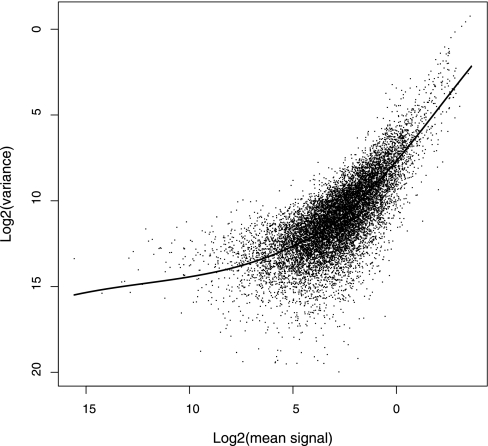
The logarithm transformation has been suggested previously for iTRAQ data with the objective of addressing the heterogeneity of variance (19, 21). However, Fig. 1, A and B, show that the logarithm transformation does not sufficiently stabilize the variance. To further investigate the error structure, the relationship between the mean and the variance on the log scale for the four tags for each peptide reading after normalization was assessed for each data set; a representative case is shown in Fig. 2. The plot is consistent with the additive-multiplicative (two-component) error model: a multiplicative component, with a leading exponent of 1 on the log-log plot, dominates at high intensities. At low intensities, the variance tends to be a constant, signal-independent value because of an additive component.

Fig. 2.

Relationship between logarithm (base 2) of mean signal and logarithm (base 2) of its variance. The solid line shows a smooth regression line calculated by local polynomial regression. Shown is Erwinia data set B. No prior intensity-based data filtering was performed.

Variance-stabilizing Transformation

Many measurements in physics and chemistry follow a multiplicative error model. Consider a quantity whose true value is x and measurements of which result in observed values x(1 + ε) where ε represents small, positive or negative random numbers. Then the standard deviation of the measurements is x times the standard deviation of ε. When transformed to the logarithmic scale, the measured values are (to good approximation) log x + ε, and the standard deviation is simply the standard deviation of ε, independent of the true value x. This transformation is therefore referred to as a variance-stabilizing transformation, and the concept can be generalized to the additive-multiplicative error model. The variance-stabilizing transformation in that case is called the generalized logarithm (34–36), and it resembles the usual logarithm transformation at the upper end of the intensity scale (where multiplicative effects dominate), a linear transformation at the lower end (where additive effects dominate), and interpolates smoothly in between (supplemental Fig. 3). Furthermore, if we define the usual log ratio between two peak intensities I₁ and I₂ as

then a generalized log ratio can be defined as follows.

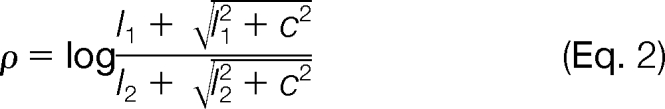Here c is a data-dependent constant; more specifically, it depends on the mean and standard deviation of the additive error component. For values of I₁ and I₂, both much larger than c, the generalized log ratio ρ simplifies to the usual log ratio. ρ is compressed toward 0 compared with q; i.e. its absolute value |ρ| is always smaller than |q|. The size of this shrinkage depends on the size of I₁ and I₂, becoming more pronounced as I₁ or I₂ gets smaller. The VSN software (33) can be used to fit the parameter c of the generalized logarithm. In addition, it allows a simultaneous affine-linear (shift and scale) normalization to adjust the data for systematic, label-, or sample processing-associated biases. Like other global normalization methods, the VSN algorithm uses the assumption that the majority (50% or more) of intensity values are truly not changing in expression.

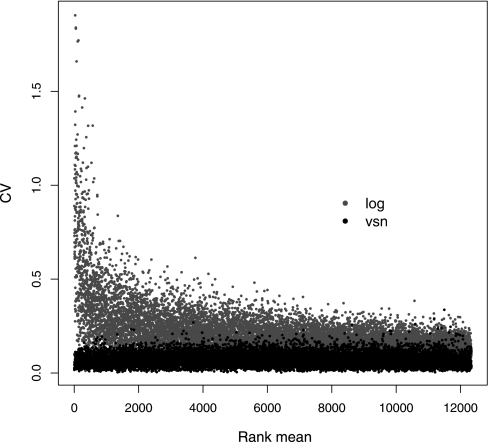
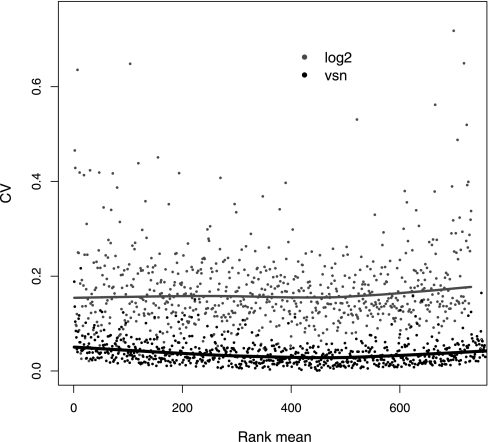
The result of the generalized log (VSN) transformation on the Erwinia same-same data set is shown in Fig. 1, C and D: the variation of the generalized log ratio is independent of the signal strength. The CV is frequently used as a measure of variability. Fig. 3 shows, with the grey dots, the heterogeneity of the CV as a function of average signal seen with log₂-transformed data. In the proteomics community, techniques are frequently compared via single CV summary values (21). However, as Fig. 3 shows, because of the heterogeneity and intensity dependence of the CV, summaries such as “median CV” are generally too simplistic and may be misleading. Fig. 3 also contrasts this behavior with that of the data transformed by the VSN transformation: their CV is approximately constant, and it coincides with the CV of the logarithm-transformed data at high intensity levels. For medium or low intensities, the CV of the VSN-transformed data is reduced compared with that of the logarithm-transformed data.

Fig. 3.

CV versus signal intensity comparison for log₂-(grey) and VSN (black)-transformed data for Erwinia data set B. No prior intensity-based data filtering was performed.

In the Erwinia data set of Fig. 3, the high intensity convergence is not reached, which suggests that the MS data were not collected over the full dynamic range. However, it was seen with the phosphorylase b data set (supplemental Fig. 4). The phosphorylase b sample is a simpler sample with individual peptides at much higher signal strengths. The CV following VSN transformation was smaller with the phosphorylase b data set compared with the Erwinia data sets but was similar between the Erwinia experiments. This is unsurprising as the Erwinia data sets had an additional separation stage (SCX) and were derived from a more complex sample.

To demonstrate that the phenomena reported here are independent of the analysis software and MS/MS collection system, the phosphorylase b QSTAR 4-plex data were reprocessed with Mascot v2.2.0 (Matrix Science, London, UK), and the LTQ-OrbitrapXL 4-plex data were processed with Proteome Discoverer (Thermo Fisher) and Mascot v2.2.0 (Matrix Science) using the default settings for quantitation. For both packages, the data behavior was essentially identical to that reported above: no significant systematic intensity-dependent bias of the mean, presence of heterogeneity of variance, consistency with the additive-multiplicative error model, and variance stabilization by the generalized logarithm transformation as fit by the VSN software (supplemental Figs. 4–6).

To increase throughput, an 8-plex iTRAQ version has been released (Applied Biosystems). The 8-plex version relies on the same amine-labeling chemistry of peptides as with the 4-plex reagents. The 8-plex version has a modified tag compared with the 4-plex version and a larger balance group. Additional reporter ions at 113, 118, 119, and 121 m/z are liberated during CID of the 8-plex tags enabling increased multiplexing of samples in experiments quantifying protein expression. To ensure that the behavior being addressed is universal to iTRAQ irrespective of which sets of tags are used, same-same phosphorylase b 8-plex labeled sample was injected on the LTQ-OrbitrapXL. The data were processed with Mascot v2.2.0 (Matrix Science) for quantitation using the default settings for quantitation. Again, data behavior was essentially identical to that reported above (supplemental Fig. 7).

From Peptides to Protein: Complex Structure

Although the measurements are made at the peptide level, interest often lies at the protein level, and a method is needed to summarize the peptide-level readings into a single, robust relative abundance estimate for each protein. A variety of approaches have been suggested for this task; they differ in how they address the different potential biases and the potentially different amount of confidence (precision) in each peptide-level reading. Here, we first discuss these issues and then present our approach.

Issues within Reducing Peptide Measurements to a Value per Protein

We have broken down issues surrounding the combining of peptide-level measurements to form a single protein measurement into four subsections as follows.

Fraction Effect

We define a “fraction effect” within a peptide as a significant dependence between the measured ratio and the fraction in which the reading was taken. The top 10 sampled peptides from Erwinia data sets B and C were examined for a fraction effect by grouping the VSN-transformed data by fraction and using a one-way analysis of variance to assess a significant difference in the mean between groups. Only fractions that were sampled more than three times were included in the analysis. 45% of the peptides had a statistically significant difference between fraction groups, and the percentage of the variance explained by the fraction effect varied between 37.0 and 86.5% (average, 57.1%). From this analysis, we concluded for these peptides that the fraction effect was significant. With the phosphorylase b data set, no statistically significant differences were seen between repeat injections, indicating that the fraction effect arose not from the repeat injections but rather from the separation (SCX) stage. Note that a fraction effect was also seen with log-transformed or raw data when a Kruskal-Wallis test was used (data not shown). These results indicate that the error within a fraction group for a peptide is smaller than the error between fraction groups and is arising not from the repeat injections but from additional variance from the repeated SCX separation.

Peptide Effect

We define a “peptide effect” within a protein as a significant dependence between the measured ratio and the precursor ion (i.e. peptide). Because of the fraction effect, insufficient numbers of readings were obtained per peptide to consider a peptide effect for the Erwinia data sets. The phosphorylase b data sets, however, were designed to get multiple readings for each peptide, and an analysis of variance was used to test for a significant difference in the mean ratio between peptides. Only peptides that were sampled more than three times were included in the analysis. The percentage of the variance explained by the peptide effect varied between 13.1 and 78.5% (average, 54.0%) depending on the tag combination examined. This peptide effect was observed for both MS instrumentations and for all software packages analyzed. These results indicate that the measurement error within a peptide group for a protein is smaller than the error between peptide groups.

Intensity Effect

As described in the previous section, the variance and hence the confidence intervals of the readings are different in different parts of the dynamic range. It is uncommon to have a large number of replicate readings for each peptide; hence estimating that variance directly is impractical. We proposed applying the VSN, which puts the data on a scale on which intensity effects on the variance are removed but are traded for an intensity-dependent conservative bias, that is, shrinkage toward ratios of 1 when the intensities are small.

Data Distribution

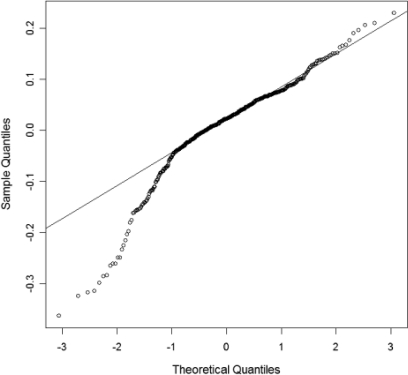
To investigate the data distribution and ensure the appropriate application of statistical tools, we plotted frequency histograms and normal quantile-quantile plots for the readings of the top 10 sampled peptides from the phosphorylase b data set after VSN normalization (Fig. 4). The data distributions were localized and unimodal, resembling a combination of a normal distribution with outliers. This was found for data obtained with or without the i-Tracker standard low volume filter which discards a precursor ion if fewer than three of the resulting reporter ions are above a threshold of 15 counts (37).

Fig. 4.

Example normal quantile-quantile plot as typical distribution profile for peptide from the phosphorylase b data set with standard i-Tracker low volume filtering.

Estimating Protein Ratio

First, we compute a robust central tendency measure for each protein, such as the trimmed average of the VSN-transformed peak intensities of all the peptides belonging to the protein. Differences between these quantities for different conditions then measure the differential abundance of the protein between the conditions. In doing so, we ignore the fraction and peptide effects described under “Fraction Effect” and “Peptide Effect” and accept the conservative variance-bias trade-off of the generalized log-ratio described under “Intensity Effect.” Although it is conceivable that a mathematical model could be constructed that explicitly models and adjusts for these effects, such an approach would likely be complicated by unbalanced data structure (“Data Sampling Characteristics of iTRAQ”), often with few readings at each level, and by fragility to outliers and model misspecification. Here we argue that although ignoring these effects might potentially incur suboptimal estimates the disadvantage is by far offset in practice, at least with data from current experiments, by the simplicity and robustness of the above approach.

Fig. 5 shows the CV, at the protein level, of protein abundance estimates where peptide data were combined with a 20% trimmed mean. The CV was calculated at the protein level using the ratio obtained from the six different possible tag combinations. For comparison, the CVs of protein abundance estimates are also shown when the ordinary logarithm transformation was used instead of the generalized logarithm of VSN. With VSN, the CV showed no signal strength dependence and was generally lower than with the logarithm.

Fig. 5.

Comparison of CV versus mean behavior for log₂- versus VSN-transformed data at protein level when trimmed mean (20%) approach was used. The solid line shows a moving average calculated with a local polynomial regression. One data point from the log data set was removed for visual clarity as it had a high CV of 1.5. This analysis was completed on Erwinia data set B where no intensity-based data filtering had been performed beyond the peptides being unique for a protein and the peptide being confident in its assignment to a protein.

Selecting Significance Threshold

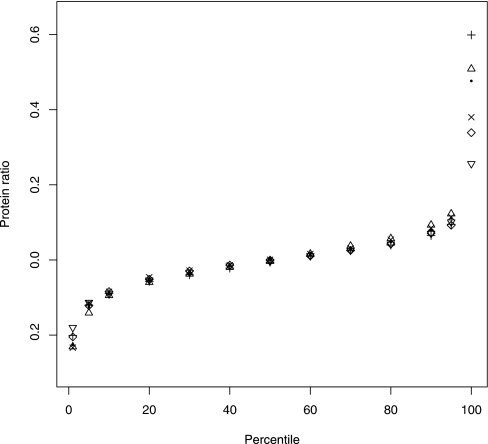
In the simplest situation, iTRAQ is used in a pairwise comparison (10, 18, 21, 38, 39). A protein is deemed to be differentially abundant if measured ratios exceed a certain threshold. The threshold is chosen such that it encompasses the majority of technical variation in a same-same comparison. This analysis approach assumes that the samples being compared are representative of the population and takes no account of biological variation. The thresholds that encompass 90 and 95% of the experimental variation were found to be reproducible across different tag combinations (Fig. 6 and Table III). For the Erwinia data sets a ±1.1-fold change threshold encompassed 95% of the experimental variation after a trimmed mean estimation of protein ratio using VSN-transformed data was used. Thus, the experimental variation is so low that proteins with low changes in expression will be detectable in a pairwise comparison, although the researcher will need to assess whether such a change is biologically significant.

Fig. 6.

Example of reproducibility of protein VSN ratio in same-same experiment across various tag combinations. The protein ratio was estimated by calculating a 20% trimmed mean using all the unique peptide readings for a protein. This analysis was completed on Erwinia data set B where no filtering was done beyond the peptides being unique for a protein and the confidence of the peptide to protein assignment. The tag combinations are represented as follows: dot, 115-114; triangle, 116-114, plus, 117-114, ×, 116-115, diamond, 117-115; and upside-down triangle, 117-116.

Table III. Average experimental thresholds as VSN ratio and -fold change that would encompass either 95 or 90% of naturally occurring technical variation for both same-same Erwinia data sets.

The average threshold was calculated for each data set as with four tags there are seven possible pairwise comparisons, and a 95% confidence interval is reported to give a measure of consistency. This analysis was completed where no filtering had occurred beyond the peptides being unique for a protein and the peptide being confident in its assignment to a protein.

Percentile	Mean log ratio (VSN1−VSN2)	95% confidence intervals for the mean log ratio		Mean-fold change	95% confidence intervals for mean -fold change
		Lower	Upper		Lower	Upper
Erwinia B
2.5	−0.15	−0.16	−0.13	0.90	0.89	0.91
5	−0.12	−0.13	−0.10	0.92	0.92	0.93
95	0.11	0.11	0.12	1.08	1.08	1.09
97.5	0.14	0.14	0.15	1.11	1.10	1.11
Erwinia C
2.5	−0.12	−0.13	−0.11	0.92	0.91	0.93
5	−0.09	−0.10	−0.09	0.94	0.93	0.94
95	0.09	0.09	0.09	1.06	1.06	1.06
97.5	0.11	0.11	0.12	1.08	1.08	1.09

Validation: Application to Real Data

Both a log transformation with ratiometric normalization and the VSN transformation were applied to data from a biological study comparing yeast grown under various nutritionally limiting conditions (40). The variability of the data from yeast samples was found to be higher than in the Erwinia study (Table IV). For both the VSN- and log-transformed data, when biological differences were present, they were reflected by the protein ratios (Fig. 7). For example, for the carbon- versus nitrogen-limited samples, the top 10 proteins, as judged by the largest -fold change, were searched for function information in the Saccharomyces cerevisiae genome database. Eight of the 10 proteins had database information indicating change in expression triggered by carbon or nitrogen source change limitation. The findings were also in agreement with the transcriptome, endometabolome, and exometabolome metabolic control analysis of yeast grown under nutritionally limiting conditions by Castrillo et al. (40).

Table IV. Thresholds calculated from same-same sample comparison of pooled sample in yeast study for various percentile positions for both log- and VSN-transformed data.

Percentile position	log2-transformed		VSN-transformed
	Protein ratio	-Fold change	Protein ratio	-Fold change
2.5	−0.37	0.77	−0.25	0.84
5	−0.29	0.82	−0.2	0.87
95	0.27	1.2	0.2	1.15
97.5	0.33	1.26	0.24	1.18

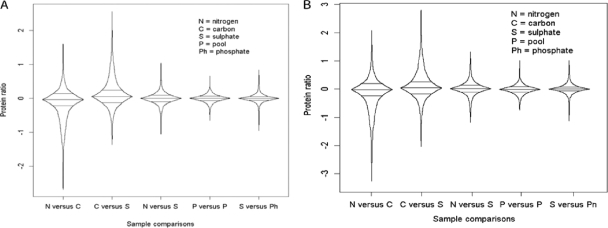
Fig. 7.

Box percentile plot comparing protein ratio distribution across various sample comparisons where protein ratio was calculated as 20% trimmed mean from peptides contributing to that protein. A, VSN-transformed data. B, log₂-transformed data with ratiometric normalization. x versus y indicates that sample x values have been divided by sample y values.

The VSN-transformed data identified considerably more proteins as having significant change in expression compared with the log-transformed data (Table V). The greater sensitivity with the VSN method arose from the reduced variability of the peptide readings used to estimate the protein ratio (supplemental Fig. 9) and was also reflected by the lower sensitivity threshold with VSN (Table IV).

Table V. Percentage of proteins identified as having significant changes in expression between various samples compared when 97.5 and 2.5% threshold were used.

Samples compared	Number of proteins		Protein identified as having significant changes in expression (%)
	VSN	log	log2		VSN
			Up-regulated	Down-regulated	Up-regulated	Down-regulated
Nitrogen-limited versus carbon-limited	1042	1038	7.10	17.18	14.26	22.74
Carbon-limited versus sulfate-limited	1042	1040	21.02	11.13	25.29	14.23
Nitrogen-limited versus sulfate-limited	1042	1036	7.10	4.51	5.89	5.41
Sulfate-limited versus phosphate-limited	923	923	2.71	1.63	0.29	0.18

Accuracy

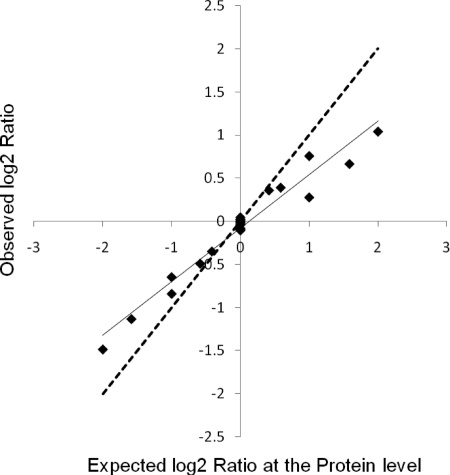
The above analysis focused on the precision of the iTRAQ technology. Concerns have been raised that iTRAQ might have problems with accuracy by systematically underestimating ratios (23–27). To assess this question, we prepared a sample with proteins at known ratios. Our findings confirmed that there is systematic ratio underestimation in iTRAQ quantitation. However, we observed a linear relationship between the observed and the expected ratios at the protein level over the 4-fold range difference examined (Fig. 8). Consistent with underestimation, the gradient of the linear relationship was less than 1, and the underestimation became more obvious for larger ratio changes. This effect was seen on both data collected with a QSTAR and with a QTof Premier, suggesting that the effect is ubiquitous and not dependent on the MS technology used. It has been suggested that this underestimation arises from contaminating peptides with similar m/z ratios during ion selection prior to collision-induced dissociation (23, 27). A quantitative model reveals that when the relative amount of contamination is the same within an experiment a linear relationship between observed and true ratios is expected and would be independent of signal strength. We observed this in our data: RI plots at the peptide and protein levels show no systematic deviations in the ratio observed with signal strength (data not shown). If the relative amount of contamination increases, the underestimation becomes more pronounced. In fact, this was seen when the isolation width was increased in a study of iTRAQ-labeled BSA digest (23). To investigate the effect of contamination within the ion selection process, the selection window settings used with the QTof Premier were changed as described under “Experimental Procedures.” No statistically significant difference was seen between the three settings (data not shown); in agreement with that, the quantitative model predicted that even a 2-fold increase in the contamination (10–20%) would only result in a minor impact on the linear relationship seen (supplemental Fig. 10). We conclude that we were not able to achieve such strong changes in contamination levels with the ranges of ion selection parameters we used, suggesting that factors other than the ion selection window give rise to this effect.

Fig. 8.

Observed versus expected protein ratio for VSN-normalized data from known ratio samples processed with QSTAR. The dotted line indicates the equivalence relationship between the observed and expected. No intensity-based data filtering was performed.

The underestimation could arise from the MS, the protein, the sample complexity, or a mixture of all three. Our results, although limited to two proteins changing in ratio, indicate that the underestimation is independent of the protein. The peptides for a protein were found to be scattered randomly around the estimated ratio, suggesting that a peptide-specific component is not significant in the degree of underestimation. No difference was seen between the ratios when three different amounts of sample were injected, suggesting that peptide ion abundance is not a crucial component to the degree of underestimation. Although it is conceivable that larger changes in sample complexity might trigger differences, in the system used in this study, the sample complexity was reasonably high in all cases with utilization of minimal prefractionation of the peptides by a single short chromatography run prior to MS analysis. Further studies to pinpoint the true source of underestimation are beyond the scope of this work.

Kuzyk et al. (26) reported that an intensity-dependent bias was seen at high ratio changes (≥5:1) with the QSTAR and was possible with an LC-MALDI-TOF/TOF instrument at a 10:1 ratio. This bias led to greater underestimation. For the QTof Premier known ratio mixture data, no significant intensity-dependent bias was seen (supplemental Fig. 11); however, an intensity-dependent deviation in the ratio reported was observed in the QSTAR data, including peptides at a ratio of 1:1 (supplemental Fig. 12). The bias was not seen in the 1:1 ratio with the Erwinia sample that has a more typical sample complexity and dynamic range (“Heterogeneity of Variance: Variance-Mean Dependence”). This issue with the QSTAR needs further investigation that is beyond the scope of this study but highlights a need to be cautious with high signal intensity data that arise when relatively large amounts of a few proteins are labeled using standard protocols.

DISCUSSION

Both accuracy and precision of measurements in quantitative analyses rely on reproducible and exact values being returned from the experiment. The iTRAQ ratio data exhibit heterogeneity of variance where the variance is higher for low intensity signals. This is a significant problem as low signals dominate the data sets, and in a typical iTRAQ experiment, many proteins have only a few peptide readings. Furthermore, the commonly used requirement of a minimum of two peptides for confident identification of a protein results in the desire to keep as many readings as possible in an analysis. Consequently, methods that discard peptide readings below a threshold significantly limit the depth of proteins sampled in a study. Other methods, such as weighted mean or weighted regression, also aim to address the issue of heterogeneity of variance; however, these methods do not work well for proteins with few peptide readings that dominate iTRAQ studies.

A two-component error model consisting of additive and multiplicative components is proposed to account for the variance structure. The presence of both components was verified with both the 4-plex and 8-plex iTRAQ tag systems independently of the analytical software and LC-MS/MS instrumentation used. The additive-multiplicative error model suggests that an appropriate data transformation will be useful, the so-called generalized logarithm (glog) transformation, which stabilizes the variance across the entire intensity range. After such transformation, the decoupling of the variance from the signal significantly simplifies the downstream analysis as each peptide reading for a protein can be treated equally. Furthermore, it allows using low intensity readings (rather than discarding them). In data from a biological system, low intensity readings may be among the most interesting readings when a peptide is seen at low abundance in some of the biological samples and at higher abundance in others. The price that we pay for using variance stabilization is that ratios of small peak areas are compressed toward 1 (or glog ratios are compressed toward 0). This is a conservative effect and is called the “variance-bias” trade-off where a (hopefully large) improvement in precision is traded for the (hopefully small) cost of a bias. For the data sets of interest, we feel that this trade-off is justified, giving the benefit of being able to include all peptides and having robust estimates for all proteins even if few peptides are present.

The additive-multiplicative error structure has also been reported with quantitation by other MS-based methodologies, and the additive component may arise from the integration of count-based signal inherent with the majority of MS instrumentation (29, 31, 32) and/or the presence of a small basal unspecific background signal. As a consequence, heterogeneity of variance is, to varying degree, likely to be an inherent feature of all peptide quantitation methodologies, and estimation that uses the glog transformation may play a useful role for these techniques.

The VSN software for fitting the error model and transformation parameters is available freely and with open source as a package for the statistics and programming environment R, downloadable from the Bioconductor web site. To apply this software, all that is required are the raw reporter ion areas at the peptide level.

iTRAQ, like other MS-based quantitation techniques, faces the problem of how to combine readings from multiple peptides to estimate an abundance ratio for the parent protein. Nesvizhskii and Aebersold (41) have suggested that inconsistent relative abundance ratios from distinct peptides may point to the presence of novel biologically significant forms (e.g. novel splice variants, a product of protein degradation, post-translational modification, etc.). It is thus worth considering the distribution of readings for a protein at the peptide level. This has been incorporated into a freely available visualization package for the R environment that compares expression changes for the peptides from the same protein (13). In our same-same data, all differences arose purely from technical effects. Some substructure was identified in peptide readings where readings from a specific peptide or fraction clustered. Ideally, a hierarchical process that takes a central tendency measure at each level would be used to estimate the overall protein ratio. In our opinion, there are too few readings in a typical study at each level for this approach to be robust; outliers would be too influential on the result. We therefore propose the use of a trimmed mean as a robust measure of central tendency for the VSN-transformed peptide readings for a protein as these readings were found to be unimodal in distribution with some outliers. In the case of proteins with only a few peptides, a standard mean would be calculated as there is no alternative in this situation. This can be combined with visual inspection to assess whether the assignment of peptides to a parent protein is appropriate.

The simplest iTRAQ experiment is a pairwise comparison between sample types looking for changes above a threshold determined from experimental variation assessed by looking at a same-same comparison. For both raw and log-transformed data, the threshold is difficult to determine as it should have an intensity-dependent element. This is complicated even more by the fact that on the protein level the estimated protein ratios are obtained from peptides at various intensities; consequently, the majority of current methodologies fail to consider this problem. With the VSN transformation, this intensity dependence is removed, and 90 and 95% thresholds were found to lead to reproducible results across tag combinations. The thresholds varied with sample type but were low and indicated the sensitivity of the technology to expression changes. In practice, of course, the experimenter will use larger thresholds that also take into account biological variation. The thresholds reported here are not intended as a universal benchmark, and the reality is that for each new system (be it MS, chromatography, or sample) a new same-same sample study should be run. If the compared samples are such that “most” protein abundances are the same across samples, then the distribution of observed glog ratios can also be used to set the significance threshold. A threshold methodology was applied to a biological study, and the iTRAQ findings were in keeping with those published for this system.

Compared with the previous iTRAQ data processing methodologies, we showed that the VSN processed data are more precise and sensitive to detecting changes. The advantages of the VSN methodology will be greatest in situations where hypothesis tests are used to detect changes in expression. Such tests are particularly useful in studies that include biological replicates to ensure the differences highlighted arise from a treatment difference rather than from a sampling effect. Underlying the more powerful hypothesis tests are assumptions such as normality and homogeneity of variance, which tend to be more appropriate with the VSN-transformed data.

The study on a sample with known ratios in two independent MS systems confirmed that the iTRAQ technology does have an accuracy problem: ratios tend to be underestimated. The experiments here, spanning a 1–4-fold ratio, suggest that this effect is independent of signal strength and leads to a linear relationship between the observed ratio and the expected ratio, which goes through the origin. Data modeling supports the suggestion of Bantscheff et al. (23) that this under-estimation arises from contamination in the precursor ion selection process and indicates that a linear relationship would be obtained when the proportion of contamination is consistent within an experiment. With this linear relationship, a single correction factor can be calculated to adjust for this underestimation from readings of known proteins that span a range of expected ratios. Therefore, we recommend that for a typical sample an experiment similar to that described here is carried out and that a gradient value estimated from the linear relationship is used as a correction factor for the system. Alternatively, if sample complexity is thought to influence this relationship, we envisage that a kit could be developed that consists of a mixture of proteins at known ratios that are added to samples prior to iTRAQ labeling and that would allow the calculation of the correction factor.

To support further development in data analysis, raw data for an example same-same study (Erwinia C), the yeast study, and the spiked study are downloadable from the PRIDE database (42) (http://www.ebi.ac.uk/pride/, accession numbers 9266–9283 (Erwinia C study), 8761–8763 (yeast study), and 10635–10637(spike study)). Excel spread sheets including both raw and normalized quantitation data are also available in the supplemental material.

In summary, this study proposes methodologies to address the precision and accuracy limitations of iTRAQ. The accuracy issue, arising from contamination during precursor ion selection specific to MS/MS quantitation, can be addressed by calculation of a correction factor from spiked samples, whereas the precision issue can be addressed by the VSN transformation. This then allows a robust estimation of the ratio at the protein level as all peptides have near equivalent precision. Together these methodologies will allow iTRAQ to provide robust quantitative data even when a protein is quantified from only two peptides. The potential application of the VSN method in MS studies is not restricted to iTRAQ quantitation or even to proteomics as many MS-based applications have reported precision problems related to heterogeneity of variance.