Cost Function Masking during Normalization of Brains with Focal Lesions: Still a Necessity?

Abstract

Although normalization of brain images is critical to the analysis of structural damage across individuals, loss of tissue due to focal lesions presents challenges to the available normalization algorithms. Until recently, cost function masking, as advocated by Brett and colleagues (2001), was the accepted method to overcome difficulties encountered when normalizing damaged brains; however, development of the unified segmentation approach for normalization in SPM5 (Ashburner & Friston, 2005) offered an alternative. Crinion et al. (2007) demonstrated this approach produced normalization results without cost function masking that appeared to be robust to lesion effects when tested using the same simulated lesions studied by Brett et al. (2001). The present study sought to confirm the validity of this approach in brains with focal damage due to vascular events. To do so, we examined outcomes of normalization using unified segmentation with and without cost function masking in 49 brain images with chronic stroke. Lesion masks were created using two approaches (precise and rough drawings of lesion boundaries), and normalization was implemented with both smoothed and unsmoothed versions of the masks. We found that failure to employ cost function masking produced less accurate results in real and simulated lesions, compared to masked normalization, both in terms of deformation field displacement and voxelwise intensity differences. Additionally, unmasked normalization led to significant underestimation of lesion volume relative to all four masking conditions, especially in patients with large lesions. Taken together, these findings suggest cost function masking is still necessary when normalizing brain images with chronic infarcts.

Introduction

Normalization of brain images into a common space allows for comparison and aggregation of data across individuals. This is typically accomplished through affine (i.e., linear) and non-linear transformations. In order to automate the registration process, most algorithms calculate a cost function, that is, a measure of the degree of difference in signal intensity between the source image and a standard template (Brett, Leff, Rorden, and Ashburner, 2001). When normalizing brains with focal damage, such as that resulting from chronic stroke, the loss of brain tissue in the area of the infarct and secondary dilation of CSF-filled spaces (e.g., ventricles, sulci, and fissures) presents a challenge for normalization algorithms. Even when images are well aligned to the template, the cost function will be high in such cases because there are areas of low or no signal in the region of damage. Thus, in order to achieve the solution with the lowest total cost function, the lesion and surrounding tissue can be markedly distorted. This distortion typically reduces lesion size, as was noted by Brett et al. (2001).

To address this issue, Brett et al. (2001) recommended the use of cost function masking wherein the damaged portion of the brain is identified in the form of a binary lesion definition image. The region is masked during calculation of the normalization parameters, and subsequently normalized by a continuation of the warping parameters derived from the unmasked areas. Brett and colleagues (2001) examined the influence of cost function masking in the context of normalization of ten healthy brains compared to the same brains normalized with a set of simulated lesions. Ten different lesion configurations were derived from true examples of brain pathology resulting from diverse etiologies (e.g., stroke, tumor, cortical atrophy, and cortical dysplasia); in each case the area of lesion was defined on the abnormal brain and then pasted into a healthy brain. This approach allowed for a comparison of true normalization of the brain without a lesion and normalization of the same brain with one of the lesion configurations performed with and without cost function masking. Evaluation of the deformation field for the normalized, lesioned brain relative to true normalization (calculated using the root mean squared displacement) showed that cost function masking yielded more accurate and less variable results. Additionally, Brett et al. (2001) tested several smoothing parameters applied to the mask prior to normalization and found that an 8mm kernel thresholded at 0.1% produced the least displacement from true normalization and the most consistent results across lesion types.

One of the drawbacks of cost function masking is the time involved in creating the lesion mask. If generated by precise tracing of the lesion borders for each relevant slice, this can require about 6 minutes per slice. Consequently, a moderately large lesion that extends 80 mm in the vertical plane may require approximately 8 hours to create. However, Brett et al. (2001) noted that the precision of the mask was not a key factor in the success of cost function masking. They emphasized that the effectiveness of masking lies in eliminating the major areas of intensity difference from the parameter estimation, so that a roughly drawn mask that obscures the lesion should yield adequate results. Because quick tracing of lesion boundaries can be accomplished in about 20-25 seconds per slice, creating a rough mask for the same large lesion alluded to above would only require approximately 30 minutes.

With the recent development of the unified segmentation technique for normalization by Ashburner and Friston (2005) in the SPM5 software package (Wellcome Trust Centre for Neuroimaging, London, UK, http://www.fil.ion.ucl.ac.uk/spm), the question arose as to whether masking is still necessary when normalizing brains with lesions (Crinion et al. 2007). The unified segmentation algorithm iteratively registers, segments tissue classes, and corrects for bias due to magnetic field inhomogeneity. The bias correction, in particular, was thought to make the normalization process less susceptible to lesion effects because it may model the lesion as an area of inhomogeneity, thus implicitly masking the lesion. To test this hypothesis, Crinion and colleagues (2007) examined the outcomes of normalization with and without cost function masking using the same set of brains with simulated lesions that were evaluated by Brett et al. (2001). When comparing the results of unified segmentation to standard affine and non-linear normalization implemented in SPM5, Crinion and colleagues (2007) found that unified segmentation resulted in less error and variability. They also examined the effect of cost function masking relative to regularization, which constrains the smoothness of the transform (warp field). They found that for low regularization, where the smoothness of the warp field is not highly constrained, cost function masking minimized the error between images; but for medium and high regularization, where the smoothness of the warp field is constrained, cost function masking did not offer any additional advantage. Thus, if one applies the findings from these simulated lesions to real brains, it suggests that cost function masking might not be necessary during normalization of brain images with lesions when using the unified segmentation algorithm.

The present study was prompted by our observation that real patient brains normalized using unified segmentation in SPM5 without masking appeared to be abnormally warped during the normalization process. To the naked eye, some lesions were “crushed” when cost function masking was not applied (see Figures 1 and 2). Problems were most notable in chronic lesions due to stroke where the evolution of the cerebral infarct commonly leads to secondary perilesional effects, such as dilation of CSF spaces, including enlarged ventricles and widened sulci and fissures. Such structural changes were not modeled in the Crinion et al. (2007) study because they examined normalization of healthy brains with simulated lesion cut-outs. Thus, the question arose as to whether or not normalization of real brains with chronic lesions due to stroke requires masking in order to minimize the effects of changes in brain morphology that often occur over time. To address this question, the present study examined the deformation field displacements in a large cohort of brain images from actual patients with chronic damage due to stroke that were normalized with and without cost function masking. We also used two additional measures (root mean squared intensity difference and lesion size) to directly compare the outcomes of normalization under several different masking conditions. We examined the effects of the precision of the mask (considering that rough masks may offer a more time-efficient option in some circumstances) and smoothing of the lesion mask. Finally, we created a set of simulated lesions from our patient cohort in order to examine the deformation field relative to normalization of healthy brains without lesions. Our goal was to determine whether cost function masking of brain damage was necessary when normalizing real brains with chronic, focal lesions, and to evaluate the effects of masking conditions (precise vs. rough, and smoothed vs. unsmoothed lesion masks).

Figure 1.

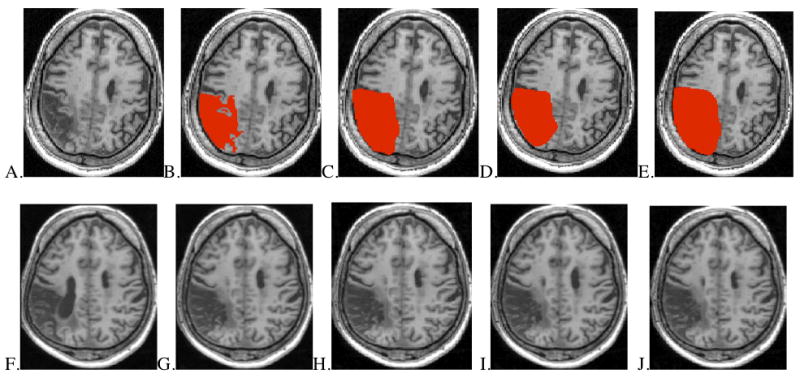
Methods of lesion masking in approximately aligned axial slices from one MCA stroke patient. Upper images (A-E): lesion in native space and shown with four masking conditions. Lower images (F-J): results after spatial normalization.

A. Native space lesion without mask B. Native space brain with unsmoothed, precise lesion mask C. Native space brain with smoothed, precise lesion mask D. Native space brain with unsmoothed, rough lesion mask E. Native space brain with smoothed, rough lesion mask F. Normalized brain using no lesion mask G. Normalized brain using unsmoothed, precise lesion mask H. Normalized brain using smoothed, precise lesion mask I. Normalized brain using unsmoothed, rough lesion mask J. Normalized brain using smoothed, rough lesion mask

Figure 2.

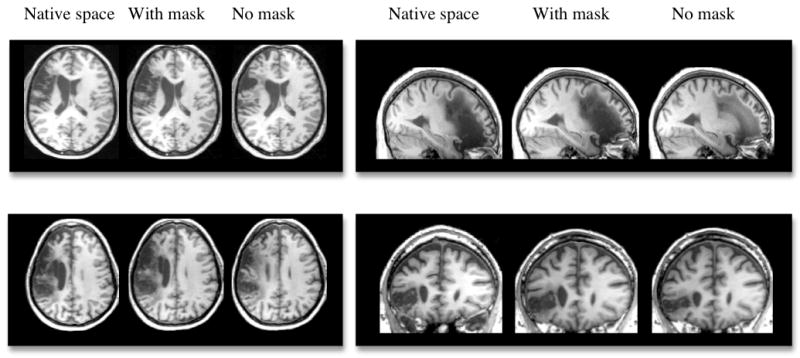
Examples of four different brains with left hemisphere lesions in native space and normalization results accomplished with and without cost function masking (using a smoothed, precise mask).

Materials and methods

High-resolution MRI brain scans were obtained from 49 consecutive individuals with focal damage due to vascular events resulting in language impairment. This cohort included 37 individuals with damage affecting left perisylvian regions supplied by the middle cerebral artery (MCA), 1 individual with crossed aphasia due to damage to right perisylvian regions, and 11 individuals with damage to temporo-parieto-occipital regions associated with left posterior cerebral artery (PCA) strokes. The participants ranged in age from 30 to 86, with an average time post onset of 3.6 years (see Table 1).

Table 1.

Patient demographics.

Lesion area	Number of participants	Sex Male:Female	Mean Age in years (range)	Mean Time Post Onset in years (range)
MCA	38	29:9	62.4 (30.1-81.9)	4.1 (0.2-12.8)
PCA	11	10:1	69.5 (53.8-86.0)	2.1 (0.1-5.8)
Total	49	39:10	64.0 (30.1-86.0)	3.6 (0.1-12.8)

MCA = Middle Cerebral Artery; PCA = Posterior Cerebral Artery

Three dimensional, spoiled gradient recall (SPGR) images with inversion recovery were obtained from all patients on either a 3 T (n = 39) or 1.5 T (n = 10) magnet. Scans were acquired sagittally with the following parameters on the 3 T magnet: TR = 7.4, TE = 3.0, TI = 500, flip angle = 15°, FOV = 25.6, voxel size = 1 × 1 × 1.5 mm, NEX = 1. On the 1.5 T magnet, scans were acquired using the same parameters except for the following slight differences: TR = 5.6, TE = 2.2, TI = 450, FOV = 26.

Binary images were created depicting the precise boundaries of the lesion for each brain by manually outlining damaged areas directly on the T1 images in native space using MRIcron software (Rorden & Brett, 2000: http://www.sph.sc.edu/comd/rorden/mricron/). Damage was restricted to one hemisphere except in two patients with left-hemisphere lesions where there was evidence of additional damage to the right frontal lobe that was clinically silent. In those cases, the right hemisphere lesions were drawn as well. A second set of binary images was created by roughly drawing the lesion outline on each slice so that the damaged region was fully obscured, but without regard for fine, local detail of the lesion. Drawing of precise lesion maps required from 1 to 8 hours per brain, depending on lesion size, whereas rough masks could be constructed in about 5 to 30 minutes.

Each brain was subsequently normalized in SPM5 using unified segmentation and medium regularization (as per Crinion et al. 2007) under five conditions: without masking; using precise, unsmoothed masks; using precise, smoothed masks; using rough, unsmoothed masks; and using rough, smoothed masks (see examples in Figure 1). The smoothing parameters were those recommended by Brett et al. (2001) (8mm FWHM Gaussian filter with 0.1% threshold), with the masks constrained so they did not extend outside of the brain. In all cases, the spatial normalization parameters generated during unified segmentation were applied to the brain image and to the precise, binary lesion image so that comparisons could be made across masking conditions.

For consistency with Brett et al. (2001) and Crinion et al. (2007), the normalization parameters were used to create deformation fields, and root mean squared displacement values were calculated for each masking condition. We evaluated deformation fields derived from the real brain images as well as a set of images with simulated lesions. First, we examined the deformation fields obtained from normalization of the 49 real brains using the smoothed, precisely masked images as the referent for “true” normalization¹. The root mean squared displacement values were compared using repeated measures ANOVA with follow-up t-tests (Bonferroni correction set at p = .0083 for 6 contrasts). The normalized brain images were also examined for voxelwise intensity differences relative to the referent (smooth, precise mask) using Advanced Normalization Tools (ANTS; http://picsl.upenn.edu/ANTS/).

In order to determine which normalization procedure better approximated true normalization of healthy brains, a second set of analyses were performed wherein deformation fields were examined in 20 brains with simulated lesions. These lesions were created using ten T1 SPGR images from neurologically normal participants (mean age = 63.4 years), and areas of damage were inserted into these normal images using the same methods as Brett et al. (2001). Specifically, the abnormal (i.e., lesioned) brain and the healthy brain were co-registered using affine-only transforms and then the lesion from the injured brain was inserted into the healthy brain (for example, see Figure 3). We created 20 brain images with simulated damage using lesions from the 10 patients with the largest infarcts and another 10 from patients with the smallest infarcts. Once the simulated lesions were created, the healthy brain and the same brain with the simulated lesion inserted were each normalized using unified segmentation in SPM5. The brain with the simulated lesion was normalized twice, once without cost function masking and again with masking applied using a smoothed, precise lesion mask. Root mean squared displacement values were calculated by comparing the deformation fields from the two normalizations of each brain with a simulated lesion to the normalization of the corresponding healthy brain without a lesion. The displacement values for the masked and unmasked condition were then compared using a paired t-test.

Figure 3.

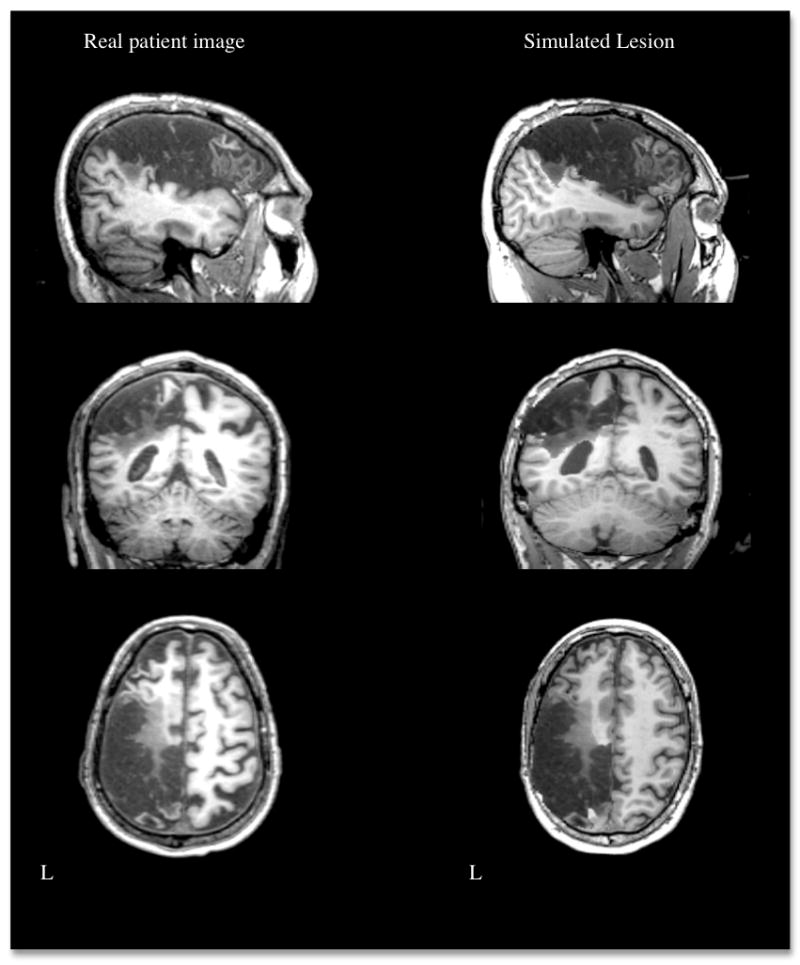
Example of a real brain lesion and a simulated lesion generated by inserting the region of damage in a healthy brain. L = left.

In addition to these global measures of normalization accuracy, lesion volumes were calculated from all conditions, masked or not, using MRIcron software (Rorden & Brett, 2000) and compared using repeated measures ANOVA with planned follow-up t-tests (p set at .0083). The effects of masking on lesion volume were also investigated by varying both warping and bias regularization parameters in the unmasked condition.

In order to estimate reliability for lesion mapping, a cohort of 10 brain images was randomly selected. The rough lesion boundaries were redrawn by both the first author (SA) and a second trained, but relatively inexperienced person. These unsmoothed, rough lesion masks were then used during normalization with the same procedures described above. Total lesion volumes were compared with those obtained from the original analysis. There was good intra-rater reliability, with no significant difference in lesion volumes when mapped two different times by the same observer (t = .67, p = .520). Inter-rater reliability was also good in that there was no significant difference between volumes mapped by the two different observers (t = .053, p = .959).

Results

For normalization of the brains with real lesions, a comparison of the root mean squared displacement values showed significant differences among the masking conditions relative to the referent deformation field (i.e., normalization using a smoothed, precise mask), F(3, 144) = 55.59, p < .001. As shown in Figure 4, the displacement in the unmasked condition (1.07 mm) was significantly larger than each of the other conditions (0.347 mm for unsmoothed, precise mask, 0.403 mm for unsmoothed, rough mask, 0.370 mm for smoothed, rough mask; all contrasts p < .001). However, there were no significant differences among the displacement values generated by the different masking conditions. The analysis of variance for the measures of voxelwise intensity difference relative to the referent image was also significant, F(3, 144) = 30.82, p < .001. Specifically, the average root mean squared difference for the unmasked brains (6.3) was significantly larger than each of the other conditions (4.3 for unsmoothed, precise mask, 4.0 for unsmoothed, rough mask, 3.8 for smoothed, rough mask; all contrasts p < .001), but the masked conditions were not different from one another (see Figure 5). Taken together, these findings indicate significant whole-brain differences between images normalized with and without cost function masking.

Figure 4.

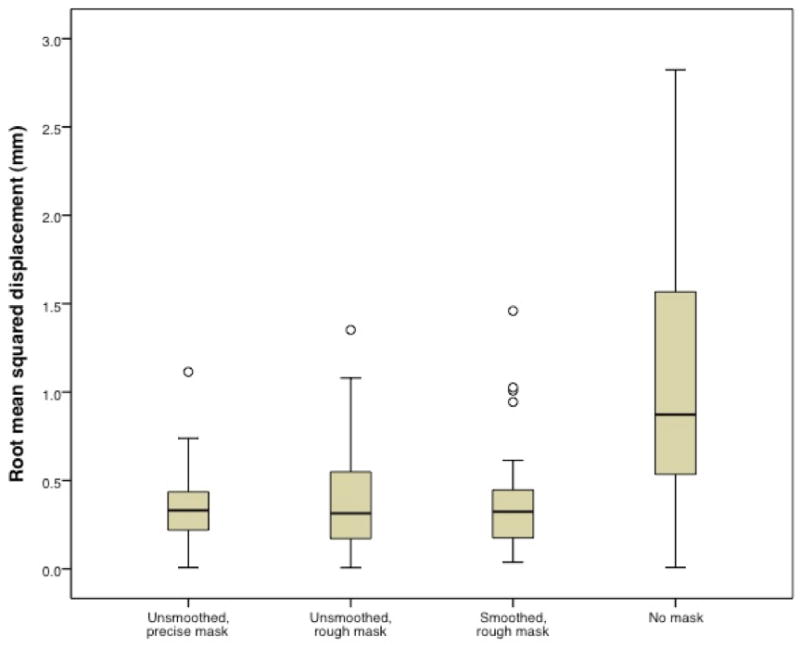
Root mean squared displacement values comparing outcomes using the smoothed, precise mask relative to the other masking conditions. Open circle indicates outlier. Root mean squared difference for the unmasked condition (mean = 1.07, s.d. = 0.72) is significantly larger than for each of the other conditions (unsmoothed, precise mask mean = 0.347, s.d. = 0.203; unsmoothed, rough mask mean = 0.403, s.d. = 0.311; smoothed, rough mask mean = 0.370, s.d. = 0.275).

Figure 5.

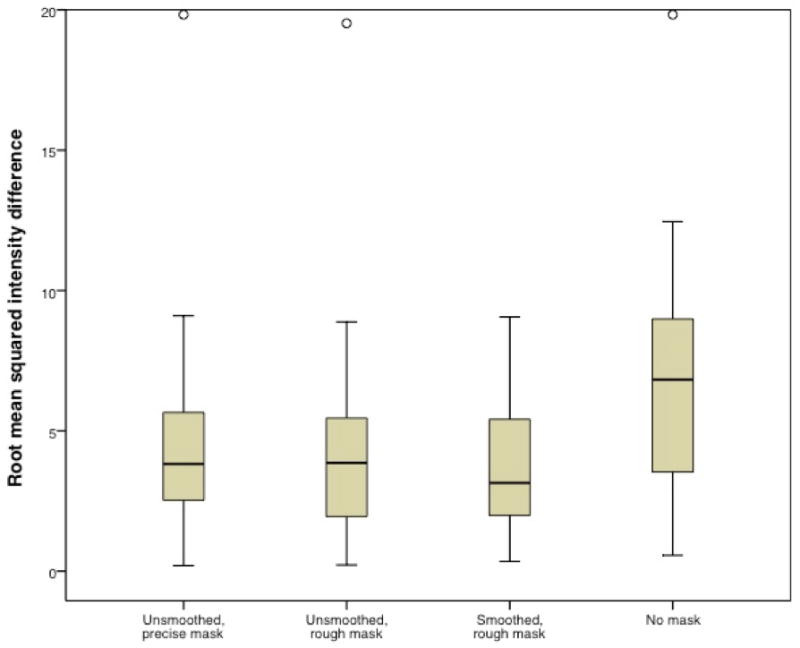
Root mean squared intensity difference comparing outcomes using the smoothed, precise mask relative to the other masking conditions. Open circle indicates outlier. Root mean squared difference for the unmasked condition (mean = 6.3, s.d. = 3.8) is significantly larger than for each of the other conditions (unsmoothed, precise mask mean = 4.3, s.d. = 3.2; unsmoothed, rough mask mean = 4.0, s.d. = 3.2; smoothed, rough mask mean = 3.8, s.d. = 2.2).

In the cohort of 20 simulated lesions, the normalization using cost function masking (with the smoothed, precise mask) led to deformation fields that were closer to that of the normalized healthy brain (without a lesion) than those generated in the unmasked condition (mean root mean squared displacement = 0.626 mm with masking vs. 1.047 mm without masking). The mean displacement was significantly less for the masked condition compared to the unmasked condition, t = 3.19, p = .005. When large and small lesions were evaluated separately, it was evident that this difference in normalization was driven by the larger lesions, with the group of 10 large simulated lesions having an average displacement of 1.07 mm in the masked condition compared to 1.90 mm in the unmasked condition (t = 4.61, p = .001). This difference was not significant in the group of small simulated lesions (0.17 mm in the masked condition vs. 0.19 mm in the unmasked condition; t = .191, p = .853).

With regard to the local effects of masking, the analysis of normalized lesion volumes indicated that masking had a significant effect on lesion size, F(4, 192) = 9.847, p < .001 (see Figure 6). Specifically, the unmasked lesion volumes were significantly smaller than the precisely masked volumes, whether smoothed or not (t = 4.07, p < .001; t = 3.85, p < .001, respectively). Similarly, the unmasked lesion volumes were smaller than the roughly masked lesion volumes, whether smoothed or not (t = 3.56, p = .001; t = 3.57, p = .001, respectively). When compared directly, there was no significant difference between the precisely masked and roughly masked lesion volumes without smoothing (t = 1.47, p = .149), or when smoothing was implemented (t = -1.74, p = .089).

Figure 6.

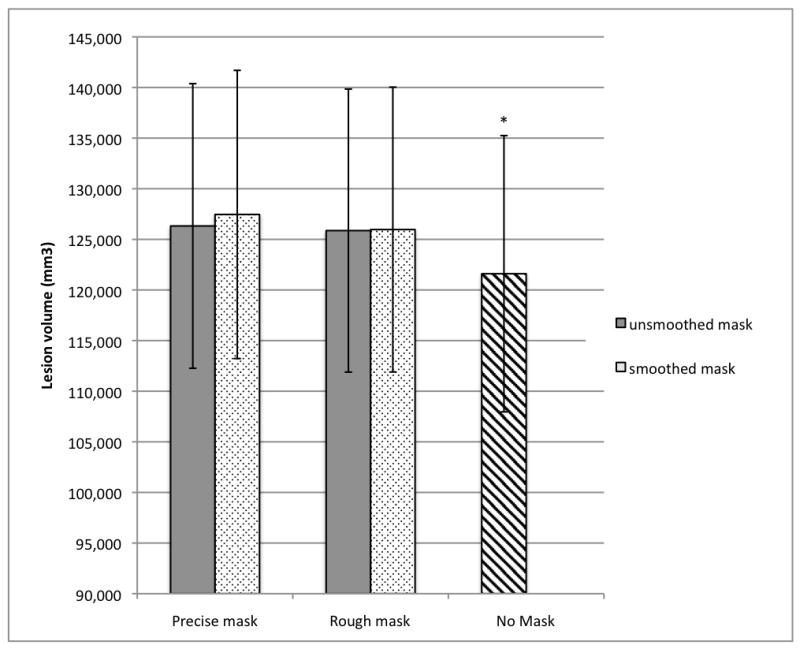
Mean lesion volumes obtained with the different normalization methods (n = 49).

*Unmasked lesion volume (121,602 mm³, S.E. = 13,646) significantly smaller than lesion volumes obtained in all masked conditions (unsmoothed, precisely masked lesion volume = 126,322 mm³, S.E. = 14,056; smoothed, precisely masked lesion volume = 127,458 mm³, S.E. = 14,232; unsmoothed, roughly masked lesion volume = 125,863 mm³, S.E. = 13,975; smoothed, roughly masked lesion volume = 125,967 mm³, S.E. = 14,069).

The effects of masking were further explored by varying the normalization parameters in the unmasked condition. When warping regularization was varied, there was still a significant effect of masking on lesion volume, F(1, 48) = 80.849, p < .001 (i.e., smooth, precise masks with medium regularization compared to unmasked with low, medium, and high regularization. See Figure 7). Specifically, each unmasked condition was significantly smaller than the masked condition, regardless of the regularization parameters used (p < .001 for all pairwise comparisons). When comparing among the unmasked conditions, there was no significant difference in lesion volume between the medium and high regularizations (t = -0.764, p = .449); however, unmasked low regularization led to lesion volumes that were significantly smaller than the outcomes using medium or high regularizations (t = 3.908, p < .001; t = 3.73, p = .001, respectively). When bias regularization was manipulated (low, medium, and high bias²) and warping regularization was held constant at medium level, there was again a significant difference among the lesion volumes derived from the masked and unmasked conditions, F(1, 48) = 79.913, p < .001. For all levels of bias regularization used, each unmasked condition was significantly smaller than the masked condition (p ≤ .001 for all pairwise comparisons. See Figure 8). With respect to the unmasked conditions, medium bias resulted in smaller lesion volumes than high bias (t = 2.82, p = .007), but none of the other comparisons were significant. In summary, the critical finding from these analyses is that the unmasked condition consistently underestimated lesion volume relative to the masked condition, regardless of the normalization parameters applied.

Figure 7.

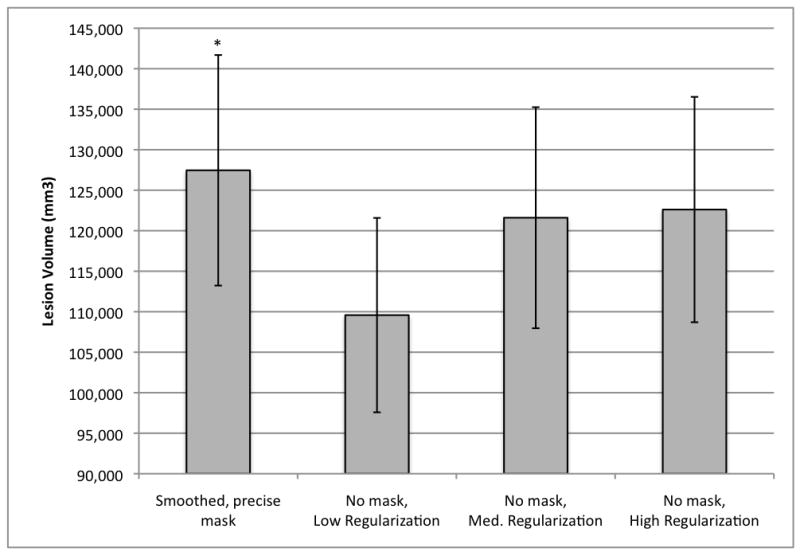
Mean lesion volumes obtained with variations of the warping regularization parameter in the unmasked condition (n=49). Bias regularization was held constant at 0.0001 for all conditions.

* Smoothed, precisely masked lesion volume (127,458 mm³, S.E. = 14,232) significantly larger than lesion volumes obtained in all unmasked conditions (low regularization = 109,580 mm³, S.E. = 11,999; medium regularization = 121,602 mm³, S.E. = 13,646; and high regularization = 122,611 mm³, S.E. = 13,911).

Figure 8.

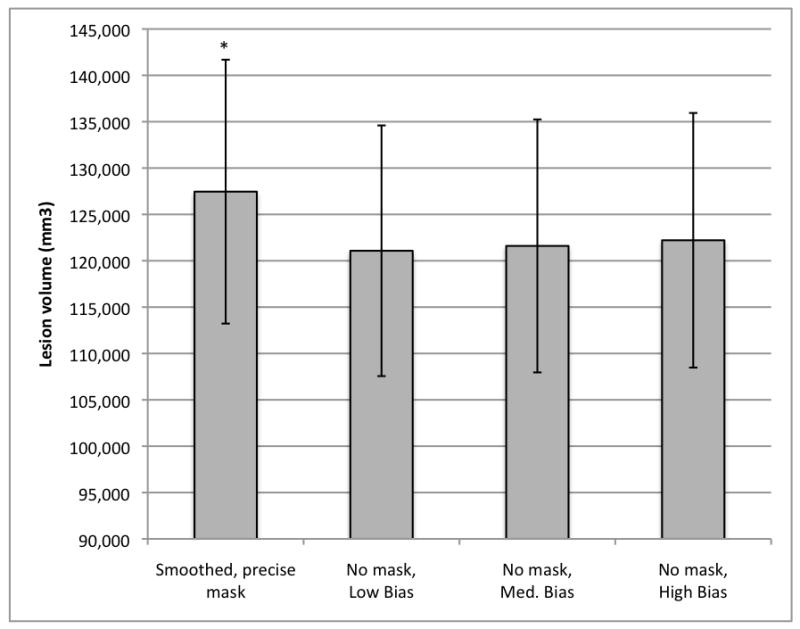
Mean lesion volumes obtained with variations of the bias regularization parameter in the unmasked condition (n=49). Warping regularization was held at medium for all conditions. Low bias = 0.00001; medium bias = 0.0001; high bias = 0.001.

*Smoothed, precisely masked lesion volume (127,458 mm³, S.E. = 14,232) significantly larger than lesion volumes obtained in all unmasked conditions (low bias = 121,079 mm³, S.E. = 13,519; medium bias = 121,602 mm³, S.E. = 13,646; and high bias = 122,211 mm³, S.E. = 13,731).

Finally, to investigate whether the observed differences in the masked versus unmasked conditions were related to total lesion volume, such that larger lesions showed greater differences in the effects of masking, we assigned the brain images to large and small lesion groups. To do so, we ordered the smoothed, precisely drawn lesion volumes by size and used the median value to divide our sample into two groups. For each patient brain, the difference in lesion volume between the masked and unmasked lesions was calculated, and these difference scores were compared for the large and small lesion groups using an independent samples t-test. The group with large lesions had significantly greater differences between the masked and unmasked lesion volumes relative to the cohort with smaller lesions (for unsmoothed, precise masks t = -2.93, p = .007; for smoothed, precise masks t = -3.68, p = .001; for unsmoothed, rough masks t = -2.59, p = .015; for smoothed, rough masks t = -2.96, p = .006). Consistent with these findings, for the group of 49 patients as a whole, there was a significant positive correlation between total lesion volume and the difference score for all masking conditions (unsmoothed, precise mask r = .358, p = .011; smoothed, precise mask r = .449, p = .001; unsmoothed, rough mask r = .301, p = .036; smoothed, rough mask r = .374, p = .008).

Discussion

The results from this study showed that when normalizing brains with chronic focal lesions due to stroke, the use of cost function masking significantly influenced normalization accuracy. Using root mean squared displacement values to examine the success of different normalizations (cf., Crinion et al., 2007), there was evidence of significantly greater displacement of the unmasked deformation fields relative to the masked conditions. There were also differences in the normalization results accomplished with and without masking when examining whole-brain intensity differences. Compared to a common referent image, the unmasked normalizations resulted in significantly greater differences in voxelwise intensities (i.e., root mean squared intensity differences) relative to the masked normalization conditions. Therefore, when brains with lesions were normalized without masking, there was greater distortion of the images during the normalization process than when masking was applied. These findings suggest that unmasked normalization is not as accurate as normalization that utilizes cost function masking, even when the unified segmentation routine is used.

Simulated lesions allowed for determination of the directionality of the difference between normalization methods because they provide a referent for normalization of brains without structural abnormality. In this study we found the masked conditions resulted in outcomes that were significantly closer to true normalization, especially in the case of large lesions. By contrast, normalization without masking tended to result in distortion of brain morphology.

The different normalization methods also influenced the calculated lesion size, with the unmasked condition producing smaller lesion volumes relative to normalization with masking, regardless of warping or bias regularization parameters utilized. As Brett et al. (2001) described, but did not quantify, some lesions appeared to be “crushed” when normalized without masking, as if the algorithm had the effect of pulling healthy tissue into the lesion in order to minimize the cost function. This was especially evident in large strokes, where lesions tended to be associated with greater secondary perilesional effects (e.g., dilated CSF spaces). When the lesion was not masked during normalization, the lateral ventricle in the affected hemisphere often enlarged toward the lesion and portions of the damaged area were re-classified as ventricle (as shown in Fig. 1); this had the effect of decreasing the total lesion volume. As a result, large lesions, which typically resulted in greater distortion of surrounding brain architecture, were underestimated when normalized without masking.

It is important to consider why we found significant differences between masked and unmasked normalization, when Crinion and colleagues (2007) did not. The primary purpose of the Crinion et al. (2007) study was to examine the effectiveness of unified segmentation across a range of lesion types, including but not limited to, damage due to stroke. In their cohort of ten brains, there were seven that had damage due to vascular infarct, and, of these, none appeared to be large with significant distortion of brain morphology. By contrast, we restricted our patient cohort to those with focal damage due to MCA or PCA stroke. The difference in the outcomes of the two studies suggests that cost function masking may not be necessary in cases where changes are more restricted to the region of primary pathology with limited secondary effects; however, it does appear to be important when there are large areas of damage and significant dilation of CSF spaces. It could also be the case that our larger sample size (49 vs. 10) simply provided greater statistical power to detect differences between masked and unmasked normalization methods than in the Crinion et al. (2007) study.

With regard to the precision with which lesions need to be masked, there was no significant difference between cost function masking performed with masks that precisely followed the lesion boundaries and those that only roughly track the borders. Because one of the major drawbacks to cost function masking is the time commitment to precisely map the lesion borders, it is important to note there was no significant difference between the two masking methods with regard to normalization accuracy (i.e., deformation field displacement or intensity difference) or lesion size. Therefore, if a normalized, precise lesion map is not needed for other purposes, then one can save hours of work while retaining the greater normalization accuracy of cost function masking by using a rough mask. The same method can also be applied when normalizing damaged brains in order to analyze functional imaging results.

We also found that smoothing of the lesion mask did not appear to play an important role in the normalization accuracy or the resultant normalized lesion volume, as there were no significant differences between any of the smoothed volumes compared to their unsmoothed counterparts³, and both the smoothed and the unsmoothed masks resulted in significantly less displacement and greater lesion volumes relative to the unmasked image. Therefore, how the mask is generated (precise vs. rough) and whether or not smoothing is applied seem to have little impact on normalization accuracy and lesion volume compared to the strong effect of whether or not cost function masking is utilized.

As new normalization methods are designed and tested, it is important that the issue of anatomical distortion due to tissue loss is addressed, regardless of whether or not it is resolved through cost function masking. Enantiomorphic normalization (Nachev, Coulthard, Jager, Kennard, and Husian, 2008) is a new method that is somewhat analogous to cost function masking. In this method, the user defines the lesion mask, and rather than being ignored during normalization, it is replaced with unaffected tissue from the contralateral hemisphere. In this way, the lesioned area is filled with healthy tissue, circumventing the issue of distortion due to tissue loss. This technique was tested using simulated lesions (Nachev et al., 2008) and awaits validation in true lesions as well. Another newly developed approach, Symmetric Normalization (SyN) with constrained cost function masking (CCFM), combines masking with diffeomorphic normalization implemented in the ANTS toolbox (Kim, Avants, Patel, and Whyte, 2007). Diffeomorphic normalization is an approach that registers images through the calculation of velocity fields. The authors explain that the missing data (due to damage) can be estimated by a smooth inference of the field around the lesion borders. One benefit of this technique is that it takes advantage of diffeomorphic normalization, which has been shown to produce more accurate normalizations in healthy brains (Klein et al., 2009), while constraining the algorithm so that lesions are not over-fitted. This approach has been shown to have promising qualitative results in two patients with brain damage, however it awaits a more quantitative evaluation in a larger patient cohort. A final approach provides an automated procedure to define brain lesions using a modified unified segmentation technique with a fourth “extra” tissue class for lesions (Seghier, Ramlackhansingh, Crinion, Leff, and Price, 2008). In this technique, the lesion is isolated from the other tissues during segmentation and normalization; an approach that appears to be analogous to cost function masking by removing the extra tissue class from parameter estimation. Thus, even in this automated routine, cost function masking is implicitly performed. Clearly, an automated approach has many advantages; however, visual inspection of outcomes reported by Seghier et al. (2008, p. 1263) suggests problems with accuracy of lesion delineation are yet to be fully resolved. This would need to be addressed prior to abandonment of manual demarcation methods.

Conclusion

Our results build on the findings of Crinion et al. (2007) that unified segmentation in SPM5 allows for more accurate normalization of brains with focal lesions. However, we find that failure to employ cost function masking during normalization of real brains with focal lesions is associated with a loss of accuracy, both in terms of deformation field displacement and voxelwise differences in image intensity. This is verified in simulated lesions, where the masked condition produces a solution that is closer to true normalization. In addition, unmasked normalization can lead to an underestimation of lesion volume, regardless of warping or bias regularization parameters employed. This is particularly true in the case of large strokes and may have important implications for lesion-deficit correlation studies. On the other hand, our results suggest that there are no differences between lesions that are roughly or precisely masked, allowing investigators significant time savings while maintaining the greatest normalization precision. Similarly, smoothing of the lesion mask prior to normalization did not have a significant effect on normalization accuracy or lesion size. In summary, our findings suggest that cost function masking should still be used when normalizing brains with chronic lesions, particularly when the damage is extensive.