Abstract
An allosteric model is used to describe changes in lifetimes of biological receptor-ligand bonds subjected to an external force. Force-induced transitions between the two states of the allosteric site lead to changes in the receptor conformation. The ligand bound to the receptor fluctuates between two different potentials formed by the two receptor conformations. The effect of the force on the receptor-ligand interaction potential is described by the Bell mechanism. The probability of detecting the ligand in the bound state is found to depend on the relaxation times of both ligand and allosteric sites. An analytic expression for the bond lifetime is derived as a function of force. The formal theoretical results are used to explain the anomalous force and time dependences of the integrin-fibronectin bond lifetimes measured by atomic force microscopy (Kong, F. et al J. Cell Biol., 2009, 185, 1275–1284). The analytic expression and model parameters describe very well all anomalous dependences identified in the experiments.
Keywords: catch bond, allostery, receptor-ligand complex, atomic force spectroscopy, external force, relaxation time
Introduction
Recent years have witnessed active research efforts aimed at elucidating the origin of the catch-binding phenomenon between biological molecules subjected to external forces 1–14. The paradoxical aspect of catch-binding resides in the anomalous dependence of the lifetimes of some biological bonds on the magnitude of the applied force. Within a certain force range the bond lifetime grows with increasing force. Only above a critical force value, having reached a maximum, the bond lifetime starts decreasing with further force increase, following the well-known slip behavior.
In the past, the catch-slip transition was discovered in the receptor/ligand complexes between P-selectin (L-selectin) and PSGL-1 2,3, actin and myosin 9, FimH and mannose 11,15, as well as glycoprotein Ibα and von Willebrand factor 12. Recently, the list was exteneded with an integrin α5β1 − Fc fusion protein or membrane α5β1 and fibronectin (FN) complex 13. The integrin/fibronectin bond lifetime showed a more complicated dependence on the applied force, compared to the other catch-systems. First, at small forces, the lifetime decreased with increasing force strength and reached a minimum. Then, the lifetime grew, exhibiting catch-binding. Finally, the lifetime attained a maximu and decreased again as a result of a catch/slip transition.
The original models used for the description of the catch/slip anomaly assumed that the potential energy profile created by the receptor and governing the motion of the ligand contains one or several minima, and several pathways for the ligand escape 6,7,10,14,16. The effect of the force on the energy profile was described by the Bell mechanism 17, which added a term that was linear in the interaction coordinate. Catch-binding was achieved by an appropriate orientation of the potential energy profile with respect to the direction of the applied force, such that the force increased the transition barrier.
The theoretical models 18–20 allowed force-induced changes in the receptor/ligand interaction potential that were different from the simple Bell mechanism 17. The deformation 18 and sliding-rebinding 19 models took into account the fact that the receptor and ligand proteins subjected to a force can change their structure, the interacting residues can shift with respect to each other, and the overall receptor/ligand interaction can become stronger as a result of the such changes. In these models, catch-binding is achieved within a certain force interval, in which the deformation mechanism of bond strengthening overwhelms the Bell mechanism of bond weakening. Slip-binding is recovered, when bond deformation stops, and the Bell mechanism becomes dominant.
The models 6,10 assumed that the bound receptor/ligand complex can exist in two conformations, corresponding to the strongly and weakly bound states. The catch-slip anomaly in the lifetime of the complex subjected to force was related to transitions between these conformations. Reference 10 proposed that the conformational changes were driven by an allosteric transition involving a two-domain fragment of the receptor protein. Reference 21 employed the two-state model as part of a more complex description of the shear threshold phenomena. It pointed out that a two-state model can produce not only a catch-slip transition, but also a slip-catch-slip transition.
In addition to the discrete pathway representations, a number of models attributed the catch-slip transition to a continuous change in the bond properties.18,22,23 Reference 18 developed a continuous bond deformation model of the catch-binding mechanism. Reference22 rationalized the catch anomaly by strong positive correlations between the energy and distance of the fluctuating barrier. Referene23 explained the phenomenon within the framework of the Smolukhovski equation by considering interaction between the conformation and reaction coordinates of the system.
The current work describes the force dependence of the lifetime of the integrin/fibronectin complex over the whole force range, including both the small-force and the catch-slip anomalies. The model develops the bond-deformation concept8,18 further by considering two sets of coordinates that determine the receptor/ligand interaction. One set characterizes the local interaction region around the binding site, while the other set represents the global state of the receptor protein that depends on large-scale conformational rearrangements. The two sets of coordinates are coupled by an allosteric interaction.
The idea of Monod et al. 24 that binding of a ligand at one subunit of the oligomer leads to a change in the quaternary structure by rotation of the subunits in concerted manner from the relaxed state to the tense state found wide applications in the biophysical science and stimulated many subsequent developments 25–37. Currently, allostery is understood as propagation of the effect of ligand binding at one end of a protein to an active site at another end. In order to understand and interprete the allosteric effect, it is necessary to consider an ensemble of protein conformations 25,27,32,33,38–46. Each conformation in the ensemble is given a statistical-mechanical weight. The allosteric site is a particular part of the protein, by perturbing which one can change the ensemble distribution. By interacting with the allosteric fragment of a protein, ligands and other effectors shift the conformation equilibrium. Each protein conformation creates its own potential energy profile in the active site. Hence, there exists a statistical-mechanical ensemble of potential energy profiles of the active site, and the allosteric effect allows one to control the distribution of the active site interactions.
The distribution of the conformation ensemble of a biological molecule can be controlled not only by ligand binding, but also by application of an external force to the allosteric fragment. The current work assumes that the shift in the conformation equilibrium is achieved by force applied to the receptor/ligand complex in the atomic force microscopy (AFM) and related experiments 10,43,47. Alternatively, a mechanical stress on the allosteric subunit can be exerted by interactions with short pieces of DNA of varying length 31,41.
In the simplest picture, the ensemble of protein conformations can be represented by two members. In such case, both allosteric and active sites exist in two states. The allosteric site governs the protein conformation. Transition of the allosteric site from one state to the other causes the corresponding transition in the active site.
Theory
The two-state allosteric model developed earlier 43,48 for the analysis of the experimental data for the P-selectin/PSGL-1 and FimH/mannose catch-slip complexes used several simplifications. For instance, it assumed that the probabilities to find the allosteric system in each of the two states were given by the equilibrium distribution. Description of the experimental data for the integrin/fibronectin complex requires a more general model, in particular, since the data contains both an anomalous force-dependence of the average bond lifetime and an anomalous time-dependence of the number of bound complexes subjected to the external force 13.
Compared to the allosteric model developed in Ref. 10, our allosteric description assumes that the conformational dynamics of the allosteric site is independent of the dynamics of the ligand in the active site, and that the former site governs the dynamics of the latter site. This assumption greatly simplifies the calculation of the time-dependent characteristics of the allosteric site. The separation of the dynamics of the two subsystems in the receptor/ligand complex leads to a simple prescription for the initial conditions in the corresponding time-dependent differential equations. The initial conditions become less straightforward for the model developed in Ref. 10.
a) Kinetics of the Two-State Model of Allostery with Force
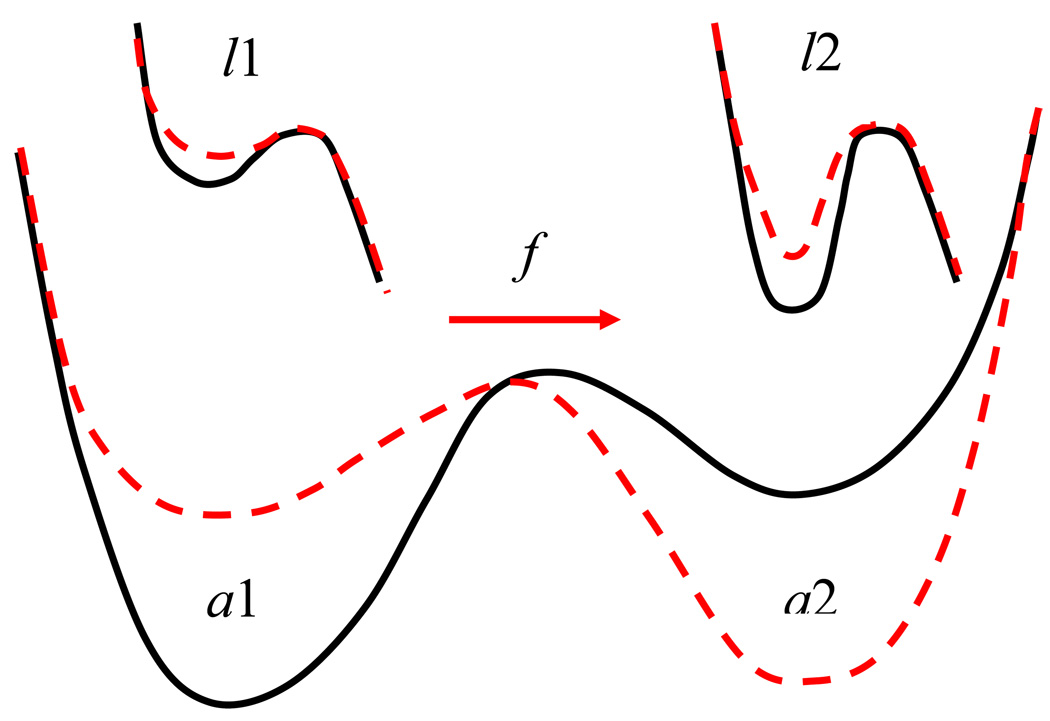
Figure 1 presents a schematic of our two-state allosteric model. The bottom two curves depict the potential energy profile of the allosteric site. The solid-black and dashed-red lines describe the potential energies in the absence and presence of the external force. Let P1(t, f) denote the probability for the allosteric site subjected to force f to exist in state a1 at time t. P2(t, f) is the corresponding probability for state a2. Naturally, the two probabilities add to one: P1(t, f) + P2(t, f) = 1.
Figure 1.
Schematic of the potential energy profiles of the allosteric site (bottom) and the ligand-binding site (top). The allosteric site can exist in two distinct states, corresponding to the potential energy minima a1 and a2. The conformation of the ligand site, l1 and l2 respectively, depends on the allosteric state. An applied force f (red arrow) transforms the potential energy profiles from the black solid curves to the dashed red curves.
The evolution of the allosteric site probabilities is given by the ordinary kinetic equations
| (1) |
where k12(f), k21(f) are the rate constants for transitions from state a1 to state a2 and back, respectively. The force dependence of these coefficients is introduced using the Bell approximation for the change in the barrier height 17: are the rate constants in the absence of force, and x12, x21 are the distances from the first (a1) and second (a2) minima, respectively to the top of the barrier, kB is the Boltzmann constant, T is temperature. Note the difference in the signs in the two exponents. The signs depend on the direction of the applied force and represent the fact that the force favors transitions from a1 to a2 and hampers transitions from a2 to a1.
It is natural to assume that at the beginning of each AFM experiment, when f = 0, the probabilities in Eq. 1 at t = 0 correspond to thermodynamic equilibrium. The initial probabilities can be found from the steady-state solution of Eq. 1. By setting the right-hand-sides to zero, one finds .
Subject to the above initial conditions, the solution of Eq. 1 for f ≠ 0 is given by
| (2) |
where
| (3) |
Therefore, according to Eq. 2, τa(f) is the characteristic relaxation time of the two-state allosteric site subjected to force f.
The conformations of the receptor governed by the allosteric site determine the potential energy profiles experienced by the ligand in the active site. If the allosteric site exists in state a1, the ligand moves in the potential l1, top panels of Fig. 1. Similarly, allosteric state a2 corresponds to the ligand state l2. The black-solid lines in the top panel of Fig. 1 describe the ligand potentials in the absence of the force, while the red-dashed lines show the force-induced lowering of the barrier experienced by the ligand. The rate constants for the escape of the ligand from the potentials l1 and l2 are given by . Here, are the rate coefficients in the absence of the force f = 0, and x1, x2 are the distanced from the minimum to the barrier maximum for each potential.
In the majority of the AFM experiments in Ref. 13, the integrin is imbedded into the substrate-cantiliver chain using two sequential biophysical contacts. The first one is the fibronectin/integrin contact, whose properties are governed by the allosteric system, as described above. The second contact is between the crystallizable fragment of the immunoglobulin molecule Fc and the GG-7 (Fab of the anti-Fc mAb). This second contact forms a simple slip-bond, whose rate coefficient can be expressed as . As usual, is the rate coefficient at zero force, and xs is the distance between the minimum and the maximum in the corresponding slip barrier.
In the presence of the sequential chain of the allosteric and slip contacts, the probability P(t, f) that the chain remains intact and the ligand is bound to the receptor at time t subject to force f obeys the following kinetic equation
| (4) |
In this equation, the first rate coefficient kr(t, f) is due to the integrin/fibronectin interaction that is governed by allostery. It is given by the sum of the rate coefficients for the ligand escape from barriers l1 and l2, Fig. 1, weighed by the corresponding probabilities, as determined by the allosteric site, Eq. 1.
| (5) |
Using Eqs. 2 and 5, together with the initial condition P(0, f) =1, Eq. 4 can be solved to give
| (6) |
where
| (7) |
According to Eq. 6, the probability for the ligand to exist in the bound state depends on two characteristic times, τa(f) in Eq. 3 and τc(f) in Eq. 7. Provided that the relaxation of the allosteric site subjected to the external force proceeds much faster than the dissociation of the receptor/ligand complex, i.e. that τa(f) ≪ τc(f), Eq. 6 shows that the survival probability of the complex decays exponentially with time over a broad time interval. The timescale of the exponential decay is τc(f). It gives the relaxation time for the dissociation of the receptor/ligand complex. Hence, τ has the subscript “c” for “complex”. Further details of the relaxation characteristics of the integrin/fibronectin system are considered in the section below, where the theory is applied to the experimental data 13.
b) Average Bond Lifetime
The average lifetime τ̄(f) of the receptor/ligand complex
| (8) |
is a key properties measured in experiments. Using the probability from Eq. 6, the bond lifetime in Eq. 8 can be transformed into
| (9) |
where
| (10) |
and d(f) = τc(f)/τa(f). Eq. 10 contains a difference of the two special functions: Γ(x) is the Euler gamma function and Γ(x, y) is the incomplete gamma function. Since the integral in Eq. 10 is calculated using continuation into the complex plane, the expression contains an explicit real-part operator “Re”, eliminating the imaginary part that can possibly appear during the calculation. The calculations were peformed using the Mathematica-7.0 Software.
Notice, if d(f) = τc(f)/τa(f) ≫ 1 and h(f) ≈<1, it follows from the integral Eq. 10 for G(f) that the exponential function under the integral can be replaced with the unit, and that G(f) ≈ 1. In this case, the average lifetime of the receptor/ligand complex is given by the following simple and transparent expression
| (11) |
c) Time-Dependence of the Number of Surviving Bonds
In addition to the average bond lifetime, experimental papers including Ref. 13 report the time-dependent bond-survival probability, often presented as the logarithm of the number of bonds that have survived by time t, when subjected to force f. In order to derive this observable within the two-state model of allostery with force, consider Eq. 6 for the bond-survival probability. Given the total of N0 measurements performed with force f, the number of complexes that are still bound at time t equals to
| (12) |
Using Eq. 6, the natural logarithm of the above expression becomes
| (13) |
This general expression can be simplified in the short, t < τa(f), and long, t > τa(f), time limits, namely
| (14) |
Clearly, if
| (15) |
then at short times the absolute value of the slope of ln N(t, f) as a function of time is large, and the slope itself is approximately equal to −h(f)/τa(f). As follows from the second line of Eq. 14, at long times the slope of ln N(t, f) is small in its absolute value and approximately equals to −1/τc(f). Provided that Eq. 15 is satisfied, the initial value ln N0 rapidly drops to ln N0 − h (f).
Comparison with Experiment
The two-state allosteric model developed in the previous section is applied here in order to describe the experimental data for a variety of the integrin/fibronectin complexes that were investigated in Ref. 13 using AFM. Due to their unusual structure and properties, integrins have been considered candidates for catch-binding for quite a while. Integrins contain a large head region that is supported by two long legs. It was well-known 49,50 that the bent conformation of the knees corresponds to the less active state of integrin, while the straight conformation makes integrin more biologically active. Hence, it was supposed that application of a force to a complex containing integrin would straighten the legs and strengthen the integrin bonds 8,19,51–53. More recent experiments, e. g. Ref. 54, confirmed this possibility. A similar conclusion was deduced on the basis of steered molecular dynamics simulations 55,56. Therefore, it was assumed that the legs fragment of integrin contains the allosteric site governing the binding affinity of the active site 57,58. In order to test this hypothesis, Ref. 13 investigated the properties of the integrin/fibronecin complex formed with a full integrin α5β1 − Fc containing the legs as well as a transacted integrin trα5β1 − Fc without the legs. Below we consider the properties of the integrin/fibronectin complex containing the full and transacted integrins, and study the force dependence of the average bond lifetime as well as the time-dependence of the bond survival probability.
a) Full Integrin: Average Bond Lifetime
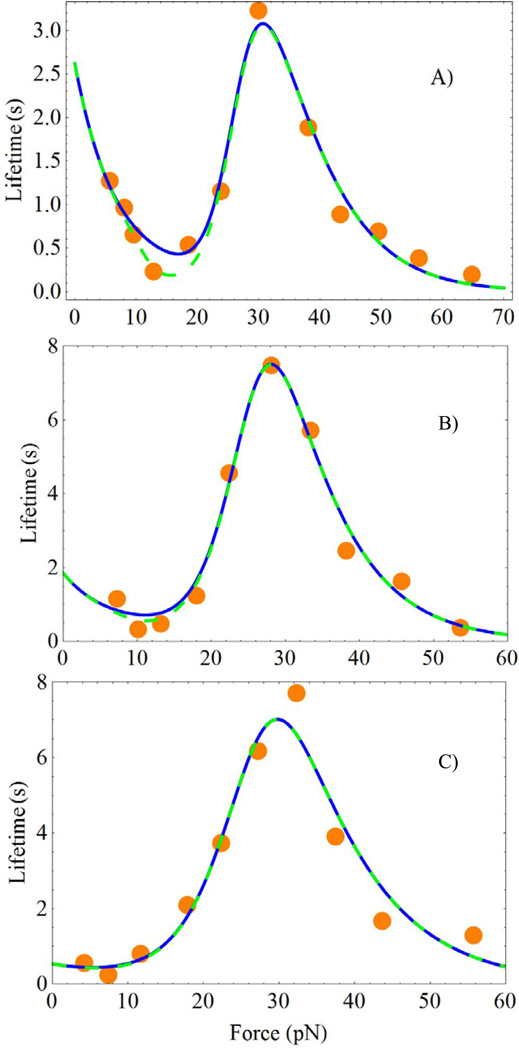
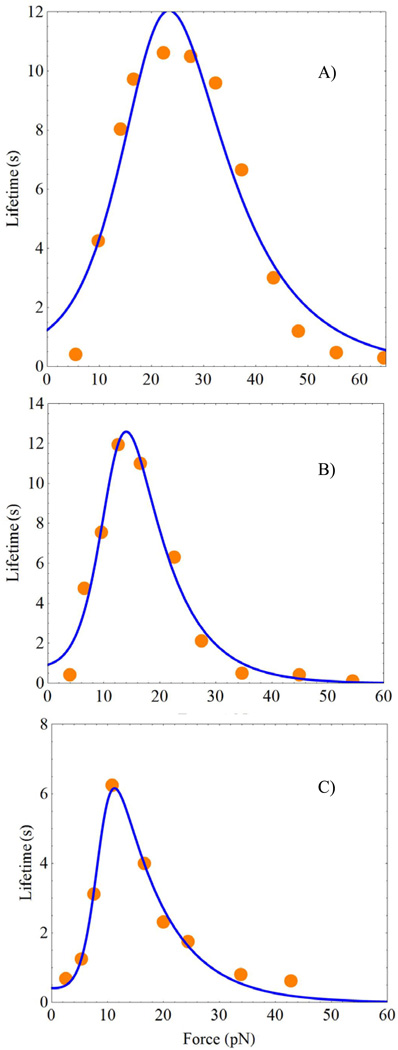
Figure 2 shows the experimental data 13 together with the theoretical curves for the force dependence of the average lifetime of the FN/α5β1 − Fc/GG − 7 complex involving Ca2+/Mg2+ in part (A), Mg2+/EGTA in part (B) and Mn2+ in part (C). All three systems show a well-pronounced catch-slip maximum in the bond lifetime around the force equal to 30pN. In addition to the catch-slip transition, the data show another anomaly around f = 10pN. At this low force, the lifetime exhibits a minimum that preceeds the catch-binding regime.
Figure 2.
Force dependence of the lifetimes of the FN/α5β1 − Fc/GG − 7 complex with the following cations: A) Ca2+/Mg2+, B) Mg2+/EGTA, and C) Mn2+. The orange circles depict the experimental data, Figs. 3A–C of Ref. 13. The blue solid curves are obtained using the exact equation, Eq. 9. The green dashed curves show the approximate result, Eq. 11. The six parameters of the model obtained by fitting Eq. 9 to the experimental data are shown in Table 1.
These experimental trends are well described by Eq. 9 in combination with Eq. 7 for τc(f), in which the ks(f) term has been dropped, as rationalized by the following difficulty with the experimental data. The function 1/ks(f) reflects the properties of the second bond in the FN/α5β1 − Fc/GG − 7 chain. The authors of Ref. 13 conjectured that the parameters of the second bond could be deduced by an independent study of the α5β1 − Fc/GG − 7 slip contact, see the curves with squares in Figs, 3A–C of Ref. 13. Analysis of these curves lead to the following slip-bond parameters, , which are essentially independent of the cation type. The parameters describe very well the force dependence of the average lifetime of the α5β1 − Fc/GG − 7 complex, as well as the characteristic time at which the logarithm of the number of surviving bonds becomes zero. In particular, for f = 30pN , corresponding to the catch-slip maxima in Fig. 2, this characteristic time (ln N0 ≈ 4.1) equals to 4.1/ks ≈ 34s, see Fig.S5D of Ref. 13. If one assumes that the properties of the isolated α5β1 − Fc/GG − 7 bond remain unchanged in the FN/α5β1 − Fc/GG − 7 chain, the characteristic time at which the logarithm of the number of surviving FN/α5β1 − Fc/GG − 7 chains becomes zero for f = 30pN should be smaller than 34s. This is because the full FN/α5β1 − Fc/GG − 7 chain can break in more places than the isolated α5β1 − Fc/GG − 7 fragment, and therefore, the full chain should break faster. In contrast to this expectation, the characteristic time for the FN/α5β1 − Fc/GG − 7 chain was on the order of 50s or even more, see Figs. S5A–C of Ref. 13 and discussion below. In order to resolve this contradiction, one can assume that the α5β1 − Fc/GG − 7 bond exposed to the AFM cantilever is significantly weaker than the same bond that is part of the FN/α5β1 − Fc/GG − 7 chain. Hence, we will focus on the properties of the allosteric FN/α5β1 − Fc bond and assume that the strong α5β1 − Fc/GG − 7 bond breaks only rarely when it is inside the FN/α5β1 − Fc/GG − 7 chain.3
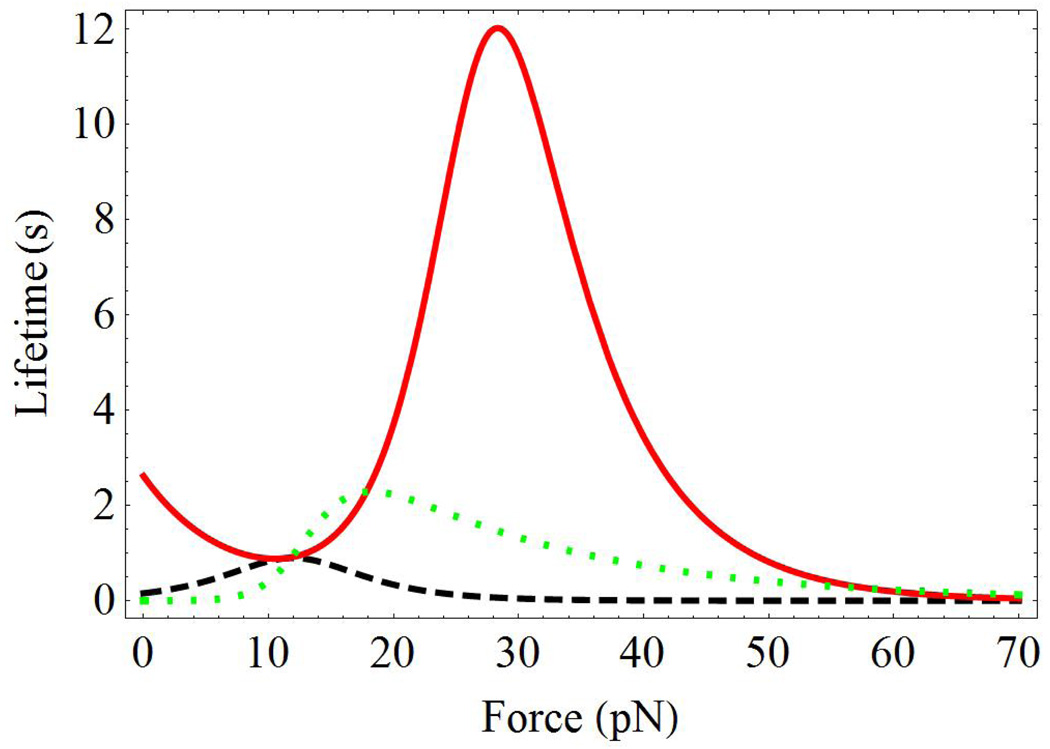
Figure 3.
The force dependence of the relaxation time of the allosteric site τa(f) (black-dashed line), the lifetime of the receptor/ligand complex τc(f) (red-solid line), and the dimentionless function h(f) (green-dotted line) for case A in Table 1 and Fig. 2.
Neglecting the ks(f) term in Eq. 7, as rationalized in the preceeding paragraph, our model contains 8 parameters: 4 parameters describe the properties of the allosteric site, including the rate constants and the distances between the bound state minima and the barrier top for the forward and backward transition, and another 4 parameters characterize the fluctuating potential energy profile of the active site, including the rate constants and barrier widths for the shallow and deep potentials. In order to reduce the number of parameters further, without sacrificing the quality of the fitting of the experimental data, we assume that the barrier widths for the two states a1 and a2 of the allosteric site are the same, i.e. x21 = x12, Fig. 1. The same assumption is made for the two states l1 and l2 of the ligand site, i.e. x2 = x1. The remaining 6 parameters, 3 for the allosteric site and 3 for the active site, will be obtained by comparing the theoretical lines with the experimental points.
In addition to the experimental data taken from Figs. 3A–C of Ref. 13, Figs. 2A–C of the present work contain two sets of theoretical lines. The solid-blue lines were obtained according to the more accurate Eq. 9, while the dashed-green lines were calculated using the simplified Eq. 11. Both sets of curves give good description of the experiments. The differences between the accurate Eq. 9 and the approximate Eq. 11 are most clearly seen in Fig. 2A. They can be rationalized by considering the force dependence of the relaxation times of the allosteric site τa(f) and the receptor/ligand complex site τc(f) , and the dimensionless function h(f), Eq. 7. These dependencies are shown in Fig. 3 by the black-dashed, red-solid and green-dotted lines, respectively. Fig. 3 shows that the approximations made to derive Eq. 11 break down for forces between 10 ÷ 20pN. In this force region, τa(f)/τc(f) ~ 1, and h(f) > 1. Note that the deviations of h(f) from zero explain the differences in the simplified expressions for the bond lifetime used here, Eq. 11, and in Ref. 43. Further, the properties of function h(f) rationalize the rapid drop in the number of bonds surviving by time t, as discussed below.
Table 1 presents the fit parameters. Since for zero force, at small forces the allosteric site exists predominantly in the a1 state with a deeper minimum, Fig. 1. Therefore, with high probability, the ligand experiences the potential energy profile l1, when the force is weak. Since , the potential well l1 is much more shallow than l2.
Table 1.
Parameters of the two-state model of allostery with force, Eq. 9, describing the lifetimes of the FN/α5β1 − Fc/GG − 7 complex with the following cations: A) Ca2+/Mg2+, B) Mg2+/EGTA, and C) Mn2+, see Fig. 2.
| x1, Å | x12, Å | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| A) | 5.89 | 0.38 | 0.00089 | 8.30 | 0.049 | 6.37 | ||||
| B) | 5.95 | 0.56 | 0.00074 | 7.79 | 0.20 | 4.96 | ||||
| C) | 4.49 | 2.22 | 0.0028 | 6.18 | 2.03 | 10.37 |
The force applied in the direction shown in Fig. 1 lowers the barriers of states l1, l2 and a1, while increasing the barrier for state a2, according to the Bell mechanism. In the neighborhood of small forces, the lowering of the barrier in the well l1 with increasing force is the main force effect. It explains the initial decrease of the bond lifetimes τ̄(f) in Fig. 2. This initial slip-behavior is particularly dramatic in the system containing the Ca2+/Mg2+ cations, Fig. 2A. It is for this system that the ratio is smallest. The ratio increases from line A) to B) and then to C) in Table 1. As a result, the initial slip-behavior becomes less pronounced in parts B) and C) of Fig. 2, compared to part A).
As the force grows, the probability for the allosteric site to exist in conformation a2 increases, and the ligand experiences the deeper potential l2 more frequently. The increase of the population of the deeper potential l2 dominates over the decrease of the barrier height of the l1 and l2 potentials by the Bell mechanism. This regime governs the properties of the bonds within the force interval between 10 ÷ 30pN. In this force interval the average bond lifetime increases with force, and the integrin/fibronectin complexes behave as catch-bonds. When the force exceeds a critical value around 30 pN, the population of the allosteric site has already shifted from state a1 to a2, and the ligand experiences the deeper l2 potential most of the time. At this point, the integrin/fibronectin complex becomes a slip-bond once again, and the lifetime decreases with increasing force by the Bell mechanism that lowers the height of the l2 barrier, Fig. 1.
Notice, x12 > x1 implies that the characteristic linear dimension of the allosteric site exceeds that of the active site. Replacing the cations from Ca2+/Mg2+ to Mn2+, lines A), B) and C) of Table 1, decreases the allosteric site dimension. The heights of the corresponding barriers decrease as well, since the rate constants for the transitions between the two states of the allosteric site grow substantially.
b) Full Integrin: Number of Bonds Surviving by Time t
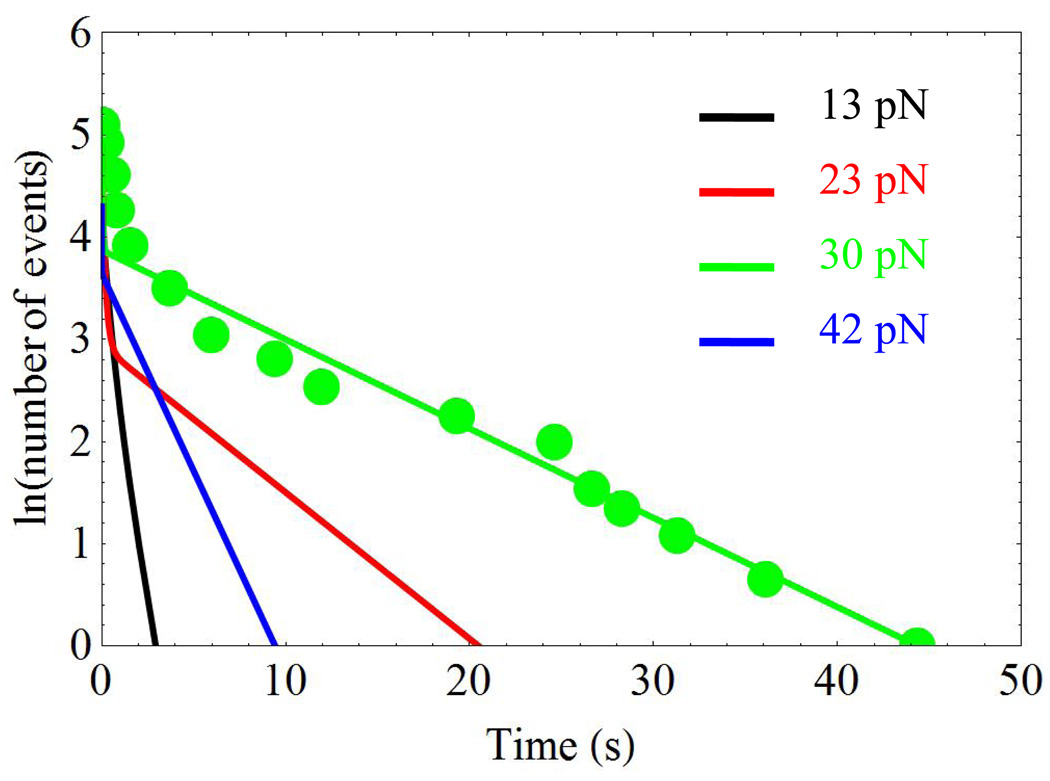
In addition to the two extrema in the average lifetime as a function of force, Fig. 2, the integrin/fibronectin complex subjected to external force f shows an anomaly in the time-evolution of the logarithm of the number of bonds surviving by time t 13, as shown in Fig. 4. In an ensemble of bond-rupture measurements, a sub-emsemble of bonds breaks very rapidly, while the remaining complexes live quite long. As a result, the logarithm of the number of bonds surviving by time t in the presence of force f, exhibits two linear time regimes, Fig. 4. A steep decrease in the number of surviving bonds is seen at the early time, and a much less steep decay takes place at a later and much broader time-interval. The allosteric model developed in this work fully rationalizes this anomaly.
Figure 4.
Time-dependence of the logarithm of the number of bonds surviving by time t for the FN/α5β1 − Fc/GG − 7 complex with the Ca2+/Mg2+ cations. The solid lines are obtained using Eq. 13 with the parameters listed in Table 1. The initial values for the logarithms of the number of bonds at t = 0 are taken from experiment, Fig. S5A of Ref. (12). The green circles show the experimental points for f = 30pN taken from the above reference.
Figure 4 shows the logarithm of the number of surviving bonds for the FN/α5β1 − Fc/GG − 7 complex with the Ca2+/Mg2+ cations. The experimental data are taken from Fig. S5 of Ref. 13. The theoretical lines are obtained using Eq. 13 with the model parameters presented in the first line of Table 1. The magnitudes of the applied force are indicated in the figure. For clarity, a subset of the experimental data is shown with circles only for f = 30pN. For this force value in particular, the fast short-time decay occurs with the slope of 29s−1, while the slow long-time decay has the slope that is over 300 times smaller, 0.087s−1. These data obey the condition expressed in Eq. 15: The calculated magnitude of the rapid initial drop in the logarithm of the number of bonds corresponds to h ≈ 1.3 for f = 30pN, which is in good agreement with the experiment. The experimental and theoretical results agree for the other force values as well, compare Fig. 4 of this work with Fig. S5A of Ref. 13.
The theoretical rationalization of the observed two regimes in the time-dependence of the bond-survival probability indicates that the relaxation of the allosteric site subjected to an external force is fast. And therefore, the equilibrium ensemble of the two potential energy profiles felt by the ligand is rapidly established. In comparison, the dissociation of the receptor/ligand complex takes significantly longer than the equilibration of the allosteric site.
c) Transacted Integrin and Integrin with Antibody
AFM studies of the integrin/fibronectin complex allow experimentalists to probe the complex properties using a continuous range of perturbations. The distribution of conformations of integrin and its allosteric site varies smoothly with increasing magnitude of the external force, and the analysis of the experiental data can be performed using a theoretical model with a single set of parameters. In addition, discrete modification to the integrin structure and composition will lead to further changes in the ensemble of protein conformations. Such focused local perturbations to the protein structure constitute an important complementary approach that can allow researchers to pin-point the location of single or multiple allosteric sites within integrin with better accuracy.
Two types of local perturbations were made to integrin in Ref. 13. Antibodies were bound to the head part of the protein. Additionally, the legs of the integrin molecule were removed. The removal of the legs led to a particularly interesting study, since until recently, the legs were considered the primary candidates for the allosteric fragment of integrin.
Surprisingly, the experiments 13 showed that both the transacted α5β1 (trα5β1) construct containing the head part but no legs, and the systems with the mAbs antibodies bound to α5β1 and trα5β1 continued to exhibit the catch-slip anomaly in the force dependence of the bond lifetime. The developed model, Eq. 9, allows us to describe the catch-slip transition in all systems studied in Ref. 13.
Figure 5 demonstrates the application of our allosteric model to three modified integrin systems. Fig. 5A shows the data for the transacted integrin system FN/trα5β1 − Fc/GG − 7 with Ca2+/Mg2+. Fig. 5B applies the model to the full integrin system FN/α5β1 − Fc/GG − 7 containing the Mn2+ ion and interacting with the monoclonal antibody TS2/16. Finally, Fig. 5C presents the results for the transacted integrin system FN/trα5β1 − Fc/GG − 7 containing Mn2+ and interacting with the TS2/16 antibody. The blue curves were obtained using Eq. 9. The experiental data are shown by the orange circles. The fitting parameters are presented in Table 2.
Figure 5.
Force dependence of the lifetimes of the complexes involving transacted integrins (A, C) and monoclonical antibody (B,C). The orange circles represent the experimental data taken from Figs. 5A, 6A, and 6C of Ref. 13. The solid blue curves are obtained using Eq. 9 with the parameters presented in Table 2.
Table 2.
Parameters of the two-state model of allostery with force, Eq. 9, describing the lifetimes of the complexes involving transacted integrins (A, C) and monoclonical antibody (B,C). Lines A), B), and C) correspond to the experimental data of Figs. 5A, 6A, and 6C of Ref. 13, see Fig. 5.
| x1, Å | x12, Å | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| A) | 3.15 | 1.11 | 0.0098 | 5.24 | 10.63 | 13.77 | ||||
| B) | 5.59 | 1.32 | 0.0083 | 9.71 | 23.74 | 45.76 | ||||
| C) | 4.71 | 2.73 | 0.036 | 14.21 | 60.36 | 414.20 |
Comparison of the model parameters for the full and transacted integrin systems, see the first lines of Tables 1 and 2 respectively, shows that the leg removal increases all rate constants. The lifetime of the complex of fibronectin with transacted integrin is shorter than the lifetime of the original complex, compare Figs. 2A and 5A. In contrast to the rate constants, the linear dimensions of the allosteric and active sites, x1 and x12 respectively, became smaller in the transacted integrin system. While in general, changes in the model parameters can eliminate the catch-slip anomaly, the relationship between the parameters of the transacted system is such that the catch-behavior is still present. With increasing force, the lifetime of the transacted integrin complex rapidly grows, proving that the system remains a catch-bond. Further force increase drives the lifetime through a maximum and ultimately makes it drop, as a result of the catch-slip transition.
Quite noteworthy, the maximum lifetime of the transacted integrin complex is almost four times higher than that of the full integrin. This means that the allostery feature remained present in the transacted integrin and even became stronger. Since previous publications suggested that the allosteric feature of integrin could reside in the leg curvature 26 as well as in the swing of the β -subunit hybrid domain away from the α -subunit in the integrin head 50,59, one can expect that the integrin molecule contains at least two allosteric fragments.
Binding of monoclonical antibodies, in particular TS2/16, to the head unit of integrin maintains the allosteric effect that is reflected in the catch-slip transition in the force dependence of the bond lifetime. In the presence of the bound antibody, the catch-slip transition is observed in the complexes containing both full and transacted integrins, see the data in Figs. 5B, 5C, and the model parameters in the second and third lines of Table 2, respectively.
In contrast to Figs. 2A–C, Figs. 5A–C do not show the theoretical curves obtained with Eq. 11. This is because the curves generated using Eq. 11 with the parameters from Table 2 coincide with the lines plotted in Fig. 5 on the basis of Eq. 9 with the same parameters. In all cases in Fig. 5 over the considered force range, the function G(f), Eq. 10, is close to one. Moreover, in all cases the function h(f), Eq. 7, is close to zero. As a result, the average lifetimes of the systems shown in Fig. 5 are well described using the following particularly simple expression
| (16) |
that was used in our earlier work 43. The lines computed using Eq. 16 with the parameters taken from Table 2 track the curves shown in Figs. 5A–C with high degree of accuracy. The applicability of Eq. 16 is rooted in the fact that the relaxation of the allosteric site proceeds much faster than the relaxation of the ligand site, τa ≪ τc, over the relevant force range. This feature can be expected generally in many situations. Therefore, the force dependence of the bond lifetime in a variety of allosteric systems analogous to the ones considered here can be described using the simple Eq. 16. At the same time, the time-dependence of the bond survival probability similar to that shown in Fig. 4 requires the more sophisticated approach.
Note that the lifetime defined in Eq. 16 depends only on the ratio of the rate coefficients for the allosteric site and not on the coefficients themselves. Hence, these coefficients are given in Table 2 with higher accuracy.
Conclusions
We have presented a model of receptor/ligand binding that is controlled allosterically by an applied force. The model includes two protein conformations, which is the minimum number required for allostery. The statistical mechanical weight of each conformation in the thermodynamic ensemble is governed by the allosteric site, which spans a relatively local fragment of the protein. Transition of the allosteric site from one state to the other changes the overall conformation of the protein. In particular, the change propagates to protein’s active site that facilitates the receptor/ligand binding. The active site is described by a simple potential with a single minimum and a single barrier. The height of the barrier depends on the protein conformation. Hence, the strength of the receptor/ligand binding can be controlled allosterically by the applied force.
The dynamics of the ligand trapped in the active site takes place in an average potential. The weights of the potentials corresponding to states 1 and 2 of the active site depend on the populations of the two states of the allosteric site. The latter is described by a double-well potential. The applied force tilts the double-well potential according to the Bell mechanism 17 and changes the populations of the two states. The properties of the potential energy profiles for the allosteric and active sites can be altered by perturbations other than the applied force. For instance, a part of the protein can be removed, or another protein can bind to the receptor near its allosteric or active site.
The formulated model contains 8 parameters. This number can be reduced by further approximations, for instance to 6 parameters assuming that the widths of the barriers in the allosteric and active sites are the same. If the populations of the two states of the allosteric site rapidly reach equilibrium, this number can be reduced to 5, as in Ref. 43.
The analysis of the developed model has led to an analytic expression for the bond-survival probability. It is found to depend on two characteristic times, which are the relaxation times for the allosteric and active sites. The allosteric relaxation time depends only on the parameters of the allosteric site, while the relaxation time of the active site depends on all parameters, including those of both active and allosteric sites. If the relaxation time of the allosteric site is much shorter than that of the active site, the bond-survival probability rapidly drops over a short period of time and then decays exponentially over a second, much longer characteristic timescale. These features of the allosteric model suggest that a detailed understanding of the conformational properties of the receptor protein can be obtained by performing force-induced bond rupture experiments for the following regimes. In the constant force experiments, one should focus on the time-dependence of the bond-rupture probability at short times. In the jump-ramp experimens, one should investigate the force-dependence of the bond-rupture probabioity at small forces.
An analytic expression for the average bond lifetime as a function of the applied force has been derived for an arbitrary set of model parameters. The lifetime expression notably simplifies, if the relaxation time of the allosteric site is significantly shorter than the bond dissociation time.
The developed model of allostery with force has been applied to the integrin/fibronectic complex. The anomalies in both the bond lifetime as a function of applied force and the bond survival probability as a function of time are represnted by the allosteric model with excellent accuracy. A variety of integrin/fibronectin systems have been considered, including those containing the full integrin, the transacted integrin that is missing its legs, and the integrin with monoclonical antibodies interacting with its head. Integrins containing different cations have been analyzed as well. The parameters of the allosteric model have been determined for all systems under investigation. These parameters include the width of the corresponding barriers and the reaction rate constants that are exponentially dependent on the barrier heights.
In most systems the relaxation of the allosteric site is faster than that of the ligand site, allowing us to use simplified theoretical expressions. However, within a certain force range, the integrin/fibronectin complex with Ca2+/Mg2+ exhibits similar timescales for the allosteric site relaxation and the bond dissociation, Fig. 3. In this case, the general theoretical expressions must be used, Eqs. 6,9.
The allosteric site relaxation and bond dissociation processes define two characteristic timescales in the receptor/ligand system, giving rise to the two distinct time-regimes of the decay of the bond-survival probability, Fig. 4. As a result of this connection, the time-dependent studies of the receptor/ligand bond dissociation can provide the timescale of the allosteric site relaxation and other valuable information regarding conformational transitions in biological molecules in general.
The developed allosteric model gives the following rationalization of the catch-slip transition. In the absence of force, the system exists in a conformation that provides the ligand with a shallow binding potential. The force shifts the conformational equilibrium toward another receptor conformation that creates a stonger receptor/ligand interaction. The force dependence of the statistical weights of each conformation and the bond dissociation barriers, provided by the simple Bell approximation, allows one to understand the origins of all anomalies observed experimentally in the integrin/fibronectin complexes, and to describe these anomalies quantitatively.
It is straightforward to extend the current model by including a larger number of protein conformations, bound states and bond dissociation pathways. If needed, finer details of the experimental data can be described by considering more complicated potential energy profiles of the allosteric and active sites. For instance, one can uncover interesting dynamical features of proteins by looking for resonances in response to a periodically oscillating force. A resonance is signified by an enhanced response of a protein to a specific perturbation frequency. The resonance frequencies may correspond to protein motions that carry biological significance. An example of such study is provided by Ref. 60 that investigated the behavior of a catch-bond described by the two-pathway model as a function of force frequency and amplitude. The study found a major change in the bond litetime properties at the physiologically relevant frequency of 30 beats per minute. In allosteric systems, the particular states exhibiting resonant behavior among all states within the ensemble of protein conformations may govern the stability of receptor-ligand bonds.
Acknowledgments
Financial support of National Science Foundation grant CHE-0957280, National Institute of Health grant NIH R01 AI50940, and Petroleum Research Fund of the American Chemical Society grant 46772-AC6 is gratefully acknowledged.
Footnotes
The authors thank Prof. C. Zhu for discussing this experimental issue
References
- 1.Dembo M, Torney DC, Saxman K, Hammer D. Proc. Royal Soc. London Series B-Biol. Sci. 1988;234:55. doi: 10.1098/rspb.1988.0038. [DOI] [PubMed] [Google Scholar]
- 2.Marshall BT, Long M, Piper JW, Yago T, McEver RP, Zhu C. Nature. 2003;423:190. doi: 10.1038/nature01605. [DOI] [PubMed] [Google Scholar]
- 3.Sarangapani KK, Yago T, Klopocki AG, Lawrence MB, Fieger CB, Rosen SD, McEver RP, Zhu C. J Biol. Chem. 2004;279:2291. doi: 10.1074/jbc.M310396200. [DOI] [PubMed] [Google Scholar]
- 4.Bartolo D, Derenyi I, Ajdari A. Phys Rev E Stat Nonlin Soft Matter Phys. 2002;65:051910. doi: 10.1103/PhysRevE.65.051910. [DOI] [PubMed] [Google Scholar]
- 5.Evans E, Leung A, Heinrich V, Zhu C. Proc. Nat. Acad. Sci. USA. 2004;101:11281. doi: 10.1073/pnas.0401870101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Barsegov V, Thirumalai D. Proc. Nat. Acad. Sci. USA. 2005;102:1835. doi: 10.1073/pnas.0406938102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Pereverzev YV, Prezhdo OV, Forero M, Sokurenko EV, Thomas WE. Biophys. J. 2005;89:1446. doi: 10.1529/biophysj.105.062158. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Zhu C, Lou JZ, McEver RP. Biorheology. 2005;42:443. [PubMed] [Google Scholar]
- 9.Guo B, Guilford WH. Proc. Nat. Acad. Sci. USA. 2006;103:9844. doi: 10.1073/pnas.0601255103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Thomas W, Forero M, Yakovenko O, Nilsson L, Vicini P, Sokurenko E, Vogel V. Biophys. J. 2006;90:753. doi: 10.1529/biophysj.105.066548. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Yakovenko O, Sharma S, Forero M, Tchesnokova V, Aprikian P, Kidd B, Mach A, Vogel V, Sokurenko E, Thomas WE. J. Biol. Chem. 2008;283:11596. doi: 10.1074/jbc.M707815200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Yago T, Lou J, Wu T, Yang J, Miner JJ, Coburn L, Lopez JA, Cruz MA, Dong JF, McIntire LV, McEver RP, Zhu C. J Clin Invest. 2008;118:3195. doi: 10.1172/JCI35754. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Kong F, Garcia AJ, Mould AP, Humphries MJ, Zhu C. J Cell Biol. 2009;185:1275. doi: 10.1083/jcb.200810002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Suzuki Y, Dudko OK. Physical Review Letters. 2010;104:048101. doi: 10.1103/PhysRevLett.104.048101. [DOI] [PubMed] [Google Scholar]
- 15.Thomas WE, Trintchina E, Forero M, Vogel V, Sokurenko EV. Cell. 2002;109:913. doi: 10.1016/s0092-8674(02)00796-1. [DOI] [PubMed] [Google Scholar]
- 16.Barsegov V, Thirumalai D. Journal of Physical Chemistry B. 2006;110:26403. doi: 10.1021/jp0653306. [DOI] [PubMed] [Google Scholar]
- 17.Bell GI. Science. 1978;200:618. doi: 10.1126/science.347575. [DOI] [PubMed] [Google Scholar]
- 18.Pereverzev YV, Prezhdo OV. Phys Rev E Stat Nonlin Soft Matter Phys. 2006;73:050902. doi: 10.1103/PhysRevE.73.050902. [DOI] [PubMed] [Google Scholar]
- 19.Lou JZ, Zhu C. Biophysical Journal. 2007;92:1471. doi: 10.1529/biophysj.106.097048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Pereverzev YV, Prezhdo OV, Sokurenko EV. Journal of Physical Chemistry B. 2008;112:11440. doi: 10.1021/jp803819a. [DOI] [PubMed] [Google Scholar]
- 21.Beste MT, Hammer DA. Proc Natl Acad Sci U S A. 2008;105:20716. doi: 10.1073/pnas.0808213105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Liu F, Ou-Yang ZC, Iwamoto M. Phys Rev E Stat Nonlin Soft Matter Phys. 2006;73:010901. doi: 10.1103/PhysRevE.73.010901. [DOI] [PubMed] [Google Scholar]
- 23.Liu F, Ou-Yang ZC. Phys Rev E Stat Nonlin Soft Matter Phys. 2006;74:051904. doi: 10.1103/PhysRevE.74.051904. [DOI] [PubMed] [Google Scholar]
- 24.Monod J, Wyman J, Changeux JP. J. Mol. Biol. 1965;12:88. doi: 10.1016/s0022-2836(65)80285-6. [DOI] [PubMed] [Google Scholar]
- 25.Gunasekaran K, Ma B, Nussinov R. Proteins. 2004;57:433. doi: 10.1002/prot.20232. [DOI] [PubMed] [Google Scholar]
- 26.Xiao T, Takagi J, Coller BS, Wang JH, Springer TA. Nature. 2004;432:59. doi: 10.1038/nature02976. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Hilser VJ, Garcia-Moreno B, Oas TG, Kapp G, Whitten ST. Chemical Reviews. 2006;106:1545. doi: 10.1021/cr040423+. [DOI] [PubMed] [Google Scholar]
- 28.Clarkson MW, Gilmore SA, Edgell MH, Lee AL. Biochemistry. 2006;45:7693. doi: 10.1021/bi060652l. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Hawkins RJ, McLeish TC. Biophys J. 2006;91:2055. doi: 10.1529/biophysj.106.082180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Popovych N, Sun S, Ebright RH, Kalodimos CG. Nat Struct Mol Biol. 2006;13:831. doi: 10.1038/nsmb1132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Choi B, Zocchi G. Biophys J. 2007;92:1651. doi: 10.1529/biophysj.106.092866. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Henzler-Wildman K, Kern D. Nature. 2007;450:964. doi: 10.1038/nature06522. [DOI] [PubMed] [Google Scholar]
- 33.Bahar I, Chennubhotla C, Tobi D. Curr Opin Struct Biol. 2007;17:633. doi: 10.1016/j.sbi.2007.09.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Goodey NM, Benkovic SJ. Nat Chem Biol. 2008;4:474. doi: 10.1038/nchembio.98. [DOI] [PubMed] [Google Scholar]
- 35.Cui Q, Karplus M. Protein Science. 2008;17:1295. doi: 10.1110/ps.03259908. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Gleitsman KR, Shanata JA, Frazier SJ, Lester HA, Dougherty DA. Biophys J. 2009;96:3168. doi: 10.1016/j.bpj.2008.12.3949. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Formaneck MS, Ma L, Cui Q. Proteins-Structure Function and Bioinformatics. 2006;63:846. doi: 10.1002/prot.20893. [DOI] [PubMed] [Google Scholar]
- 38.Tobi D, Bahar I. Proc Natl Acad Sci U S A. 2005;102:18908. doi: 10.1073/pnas.0507603102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Whitten ST, Garcia-Moreno EB, Hilser VJ. Proc Natl Acad Sci U S A. 2005;102:4282. doi: 10.1073/pnas.0407499102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Ming D, Wall ME. Proteins. 2005;59:697. doi: 10.1002/prot.20440. [DOI] [PubMed] [Google Scholar]
- 41.Choi B, Zocchi G, Wu Y, Chan S, Jeanne Perry L. Phys Rev Lett. 2005;95:078102. doi: 10.1103/PhysRevLett.95.078102. [DOI] [PubMed] [Google Scholar]
- 42.Chodera JD, Singhal N, Pande VS, Dill KA, Swope WC. J Chem Phys. 2007;126:155101. doi: 10.1063/1.2714538. [DOI] [PubMed] [Google Scholar]
- 43.Pereverzev YV, Prezhdo OV, Sokurenko EV. Phys Rev E Stat Nonlin Soft Matter Phys. 2009;79:051913. doi: 10.1103/PhysRevE.79.051913. [DOI] [PubMed] [Google Scholar]
- 44.Kidd BA, Baker D, Thomas WE. PLoS Comput Biol. 2009;5:e1000484. doi: 10.1371/journal.pcbi.1000484. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Zuckerman DM. Journal of Physical Chemistry B. 2004;108:5127. [Google Scholar]
- 46.Miyashita O, Wolynes PG, Onuchic JN. J Phys Chem B. 2005;109:1959. doi: 10.1021/jp046736q. [DOI] [PubMed] [Google Scholar]
- 47.Dudko OK, Hummer G, Szabo A. Proceedings of the National Academy of Sciences of the United States of America. 2008;105:15755. doi: 10.1073/pnas.0806085105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Prezhdo OV, Pereverzev YV. Acc Chem Res. 2009;42:693. doi: 10.1021/ar800202z. [DOI] [PubMed] [Google Scholar]
- 49.Xiong JP, Stehle T, Diefenbach B, Zhang R, Dunker R, Scott DL, Joachimiak A, Goodman SL, Arnaout MA. Science. 2001;294:339. doi: 10.1126/science.1064535. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Takagi J, Petre BM, Walz T, Springer TA. Cell. 2002;110:599. doi: 10.1016/s0092-8674(02)00935-2. [DOI] [PubMed] [Google Scholar]
- 51.Chigaev A, Buranda T, Dwyer DC, Prossnitz ER, Sklar LA. Biophys J. 2003;85:3951. doi: 10.1016/S0006-3495(03)74809-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.McEver RP, Zhu C. Nat Immunol. 2007;8:1035. doi: 10.1038/ni1007-1035. [DOI] [PubMed] [Google Scholar]
- 53.Alon R, Dustin ML. Immunity. 2007;26:17. doi: 10.1016/j.immuni.2007.01.002. [DOI] [PubMed] [Google Scholar]
- 54.Friedland JC, Lee MH, Boettiger D. Science. 2009;323:642. doi: 10.1126/science.1168441. [DOI] [PubMed] [Google Scholar]
- 55.Jin M, Andricioaei I, Springer TA. Structure. 2004;12:2137. doi: 10.1016/j.str.2004.10.005. [DOI] [PubMed] [Google Scholar]
- 56.Puklin-Faucher E, Gao M, Schulten K, Vogel V. J Cell Biol. 2006;175:349. doi: 10.1083/jcb.200602071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Hynes RO. Cell. 2002;110:673. doi: 10.1016/s0092-8674(02)00971-6. [DOI] [PubMed] [Google Scholar]
- 58.Luo BH, Carman CV, Springer TA. Annu Rev Immunol. 2007;25:619. doi: 10.1146/annurev.immunol.25.022106.141618. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Mould AP, Barton SJ, Askari JA, McEwan PA, Buckley PA, Craig SE, Humphries MJ. J Biol Chem. 2003;278:17028. doi: 10.1074/jbc.M306655200. [DOI] [PubMed] [Google Scholar]
- 60.Pereverzev YV, Prezhdo OV. Biophys J. 2006;91:L19. doi: 10.1529/biophysj.106.087288. [DOI] [PMC free article] [PubMed] [Google Scholar]