Abstract
Aim
This study introduces a new method for graphical and numerical evaluation of time lags typically associated with subcutaneous glucose sensing, based on Poincaré-type plot and a maximum statistical agreement criterion.
Methods
The proposed method is illustrated by retrospective analysis of 56 continuous glucose monitor (CGM) time series collected by the FreeStyle Navigator™ (Abbott Diabetes Care, Alameda, CA) from 28 patients with type 1 diabetes mellitus, each wearing simultaneously two sensors (on arm and abdomen) and parallel reference blood glucose (BG) collected with a reference YSI (Yellow Springs, OH) analyzer every 15 min. The average duration of a time series was 111 h; there were approximately 10,000 sensor–reference data pairs.
Results
When sliding in time CGM readings versus BG, the point of minimal spread of a Poincaré-type plot marks visually the time of CGM delay. The same point is numerically estimated by minimizing the distance between BG and CGM readings. The average observed time lag between reference BG and CGM was 12.5 min. Stratified by BG rate of change, the time lag was longer (16.8 min) when BG was falling, compared to steady or rising BG (11.7 min and 9.9 min, respectively) (P < 0.005). The time lags at the two sensor locations were not significantly different: 12.4 min on the arm, 12.6 min on the abdomen.
Conclusions
In this data set, substantial blood-to-sensor time delays were observed, possibly because of both blood-to-interstitial glucose transport and instrumental delay. Analysis of BG-CGM co-dynamics that is free from mathematical approximation of glucose fluctuations resulted in convenient visualization and numerical estimation of these delays.
Introduction
Blood glucose (BG) fluctuations represent the measurable result from the action of an underlying dynamical system. In healthy individuals this system is governed by internal feedback control; in those with diabetes the internal feedback loops are disrupted or inefficient, which results in abnormal glucose fluctuations and the need for their external regulation. Subcutaneous continuous glucose monitors (CGMs) assist this regulation by providing frequent data for the dynamics of BG. However, CGMs measure glucose concentration in a different compartment—the interstitium. Interstitial glucose (IG) fluctuations are related to BG presumably via a diffusion process between the two compartments.1–4
To account for the gradient between BG and IG, CGMs are calibrated with capillary glucose, which brings the typically lower IG concentration to BG levels. Successful calibration would adjust the amplitude of IG fluctuations with respect to BG, but would not eliminate the possible time lag due to BG-to-IG glucose transport and sensor processing time (instrumental delay). Because such a time lag could greatly influence the accuracy of CGM, a number of studies were dedicated to its investigation.5–8 The estimates of the physiologic BG-to-IG time lag vary in different study conditions. For example, it was hypothesized that if glucose fall is due to peripheral glucose consumption the physiologic time lag would be negative, i.e., fall in IG would precede fall in BG.1,9 In other studies IG lagged behind BG (most of the time) by 4–10 min, regardless of the direction of BG change.3,5 The formulation of the push-pull phenomenon offered reconciliation of these results and provided arguments for a more complex BG-IG relationship than a simple constant or directional time lag.8,10 Sensor instrumental delay, which appears negligible for needle-type sensors but could be substantial with microdialysis,8,11 should be added to BG-to-IG time lag, resulting in combined, potentially substantial BG-to-CGM delay.
However, the quantifying of BG-to-IG or combined BG-to-CGM time lag in sensor accuracy studies is quite complex because of the nature of the data—dense time series of fluctuating BG and IG concentrations. Several methods have been proposed, ranging from estimates of the derivatives (slopes) of BG and IG fluctuations5 to spline approximation and horizontal translation of the BG/IG time series.8 While these methods are built over sound assumptions and produce similar results, certain improvements could be offered in two directions: (1) simple visualization of the time lag observed in potentially thousands (BG, CGM) data pairs and (2) numerical estimation of the time lag that does not rely on an underlying model or approximation (e.g., spline or polynomial). Both of these directions are important in view of the complex temporal relationship between BG and CGM.
In order to address these issues, we introduce the notion of co-dynamics of BG and CGM and propose tools for its quantifying and visualization. As a base we use the classical approach to visualization nonlinear system dynamics—the Poincaré plot, which takes a sequence of sample values and plots each sample against the following sample.12 The significance of this plot is that it is the two-dimensional reconstructed phase space—the projection of the system attractor that describes the dynamics of the time series.13,14 The geometry of the Poincaré plot reveals properties of the system dynamics. For example, a cigar-shaped plot along the principal diagonal (x = y) would reveal high autocorrelation within the time series, while a circular plot would reveal periodicity (the Poincaré plot of a sine wave or a pendulum is a circle). The Poincaré plot has been used extensively to describe heart rate variability15–19 and was also introduced to the analysis of CGM time series.20 In this paper, we propose an altered Poincaré-type plot, which extends the visualization of system dynamics to depiction of the co-dynamics of BG and CGM. Then, we equip the resulting pictures with a measure of proximity between BG and sensor data based on the notion of statistical agreement and maximum likelihood. This technique is applicable to evaluating both BG-to-IG and BG-to-CGM time differences, depending on the data in hand, as well as to evaluation of the delay in any direction—BG preceding or lagging behind IG.
Materials and Methods
Data and procedure
This study utilizes data from an accuracy study of the FreeStyle Navigator™ (Abbott Diabetes Care, Alameda, CA). The data were collected under controlled hospital conditions from 28 study participants with type 1 diabetes. Each subject wore simultaneously two sensors—one on the arm and the other on the abdomen. Thus 56 CGM data series were generated; these CGM time series had resolution of 1 min and average duration of 111 h. Reference BG was measured every 15 min using a YSI (Yellow Springs, OH) BG analyzer. After elimination of missing data and nonfunctioning sensors, the final data set was composed of approximately 10,000 BG–sensor data pairs.
Poincaré-type plot of sensor delay
The classic Poincaré plot of system dynamics presents system state at time t plotted versus system state at time t + Δt, e.g., BG(t) on the y-axis is plotted against BG(t + Δt) on the x-axis for a time series of BG readings designated BG(t + nΔt), n = 1,2,3, … We modify the plot to depict the co-dynamics of BG and (recalibrated) sensor interstitial readings by placing BG(t) on the x-axis and CGM(t − Δt) readings on the y-axis for any fixed time delay Δt and a time series of sensor–reference data pairs designated [BG(tn), CGM(tn − Δt)], n = 1,2,3, …. Further, we vary Δt with increments of 1 min (which is permitted by the high resolution of the Navigator data collected in this study) and repeat the plot for each Δt. Because the discrepancy between BG and CGM dynamics will be minimized when Δt reaches the true underlying sensor delay Δt0, the Poincaré plot of BG-CGM co-dynamics will have minimal spread at Δt0. In other words, the data cloud in the Poincaré plot of BG–sensor co-dynamics will appear most orderly at the true value of sensor delay Δt0.
Numerical evaluation of sensor delay
Following the idea presented in the previous paragraph, we must now find a metric corresponding to the visual impression of “most orderly” Poincaré plot. Intuitively, the Poincaré plot would be most orderly if the statistical agreement between BG fluctuations and CGM is maximized. To compute an appropriate agreement criterion (AC), we first normalize the data, converting the typically asymmetric distributions of CGM and reference BG into distributions that are closed to normal (Gaussian). In order to do so, we use a previously introduced logarithmic transformation that has been shown effective in that regard21: each CGM or BG reading (measured in mg/dL) is first transformed using the formulas CGMT = 1.509 × [(ln (CGM))1.084 − 5.381] and BGT = 1.509 × [(ln (BG))1.084 − 5.381].21 After the transformation, the (BGT, CGMT) data pairs will have approximately bivariate normal distribution. Normalizing the data before computing AC is important for the following statistical reason: if a bivariate normal distribution is in place, we can claim that the R2 coefficient of a linear regression of CGM readings along BG is proportional to the information that CGM extracts from the reference data. Thus, when the data are normalized, maximum agreement between BG and CGM measured by R2 would correspond to maximal information carried by CGM about BG fluctuations. We can therefore define AC = R2 of a linear regression of BGT along CGMT, measured in percentages. As with the plots explained in the previous paragraph, we vary Δt with increments of 1 min and repeat a linear regression for each Δt. Maximal AC will be then reached when Δt reaches the true underlying CGM delay Δt0. Thus, this procedure provides a numerical estimation of Δt0 that corresponds to the visual impression conveyed by a Poincaré plot.
Data analysis
In order to perform data analysis, the AC and the corresponding CGM delay Δt0 are computed from each CGM data set, yielding two delay estimates (arm and abdomen) per participant in the study. Then, repeated-measures analysis of variance is used to compare the time delays across sensor placements and BG rates of change. Mean and standard deviation (SD) of the time delays across subjects are presented as well. Using the Kolmogorov-Smirnov test for Gaussian distribution, we have also confirmed that the data transformation described in the previous section indeed normalized the BG data—for all but three subjects, the BG data prior to transformation did not have normal distribution (P < 0.001), while post-transformation the normality hypothesis was rejected for only one subject.
Results
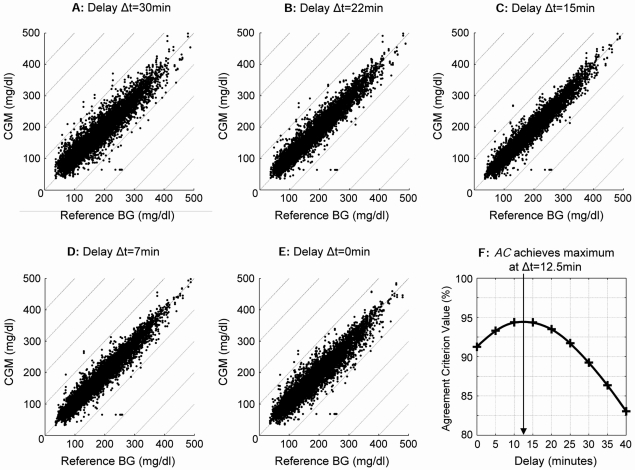
Figure 1 presents a set of Poincaré plots of BG-sensor co-dynamics over the entire BG delay values of Δt = 30 min (Fig. 1A), 22 min (Fig. 1B), 15 min (Fig. 1C), 7 min (Fig. 1D), and 0 min (Fig. 1E). It is evident that the most orderly plot with minimum spread of the data is in Figure 1C, e.g., at a delay of 15 min. This visual impression is confirmed by the graph of the AC in Figure 1F, which shows that AC achieves a maximum at 12.5 min. Thus, in this data set across the entire BG range the true sensor delay value appears to be Δt0 = 12.5 min (SD = 6.1 min).
FIG. 1.
Poincaré plots of BG–sensor co-dynamics at delay values of (A) 30 min, (B) 22 min, (C) 15 min, (D) 7 min, and (E) 0 min. (F) AC achieves a maximum at 12.5 min, which coincides with the visual impression of minimal spread of the plot at 15 min.
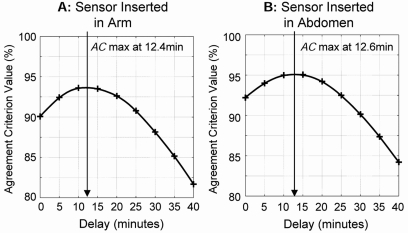
Because each participant in the study was wearing two sensors simultaneously, it was possible to compare the time lags at the two sensor locations. Figure 2 presents the AC of sensors inserted in the arm (Fig. 2A) and the abdomen (Fig. 2B). The average time lag of sensors inserted in the arm was Δt0 = 12.4 min (SD = 4.9 min); the average time lag of sensors inserted in the abdomen was similar: Δt0 = 12.6 min (SD = 7.1 min). Paired t test showed no statistical difference between the two sensor sites (t = 0.1, difference not significant).
FIG. 2.
Graphs of AC for sensors worn on the (A) arm and (B) abdomen, showing no difference between the sensor delays at the two sites.
Further, we compute the values of the time lag for different glucose rates of change. When CGM was falling at 1 mg/dL/min or faster, the AC achieved a maximum at 16.8 min. Thus, at fast negative rate of change the true sensor delay value appears to be Δt0 = 16.8 min (SD = 9.8 min). When glucose fluctuations were relatively steady—rate of change within the range of [-1,1] mg/dL/min—the AC achieved a maximum at 11.7 min. Thus, the true sensor delay value appears to be Δt0 = 11.7 min (SD = 7.2 min). When CGM was rising at 1 mg/dL/min, or faster, the AC achieved a maximum at 9.9 min corresponding to true sensor delay Δt0 = 9.9 min (SD = 8.9 min). Repeated-measures analysis of variance showed that the time lags at different glucose rates of change were statistically different (F = 8.3, P < 0.005). A contrast revealed that this significant difference was primarily due to longer time lag at fast negative rates of change (t = 3.7, P < 0.005).
Discussion
In this paper we present a new method for graphical and numerical evaluation of the possible time lag between BG and CGM readings observed in a number of studies of subcutaneous glucose monitoring.5–8 The method is based on the notion of co-dynamics of BG fluctuations and their corresponding CGM readings and on the representation of these co-dynamics via Poincaré-type plots. The principal idea is that the plot would appear most orderly and aligned along the true underlying relationship between BG levels and CGM values when its lag is at the exact time of sensor delay. If the relationship between BG and CGM is strictly linear, the points of the plot will coalesce along a straight line—the principal diagonal of the plot. In such a linear case the Poincaré plot would also be a correlation plot and its minimum spread would be at the point of maximal correlation, i.e., the true sensor delay will occur at the point where the correlation between BG and sensor readings is maximized. However, in many cases the relationship between BG and CGM is not linear and is not exactly known. For example, if the sensor tends to overestimate hypoglycemia and underestimate hyperglycemia, the relationship would be S-shaped. The approach adopted in this paper does not assume linear relationship between BG and CGM. Instead, the identification of the likely value of a delay is first done visually; then the numerical estimation relies on normalizing the data and on the information properties of the resulting normal distribution. If such a distribution is in place, we can claim that the R2 of a linear regression of CGM along BG data is proportional to the information, which CGM extracts from the reference data. In other words, maximum agreement between the normalized reference and CGM data would imply maximum information carried by CGM.
Because the proposed technique does not rely on mathematical approximation of the data, it offers certain advantages over techniques that rely on numerical derivatives,5 linear approximation, or spline smoothing of BG and sensor fluctuations.8 The principal advantage is non-vulnerability to missing data. For example, if some sensor data points are missing, the time sequence of CGM data would contain gaps, which would distort the computation of derivatives or the spline approximation of the data. The advantage of having gaps in the data without penalty on the delay estimation is important: it translates into the ability of the proposed method to estimate time delays at data strata defined by different rates of change or different BG levels. For example, the method does not need long streaks of rapidly falling BG values to estimate the delay at negative BG rates of change—a task that is difficult with model-based approaches relying on mathematical approximation of the data sequence. Further, consecutive CGM readings are highly interdependent,22 which presents problems to statistical tests, particularly when there is a need to determine degrees of freedom. The AC proposed here does not rely on independence of the data points involved in its computation, and therefore its application to CGM data is statistically justified. Alternative methods quantifying the visual impression of most orderly Poincaré plot can be used as well, as long as independence of consecutive BG–CGM data pairs is not assumed. For example, standard clustering criteria can be adopted to provide numerical evaluation of the spread of the Poincaré plot.
To illustrate the proposed technique, we analyzed a data set from an accuracy clinical trial of the FreeStyle Navigator. In these data, the average overall time delay between reference BG and sensor readings was 12.5 min, which is comparable to literature results. The data did not permit separating the possible delays because of BG-to-IG transport and instrument time. With this data set, we were also unable to separate the delay that can be potentially introduced by the smoothing and filtering algorithms used by the CGM for processing raw current data. However, we used Navigator data derived in “engineering mode” at a frequency of one reading per minute, thus, the influence of data preprocessing on these data should be minimal.
Negative rates (e.g., rapid glucose fall) caused longer delay—16.8 min—compared to 11.7 min at steady glucose and 9.9 min at rising glucose. This effect could be attributable to the static description of the delay process—a dynamic approach that accounts for the evolution of glucose fluctuations could ameliorate these differences. Or, we can speculate that the sensor time delay may have a physiologic component that depends on the rate of glucose change. In addition, because each participant in the study wore two sensors, it was possible to compare the delays at different locations—arm and abdomen—with no significant differences found.
In summary, we have proposed a new graphical and numerical analysis of BG-CGM co-dynamics that is free from underlying approximation of glucose fluctuations and thus results in model-free estimation of blood-to-sensor time delays. The method is applicable to estimating delays in any direction, positive or negative, corresponding to sensor lagging behind or running ahead of BG, and is not sensitive to gaps in the data, which is important for stratified analysis of sensor delay. We should emphasize that, although significant delays were identified, the purpose of this paper is to introduce a new technique, not to prove or disprove the existence of possible interstitial time lag.
Acknowledgments
The development of the proposed methods was supported by NIH/NIDDK grant RO1 DK 51562. The authors thank Abbott Diabetes Care, Alameda, CA for sharing their data.
Author Disclosure Statement
The authors have received grant support from Abbott Diabetes Care, Alameda, CA, a manufacturer of continuous glucose monitors. B.K. has received an honorarium from Amylin Pharmaceuticals.
References
- 1.Rebrin K. Steil GM. van Antwerp WP. Mastrototaro JJ. Subcutaneous glucose predicts plasma glucose independent of insulin: implications for continuous monitoring. Am J Physiol Endocrinol Metab. 1999;277:E561–E571. doi: 10.1152/ajpendo.1999.277.3.E561. [DOI] [PubMed] [Google Scholar]
- 2.Rebrin K. Steil GM. Can interstitial glucose assessment replace blood glucose measurements? Diabetes Technol Ther. 2000;2:461–472. doi: 10.1089/15209150050194332. [DOI] [PubMed] [Google Scholar]
- 3.Steil GM. Rebrin K. Hariri F. Jinagonda S. Tadros S. Darwin C. Saad MF. Interstitial fluid glucose dynamics during insulin-induced hypoglycaemia. Diabetologia. 2005;48:1833–1840. doi: 10.1007/s00125-005-1852-x. [DOI] [PubMed] [Google Scholar]
- 4.King CR. Anderson SM. Breton MD. Clarke WL. Kovatchev BP. Modeling of calibration effectiveness and blood-to-interstitial glucose dynamics as potential confounders of the accuracy of continuous glucose sensors during hyperinsulinemic clamp. J Diabetes Sci Technol. 2007;1:317–322. doi: 10.1901/jaba.2007.1-317. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Boyne M. Silver D. Kaplan J. Saudek C. Timing of changes in interstitial and venous blood glucose measured with a continuous subcutaneous glucose sensor. Diabetes. 2003;52:2790–2794. doi: 10.2337/diabetes.52.11.2790. [DOI] [PubMed] [Google Scholar]
- 6.Kulcu E. Tamada JA. Reach G. Potts RO. Lesho MJ. Physiological differences between interstitial glucose and blood glucose measured in human subjects. Diabetes Care. 2003;26:2405–2409. doi: 10.2337/diacare.26.8.2405. [DOI] [PubMed] [Google Scholar]
- 7.Stout PJ. Racchini JR. Hilgers ME. A novel approach to mitigating the physiological lag between blood and interstitial fluid glucose measurements. Diabetes Technol Ther. 2004;6:635–644. doi: 10.1089/dia.2004.6.635. [DOI] [PubMed] [Google Scholar]
- 8.Wentholt IME. Hart AAM. Hoekstra JBL. DeVries JH. Relationship between interstitial and blood glucose in type 1 diabetes patients: delay and the push-pull phenomenon revisited. Diabetes Technol Ther. 2004;9:169–175. doi: 10.1089/dia.2006.0007. [DOI] [PubMed] [Google Scholar]
- 9.Wientjes KJ. Schoonen AJ. Determination of time delay between blood and interstitial adipose tissue glucose concentration change by microdialysis in healthy volunteers. Int J Artif Organs. 2001;24:884–889. [PubMed] [Google Scholar]
- 10.Aussedat B. Dupire-Angel M. Gifford R. Klein JC. Wilson GS. Reach G. Interstitial glucose concentration and glycemia: implications for continuous subcutaneous glucose monitoring. Am J Physiol Endocrinol Metab. 2000;278:E716–E728. doi: 10.1152/ajpendo.2000.278.4.E716. [DOI] [PubMed] [Google Scholar]
- 11.Feldman B. Brazg R. Schwartz S. Weinstein R. A continuous glucose sensor based on wired enzyme technology—results from a 3-day trial in patients with type 1 diabetes. Diabetes Technol Ther. 2003;5:769–778. doi: 10.1089/152091503322526978. [DOI] [PubMed] [Google Scholar]
- 12.Liebovitch LS. Scheurle D. Two lessons from fractals and chaos. Complexity. 2000;5:34–43. [Google Scholar]
- 13.Takens F. Detecting strange attractors in turbulence. In: Rand DA, editor; Young LS, editor. Dynamical Systems and Turbulence. Vol. 898. Berlin: Springer-Verlag; 1981. pp. 366–381. Series Lecture Notes in Mathematics. [Google Scholar]
- 14.Thuraisingham RA. Enhancing Poincaré plot information via sampling rates. Appl Math Computation. 2007;186:1374–1378. [Google Scholar]
- 15.Denton TA. Diamond GA. Helfant RH. Khan S. Karagueuzian H. Fascinating rhythm: a primer on chaos theory and its application to cardiology. Am Heart J. 1990;120:1419–1440. doi: 10.1016/0002-8703(90)90258-y. [DOI] [PubMed] [Google Scholar]
- 16.Kamen PW. Krum H. Tonkin AM. Poincare plot of heart rate variability allows quantitative display of parasympathetic nervous activity in humans. Clin Sci (Lond) 1996;91:201–208. doi: 10.1042/cs0910201. [DOI] [PubMed] [Google Scholar]
- 17.Brennan M. Palaniswami M. Kamen P. Do existing measures of Poincare plot geometry reflect nonlinear features of heart rate variability? IEEE Trans Biomed Eng. 2001;48:1342–1347. doi: 10.1109/10.959330. [DOI] [PubMed] [Google Scholar]
- 18.Brennan M. Palaniswami M. Kamen P. Poincare plot interpretation using a physiological model of HRV based on a network of oscillators. Am J Physiol Heart Circ Physiol. 2002;283:H1873–H1886. doi: 10.1152/ajpheart.00405.2000. [DOI] [PubMed] [Google Scholar]
- 19.Javorka M. Javorkova J. Tonhajzerova I. Calkovska A. Javorka K. Heart rate variability in young patients with diabetes mellitus and healthy subjects explored by Poincare and sequence plots. Clin Physiol Funct Imaging. 2005;25:119–127. doi: 10.1111/j.1475-097X.2004.00601.x. [DOI] [PubMed] [Google Scholar]
- 20.Kovatchev BP. Clarke WL. Breton M. Brayman K. McCall A. Quantifying temporal glucose variability in diabetes via continuous glucose monitoring: mathematical methods and clinical application. Diabetes Technol Ther. 2005;7:849–862. doi: 10.1089/dia.2005.7.849. [DOI] [PubMed] [Google Scholar]
- 21.Kovatchev BP. Cox DJ. Gonder-Frederick LA. Clarke WL. Symmetrization of the blood glucose measurement scale and its applications. Diabetes Care. 1997;20:1655–1658. doi: 10.2337/diacare.20.11.1655. [DOI] [PubMed] [Google Scholar]
- 22.Kovatchev BP. Clarke WL. Peculiarities of the continuous glucose monitoring data stream and their impact on developing closed-loop control technology. J Diabetes Sci Technol. 2008;2:158–163. doi: 10.1901/jaba.2008.2-158. [DOI] [PMC free article] [PubMed] [Google Scholar]