Evaluating diagnostic accuracy of genetic profiles in affected offspring families

Abstract

Diagnostic accuracy of a genetic test involving multiple disease genes is evaluated using sensitivity and specificity. For estimation, data from both affected and unaffected subjects are required. For early onset diseases such as autism spectrum disorder only data from families with affected offspring is available. To enable estimation of specificity when no data for unaffected offspring are available (single affected offspring, SAO, data), we combine the pseudocontrol method of Cordell and Clayton [2002 Am J Hum Genet 70:124-41] with the approach of DeLong et al. [1985 Biometrics 41:947-58] in a logistic regression model for disease outcome with a risk score (RS) constructed from genotype information as prognostic variable. The area under the receiver operating characteristic curve (AUC) is then computed using the nonparametric Mann-Whitney method. Extensive simulation studies show that, analogously to other approaches utilizing pseudocontrols, resulting estimates of AUC using SAO data are slightly conservative when compared to estimates computed using the full population-based data. The method is illustrated using data from a study of autism spectrum disorder.

Introduction

Many common complex diseases are influenced by genetic factors, and the recent identification of some complex disease genes through genome-wide association studies (GWAs) has resulted in interest in the use of genetic variants for diagnostic and prognostic purposes. The contribution to disease risk for each identified individual gene is generally low in common diseases [1], and the predictive power is typically too small to be of clinical utility. In contrast, multiple studies have shown the potential value of genetic tests that combine a number of disease genes to a risk score (RS), where the number of risk alleles is summed [2-6]. However, before a genetic test may be used in clinical routine, its clinical validity has to be demonstrated. This includes the validation in a second, independent group of subjects, i.e., in a replication study [7]. Even more important, reliable and valid estimates of diagnostic accuracy of the test have to be provided [8]. The two most important measures for diagnostic accuracy are sensitivity and specificity because they form the basis of further relevant measures including the receiver operator characteristic (ROC) curve or likelihood ratios (LR). To estimate sensitivity and specificity, the availability of both affected and unaffected subjects from an appropriate spectrum of patients is required [7, 9]. In some instances, this is given through cohort or case-control populations from genetic association studies. However, for other diseases, especially early onset diseases, very few such samples are available. Instead, nuclear families consisting in one or more affected offspring together with their parents have been collected for studying transmission disequilibrium tests (TDT) that jointly test for both linkage and association [10].

In this work, we show how both sensitivity and specificity and subsequently other measures of diagnostic accuracy for judging clinical validity of a genetic test based on a RS can be estimated from single affected offspring trio (SAO) data consisting in an affected child and his/her both parents. To this end, we combine the pseudocontrol approach of Cordell and Clayton [11] with the method for estimating specificity from sensitivity and odds ratio (OR) estimates of DeLong et al. [12]. We show the validity in an extensive Monte-Carlo simulation study and illustrate its application by combining information from four genes for risk assessment of autism spectrum disorder (ASD). Finally, in the Discussion, we contrast the RS model with alternative models described in the literature, none of which are capable of estimating specificity from SAO data.

Material and Methods

Statistical Model

Suppose there is a sample of n_a affected (y = 1) and n_u unaffected (y = 0) subjects. To avoid haplotyping which would require substantial laboratory efforts for a test to be used in clinical routine, assume that one SNP per disease susceptibility gene has been selected. Let g_k denote the number of risk alleles of the subject at SNP k, k = 1,…, K, which corresponds to the additive score coding [13]. For dominant models, g_k = 2(0) if the number of risk alleles at SNP k is at least one (none); for recessive models, g_k = 2(0) if the number of risk alleles at SNP k is two (up to one). For simplicity, we assume that genotypes are available for all SNPs and all subjects. To combine the information across SNPs, we consider the $\text{RS}={\sum }_{k=1}^K{g}_k$ which is the number of risk alleles. Parameters are estimated using the logistic regression model

$$\text{logit}P(y=1|\mathit{\text{g}})={\eta }_1=\alpha +\beta \text{RS}=\alpha +\beta {\sum }_{k=1}^K{g}_k.$$ (1)

The test is considered to be positive if the linear predictor η₁ exceeds a pre-specified threshold γ. This model involves only two parameters, the regression constant and the parameter for the RS, and it has been used in many applications [see, e.g., 4, 14-16]. The disadvantage is that all SNPs are assumed to follow dosage models with identical weights for all SNPs. Specifically, in a three SNP model with additive coding, two risk alleles at SNP 1 have the same effect as one risk allele at SNP 2 and another one at SNP 3. Alternative models are two weighted risk score (WRS) models and the polygenic (PG) model which are described and compared in detail in the Appendix.

Measures of Diagnostic Accuracy

The log odds ratios (logOR) β of eq. (1) can be estimated with standard approaches, and measures of diagnostic accuracy can be derived from the pre-specified threshold γ for the linear predictor η₁ if unrelated affected and unaffected subjects are available. Specifically, the sensitivity is given by the probability that the linear predictor exceeds the threshold given the subject is affected sens_γ = P(RS > γ|y = 1). Similarly, the specificity, i.e., the probability that the linear predictor does not exceed the threshold in an unaffected subject is spec_γ = P(RS ≤ γ|y = 0). From sens and spec, other measures of diagnostic accuracy can be derived, e.g., the likelihood ratio (LR) of a positive test result LR+_γ = sens_γ/(1 − spec_γ), the likelihood ratio of a negative test result LR−_γ = (1 − sens_γ)/spec_γ, or the ROC curve for which sens_γ is plotted against (1 − spec_γ) for the entire range of γ. Finally, the C–statistic, i.e., the area under the curve (AUC) can be calculated. Because SNPs are ordinally scaled at most, the Mann-Whitney approach to the C–statistic should be used instead of trapezoid methods [17]. Specifically, let S^a and S^u be the risk score values in affected and unaffected subjects, respectively. Then the C-statistic is given by

$$C=\sum _{i=1}^{n_a}\sum _{j=1}^{n_u}\left(I({\mathit{\text{S}}}_i^a>{\mathit{\text{S}}}_j^u)+\frac{1}{2}I({\mathit{\text{S}}}_i^a={\mathit{\text{S}}}_j^u)\right)/(n_a{n}_u)$$

with I denoting the indicator function.

Estimation of Sensitivity and Specificity in Single Affected Offspring Trio Data

While sensitivity can be estimated from the affected offspring in SAO data, specificity cannot be estimated directly because only pseudocontrols and no data from truly unaffected subjects are available. Since competing methods are lacking, we propose estimation of specificity as follows. As only one SNP per gene has been selected, phase is irrelevant, and method 3 of Cordell and Clayton [11] can be used. Here, one matched pair consisting in a case and a pseudocontrol is formed per family. The case genotypes consist in the genotypes of the affected offspring, and the pseudocontrol is constructed with the genotypes consisting in the non-transmitted parental alleles. For example, suppose that a family is typed at two SNPs, with the father having genotypes (1/1 and 1/2) at loci (1 and 2), respectively; the mother having genotypes (1/2 and 1/2); and the affected offspring having genotypes (1/1 and 1/2). We have a single case with genotypes (1/1 and 1/2) and form a single matched pseudocontrol with genotypes (1/2, and 1/2). For estimation of logORs, conditional logistic regression is used. The sensitivity sens_γ is estimated as the proportion of affected subjects with RS > γ. For every threshold γ, a conditional logistic regression is fitted to obtain threshold specific odds ratios OR_γ = exp(β_γ). DeLong et al. [12] have shown that the specificity can be estimated given the OR and sensitivity as ${\text{spec}}_{\gamma }=\frac{(1-{\text{sens}}_{\gamma }){\mathit{\text{OR}}}_{\gamma }}{(1-{\text{sens}}_{\gamma }){\mathit{\text{OR}}}_{\gamma }+{\text{sens}}_{\gamma }}$.

Measures of variability can be obtained using the leave-one-out jack-knife approach which is asymptotically equivalent to the robust estimator of variance [18]. Specifically, let ${\widehat{\text{spec}}}_{\gamma ,(i)}$ denote the specificity estimated at threshold γ when the i^th family from a total of n SAO families is left out from the analysis. Then the asymptotic variance of the specificity is estimated by $\widehat{\mathit{\text{Var}}}({\widehat{\text{spec}}}_{\gamma })=\frac{n-2}{n}{\sum }_{i=1}^n{({\widehat{\text{spec}}}_{\gamma ,(i)}-{\widehat{\text{spec}}}_{\gamma })}^2$. Estimates of likelihood ratios and the C–statistic estimated by the Mann-Whitney approach are obtained analogously.

Knapp et al. [19] showed that the haplotype relative risk which is estimated from SAO families is always stochastically closer to 1 than the relative risk estimated from population-based samples. We demonstrated for the genotype relative risk method that biases may occur when marker and trait locus are different [20]. The biases result in conservative estimates in all practical situations, and it is negligible for practical purposes. We therefore expect that likelihood ratios should be closer to 1 when estimated from family data compared to estimates from population-based samples. Similarly, specificities and C-statistics should be closer to 0.5 for SAO families compared with those from population-based samples.

Simulation Study

To investigate the validity of our novel approach for estimating sensitivity, specificity, the positive likelihood ratio LR+, the negative likelihood ratio LR−, and the AUC C as measures of diagnostic accuracy from SAO families, we performed a Monte-Carlo simulation study. Parental genotypes were simulated according to specified allele frequencies under the assumption of Hardy-Weinberg equilibrium. Mendelian transmission was used to generate genotypes in offspring. The disease risk in a child given his/her genetic profile was calculated as in Janssens et al. [2, 21] by means of the LR under an additive effect of the deleterious alleles and assuming no statistical interaction between genes. The computed disease risk was compared to a random variable drawn from a continuous uniform distribution on the interval [0;1]. A subject was defined as affected when the disease risk was higher than the value of the random variable, and unaffected, otherwise.

Parent-offspring trios with an affected child defined the SAO samples. To compare the estimates of diagnostic accuracy from SAO families with a population-based sample consisting of independent subjects, parental information was discarded, and affected children were compared with unaffected children. Thus, data from exactly the same affected subjects were used in the population-based samples and the SAO families.

The disease prevalence was assumed to be 0.1. The investigated genetic profiles had 2, 4, 10, 20 and 40 SNPs that were in linkage equilibrium. For stable estimation and for retaining a high number of events per variable (EPV), the number of SAO families was 200, 400, 1,000, 2000, and 4000, respectively. Because an SAO family consists of one affected subject and one pseudocontrol, the identical number of affected and unaffected subjects was simulated for the population-based sample. For each genetic profile, two different scenarios were studied. In the first (scenario I), all markers had identical deleterious allele frequencies (MAF) of 0.3 and allelic ORs of 1.3. The second scenario (scenario II) was characterized by a combination of three different MAFs corresponding to three different ORs. Specifically, one SNP was assumed to have a MAF of 0.1 and an allelic OR of 1.5, two SNPs were assumed to have a MAF of 0.3 and an OR of 1.3. All other SNPs were assumed to have a MAF of 0.5 and an OR of 1.1. In the model with two SNPs only, one SNP had a MAF of 0.1 and an OR of 1.5 and the other a MAF of 0.3 and an OR of 1.3. The number of replicates was 10,000 for each scenario and genetic profile. All simulations were done in C, and all calculations were performed in R version 2.4.1.

Application to Autism Spectrum Disorders (ASD)

Families were selected from the Autism Genetic Resource Exchange (AGRE) repository (www.agre.org), ascertained in the United States of America through a proband with ASD and a potentially affected sibling. Details of AGRE have been given elsewhere [22]. In this study, 226 families had complete genotypes at all investigated SNPs, and 159 (69%) of the families were Caucasian. The AGRE families consisted in families including at least two affected offspring, and the first sibling to the proband was considered for analysis.

One SNP was chosen per gene. rs2292813 (risk allele C) and rs1861972 (risk allele A) were selected for SLC25A12 and EN2, respectively, both with an additive 0/1/2 allele coding because of the previous positive associations [23-24]. Similarly, rs6872664 (risk allele C) and rs35678 (risk allele T) were selected from our own findings for PITX1 [25] (replication unpublished) and ATP2B2 [Pub. No.: WO/2006/100608] with additive and a recessive codings for the risk allele, respectively. Minor allele frequencies of individual SNPs are provided in Supplementary Table S1.

Stability of parameter estimates was checked using five-fold cross-validation (5-fold CV) using the family as unit and a Caucasian families only subgroup analysis.

Extension to the Ascertainment Scheme “Sibling to Proband”

The ascertainment scheme of the AGRE families does not match the situation of SAO families considered above. In some applications including ASD it is, however, important to investigate the clinical validity of a test in siblings to probands. Here, families with a first child that is already diagnosed with ASD present a second child to the physician. The aim is estimating the risk for ASD in the sibling to the proband without genotyping the proband. We thus have to consider the prospective model P(y₂|g₂, y₁), where y₂ and y₁ are the phenotypes of a second sibling and the proband, respectively, and g₂ denotes the vector of genotypes of the sibling to the proband. The different ascertainment scheme is thus different to the simpler prospective model P(y|g) from above. Because all information on the phenotype y₂ of the second sibling is contained in his/her genotype g₂, the phenotype y₁ of the proband is irrelevant. The prospective model thus reduces to P(y₂|g₂) if the model is correctly specified.

Because families with two affected offspring are ascertained in this study, we need to consider the retrospective model P(g₂|y₁, y₂). Using the same arguments as Prentice and Pyke [26], it can be shown that the retrospective likelihood from a logistic regression is identical to the prospective likelihood except for the intercept even under the sibling to the proband ascertainment scheme.

Results

Simulation Study

Results of the simulation study are displayed in Table 1 for the AUC over all models. Detailed results for the four SNP model are presented in Table 2. The findings for the Monte-Carlo simulations involving 2, 10, 20 and 40 SNPs in the genetic profile are given in Supplementary Tables S2-S5, respectively. The number of NA values increases with the number of SNPs investigated because the probability to observe a specific number of risk alleles is low. For example, in the case of 40 independent SNPs, the probability to observe a subject with RS ≤ 9 is < 10^-4 in scenario I. Similarly, the probability of RS ≥ 40 is < 10^-4 in this scenario. We thus expect NA values for 50 out of 80 values in this part of the simulation study. Furthermore, calculation of both LR values is only possible if sens and spec are not equal to 0 and 1, respectively

Table 1.

Results from Monte-Carlo simulation study for genetic profiles involving different numbers of independent SNPs. Displayed are mean and range of the area under the curve (C-statistic) from 10,000 replicates for two scenarios from the population-based study and the single affected offspring families.

# SNPs	Scenario I				Scenario II
	Population-based		Family-based		Population-based		Family-based
	Mean	Range	Mean	Range	Mean	Range	Mean	Range
2	0.566	(0.456–0.67)0	0.560	(0.452–0.661)	0.564	(0.435–0.667)	0.558	(0.456–0.662)
4	0.595	(0.519–0.666)	0.585	(0.507–0.660)	0.577	(0.502–0.656)	0.567	(0.491–0.654)
10	0.648	(0.601–0.694)	0.633	(0.587–0.677)	0.583	(0.532–0.633)	0.575	(0.526–0.621)
20	0.702	(0.674–9.731)	0.682	(0.645–0.713)	0.600	(0.564–0.638)	0.590	(0.555–0.625)
40	0.767	(0.746–0.785)	0.741	(0.717–0.762)	0.628	(0.606–0.651)	0.615	(0.591–0.637)

Table 2.

Results from Monte-Carlo simulation study for four SNPs with 10,000 replicates per scenario. Displayed are mean and range of measures of diagnostic accuracy (sensitivity (sens), specificity spec, positive likelihood ratio (LR+), negative likelihood ratio (LR−)) for all score values (0 to 8). Sensitivity is displayed in the columns for the population-based samples only because the same cases were used for both the population-based study and the single affected offspring families.

		Scenario I				Scenario II
		Population-based		Family-based		Population-based		Family-based
Score	Measure of accuracy	Mean	Range	Mean	Range	Mean	Range	Mean	Range
0	sens	0.969	(0.928–0.992)			0.970	(0.925–0.998)
	spec	0.061	(0.017–0.108)	0.058	(0.020–0.173)	0.051	(0.012–0.098)	0.049	(0.013–0.132)
	LR+	1.032	(0.972–1.098)	1.029	(0.970–1.195)	1.022	(0.964–1.078)	1.020	(0.958–1.138)
	LR−	0.530	(0.083–1.917)	0.556	(0.069–1.935)	0.622	(0.050–2.375)	0.651	(0.028–3.000)
1	sens	0.834	(0.758–0.900)			0.830	(0.748–0.898)
	spec	0.265	(0.185–0.350)	0.256	(0.157–0.362)	0.248	(0.162–0.342)	0.240	(0.158–0.344)
	LR+	1.136	(0.969–1.305)	1.121	(0.955–1.345)	1.104	(0.975–1.255)	1.093	(0.946–1.265)
	LR−	0.631	(0.352–1.132)	0.655	(0.344–1.184)	0.693	(0.373–1.108)	0.715	(0.379–1.253)
2	sens	0.575	(0.490–0.665)			0.555	(0.465–0.652)
	spec	0.566	(0.478–0.670)	0.552	(0.466–0.653)	0.561	(0.468–0.650)	0.549	(0.452–0.654)
	LR+	1.332	(1.000–1.773)	1.289	(1.030–1.704)	1.268	(0.967–1.680)	1.236	(0.953–1.643)
	LR−	0.751	(0.549–1.000)	0.771	(0.584–0.969)	0.795	(0.586–1.037)	0.812	(0.598–1.047)
3	sens	0.295	(0.198–0.382)			0.264	(0.190–0.352)
	spec	0.817	(0.738–0.885)	0.806	(0.727–0.885)	0.827	(0.758–0.895)	0.817	(0.751–0.891)
	LR+	1.632	(0.926–2.915)	1.540	(0.880–2.800)	1.542	(0.926–2.690)	1.465	(0.874–2.826)
	LR−	0.863	(0.740–1.023)	0.875	(0.743–1.038)	0.891	(0.767–1.023)	0.901	(0.763–1.036)
4	sens	0.106	(0.055–0.168)			0.083	(0.038–0.140)
	spec	0.947	(0.905–0.980)	0.942	(0.895–0.984)	0.956	(0.910–0.988)	0.952	(0.908–0.989)
	LR+	2.104	(0.788–6.000)	1.913	(0.714–6.316)	2.021	(0.593–8.200)	1.854	(0.527–8.929)
	LR−	0.944	(0.872–1.019)	0.949	(0.874–1.029)	0.959	(0.892–1.029)	0.963	(0.886–1.047)
5	sens	0.025	(0.002–0.060)			0.016	(0.000–0.045)
	spec	0.990	(0.968–1.000)	0.989	(0.965–1.000)	0.993	(0.968–1.000)	0.992	(0.000–1.000)
	LR+	NA	NA	NA	NA	NA	NA	NA	NA
	LR−	0.985	(0.947–1.018)	0.986	(0.945–1.023)	0.990	(0.957–1.018)	NA	NA
6	sens	0.003	(0.000–0.018)			0.000	–
	spec	0.999	(0.988–1.000)	1.000	–	1.000	–	1.000	–
	LR+	NA	NA	NA	NA	NA	NA	NA	NA
	LR−	0.998	(0.982–1.010)	NA	NA	NA	NA	NA	NA
7	sens	0.000	–			NA	NA
	spec	1.000	–	NA	NA	NA	NA	NA	NA
	LR+	NA	NA	NA	NA	NA	NA	NA	NA
	LR−	NA	NA	NA	NA	NA	NA	NA	NA
8	sens	NA	NA			NA	NA
	spec	NA	NA	NA	NA	NA	NA	NA	NA
	LR+	NA	NA	NA	NA	NA	NA	NA	NA
	LR−	NA	NA	NA	NA	NA	NA	NA	NA

NA: Score was never observed; –: not assessed.

Diagnostic accuracy was always slightly underestimated when determined from SAO families compared with population-based affected/unaffected data involving the same affected subjects as the SAO families. This is consistent with our expectations from other studies involving pseudocontrols [19-20].

The bias increased with the number of SNPs involved, but even for the 40 SNPs scenarios, difference in the mean AUC from 10,000 replicates was only 0.02 (0.767 for affected/unaffected data; 0.741 for SAO families).

Application to Autism Spectrum Disorders (ASD)

For the RS model, the increase per risk allele was 1.35 (95% confidence interval (CI): 1.16-1.58) for ASD. Sensitivities, ORs and 1 minus specificities for the binary tests on the RS are shown in Table 3. Figure 1 depicts the ROC curve which was constructed from the estimates of Table 3. The estimated AUC was 0.61 (95% CI: 0.59 – 0.64; p = 1.4 × 10^-6 for test of random guessing). Test performance of single SNPs is given in Supplementary Table S6. Stability of estimated sensitivities, specificities and ORs was investigated using 5-fold CV (Table S7) and a subgroup analysis in Caucasian families only (Table S8).

Table 3.

Sensitivity (Sens), 1 minus specificity (1-Spec), odds ratio (OR) with 95% confidence intervals (95% CI) and two-sided p-values as estimated from 2 × 2 tables for a binary test on the risk score (RS) with ≤ γ vs. > γ risk alleles.

RS ≤	Sens	95%CI	1-Spec	95% CI	OR	95%CI	p-value
3	0.95	0.93 - 0.96	0.94	0.91 - 0.95	1.30	0.53 - 2.37	0.530
4	0.83	0.81 - 0.85	0.71	0.68 - 0.74	2.04	1.21 - 2.85	0.003
5	0.50	0.47 - 0.54	0.33	0.29 - 0.36	2.09	1.14 - 2.25	0.0005
6	0.21	0.19 - 0.24	0.11	0.09 - 0.13	2.17	1.39 - 3.46	0.007
7	0.10	0.08 - 0.11	0.03	0.02 - 0.04	3.33	1.22 - 3.72	0.010
8	0.00	–	0.00	–	1.00	–	–

Figure 1.

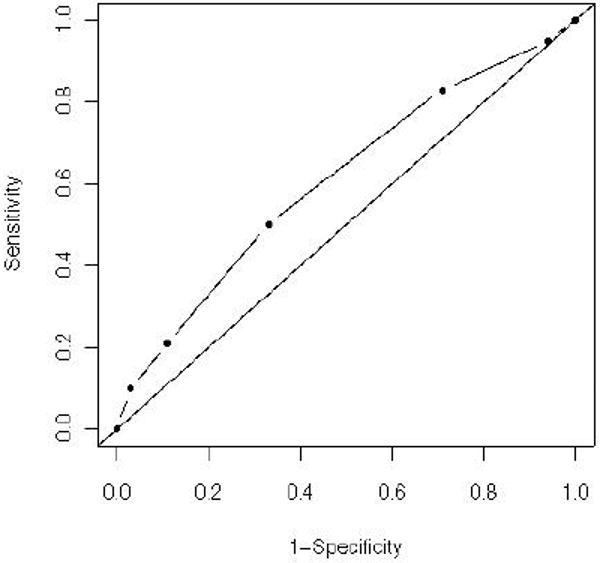
Receiver operating characteristic associated with the risk score. Specificity was estimated using sensitivity and the odds ratio. The estimated area under the curve (AUC) was 0.61 (95% CI: 0.59 – 0.64).

Discussion

The contribution of a single gene to the disease risk is generally low in complex diseases but the use of a combination of a number of SNPs from different genes generally improves risk prediction. This holds true for both genomic profiling and the analysis of multiple genes added to traditional clinical risk factors [3-6]. The addition of classical clinical variables is not only reasonable but strongly indicated for some diseases including coronary artery disease in which well-established risk scores based on clinical features are already available. Genetic profiles that do not incorporate clinical variables could, however, be particularly useful for early onset diseases such as ASD, where reliable clinical measures are not available when first clinical signs become apparent and early therapeutic intervention can improve long-term outcome [27].

Irrespective of the question whether only genetic variables or both genetic and clinical variables are to be included in a risk model, an important question is how the best model is selected and validated. This issue has been discussed in detail in several articles in this journal, see, e.g., Refs. [28-30]. However, in the area of genetics an important different aspect needs to be considered. A genotype-phenotype association is only credible if the initial association has been reproduced in follow-up studies and/or in different study groups within the same study [31]; this process is termed replication [32]. The replication should be considered a sine qua non condition before a SNP is included in a risk score model. As a result, we have included four SNPs in our application that have been shown to be associated with ASD in at least two studies. Currently, we recommend to include as many replicated, i.e., truly associated SNPs as possible in the RS model for the following reasons:

• The effect size of different SNPs is weak but similar for complex genetic diseases.

• Results from several simulation studies indicate that the performance of a risk score model improves with the number of SNPs [2, 21].

• The genotyping cost of an additional SNP is substantially lower than 50 cents when genotyping is done on a customized array, thus practically negligible.

Although we recommend adding as many SNPs as possible, this need not improve the classification.

To combine the information across the available SNPs, four standard models are considered in the literature, and all of them are based on the logistic regression because of its simple interpretation, and the possibility of estimating parameters from a retrospective likelihood [26]. A detailed description and a comparison of the four models is given in the Appendix.

One approach that has received great interest is the polygenic (PG) model, where two dummy variables are used per SNP. However, with four diallelic SNPs as in the ASD study, one in recessive coding, there are 54 different genotype combinations. Thus, risk assessment and interpretation of results are difficult. Even worse, the complexity increases exponentially with the number of SNPs. The PG model is, however, an appropriate choice for large data sets because these allow stable risk assessments for a large number of SNP combinations. Nevertheless, in the illustrative example only 25 of the 54 possible combinations were observed. A risk assessment of new subjects having one of the non observed SNP combinations would be impossible because no estimates of sensitivity and specificity are available. These concerns against the use of the PG model are analogous to those against subgroup analyses in clinical trials where decisive conclusions often cannot be achieved.

The stable estimation of measures of diagnostic accuracy is important for early onset diseases such as ASD, where very few cohort or case-control populations are available. We therefore developed an approach allowing estimation of measures for judging diagnostic accuracy from SAO trio data for the simple RS model. We are not aware of further methods for estimating measures of diagnostic accuracy from SAO families. The novel method should not be considered a replacement for cohort or case-control studies for final clinical validation because SAO trio data need not represent an appropriate spectrum of patients to whom the test may be applied. Because findings need replication in an independent study, we propose that the SAO data are used as first stage and that the replication is performed in an appropriate study of independent subjects.

The low flexibility of the simple RS model may on the one hand be considered a weakness because all SNPs contribute equally to the score, irrespective of their true effect. On the other hand, the simple RS model is explicitly not considered an in vitro diagnostic multivariate index assays (IVDMIA) according to the Food and Drug Administration (FDA) [33]. IVDMIAs are developed based on multivariate data and clinical outcome, and the claim of their clinical validity is not transparent to patients, laboratorians, and clinicians who order these tests. Since the FDA has to ensure that an IVDMIA has been clinically validated, it regulates these devices to ensure that the IVDMIA is safe and effective for its intended use. As a result, pre- and postmarket requirements differ substantially between IVDMIAs and an assay not considered to be an IVDMIA. Simply speaking, an IVDMIA needs premarket approval by the FDA so that developing costs are substantially higher for an IVDMIA compared to other genetic tests not considered to be IVDMIAs.

In summary, we developed a novel approach based on the simple RS model that is appropriate for estimating measures of diagnostic accuracy from SAO families. It was contrasted with the PG model, validated in an extensive Monte-Carlo simulation study and illustrated using ASD families. In line with other studies utilizing pseudocontrols that are constructed from non-transmitted alleles our novel approach yields valid estimates that are slightly conservative.

Appendix

Weighted Risk Score Model I

Weighted risk score (WRS) models are natural extensions of the RS model because different weights are assigned to the SNPs. Two different WRS models have been proposed in the literature. The simpler WRS (WRSI) model assumes pre-specified fixed weights w_k

$$\text{logit}P(y=1|\mathit{\text{g}})={\eta }_2=\alpha +\beta \text{RS}=\alpha +\beta {\sum }_{k=1}^K{w}_k{g}_k.$$ (2)

This model involves only two parameters but requires weights for the index ${\sum }_{k=1}^K{w}_k{g}_k$ which need to be defined externally. Because the specification of external weights is almost impossible in practice, this approach has rarely been followed in applications.

Weighted Risk Score Model II

The second WRS (WRSII) model involves K + 1 parameters and is given by

$$\text{logit}P(y=1|\mathit{\text{g}})={\eta }_3=\alpha +{\sum }_{k=1}^K{\beta }_k{g}_k.$$ (3)

It relies on the dosage effects of all SNPs and excludes the possibility of statistical interactions between SNPs. It has therefore rarely been employed in practice.

Polygenic Model

The polygenic (PG) model with or without interactions can be considered the natural competitor of the simple RS model. In the PG model, there are multiple genes with varying effects, and the effect of the genes need not be additive in nature. The PG model allows for non-additive and non-standard effects of genotypes, and this means that a dosage effect of each SNP is not assumed. Usually, two dummy variables are considered per SNP if the mode of inheritance is unknown. Specifically, x_k1 = 1 if a subject is heterozygous at SNP k, 0 otherwise, and x_k2 = 1 if a subject is homozygous for the risk allele at SNP k, 0 otherwise. A general discussion of codings can be found in the literature [11, 34-35]. Genotypes and dummy variables are collected in column vectors. g = (g₁,…, g_K)′ and x = (x₁₁, x₂₁,…, x_K1, x_K2)′.

The PG model without interaction involves 2K + 1 parameters, has been employed in applications [36-37], and it is given by

$$\text{logit}P(y=1|\mathit{\text{g}})={\eta }_4=\alpha +{\sum }_{k=1}^K{\beta }_{k1}{x}_{k1}+{\sum }_{i=1}^K{\beta }_{k2}{x}_{k2}.$$ (4)

A further generalization of Eq. (4) is to allow for pair-wise and higher-order statistical interactions between SNPs which has often been considered [21, 38-41], and this model may lead to a total of 2^K − 1 parameters.

Comparison of Models

To compare the different sketched methods, a number of criteria need to be considered. First, the greatest flexibility is offered by the PG model, where single locus genotypes are combined into a polygenic profile. Therefore, the prediction of the risk of affection is assumed to be more accurate in the PG compared with both WRS approaches and the simple RS method.

Second, the methods differ greatly regarding their complexity. Specifically, the RS model requires the estimation of only one logOR and one specificity per threshold γ, whereas the complexity of the PG model increases exponentially with the number of SNPs. For instance, with only four diallelic SNPs there are 81 different possible genotype combinations. This has profound implications for the sample sizes required for risk assessments and reasonable interpretations. Specifically, several authors advocated that the minimum number of EPV required in logistic regression analyses should be 10-20 [28, 42]. While the number of SNP parameters to be estimated in a logistic regression is independent from the number of SNPs considered and therefore always identical to one in the RS model, the number of parameters increases linearly for the WRS models and exponentially for PG (Table A.1). According to this, for the setting of four diallelic SNPs, the simple RS model and the WRS I model require 160 SAO families for estimation of both sensitivity and specificity (2 parameters × 8 thresholds × 10), but the PG model 1600 – and the PG model still does not allow estimation of specificity. Clearly, such large data sets are hardly available in family analysis. To obtain reliable parameter estimates, the required sample size thus is only a third for the simple RS model and the WRS I model when compared with the full PG model even when only four SNPs are considered. This advantage of the simple RS model increases with the number of SNPs because the RS model increases exponentially with the number of SNPs. Compromises are the WRSII model and the PG model without interaction.

Finally, as discussed in detail in the Discussion, the simple RS approach has one further general advantage when aimed at use in clinical routine. In contrast to the PG and the WRS II models, the simple RS model is not considered to be an IVDMIA.

Table A1.

Number of SNPs (# SNPs) used for risk prediction, number of parameters in a logistic regression required for SNP modeling, required number of single affected offspring trios (SAO) for estimating sensitivity in a logistic regression required to obtain 10 events per variable (EPV; # SAO for sens), and required number of single affected offspring trios for estimating specificity using the risk score (RS) and WRS I model to obtain an EPV of 10 (# SAO RS for spec). Specificity cannot be estimated for the second weighted risk score (WRS II) and the polygenic (PG) models from SAO.

# SNPs	# SNP parameters		# SAO for sens			# SAO for spec
	RS	WRS II	PG	RS	WRS II	PG	RS
1	1	1	2	20	20	40	40
2	1	2	8	20	40	160	80
4	1	4	80	20	80	1,600	160
10	1	10	6,560	20	200	> 105	400
20	1	20	59,048	20	400	> 105	800
50	1	50	3.5·107	20	1,000	> 108	2,000
100	1	100	5.2·1047	20	2,000	> WP	4,000
500	1	500	3.6·10238	20	10,000	> WP	20,000
1,000	1	1,000	> 1·101,000	20	20,000	> WP	40,000

^*WP: world population