Detecting Selection in Population Trees: The Lewontin and Krakauer Test Extended

Abstract

Detecting genetic signatures of selection is of great interest for many research issues. Common approaches to separate selective from neutral processes focus on the variance of F_ST across loci, as does the original Lewontin and Krakauer (LK) test. Modern developments aim to minimize the false positive rate and to increase the power, by accounting for complex demographic structures. Another stimulating goal is to develop straightforward parametric and computationally tractable tests to deal with massive SNP data sets. Here, we propose an extension of the original LK statistic (T_LK), named T_F–LK, that uses a phylogenetic estimation of the population's kinship (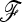) matrix, thus accounting for historical branching and heterogeneity of genetic drift. Using forward simulations of single-nucleotide polymorphisms (SNPs) data under neutrality and selection, we confirm the relative robustness of the LK statistic (T_LK) to complex demographic history but we show that T_F–LK is more powerful in most cases. This new statistic outperforms also a multinomial-Dirichlet-based model [estimation with Markov chain Monte Carlo (MCMC)], when historical branching occurs. Overall, T_F–LK detects 15–35% more selected SNPs than T_LK for low type I errors (P < 0.001). Also, simulations show that T_LK and T_F–LK follow a chi-square distribution provided the ancestral allele frequencies are not too extreme, suggesting the possible use of the chi-square distribution for evaluating significance. The empirical distribution of T_F–LK can be derived using simulations conditioned on the estimated matrix. We apply this new test to pig breeds SNP data and pinpoint outliers using T_F–LK, otherwise undetected using the less powerful T_LK statistic. This new test represents one solution for compromise between advanced SNP genetic data acquisition and outlier analyses.

THE development of methods aiming at detecting molecular signatures of selection is one of the major concerns of modern population genetics. Broadly, such methods can be classified into four groups: methods focusing on (i) the interspecific comparison of gene substitution patterns, (ii) the frequency spectrum and models of selective sweeps, (iii) linkage disequilibrium (LD) and haplotype structure, and (iv) patterns of genetic differentiation among populations (for a review see Nielsen 2005). Tests based on the comparison of polymorphism and divergence at the species level inform on mostly ancient selective processes. Population-based approaches, however, are designed to pinpoint modern processes of local adaptation and speciation occurring among populations within a species. Such approaches also become crucial in the fields of agronomical and biomedical sciences, for instance, to pinpoint possible interesting (QTL) regions and disease susceptibility genes. Especially, human, livestock, and cultivated plants genetics may benefit from such methods while whole-genome single-nucleotide polymorphisms (SNPs) genotyping technologies are becoming routinely available (e.g., Barreiro et al. 2008; Flori et al. 2009).

In the population genomic era (Luikart et al. 2003), identifying genes under selection or neutral markers influenced by nearby selected genes is a task in itself for quantifying the role of selection in the evolutionary history of species. Conversely, the accurate inference of demographic parameters such as effective population sizes, migration rates, and divergence times between populations relies on the use of neutral marker data sets. One approach of detecting loci under selection (outliers) with population genetic data is based on the genetic differentiation between loci influenced only by neutral processes (genetic drift, mutation, migration) and loci influenced by selection.

Lewontin and Krakauer's (LK) test for the heterogeneity of the inbreeding coefficient (F) across loci was the first to be developed with regard to this concept (Lewontin and Krakauer 1973). The LK test was immediately subject to criticisms (Nei and Maruyama 1975; Lewontin and Krakauer 1975; Robertson, 1975a,b; Tsakas and Krimbas 1976; Nei and Chakravarti 1977; Nei et al. 1977). Indeed, its assumptions are likely to be violated due to loci with high mutation rate, variation of F due to unequal effective population size (N_e) among demes, and correlation of allele frequencies among demes due to historical branching. The robustness of the LK test to the effects of demography was tested through coalescent simulations by Beaumont and Nichols (1996). They tested the influence of different models of population structure on the joint distribution of F_ST (i.e., the inbreeding coefficient F) and heterozygosity (H_e). The F_ST distribution under an infinite-island model is inflated for low H_e values under both the infinite-allele model (IAM) and the stepwise mutation model (SMM) (Beaumont and Nichols 1996). This tendency becomes, however, more marked when strong differences in effective size N_e and gene flow among demes occur, that is, when allele frequencies are correlated among local demes. This suggests an excess of false significant loci when one assumes an infinite-island model as a null hypothesis, while correlations of gene frequencies substantially occur. However, the F_ST distribution shows robustness properties for high H_e values (typical from microsatellite markers). Therefore, Beaumont and Nichols (1996) suggested the possibility of detecting outliers by using the distribution of neutral F_ST conditionally on H_e under the infinite-island model of symmetric migration, with mutation.

The problem of accounting for correlations of allele frequencies among subpopulations was discussed by Robertson (1975a), who showed how these correlations inflated the variance of the LK test. Different approaches were taken to cope with the problem. It was, for instance, proposed to restrict the analysis to pairwise comparisons (Tsakas and Krimbas 1976; Vitalis et al. 2001). However, as pointed out by Beaumont (2005), reducing the number of populations to be compared to many pairwise comparisons raises the problem of nonindependence in multiple testing and may reduce the power to detect outliers. Another way was to assume that subpopulation allele frequencies are correlated through a common migrant gene pool, that is, the ancestral population in a star-like population divergence. In this case, subpopulations evolve with an unequal number of migrants coming from the migrant pool and/or to different amounts of genetic drift. This demographic scenario can be explicitly modeled using the multinomial-Dirichlet likelihood approach (Balding 2003). This multinomial-Dirichlet likelihood (or Beta-binomial for biallelic markers such as SNPs) was implemented by Beaumont and Balding (2004) and subsequently by Foll and Gaggiotti (2008), Gautier et al. (2009), Guo et al. (2009), and Riebler et al. (2010), in a Bayesian hierarchical model in which the F_ST is decomposed into two components: a locus-specific (α) effect and a population-specific (β) effect. This Bayesian statistical model together with prior assumptions on α and β was implemented in a Markov chain Monte Carlo (MCMC) algorithm. A substantial improvement made by Foll and Gaggiotti (2008) was to use a reverse-jumping (RJ)-MCMC to simultaneously estimate the posterior distribution of a model with selection (with α and β) and of a model without selection (with β only). More recently, Excoffier et al. (2009) addressed the issue of accounting for “heterogeneous affinities between sampled populations”—in other words, accounting for migrant genes that do not necessarily originate from the same pool—by using a hierarchically structured population model. They showed by simulations that the false positive rate is lower under a hierarchically structured population model than under a simple island model, for the IAM and the SMM applicable to microsatellite markers and for a SNP mutation model. Excoffier et al.(2009) thus proposed to extend the Beaumont and Nichols (1996) method to a hierarchically structured population model.

Nowadays, a computational challenge is to analyze data sets with increasing numbers of markers and populations, under complex demographic histories, in a reasonable amount of time. This is especially the case in agronomical and biomedical sciences with the increasingly used biallelic SNP markers. A question arises as to whether F_ST-based methods would be sufficiently powerful to detect outliers with SNP markers. Indeed, for low H_e values, the inflation of the F_ST distribution under the infinite-island model accentuates dramatically when assuming a mutation model typical for SNPs (simulations of Eveno et al. 2008). Excoffier et al. (2009) corroborated these results and also indicated that the F_ST distribution is generally broader under a model of hierarchically structured populations when using SNP markers. In addition, as the authors pinpoint, although the hierarchical island model is more conservative than the island model, an excess of false positives can be obtained “if the underlying genetic structure is more complex …, for instance in case of complex demographic histories, involving population splits, range expansion, bottleneck or admixture events” (Excoffier et al. 2009, p. 12). The Bayesian hierarchical models developed by Beaumont and Balding (2004) and Foll and Gaggiotti (2008) effectively account for strong effective size and migration rate variation among subpopulations, but they still impose a star-like demographic model in which the current populations share a common migrant pool and are not supposed to have undergone historical branching. More practically, MCMC-based methods might suffer from a computational time requirement when analyzing large marker data sets such as SNP chips data sets. Therefore, the development of simple parametric tests potentially dealing with a summary of the population tree, including historical branching as well as population size variation, remains an alternative solution to achieve a good compromise between advanced genetic data acquisition and outlier analyses.

In this article, we describe an extension of the original parametric LK test for biallelic markers that deals with complex population trees through a statistic that takes into account the kinship (or coancestry) matrix between populations, under pure drift with no migration. The statistics of the classical test (T_LK) and its extension (T_F–LK) are expected to follow a chi-square distribution with (n – 1) d.f., where n is the number of populations studied. Through forward simulations of neutral SNPs data under increasingly complex demographic histories, we obtained the empirical distribution of both statistics and showed that they follow a chi-square distribution provided the ancestral allele frequencies are not too extreme. These results also emphasize the robustness of these statistics to variation in demographic histories. Forward simulations of the same demographic models but including selection in one population allowed us to evaluate the power of both statistics to detect selection. We show that the extension of the LK test is more powerful at detecting outliers than the classical LK test for complex demographic histories. A comparison with one of the MCMC methods for multinomial-Dirichlet models (Foll and Gaggiotti 2008) also revealed substantial additional power. We apply this new statistical test to a data set of SNP markers in known genes of the pig genome, taking advantage of the availability of microsatellite markers for the estimation of the kinship matrix. This new parametric test can help to screen large marker data sets and large numbers of populations for outliers in a reasonable amount of time, although we recommend to simulate the empirical distribution of the T_F–LK statistics conditionally on the estimated kinship matrix.

POPULATION MODEL AND NOTATIONS

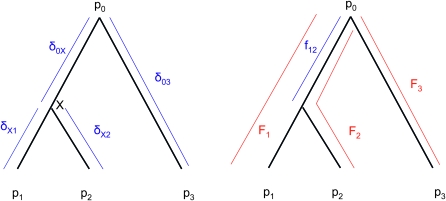
We consider a set of n populations derived from a common ancestor and the frequencies (p₁, p₂, …, p_n) of one allele at a neutral biallelic locus. We assume their phylogeny is described by a tree (Figure 1), in which each branch is characterized by some amount of drift.

Figure 1.—

Example of tree-like evolution: construction of the kinship matrix.

The kinship matrix:

Due to drift and coancestries, frequencies p_i's are correlated, so that

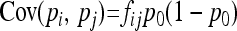(1)

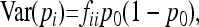(2)

where p₀ is the frequency of the allele in the ancestor population, f_ii is the mean expected inbreeding coefficient of the ith population, and f_ij the kinship coefficient between populations i and j equal to the inbreeding coefficient of the most recent ancestor population common to i and j.

In Figure 1, for example, the calculations proceed as follows. Let δ_UV be the fixation index corresponding to the branch from U (an internal node or the root of the tree) to V (an internal node or a leaf of the tree, i.e., one of the n populations). If the branch UV corresponds to t generations in a population of effective size N, 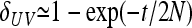provided mutations are ignored. The tree of Figure 1 includes the root (O), the internal node (X), and the three populations 1, 2, and 3. Setting f₀₀ = 0, we have

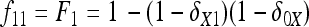(3)

(4)

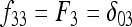(5)

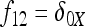(6)

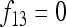(7)

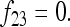(8)

In the following, 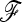stands for the matrix of the f_ij. For simplicity, diagonal elements f_ii are simply denoted as F_i. Under pure drift (without mutation) it can be demonstrated that 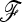is invertible and positive definite.

Estimation:

Let us consider L biallelic loci indexed by ℓ, whose first allele frequency in population i is p_i,ℓ. A sample of genotyped individuals in each population provides an empirical estimate 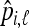of this allele frequency by simple counting.

We propose to make use of the neighbor-joining (NJ) tree (Saitou and Nei 1987) built from the Reynolds' genetic distances between pairs of populations (Reynolds et al. 1983), adding an outgroup so that the tree linking the n populations can be rooted. Then branch lengths of the NJ tree are estimates of the δ's and provide estimates of the elements of the matrix. Since we assume in the following that frequency distributions are approximately Gaussian, an alternative approach could be to estimate δ-values by a likelihood approach as suggested by Weir and Hill (2002). However, these authors considered only the case where is diagonal. Accounting for a general tree structure would make their approach more complicated and probably not needed since we did not find any strong difference between results obtained using true or estimated values.

Loci used to estimate must be neutral. When genome-wide genotyping is available, one can consider that only a small fraction of genomic regions and hence of genotyped markers is or has been a target of selection, so that averaging over all loci will provide a good estimate of . We used this approach in our simulation-based study, where was estimated from the simulated SNPs to be tested. Another possibility is to make use of a subset of markers (supposed neutral) to estimate and then use it for testing departures from neutrality of another subset of markers. We used this approach to test for signature of selection in a real data set from pig populations. We took advantage of the availability of microsatellite markers for estimating , to test SNP markers in candidate genes.

TESTS OF SELECTION: LEWONTIN AND KRAKAUER AND EXTENSIONS

Distribution of the LK test:

Consider L biallelic loci genotyped for a large set of individuals structured in n populations. Lewontin and Krakauer (1973) focused on the distribution of the F_ST statistic per locus and proposed a test statistic denoted here by T_LK. To simplify notations, the subscript ℓ per locus is omitted in the following. Note that the allele frequencies and the corresponding statistics depend on the current locus, while the kinship matrix 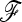does not. Let p = (p₁, …,p_j, …,p_n)′ be the n-vector of allelic frequencies of the first allele (say) in the n populations. The quantity F_ST is defined as

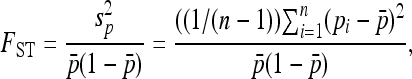(9)

where 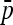and 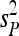are the sampling estimates of the mean and variance, respectively, of the vector p. The test statistic is equal to

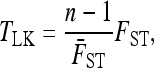(10)

where 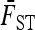is the average of F_ST in (9) over the L loci. Under the reference conditions considered by Lewontin and Krakauer (equal branch lengths, F_i = f_ii = F, and no correlations, f_ij = 0 for i ≠ j), this test was shown to follow approximately a χ²-distribution with n – 1 d.f.

In the following, we propose a new calculation of the first two moments of the F_ST statistic, in the case of a tree-like history of the n populations. Under genetic drift, the first two moments of p are

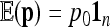(11)

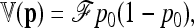(12)

where p₀ is the founder allele frequency, 1_n is the n-vector of 1's, and 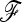is the kinship (or coancestry) (n × n) matrix linking the n populations.

It can be shown (see appendix a) that

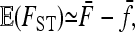(13)

provided the number of populations is large enough, that

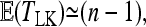(14)

and that, approximating frequency distributions by the normal if F values are small,

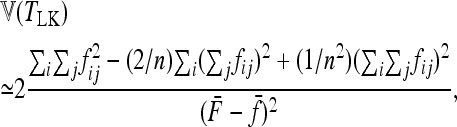(15)

with

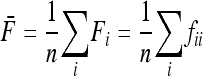(16)

and

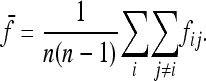(17)

With a star-like evolution (the nondiagonal elements in 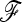= 0, 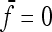) and with equal branch lengths ( 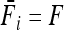for all i as in Lewontin and Krakauer 1973), the p_i's are assumed to be independent, identically distributed, and normal, so that T_LK follows the distribution of a chi square with (n − 1) d.f. This is the basic version of the test. In other cases, the test can be adapted, either recalculating its moments or defining another statistic to test the fit of data with the null hypothesis.

As shown in appendix a, the general expression (15) takes simpler forms in special cases of departure from the basic situation:

• The phylogenetic tree of populations is structured but branch lengths are equal (F_i = f_ii = F for all i). Then Robertson (1975b) showed that

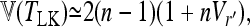(18)

where V_r′ stands for the variance of correlation coefficients between gene frequencies (see appendix a for the correspondence with the present notations). This result suggests that such correlations may imply a strong increase of the expected variance of the test.

• Populations are independent (i.e., the tree representing the phylogeny of populations has the structure of a star) but F values are heterogeneous. In that case one has

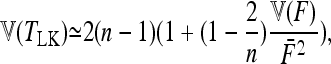(19)

where 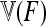is the variance of F_i values.

Provided the departure from normality is not too strong, we propose an extension of the LK test to take account of any structuration on the moments of allele frequency distributions.

An extension of the LK test when the populations are structured—use of the matrix:

The previous calculation allows one to obtain the correct variance of the test. However, the chi-square distribution of the test is anyway only approximate, even assuming normality, because (i) the F_i's are heterogeneous, which implies that T_LK is a sum of squared random variables with different variances, and (ii) the denominator in (9) depends on the allele frequencies.

Assuming normality the joint distribution of allele frequencies is fully characterized by the initial frequencies p₀ and by the matrix.

Let

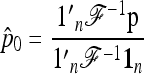(20)

be the unbiased linear estimate of p₀ with minimum variance, with 1_n denoting the n-vector made of 1's. It may be noted that this estimate of p₀ is not the maximum-likelihood estimate, even under the normal assumption. When the n populations diverge from the founder in a star-like manner, but with different coancestry coefficients, then 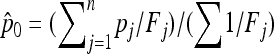. Further, when the populations have the same size, as in the Lewontin and Krakauer test, then this estimator is the sample mean .

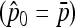Let us note 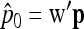, with w the n-vector

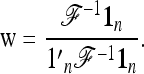(21)

Then the first two moments of the estimator 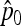of p₀ can be calculated:

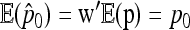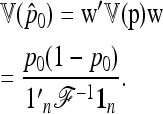It follows that

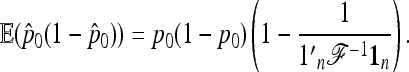(22)

If the ancestral allele frequencies p₀ were known, then the most interesting quadratic form in p would be

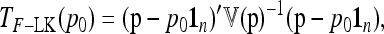(23)

which follows a chi-square distribution with n d.f. However, since p₀ is unknown, it is replaced by its estimator 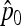, suggesting to define the test as

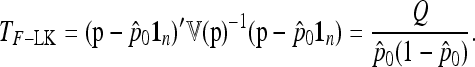(24)

In practice, the above expression of T_F–LK is multiplied by the bias correction term 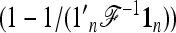(see Equation 22), which is omitted in the following, for the sake of simplicity. When 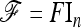, the only difference between T_LK and T_F–LK, apart from the bias correction term, resides in the estimation of F, either with 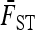or with the estimation method proposed in this article (Estimation section).

The quadratic form

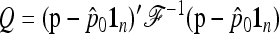(25)

can be written as p′M p, where

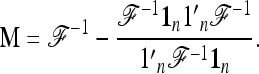(26)

Its first moment can be calculated as

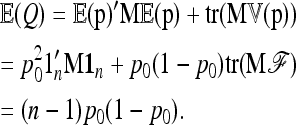The second moment of Q is

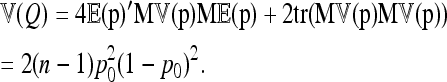Then T_F–LK has approximate expectation

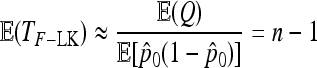(27)

and approximate variance

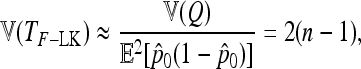(28)

so that T_F–LK follows approximately a 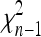-distribution under genetic drift. The case of a multiallelic locus is derived in appendix b, but is not investigated further in this article.

SIMULATIONS

Simulation settings:

We simulated haplotype samples of partially linked loci, under neutrality (H₀) and directional selection on one locus in one population (H₁). The choice of simulating partially linked loci was technically relevant because most SNPs data sets nowadays come from dense whole-genome scans. In all simulated scenarios of population divergence, the populations originate from an equilibrium ancestral population of constant size.

Neutral haplotype samples from this ancestral population were obtained by coalescent simulations using the MS software (Hudson 2002). The generated haplotypes consisted of 1000 SNPs (or biallelic segregating sites) randomly distributed along a 100-Mb chromosome, resulting in a 100-kb distance between two SNPs, on average. Assuming a recombination rate of 1 cM/Mb, the recombination rate between two SNPs was fixed at 0.1 cM.

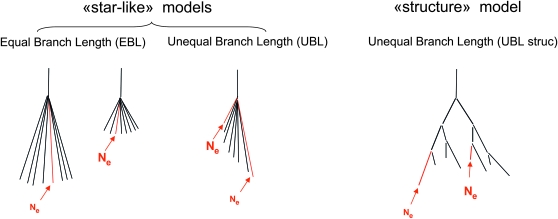
To simulate the evolution of the populations from the ancestral one in the same way for both neutrality and selection, we used forward simulations of the Wright–Fisher diploid model, further assuming stepwise changes in population size, population dichotomy, no mutations, and a uniform recombination rate. Different sorts of demographic models were simulated to explore the influence of demographic history on the statistical properties of both the classical LK statistic and the extension we propose. The first demographic model is a model of star-like population divergence with equal branch lengths (EBL) among populations, in which all populations evolve spontaneously from a common ancestor, independently from each other with the same inbreeding coefficient F. The second model is also a star-like divergence scenario but with unequal branch lengths (UBL) among populations. The third model is a model of populations structured by common ancestries with variation of branch length (UBL struc) (see Figure 2 and Table 1 for population schemes and the demographic parameters used).

Figure 2.—

Models of population divergence simulated in this study. This schematic illustrates three sorts of demographic models simulated in this study: EBL, UBL, and UBL struc. Populations highlighted in red are those in which directional selection occurs. For the UBL models, we simulated selection in a large (big N_e) and a small (little N_e) population, in separate simulations. For the EBL model we simulated two scenarios, one with large and one with small populations, in which one population is selected.

TABLE 1.

Demographic parameters of the different models simulated in this study

	Model
	EBL (F = 0.05)a (8 pop)			UBLa (8 pop)			UBL struc (8 pop)
	Groups
	Outgroup	Ancestor	Population	Outgroup	Ancestor	Population	Outgroup	Ancestor	Ancestor	Ancestor	Population
	Population size
	Ne = 900	Ne = 900	Ne = 900bc	Ne = 500	Ne = 500	Ne = 100bd	Ne = 500				Ne = 100bd
			Ne = 900			Ne = 200					Ne = 200
			Ne = 900			Ne = 300				Ne = 100
			Ne = 900			Ne = 350				Ne = 500
			Ne = 900			Ne = 400			Ne = 500		Ne = 300
			Ne = 900			Ne = 600					Ne = 100
			Ne = 900			Ne = 800		Ne = 500
			Ne = 900			Ne = 1000bc					Ne = 400
									Ne = 500		Ne = 600
	EBL (F = 0.4)a									Ne = 100
										Ne = 500
	Ne = 100	Ne = 100	Ne = 100bd								Ne = 800
			Ne = 100								Ne = 1000bc
			Ne = 100
			Ne = 100
			Ne = 100
			Ne = 100
			Ne = 100
			Ne = 100
Generation nos.	t = 200	t = 100	t = 100	t = 200	t = 100	t = 100	t = 200	t = 100	t = 25	t = 25	t = 50

^aIn “star-like” models, the inbreeding coefficient F = 1 − (1 − t/2N)^t = F_ST. 8 pop, eight populations.

^bPopulation in which directional selection occurs in the simulations (only one population is under selection in each simulation type).

^cLarge population.

^dSmall population.

Selection was modeled as follows: (i) selection occurs on a single locus (SNP) of the haplotype, (ii) selection occurs on the less frequent allele of the SNP (“0” and “1” are the ancestral and derived states, respectively), (iii) the allelic fitness k is linked to the selection coefficient s by k = 1 + s, leading to the genotypic fitness scheme

00	01	11
1	1 + s	(1 + s)2

Note that in this case it is the derived allele that is under selection. Hence, the probability of drawing a given parental genotype to generate the next generation depends on the genotype frequency, which changes at each generation according to this selection scheme. In UBL models, we chose to simulate separately selection on “large” and “small” populations to better account for the heterogeneity of F among populations when selection acts (Table 1). Selection was simulated for two intensities, s = 0.05 and s = 0.20.

We performed 10,000 simulations in each demographic scenario to cover small type I error. For each simulation, a matrix of unbiased Reynolds' genetics distances was computed from frequency data of the 1000 partially linked SNPs simulated. The 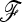matrix was then estimated from branch lengths of a neighbor-joining tree (see Estimation section). The ancestral allele frequency p₀ was estimated using 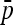for T_LK and using 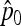(Equation 20) for T_F–LK. Then the T_LK and T_F–LK statistics were calculated for each SNP, excluding the cases of complete fixation of any of the two alleles in the whole population set. To construct the H₁ distribution of both statistics, we recorded the T_LK and T_F–LK values for the SNP under selection for each simulation. To construct the H₀ distribution, we drew at random one SNP position and recorded its associated T_LK and T_F–LK values for each simulation under neutrality.

To allow an unbiased comparison of the empirical distributions to the theoretical distribution, we considered the ideal situation in which the true 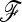matrix and ancestral allele frequency p₀ are known. In each simulation, we recorded the value of the ancestral allele frequency p₀ for each SNP, and we calculated T_LK(p₀) and T_F–LK(p₀) accordingly (refer to Equations 9 and 10, where 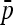is replaced by p₀, and Equation 23). The calculation of T_F–LK(p₀) included the true 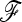matrix.

The different empirical H₀ distributions of T_LK and T_F–LK were compared to their theoretical expectations (i.e., chi-square distribution with n or n − 1 d.f., depending on whether parameters had to be estimated or not). The power of each statistic to detect selected SNPs was evaluated as follows: first, we determined the 0.9, 0.95, 0.98, 0.99, and 0.999 quantiles of the empirical null distribution of each test from the simulations under neutrality. Then, the power of the tests was determined as the proportion of simulations for which the statistic was greater than a given quantile of the null. This allows power to be recorded as a function of the empirical type I error.

To compare the LK-based tests to the method of Foll and Gaggiotti (2008), we used their Bayes factor for selection of the selected SNP as a test statistic. As an implementation of the Foll and Gaggiotti (2008) method, we used the BAYESCAN software run with the default parameters. As this method requires a rather long computation time, comparisons were performed on 1000 simulations only, under UBL and UBL struc models for two selection intensities (0.05, 0.20). The power of this method and of the LK-based tests was evaluated as explained above.

Simulation results:

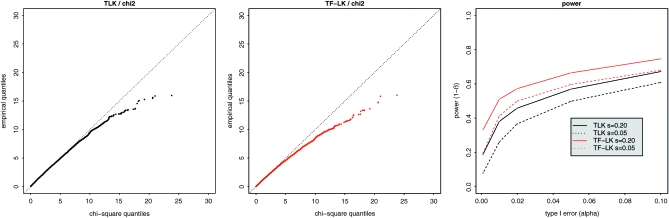
The empirical distributions of T_LK and T_F–LK under neutrality, and the chi-square distribution:

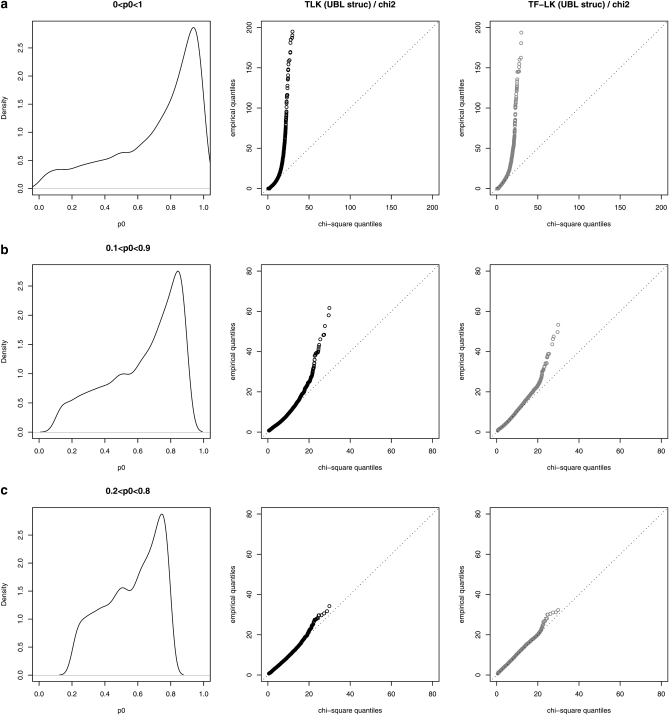
The empirical distributions of T_LK(p₀) and T_F–LK(p₀) have similar shapes in each demographic model (EBL, UBL, and UBL struc), with the same number of populations (i.e., eight populations were simulated). We illustrate this under the more complex UBL struc model, with Q–Q plots that compare the empirical distribution of T_LK(p₀) and T_F–LK(p₀) with the theoretical chi-square distribution (Figure 3). For each statistic, however, the right tail of the distribution varies slightly depending on the demographic model (Figure 3 for UBL struc and supporting information, Figure S1 and Figure S2 for EBL and UBL models). Overall, the empirical distributions of T_LK(p₀) and T_F–LK(p₀) under neutrality appear relatively robust to increasingly complex demographies, whatever the range of ancestral allele frequencies (Figure 3, Figure S1, and Figure S2). In addition, we observed that the shape of the empirical distributions of T_LK(p₀) and T_F–LK(p₀) appears to depend on p₀. When all simulated ancestral frequencies are included (0 < p₀ < 1), they do not fit the right tail of the chi-square distribution (Figure 3). Extreme p₀ values represented a high proportion of the simulations (Figure 3a). When accounting for less extreme p₀ values (i.e., 0.2 < p₀ < 0.8), the empirical distribution fit the chi-square distribution (Figure 3, b and c).

Figure 3.—

Fit of T_LK and T_F–LK empirical distributions to a χ²-distribution under the UBL struc scenario with eight populations, and dependency on p₀. (a–c) Left column, distribution of ancestral allele frequencies; center (resp. right) column, Q–Q plots of the empirical distribution of T_LK (resp. T_F–LK) under neutrality (H₀) against the χ²(8) distribution. For unbiased comparison of the empirical and theoretical distributions, we illustrate the ideal case in which p₀ and 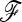are known.

In the real situation of parameter estimation (see Estimation in population model and notations for the estimation of p₀ and the 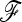matrix), both estimators of p₀ ( 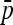and 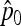in Equation 20) approximate well the true p₀ values (Figure S3). Moreover, the empirical distribution of T_F–LK values based on various 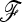-matrix estimates is highly similar to the one calculated with the true 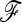matrix (not shown). These results indicate that for both statistics the departure from the theoretical chi-square distribution under neutrality is mainly due to extreme p₀ values rather than problems related to parameter estimations.

Power comparison of the T_LK and T_F–LK statistics:

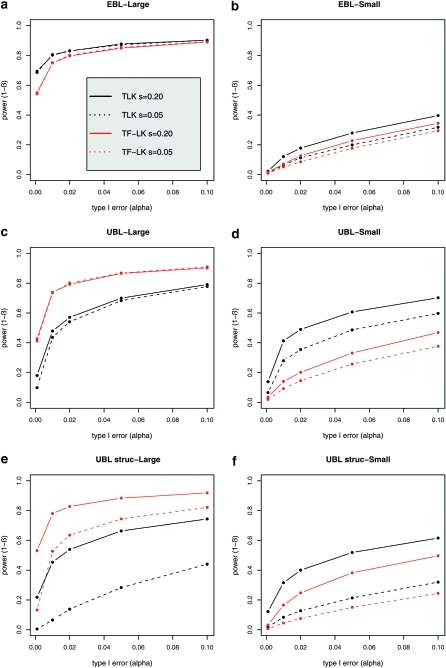
Power was calculated using the empirical distributions of the statistics, on the basis of simulations under neutrality and selection (see Simulation settings section). Some power properties common to both T_LK and T_F–LK arise from this simulation study. First, the population size of the selected population has a major impact on the power to detect selected loci. For a given selection coefficient and whatever the type I error, we found that the power to detect selection is higher in a large population than in a small population (Figure 4), for both T_LK and T_F–LK. This was expected because the strength of a selection event is mainly determined by the product N_es. The explanation is, however, more complex, since the population sizes also intervene in the weights T_F–LK puts on each population. Second, the selection coefficient has a differential impact on the power, depending on the underlying demographic model. A larger selection coefficient does not result in a higher level of power in EBL and UBL models. However, a larger selection coefficient has a positive impact for detecting selected SNPs in UBL struc models. This can be explained by the fact that complete fixation was reached in some models but not in all of them.

Figure 4.—

(a–f) Power of T_LK and T_F–LK to detect selection in a large (a, c, and e) or small (b, d, and f) population, for different type I error values. Results are shown for different demographic models with eight populations and two selection coefficients (s = 0.05 and 0.20). The matrix and p₀ are set to their estimated values.

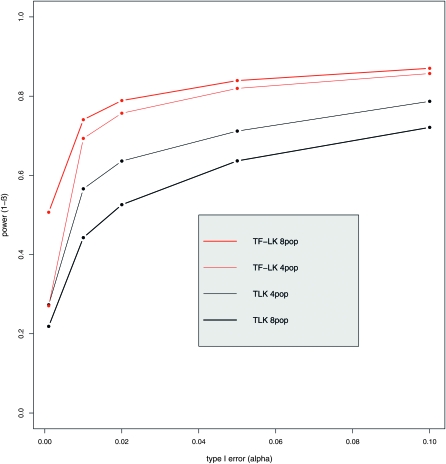
Substantial differences in power occur between T_LK and T_F–LK. We first consider the case in which selection acts on a large population relative to other populations. In UBL and UBL struc models, the detection power of T_F–LK is >20% greater than that of T_LK (Figure 4). In an EBL model, T_F–LK and T_LK have similar detection power, from 60 to 85% for 0.001 < α < 0.1. If selection acts on a small population relative to other populations, however, T_LK is more powerful than T_F–LK but it should be noted that the absolute power of both statistics is small in that case, especially at low type I errors. Restricting the window of possible p₀ values, for instance to 0.2 < p₀ < 0.8, has a general negative effect on the power of the T_LK statistic, whatever the size of the population under selection (not shown). However, in complex UBL models when selection acts on a large population, the power of T_F–LK seems to benefit from intermediate ancestral frequencies (0.2 < p₀ < 0.8) for low type I error (α < 0.001). We also investigated the impact of the population sampling on power properties. For a given population tree, the power to detect selected SNPs with T_F–LK is increased by sampling more populations (Figure 5). This is not the case with T_LK for which the signal of selection seems masked by an increasing number of populations sampled.

Figure 5.—

Influence of population sampling on the power of T_F–LK when eight populations are simulated under a UBL struc model and the power is calculated on the basis of samples of four or eight populations. Each population sampling contains the selected population. The matrices calculated on the basis of both kinds of population sampling do not have the same dimension but reflect similar amounts of genetic drift.

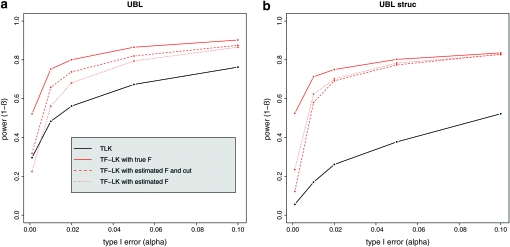
We investigated the effect of estimating the matrix on power. Selection may introduce a bias in the estimation of the matrix, resulting in a loss of power for the tests based on T_F–LK. Indeed, in EBL, UBL, and UBL struc models, the detection power obtained when estimating (Figure 4) was reduced compared to that obtained when is known (Figure S4), especially for small type I errors, i.e., 0.001 < α < 0.01. In addition, for tests based on the T_F–LK statistic, the phylogenetic reconstruction may lead to the emergence of small internal branches and hence to small extradiagonal (f) values in the estimated matrix. In the UBL models simulated, cutting small branch lengths had a positive effect on the power of T_F–LK (Figure 6a, cutoff values = 0.005). Indeed, the branch-cutting procedure transformed some trees inferred as (falsely) “structured” into “star-like” trees closer to the population trees simulated. In UBL struc models, however, cutting small branch lengths had a slightly negative effect on the power of T_F–LK (Figure 6b, cutoff value = 0.001). In some simulations, indeed, small branch lengths were neglected whereas they truly described the population tree and hence led to a decrease of power.

Figure 6.—

Influence of a branch-cutting procedure on the power of T_F–LK. This illustrates the effect on the power of T_F–LK of estimating the matrix and of cutting small branch lengths in the phylogenetic tree. Branch lengths are cut as they correspond to f (extra diagonal) values <0.005 and <0.001, in (a) UBL and (b) UBL struc models, respectively.

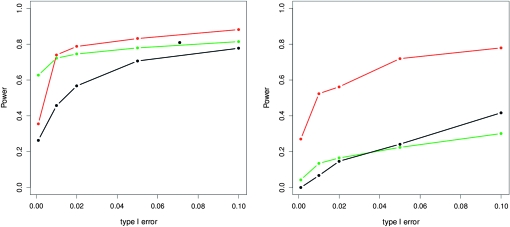
Finally, we compared the T_LK and T_F–LK tests with the MCMC method of Foll and Gaggiotti (2008) under UBL and UBL struc scenarios. We found that under a UBL scenario, the method of Foll and Gaggiotti (2008) had more detection power than T_LK, but not as much as T_F–LK whether one assumes the number of simulations was not enough for low type I errors (<0.001) (Figure 7, left). Under a UBL struc scenario, however, T_F–LK clearly outperformed the MCMC method for a wide range of type I errors (Figure 7, right). Indeed, T_F–LK detected 20–50% more selected SNPs than the MCMC method for type I errors ranging from 0.001 to 0.05. Similar results are obtained for s = 0.20 under both demographic scenarios (Figure S5). This difference in power under UBL struc scenarios may stem from the fact that the method of Foll and Gaggiotti (2008) does not account for the hierarchical structure of populations, while T_F–LK does.

Figure 7.—

Detection power obtained with T_LK (black), T_F–LK (red), and the method of Foll and Gaggiotti (2008) (green) under a UBL (left) and a UBL struc scenario (right), for a selection coefficient of 0.05.

APPLICATION TO PIG SNPS DATA

One SNP data set was tested as an illustrative example for signature of selection: 34 SNPs located in candidate genes (Blott et al. 2003; A. Day, G. Evans, and S. Blott, unpublished data). The associated commercially important phenotypes concern reproductive performance, growth and fatness, meat quality, and disease resistance. Samples of four major European pig breeds were genotyped: the Landrace (LR) (LR01), the Large White (LW) (LW05), the Piétrain (PI) (PI03), and the Duroc (DU) (DU02). To estimate the 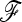matrix for calculating the T_F–LK statistic, we made use of 50 genome-wide distributed microsatellite markers previously studied on the same samples in a previous project (PigBioDiv, see http://www.projects.roslin.ac.uk/pigbiodiv/ and Sancristobal et al. 2006). We used an Asian breed, the Meishan (MS01), as outgroup. We first explored the fit of the empirical distributions of T_LK and T_F–LK to the chi-square distribution. The empirical distributions were generated by simulating population history conditional on the previously estimated 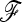matrix. To do so, we used forward simulations with parameterizations of N_e and split times that led to the estimated 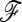matrix. Then, we simulated selection on one SNP in one population under the same conditions, to assess the power to detect selection in a real case. The empirical H₀ distribution of T_LK and T_F–LK in this case has a slightly shorter right tail than the chi-square distribution, (Figure 8). Moreover, T_F–LK was more powerful than T_LK (Figure 8). We performed single tests on the basis of the empirical distribution of T_LK and T_F–LK, on each SNP, and we accounted for multiple testing using the Benjamini–Hochberg (BH) correction, which controls the false discovery rate (Benjamini and Hochberg 1995). The threshold for significance was set at 0.05. We also performed tests on the basis of the chi-square distribution (as in tests of selection section).

Figure 8.—

Fit to the χ²-distribution and power analysis of T_LK and T_F–LK for a scenario mimicking the pig data set. The 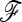matrix was estimated using data on 50 microsatellites. Forward simulations were parameterized conditionally on the matrix.

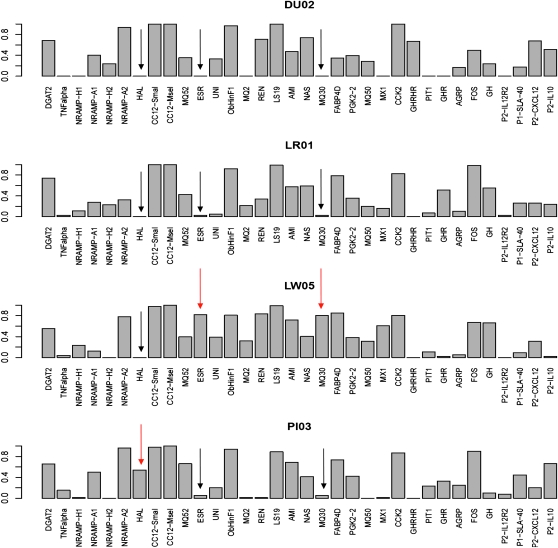
Single tests performed using T_LK, with either its empirical distribution or the chi-square distribution, pinpointed three outliers, ESR, MQ30, and GHRHR (Table 2). After correction for multiple tests (BH), there was no significant outlier. Single tests performed using T_F–LK with its empirical distribution pinpointed seven outliers (NRAMP, HAL, ESR, REN, MQ30, MX1, and GHRHR). Using the chi-square distribution, four outliers were detected (HAL, ESR, REN, and MQ30). After correction for multiple tests, only ESR and MQ30 were significant. Overall, after correction for multiple tests, results of the chi-square test were similar to those obtained using the empirical distributions, but P-values were higher (Table 2), as expected since the chi-square distribution was more conservative in this case (Figure 8). Population SNP allele frequencies allowed us to identify the population(s) in which selection occurred. In our case, directional selection seems to have occurred in the Large White breed for a gene involved in reproductive performance (ESR) and for another gene MQ30 (Figure 9). In addition, we confirmed that directional selection had occurred at the Halothane gene (HAL) in the Piétrain breed (Figure 9).

TABLE 2.

Nominal and corrected P-values on a 34-SNPs data set from PigBioDiv2, based on the empirical distribution of T and TF–LK and on the theoretical χ2-distribution

	Empirical test				Chi-square test
	TLK		TF–LK		TLK		TF–LK
SNP name	P-value	BH	P-value	BH	P-value	BH	P-value	BH
9CP-DGAT2	0.9584	1.0000	0.9339	1.0000	0.9523	1.0000	0.9314	1.0000
23CP-TNFα	0.8150	1.0000	0.7344	1.0000	0.7934	1.0000	0.7323	1.0000
32CP-NRAMP-H1	0.6540	1.0000	0.5565	1.0000	0.6337	1.0000	0.5652	1.0000
41CP-NRAMP-A1	0.7213	1.0000	0.6128	1.0000	0.6967	1.0000	0.6185	1.0000
42CP-NRAMP-H2	0.5562	1.0000	0.4985	1.0000	0.5424	1.0000	0.5094	1.0000
43CP-NRAMP-A2	0.1313	0.6377	0.0333	0.1887	0.1361	0.6612	0.5090	0.3345
66CP-HAL	0.0521	0.4428	0.0048	0.0544	0.0583	0.4954	0.0168	0.1907
68CP-CC12-Smal	0.9833	1.0000	0.9751	1.0000	0.9803	1.0000	0.9707	1.0000
67CP-CC12-Msel	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000
69CP-MQ52	0.8420	1.0000	0.7756	1.0000	0.8236	1.0000	0.7717	1.0000
105CP-ESR	0.0074	0.1513	0.0005	0.0085	0.0129	0.2465	0.0022	0.0447
106CP-UNI	0.7148	1.0000	0.5689	1.0000	0.6907	1.0000	0.5760	1.0000
107CP-ObHinF1	0.8841	1.0000	0.8544	1.0000	0.8681	1.0000	0.8454	1.0000
108CP-MQ2	0.4934	1.0000	0.3838	1.0000	0.4775	1.0000	0.4040	1.0000
109CP-REN	0.0792	0.5385	0.0204	0.1734	0.0846	0.5754	0.0427	0.3345
110CP-LS19	0.8117	1.0000	0.7115	1.0000	0.7901	1.0000	0.7086	1.0000
111CP-AMI	0.8985	1.0000	0.9049	1.0000	0.8839	1.0000	0.8996	1.0000
112CP-NAS	0.7641	1.0000	0.7703	1.0000	0.7409	1.0000	0.7661	1.0000
113CP-MQ30	0.0089	0.1513	0.0005	0.0085	0.0145	0.2465	0.0026	0.0447
8CP-FABP4D	0.4267	1.0000	0.5327	1.0000	0.4105	1.0000	0.5415	1.0000
100CP-PGK2-2	0.9993	1.0000	0.9985	1.0000	0.9983	1.0000	0.9969	1.0000
104CP-MQ50	0.7092	1.0000	0.5852	1.0000	0.6862	1.0000	0.5913	1.0000
219CP-MX1	0.0991	0.5615	0.0291	0.1887	0.1054	0.5970	0.0541	0.3345
220CP-CCK2	0.8598	1.0000	0.8877	1.0000	0.8426	1.0000	0.8824	1.0000
228CP-GHRHR	0.0171	0.1938	0.0468	0.2273	0.0225	0.2555	0.0731	0.3551
229CP-PITI	0.7637	1.0000	0.7041	1.0000	0.7402	1.0000	0.7006	1.0000
230CP-GHR	0.2283	0.8998	0.1555	0.5874	0.2260	0.8888	0.1860	0.7025
231CP-AGRP	0.8873	1.0000	0.8219	1.0000	0.8713	1.0000	0.8160	1.0000
232CP-FOS	0.3783	1.0000	0.3247	1.0000	0.3637	1.0000	0.3439	1.0000
233CP-GH	0.3426	1.0000	0.1914	0.6507	0.3307	1.0000	0.2182	0.7419
234CP-P2-IL12R2	0.8972	1.0000	0.8613	1.0000	0.8821	1.0000	0.8525	1.0000
235CP-P1-SLA-40	0.7084	1.0000	0.5956	1.0000	0.6856	1.0000	0.6025	1.0000
236CP-P2-CXCL12	0.5138	1.0000	0.5993	1.0000	0.4987	1.0000	0.6053	1.0000
237CP-P2-IL10	0.2382	0.8998	0.1211	0.5146	0.2353	0.8888	0.1521	0.6463

P-value is for a single test. BH is P-value corrected for multiple testing, according to the Benjamini–Hochberg method (controlled for false discovery rate). P-values considered as significant at the 5% level are in boldface type, showing outlier SNPs most likely under directional selection. Four populations are studied: DU02, LW05, PI03, and LR01.

Figure 9.—

Allelic frequencies of 34 SNPs in four major pig breeds of the PigBioDiv2 project. Arrows pinpoint the outlier SNPs, black in populations where no selection occurs, red in populations where selection occurs.

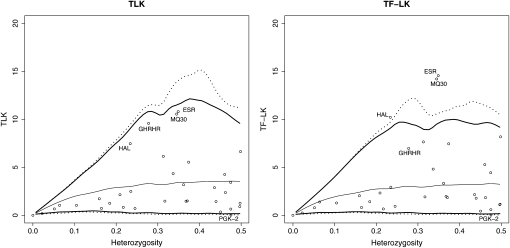
Figure 10 shows the neutral distribution of T_LK and T_F–LK conditional on heterozygosity (following the work of Beaumont and Nichols 1996), for the four pig breeds studied. T_LK and T_F–LK have similar shapes although T_LK has a slightly broader distribution for heterozygosity values >0.2. The SNPs ESR, HAL, and MQ30 lie beyond the 0.999 quantile of the T_F–LK neutral envelope, with similarity to the single-test P-values we obtained (Table 2).

Figure 10.—

Distributions of T_LK and T_F–LK conditional on heterozygosity and test for outliers with 34 SNPs (candidate genes) of the PigBioDiv2 project. Top, middle, and bottom solid lines delineate the neutral envelope containing 98% of the values, with the mean values. Top and bottom dotted lines delineate the 99.8% envelope.

DISCUSSION

We proposed an extension of Lewontin and Krakauer's (1973) method to detect signatures of selection in species with complex population trees, under pure genetic drift. We focused here on SNP data, but the method can also be applied to multiallelic loci. Using simulations of various population trees with or without selection, we compared the robustness and power of the original LK test, based on the T_LK statistic, and of the extension we proposed, based on the T_F–LK statistic. In some simulation scenarios, comparisons with a model-based MCMC method (Foll and Gaggiotti 2008) were also performed.

Empirical distributions of T_LK and T_F–LK under neutrality:

Simulations under neutrality indicate that the empirical distributions of T_LK and T_F–LK are similar. They both do not fit the right-tail side of the chi-square distribution when including extreme p₀ values (0 < p₀ < 1), while they fit the chi-square distribution when considering only intermediate p₀ values (i.e., 0.2 < p₀ < 0.8). These observations hold whatever the demographic history of the populations (EBL, UBL, or UBL struc) and whether the parameters p₀ and are estimated or not. The long right tail of the test distributions in the presence of extreme p₀ values results in an excess of false positives if the chi-square distribution is used as the null distribution for the test. Therefore, it is recommended rather to use the empirical distribution of the tests, which we did when evaluating the power of the methods. Alternatively, p₀ estimates at each tested SNP could be used as a proxy for choosing which distribution (empirical or theoretical) should be preferred to perform tests based on T_LK and T_F–LK.

The lack of fit of the T_LK and T_F–LK distributions to the chi-square distribution in the case of extreme p₀ values can be explained as follows. First, these statistics are ratios (see Equations 9 and 24) and our derivations of their expected values and variances imply a first-order approximation of these ratios. When p₀ tends to zero or one, the denominators of the statistics become very large and this approximation is less accurate. Second, our derivations assume that the allele frequencies are normally distributed, which is also violated for extreme p₀ values.

Focusing on intermediate allele frequencies makes our derivations more accurate, and the good fit of the T_F–LK distribution with the chi-square distribution is thus natural. More surprising is the equally good fit for UBL scenarios of the T_LK distribution with the chi-square distribution in this case. We note, however, that this result is consistent with the ones obtained by Beaumont and Nichols (1996), who showed that the F_ST distribution is robust to variations in the population structure for intermediate heterozygosity values. In the case of the UBL models, one likely explanation for the robustness of T_LK is that restricting to intermediate p₀ values effectively conditions on allele frequency trajectories that are compatible with the EBL hypothesis, therefore reducing the effect of population size differences. In the case of more complex structured models, this explanation alone may not be sufficient. But, as pointed out by Beaumont (2005), we can advocate the separation-of-timescales approximation (Nordborg 1997; Wakeley 1999, 2001; Wakeley and Aliacar 2001), which implies that in a wide range of structured population models, the allele frequencies can be approximated by the ones of a UBL model where several populations evolve independently from a common ancestral pool.

Another interesting issue is that the use of SNP data satisfies in principle one assumption underlying LK tests, i.e., that mutations occur only in the ancestral population (the collecting phase of the separation-of-timescales approximation). Indeed, one criterion of the SNP ascertainment phase is that both alleles at a SNP marker must segregate in several of the populations studied, implying that the mutated allele is relatively ancient. Therefore, LK tests with SNP data can be applied to recently bifurcating populations (i.e., livestock, recently colonizing or invasive populations), but also in principle to deeply divergent populations, provided the selected SNPs segregate in several of the populations studied. In contrast, the use of multiallelic loci (i.e., microsatellites) should be handled with caution because they can potentially have mutated more recently (in the scattering phase of the separation-of-timescales approximation). This can affect the distribution of F_ST (Flint et al. 1999; Storz et al. 2004) and therefore the results of LK tests.

Power of T_LK and T_F–LK:

If selection acts on a large population, T_F–LK is more powerful than T_LK. This difference of power is remarkable at low type I errors. In UBL and UBL struc models T_F–LK detects 20% and 15–35% more selected SNPs than T_LK, respectively. However, if selection acts on a small population, T_LK may be more powerful than T_F–LK for UBL models, although this trend disappears for low type I errors. To interpret these observations, let us consider the simpler case of a UBL model where the matrix is known. In this case, T_F–LK is proportional to 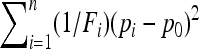, so that populations with a large F_i (i.e., a small population size) have little influence on the distribution of the statistic. Thus, the relative size of the population where selection occurs has a strong impact on the power of the test. On the other hand, T_LK is proportional to 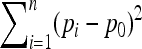, so that all populations have the same weight and the size of the population where selection occurs does not directly matter. In fact, the disadvantage of T_LK compared to T_F–LK is its larger variance, due to the fact that it does not account for the F_i's. For large type I errors, the power of the test is essentially determined by the difference between the expected value of the statistic under selection and under neutrality, so the larger variance of T_LK is not an important problem. However, for very small type I errors, this problem of variance has a clear negative impact on T_LK's power. It is important to note here that the small type I errors are the most relevant in practical applications, because genomic scans for selection have to deal with an important multiple-testing issue.

In practice, the 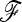matrix is unknown and the power of T_F–LK will depend on how well it can be estimated. In our simulations, only a small percentage of SNPs were influenced by selection due to hitchhiking. Consequently, 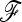was in general well estimated and the power of T_F–LK with an estimated 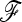was almost as good as with a known 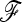. However, it is advisable to be cautious when testing dense SNP genotyping data in only a few genomic regions. In our application to pig SNP data, we avoided this bias by estimating the 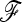matrix with an independent data set of microsatellite loci. Remarkably, the power of T_F–LK depends on a comprehensive population sampling in a given population tree, because the estimation of the 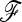matrix is less biased when the population in which selection occurs is “diluted” among a high number of populations.

When lots of populations are tested and nearly neutral multilocus genotypes are available, the phylogenetic framework is perhaps the most convenient way of estimating the 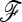matrix, as was proposed in this work. However, when the population number is not too large, alternative methods such as approximate Bayesian computation (ABC) methods (Beaumont et al. 2002; Marjoram et al. 2003) could be considered, as they potentially deal with more summary statistics than only one distance to infer the population tree necessary to calculate the matrix.

The ancestral allele frequency p₀ of the selected allele has a complex influence on the detection power of T_LK and T_F–LK. On one hand, extreme p₀ values induce a long right tail of the statistic distributions under neutrality, which reduces the power. On the other hand, the evidence of selection is stronger if the selected allele was initially at low frequency (saying it differently, the difference between the expected value of the statistics under selection and under neutrality is larger for small p₀ values). The combination of these two antagonistic effects implies that conditioning on intermediate p₀ values may lead to either an increase or a decrease of power, depending on the evolution scenario and on the test. As already outlined above, the size of the population where selection occurs will have more effect on the results obtained with T_F–LK than on those obtained with T_LK. Indeed, conditioning on intermediate p₀ values will increase the power of T_F–LK if selection acts in a large population, but decrease it if selection acts in a small population. These observations may be important to understand the influence of SNP ascertainment, which typically favors alleles with intermediate ancestral frequencies, on the detection power of the tests.

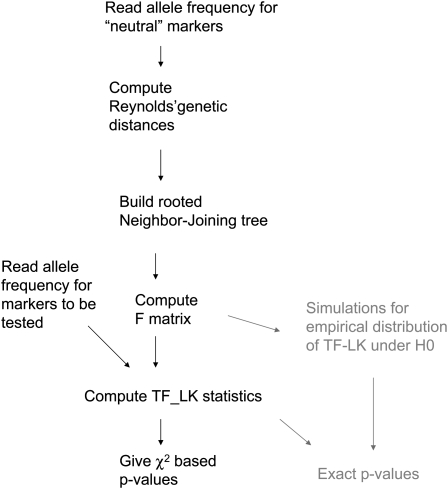
Software:

A general workflow for the application of the test to a real data set is presented in Figure 11. We implemented R and python codes that (i) compute the matrix of Reynolds' genetic distances (Laval et al. 2002) between populations from a matrix of SNP genotype frequencies, (ii) compute a NJ tree from this Reynolds' matrix (or another Reynolds' matrix if provided), (iii) build an estimate of the matrix from the output of the NJ tree, (iv) compute the test statistics, and (v) compute the χ²-approximated P-values, the empirical distribution of the test statistics under the null (conditioned on ), and the null envelope conditioned on heterozygosity. The codes and the pig data files are available at http://qgp.jouy.inra.fr/flk or as File S1 and File S1 cont.

Figure 11.—

Workflow for the F–LK test. Shaded terms illustrate optional items.

Methodological perspectives:

Some methodological issues arise from these observations. First, the F_ST distribution (analogous to the T_LK statistic) was shown to be sensitive to complex patterns of migration and sharp differences in the migration rate among populations [island models, hierarchically structured models (Beaumont and Nichols 1996; Excoffier et al. 2009)]. The sensitivity of T_F–LK to correlations of allele frequencies among populations due to migration events should also be considered with regard to robustness and power. Although gene flow among closely related populations should not in principle bias the estimation of the population tree—the bias would concern only branch lengths after the split—gene flow among distantly related populations is expected to mask the true population tree. Second, a simulation study of the robustness and power of T_F–LK when testing multiallelic loci with a high mutation rate, such as microsatellite loci or haplotypes, would be interesting.

CONCLUSION

A practical motivation for the development of an extension of the LK test was to provide a powerful and rapid parametric statistical test for detecting the signature of selection in somewhat complex population trees with large marker data sets in many populations. Beaumont and Balding (2004) and Foll and Gaggiotti (2008) developed Bayesian hierarchical models on the basis of a multinomial-Dirichlet likelihood that arises naturally under the separation-of-timescales approximation. These methods explicitly model population-specific (β-) effects that actually correspond to variation of the inbreeding coefficient F (or F_ST) among populations. The fact that these methods implement robust statistical modeling, including likelihood expression and estimation using MCMC, makes them computationally prohibitive for large marker data sets and large numbers of populations. On the other hand, methods based on an island model (Beaumont and Nichols 1996) or a hierarchically structured model (Excoffier et al. 2009) are computationally convenient and quite conservative, but may tend to omit more complex demographic histories involving N_e variation among populations and historical branching. To help in screening large marker data sets for outliers in relatively complex population trees, we propose an additional method that accounts for N_e variation among populations and historical branching, assuming pure genetic drift and no migration in its current state. The statistical test based on either the empirical distribution of the T_F–LK statistic or the theoretical chi-square distribution is generally more powerful than a classical LK test based on T_LK. In scenarios where the populations are hierarchically structured, it is also more powerful than the MCMC method of Foll and Gaggiotti (2008). This extended LK test thus represents a quick and powerful tool in the context of genomic scans for selection using population data.

APPENDIX A: DISTRIBUTION OF LEWONTIN AND KRAKAUER'S TEST IN A STRUCTURED POPULATION

In the following, we derive the first two moments of the basic test (Equation 10).

We first write the sum of the numerator in Equation 9, in matrix product,

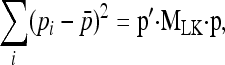(A1)

where p is the n-vector of p_i's, M_LK is the n × n matrix equal to I−(1/n)E, I is the n × n identity matrix, and E is the n × n matrix made up of 1's. The expectation can be written as

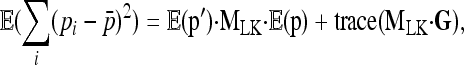(A2)

where 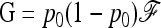is the variance–covariance matrix of frequencies. The first term is 0 since all p_i's have the same expectation p₀ (hence M_LK·E(p)=0). Further,

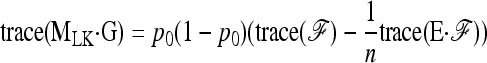(A3)

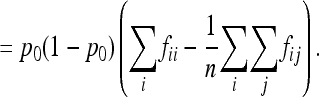(A4)

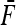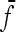Denoting by and the mean value of fixation indexes F_i and the mean value of the fixation indexes f_ij attached to ancestral populations common to all pairs of observed populations (Equations 16 and 17), one gets

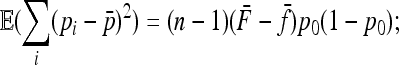(A5)

hence

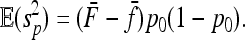(A6)

Similarly, we have

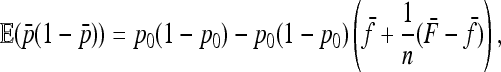(A7)

where the second term is equal to minus the variance of 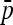. In fact the expression 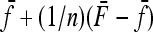can be shown to be small, in general smaller than the reciprocal of the number n of populations.

Turning to the expectation of F_ST, the error made when replacing the expectation of the ratio by the ratio of expectations is of the same order of magnitude (<1:n), so that we can write

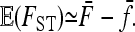(A8)

Assuming normality, the sum of squares (Equation A1) has a variance equal to

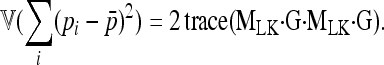(A9)

We have

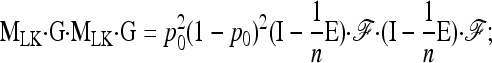(A10)

hence

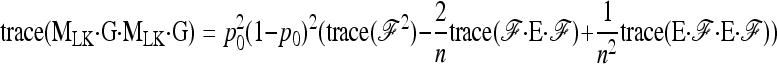(A11)

since the trace operator is commutative. Denoting by a dot the summation over indexes 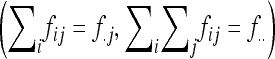, we have

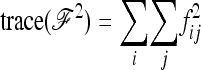(A12)

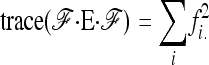(A13)

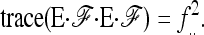(A14)

As before, we assume that the number of populations is large enough for the variance of F_ST to be approximated by the ratio of the variance of the numerator, as calculated above, to the square of the expectation of 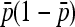(Equation A7).

Assuming that the number of loci is large enough for the variance of 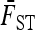(Equation 10) to be neglected, the previous expressions allow the first two moments of the test to be derived for any coancestry structure (matrix 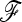) of the populations, Equations 13 and 15.

Robertson (1975a) considered the case of a structured history causing correlations between allele frequencies (nonzero f_ij values, with equal branch lengths (F_i = f_ii = F). With these conditions expressions (A12), (A13), and (A14) become

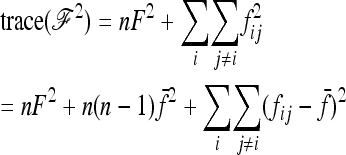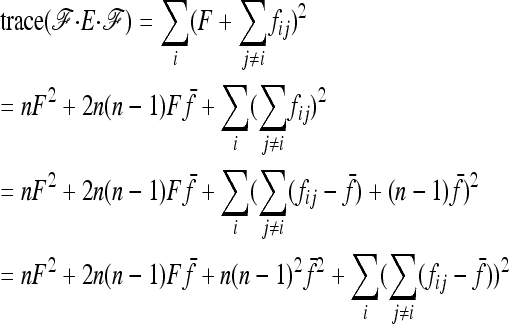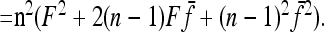Setting

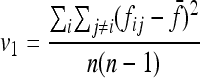and

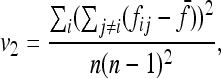the sum

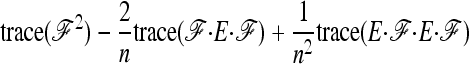in Equation A11 becomes equal to

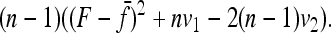Comparing with Robertson's notations (Robertson 1975a, p. 785), his δ_ij is

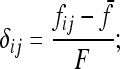v₁ = 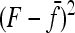times his V_r′ term, which is the variance of “internal” correlation coefficients between gene frequencies in different populations defined as

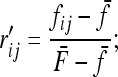and v₂ corresponds to a second term he found small with respect to the first one, to get Equation 18.

In the case of independence between populations (the tree has a star structure), but heterogeneous F_i values (the populations show different heterozygosities), we get another simplified expression. Assuming no correlation between allele frequencies (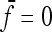), the expectation is not changed,

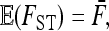(A15)

and the previous expressions for the variance become

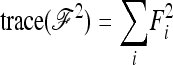(A16)

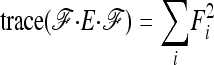(A17)

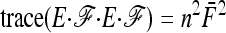(A18)

so that we get

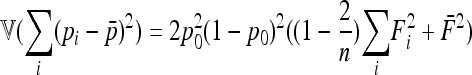(A19)

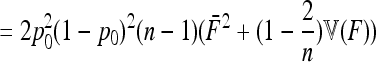(A20)

if we set

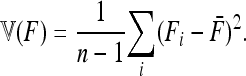(A21)

Then, the variance of T_LK is changed from 2(n – 1), the value corresponding to a chi-square distribution, to

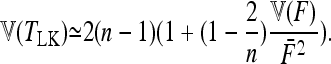(A22)

Evaluating the variance of F_i values can be obtained from the variance of Reynolds' distances R_ij, which estimate the mean F values of populations i and j from their proximal common ancestor population. Indeed, with no correlation (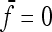), , 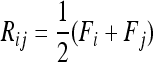so that

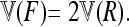(A23)

APPENDIX B: MULTIALLELIC VERSION OF BASIC AND EXTENDED LK TESTS

In the following we extend the test to the case of multiallelic markers.

Consider a locus with A alleles. Let P = (p′₁, …, p′_a, …, p′_A)′ denote the nA-vector of allele frequencies sorted by population within allele number: p_a denotes the n-vector of frequencies of allele a in the n populations. Under drift,

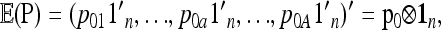(B1)

where ⊗ denotes the Kronecker product and p₀ is now the A-vector of founder allele frequencies. The variance of P,

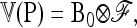(B2)

involves the (n × n)-matrix 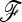and the (A × A)-matrix 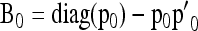. The estimator of founder frequencies is now 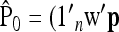and can be written as 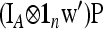, with w as in Equation 21. The multiallelic equivalent of 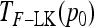in (23) is

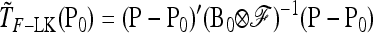(B3)

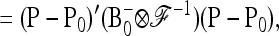(B4)

where 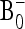is the Moore–Penrose generalized inverse of B₀. It can be explicitly written as (Tanabe and Sagae 1992)

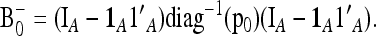(B5)

Replacing p₀ with 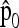in P₀ and B₀ leads to the quadratic form

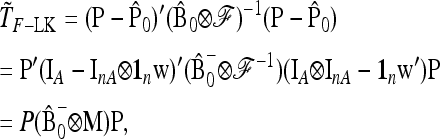where M is the (n × n) matrix in Equation 26.

In the particular case when the number of alleles is two, reduces to T_F–LK in (24), so that considering one of the two alleles or both alleles is equivalent.

From the calculation of the moments of (see below), we get

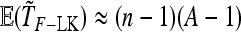(B6)

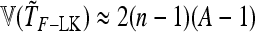(B7)

so that 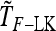has approximately a χ²_{(n−1)(A−1)}-distribution under the null hypothesis of genetic drift.

Moment calculations:

The same type of demonstration as in appendix a is used for the extension of the LK test, so that only main results are presented.

When P₀ is known:

The expectation of the statistic test is

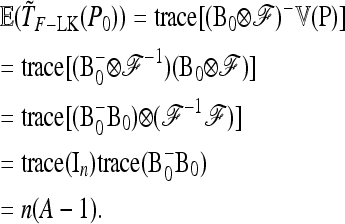Similarly, assuming approximate normality,

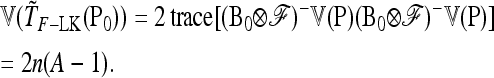When P₀ is unknown:

First, note that 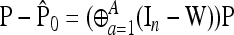, where W is the (n × n) matrix built with identical lines equal to w (Equation 21). It can also be shown that the ath diagonal element of B₀ is 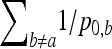and the (a, b) element is equal to .

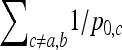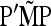The quadratic form can be written as , with

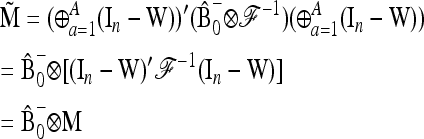with M defined in Equation 26. Then, incidently, can be written as

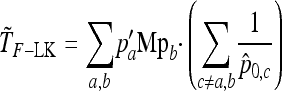(B8)

with .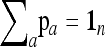

Coming back to the matrix notations, and following calculation lines of the biallelic case (Equations 22, 27, and 28), but neglecting the bias term in (22), 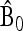is replaced by its expectation B₀, and

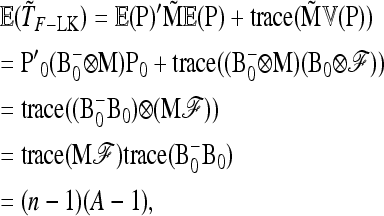since

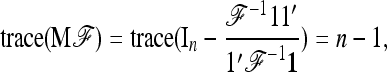(B9)

and B₀ has rank (A − 1).

Similarly, assuming approximate normality,

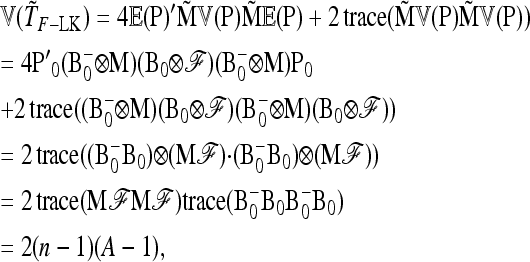since 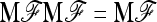and 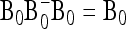by definition of the generalized inverse.