Nested Association Mapping for Identification of Functional Markers

Abstract

Identification of functional markers (FMs) provides information about the genetic architecture underlying complex traits. An approach that combines the strengths of linkage and association mapping, referred to as nested association mapping (NAM), has been proposed to identify FMs in many plant species. The ability to identify and resolve FMs for complex traits depends upon a number of factors including frequency of FM alleles, magnitudes of their genetic effects, disequilibrium among functional and nonfunctional markers, statistical analysis methods, and mating design. The statistical characteristics of power, accuracy, and precision to identify FMs with a NAM population were investigated using three simulation studies. The simulated data sets utilized publicly available genetic sequences and simulated FMs were identified using least-squares variable selection methods. Results indicate that FMs with simple additive genetic effects that contribute at least 5% to the phenotypic variability in at least five segregating families of a NAM population consisting of recombinant inbred progeny derived from 28 matings with a single reference inbred will have adequate power to accurately and precisely identify FMs. This resolution and power are possible even for genetic architectures consisting of disequilibrium among multiple functional and nonfunctional markers in the same genomic region, although the resolution of FMs will deteriorate rapidly if more than two FMs are tightly linked within the same amplicon. Finally, nested mating designs involving several reference parents will have a greater likelihood of resolving FMs than single reference designs.

THE primary purpose for identifying functional markers (FMs) associated with complex traits in plant species is to provide molecular genetic information underlying variability upon which both artificial and natural selection are based. FMs are defined as polymorphic sites within genomes that causally affect phenotypic trait variability (Andersen and Lubberstedt 2003). This definition is a pragmatic recognition that phenotypic variability can be due to genomic variability located outside of open reading frames. Forward genetics approaches to associate naturally occurring structural genomic variants with phenotypic variability can be broadly categorized as (1) linkage mapping, also referred to as quantitative trait locus (QTL) mapping, (2) association genetic mapping, also known as linkage disequilibrium (LD) mapping, and (3) designs that combine linkage and LD mapping.

The third approach based on the concept of combining LD with QTL mapping is a natural extension of the multifamily QTL approach and has been referred as joint linkage and linkage disequilibrium mapping (JLLDM) (Xiong and Jin 2000; Farnir et al. 2002; Wu et al. 2002; Perez-Enciso 2003; Jung et al. 2005) in samples from natural populations. The combined approach also has been applied to designed mapping families sampled from plant breeding populations (Xu 1998a; Jannink and Jansen 2000; Jannink and Wu 2003; Jansen et al. 2003). A special case of designed mapping families that are interconnected, known as nested association mapping (NAM), was proposed by Yu et al. (2008). As originally proposed, a NAM population consists of multiple families of recombinant inbred lines (RILs) derived from multiple inbred lines crossed to a single reference inbred line. Implicitly, genomic information is composed of high-density genotypes of parental inbred lines and low-density genotypes from segregating progeny. If the segregating progeny are RILs or doubled haploid lines (DHLs), then the genomic information can be “immortalized” for associations with phenotypes obtained through long-term longitudinal studies (Nordborg and Weigel 2008).

A NAM population consisting of 25 families with 200 RILs for each family has been developed and released as a genetic resource for identification of FMs in maize (Yu et al. 2008). Other publicly available NAM populations are being developed for several species including Arabidopsis thaliana (Buckler and Gore 2007), barley (R. Wise, personal communication), sorghum (J. Yu, personal communication), and soybean (B. Diers, personal communication).

The power, accuracy, and precision of identifying FMs in experimental NAM populations have not been investigated for complex genetic architectures. These statistical properties depend upon a number of factors including the following:

1. Data analysis method: Some methods are more powerful than others; however, experimental biologists prefer methods implemented in existing software packages. Are least-squares methods sufficiently powerful to identify FMs in established and developing NAM populations?

2. Frequency of functional markers and magnitudes of genetic effects: Development of a NAM population will change the allele frequencies of the FM relative to the reference population from which the lines are sampled. How will allele frequency and magnitude of genetic effects in a typical NAM population affect the ability to identify FMs?

3. Disequilibrium among functional and nonfunctional markers: Disequilibrium may exist among alleles within subpopulations even when there is no physical basis for genetic linkage. To what extent can the NAM design address consequences of gametic disequilibrium (population structure) in the reference population?

4. Multiple FMs in the same genomic region: If multiple FMs are physically located in the same genomic region, will equilibrium among the parental lines enable resolution of multiple FMs?

5. Mating design: An appropriate mating design can maximize the number of families that are informative for FMs. Will multiple-reference mating designs improve the probability of identifying FMs?

These five questions were addressed.

METHODS

Models:

Consider multiple families of segregating progeny with only two genotypic classes per locus, such as will occur with DHLs and RILs derived from a cross of two inbred lines (Figure 1). For the sake of brevity, we refer to such loci as Q loci; i.e., these are potential FMs. Segregating progeny with three genotypic classes per locus, such as will occur in an F₂, are obvious (Xu 1998a) and are not explicitly developed herein. A pooled analysis of data from multiple families is enabled through the linear genetic model first proposed by Haley and Knott (1992), extended to multiple families by Xu (1998a) and to account for background QTL by Guo et al. (2006),

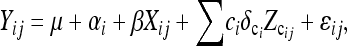(1)

where Y_ij is the observed trait value of the jth segregating line in the ith family, μ is the overall mean, and α_i is the effect of the ith family. X_ij represents a Q locus under consideration and assumes the values of −1 and +1 for the two homozygous genotypic classes. The vast majority of SNP loci have only two alleles. Thus most SNP loci that are FMs will be detectable as a biallelic system across families in which these alleles are segregating. Given current sequencing capabilities and costs, the alleles at the Q locus will be known in the parental lines, but unknown in the segregating progeny (Figure 1). The values for X_ij can be imputed in the segregating progeny by the conditional expectation, E(X_ij | I_P, I_M) (Xu 1998a), where I_P includes the known genotypes of the parental alleles at the Q locus, and I_M is the genotypic information from the flanking markers in both parents and progeny (see below). c_i is a cofactor marker in family i used for the effects of background QTL. Z_cij is an indicator of cofactor marker in the jth line of the ith family. The values for Z_cij assume values of 1 or −1 for the two known genotypic classes in the segregating progeny and are identified on the basis of analyses within individual families (see below). α_i, β, and δ_ci are parameters that need to be estimated. It is assumed that ɛ_ij are sampled from an identical and independent normal distribution. Epistasis among Q loci was not modeled.

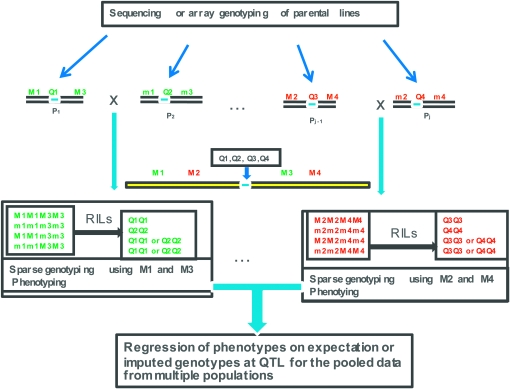
Figure 1.—

Generalized design for development of a nested association mapping (NAM) population. Essential elements depicted include (1) structure (nested) and purpose (association mapping) of a population of segregating progeny, (2) high-density genotypic data from genomic regions of interest in parental inbred lines, and (3) low-density genotypic data throughout the genomes of the parental lines and the segregating progeny.

Under the null hypothesis model, (1) is reduced to

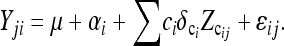(2)

Identification of functional markers:

Cofactor markers associated with background QTL were identified with an initial scan of the genome in individual families, using composite-interval mapping (Zeng 1994). This is amenable to least-squares computation that is readily available through standard software packages and search procedures routinely used for multiple-regression problems (Christensen 2002).

After background QTL were identified, all Q loci within the genomic region of interest were tested for significant associations with simulated phenotypic variability. Q loci included in model (1) were declared to be FMs if the variability explained by the model with a parameter representing the locus exceeds that of the model without the locus (Equation 2) at a predetermined threshold value. The threshold for declaring a Q locus as a FM with a type 1 error rate of 0.01 was determined initially using 3000 replicates of data generated under the null hypothesis of no genetic effects. The resulting threshold was −log₁₀(p) = 3.80. Because SNP loci in sh1 amplicons were used to simulate FMs (see below), we noted that this value is very close to a Bonferroni adjusted value of 4.09 = log₁₀(0.01/123), where 123 represents the number of tagged SNPs among sh1 amplicons. Therefore, for simulations involving both sh1 and bt2 amplicons, threshold values were based on Bonferroni adjusted values of 4.2 (= log₁₀(0.01/150)), where 150 represents the total number of tagged SNP loci in both amplicons.

If a FM was identified (conditional on background QTL), additional Q loci were evaluated for significance using two variable selection methods: forward selection and a modified stepwise procedure. The forward selection procedure has been used previously in association mapping (Nair et al. 2009), so it was chosen as a comparator for the modified stepwise procedure. The modified stepwise procedure consisted of an adding step and an updating step (Christensen 2002). In the adding step, all possible Q loci are tested conditional on covariate FMs and background QTL. In the updating step, previously identified FMs are reevaluated as each FM is sequentially excluded while all other FMs are included in the model as covariate(s). This updating step is repeated for each of the previously identified FMs. The adding and updating steps are repeated until no further significant associations are identified.

Imputation of parental SNPs onto segregating progeny:

Assume a Q locus is genotyped in parental lines but not in their progeny and this locus is flanked by two SNP loci, A and B, which are genotyped in parental lines and their progeny within a family, and the expectation of genotype score is based on the following:

1. The transition probabilities from one genotype at one locus to one genotype at another locus [P(Q = q | A = a), P(B = b | Q = q)] are obtained from Jiang and Zeng (1995). These transition probabilities are functions of the frequency of recombinants between the two flanking loci and the number of selfing generations.

2. The conditional probability of genotypes at Q given flanking SNP loci A and B is computed as P(Q = q | A = a, B = b) = P(Q = q | A = a)P(B = b | Q = q)/∑_qP(Q = q | A = a)P(B = b | Q = q) (Jiang and Zeng 1995).

3. The expectation of genetic score at Q is computed as (1)P(Q = 1 | A = a, B = b) + (0)P(Q = 0 | A = a, B = b) + (−1)P(Q = −1 | A = a, B = b) = P(Q = 1 | A = a, B = b) − P(Q = −1 | A = a, B = b). In situations where computation is needed at terminal ends of a linkage group, SNP locus Q will have only one adjacent polymorphic SNP locus. For this situation, the conditional probability is computed as P(Q = q | A = a) = P(Q = q | A = a)/∑_qP (Q = q | A = a). The expectation of genetic score is computed by (1)P(Q = 1 | A = a) + (0)P(Q = 0 | A = a) + (−1)P(Q = −1 | A = a) = P(Q = 1 | A = a) − P(Q = −1 | A = a).

Statistical properties:

The ability to identify FMs was characterized using power, accuracy, and precision from replicated simulations (see below). Power was estimated as the frequency, among 100 replicates, of significant associations for one or more Q loci within the sequenced amplicon containing a simulated FM. Note that this definition of power indicates that a segregating Q locus within the amplicon containing the FM is significantly associated with the phenotypic variability; the identified Q locus may not be the actual FM. Accuracy was evaluated by two criteria: (1) as the frequency of correctly identified FM(s) and (2) as the difference between estimated genetic effects and the actual simulated genetic effects. Precision is a measure of consistency among the replicates. Identified FMs from all replicates were used to construct a 95% linkage disequilibrium confidence interval (LD C.I.) to represent the lack of consistency among the replicate data sets. Explicitly, let the statistically identified FM be the Q locus with the largest −log₁₀(p) exceeding a threshold value be designated as R², and let r² be the LD between the identified FM and the “true” simulated FM. The 1 − α LD C.I. is defined as P(r² ≥ R²) ≥ 1 − α, where r² ≥ R² includes the simulated FM with probability ≥1 − α. The 95% confidence interval was obtained as the interval that included 95% of the replicates after ranking their r² values among alleles from the largest to the smallest. All SNP loci contained in this interval were referred to as the C.I. SNPs and might be regarded as candidate FMs.

Simulations of FMs:

The genomes of 28 segregating families in a NAM population, each consisting of 100 DHLs, were simulated using R/QTL (http://www.rqtl.org/). The genomes of the simulated families consisted of five independent linkage groups. Each linkage group consisted of 100 cM of recombination with 11 anonymous biallelic markers placed every 10 cM. In addition to simulated polymorphic marker loci actual sequences of the sh1 and bt2 amplicons from 28 maize inbreds were assigned to the segregating families. Depending upon the genetic architecture and their relative genomic locations (see below), SNPs within these sequences were selected to serve the role of FMs in the expression of quantitative phenotypes. The majority of SNP loci have two alternate alleles and only in rare cases will a SNP locus have three or four alternative alleles. For these rare cases, multiple classes of alleles can be reduced to two classes: one representing the allele of highest frequency and one representing all other alleles. Thus, for purposes of these studies, we considered only biallelic FMs.

Sequences from the sh1 amplicons were placed in the middle of one linkage group, midway between the fifth and sixth markers. For genetic architectures involving two FMs, sequences of the bt2 amplicon also were placed at various locations in the simulated genomes of the parental lines. In addition to the FMs, three background QTL were simulated on independently segregating chromosomes in all families, including families for which no simulated FMs were segregating. Each background QTL contributed an equal amount to the overall phenotypic variability. Note that while the genotypes of the SNP loci within the sequences are known in the parental lines, in a NAM analysis they may not be genotyped in the segregating progeny (Figure 1). Thus, the actual SNP data were deleted from the simulated data sets and expected genotypic values, as described above (Xu 1998a), were used in data analyses.

Sequences of sh1 and bt2 amplicons from the maize diversity project (http://www.panzea.org) consist of 7029 bp and 6196 bp, respectively. Among maize accessions 235 SNPs have been identified on sh1 and 46 SNPs on bt2. While LD (r²) among these SNPs decays rapidly with distance, sets of 110 SNPs within sh1 and 22 within bt2 are in complete LD (r² = 1) among the maize accessions at http://www.panzea.org. For purposes of these simulations, a single SNP was used to represent sets of SNPs that are in complete LD, resulting in a total of 123 tagged SNPs on sh1 and 24 tagged SNPs on bt2.

Phenotypes were simulated as the sum of additive genetic effects from FMs, additive genetic effects from background QTL, and random error. Three studies involving multiple genetic architectures were used to evaluate the ability to identify FMs. The goals of these studies were to (1) determine impacts of multiple allelic frequencies and magnitudes of simple additive genetic effects, (2) determine whether the NAM design can reduce false positive consequences of disequilibrium (population structure) between FMs and non-FMs in the reference population, and (3) determine if equilibrium among the parental lines enables resolution of linked FMs within families.

Study 1. Impact of frequencies and genetic effects of functional markers:

SNPs that occur at two different frequencies in the reference population (http://www.panzea.org) were simulated as FMs (Table 1). These SNPs occur at positions 3822, 4884, and 5769 on the sh1 amplicon and are designated as sh1-3822, sh1-4884, and sh1-5769. The allele frequencies for the sh1-4884 and sh1-5769 loci each have an estimated frequency of 0.19 in the reference population, but they were associated with different numbers of informative NAM families: 24 and 5, respectively. The minor allele at sh1-3822 occurs at a frequency of 0.47 and was informative in 15 simulated NAM families. Differences in additive genetic effects of the FMs accounted for 1, 2, 5, 10, 15, and 20% of the total phenotypic variability within families that were segregating FMs. Three additional independently segregating background QTL were simulated such that the total additive genetic variability from all sources explained 70% of the phenotypic variability within families. The remaining phenotypic variability was due to random variability from a random normal distribution. Phenotypes were simulated across all DHL families 100 times. Thus for each of the three FMs with six different magnitudes of genetic effects there were 100 replicates, i.e., 1800 data sets, used to characterize the statistical properties.

TABLE 1.

Power, accuracy, and precision in identification of simulated functional markers (FMs) based on Minor Allele Frequencies (MAF), number of segregating families (SF) and magnitude of genetic effects

		Simulated additive genetic effects (% of phenotypic variability within segregating families)
Simulated FMa	Statistical measure	0.183 (1%)	0.258 (2%)	0.409 (5%)	0.577 (10%)	0.707 (15%)	0.817 (20%)
sh1-5769	Powerb	0.07	0.42	0.95	1.0	1.0	1.0
MAFR = 0.19 SF = 5	Accuracy: f(AIFM)c	1.0	0.93	0.99	1.0	1.0	1.0
	Average estimated genetic effectsd	0.305	0.310	0.424	0.597	0.704	0.833
	Precision: 95% LD C.I. (r2)e	NA	≥0.14	1.0	1.0	1.0	1.0
	SNP loci included in the C.I.	NA	sh1-5769, 6027	sh1-5769	sh1-5769	sh1-5769	sh1-5769
sh1-3822	Power	1.0	1.0	1.0	1.0	1.0	1.0
MAFR = 0.47 SSF = 15	f(AIFM)	0.33	0.51	0.81	0.94	1.0	0.99
	Average estimated genetic effects	0.171	0.226	0.409	0.574	0.705	0.817
	95% LD C.I. (r2)	≥0.51	≥0.66	≥0.88	≥0.88	1.0	1.0
	SNP loci included in the C.I.	sh1-3822, 3982, 3564, 4325, 4133, 3861	sh1-3822, 3564, 4325	sh1-3822, 3982	sh1-3822, 3982	sh1-3822	sh1-3822
sh1-4884	Power	1.0	1.0	1.0	1.0	1.0	1.0
MAFR = 0.19 SSF = 24	f(AIFM)	0.90	0.98	1.0	1.0	1.0	1.0
	Average estimated genetic effects	0.1984	0.2665	0.4194	0.5895	0.7167	0.8294
	95% LD C.I. (r2)	≥0.44	1.0	1.0	1.0	1.0	1.0
	SNP loci included in the C.I.	sh1-4884, 3870	sh1-4884	sh1-4884	sh1-4884	sh1-4884	sh1-4884

^aMAF_R designates minor allele frequency among maize lines at http://www.panzea.org, SF designates the number of families in the NAM population that segregate the FM.

^bPower indicates that a segregating Q locus within an amplicon containing the FM has a statistically significant association with the phenotypic variability; the significant Q locus may not be the actual FM.

^cFrequency of accurately identified functional markers.

^dThe average consists only of estimates for correctly identified FMs.

^eThe 1 − α LD C.I. is defined as P(r² ≥ R²) ≥ 1 − α, where r² is the LD between the identified FM and the “true” simulated FM and R² is designated as a threshold value associated with the probability ≥1 − α.

Study 2. Disequilibrium among functional and nonfunctional markers:

To evaluate the ability of the NAM design to alter consequences of disequilibrium in the reference population, a SNP allele in complete disequilibrium with the allele at the sh1-3822 locus was simulated and used as a FM (Table 2). No genetic effects were simulated at the sh1-3822 locus, while the simulated FM was located at 10, 20, 30, and 40 cM and independent of sh1 in segregating families. Because the FM was in complete disequilibrium with sh1-3822, it also is informative in 15 of the 28 families. Differences in additive genetic effects of the FMs accounted for 5, 20, and 30% of the total phenotypic variability among progeny within families in which the FMs were segregating. Three additional independently segregating background QTL were simulated such that the total additive genetic variability accounted for 70% of the phenotypic variability within families. A total of 15 combinations (3 additive genetic effects × 5 genomic locations) were simulated 100 times, providing a total of 1500 data sets.

TABLE 2.

Ability of NAM populations to distinguish functional and nonfunctional markers that are in complete disequilibrium in the reference population, but located on separate amplicons in segregating families (SFs)

Simulated additive genetic effect, as a percentage of phenotypic variability in SFs	Genetic linkage between functional marker and sh1-3822a (cM)	False positive associations with sh1 locib	Frequency of correctly identified functional markersc	Difference between modelsd
5%	10	1.0	0.98	4.97
	20	1.0	1.0	16.16
	30	1.0	1.0	22.28
	40	1.0	1.0	27.59
	Independent	0.01	1.0	33.53
20%	10	1.0	1.0	21.24
	20	1.0	1.0	65.24
	30	1.0	1.0	86.35
	40	1.0	1.0	103.06
	Independent	0.01	1.0	132.37
30%	10	1.0	1.0	33.27
	20	1.0	1.0	97.00
	30	1.0	1.0	127.90
	40	1.0	1.0	149.26
	Independent	0.0	1.0	193.27

^aAmong the parental lines, the simulated FM exhibits complete disequilibrium with sh1-3822.

^bFrequency of false positive sh1 loci that exhibit a significant association with the phenotype.

^cFrequency of correctly identified FMs when the FM is included in the model.

^dThe average difference of the −log₁₀(p) between models that included the correct FM and models that included only false positive sh1-3822 markers.

Study 3. Multiple functional markers in the same linked genomic region:

To evaluate whether the NAM design can resolve multiple FMs located in the same genomic region, four cases were simulated (Table 3): (a) two FMs within a single amplicon, (b) three FMs within a single amplicon, (c) two FMs located in two linked amplicons, and (d) two FMs within one amplicon and a third FM in a linked amplicon.

TABLE 3.

Accuracy in identification of multiple functional markers (FMs) within the same linked genomic region using two variable selection procedures

Amplicons	Genetic Distance (cM)	Sets of simulated functional marker loci	% contribution of additive genetic effects to phenotypic variability within segregating families	Accuracya (modified stepwise procedure)	Accuracy (forward selection procedure)
sh1		sh1-3822, sh1-819	10, 10	0.94	0.24
		sh1-3822, sh1-819	5, 5	0.93	0.32
		sh1-3822, sh1-819	10, 5	0.95	0.73
		sh1-3822, sh1-5769	10, 5	0.97	0.95
		sh1-3822, sh1-5769	5, 10	0.81	0.43
		sh1-3822, sh1-5769, sh1-819	5, 10, 5	0.44	0.07
sh1, bt2	10	sh1-3822, bt2-2854	10, 5	0.93	0.98
	40	sh1-3822, bt2-2854	10, 5	0.95	1.0
	10	sh1-3822, bt2-900	10, 5	0.95	0.88
	40	sh1-3822, bt2-900	10, 5	0.97	0.93
	10	sh1-3822, bt2-900	5, 10	0.86	0.78
	40	sh1-3822, bt2-900	5, 10	0.73	0.67
	10	sh1-3822, sh1-5769, bt2-2854	5, 10, 5	0.88	0.82
	40	sh1-3822, sh1-819, bt2-900	5, 5, 10	0.75	0.23

Analyses were able to identify a statistically significant association between segregating Q loci within an amplicon containing the FMs in all data sets; i.e., the power was 1.0 for both variable selection methods.

^aThe frequency of correctly identified sets of functional markers across all replicates of simulated phenotypes.

For cases a and b three SNP alleles, located at positions 819, 3822, and 5769 in the sh1 amplicons were used to simulate FMs. The minor alleles at sh1-819 and sh1-3822 have estimated frequencies of 0.41 and 0.47 in the reference population and were segregating in 13 and 15 families, respectively. The minor allele at sh1-5769 has an estimated frequency of 0.19 in the reference population and was segregating in 5 families. For the three pairwise combinations of FMs within a single amplicon, differences in additive genetic effects of the FMs accounted for 5 and 10% of the total phenotypic variability among progeny within families in which the FMs were segregating. For the triplet, differences in additive genetic effects at sh1-819 and sh1-5769 accounted for 5% and those at sh1-3822 accounted for 10% of the phenotypic variability among progeny within families in which these FMs were segregating.

For case c position 3822 in the sh1 amplicon was designated as one of the FMs and alleles at positions 900 and 2854 in the bt2 amplicon (designated as bt2-900 and bt2-2854, respectively) were used as FMs in the same genomic region. Sequences from the bt2 amplicon were located at 10 or 40 cM from sh1 within segregating families. The estimated minor allele frequency at bt2-900 is 0.16 and is segregating in 5 families, while the estimated allele frequency for bt2-2854 is 0.5 and is segregating in 16 of the NAM families. The alleles at sh1-3822 were used to simulate additive genetic effects that accounted for 10% of the phenotypic variability and the FMs at bt2-900 and bt2-2854 were responsible for 5% of the phenotypic variability among progeny within families in which these FMs were segregating. The magnitudes of additive genetic effects were also reversed between the pairs of loci (Table 3).

The fourth case of two FMs within one amplicon and a third FM in a second amplicon was evaluated using SNP alleles at sh1-3822, sh1-5769, and bt2-2854. The bt2 locus was placed 10 and 40 cM from the sh1 loci in segregating families. Simulated additive genetic effects at the sh1-3822, sh1-5769, and bt2-2854 loci were respectively responsible for 5, 10, and 5% of the phenotypic variability in segregating families, while the simulated genetic effects at the sh1-3822, sh1-819, and bt2-900 loci were respectively responsible for 5, 5, and 10% of the phenotypic variability in segregating families.

For all simulated phenotypes in all four cases, three additional independently segregating background QTL were simulated to contribute 60% of the phenotypic variability within all families. Thus, the total contribution to phenotypic variability from genetically segregating loci was 60%, 70%, or 80%, depending upon the magnitude of additive genetic effects at segregating FMs. For all four cases 100 replicates were simulated, producing 1400 data sets for analyses.

Mating designs:

For the simulation studies it was straightforward to determine the number of polymorphic families associated with SNPs that were designated as FMs. However, experimentalists must choose a mating design without such knowledge. With the emergence of current sequencing and genotyping technologies, consider use of sequence data to determine the relationships between minor allele frequencies (MAFs) and number of informative families. Eleven maize amplicons representing Id1, d8, sh2, su1, fea2, bt2, ae1, wx1, d3, sh1, and zfl1 loci have been resequenced in 30 maize inbreds (http://www.panzea.org/). Among the resulting 65,966 bp of sequence there are 1552 SNPs with estimated MAFs ranging from 0.03 to 0.50. For three single reference mating designs, sequences from 27 maize inbred lines were contrasted with sequences from 3 lines selected as least similar to the remaining 27. These 3 lines were also used in a multi-reference design where the 27 lines were randomly distributed into 3 subgroups of 9. SNPs in each subgroup were compared with the three references to determine the number of informative families in a multi-reference design.

RESULTS

Frequencies and genetic effects of functional markers:

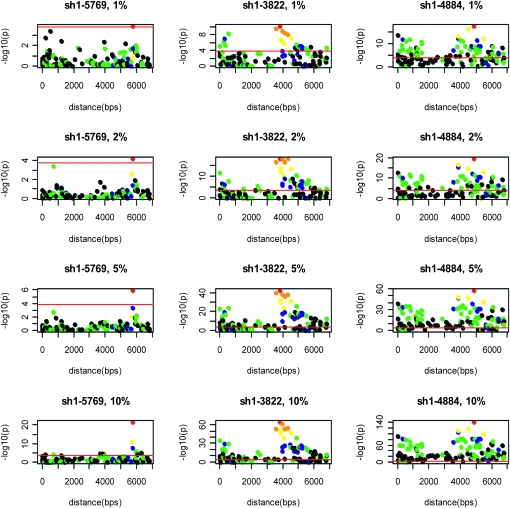
Typical association profiles in the genomic region associated with the sh1 amplicon for some of the simulated phenotypes are presented in Figure 2. The simulated FMs are at the sh1-3822, sh1-4884, and sh1-5769 loci, where the magnitudes of the genetic effects account for 1–10% of the phenotypic variability in families with segregating FMs. FMs with larger simulated genetic effects reveal similar association profiles except that the statistical significance, −log₁₀(p), has larger values.

Figure 2.—

Typical association profiles obtained from simulated NAM populations. Each solid circle represents analysis results at a SNP within the amplicon. Circle colors represent correlation coefficients with the simulated functional marker that is represented by the red circle (orange, 0.8–1.0; yellow, 0.6–0.8; blue, 0.4–0.6; green, 0.2–0.4; black, 0–0.2). The red horizontal line represents the significance threshold at −log₁₀(p) = 3.8. Results are shown for simulated genetic effects that account for 1, 2, 5, and 10% of the total phenotypic variability within segregating families. Note that the vertical scales are unique to each plot.

A summary of all analyses involving FMs responsible for 1–20% of the phenotypic variability reveals that if there are a large number of informative progeny at the locus (1500 for sh1-3822), the power of the test is 1.0, across all magnitudes of genetic effects (Table 1). For FMs that may be at lower frequencies (0.19) in the reference population, but are informative in most families (sh1-4884), the power of the test is also close to certainty, even for small additive genetic effects. For FMs that were segregating in only a few families the power to identify the FM is low if the FM contributes little to the overall phenotypic variability. If the magnitude of the genetic effects accounts for at least 5% of the phenotypic variability and segregates in at least 500 of the 2800 progeny, the power to identify the FM is very high. Thus, except in cases where low-frequency FMs contribute little to the phenotypic variability and are segregating in <18% of at least 2800 progeny, the NAM design will have adequate power to identify FMs involved in simple additive genetic architectures.

Accuracy, assessed as the frequency of accurately identified functional markers, f(AIFM), increased with the number of families segregating for the simulated FM and the magnitude of the simulated genetic effect (Table 1). Accuracy, as assessed by the estimated genetic effects relative to the actual simulated genetic effects, indicated that all estimates were slightly inflated, except in cases where there was low power, such as the FM (sh1-5769). As with power, the ability to accurately identify a FM and estimate its genetic effects is extremely good as long as the segregating genetic effect contributes at least 5% to the total phenotypic variability.

Inaccurate identification of non-FMs is a function of LD for those SNP loci in close proximity to the FM. In contrast to association mapping where the rapid decay of LD with physical distance from the FM will result in few false positive associations (Kathiresan et al. 2008; Sabatti et al. 2009), replicates of the simulated NAM population resulted in some false positive associations; i.e., the f(AIFM) < 1.

Precision was quantified using a 95% LD C.I. based on an amplicon (gene)-wise significance threshold (Table 1). The size of the LD C.I. decreased with increasing FMs responsible for larger amounts of phenotypic variability. Simulated FMs responsible for >5% (sh1-5769), 15% (sh1-3822), and 2% (sh1-4884) of the phenotypic variability were the sole loci contained in the LD C.I. Occasionally, nonfunctional SNPs that are in LD with the simulated FM were included in the LD C.I. For example, the simulated FMs at sh1-4884 and sh1-5769 are in LD (r² = 0.50) with the minor alleles at sh1-5469 and sh1-5715 and both are included in their respective LD C.I. Also note that sh1-3822 has a larger LD C.I. than sh1-5769 in situations where the simulated genetic effects were responsible for 5 and 10% of the phenotypic variability. This is somewhat counterintuitive given the greater number of informative families for sh1-3822. It was noted, however, that there are a larger than average number of SNP loci in LD with the simulated FM at this locus (data not shown).

Disequilibrium between functional and nonfunctional markers:

An allele in complete disequilibrium with the minor allele at the sh1-3822 locus was simulated and placed at 10, 20, 30, and 40 cM from the sh1 amplicons as well as on an independently segregating linkage group (Table 2). An initial scan (excluding the simulated FM) of all SNP loci indicated that the sh1-3822 alleles were significantly associated with the segregating trait in all replicates. These represent false positive associations. If the FM was simulated on an independent chromosome, no false positive associations were detected. Application of the variable selection procedure to data sets that included the simulated FM resulted in correctly identifying the FM instead of the sh1-3822 locus. The impact of tighter linkage, the number of segregating progeny, and the ability to resolve FM with non-FM was not investigated but needs to be.

Multiple functional markers within a linked genomic region:

Phenotypes were simulated on the basis of two or three FMs within a single candidate amplicon or two or three FMs located in two amplicons located in a linked region, with additive genetic effects at the FMs accounting for 5 or 10% of the total phenotypic variability (Table 3). The correct sets of FMs were identified in >70% of the simulated data sets, indicating that it is usually possible to distinguish two FMs within the same candidate gene or whether there are two or three FMs located in two candidate genes (amplicons) located in a linked region. Note that this ability to accurately identify FMs depends upon the variable selection procedure; i.e., frequencies of correctly identified FMs using forward selection were less than those using the modified stepwise procedure (Table 3).

Simulated phenotypes in NAM families involving sh1-3822 paired with either sh1-819 or bt2-2854 produced the largest frequencies of correctly identified FMs. For each of these three loci the frequency of segregating families was ∼0.5 while the number of cosegregating loci occurred in 5 (sh1-3822, sh1-819) or 8 (sh1-3822, bt2-2854) of 28 families. By way of contrast, the least favorable resolution of pairs of loci involved sh1-3822 and either sh1-5769 or bt2-900. The frequency of segregating families for the latter two loci was 5/28 and the number of cosegregating loci occurred in only 2 (sh1-3822, sh1-5769) or 3 (sh1-3822, bt2-900) families. The ability to resolve the pair of FMs was strengthened if the more prevalent locus (sh1-3822) was responsible for a larger amount of phenotypic variability than its less prevalent partner (sh1-5769). These results suggest that if there is a large difference in genetic effects between FMs and the number of cosegregating families is small, it will be possible to resolve pairs of FMs on the same amplicon. In contrast, if the genetic effects of multiple FMs are responsible for similar amounts of phenotypic variability and the numbers of cosegregating families are large, resolution of FMs will be poor. These results are somewhat counterintuitive and need further investigation.

In the case of three FMs within a single candidate gene (amplicon) only 44% of the analyses managed to correctly include all three FMs, indicating that the NAM design and the variable selection procedure are limited in their ability to resolve multiple FMs within a single ampiicon.

Mating designs:

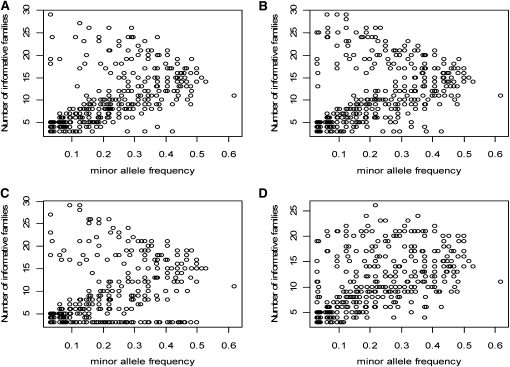
The results (Figure 3) indicate that regardless of choice of reference, SNP loci with rare alleles will be either highly informative (segregating in a large number of families) or largely noninformative (fewer than five informative familes) for the single reference design (Figure 3, A–C). Alternatively, use of three references resulted in about one-third as many SNP loci in noninformative families as there are in the single reference designs (Figure 3D). On the basis of these results the single reference design is not optimal, particularly if the frequencies of FMs are rare. If the reference line carries a minor allele that occurs at low frequency in the reference population, then expected heterozygosity for the locus could approach 1.0 among NAM crosses, providing considerable power to identify the FM. On the other hand, if the MAF is low and the common reference does not have this allele, then the expected heterozygosity could approach 0.0, resulting in failure to detect the FM (Xu 2003).

Figure 3.—

Number of informative families based on expected heterozygosity, between pairs of parental lines plotted against the minor allele frequencies for 11 resequenced amplicons sampled from the worldwide collection of maize. The set of 27 maize inbred lines includes (1) A272, (2) D940Y, (3) EP1, (4) F₂, (5) I205, (6) T232, (7) B103, (8) B97, (9) CI187-2, (10) Ki21, (11) Ky21, (12) M162W, (13) Mo17, (14) NC260, (15) Oh43, (16) Pa91, (17) W153R, (18) II101, (19) P39, (20) N28Ht, (21) A6, (22) CML254, (23) CML258, (24) CML333, (25) Ki3, (26) NC348, and (27) Tx601 (Liu et al. 2003). Sequences from the 27 lines are compared with B14A (A), Ia2132 (B), and IDS28 (C). The 27 lines also were randomly divided into three subgroups. (D) Group 1 includes 1, 4, 7, 10, 13, 16, 19, 22, and 25. Group 2 includes 2, 5, 8, 11, 14, 17, 20, 23, and 26. Group 3 includes 3, 6, 9, 12, 15, 18, 21, 24, and 27. Group 1 is compared with B14A, group 2 with Ia2132, and group 3 with IDS28 and the number of informative families were tallied across all three.

DISCUSSION

Replication of genetic effects, genomic architecture, and population structure with simulations provided quantitative measures of power, accuracy, and precision in identification of FMs in NAM populations. By using sequences from the maize diversity project (http://www.panzea.org) the simulations were based on realistic representations of allelic diversity and disequilibrium among SNPs. Although resequenced amplicons from maize show greater diversity and less disequilibrium per kilobase than those from most plant species, the results are applicable to all NAM populations because results are based on disequilibrium among markers regardless of their density per kilobase of sequence. However, the results also suggest caution should be exercised if a candidate gene approach is pursued with a NAM population. An actual statistical test based on the variable selection procedure was needed to eliminate false positives from the model. It is important to recognize that such ability to resolve FMs was possible only because genotypic information from the actual FMs was available. If the FMs are not genotyped, false positive associations may be declared (Nair et al. 2009).

Data analyses:

The data analyses are based on a biallelic model per SNP locus, which is reasonable for the vast majority of SNP loci. This FM model can be extended to the concept of multiple haplotypes, i.e., multiple FM alleles. The concept of multiple FM alleles can be regarded as a combination of biallelic variants within a haplotype (or amplicon) and the goal of identifying multiple FM alleles within an amplicon would be addressed exactly as we proposed in our third study on identifying multiple functional markers in the same genomic region. However, the model will need to be extended to account for epistasis among the alleles at the SNP loci.

Conceptually, the data analyses used herein and by Yu et al. (2008) are similar to that proposed for quantitative trait transmission disequilibrium tests (QTDT) in human families when combined with imputation of genotypes of relatives (Abecasis et al. 2000; Burdick et al. 2006). The data analysis method proposed herein has the following distinctive features from these other approaches: (1) Background QTL are controlled with cofactor markers identified in a model-building process, whereas they are controlled with a covariance matrix based on family relationships in QTDT (Abecasis et al. 2000) or based on a forward selection process (Yu et al. 2008); (2) genotypes at Q loci are imputed in the progeny using the conditional expectation based on known genotypic information of the parental alleles and genotypic information from anonymous flanking markers, whereas they are imputed using a random draw from a conditional distribution by Yu et al. (2008); and (3) implementation herein is through least squares, whereas maximum-likelihood algorithms are used in the other two.

The decision to use cofactors to represent background QTL in the modeling process is idealistic because it assumes that background genetic effects are fully explained by the identified cofactors. For the simulated data sets this assumption was not violated, and thus the results represent a set of “best cases.” It should be recognized, however, that such an assumption is not reasonable for experimental NAM populations. Further, it is very difficult to test the assumption. Intuitively, it seems that a more reasonable approach for experimental NAM populations is to model the background genetic effects as a random effect variance component in a mixed-model framework. At this point, however, it remains an open question as to which approach to modeling the background QTL is better for various possible genetic architectures and population structures.

The challenge of imputing genotypes in segregating progeny on the basis of parental genotypes has been addressed using three approaches (Yi and Shriner 2008): (1) Estimate all missing genotypes by their expected values conditional on observed flanking markers (Haley and Knott 1992), (2) consider QTL genotypes as unknowns to be predicted using an MCMC update procedure, and (3) perform multiple sampling of genotypes from a conditional probability distribution for each unknown locus (Sen and Churchill 2001). Given the large number of SNP loci and large number of families and progeny of NAM populations, the latter two approaches are computationally daunting. We found the first to be accurate while computationally feasible. Using publicly available data resources for maize and the methods described herein, we found that it is possible to assign 90% of 1.5 million genotyped SNPs from the maize HapMap project to linkage map positions in the maize NAM progeny using ∼1100 mapped markers (B. Guo and W. D. Beavis, unpublished results).

The motivation for development of a least-squares algorithm to map FMs is that it is accessible to experimentalists through many statistical software packages and is computationally fast even in situations with large numbers of SNPs in a large NAM population. It is well known that variable selection methods may not result in the correct model (Christensen 2002), although for the situations simulated herein, FMs were correctly identified in most cases, even when the model was built under potentially confounding influences of disequilibrium among functional and nonfunctional makers in the reference population. Another modification to variable selection is to consider an iterative reweighted least-squares algorithm and likelihood-ratio test, such as described by Xu (1998b).

The i.i.d. assumption associated with error in model (1) may not be seriously violated if all families are evaluated under relatively uniform conditions and cofactor markers are used to reduce background QTL effects among different families. It is possible, however, that some families may be evaluated in different environments. This can occur when data are pooled from multiple single-family studies or if different families are adapted to different sets of environments. In addition to transformations, standardized phenotypes have been suggested for handling this issue (Walling et al. 2000; Guo et al. 2006). Another solution is the use of permutation tests (Churchill and Doerge 1994), but in a nested model (Anderson and Ter Braak 2003), although it is unclear how heterogeneous error variances among families will affect permutation tests. Finally, we recognize that thresholds are essential for inferential statistics but irrelevant to Bayesian approaches.

We also recognize that a measure of precision for NAM experiments is needed. While the LD C.I. was possible with 100 replicates of the simulated genotypic effects, an individual NAM experiment needs a method to estimate precision for the identified FMs. An estimator that is conceptually related to the LD C.I. would be bootstrapping (Visscher et al. 1996; Lebreton and Visscher 1998), but would likely require significant computational resources. An alternative method proposed for linkage mapping is the confidence interval based on population size and the estimated QTL effect (Darvasi and Soller 1997) and can be adapted to the multiple-family situation of a NAM design.

Mating designs:

While the originally proposed NAM design was based on use of a single reference, it is reasonable to consider alternative designs such as the North Carolina Design I (NC-DI), routinely used by commercial maize and soybean breeders. The choice of a single reference for the maize NAM population was based on the desire to identify FMs from the breadth of maize germplasm while reducing the potential confounding of photoperiod on most traits through use of a single reference line adapted to temperate day length (Myles et al. 2009). Alternatively if all parental lines used in the NAM design are adapted to a set of target environments, results reported herein suggest that the mating design should be based upon the criterion of maximizing the number of informative families.

While three references are more optimal than one for adapted NAM populations, the optimum number of references was not determined. Determination of an optimum will depend upon the power of the experiment. It is reasonable to expect power to increase with family size and number of families (Xu 1998a). Power also will be affected by family heterogeneity arising from a variety of genetic mechanisms and experimental protocols. An investigation of optimal NAM designs will need to be based on multiple criteria and will require development of constraints in the context of an appropriate objective function (Hillier 2005).