Nonparametric Bayesian Variable Selection With Applications to Multiple Quantitative Trait Loci Mapping With Epistasis and Gene–Environment Interaction

Abstract

The joint action of multiple genes is an important source of variation for complex traits and human diseases. However, mapping genes with epistatic effects and gene–environment interactions is a difficult problem because of relatively small sample sizes and very large parameter spaces for quantitative trait locus models that include such interactions. Here we present a nonparametric Bayesian method to map multiple quantitative trait loci (QTL) by considering epistatic and gene–environment interactions. The proposed method is not restricted to pairwise interactions among genes, as is typically done in parametric QTL analysis. Rather than modeling each main and interaction term explicitly, our nonparametric Bayesian method measures the importance of each QTL, irrespective of whether it is mostly due to a main effect or due to some interaction effect(s), via an unspecified function of the genotypes at all candidate QTL. A Gaussian process prior is assigned to this unknown function. In addition to the candidate QTL, nongenetic factors and covariates, such as age, gender, and environmental conditions, can also be included in the unspecified function. The importance of each genetic factor (QTL) and each nongenetic factor/covariate included in the function is estimated by a single hyperparameter, which enters the covariance function and captures any main or interaction effect associated with a given factor/covariate. An initial evaluation of the performance of the proposed method is obtained via analysis of simulated and real data.

TRAITS showing continuous variation are called quantitative traits and are typically controlled by multiple genetic and nongenetic factors, which tend to have relatively small effects individually. Crosses between inbred lines produce suitable populations for quantitative trait locus (QTL) mapping and are available for agricultural plants and for animal (e.g., mouse) models of human diseases. Such crosses are often used to detect QTL. For these inbred line crosses, uniform genetic backgrounds, controlled breeding schemes, and controlled environment ensure that there is little or no confounding of uncontrolled sources of variability with genetic effects. The potential for such confounding complicates and limits the analysis and interpretation of human data. Because of the homology between humans and rodents, rodent models can be extremely useful in advancing our understanding of certain human diseases. In the past 2 decades, various statistical approaches have been developed to identify QTL in inbred line crosses (see, for example, Doerge et al. 1997 for review). To perform QTL mapping (identification), a large number of candidate positions (candidate QTL) along the genome are selected. These candidate QTL may all be located at genetic markers (positions of sequence variants in the genome where the genotypes of all individuals in a mapping population can be measured) or also in between markers if the marker density is not high. QTL mapping may then be performed by considering one candidate QTL at a time or multiple candidate QTL simultaneously. For inbred line crosses with low marker density and considering a single candidate QTL at a time, the interval-mapping method was proposed by Lander and Botstein (1989). However, these authors showed that interval mapping tends to identify a “ghost” QTL located in between two actual linked QTL if two or more closely linked QTL exist. This problem can be reduced or eliminated in two ways: (1) by using composite-interval mapping (Jansen and Stam 1994; Zeng 1994) which still performs a one-dimensional QTL search but conditional on the genotypes at a pair of markers flanking the marker interval containing the current QTL, to absorb the effects of background (nontarget QTL) outside of the target interval; or (2) by performing multiple QTL mapping, where two or more QTL are mapped simultaneously. Furthermore, if several QTL affect a quantitative trait mostly through their interactions (epistasis) while having nonexistent or weak main effects, then interval mapping or single-marker analysis will fail to detect such QTL. QTL interactions may not be limited to pairwise interactions. Marchini et al. (2005) have shown by simulation that searching for three loci jointly in the presence of a three-way interaction is more powerful than searching for a single or a pair of QTL. There are various different implementations of multiple QTL mapping. Most methods still perform only pairwise searches, with and without epistasis. The most recent methods are based on Bayesian variable selection and consider a group of candidate QTL or all candidate QTL in the genome simultaneously (e.g., Yi et al. 2007). These methods are typically still limited to pairwise interactions among QTL and do not consider gene–environment interactions.

The identification of QTL can be viewed as a very large variable selection problem: for p candidate QTL, with p typically in the hundreds or thousands and sample size in the low hundreds, there are 2^p possible main-effect models, 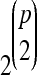possible two-way interactions, and 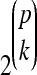possible higher-order (k > 2) interactions. For inbred line crosses, where multiple-QTL mapping models can be represented as multiple linear regression models, classical variable selection methods such as forward and stepwise selection (Broman and Speed 2002) have been used in searching for main and two-way interaction effects. Bayesian analysis implemented by Markov chain Monte Carlo (MCMC) and based on the composite model space framework (Godsill 2001, 2003) has been introduced to genetic mapping (Yi 2004). Well-known Bayesian variable selection methods such as reversible jump MCMC (Green 1995) and stochastic search variable selection (SSVS) (George and McCulloch 1993) are special cases. SSVS and similar methods employ mixture priors for the regression coefficients, which specify different distributions for the coefficients under the null (effect negligible) and alternative (effect nonnegligible) hypotheses. The marginal posterior probabilities of the alternative hypotheses can be used to identify a subset of important parameters on the basis of Bayesian multiple comparison rules, including the median probability model (with a threshold of 0.5) and Bayesian false discovery rate control (e.g., Müller et al. 2006).

An alternative to variable selection with mixture priors is classical and Bayesian shrinkage- or penalty-based inference. For the classical approach of penalized regression, while an L₂-based shrinkage method (ridge regression) cannot perform variable selection, other methods, in particular the L₁-based lasso of Tibshirani (1996) and later lasso extensions, are capable of performing variable selection by reducing the effects of unimportant variables effectively to zero. The lasso has been applied to parametric, regression-based QTL mapping (Yi and Xu 2008). The penalized regression methods can be interpreted as Bayesian regression models with particular sparsity priors imposed on the regression coefficients (Park and Casella 2008).

Regression methods are also used for association mapping in human populations. Recently, Kwee et al. (2008) proposed a semiparametric regression-based approach for candidate regions in human association mapping, where a quantitative trait is regressed on a nonparametric function of the tagSNP genotypes within a region. They analyzed a (small) subset of the genome and tested for the joint significance of the subset. Their method potentially can be used to model interactions among SNPs and covariates. However, Kwee et al. (2008) fit their model using least-squares kernel machines, a dimension-reducing technique that is identical to an analysis based on a specific linear mixed model. Model selection for different types of kernels and different sets of variables is performed using criteria such as Akaike's information criteria (Akaike 1974) and Bayesian information criteria (Schwarz 1978), which may not be appropriate or feasible in large-scale, sparse variable selection situations.

We (Huang et al. 2010) recently developed a Bayesian semiparametric QTL mapping method, where nongenetic covariate effects are modeled nonparametrically. This method was implemented via MCMC, and a Gaussian process prior (O'Hagan 1978; Neal 1996, 1997) was placed on the unknown covariate function. The Gaussian process is particularly well suited for curve estimation due to its flexible sample path shapes. This method allows one or more nongenetic covariates to have an arbitrary (nonlinear) relationship with the phenotype. Another strong advantage of the Gaussian process is its ability to deal with high-dimensional data compared to other nonparametric techniques such as spline regression (Wahba 1984; Heckman 1986; Chen 1988; Speckman 1988; Cuzick 1992; Hastie and Loader 1993). There has been a growing interest in using Gaussian processes as a unifying framework for studying multivariate regression (Rasmussen 1996), pattern classification (Williams and Barber 1998), and hierarchical modeling (Menzefricke 2000). In this article, we build on this work and propose a nonparametric Bayesian method for multiple QTL mapping by including not only nongenetic covariates but also all candidate QTL in the unknown function. A Gaussian process prior (GPP) is again placed on the unknown function, and a variable selection approach is implemented for the hyperparameters of the GPP (one for each QTL and nongenetic covariate). Here, we rely on mixture priors and MCMC implementation, and we focus on linkage mapping in inbred line crosses, while in ongoing and future work we are considering shrinkage priors, deterministic algorithms, and association mapping. Our application of the GPP differs from “standard” applications in that the QTL covariates included in the unknown function are discrete, not continuous, with a small number (two or three) of possible values (the genotype codes). The goal of using a GPP here is not curve or response surface modeling but rather high-dimensional variable selection (QTL and nongenetic covariates) with a method requiring only a single parameter for each variable while accounting for any multiway interactions among the candidate variables.

To improve current methods for linkage mapping in inbred line crosses and for association analysis of human populations, we need to be able to detect QTL irrespective of whether they act mostly through main effects, interactions with other QTL, or interactions with environment. Fitting a parametric model including all these potential effects for a genome-wide search would substantially increase the multiple-testing problem, in addition to being computationally extremely demanding. Here we offer an alternative. We show that our nonparametric Bayesian method can identify QTL irrespective of whether they act through main effects, through interactions with other QTL, or with environmental factors. This method cannot identify the source(s) of a QTL's importance (main or interaction effects involving this QTL). Therefore, once a small number of important QTL have been identified in a genome-wide scan, then these QTL can be further analyzed with detailed parametric models to determine the source(s) of their importance.

The remainder of the article is organized as follows. We first present the nonparametric multiple-QTL model and outline the MCMC sampler in the next section. Simulation results and the analysis of a real data set are presented in the section following that. And we end the article with a discussion and conclusions.

NONPARAMETRIC REGRESSION WITH GAUSSIAN PROCESS

Model and prior:

For the ith individual, we observe (i) the genotype codes 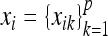at p markers, where x_ik is the genotype code at the kth marker; (ii) q nongenetic covariates or factors 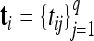, where t_ij is the value of nongenetic covariate j; and (iii) the phenotype or trait value y_i. The primary goal of the analysis is to map QTL (also loosely referred to as “genes”) associated with the phenotype. Assuming for simplicity of presentation that the set of candidate QTL is the set of markers, the problem reduces to identifying which markers influence the phenotype through their genotypes. We considered the following semiparametric QTL mapping model in Huang et al. (2010),

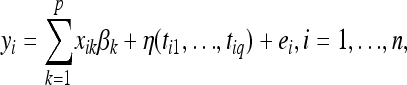(1)

where η is an unknown function of nongenetic covariates that we modeled via a Gaussian process prior; β_k is the partial regression coefficient associated with the kth marker; and e_i is a random error with distribution N(0, 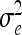). Model (1) considers only main QTL effects, which of course can be extended to pairwise interactions by including the terms 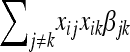, into (1) and similarly to higher-order interactions. The explicit modeling of interactions among genes causes an increase in the number of parameters in (1) which is exponential in the order of the interactions considered. Consequences are computational difficulties and poor inferences due to small sample sizes. To overcome this problem, we can alternatively consider the following model:

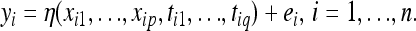(2)

This model is flexible and considers all interactions among genes and gene–environment interactions nonexplicitly. For example, if the unknown function η(x_i1, …, x_ip, t_t1,…, t_tq) = x_i1x_i2 + x_i3t_i1, then Equation 2 nonexplicitly models the two-way interaction between genes 1 and 2 and the gene–environmental interaction between gene 3 and environmental covariate 1. Let η_i = η(x_i1,…, x_ip, t_i1,…, t_iq) and define .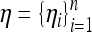

To estimate η, we again assume that η has a Gaussian process prior (as in Huang et al. 2010) with mean 0 and with a covariance matrix Σ whose element ii′ (i ≠ i′) associated with individuals i and i′ is

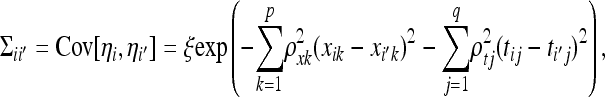(3)

where ξ, the 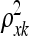's, and the 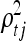's are hyperparameters. This is the most commonly employed stationary covariance function for a Gaussian process (a detailed presentation of Gaussian processes with many valid covariance functions is in Abrahamsen 1997; see also MacKay 1998). Hyperparameter ξ defines the vertical scale of variations, i.e., controls the magnitude of the exponential part. Hyperparameters 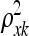and 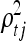are related to length scales that characterize the distance in that particular direction over which y is expected to vary significantly. When for example, 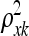= 0, then η is expected to be essentially a constant function of variable (gene) x_k, which is therefore deemed irrelevant (MacKay 1998). When 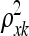is large, then the resulting function has a short characteristic length and will vary rapidly along the corresponding axis of x_k, indicating that variable x_k is of high importance. Similarly, 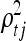indicates the importance of nongenetic covariate j in combination with the genetic factors and other nongenetic covariates.

The original articles on the Gaussian process (Neal 1997; MacKay 1998) did not view this method as an approach for variable selection and imposed an inverse Gamma prior on the ρ² parameters. Though 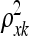does provide information about the relevance of any QTL k with values near zero indicating an irrelevant QTL [similar to the parameters β_k in the parametric linear QTL model (1)], determining which 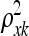's are significantly nonzero is challenging. It is convenient to represent the hyperparameters 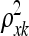in terms of their reciprocals, defined to be τ_xk = 1/ 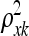and 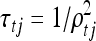. We perform Bayesian variable selection by imposing Gamma mixture priors on the parameters τ_xk and τ_tj. We introduce the latent variables γ_xk (γ_xk = 0 or 1) and γ_tj (γ_tj = 0 or 1). Then the Gamma mixture priors for the QTL associated parameters are represented as

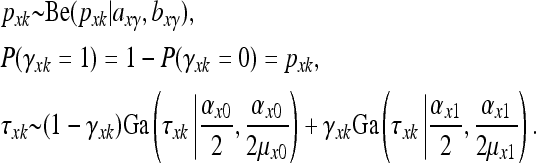(4)

Here Be(p | a, b) represents the Beta density p^a−1(1 − p)^b−1/B(a, b), Ga(τ | a, b) represents the Gamma density τ^a−1exp(−bτ)b^a/Γ(a), with E(τ) = μ and 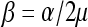, and (α_x0, μ_x0, α_x1, μ_x1, a_xγ, b_xγ) are hyperparameters to be specified or inferred. Similarly, for the nongenetic covariate associated parameters, we assume the mixture priors

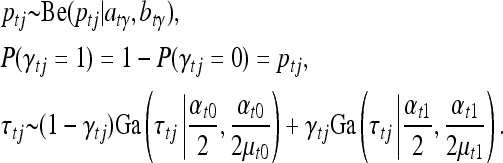(5)

Note that here μ_x0, μ_x1, μ_t0, and μ_t1 are the means of the two Gamma distributions in (4) and in (5), respectively. Setting μ_x0 (as well as μ_t0) to a large value ensures that if γ_xk = 0, then ρ_xk will take on very small values, and thus the corresponding variable is irrelevant. In contrast, setting μ_x1 (as well as μ_t1) to a smaller value ensures that if γ_xk = 1, then a nonzero value of ρ_xk will be included in the model.

Define τ_ξ = 1/ξ², 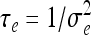and let the prior distributions of the two parameters be Gamma and given by

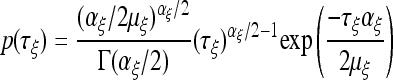(6)

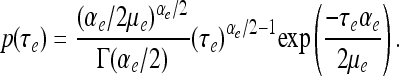(7)

Values for the parameters (α_ξ, μ_ξ, α_e, μ_e) are chosen prior to analysis.

The Gaussian process was originally proposed for modeling curves with continuous covariates, where the smoothness assumption on Gaussian process guarantees the smoothness of the estimated curves. However, in QTL mapping and other similar genetics analysis (Kwee et al. 2008), the primary goal is to map genes. The violation of the continuity assumption may be highly influential on the QTL effect estimation, but since the QTL effect estimation is only a secondary task in QTL mapping, the discreteness of genetic variables is less of a concern. As one extreme example, when only one gene is included, the Gaussian process model is equivalent to the random effect model where the genetic effect is treated as random with a normal distribution.

MCMC algorithm for posterior computation:

Inference is based on the joint posterior distribution of the unknown parameters (τ_x1, …, τ_xp, τ_t1, …, τ_tq, τ_ξ, τ_e) and the unknown function vector η, conditional on the phenotype (y), covariate (t), and marker (x) data. One potential problem in working with this joint posterior arises due to the discrete nature of the marker data: When the number of significant markers (i.e., markers with distinctly nonzero ρ_xk) is small, then the covariance matrix of η, Σ, may become (nearly) singular, because multiple individuals will share the same genotype configuration at these few markers. In this case the performance of the method deteriorates, and we therefore prefer to work with the joint posterior of the unknown parameters, or the joint posterior marginalized with respect to η. Because of the normal prior on η, this marginalization is equivalent to substituting the likelihood function of y conditional on η by the unconditional likelihood of y, or

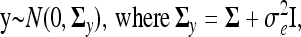(8)

where Σ_y is nonsingular even if Σ is singular. We compared inferences based on the joint posterior of the unknown parameters and η vs. the joint posterior of the parameters (using the same simulated data as presented below) and found the latter to provide clearly superior results. Therefore, from here on we consider only the marginalized posterior.

Most of the posterior computation is quite straightforward, and details can be found in supporting information, File S1. Below we describe an efficient sampling scheme, hybrid MCMC, that is essential for dealing with the large-scale QTL mapping data.

Let υ = (log(τ_x1), …, log(τ_xp), log(τ_t1), …, log(τ_tq), log(τ_ξ), log(τ_e)). Due to the complexity of the covariance form (3), one cannot sample from the full conditional posterior distributions of υ directly. The Metropolis–Hastings algorithm could be used with some proposal distribution, but it would explore the region of high probability by an inefficient random walk. To overcome this problem, the hybrid Monte Carlo method was proposed for sampling the hyperparameters in Gaussian process regression (Neal 1993, 1996; Rasmussen 1996; Barber and Williams 1997), and we adopt this approach here. The hybrid Monte Carlo method merges the Metropolis–Hastings algorithm with sampling techniques based on dynamics simulation.

To sample the p + q + 2 elements of vector υ from their posterior distribution p(υ|y, θ_–υ), we consider a physical system including p + q + 2 particles with the coordinate of the ith particle being υ_i. The potential energy of this system is defined in such a way that 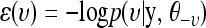. To allow the use of the dynamic method, we introduce a “momentum” variable, φ, which has p + q + 2 real-valued components, φ_i, in one-to-one correspondence with the components of υ. The kinetic energy of this system is defined as 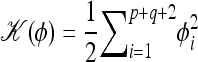. Therefore, sampling υ from 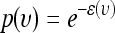is equivalent to sampling (υ, φ) from 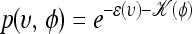by simply ignoring the momentum φ. The canonical distribution over (υ, φ) is defined to be 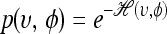, where 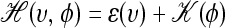is the “Hamiltonian” function, which gives the total energy of the system. It is well known in physics that the evolutions of such a canonical dynamical system through fictitious time s are governed by the following differential equations:

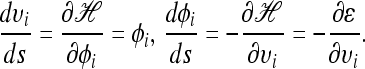(9)

By simulating this dynamical system, the transitions of the Markov chain in the hybrid Monte Carlo method take place as follows:

1. Starting from the current state (υ(s), φ(s)), perform L steps on the basis of the discretized Equation 9 with step size ɛ, resulting in the state (υ*, φ*) = (υ(s + Lɛ), φ(s + Lɛ)). A single step from s to s + ɛ can be explicitly written as

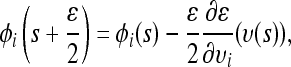
   (10)

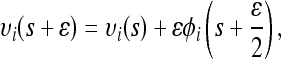
   (11)

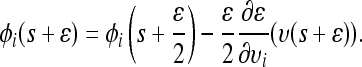
   (12)

2. With probability min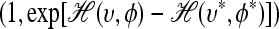, accept the new state (υ, φ) = (υ*, φ*); otherwise reject the new state and retain the old state with negated momentum (υ, φ) = (υ, −φ).

3. Update the total energy of the system by perturbing the momenta according to 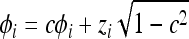for all i, where z_i is drawn randomly from the standard normal distribution. The momentum causes the particle to continue in a consistent direction until a region of high energy (low probability) is encountered. Following Rasmussen (1996), we set ɛ = 0.5n^−1/2 and c = 0.95.

SIMULATION AND REAL DATA ANALYSIS

Simulation of multiple-QTL models with or without higher-order interactions:

We simulated a backcross population with 200 individuals and a single chromosome with 151 evenly spaced markers at 5-cM intervals. To investigate the ability of the nonparametric Bayesian multiple-QTL analysis based on (2) to map higher-order interacting QTL that have no main effects, we simulated four interacting QTL without main effects and without lower-order interactions. The four simulated QTL are located at markers 9, 39, 69, and 99, respectively. The simulated function η = η(x_i1, …, x_i151) = x_i9x_i39x_i69x_i99, where the x_ik, k = 9, 39, 69, 99, are the genotype codes (1 and −1) of the four simulated QTL of individual i and 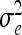= 1. The total heritability of this model is 50%.

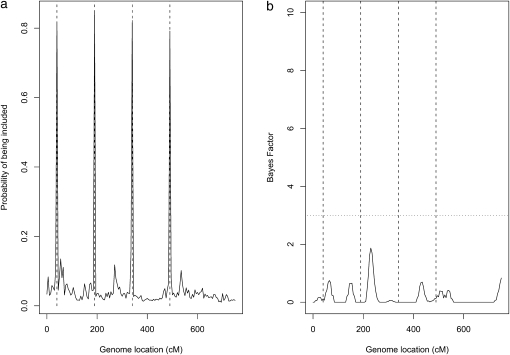
For the analysis, we set α_x0 = α_t0 = α_x1 = α_t1 = 1, α_ξ = α_e = 0.5, C = 100, and μ_ξ = μ_e = 400. We also set a_xγ = a_tγ = 0.95 and b_xγ = b_tγ = 0.05, so that the prior probabilities that each variable (QTL or nongenetic covariate) is relevant or irrelevant for the phenotype are 0.05 and 0.95, respectively. Figure 1a provides a plot of the posterior mean estimate of the hyperparameter γ_xk for each marker k vs. the marker position from the general model (2). As we hoped, the estimates of the hyperparameters associated with the true QTL markers are much larger than the estimates of the hyperparameters associated with the irrelevant markers, and all four, purely interacting QTL were identified on the basis of the marginal posterior probability of inclusion >0.5. Selecting all variables with marginal posterior probability of inclusion >0.5 produces the median probability model that is known to frequently correspond to the optimal predictive model while often differing from the highest probability model.

Figure 1.—

Four-way interaction model. (a) Average marginal posterior probabilities of being included in the model for each marker. (b) Estimated marginal Bayes factor for each marker from R/qtlbim. The dashed vertical lines indicate the true QTL positions. The dotted horizontal line is the threshold suggested by R/qtlbim for weak support of significance.

For comparison, we also ran R/qtlbim (www.qtlbim.org/), a popular software for Bayesian multiple-QTL mapping developed by Yandell et al. (2007). R/qtlbim is an extensible, interactive environment for parametric Bayesian analysis of multiple interacting QTL models for experimental crosses (limited to two-way interactions). The results are summarized in Figure 1b. In the R/qtlbim manual (Banerjee et al. 2008), the following criteria are suggested for judging the significance of QTL: weak support if the Bayes factor (BF) falls between 3 and 10, moderate support if the BF falls between 10 and 30, strong support if the BF > 30, and no support if BF < 3. According to these criteria, R/qtlbim fails to detect any QTL simulated.

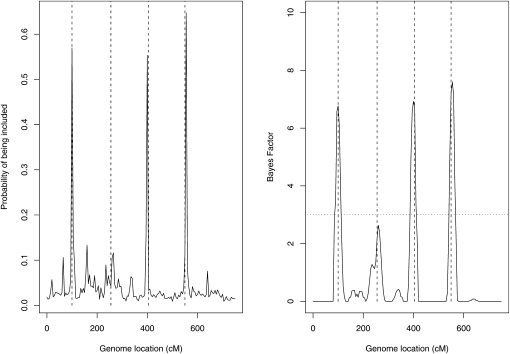
To further test the method, we then simulated data sets containing QTL that have only main effects (η(x_i1,…, x_i151) = 0.25(x_i21 + x_i51 + x_i81 + x_i111)) or main and two-way interaction effects (η(x_i1, …, x_i151) = 0.25 · (x_i21 + x_i81 + x_i21x_i51 + x_i81x_i111)). These are situations that R/qtlbim was specifically designed for. All other simulation parameters remained the same as in the previous simulation. Both models have a total heritability of 20% (∼5% heritability for each QTL). We used the same priors as in the previous simulation for the nonparametric method, and as before we used the default priors of R/qtlbim. Figure 2 summarizes the results for the additive model. Our nonparametric method detects three of the four QTL on the basis of the marginal posterior probability of inclusion (>0.5) and misses one QTL. Similarly, R/qtlbim detects the same three QTL with weak support (3 < BF < 10). For the model with the two-way interactions, results were very similar and are therefore not shown.

Figure 2.—

Additive (main effects only) model. See Figure 1 for details.

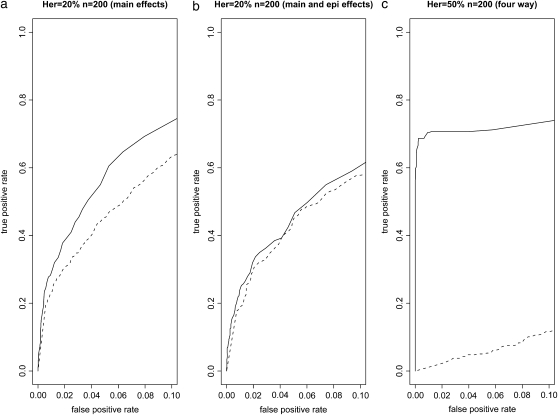
Our method and R/qtlbim use different criteria (median inclusion probability vs. BF-based selection) for the selection of a relevant subset of QTL. This difference is confounded with the comparison between the nonparametric and the linear parametric method in terms of their ability to detect existing QTL correctly. To overcome this problem, we varied the cutoffs imposed on the inclusion probability and BF, respectively, for declaring the significance of QTL, and we generated receiver operating characteristic (ROC) curves. For each scenario (four-way interaction, additive, and additive plus two-way interaction models as above), we ran 100 simulations. Instead of fixing the positions of the four simulated QTL, we uniformly generated their positions subject to the restriction that any pair of QTL had to be at least 10 cM apart. We divided the whole genome into nonoverlapping 10-cM-wide intervals. For a given cutoff (on inclusion probability or BF), a significant interval was defined as an interval that contains at least one marker whose significance measure exceeds the cutoff. A significant interval is defined as a true positive if it includes one of the simulated QTL. Otherwise, it is called a false positive. We defined true positive rate = (no. of significant, true intervals)/(no. of significant intervals) and false positive rate = (no. of significant, false intervals)/(no. of significant intervals). The ROC curves up to a false positive rate of 0.1 are given in Figure 3 for all three models simulated. For the four-way interaction model, our nonparametric method performed much better than R/qtlbim, which essentially failed to detect any QTL. It is interesting to see that our method appears to perform essentially as well as R/qtlbim for the model with both main and two-way interactions. It is even more interesting to find that our method is superior to R/qtlbim for the main effects model. This is because we ran R/qtlbim by searching for both main effects and two-way interactions simultaneously, even when analyzing the data generated under the pure main effects (additive) model.

Figure 3.—

ROC curves estimated for the three models simulated. The solid lines represent the nonparametric method and the dotted lines the linear parametric method in R/qtlbim. (a) Additive (main effects) model; (b) main plus two-way interaction effects model; (c) four-way interaction model.

Real data analysis:

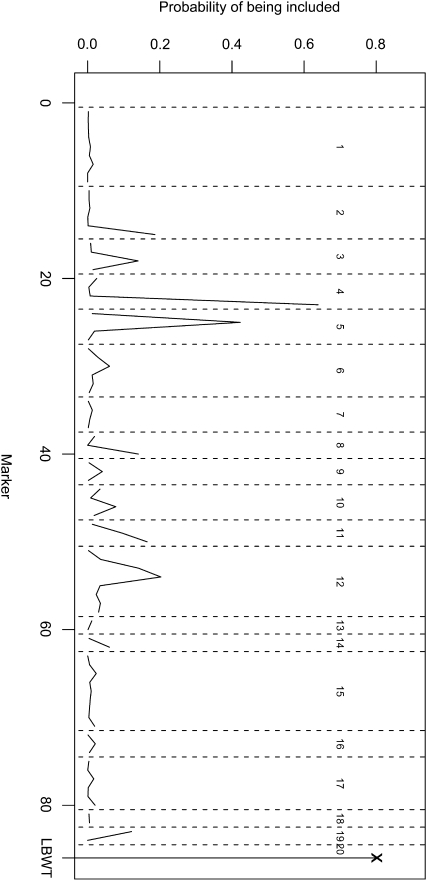
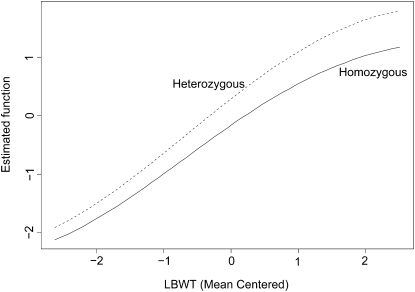
In addition to the simulation, we tested our method on a real mouse study on obesity, a major risk factor for type II diabetes. To genetically dissect a polygenic mouse model of obesity-driven type II diabetes, Reifsnyder et al. (2000) outcrossed the obese, diabetes-prone, New Zealand obese (NZO)/HlLt strain to the relatively lean nonobese nondiabetic (NON)/Lt strain and then reciprocally backcrossed obese F₁ mice to the lean NON/Lt parental strain. They measured the body weights of 187 backcross males. In addition, inguinal, gonadal, retroperitoneal, and mesenteric fat pad weights were also measured. Stylianou et al. (2006) studied the fat pad weights using F₂ progeny between the SM/J and NZB/BINJ inbred mouse strains. They identified several QTL associated with the gonadal fat pad weight after adjusting for the total lean body weight (LBWT). Following Stylianou et al. (2006), we first calculated the total fat pad weight as the mesenteric fat pad weight plus twice the sum of the inguinal, gonadal, and retroperitoneal fat pad weights. Then the LBWT was obtained as the difference between the total body weight and the total weight of the fat pads. We applied our nonparametric Bayesian variable selection method to the Reifsnyder et al. (2000) data. The results are presented in Figure 4. Clearly, 2 among the 86 predictors (85 markers plus the continuous covariate LBWT) are selected. The first ranked predictor is the covariate LBWT, and the second ranked predictor is marker D4Mit311 located on chromosome 4. Figure 4 strongly indicates a QTL on chromosome 4 while other QTL in the genome are (much) less likely. Further studies based on this observation can be done by investigating the relationship between the phenotype and these two variables in more detail. For each genotype of the QTL identified on chromosome 4, we estimated the weight curve function on LBWT, and the results are reported in Figure 5. From the two estimated curves, there is no clear evidence for an interaction between the QTL and LBWT.

Figure 4.—

Nonparametric Bayesian analysis of the backcross mesenteric fat pad data.

Figure 5.—

Estimated η function separated for the QTL genotypes of marker D4Mit311 on chromosome 4.

DISCUSSION

In this article, we have proposed a novel nonparametric QTL mapping method where the genetic as well as nongenetic factors are modeled via a function η, whose form is unspecified. The advantage of our approach is that it models all potential genetic and nongenetic effects, including main effects and all interaction effects of any order, nonexplicitly. It determines only which of the genetic and nongenetic factors are important, on their own through main effects and/or in combination with other factors. This was achieved by combining the Gaussian process prior for the unknown function with variable selection. Although in this article we assumed that all putative QTL are located at the marker positions, it is straightforward to extend the method to consider any candidate QTL in between marker positions as in Wang et al. (2005) and Huang et al. (2010). A similar nonparametric variable selection procedure has been proposed for computer experiments by Linkletter et al. (2006). These authors mainly focused on identifying active factors having nonlinear relationships with the response variable. However, mapping multiple interacting QTL is our main purpose, and our article appears to be the first one to propose modeling the joint action of multiple QTL with an unknown function having a Gaussian process prior, which accommodates any multiway interactions. Moreover, Linkletter et al. (2006) consider only a relatively small (<50) number of continuous covariates while in our article and in QTL linkage and association mapping in general, there are a large number of discrete marker covariates (hundreds or thousands) in addition to a small number of environmental, continuous covariates or discrete factors. Therefore, an efficient sampling scheme, such as the hybrid MCMC described in this article, is essential for dealing with these large-scale data sets.

While the linear parametric method in R/qtlbim may have little or no power to detect QTL acting through higher-order interactions, computationally it is fast, and it can handle large numbers of individuals and markers. We do not recommend replacing the linear parametric analysis with the nonparametric method, but rather using it as an additional or preliminary tool to screen the genome for QTL acting through higher-order interactions, which existing QTL mapping methods fail to detect. Once important factors have been identified with the nonparametric method, they then can and should be further analyzed with a detailed parametric model to elucidate the mode of action of the identified QTL (and environmental factors). Application of a detailed parametric method on a genome-wide scale to search for all possible main and interaction effects would dramatically increase the multiple-testing problem, in addition to the computational burden, while the nonparametric method can identify all these effects with a single parameter per candidate QTL (and environmental factor).

Our current research focuses on further improving the computational feasibility of our nonparametric method. Our current implementation of the Bayesian Gaussian process prior method, with the mixture priors on the variable selection parameters (ρ's) and using the hybrid Monte Carlo method, allows us to analyze data sets with up to several hundred individuals and several hundred markers, in hours rather than in minutes as with R/qtlbim. A major reason for this increase in computing time is the need to compute the inverse of an n × n matrix in each MCMC cycle to sample υ. This is particularly a problem for genome-wide association studies (GWAS), for which our nonparametric method is also potentially useful. GWAS typically require a larger sample size than linkage studies (in the order of thousands or tens of thousands) and several hundred thousand markers (tag SNPs). Further, in this article, we propose a simple Gibbs sampler for the latent binary variables that code for inclusion of a marker in the covariance function. For QTL mapping with only hundreds of markers, this algorithm works well. For very large p, it is likely that the algorithm may not properly mix over the huge sample space, a legitimate concern when we apply the method directly to GWAS data where hundreds of thousands of SNPs are available. Berger and Molina (2005) propose an approach to search for important models through large model space without visiting every model. Their approach provides a nice alternative, which deserves further investigation for GWAS data. Besides alternative sampling schemes we are currently investigating shrinkage priors to replace the mixture priors and increase computational efficiency, and we are exploring deterministic algorithms to replace MCMC sampling, in particular a conjugate gradient optimization technique to compute the maximum a posteriori estimates of the parameters (Rasmussen 1996). A genome-wide data set may first be analyzed with the deterministic implementation to screen out many variables (predictors) that are clearly irrelevant. Then the selected, promising subset of predictors (markers, genomic regions) may be reanalyzed by full MCMC, which provides much more information than a deterministic mode-finding algorithm. With an initial implementation of shrinkage priors and the conjugate gradient optimization technique we have been able to analyze a data set in a candidate gene association study with ∼900 participants and 2500 tag SNPs.

Selection of a subset of QTL can be performed on the basis of the estimated marginal posterior probabilities of inclusion with cutoff determined using the median probability model or Bayesian false discovery rate. Alternatively, we may add pseudonull variable(s) into the model and use the posterior distribution of their γ's to guide the variable selection. Linkletter et al. (2006) suggested adding a single pseudonull variable but running the analysis many times (say 100). For computational reasons, this approach works for their smaller size problems but is computationally very demanding or infeasible in the QTL mapping context. Furthermore, adding a single pseudonull variable would not work (well) for QTL mapping because marker (null) variables are correlated due to linkage. Wu et al. (2007) proposed a similar idea for variable selection in linear regression models using a set of pseudonull variables. Their method requires no additional repeated analysis as in Linkletter et al. (2006) and can also incorporate the linkage structure of the observed markers into the generation of the pseudonull variables. We are planning to extend the method of Wu et al. (2007) to our Gaussian process-based QTL selection methodology.

Much work has been done recently on sparse signal detection in (generalized) linear regression models, where there are two groups of sparsity priors, shrinkage or one-group priors, and mixture or two (multiple) group priors. Here we have employed a mixture prior for the parameters related to variable selection. Our current and future work focuses on further studies and modifications of this mixture prior and of alternative shrinkage priors. The goal of our present article was to convincingly demonstrate that the nonparametric Bayesian analysis based on the Gaussian process prior is indeed able to detect QTL irrespectively of whether they act on the trait of interest through main effects, any order of interaction among QTL, or interactions of QTL with environmental factors.