The Genetic Architecture of Grain Yield and Related Traits in Zea maize L. Revealed by Comparing Intermated and Conventional Populations

Abstract

Using advanced intermated populations has been proposed as a way to increase the accuracy of mapping experiments. An F₃ population of 300 lines and an advanced intermated F₃ population of 322 lines, both derived from the same parental maize inbred lines, were jointly evaluated for dry grain yield (DGY), grain moisture (GM), and silking date (SD). Genetic variance for dry grain yield was significantly lower in the intermated population compared to the F₃ population. The confidence interval around a QTL was on average 2.31 times smaller in the intermated population compared to the F₃ population. One controversy surrounding QTL mapping is whether QTL identified in fact represent single loci. This study identifies two distinct loci for dry grain yield in the intermated population in coupling phase, while the F₃ identifies only a single locus. Surprisingly, fewer QTL were detected in the intermated population than the F₃ (21 vs. 30) and <50% of the detected QTL were shared among the two populations. Cross-validation showed that selection bias was more important in the intermated population than in the F₃ and that each detected QTL explained a lower percentage of the variance. This finding supports the hypothesis that QTL detected in conventional populations correspond mainly to clusters of linked QTL. The actual number of QTL involved in the genetic architecture of complex traits may be substantially larger, with effect sizes substantially smaller than in conventional populations.

QUANTITATIVE trait loci (QTL) mapping provides insight into the genetic architecture of complex quantitative traits and generally relies on segregating populations derived from two parental inbred lines. Backcrosses or F₂ populations of a few hundred individuals lead to relatively large confidence intervals (CI) for detected QTL. Expanding the population size and increasing the marker density increases the precision of QTL mapping. This strategy incurs substantial costs and it is important to identify efficient and economical alternatives.

Populations of advanced intermated lines (AILs) have been proposed as an approach to increase the number of recombination events, while keeping population size constant (Darvasi and Soller 1995). AILs can be created from a cross between two inbred lines by performing several generations of random intercrossing after the F₂ stage. This cross leads recombination events to accumulate and breaks down linkage disequilibrium. As a consequence, map expansion is observed (Liu et al. 1996; Coe et al. 2002; Lee et al. 2002) when using mapping function developed for conventional populations.

Mapping experiments using AILs in animals and plants have been published (Iraqi et al. 2000; Hazen et al. 2003; Wang et al. 2003; Jagodic et al. 2004; Hernandez-Valladares et al. 2004; Scott and Duvick 2005; Yu et al. 2007; Balint-Kurti et al. 2007, 2008; Rodriguez et al. 2008; Capelle et al. 2010). In maize, the IBM population (for Intermated B73 × Mo17, Lee et al. 2002), is widely used by the maize international community for high-density genetic mapping (Falque et al. 2005; Fu et al. 2006) and fine mapping of traits of interest (Hazen et al. 2003; Scott and Duvick 2005; Balint-Kurti et al. 2007, 2008; Rodriguez et al. 2008). Balint-Kurti et al. (2007, 2008) were the first to compare the precision of QTL detection in conventional recombinant inbred lines (RILs) and intermated RILs, derived from the same parental lines, for two disease resistance traits in maize. These authors found a dramatic reduction of QTL confidence interval for some regions in the intermated population, reaching up to 50-fold in the case of two distinct QTL in repulsion detected as one unique QTL in the conventional population. In this study, however, the phenotypic evaluations were conducted separately for each population, and population sizes were variable (158 individuals for conventional RILs and 258 for intermated RILs). In a more recent study, Balint-Kurti et al. (2008) compared QTL detected in both types of populations for a different resistance trait. The populations had different sizes (288 for intermated population vs. 204 for conventional population) and were not evaluated in the same environments (only one environment was common). Although the authors found a relatively poor consistency between the QTL detected in each population, they were unable to exclude the hypothesis that those differences could be explained by differences in experimental conditions.

The present study was intentionally designed to compare an intermated F₃ population derived after four intermating cycles (called LHRF-F₃) to an F₃ population, both derived from the same parental lines, with equivalent population sizes (300 and 322 for the F₃ and LHRF-F₃, respectively). To allow a more direct comparison than in previous studies, these populations were jointly evaluated for dry grain yield (DGY), grain moisture (GM), and silking date (SD). Linkage maps, observed genotypic variation, and QTL mapping results all differ between the two populations. Using intermated populations for complex traits analysis and more broadly, fine mapping, appears beneficial in reducing the size of confidence intervals; however, caution is warranted because for highly complex traits, it may also reduce the number of detected QTL.

MATERIALS AND METHODS

Plant materials:

Two maize populations were analyzed in this study. One was an F₃ population used in previous QTL studies (Moreau et al. 1999, 2004a). This population was obtained by single-seed descent from the F₁ hybrid between F2, an early European flint inbred line, and F252, an early dent line from US origin. This population of 300 F₃ plants was selfed to produce F_3:4 seed stock. The LHRF-F₃ population was also derived from F2 and F252, with four generations of random mating after the F2. During random mating, each plant was used once as a parent. A total 80–100 crosses were produced for each subsequent next generation. The random mating generations were followed by one generation of selfing. The end result is an intermated population with genotypic frequencies per locus equivalent to an F₃. The 322 genotypes were selfed to obtain LHRF-F_3:4 seed stock. A testcross progeny was produced for all F_3:4 families by mating a representative sample of individuals to the inbred line MBS847, a US dent mid-to-late inbred line unrelated to F252.

Field experiments:

The testcross progenies for the two populations were grown in five sites in France in 1999 and 2000. During both years, the same design was used for all sites: 35 blocks, 17 blocks for F_3:4 testcross progenies and 18 blocks for LHRF-F_3:4 testcross progenies. A block was composed of 20 plots. Each plot consisted of two seed rows, spaced 0.8 m apart, and 4–5 m long. About 100 seeds were sown in a plot, and the plant density was adapted to the usual breeding practice at the site. Because seed stocks were not sufficient to test all the genotypes in all trials, 254 F_3:4 testcross progenies and 251 LHRF-F_3:4 testcross progenies were grown in all trials. The remaining progenies were randomly allocated to trials and each genotype was evaluated in at least five trials. A total of 292 of the 300 F_3:4 testcross progenies and 296 of the 322 LHRF-F_3:4 progenies were evaluated in each trial. To estimate environmental error, a subgroup of 31 F_3:4 progenies and 46 LHRF-F_3:4 progenies were replicated within each trial. The single-cross hybrids F2 × MBS847 and F252 × MBS847 were used as checks. One plot per block was devoted to checks, such that each check was planted every two blocks. For each plot, the silking date (SD) was recorded as the number of days after January 1 when 50% of the plants of a plot exhibited silks. Each plot was harvested in bulk to evaluate fresh grain yield. Grain moisture at harvest (GM, percentage of the fresh grain weight) was estimated for each plot by drying an 800-g sample. Fresh yield and GM were then used to estimate DGY, in tons ha⁻¹ at 0% grain moisture).

Marker genotyping and linkage map construction:

Leaves from ∼15 plants for each F_3:4 family were harvested in bulk to perform genomic DNA extraction. All genotypes were typed for 75 RFLPs (Moreau et al. 2004a) and 103 SSR markers. There was an additional marker set of 18 RFLPs and 3 SSRs for the F₃ population. There were 4 additional RFLPs and 176 additional SSR markers in the LHRF-F₃ population. All SSR primers are available at MaizeGDB (http://www.maizegdb.org). For SSR markers, electrophoresis was performed on 4% Metaphor agarose gels. For each locus, segregation distortion with respect to expected genotypic frequencies (3:2:3) and allelic frequency (1:1) was tested using a χ² test. Genetic maps were constructed using MAPMAKER v. 3.0b (Lander et al. 1987) with a LOD threshold of 3.0 to define linkage groups. Markers were ordered using multipoint analysis, with orders on each chromosome checked by the “ripple” option. Genetic distances were computed using Haldane's mapping function (Haldane 1919). Because recombination rates were estimated on the basis of the accumulation of recombination events through random mating generations (Lee et al. 2002; Winkler et al. 2003; Falque et al. 2005, 2006; Falque 2005), the unit of distance in the LHRF-F₃ population does not correspond to “true” centimorgans. We designated this unit of distance “IcM” for “intermated centimorgans,” as reported in the literature (Balint-Kurti et al. 2007).

Phenotypic data analyses:

For a given trait within a population, 0 to 0.9% of the plots were discarded for aberrant values. For each trial, experimental error variance was estimated on the basis of the subset of repeated genotypes. Bartlett's tests (Bartlett 1937) were then carried out to check homogeneity of error variances among trials. For each population, the following analyses of variance (ANOVA) models were fit:

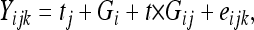where Y_ijk is the phenotypic performance of the k^th replication of genotype i in trial j; t_j is a fixed trial effect; G_i is a random genotypic effect; t × G_ij is a random genotype × trial interaction effect; and e_ijk is the residual. F tests were performed using the “random/test” option of PROC GLM and variance components with confidence intervals were estimated with PROC MIXED (Sas 1999). F tests for the genotypic effect were then used to estimate broad sense heritabilities (H²) and their 95% confidence intervals (CI) following the method proposed by Knapp et al. (1985). QTL detection was performed on adjusted mean testcross progeny performances over all 10 trials. We decided not to use genotypic BLUPs for QTL detection. As the estimated genetic variance may differ in the two populations, the variation of BLUPs may also differ, thereby complicating the comparison between the QTL detected in the two populations.

The same QTL segregated in both populations. However, generations of random mating can affect the genetic variance. First, random mating decreases the linkage disequilibrium between linked QTL. Under the hypothesis that QTL behave additively, this might have increased genetic variance in the LHRF-F₃ population if linked QTL were mainly in repulsion phase or, conversely, decreased variance if the QTL were mainly in coupling phase. If linked QTL interact, the genetic variance attributed to epistasis also depends on the linkage disequilibrium between loci (see Wang and Zeng 2006). Second, the increased number of generations in the LHRF-F₃ population might affect genotypic frequencies due to random genetic drift and/or involuntary selection. For a given QTL, q, we denote B and b as the two parental alleles. Assuming no dominance, the genetic variance associated with this QTL is:

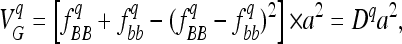where a is the additive effect (defined as half of the difference between values of genotypes BB and bb) and D^q is the variance coefficient determined by the genotypic frequencies and 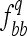of the genotypes BB and bb, respectively. In an F₃ population (conventional or intermated), the expecte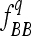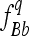d, , and 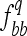are equal to 3/8, 1/4, and 3/8, respectively, leading to an expected value of coefficient 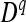= 3/4. The average D coefficient over the genome was computed for both the LHRF-F₃ and the F₃ using genotypic frequencies observed at co-dominant markers. The difference between 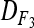and 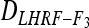yields an estimate of the difference in variances due to deviation in expected genotypic frequencies. Confidence intervals of 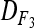and 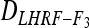(at the 95% level) were estimated by Wald's method (Vollset 1993).

QTL analysis:

A composite interval mapping method (CIM) (Jansen and Stam 1994; Zeng 1994) based on a regression approach (Haley and Knott, 1992) was implemented in PLABQTL v 1.2 software (Utz and Melchinger 2003). The input files are included as supporting information, File S1 and File S2. QTL detections were performed every 2 cM along the chromosomes for the F₃ population and every 2 IcM for the LHRF-F₃ population. The markers used as covariates in CIM were selected with a stepwise multiple regression with an F-to-enter and an F-to-drop equal to 8. This value was empirically chosen to correspond to an individual type I risk of 0.005. LOD thresholds estimated by 1000 permutation tests (Churchill and Doerge 1994), corresponding to a 10% global type I error risk at the genome level, were 2.7 and 3.12 for the F₃ and the LHRF-F₃ population, respectively. The higher threshold for LHRF-F₃ was consistent with the map expansion in this population. For each QTL detection, the individual P-values along the genome were used to compute the false discovery rate (FDR) associated with positions displaying LOD values above the 10% genome-wide threshold (Benjamini and Hochberg 1995). Digenic epistatic additive × additive effects between detected QTL were tested using “model/AA” option of PLABQTL with F-to-enter and F-to-drop values equal 8.

CIM results in LOD curves that may exhibit artificially narrow peaks around marker cofactor positions. To estimate the CI of QTL, CIM in the vicinity of each detected QTL was performed after removing the nearest cofactor from the list of cofactors selected by multiple regression. The 2-LOD fall method was then used to estimate 95% CI (van Ooijen 1992). The contribution of each detected QTL to the total phenotypic variation (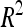) was estimated by dividing the partial sum of squares attributed to this QTL by the total sum of squares of the adjusted means. The proportion of the phenotypic variance explained by all detected QTL (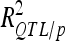) was adjusted as proposed by Hospital et al. (1997). The proportion of genetic variance explained by all the detected QTL (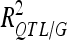) was estimated by dividing 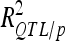by the broad sense heritability of the trait.

Phenotypic variance explained by QTL may be severely inflated due to selection bias (Beavis 1994; Moreau et al. 1998; Utz et al. 2000). Cross-validation was used to estimate unbiased 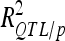(Utz et al. 2000) with “cross/p 1000” option of PLABQTL. The cross-validation process uses 4/5 of the individuals, randomly sampled, as a detection set (DS) to estimate QTL positions. The remaining 1/5 individuals are used as a validation set (VS) to estimate the effects and obtain an asymptotically unbiased estimation of the contribution of detected QTL to phenotypic variation (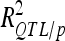). Analysis of the sampled sets provided the mean and extreme values for the number of detected QTL and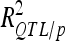. 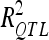obtained in VS were divided by the number of QTL detected in DS to estimate the average individual contribution of each QTL to the phenotypic and genotypic variations.

To compare positions and confidence intervals of the QTL detected in the two populations, common markers with unambiguous marker order were used. Biomercator v2.1 (Arcade et al. 2004) was used to project the QTL detected in the LHRF-F₃ population on the F₃ map. LHRF-F₃ QTL positions and CI limits were positioned on the F₃ map through a homothetic projection applying the appropriate local distance ratio between the two maps. We considered that the two populations had a QTL in common if the CI overlapped after projection.

RESULTS

Linkage maps:

The map obtained for the F₃ population was composed of 199 loci with a total length of 2115.7 cM and an average interval length between adjacent loci of 11.20 cM (Figure 1). The linkage map of LHRF-F₃ population included 358 loci with a total distance equal to 5568.3 IcM and an average interval length of 16.18 IcM between adjacent loci. In IcM unit, the linkage map of LHRF-F₃ was 2.63 times larger than the map of the F₃ population. This expansion factor varied from 2.21 for chromosome 3 to 3.11 for chromosome 2. A total of 178 loci were common between the two maps. Among them, 157 showed consistent order on the two maps and we noted that inversions mainly involved markers that were mapped at positions close to each other in the F₃ population map. Markers with consistent order were separated by 13.82 cM on average and were used for map comparison and QTL projections. Expansion factors between the two maps were also calculated for every interval between adjacent markers, yielding a 0.75- to 7.68-fold expansion factor with a median value of 2.54. Significant (P < 0.05) deviations from the expected segregation ratios (3:2:3) were observed for loci on all chromosomes of the two populations (Figure 1). Allele frequency deviated significantly (P < 0.001) from 0.5 at some markers of chromosomes 1, 3, 5, and 6 for F₃ population. A higher number of markers showed a deviation from an allele frequency of 0.5 in the LHRF-F₃ population. These makers were located on all chromosomes, with the maximum deviation being observed in regions of chromosomes 3 and 5.

Figure 1.—

Comparative linkage maps of F₃ (left) and intermated LHRF-F₃ (right) populations. Marker positions are in centimorgans (cM) for the conventional F₃ (using Haldane's function) and intermated centimorgans (IcM) (see text) for the intermated population. *0.05; **0.01; and ***0.001 indicate genotypic distortions at the respective levels of risk. Gray bars indicate regions where markers showed allelic bias at P = 0.001.

Phenotypic data analyses:

The average testcross performances of GM and SD in both populations were intermediate between the parental hybrid performances (F2 × MBS847 and F252 × MBS847). DGY mean performances observed in both populations were lower than the parental hybrid values, which suggests the presence of epistasis for this trait (Table 1). Transgressive segregation with respect to parental values was observed for all traits. Bartlett's test (Bartlett 1937) showed heterogeneity in error variance among trials, which might affect the significance levels of the effects in the analyses of variance. However, the broad sense heritability (H²) was extremely high for all traits (H² > 0.80), with the lowest value being observed for DGY in LHRF-F₃ population (0.73, Table 1). The ANOVA showed that genotypic, trial, and genotypic × trial interaction effects significantly (P < 0.001) influenced the testcross performance for all traits in both populations (Table 2). Estimated genotypic variance of DGY was almost two times lower in LHRF-F₃ than in the F₃ population (12.00 vs. 21.18) and their 95% confidence intervals did not overlap (Table 2). To determine whether this decrease in variance could be accounted for by differential drift among the two populations, we computed the variance coefficient 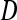and obtained values of 0.712 and 0.722 for the F₃ population and the LHRF-F₃ populations, respectively. The 95% confidence intervals for these values overlapped (0.708–0.722 for F₃ vs. 0.717–0.727 for LHRF-F₃), indicating that drift was not significantly different among the populations.

TABLE 1.

Testcross values of the parental lines and the two segregating populations

Trait	Parents		Conventional F3					LHRF-F3
	F2 × MBS847	F252 × MBS847	Means	Min	Max	H2a	CIb	Means	Min	Max	H2a	CIb
DGY (tons ha−1)	9.46	9.39	9.16	7.85	10.49	0.81	0.77–0.84	9.09	7.92	10.14	0.73	0.68–0.77
GM (%)	33.16	29.61	32.13	29.05	34.56	0.82	0.79–0.85	31.80	29.04	33.87	0.83	0.80–0.85
SD (days)	207.32	210.25	209.98	204.14	212.56	0.84	0.81–0.86	209.14	204.98	212.92	0.86	0.84–0.88

Least square means of the parental lines, means, minimal (min), and maximal (max) values for genotypes of the two segregating populations and trait heritabilities for dry grain yield (DGY), grain moisture at harvest (GM), and silking date (SD) evaluated in 10 trials.

^aBroad sense heritability.

^bConfidence interval (95%) of broad sense heritability.

TABLE 2.

Analysis of variance for dry grain yield (DGY), grain moisture (GM), and silking date (SD)

Source	Conventional F3				LHRF-F3
	d.f.	Mean squares III	F	Variance × 10−2 (CI)	d.f.	Mean squares III	F	Variance × 10−2 (CI)
DGY (ton ha−1)
Trials	9	280.19	547.92***	—	9	214.4113	447.42***	—
Genotype	295	2.67	5.23***	21.18 (17.50–26.18)	298	1.7441	3.64***	12.00 (9.73–15.17)
Genotype × trials	2474	0.52	1.58***	16.12 (12.33–21.98)	2602	0.4888	1.66***	15.69 (12.12–21.11)
Error	409	0.33		33.62 (29.62–38.50)	433	0.2949		30.92 (27.22–35.42)
GM (%)
Trials	9	1972.69	1236.11***	—	9	2594.42	1536.39***	—
Genotype	295	9.11	5.71***	0.74 (0.61–0.91)	298	9.72	5.76***	0.75 (0.63–0.92)
Genotype × trials	2495	1.63	1.66***	0.51 (0.39–0.70)	2603	1.72	1.48***	0.44 (0.31–0.65)
Error	414	0.98		1.04 (0.91–1.20)	435	1.16		1.21 (1.07–1.38)
SD (days)
Trials	9	6960.70	2785.35***	—	9	8950.32	2955.21***	—
Genotype	295	15.80	6.33***	1.34 (1.11–1.64)	298	21.99	7.26***	1.78 (1.49–2.16)
Genotype × trials	2496	2.53	1.41***	0.62 (0.44–0.94)	2621	3.07	1.34***	0.70 (0.49–1.08)
Error	416	1.80		1.83 (1.62–2.09)	437	2.29		2.27 (2.02–2.56)

For all the effects, degrees of freedom (d.f.), type III mean squares, and Fisher's test values are shown. For random effects, variance components and their 95% confidence intervals were estimated by Proc MIXED. ***P < 0.001.

QTL detection:

F₃ population:

A total of 30 additive QTL were detected: 9, 9, and 12 for DGY, GM, and SD, respectively (Table 3) with no significant digenic epistasis. A total of 22 of the 30 QTL displayed small individual effects (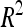 < 5%). The highest 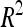was 18.2% for a GM QTL on chromosome 4. For a given trait, the sum of the detected QTL explained ∼45% of the phenotypic variance (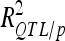) and ∼55–60% of the genetic variance (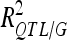) (Table 3).

TABLE 3.

QTL detected for DGY, GM, and SD in F₃ and LHRF-F₃ populations

Chr	Conventional F3						LHRF-F3
	Left marker	Pos (cM)	CI (cM)	LOD	R2	Add	Left marker	Pos (IcM)	CI (IcM)	LOD	R2	Add
DGY (ton ha−1)
1	bnlg1083	70	56–84	6.53	4.44	−1.411	Umc1397	226	218–240	4.23	3.51	−0.927
1	umc161	254	242–272	5.12	2.77	1.250	Umc161	728	716–754	5.4	5.11	1.021
2							gsy53b	88	40–168	3.43	2.25	0.882
2							Bnlg2248	208	190–220	3.81	2.73	−0.900
2	csu143	112	108–122	16.05	9.52	−2.327
2							phi127	462	448–476	6.69	8.43	−1.291
2	umc137	184	156–204	5.14	2.73	−1.381
4							Umc1511	200	174–226	6.08	6.04	−1.232
4	umc1101	212	186–230	4.16	5.88	−1.131	csu9b	476	448–506	4.46	3.20	−1.145
4							Umc1532	550	538–564	3.89	2.98	−0.868
5							Umc83b	314	296–324	3.43	3.59	−0.888
6							Bnlg249	126	108–138	6.59	9.10	−1.200
7	umc116	68	52–106	5.24	2.72	1.332
8	umc152	62	50–78	4.74	3.38	1.347
8	umc89	100	76–120	3.02	2.94	1.105
9							csu147	204	190–236	3.76	2.60	−0.939
10	umc1196	128	118–134	7.04	5.91	1.382
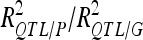					48.4	/59.75					41.5	/56.85
GM (%)
2	umc134l	102	94–112	6.33	4.05	0.374
2	umc5a	126	114–144	3.2	2.55	−0.244
2	umc137	172	160–186	7.07	4.30	−0.289
3	umc1892	22	0–72	2.93	2.00	0.21	bnl13.05b	176	166–188	3.67	3.22	−0.252
3	umc1767	158	148–180	4.59	3.42	−0.238
4	gsy4	68	62–76	19.66	18.02	−0.51	Mmc0471	154	142–188	5.98	8.94	−0.308
5	umc2115	76	58–100	2.72	1.6	−0.171
5							bnl7.71	330	314–350	3.54	4.29	−0.228
6	bnlg1702	130	118–144	4.59	2.92	−0.213
8							Bnlg1031	370	330–392	3.77	2.69	−0.254
9	phi027	56	46–66	6.62	5.23	−0.280
9							bnl5.09	378	370–386	3.66	4.67	−0.230
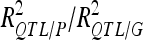					45.5	/55.49					20.6	/24.82
SD (days)
1	umc1166	48	28–62	6.49	5.58	0.391
1	umc84	282	268–292	6.45	4.76	0.366	Bnlg2123	814	800–836	3.33	5.18	0.287
3	umc1892	22	6–46	3.71	2.82	0.328
3							dupssr23	270	240–286	3.36	3.43	0.307
5	mmc0261	90	82–110	4.37	3.43	0.314	Umc43	250	240–260	8.25	9.63	0.559
5							Umc1110	324	312–340	4.79	5.05	−0.385
6	gsy189	20	8–36	3.19	2.67	−0.243
6	umc62	178	156–196	2.84	2.42	−0.246
8	umc152	64	40–86	3.51	2.88	0.324
8	umc89	96	90–104	10.95	7.30	0.56
8	umc1384	180	136–190	4.53	3.59	−0.300
9	phi027	56	48–64	6.47	6.28	−0.376
9	umc1137	200	180–208	3.55	2.60	0.261	Umc1137	472	456–492	4.72	5.07	0.376
10	umc44	102	86–136	5.27	3.88	0.315
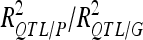					45.7	/54.40					26	/30.23

For each detected QTL are indicated the chromosome (Chr), the left marker flanking the QTL (left marker), the estimated position (Pos) on the linkage map of the population, the 95% confidence interval of the QTL position (CI), the LOD score, the percentage of phenotypic variance explained by the QTL (R²), and the additive effect (associated with F252 allele). 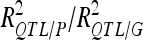is the proportion of phenotypic variance/genotypic variance explained by all the detected QTL for a given trait. QTL showing significant digenic epistasis (P < 0.01) are underlined. QTL involved in epistatic interaction with two different QTL are double underlined.

Advanced intermated LHRF-F₃ population:

A total of 21 additive QTL were detected: 11, 5, and 5 for DGY, GM, and SD, respectively (Table 3) with two digenic QTL × QTL interactions for DGY (P < 0.01). Detected QTL exhibited small individual effects and the biggest 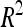was <10% (one QTL on chromosome 5 for SD). 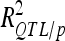was 41.5% for DGY but was only ∼20% for the other traits, consistent with the small number of detected QTL in this population. Consequently, 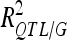was 56.85% for DGY and ∼25–30% for GM and SD (Table 3).

Cross validation:

In the validation sets (VS), the reestimate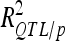d and 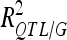were 1.36- to 3.54-fold lower than in DS (Table 4). For DGY and GM, the decrease in explained phenotypic (or genotypic) variance was more severe in LHRF-F₃ (2.5 and 3.54, respectively) than in F₃ (1.37 and 1.36, respectively). For SD, the decreases in explained variance were similar (∼2) in both populations. Using unbiaised estimates of 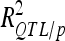, each individual QTL detected in the F₃ population contributed on average 4.4, 5.2, and 2.4% of trait variation for DGY, GM, and SD, respectively. The average contributions of each detected QTL were smaller in the LHRF-F₃ population for DGY and GM (2.2 and 1.6%, respectively) and similar (2.9%) for SD. The high heritabilities (about 0.8) and the small contributions of individual QTL to trait variation in the intermated population jointly suggest that the actual numbers of QTL involved in the architecture of traits related to grain yield must be high.

TABLE 4.

Cross-validation analysis of QTL detection and comparison to whole data (WD) set results

	Conventional F3			LHRF-F3
	DGY	GM	SD	DGY	GM	SD
QTL no.
WD	9	9	12	11	5	5
DS	8.96	6.00	8.31	5.68	3.75	5.93
Range	(5–15)	(3–10)	(1–14)	(1–11)	(1–11)	(2–12)
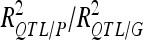WD	48.40/59.75	45.50/55.49	45.70/54.40	41.50/56.85	20.60/24.82	26.00/30.23
DS	54.03/66.70	42.29/51.57	41.02/48.83	30.58/41.89	21.4/25.78	33.86/39.37
VS	39.48/48.74	31.05/37.87	20.05/23.87	12.24/16.76	6.05/7.29	17.22/20.02
Bias	1.37	1.36	2.04	2.50	3.54	1.97
Av. R2 per QTL	4.4/5.4	5.2/6.3	2.4/2.9	2.2/2.9	1.6/1.9	2.9/3.4

The number of detected QTL (QTL no.) and the proportion of phenotypic and genotypic variance explained by the detected QTL (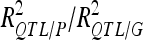) are reported for each analysis. In the cross-validation process, the number of detected QTL corresponds to the average number of detected QTL across 200 5-split cross-validation detection sets (DS). We also indicated the range of variation of the number of QTL detected (range).Two different types of percentages of variance are given: the average values across detection sets (DS) and validation sets (VS). The ratio between the DS value and the VS value gives an estimate of the selection bias for the percentage of variance explained. The VS values were divided by the average number of QTL detected in DS to estimate the average contribution of each individual QTL to the variation (Av. R² per QTL).

Comparison between conventional population and advanced intermated population:

Eight of 30 QTL for conventional F₃ and 9 of 21 QTL for intermated F₃ were “common QTL” (Table 5). One QTL of DGY on chromosome 4 in the conventional population corresponded to two distinct QTL in coupling phase in LHRF-F₃ (Table 5, Figure 2A). The average CI of all detected QTL were 32.93 cM and 14.26 cM for conventional and intermated populations, respectively. This corresponded to a global CI reduction by a factor of 2.31 in the LHRF-F₃ vs. the F₃. Considering only common QTL, with the exception of the QTL for GM detected on chromosome 3, the average CI was equal to 28.00 cM in the conventional population vs. 12.34 cM in LHRF-F₃. This yielded an average CI reduction factor of 2.27 with a variation between 1.67 and 4.77.

TABLE 5.

QTL with overlapping CI between F₃ and LHRF-F₃ populations after QTL projection

	Conventional F3			LHRF-F3
Chr	Left marker	Pos	CI (cM)	Left marker	Pos	CI (cM)	CIC/L ratio
DGY (tons ha−1)
1	bnlg1083	70	56–84	umc1397	78.43	75.04–84.36	3.00
1	umc161	254	242–272	umc161	258.97	252.62–267.40	2.03
4	umc1101	212	186–230	csu9b	188.79	176.26–202.66	1.67
4				umc1532	219.44	215.18–224.41	4.77
GM (%)
3	umc1892	22	0–72	bnl13.05b	75.32	71.04–78.97	9.08
4	gsy4	68	62–76	mmc0471	68.65	65.65–78.15	1.12
SD (days)
1	umc84	282	268–292	bnlg2123	286.3	281.93–292.22	2.33
5	mmc0261	90	82–110	umc43	105.66	103.14–108.18	5.56
9	umc1137	200	180–208	umc1137	202.51	196.39–207.58	2.50

QTL of LHRF-F₃ are projected on conventional F₃ linkage map so CI are expressed in cM. The CI_C/L ratio was obtained by dividing the conventional F₃ CI by LHRF-F₃ projected CI.

Figure 2.—

Specific examples of QTL detected in both populations after projection on the F₃ map. (A) One QTL for DGY on chromosome 4 detected in the F₃ population corresponds to two QTL in the LHRF-F₃ population. (B) A QTL for SD detected on chromosome 5 in the LHRE-F₃ population has a smaller CI than the corresponding QTL detected in the conventional population. In each case, only part of the chromosome is shown with the chromosome number above. Numbers in parentheses are marker positions along the chromosome in centimorgans. Dark lines indicate QTL detected in the F₃ population; gray lines indicate QTL detected in the intermated F₃ population.

DISCUSSION

There is a gain in precision for QTL mapped in the intermated population compared to the conventional population (Table 5). The average reduction in the CI corresponds to the expected value t/2, where t is the number of random mating generations (Darvasi and Soller 1995) and also corresponds to the map expansion coefficient. Two linked QTL in the intermated population were identified in a region where a single QTL was detected in the F₃ population. These observations are consistent with those of Balint-Kurti et al. (2007) who observed a notable gain in precision in QTL mapping in their intermated population, reaching up to 50-fold smaller CI in the specific situation of breaking linkage of two QTL in repulsion. However, we detected globally fewer QTL in the intermated population than in the conventional one (in the whole data set, we detected slightly more QTL for DGY, but much fewer for the other traits). Only 27% (8 of 30 QTL) of the QTL detected in the conventional population were also detected in the intermated population and 43% (9 of 21 QTL) of QTL detected in the intermated population were also detected in the conventional population.

Our results suggest a high number of QTL for yield-related traits in maize, with linkage occurring in both repulsion and coupling. Theory shows that with coupling phase linkages in the F₁, random mating is expected to reduce the additive genetic variance, whereas repulsion is expected to inflate it (Comstock and Robinson 1948). For SD, the genetic variance increased (even if the difference between the two variances were not significant). This suggests that some QTL may have been in repulsion phase. For GM, the genetic variance was almost identical in both populations, suggesting either limited linkage or more likely (considering results from cross-validations), a combination of both phases. Conversely, DGY genetic variance was lower in the intermated population than in the conventional population. The magnitude of reduction appears high (almost a factor of two) relative to the value expected in the case of coupling between pairs of QTL of similar effect (a factor of two when comparing complete linkage to complete independence). This may suggest coupling between higher number of QTL clustered into segments, or possibly epistatic interactions. Such a reduction of genetic variance after random mating generations was also observed in populations derived by crossing genotypes issued from a long-term divergent selection for protein or oil content (Moreno-Gonzalez et al. 1975; Dudley et al. 2004). In these studies, coupling phase linkage in the initial generation was the consequence of the divergent selection process. In this study, the parental lines did not derive from a divergent selection process, but the lines do belong to two distinct heterotic groups (European Flints vs. US dents), independently selected for grain yield that then further diverged because of complementary testers. Our results might therefore be specific to the genetic background of parental materials used to create these populations. Results of Lu et al. (2003) and Graham et al. (1997) suggest that the effect of main QTL detected for grain yield heterosis are due to smaller QTL in repulsion phase. Repulsion phase between linked loci with dominant effects generates an apparent pseudo-overdominance of the chromosome region that facilitates its detection. In our case, QTL display only statistical additive effects (testcross performance); repulsion phase cannot contribute to enhanced QTL effects, perhaps explaining a lack of QTL detected in repulsion phase.

Epistasis between linked QTL is expected to affect the genetic variance contributed by the chromosome region that carries these QTL (Wang and Zeng (2006)). We observed that testcross value for DGY was lower on average for the populations than for the parental lines, suggesting epistasis with favorable epistatic combinations between alleles originated from the same parental line. We detected epistatic interactions in the LHRF-F₃ population, but not between linked QTL. Blanc et al. (2006) also pointed out the importance of QTL-by-genetic-background epistasis and QTL × QTL interaction for grain yield in using six connected F₂ populations of maize inbred lines. In contrast, no epistasis for grain yield was reported in other studies (Hinze and Lamkey 2003; Schön et al. 2004). The importance of epistasis might be population specific. In our case, the parental lines originated from two different heterotic groups. Selection for complementarity between heterotic groups might have led to the fixation within each group of synergistic combinations of alleles at linked QTL.

Our results confirm the interest of intermated populations in reducing confidence intervals of QTL position estimates. They suggest globally that most QTL contributing to trait variation in the studied cross had small individual effects, especially for DGY and GM. In the intermated population, recombination events disrupt linkage within clusters of QTL in coupling phase. These clusters, that could be detected in conventional population, were split into individual QTL with small effects that became difficult to detect in the intermated population. In contrast, recombination events should have helped the detection of QTL in repulsion phase. But because these QTL had a small individual effect, they remained largely undetected. This led to the detection of fewer QTL in the intermated population and to a lack of consistency between the QTL detected in the intermated population compared to the conventional population. Moreover, as recombination events reduced the level of dependency between linked tests in the intermated population, the LOD threshold was increased to keep genome-wide type I error risk constant. This may further reduce the power of detection of a given individual QTL in the intermated population. This implies that, for a fixed population size the use of intermated populations might reduce the number of QTL regions that are detectable, when a large number of loci segregate.

Our results also highlight that the number of QTL segregating for traits such as grain yield, grain moisture, and silking date in maize is large even when only two alleles segregate. This is consistent with results of Openshaw and Frascaroli (1997) and Schön et al. (2004) in a conventional biparental maize population of ∼1000 individuals. Note that this number increases when considering a broader diversity (Buckler et al. 2009). Both epistasis and coupling phase “erosion” likely contribute to the inefficiency of MAS observed by Moreau et al. (2004b) after detecting QTL in the conventional population presented here and conducting generations of selection based on markers only. Such an approach might not be appropriate, especially when chromosome segment effects are diluted along generations due to the recombination effect. More efficient strategies may include “genomic selection,” first proposed by Whittaker et al. (2000) or Meuwissen et al. (2001), which uses markers located on the entire genome as predictors, without selecting the most significant ones. Such a method avoids the issue of selection bias and divides selection pressure more equally over the whole genome. Genomic selection appears more efficient than conventional MAS (see Heffner et al. 2009, for a review), especially for traits controlled by a large number of QTL and in cases of low heritability (Bernardo and Yu 2007).