In vivo validation of MRI vessel caliber index measurement methods with intravital optical microscopy in a U87 mouse brain tumor model

Abstract

The vessel caliber index (VCI), a magnetic resonance imaging biomarker of the average blood vessel diameter, is increasingly being used as a tool for assessing tumor angiogenesis and response to antiangiogenic therapy. However, although the VCI has been correlated with histological vessel diameters, good quantitative agreement with histology has been lacking. In addition, no VCI validation studies have been performed in vivo where the structural deformations frequently associated with histological tissue preparation are not present. This study employs intravital optical microscopy (IVM) measurements of cerebral blood vessel diameters in a mouse orthotopic glioma model to provide the first such in vivo validation. Two VCI correlation models, both a linear and a 3/2-power dependence on the ΔR2*/ΔR2 ratio, were compared with the IVM data. The linear VCI model, determined from steady-state susceptibility contrast (SSC) images, was found to be in excellent quantitative agreement with the intravitally determined VCI for separate tumor size matched groups of mice. In addition, preliminary data indicate that the VCI is independent of whether a dynamic susceptibility contrast or SSC measurement method is used.

Increased average tumor blood vessel diameters are a hallmark of angiogenesis driven tumor growth. Magnetic resonance imaging (MRI) measurements of a biomarker of the average blood vessel diameter, the vessel caliber index (VCI), may therefore provide an important tool for the in vivo assessment of tumor angiogenesis and response to antiangiogenic therapy.^1–7 This method is based on the differential sensitivity to vessel radius observed in the changes in transverse relaxation rates R2 and R2* induced by susceptibility-based contrast agents.^8,9 In particular, ΔR2 has a greater sensitivity to microvasculature and, above a certain radius threshold, was shown to decrease with vessel radius, whereas ΔR2* remains essentially constant. A VCI defined by the ΔR2*/ΔR2 ratio was shown by Dennie et al.¹ to provide a measure of the average blood vessel radius in both Monte Carlo simulations and in vivo studies of a rat brain tumor model. This VCI method has been validated with histology in a number of studies.^1–4,7 However, although the MRI-derived VCI was strongly correlated with the histological vessel radius, quantitative agreement has been highly variable (Table 1). In most cases, the MRI-derived VCI was found to be substantially greater than the histology derived VCI. This discrepancy has been attributed to a number of possible factors including (a) structural deformations associated with histological tissue preparation (fixation, freezing, cryosectioning, etc.), (b) the detection of all vessels by histology, but only perfused vessels by MRI, and (c) the inadequacy of the vascular models used to derive the VCI.^5,10,11

Table 1.

Comparison of MRI linear, MRI 3/2-power, and histology-derived rVCI (±SD)

Reference	rVCIhistoa	ΔR2*/ΔR2	(ΔR2*/ΔR2)3/2	Tumor model
Dennie et al.1	1.89 ± 1.19	1.92 ± 0.24	2.65 ± 0.50	Rat, C6 glioma
Packard et al.3	1.63 ± 0.14	1.59 ± 0.20	2.01 ± 0.38	Rat, U87, baseline hypercarbia group
Packard et al.3	1.63 ± 0.14	1.41 ± 0.12	1.68 ± 0.21	Rat, U87, baseline hypocarbia group
Badruddoja et al.2	2.97 ± 0.32	5.37 ± 3.56	12.43 ± 12.37	Rat, 9L gliosarcoma, control
Badruddoja et al.2	5.37 ± 0.80	3.46 ± 1.26	6.44 ± 2.61	Rat, 9L gliosarcoma, dexamethasone treated
Tropres et al.4	1.87 ± 1.54	2.70 ± 0.65	4.44 ± 1.61	Rat, C6 glioma
Valable et al.7	2.68 ± 0.61	2.18 ± 0.50	3.21 ± 1.12	Rat, C6 glioma (day 25)
Valable et al.7	1.90 ± 0.39	1.79 ± 0.42	2.39 ± 0.85	Rat, RG2 glioma (day 18)
Farrar et al., this study	1.67 ± 0.67	1.64 ± 0.10	2.10± 0.20	Mouse, U87

Abbreviation: rVCI_histo, relative vessel caliber index derived from the histology.

All rVCI are normalized by the rVCI of normal contralateral brain tissue.

^aHistology .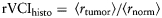

In addition, two models for calculating the MRI VCI have been proposed—a linear dependence on the ΔR2*/ΔR2 ratio¹ and 3/2-power dependence.^5,12,13 Monte Carlo simulations performed by Dennie et al.¹ originally indicated a linear dependence on the ΔR2*/ΔR2 ratio. More recent Monte Carlo simulations by Tropres et al.¹² and Mandeville et al.¹³ and analytical expressions derived by Tropres et al.¹² indicate that a 3/2-power dependence is more appropriate. The original Monte Carlo simulations of Boxerman et al.⁹ did suggest that there is a sublinear dependence of ΔR2 on the susceptibility shift Δχ for sufficiently large Δχ; however, it is unclear at what field strength and contrast agent dose this should occur. Furthermore, the VCI is derived from simulated vascular models that assume randomly oriented and uniformly distributed cylindrical vessels. Recent studies by Pathak et al.^10,11 suggest that such models are inadequate for tumors, which have very abnormal vessel morphology. An in vivo validation method is needed in order to better assess the validity of the MRI-derived VCI models without the confounding factors involved in comparisons with histology.

Intravital optical microscopy (IVM) can be used to provide just such an in vivo validation of the MRI-derived VCI. IVM directly visualizes the blood vessels by multiphoton laser-scanning microscopy with a fluorescent contrast agent (tetramethylrhodamine-labeled dextran). Since IVM and MRI are both in vivo techniques and both image perfused vessels only, discrepancies between MRI- and IVM-derived VCI cannot be attributed to differences in tissue preparation and vessels imaged, as is the case for comparisons with histology data. IVM therefore provides a powerful tool for assessing the validity of the MRI-derived VCI models.

Finally, no comparison of the VCI determined from dynamic susceptibility contrast (DSC) data acquired during injection of small gadolinium (Gd)-based contrast agents,^14–18 such as Gd-diethylenetriamine pentaacetic acid (DTPA), has been made with the VCI calculated from steady-state susceptibility contrast (SSC) measurements of R2 and R2* before and after injection of superparamagnetic iron-oxide nanoparticles (SPION).¹ Although several Gd-based contrast agents are clinically approved, their small size results in leakage of the Gd contrast agent across the disrupted blood-brain barrier (BBB) of most tumors. Such extravasation of contrast agent may compromise the VCI measurement due to R1, R2, and R2* relaxation induced by extravasated contrast agent. Methods have been developed to try to correct for the R1 relaxation enhancement induced by extravasated Gd;^18–22 however, these methods have not been validated nor do they correct for the additional R2 and R2* relaxation induced by high concentrations of extravasated Gd, frequently observed for very leaky tumors. In contrast, the large size of SPION (20–30 nm) typically precludes its leakage across the BBB of most tumors making SSC VCI methods more reliable; however, no SPION agent is currently clinically approved in the United States. Rodent tumor models, in which both DSC and SSC methods can be performed, can thus be used to explore the validity of the DSC method.

Here, we directly compare the MRI VCI models with both IVM and histological measurements of the VCI in a U87 mouse brain tumor model. In addition, the VCI calculated from the SSC SPION-based method is compared with that of the DSC Gd-based method.

Materials and Methods

Mouse Brain Tumor Model

Green fluorescent protein (GFP) expressing U87 (U87-GFP) tumor cells (human glioblastoma) were grown in vitro [Dulbecco's modified Eagle's medium (DMEM) medium with 10% serum, 37°, 20% oxygen, 5% CO₂], harvested, resuspended in serum-free DMEM medium, and used for tumor implantation in athymic (nu/nu genotype) mice. Injections consisted of 3–5 µL of a cell suspension containing 1 × 10⁶ – 5 × 10⁶ cells/µL implanted with a 28-gage microsyringe (10 µL, Hamilton, Reno, NV). Injections were performed with the mouse head fixed in a stereotaxic device (Small Animal Stereotaxic Instrument with Mouse Adaptor, David Kopf Instruments, Tujunga, California). The needle tip was positioned at an angle of 55° and depth of 1.75 mm, and cells were injected slowly over 1 minute. This injection technique ensures the implantation of a sufficient number of cells into the superficial mouse brain cortex. When the resulting tumor reached approximately 3 × 3 mm, it was harvested and divided into small fragments (∼0.5 × 0.5 mm) for implantation in the animals used for the MRI experiments. The tumor fragments were implanted into the mice by dissecting the skin from a small area of the skull, slightly anterior to the bregma and lateral to the midline. A small portion of tumor tissue was implanted with a 30-gage needle in the exposed brain. Mice were imaged 10–14 days following tumor implantation, when tumors typically reached a diameter of 2–3 mm, and again 2–3 days later when tumors were typically 3–4 mm in diameter. Immediately following the last MRI session, the mice were sacrificed and the brains perfusion fixed in 4% paraformaldehyde and OCT embedded. All experiments were approved by the Massachusetts General Hospital Subcommittee on Research Animal Care.

Intravital Optical Microscopy

GFP expressing U87-GFP tumors were implanted in athymic mice, as described above, with previously implanted cranial windows.^23,24 When tumors reached a diameter of 1.8–3.5 mm, animals were anesthetized, and 3–6 locations per animal were imaged using a multiphoton laser-scanning microscope. To visualize the vessels, 150 µL of tetramethylrhodamine-labeled dextran (MW 2 million, 10 mg/mL) was injected intravenously. Stacks of 250-μm depth with 5 µm Z-steps were acquired, and a virtual vascular cast was generated in 3D by custom image analysis software.²⁵ Length-weighted average vessel diameter was calculated based on the virtual cast. A relative VCI was derived from the IVM (rVCI_IVM) data. The rVCI is calculated from the ratio of the average radii of blood vessels in the tumor core to the contralateral cortex as given by

1

Magnetic Resonance Imaging

All experiments were performed on a 9.4-T magnet (Magnex Scientific Ltd, Oxford, UK) equipped with a 60-mm inner diameter gradient coil (Resonance Research, Billerica, Massachusetts) and interfaced with a Bruker MRI console (Bruker Biospin, Billerica, Massachusetts). The gradient coil has a maximum strength of 1500 mT/m and a rise time of 100 µs. Images were acquired using either a home built surface coil or a home built mouse head bird-cage coil. Mice were positioned on a custom made mouse cradle and anesthetized with 1.5% isoflurane in 50/50 O₂/medical air mixture with a total flow rate of 1200 mL/min. Contrast agent injections were performed using an intravenous tail vein catheter.

SSC MRI Measurement of rVCI

R2 and R2* maps were generated from multiecho spin-echo and multiecho gradient-echo images, respectively, using a custom written MATLAB program for voxel-wise fitting of the T2 or T2* relaxation times. Multiecho spin-echo image acquisition parameters were: TE = 10 milliseconds, 10 echoes with 10 millisecond increment, TR = 2.5 seconds, 2 averages, field of view (FOV) = 1.92 cm, matrix = 128 × 128 (in-plane resolution 150 µm), slice thickness = 0.5 mm, 11 image slices. Multiecho gradient-echo image acquisition parameters were: TE = 2.5 milliseconds, 8 echoes with 2.5 millisecond increment, TR = 1.0 seconds, 4 averages, FOV = 1.92 cm, matrix = 128 × 128 (in-plane resolution = 150 µm), slice thickness = 0.5 mm, 11 image slices. Images were acquired both before and after injection of SPION (16 mg Fe/kg bodyweight, r2 = 40/mM/s). The relative cerebral blood volume (rCBV) weighted for large (ΔR2*) and small (ΔR2) blood vessels was determined from the difference between the post- and pre-SPION R2* and R2 maps, respectively. Two models for calculating the MRI VCI have been proposed—a linear dependence on the ΔR2*/ΔR2 ratio¹ and 3/2-power dependence.^4,13 A tumor rVCI was calculated using both linear and 3/2-power models, where the tumor VCI was normalized to the contralateral cortex VCI as given below:

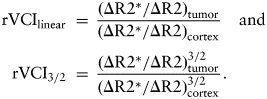2

DSC MRI Measurements of rVCI

A prebolus injection of Gd-DTPA (50 µL of 100 mM Gd-DTPA) was administered (for delayed contrast enhancement (DCE) image acquisition) prior to DSC imaging. The DSC sequence consisted of a dual gradient-echo/spin-echo echo-planar imaging (EPI) sequence. The acquisition parameters were TE_GE/TE_SE = 8.2/16.8 milliseconds, TR = 600 milliseconds, NR = 300, FOV = 2.0 cm, matrix = 80 × 80 (in-plane resolution 250 µm), 0.5 mm slice thickness, 3 image slices. A bolus of 100 µL of 100 mM Gd-DTPA (0.4 mmol/kg bodyweight) was injected ∼30 seconds after commencement of the DSC sequence. Selected regions of interest (ROI) in the tumor core, tumor periphery, and contralateral cortex were analyzed. The time dependence of ΔR2* and ΔR2 were calculated from the signal intensity using the equation given below, S_pre was taken as the average signal intensity prior to contrast agent injection:

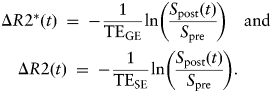3

A gamma variate function was fit to the first bolus passage time points and integrated to determine the rCBV weighted for large (ΔR2*) and small (ΔR2) vessels. The rVCI was calculated using the linear rVCI models as given in Equation (2) above.

Histology Measurement of rVCI

Brains from 4 mice with tumors ranging from 3 to 4 mm in diameter were preserved by perfusion fixation in 4% paraformaldehyde, rinsed in PBS, and infiltrated with a 30% sucrose solution prior to OCT embedding. Ten micrometer-thick cryosections were cut and immunostained with a following antibody against CD31 (Pharmingen, 1:100). Endogenous peroxidase activity was blocked by incubating with 0.03% H₂O₂ in water for 20 min. Primary antibody was applied overnight at 4°C. Secondary antibody (rabbit anti-rat, Jackson ImmunoResearch, 1:200) and DAB (Dako Envision + System Peroxidase) were used for detection following incubation with a polymer from the Envision system (Dako). Positive and negative (where antibody was omitted) controls were included in each batch.

Quantification of the microvessel density (MVD) and diameter was done on at least five fields of confirmed tumor tissue or normal brain parenchyma at ×200 magnification with an average of 100 vessels counted per section using a Canon EOS 40D digital camera. A customized analysis software tool compatible with Image J (http://rsb.info.nih.gov/ij/) was then used to determine the number of vessels, perimeter, the minor axis of best-fitted ellipse (representative of the vessel diameter), and the surface covered by the vascular space. A relative VCI was derived from the histology (rVCI_histo) data. The rVCI is calculated from the ratio of the average radii of blood vessels in the tumor core to the contralateral cortex as given by

4

Comparison of IVM and SSC MRI Measurements of rVCI

Owing to the severe susceptibility artifacts introduced by the optical window required for the IVM studies, the IVM and MRI rVCI could not be determined from the same group of mice. Instead, rVCI measurements were made from separate tumor size matched groups of mice. A total of 40 mice were imaged by IVM, all with tumors diameters between 1.8 and 3.5 mm. For the MRI studies, a total of 7 mice met the 1.8–3.5-mm tumor diameter criteria compared with IVM. The IVM rVCI was compared with both the linear and 3/2-power MRI rVCI models using an analysis of variance (ANOVA) calculation, and statistical significance was defined by a P-value of <.05.

Comparison of Histology and SSC MRI Measurements of rVCI

MRI and histology rVCI were obtained from a group (n = 4) of mice with tumors ranging from 3 to 4 mm in diameter. Immediately following MRI data acquisition, mouse brains were perfusion fixed and OCT embedded for histological analysis as described earlier. The histology rVCI was compared with both the linear and 3/2-power MRI rVCI models using an ANOVA calculation and statistical significance was defined by a P-value of <.05.

The linear and 3/2-power MRI rVCI models and the histology-derived rVCIs that have been reported previously in the literature were also compared. Since the explicit form of the MRI-derived VCI equation used in the different papers is not consistent, we have converted all VCI to a consistent form that neglects diffusion and normalizes the tumor VCI by the contralateral, normal brain tissue VCI.

Comparison of DSC and SSC Measurements of rVCI

DSC and SSC measurements were performed sequentially in the same animal for 2 animals with tumor diameters of 1.5 and 3.2 mm. DSC data were acquired and rVCI calculated as discussed above. Approximately 2 hours after Gd-DTPA injection, to allow time for Gd-DTPA clearance, animals were injected with SPION (16 mg Fe/kg bodyweight, r2 = 40/mM/s). R2 and R2* maps were acquired immediately before and after SPION injection and rVCI were calculated as described in detail above.

Results

Comparison of SSC MRI and IVM Measurements of Tumor rVCI

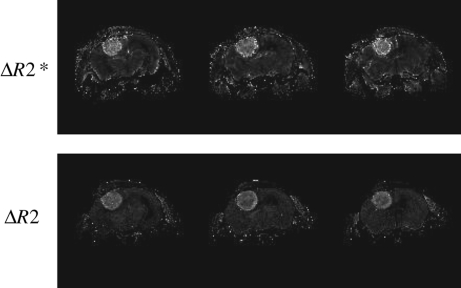
Figure 1 shows a representative rCBV map acquired from a U87-GFP mouse brain tumor model. The rCBV map is generated from the difference between R2 (or R2*) maps acquired pre- and postinjection of SPION. A significantly increased blood volume, weighted for both small (ΔR2) and large (ΔR2*) vessels, is evident in the tumor.

Fig. 1.

Three image slices from representative rCBV maps weighted for large (ΔR2*, top) and small (ΔR2, bottom) vessels. Maps were generated from the difference in R2 and R2*, respectively, before and after injection of SPION (16 mg Fe/kg bodyweight, r2 = 40/mM/s).

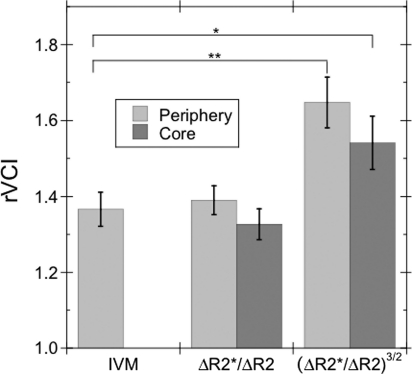
MRI and IVM rVCI were determined from 2 different groups of mice (MRI: n = 7; IVM: n = 40) with size-matched tumors. An MRI tumor rVCI was calculated for both the tumor periphery and tumor core using the 3/2-power model of Tropres et al.¹² and the linear model of Dennie et al.¹ [Equation (2)]. For the linear rVCI model, the rVCI (±SEM) for the tumor core and periphery was 1.33 ± 0.04 and 1.39 ± 0.04, respectively. For the 3/2-power model, the average rVCI for tumor core and periphery was 1.54 ± 0.07 and 1.65 ± 0.07, respectively.

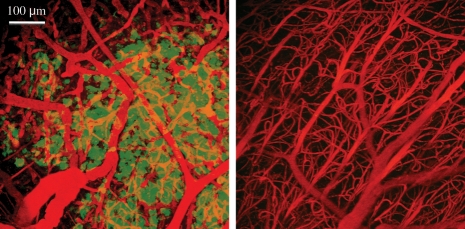
Analysis of multiphoton images from tumor and normal tissue (Fig. 2) showed an average blood vessel diameter of 9.50 ± 0.04 µm for tumor tissue and 6.95 ± 0.36 µm for normal contralateral cortex tissue. These measurements corresponded to a tumor rVCI_IVM of 1.37 ± 0.04. The IVM rVCI was in good agreement (Fig. 3) with the linear rVCI model for both the tumor core (rVCI_linear^core = 1.33 ± 0.04, P = .61) and periphery (rVCI_linear^periphery = 1.39 ± 0.04, P = .75) with no statistically significant differences. In contrast, there was a statistically significant difference between the IVM and the 3/2-power MRI model for both the tumor core (rVCI_3/2^core = 1.54 ± 0.07, P = .04) and periphery (rVCI_3/2^periphery = 1.65 ± 0.07, P < .01).

Fig. 2.

Representative IVM images of a U87-GFP mouse brain. Images of both GFP expressing tumor (left) and normal (right) tissue are shown. Blood vessels are indicated in red and GFP expressing tumor tissue in green.

Fig. 3.

Comparison of the average rVCI (±SEM) calculated from IVM images with that calculated for the tumor periphery and core from the MRI ΔR2* and ΔR2 maps using linear and 3/2-power rVCI models. An increased average vessel caliber, compared with normal contralateral cortex tissue, is observed in both the tumor periphery and core: rVCI_linear^core = 1.33 ± 0.04, rVCI_linear^periphery = 1.39 ± 0.04, rVCI_3/2^core = 1.54 ± 0.07, and rVCI_3/2^periphery = 1.65 ± 0.07 (n = 7). No statistically significant difference is observed between the IVM and linear MRI rVCI for either tumor core or periphery. A statistically significant difference is observed between the IVM (rVCI_IVM = 1.37 ± 0.04, n = 40) and 3/2-power MRI rVCI for both tumor core (*P < 0.05) and periphery (**P < 0.01).

Comparison of SSC MRI and Histology Measurements of Tumor rVCI

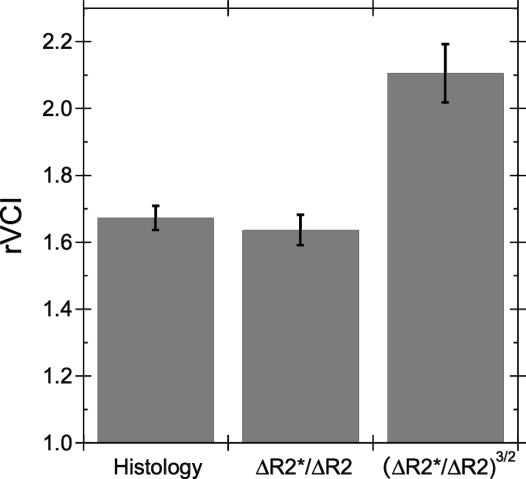
MRI and histology rVCI were determined for a group (n = 4) of mice with tumors ranging from 3 to 4 mm in diameter. An average MRI rVCI_linear of 1.64 ± 0.14 was obtained for the linear model, whereas a significantly (P < .01) larger rVCI_3/2 of 2.10 ± 0.51 was calculated for the 3/2-power model. Average vessel diameters, determined from CD31 stained images, for tumor and contralateral cortex tissue were 6.43 ± 0.13 and 3.86 ± 0.05 µm, respectively. A histology rVCI of 1.67 ± 0.03 was derived from these average vessel diameters.

Figure 4 shows a comparison of the MRI-derived rVCI and the histology rVCI. The linear rVCI model (rVCI_linear = 1.64 ± 0.14) was in better agreement with the histology rVCI (rVCI_histo = 1.67 ± 0.03) than the 3/2-power model (rVCI_3/2 = 2.10 ± 0.51); however, neither rVCI model had a statistically significant difference from the histology rVCI. Although we found good agreement between the histology rVCI and linear rVCI model, the agreement in the past literature has been more variable. In Table 1, the MRI and histology-derived rVCIs reported in the literature are compared. In most cases, the linear rVCI is in better agreement with the histology rVCI than the 3/2-power model; however, the quantitative agreement is highly variable for both MRI rVCI models and quite poor in several cases.

Fig. 4.

Comparison of the average (n = 4) histology rVCI with the linear and 3/2-power MRI rVCI models. The average rVCI (±SEM) are, respectively, rVCI_histo = 1.67 ± 0.04, rVCI_linear = 1.64 ± 0.05, and rVCI_3/2 = 2.10 ± 0.09.

Comparison of DSC and SSC MRI Measurements of Tumor rVCI

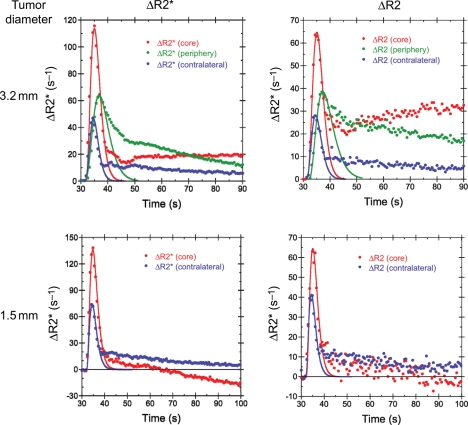
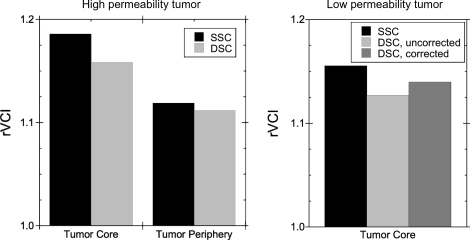
Both DSC and SSC rVCI methods were performed sequentially in the same mice (n = 2), enabling the accuracy of the DSC rVCI to be examined. Shown in Figure 5 are the DSC ΔR2* and ΔR2 temporal profiles acquired during injection of 100 µL of 100 mM Gd-DTPA (∼0.4 mmol/kg) for 2 different mice—one with a large 3.2-mm diameter tumor and one with a small 1.5-mm diameter tumor. Gamma variate functions (solid lines) were fit to the first pass bolus time points for gradient- and spin-echo DSC curves and integrated to determine ΔR2* and ΔR2, respectively. The rVCI_DSC were then calculated using the linear rVCI model for the tumor core and periphery. Figure 6 shows comparisons of the DSC determined rVCI with that determined from steady-state measurements of R2 and R2* before and after injection of SPION for both large and small diameter tumor models. For the large diameter tumor, excellent agreement was observed between the DSC and SSC methods for both the tumor core (rVCI_SSC = 1.19, rVCI_DSC = 1.16) and tumor periphery (rVCI_DSC = 1.11, rVCI_SSC = 1.12). Similarly good agreement was observed for the small diameter tumor for the tumor core (rVCI_SSC = 1.16, rVCI_SSC = 1.13). Correction for Gd-DTPA leakage, using the method of Schmainda and coworkers,^18–22 was performed for the small diameter tumor and resulted in a slightly larger rVCI (rVCI_DSC = 1.14) and improved agreement with the steady-state rVCI. The leakage correction algorithm, however, was unable to correct for the extensive leakage of Gd-DTPA in the large diameter tumor.

Fig. 5.

Temporal ΔR2* (left) and ΔR2 (right) profiles, acquired during injection of 0.4 mmol Gd-DTPA/kg bodyweight, in the tumor core (red), tumor periphery (green), and contralateral cortex (blue) for a mouse with a large 3.2-mm diameter tumor (top) and a mouse with a small 1.5-mm diameter tumor (bottom). The solid lines are the respective γ variate fits of the DSC first pass bolus time points.

Fig. 6.

Comparison of the rVCI for SSC SPION and DSC Gd-DTPA methods for both a large highly permeable tumor (left) and a small moderately permeable tumor (right). Excellent agreement is observed between the DSC and SSC methods for both tumors.

Discussion

Angiogenesis plays a critical role in tumor growth. Angiogenesis driven tumor growth is associated with increased vessel density and caliber and a disordered and tortuous vasculature structure.^26–28 Characteristics of the tumor vasculature, such as MVD and blood volume, have been shown to be major factors in predicting tumor grade, aggressiveness, and patient survival.^22,29–32 MRI is playing an increasingly important role in the in vivo characterization of tumor vascularization. MRI measurements of tumor blood volume have been shown to strongly correlate with glioma tumor grade.^18,20,22 In addition, biomarkers of vasogenic brain edema have been shown to correlate with glioblastoma patient survival.⁶ More recently, the tumor VCI has been shown to be an important biomarker for assessing tumor angiogenesis and response to antiangiogenic therapies.⁶ VCI measurements are gaining widespread use not only in animal model studies,^1,4,7 but also in clinical studies.^5,6,18,20

Although past animal model studies have shown a strong correlation between the VCI and the average vessel radius determined from histological data,^4,7 good quantitative agreement has been lacking (Table 1). In addition, several equations have been proposed for modeling the VCI, including a linear dependence¹ on the ΔR2*/ΔR2 ratio and a 3/2-power dependence.^5,12 In this study, we found that the histological rVCI (1.67 ± 0.04) is in better agreement with the linear (1.64 ± 0.05) than the 3/2-power (2.10 ± 0.09) rVCI model (Fig. 4); however, the differences are not statistically significant. Pooling data from the literature, we find highly variable quantitative agreement between the histology rVCI and both MRI rVCI models (Table 1). The large number of potential factors that may contribute to the discrepancy between histology and MRI rVCI makes validation of the VCI model difficult. An in vivo validation method is needed in order to better assess the validity of the vascular models used to derive the MRI rVCI without the confounding factors involved in comparisons with histology.

IVM has been used in this study to provide just such an in vivo validation of the MRI rVCI model. Comparison of the IVM and MRI rVCI is not confounded by either the tissue distortions associated with histological specimens or differences in the vessels imaged. Here, the IVM-derived rVCI was found to be in good agreement with the linear rVCI model for both tumor core and periphery (Fig. 3). Since the IVM method was limited to imaging only the outer 250–300 µm of the tumor, it is more representative of the tumor periphery, consistent with the improved agreement observed between the IVM rVCI and the MRI tumor periphery rVCI. In contrast, there was a statistically significant difference between the IVM and the 3/2-power rVCI model for both tumor core and periphery. The slightly increased rVCI observed in the tumor periphery relative to the core, although not statistically significant, is consistent with the increased vessel diameter observed in the tumor periphery of histology images reported in a previous study using the same mouse model.³³ These results therefore suggest that the liner rVCI model is a better quantitative predictor of the average vessel radius than the 3/2-power model.

Although the linear rVCI model was empirically shown to provide excellent agreement with IVM, more work is required to explain why. The original Monte Carlo simulations by Boxerman et al.⁹ and Dennie et al.¹ suggested that the vessel radius was proportional to the ΔR2*/ΔR2 ratio. However, for large contrast agent induced susceptibility changes (Δχ), Boxerman et al.⁹ did predict a sublinear dependence of ΔR2 on Δχ. Both the VCI derived from more recent Monte Carlo simulations^12,13 and analytical expressions^5,12 suggested that the VCI is best modeled with a 3/2-power dependence on the ΔR2*/ΔR2 ratio. Although the rVCI models considered in this study did not include a square-root dependence on the water apparent diffusion coefficient (ADC) as proposed previously,^5,12 the inclusion of an ADC term in the 3/2-power rVCI equation would only cause a further increased overestimation of the rVCI since the tumor ADC is significantly greater than that of normal tissue (ADC_tumor = 836 µm²/s and ADC_norm = 575 µm²/s for the U87-GFP mouse tumor model).

The discrepancy between the empirical data and the Monte Carlo simulations may be due to an inadequacy of the vascular model used in the simulations. In particular, the vascular network is modeled as a collection of randomly oriented and uniformly distributed perfect cylinders.^9,34 However, recent studies by Pathak et al.^10,11 suggest that such vascular models are inadequate for tumors, which have very abnormal vascular morphology. Since the susceptibility contrast is quite sensitive to the size, shape, and orientation of the perturbing blood vessels, more accurate models of the amorphous, tortuous, and chaotic tumor vasculature may be required.¹⁰

Although the rVCI can clearly be a very useful biomarker of vessel caliber, the SSC methods discussed above for determining the rVCI require contrast agents with very high relaxivity, currently achieved only with SPION. However, no SPION is currently clinically approved in the United States. Instead a DSC approach is used clinically, where the signal changes induced by the first pass of a Gd-based contrast agent are observed.^14–18 However, the small size of the Gd-based contrast agents typically used results in their leakage across the disrupted BBB of most tumors.^18–22 Such extravasation of contrast agent distorts the DSC time curves due to R1, R2, and R2* relaxation induced by the extravasated contrast agent. This is demonstrated quite dramatically in Fig. 5 for 2 cases, one with a highly permeable tumor and a second with a moderately permeable tumor. For the highly permeable tumor, the tumor core ΔR2* and ΔR2 slowly increase after the first bolus passage (Fig. 5, top row). Given the relatively low relaxivity of Gd-DTPA (r2 = 4.8/mM/s at 4.7 T),³⁵ the increased ΔR2* and ΔR2 must be due to extravasation of high concentrations of contrast agent. The accumulation of Gd-DTPA in the tumor core, but not the periphery, is likely due to an increased extravascular extracellular space and decreased vascularization with respect to the periphery, which acts to slow down clearance of Gd-DTPA from the tumor core. In addition, the peak ΔR2 and ΔR2* are delayed in both the tumor core and periphery with respect to that of contralateral tissue. The convoluted and tortuous vessels of the tumor likely lead to a slow down in the bolus passage through the tumor. This slower bolus passage is also reflected in the increased width of the bolus passage in the tumor periphery, which is significantly broader than that observed in normal tissue or the tumor core.

For the moderately permeable tumor, the tumor ΔR2* and ΔR2 become negative at late times due to R1 relaxation enhancement of the tumor caused by the extravasated contrast agent (Fig. 5, bottom row). The concentration of extravasated Gd-DTPA is low enough, however, that only an R1 enhancement effect is seen and not an additional R2 or R2* effect, as observed for the large tumor. The relatively low concentration of extravasated Gd-DTPA therefore suggests that the small tumor has a significantly reduced vessel permeability compared with the large tumor.

The extravasation correction algorithm developed previously by Schmainda and coworkers^18–22 was used to try to correct for the relaxation effects induced by extravasated contrast agent; however, the correction algorithm was unable to correct for the leakage of contrast agent in the highly permeable tumor where the extravasated contrast agent contributes significantly to R2 and R2* relaxation. Efforts are currently underway by a number of groups to extend the correction algorithm to include correction of R2 and R2* contributions from the extravasated contrast agent. However, from the DSC time curves, it is evident that the extravasation is relatively slow with respect to the first bolus passage. We therefore investigated whether a simple integration of gamma variate fits of the first pass bolus time points would provide adequate estimates of the rVCI. Excellent agreement is observed between the DSC and SSC rVCI measured sequentially in the same animals for this preliminary data set (Fig. 6), consistent with recent preliminary results from others showing a strong correlation between DSC and SSC methods.³⁶ This suggests that integration of gamma variate fits of the first pass DSC time points can provide accurate measurements of the rVCI despite extensive leakage of contrast agent.

Conclusions

A rVCI model with a linear dependence on the ΔR2*/ΔR2 ratio was found empirically to provide excellent quantitative agreement with the IVM rVCI determined from a separate tumor size matched group of mice. The IVM data provide an important validation of the MRI VCI that is independent of the confounding factors associated with histological tissue preparation. More studies are required to improve the vascular models used in Monte Carlo simulations to explain why the simple ΔR2*/ΔR2 ratio provides the best quantitative agreement. In addition, the rVCI determined for a small group of mice (n = 2) from DSC studies employing Gd-DTPA are found to be in excellent agreement with the rVCI determined from SSC measurement methods employing SPION in both highly and moderately permeable brain tumors. These preliminary findings suggest that a simple fitting of the first pass bolus DSC time points can provide an accurate measure of the rVCI, despite extravasation of Gd-DTPA due to the disrupted BBB typical of most brain tumors.

Conflict of interest statement. AGS and RKJ are consultants for AstraZenaca Pharmaceuticals.

Funding

This research was supported by the National Institutes of Health (P41-RR14075, P01-CA80124, R01-CA115767) and by gifts from AstraZeneca Pharmaceuticals. CTF gratefully acknowledges support from the National Cancer Institute (T32-CA009502-19) and the National Institute on Aging (K25-AG029415). WSK gratefully acknowledges support from the Susan G. Komen foundation. CDL gratefully acknowledges support from the Harboe Foundation, the A.P. Møller Foundation, and the Dagmar-Marshall Foundation.