Sulfur K-edge XAS of W^V=O vs. Mo^V=O Bis(dithiolene) Complexes: Contributions of Relativistic Effects to Electronic Structure and Reactivity of Tungsten Enzymes

Abstract

Molybdenum- or tungsten-containing enzymes catalyze oxygen atom transfer reactions involved in carbon, sulfur, or nitrogen metabolism. It has been observed that reduction potentials and oxygen atom transfer rates are different for W relative to Mo enzymes and the isostructural Mo/W complexes. Sulfur K-edge X-ray absorption spectroscopy (XAS) and density functional theory (DFT) calculations on [Mo^VO(bdt)₂]⁻ and [W^VO(bdt)₂]⁻, where bdt = benzene-1,2-dithiolate(2−), have been used to determine that the energies of the half-filled redox-active orbital, and thus the reduction potentials and M=O bond strengths, are different for these complexes due to relativistic effects in the W sites.

1 Introduction

Enzymes containing molybdenum or tungsten appear to be present in all organisms, ranging from ancient bacteria to humans, although only thermophilic bacteria and hyperthermophilic archaea utilize tungsten [1–4]. These enzymes catalyze a wide range of processes important in carbon, nitrogen, and sulfur metabolism. With the exception of the nitrogenases, these enzymes mostly catalyze oxygen atom transfer and are often referred to as oxotransferases.

The molybdenum oxotransferases have been divided into three families based on their protein sequences and the structures of their oxidized active sites: the DMSO reductase, sulfite oxidase, and xanthine oxidase families [1]. The tungsten oxotransferases may also be divided into three families, although this classification is based on biochemical properties rather than active site structures: aldehyde oxidoreductase, formate dehydrogenase, and acetylene hydratase [2]. Each of these enzymes contains at least one pyranopterindithiolene ligand, which is of particular interest because of its dithiolene-like chelate ring formation. Although dithiolene ligands have been shown to have non-innocent bonding interactions with metals in higher oxidation states of certain complexes [5], they appear to function as classical ene-1,2-ditholate dianions in enzyme sites and synthetic site analogues.

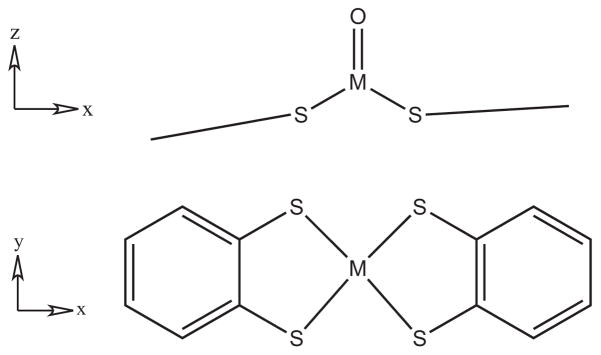
Molybdenum and tungsten mono-oxo bis(dithiolene) complexes that model the active site structures of the enzymes containing two pyranopterindithiolene cofactors (i.e. the DMSOr family and every tungsten enzyme) have been synthesized [6]. Among them are isostructural [Mo^VO(bdt)₂]⁻ and [W^VO(bdt)₂]⁻ [7, 8]. These complexes have approximately C_2v symmetry with the M=O bond along the C₂ axis (z) and a mirror plane (xz) bisecting each dithiolene ligand (Fig. 1). The M^V redox state is not directly involved in the event of oxygen atom transfer, but is involved as the enzymes and models cycle between M^IV (d²) and M^VI (d⁰) formal oxidation states on the metal center. In this investigation, the complexes provide models that probe possible differences of the redox active orbitals of molybdenum and tungsten oxotransferases.

Figure 1.

Diagram illustrating the approximate C_2v symmetry of the M^VO(bdt)₂ (M = Mo, W) complexes.

Two general trends are found without exception for molybdenum and tungsten enzymes and complexes. First, E^o_W < E^o_Mo for strictly analogous redox couples, with potential differences decreasing as bond covalency increases [6, 9–14]. Second, in Mo/W enzymes and Mo/W isostructural complexes, oxo transfer from substrate to metal (M^IV → M^VI) is faster with tungsten [6, 9, 15–16]. These trends suggest a fundamental difference between the reactivity of molybdenum and tungsten centers. Johnson, et al. [2] have suggested that these differences explain why organisms are unable to catalyze low-potential reactions using molybdenum enzymes.

In any discussion comparing a second-row transition metal with a third-row transition metal, it is important to consider relativistic effects in the latter. The general premise behind these effects is that as the atomic number increases, the speed of core electrons approaches a relativistic limit. This leads to a mass increase

$$m=\frac{m_0}{\sqrt{1-{(v/c)}^2}}$$

where m₀ is the rest mass and ν is the speed of the electron, which causes the effective Bohr radius

$$a_0=\frac{4\pi {\epsilon }_0\hslash }{m{e}^2}$$

to decrease for core s and p electrons (i.e. a radial contraction) [17]. This has two main effects on the electronic structure of a transition metal. The valence s (and p) electrons also experience radial contraction to remain orthonormal to the contracted core s electrons, and thus are stabilized in energy, while the valence d electrons experience better shielding from the nucleus, resulting in a radial expansion and energy destabilization. Relativistic effects also cause shorter bond lengths, although this is a parallel effect and not the direct result of core radial contractions [17].

Ligand K-edge X-ray absorption spectroscopy (XAS) is a direct probe of metal-ligand bonding interactions [18]. The excitation of ligand 1s orbitals to unoccupied metal-based molecular orbitals (Ψ^*) results in pre-edge features. The energies of these pre-edges have three contributions: ligand Z_eff, metal Z_eff, and ligand field effects [19]. Since, as described above, metal Z_eff can be influenced by relativistic contraction of core orbitals, ligand K-edge XAS provides a unique opportunity to study relativistic effects in W vs. Mo-oxo bis(dithiolene) complexes.

2 Experimental

A. Sample Preparation

The complexes (Et₄N)[Mo^VO(bdt)₂] and (PPh₄)[W^VO(bdt)₂] were prepared as described previously [7, 8].

B. X-ray Absorption Measurements and Data Analysis

S K-edge spectra were measured at the Stanford Synchrotron Radiation Laboratory under ring conditions of 3 GeV and 80–100 mA. The measurements utilized the 54-pole wiggler beam line 6-2 operating in high field mode of 10 kG with a Ni-coated harmonic rejection mirror and a fully tuned Si(111) double crystal monochromator. Details of the beam line optimization for S K-edge studies were published elsewhere [20]. The solid samples were ground in an inert atmospheres (N₂) dry glovebox at less than 1 ppm O₂ level and dispersed as thinly as possible on a Mylar tape to minimize the possibility of fluorescence saturation effects. A 6 μm thick, sulfur-free polypropylene window was used to prevent sample exposure to air upon mounting into the sample chamber. The photon energy was calibrated to the maximum of the first pre-edge feature of Na₂S₂O₃·5H₂O at 2472.02 eV. Data scans were averaged using MAVE, which is part of the EXAFSPAK suite of programs [21], and a smooth background of a second-order polynomial was subtracted from the average spectrum. Normalization of the data was accomplished by fitting the post-edge region with a flat first-order polynomial and scaling the data such that the value of this fit function is 1.0 at 2490 eV. In the case of the data for (Et₄N)[Mo^VO(bdt)₂], the post-edge region was above the Mo L₃-edge so it was scaled such that the region between the S K-edge and the Mo L₃-edge had the same intensity as the corresponding region in the data for (PPh₄)[W^VO(bdt)₂]. Fits to the pre-edges were modeled by pseudo-Voigt peak shapes using the program EDG_FIT [21] with a fixed 1:1 ratio of Lorentzian to Gaussian contributions. The reported intensity values are based on the average of several good fits. Error in the total pre-edge peak areas can range from ~2% for well-resolved pre-edges to ~10% for unresolved pre-edges. In addition, normalization procedures can introduce ~3% error in the total pre-edge peak areas. Conversion between peak area and sulfur covalency was accomplished using the equation

$$D_0=\frac{N}{12}{\alpha }^{2}I(S)$$

where D₀ is the peak area, N is the number of holes in the corresponding molecular orbital, α² is the sulfur covalency, and I(S) is the transition dipole integral as determined using a previously described method [22].

C. Electronic Structure Calculations

Density functional calculations were performed using the Amsterdam Density Functional 2004.01 [23–25] and Gaussian 03 [26] packages.

ADF calculations were performed using the Becke GGA exchange [27] and the Perdew 1986 nonlocal correlation [28] functionals. Scalar and spin-orbit relativistic effects were included using the Zero Order Regular Approximation (ZORA). For non-relativistic calculations, the TZP basis set [25] was used for all atoms, which is double-ζ and triple-ζ quality for core and valence functions, respectively, with a frozen core up to and including the nd shell for the metal (n = 3 for Mo, n = 4 for W). For relativistic calculations, the all-electron ZORA-adapted TZP basis set [25] was used for all atoms, which is double-ζ and triple-ζ quality for core and valence functions, respectively.

Gaussian calculations were performed using either the pure functional BP86 (Becke GGA exchange with Perdew 1986 non-local correlation) or the hybrid functional B3LYP (Becke’s three parameter functional [29] with LYP correlation). The CEP-121G basis set [30], which is triple-ζ quality for valence functions with an effective core potential (ECP) for the core functions, was used for the metal centers. The 6-311G(d) basis set was used for the sulfur and oxygen atoms and the 6-31G(d) basis set was used for the carbon and hydrogen atoms. Calculations with the SDD basis set (triple-ζ quality with an effective core potential) [31] for the metal and the 6-311G(d) for the remaining atoms were also performed, but gave similar results as the calculations with the CEP-121G basis set.

Molecular orbital compositions were analyzed using Mulliken Population Analysis [32] as implemented in PyMOlyze [33].

3 Results

3.1 S K-edge XAS

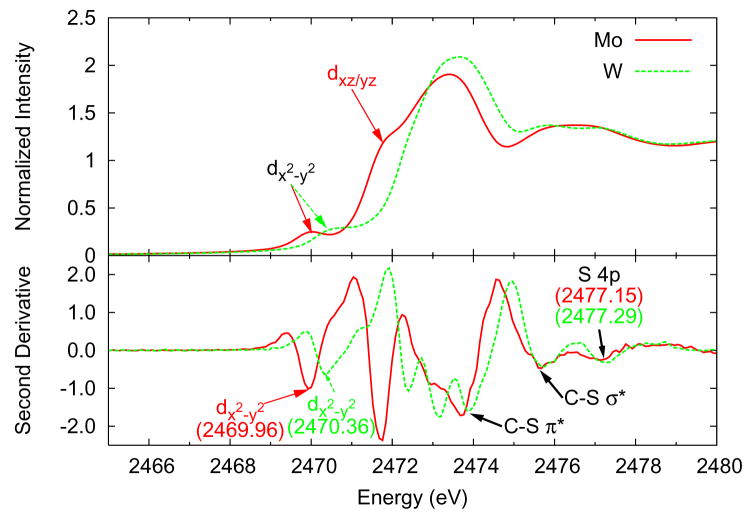
Fig. 2 shows the pre-edge (2469–2473 eV) and rising edge (2473–2480 eV) regions of S K-edge spectra of the Mo^V=O and W^V=O bis(dithiolene) complexes. These complexes have approximately C_2v symmetry which allows the spectra to be interpreted using the following qualitative bonding description. The d_x2−y2 orbital is essentially non-bonding, although it gains some intensity through mixing with S orbitals because of the bending distortion of the dithiolene ligand (Fig. 1), so transitions to it should be lowest in energy and appear as a small pre-edge feature. This pre-edge is resolved in both spectra at ~2470 eV (arrows in Fig. 2). The d_xz and d_yz orbitals have π bonds with the oxo and pseudo-σ bonds to the in-plane S orbitals of the dithiolene ligands. These orbitals are nearly degenerate because the S-Mo-S angle of the dithiolene chelate ring is ~85°, so transitions to these orbitals are not resolved and appear as a single pre-edge. This feature is visible as a shoulder only in the molybdenum spectrum at ~2472 eV (arrows in Fig. 2). The d_xy orbital has σ bonds to the in-plane S orbitals of the dithiolene ligand and the d_z2 orbital has σ bonds to the oxo and π bonds to the out-of-plane S orbitals of dithiolene ligands. The S in-plane interaction with the d_xy orbital is of comparable strength to that of the interaction of the oxo and out-of-plane S orbitals with the d_z2 orbital (see Table S1), and thus are nearly degenerate so transitions to these orbitals would not be resolved. Experimentally, this pre-edge feature is not resolved from the edge but appear as minima in the second derivative (bottom) at ~2473 eV. The remaining minima at ~2474, ~2476, and ~2477 eV correspond to S 1s → C-S π^*, S 1s → C-S σ ^*, and S 1s → S 4p transitions, respectively [5].

Figure 2.

Sulfur K-edge spectra and second derivatives of (Et₄N)[Mo^VO(bdt)₂] (solid red line) and (PPh₄)[W^VO(bdt)₂] (dashed green line).

All of the pre-edge features (minima in the 2469–2473 eV region of the second derivative) of the W complex are ~0.4–0.7 eV higher in energy than the corresponding features of the Mo complex which indicates that d orbitals have been destabilized in the W complex. As mentioned in the Introduction, this energy difference is the result of three possible contributions (i.e. ligand Z_eff, metal Z_eff, and ligand field effects). The features due to transitions to sulfur-based orbitals (minima in the 2474–2477 eV region of the second derivative) of the W complex are ~0.1–0.2 eV higher in energy than the corresponding features of the Mo complex. This suggests that the sulfur atoms of the tungsten complex are slightly more positive than those in the molybdenum complex. In particular, the energy of the S 1s → d_x2−y2 transition in the W complex is, based on the second derivative, 0.40 eV higher than that of the Mo complex, while the energy of the S 1s → S 4p transition is 0.14 eV higher (Fig. 2 bottom at ~2477 eV). The remaining 0.26 eV energy difference of the d_x2−y2 orbitals is therefore due to either the ligand field or the metal Z_eff. Density functional calculations (in Section 3.2) were used to determine which effect is the primary contribution to this difference.

Pre-edge positions, intensities, and experimental sulfur covalencies are presented in Table 1 (see Supplementary Figs. S1–S4 for representative peak fits). There are small differences in sulfur character between the molybdenum and tungsten complexes with the tungsten complex having slightly more total sulfur character (105% S and 112% S, respectively).

Table 1.

Averages of pre-edge energies (E), unfilled metal-based orbital (Ψ^*), intensities (D₀), number of holes per expected orbital (N), transition dipole integral (I(S)), and sulfur covalencies (α², %) for multiple reasonable fits.

	Ψ*	E (eV)	D0	N	I(S)	α2
(Et4N)[MoVO(bdt)2]	dx2−y2	2469.97	0.1411	1	15.01	11
	dxz/dyz	2471.83	1.0434	2		42
	dxy/dz2	2472.79	1.2908	2		52
(PPh4)[WVO(bdt)2]	dx2−y2	2470.68	0.2414	1	15.30	19
	dxz/dyz	2472.53	0.9433	2		37
	dxy/dz2	2473.23	1.4286	2		56

3.2 Density Functional Calculations

Density functional calculations were used to determine the contribution of relativistic effects to the energy of the d levels in the Mo^V=O and W^V=O bis(dithiolene) complexes. Table 2 shows key bond lengths for the crystal structure and the optimized structures without and with relativistic effects. In the crystal structure, the M=O bond length is 0.02 Å longer for the tungsten complex, while the M-S bond lengths are 0.01 Å shorter. The latter trend is not observed in the optimized structures without relativistic effects (the M-S bond lengths are 0.02 Å longer in the tungsten complex), but is reproduced once relativistic effects are included. It should be noted that the experimental and calculated bond lengths of the molybdenum and tungsten complexes are not significantly different, and thus alone do not conclusively evaluate relativistic contributions to bonding.

Table 2.

Key experimental and geometry optimized (ADF with BP86) bond lengths for [Mo^VO(bdt)₂]⁻ and [W^VO(bdt)₂]⁻.

	Crystal Structure		Non-relativistic		Relativistic
	Mo	W	Mo	W	Mo	W
M=O (Å)	1.67a	1.69b	1.72	1.75	1.71	1.72
M–S (ave, Å)	2.38a	2.37b	2.43	2.45	2.42	2.41

^aReference [29].

^bReference [8].

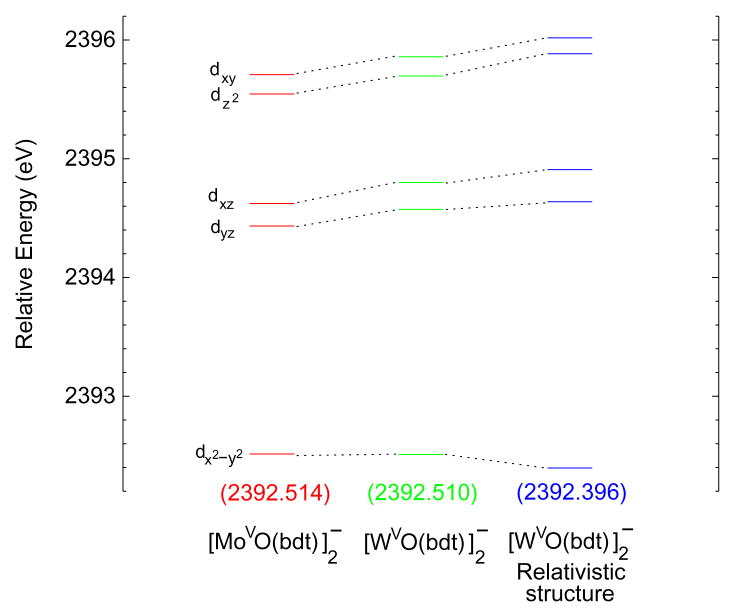
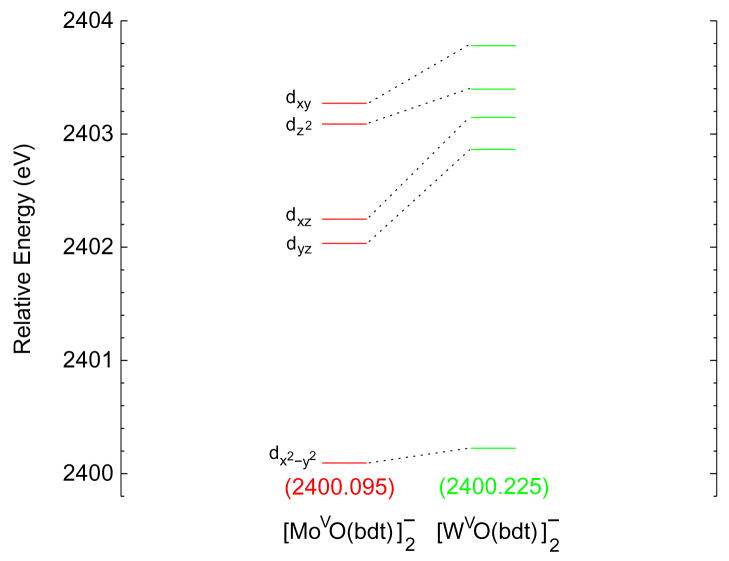
Fig. 3 shows the energy level diagram for the unoccupied β metal-based orbitals from calculations without relativistic effects included in the molecular Hamiltonian. The d_x2−y2 orbital of the W complex at the non-relativistic optimized structure (green, middle) has the same energy as the d_x2−y2 orbital of the Mo complex (red, left). This level for the W complex at the relativistic optimized structure but without the relativistic terms included in the molecular Hamiltonian (blue, right) is 0.12 eV lower in energy than in the Mo complex. These results indicate that calculations without relativistic effects included in the Hamiltonian do not reproduce the trend observed for the energies of the first pre-edge transitions (Fig. 2). Fig. 4 shows an energy level diagram for the unoccupied beta metal-based orbitals obtained from the relativistic calculations. The d_x2−y2 orbital of the W complex (green, right) is now 0.13 eV more destabilized than that of the Mo complex (red, left). These results do reproduce the trend observed for the energies of the first pre-edges (Fig. 2), although the calculated difference (which does not include final state relaxation) is smaller than observed in the data. This trend is also reproduced in calculations with spin-orbit relativistic effects also included in the Hamiltonian (Fig. S3, Supplementary data).

Figure 3.

Energy level diagram of the five β metal d orbitals for the non-relativistic ADF/BP86 calculations of molybdenum (red, left) and tungsten (green, middle) complexes at the non-relativistic optimized structures and the tungsten complex (blue, right) at the relativistic optimized structure. Energies are relative to those of the S 1s orbitals.

Figure 4.

Energy level diagram of the five β metal d orbitals for the relativistic ADF/BP86 calculations of the molybdenum (red, left) and the tungsten (green, right) complexes at the relativistic optimized structures. Energies are relative to those of the S 1s orbitals.

Table 3 compares the calculated ground state sulfur 3p covalencies of the unoccupied β metal d orbitals of [Mo^VO(bdt)₂]⁻ and [W^VO(bdt)₂]⁻. The total amount of sulfur character is the same for the molybdenum and tungsten complexes with both non-relativistic and relativistic calculations (first four columns); however; both calculations for molybdenum are slightly more covalent (~6% total S 3p) than that determined by experiment (Table 1). Additionally, the S 3p character in the molybdenum d_x2−y2 orbital is overestimated by ~10%. A more detailed presentation of the minor differences among the β metal orbitals of the molybdenum and tungsten complexes can be found in Supplimentary Table S1.

Table 3.

Calculated ground state sulfur 3p character (%) of the unoccupied β metal d orbitals of [Mo^VO(bdt)₂]⁻ and [W^VO(bdt)₂]⁻ using ADF/BP86 (first four columns) and Gaussian (last four columns).

	Non-relativistic BP86		Relativistic BP86		Non-relativistic BP86		Non-relativistic B3LYP
	Mo	W	Mo	W	Mo	W	Mo	W
dx2−y2	21	21	20	14	20	17	18	13
dxz/dyz	32	31	30	36	29	25	29	24
dz2/dxy	59	62	63	63	58	58	55	57
Total	112	113	113	112	107	100	102	94

Since it has been found that the pure functional BP86 can give an electronic structure description that is too covalent [34], both complexes were calculated using a hybrid functional (B3LYP). Table 3 shows the effect a hybrid functional has on the covalency of the molybdenum and tungsten complexes. Calculations using BP86 were repeated in Gaussian since ADF and Gaussian use fundamentally different basis functions (i.e. ADF uses Slater-type orbitals and Gaussian uses Gaussian-type orbitals). The trends for the Gaussian BP86 calculation are about the same as the relativistic ADF BP86 calculation, although in both molybdenum and tungsten complexes, there is slightly less S 3p character in the d_xz/d_yz orbitals. The hybrid functional (B3LYP) causes a decrease in the total sulfur 3p character for both complexes and gives a better description of the d_x2−y2 orbital for the molybdenum complex, although it is still too covalent compared to the data. The pure functional (BP86) gives a better description of the d_x2−y2 orbital in the tungsten complex. This suggests that a hybrid functional is more appropriate for the molybdenum complex. Additionally, the energy of d_x2−y2 orbital for the tungsten complex is higher than that of the molybdenum complex, regardless of the functional used: 0.20 eV with BP86 and 0.21 eV with B3LYP.

4 Discussion

The results of DFT calculations show that the difference in energies of the pre-edges of Mo^V=O and W^V=O bis(dithiolene) complexes are primarily due to relativistic effects. The valence d electrons in the W complex experience a greater radial expansion due to the relativistic radial contraction of the core s and p electrons. This radial expansion destabilizes the redox active d_x2−y2 orbital, which accounts for the observed differences of the pre-edge transitions (Fig. 2).

Additional DFT calculations on Mo(IV) and W(IV) forms of the complexes were used to calculate the one-electron ionization potentials. The calculations show that relativistic effects result in a significant difference in ionization potentials (IP_Mo − IP_W = 160 mV) for the M(IV)/M(V) couples, which is on the order of the difference in experimental reduction potentials (E^o_Mo − E^o_W = 260 mV), whereas non-relativistic calculations do not (IP_Mo − IP_W = 20 mV).

The strength of the metal-oxo bond also plays a role in the thermodynamics of oxygen atom transfer. Bond dissociation energy (BDE) differences for pairs of molybdenum and tungsten complexes with oxidation states ranging from M(II) to M(VI) were compared in a previous study, which found that BDE_W > BDE_Mo suggesting that the W=O bond is stronger [9]. One pair of these complexes, MOCl₄ (M = Mo, W), was studied using relativistic Dirac–Slater discrete variational calculations [35]. The authors determined that there is more electron density on the M=O bond for tungsten and noted that this is reflected in the experimentally higher W=O stretching frequency. However, they did not explore the contribution of relativistic effects towards these results.

In order to determine the contribution of relativistic effects towards the strength of the metal-oxo bond as reflected by the M=O stretching frequency, geometry optimizations and frequency calculations without and with relativistic effects were done on MOCl₄ (M = Mo, W) complexes. Table 4 compares the length of the M=O bond at the optimized square pyramidal geometry and the M=O stretching frequencies for calculations without and with relativistic effects to the bond lengths and frequencies obtained from experiment. The non-relativistic calculation results in a longer M=O bond in the tungsten complex but does not reproduce the observed trend, that is ν (W) > ν (Mo), for the M=O vibrations. The relativistic calculation does reproduce the higher M=O stretching frequency in the tungsten complex, but results in an optimized structure with a slightly shorter M=O bond. Table 5 presents the total compositions of the filled α and β valence molecular orbitals formed from interactions with the O p_z orbital for MOCl₄ (M = Mo, W). There are no significant differences for metal contributions to bonding molecular orbitals with predominately oxygen p_x or p_y character. The non-relativistic calculations show that there is a slight (4%) difference in covalency in going from molybdenum to tungsten consistent with the lower W=O stretching frequency reflecting the longer calculated W=O bond. The opposite trend is observed for the relativistic calculations: there is a slight (4%) increase in M-O covalency in going from molybdenum to tungsten which is consistent with the higher calculated and observed W=O stretching frequencies.

Table 4.

Experimental and calculated M=O bond lengths and M=O stretching frequencies for MoOCl₄ and WOCl₄.

	Experimental		Non-relativistic		Relativistic
	Mo	W	Mo	W	Mo	W
M=O length (Å)	1.66a	1.69b	1.70	1.72	1.70	1.69
M–Cl length (Å)	2.28a	2.28b	2.33	2.35	2.33	2.31
M=O stretch (cm−1)	1015c	1027c	983	969	998	1011

^aReference [31].

^bReference [32].

^cReference [33].

Table 5.

Total compositions of bonding molecular orbitals with O p_z character as determined by calculations for MOCl₄ (M = Mo, W).

	Non-relativistic		Relativistic
	MoOCl4	WOCl4	MoOCl4	WOCl4
% M d	40	33	33	30
% M s	8	10	11	17
% M p	2	3	2	3
% O	64	66	69	68
% Cl	87	88	86	82

The shorter calculated W=O bond could, in principle, be responsible for the higher W=O stretching frequency. In order to determine whether this is the primary effect resulting in a higher stretching frequency, a single-point calculation with relativistic effects included in the molecular Hamiltonian was done at the non-relativistic structure (with the longer W=O bond). This calculation resulted in a bonding description that was nearly identical to that of the relativistic calculation for the relativistic structure. This suggests that the small change in length of the M=O bond plays a minor role in determining the differences in stretching frequency, and that relativistic effects are responsible for the stronger W=O bond. For tungsten, the relativistic effects increase the amount of the 6s orbital involved in bonding with the oxygen (Table 5 shows a 7% increase in W s character when relativistic effects are included) which derives from the energetic stabilization of the 6s orbital due to radial contraction. This agrees with the result obtained from the previous study which used relativistic Dirac–Slater discrete variational calculations.

In summary, S K-edge XAS and DFT calculations of molybdenum and tungsten bis(dithiolene) complexes have shown that relativistic effects contribute to the differences in the thermodynamics and kinetics of tungsten (relative to molybdenum) oxotransferases. The reduction potential is lower for tungsten sites because of the relativistic destabilization of the redox-active d_x2−y2 orbital. The faster oxygen atom transfer reactions observed suggest a lower activation barrier that would reflect occupied metal-based orbitals being relativistically destabilized, and thus better suited for frontier molecular orbital interactions with low-energy unoccupied oxygen-based anti-bonding orbitals on the substrate. Finally, DFT calculations indicate that inclusion of relativistic effects can also strengthen metal-oxo bonds through increased 6s mixing, which would affect the thermodynamics of oxygen atom transfer.

5 Abbreviations

ADF

Amsterdam Density Functional

BDE

Bond dissocation energy

bdt

benzene-1,2-dithiolate(2−)

DFT

Density functional theory

ECP

Effective core potential

XAS

X-ray absorption spectroscopy

ZORA

Zero Order Regular Approximation