Myosin Heads Contribute to the Maintenance of Filament Order in Relaxed Rabbit Muscle

Abstract

Raising the temperature of rabbit skeletal muscle from ∼0°C to ∼20°C has been shown to enhance the helical organization of the myosin heads and to change the intensities of the 10 and 11 equatorial reflections. We show here by time-resolved x-ray diffraction combined with temperature jump that the movement of the heads to enhance the organized myosin helix occurs at the same fast rate as the change in the intensities of the equatorial reflections. However, model calculations indicate that the change in the equatorials cannot be explained simply in terms of the movement of myosin heads. Analysis of electron micrographs of transverse sections of relaxed muscle fibers cryofixed at ∼5°C and ∼35°C shows that in addition to the reorganization of the heads the thin and thick filaments are less constrained to their positions in the hexagonal filament lattice in the warm muscle than in the cold. Incorporating the changes in filament order in model calculations reconciles these with the observed changes in equatorial reflections. We suggest the thin filaments in the cold muscle are boxed into their positions by the thermal movement of the disordered myosin heads. In the warmer muscle, the packed-down heads leave the thin filaments more room to diffuse laterally.

Introduction

In vertebrate striated muscle at rest, the myosin heads are arranged helically around the shaft of the thick filament. However, the level of this organization in warm-blooded animals has been shown by x-ray diffraction to depend on the temperature. The myosin layer lines, characteristic of the helical structure, provide a quantitative measure of the degree of helical order. In skeletal muscle from rabbit, the layer lines are much more intense at 20°C and above, than they are at 5°C (1–6). The change in the helical order was assumed to be associated with ATP hydrolysis, i.e., the transition from a myosin-ATP to myosin-ADP-Pi state (1). Later, it was found that the changes in the helical order result, instead, from a transition from the open to the closed conformation of the heads at higher temperatures (7). This transition is necessary for hydrolysis although not contemporaneous with it (8). Stabilizing the closed conformation with blebbistatin improves the helical order at low temperature (9,10). Concomitant with the changes in the layer lines there are also changes in the intensities of the equatorial reflections upon raising the temperature (6,11). In particular, I₁₀ increases slightly and I₁₁ falls more dramatically so that the intensity ratio of the two reflections I₁₁/I₁₀ changes by ∼50%.

The time course of the change in the equatorials with temperature has been briefly reported by Rapp et al. (11), who showed that after a temperature jump (T-jump) from 0°C to 7°C, the change in intensity was accomplished in 50 ms, whereas at a higher temperature (T-jump from 15°C to 22°C), the half-time was 5 ms. To our knowledge, the rate of change in the layer line reflections has not been measured previously. Here we report simultaneous measurements of the time course of the changes in the equatorial reflections and in the first myosin layer line after a T-jump and show that they have the same time course. The observed change in the intensity of the equatorial reflections seems to be explained by movement of the myosin heads toward a more helical packing on the backbone of the thick filaments. However, calculations suggest that only part of the observed change can be explained in this way. An additional factor is likely to be disorder of the filaments lattice, as was early recognized by Elliott et al. (12). To investigate this further, we cryofixed relaxed muscle fibers at low and high temperature by using the T-jump technique and compared the structures by electron micrography. As we previously showed, the warm structure of muscle after a T-jump can be cryofixed for electron microscopy retaining the changes in both the 43-nm layer line and the lattice reflections (13). Analysis of the order of the thin filament arrangement in the hexagonal lattice shows it to be better maintained in the cold relaxed state. We suggest that the order of the thin and of the thick filaments in the lattice is influenced by the degree of order in the myosin heads on the thick filament.

Materials and Methods

Muscle preparation

Bundles of rabbit m. psoas fibers were dissected and stored in 50% glycerol in relaxing solution at −20°C as described before (14). The treatment rendered the muscle cells permeable. Relaxing solution contained: 3-(n-morpholino)-propanesulfonic acid (MOPS) 100 mM, MgATP 5 mM, Mg²⁺ 2 mM, ethylene glycol-bis(β-aminoethyl ether)-n,n,n′,n′-tetraacetic acid (EGTA) 5 mM, potassium propionate 80 mM, and dithiothreitol (DTT) 5 mM. Rigor solution contained MOPS 100 mM, ethylenediaminetetraacetic acid (EDTA) 5 mM, potassium propionate 100 mM, and DTT 5 mM. All solutions had ionic strength of ∼150 mM and pH 7.1 at 20°C. For electron microscopy experiments, single fibers of some 5–6 mm in length were dissected from the bundle in relaxing solution and additionally permeabilized by 0.5% Triton X-100 in relaxing solution for 15 min at ∼5°C before mounting on the CryoSnapper apparatus (Gatan, Pleasanton, CA) (13). All chemicals are from Sigma Aldrich (St. Louis, MO). Sarcomere length, measured using diffraction of a He-Ne laser beam, was adjusted to 2.4–2.45 μm.

In the x-ray experiments, bundles of 3–5 fibers were used to increase the amount of diffracting material in the beam. The bundles of parallel and untwisted fibers were chosen and knotted together at their ends to improve their mechanical stability and to keep the same sarcomere length in all fibers. Each bundle was also treated with 0.5% Triton X-100 in relaxing solution for 15–30 min and then mounted in a 140 μl trough by gluing the knots with droplets of shellac/ethanol solution to the tips of a length motor and a force transducer (15,16). Sarcomere length was adjusted to 2.4 μm in all preparations.

X-ray diffraction and analysis

The setup for x-ray diffraction experiments was described previously (15) as was the T-jump apparatus and the procedure for estimating the T-jump amplitude (13,16,17). Experiments were carried out on beamline 16.1 of the Synchrotron Radiation Source (Daresbury Laboratory, Cheshire, UK) using the RAPID x-ray detector (18). Approximately one second before exposing a muscle bundle to the x-rays the solution trough was lowered so that the bundle was suspended in air at ∼5°C. The trigger for the T-jump was synchronized with the time-frame generator of the RAPID detector. The two-dimensional x-ray diffraction patterns before and after the T-jump to 34–37°C were recorded for 350 ms. The diffraction patterns were collected into time frames of 1–50 ms with shorter frames just before and after the T-jumps. Then the solution trough was lifted and the bundle was returned to the relaxing solution at 0–1°C for 2–3 min. Thirty-five to ninety T-jumps were applied to each of five bundles.

X-ray diffraction data were analyzed using the softwares BSL (CCP13 suite, http://srs.dl.ac.uk/ncd/computing/manual.bsl.html) and BS (written by Natalia A. Koubassova, available at http://muscle.imec.msu.ru/bs_1.htm). The patterns were corrected for camera background scattering recorded after removing the bundle as well as for spatial and amplitude distortion of the detector. The four symmetrical quadrants of the corrected patterns were averaged as described previously (15). The time-resolved diffraction patterns obtained for each bundle were added together to increase signal/noise ratio. The time course of the change in the intensities of the 10 and 11 equatorial reflections was measured by integration of the intensities under the peaks after background subtraction, as previously described (19,20). The time course of the changes in the intensity I_M1 of the M1 myosin layer line was determined as follows. For each time frame, the axial intensity profile of the layer lines was obtained by integrating the averaged two-dimensional patterns radially from 0.02 nm⁻¹ to 0.087 nm⁻¹. The average intensity profile before the T-jump was subtracted from those obtained in each time frame after the T-jump; ΔI_M1 for each time frame was determined from this differential intensity using XFIT software (CCP13 software suite; latest revision: http://www.ccp14.ac.uk/tutorial/xfit-95/xfit.htm), assuming a constant position and width of the M1 peak and a variable amplitude and background level.

The mean rate constants and their standard deviations for the time course of the changes in the x-ray intensities were determined using Provencher's algorithm (21) incorporated to GIM software (kindly provided by its author A. L. Drachev, from Dr. Achev Development, Tempe, AZ).

Cryofixation and electron microscopy

Cryofixation was carried out as described in Bennett et al. (13). Briefly, a fiber was attached to two fine nickel tubes and held in a small trough filled with relaxing solution as described for previous T-jump experiments (14,16,22). The nickel tubes moved in two narrow slits in the sides of the trough so that the fiber can be brought into air. After lowering the trough, the fiber, in air, was snap-frozen using a CryoSnapper (Gatan) (13,23–25). The activation of the CryoSnapper signaled a trigger pulse that was fed into a PC equipped with an AD converter (DAS-50; Keithley Metrabyte, Taunton, MA) and a DA converter/timer card (L-154; L-Card, Moscow, Russia). The T-jump signal occurred 50 ms after the trigger (∼50 ms before freezing). For cold relaxed specimens, the T-jump was omitted; for rigor specimens, the solution was changed from relaxed, to rigor, after the fiber had been mounted and sarcomere length adjusted. Only cold rigor specimens were obtained.

After freezing, the fibers were collected and stored in liquid nitrogen until further processing. Fibers were freeze-substituted in 2% osmium tetroxide in acetone at –80°C for at least two days. After slowly warming to 0°C, they were washed in acetone, warmed to room temperature, then washed again in acetone and embedded in Araldite. Thin sections were stained with 2% KMnO₄ followed by lead citrate and examined in a 200CX transmission electron microscope (JEOL, Peabody, MA). Transverse sections were examined and micrographs of good areas taken at 10,000 or 20,000 times magnification. The micrographs were scanned on a T2500 scanner (AGFA, Mortsel, Belgium) with pixel size equivalent to ∼1 nm in the specimen.

Image analysis

Parameters of lattice disorder were obtained from computer analysis of electron micrographs of transverse sections of fibers using homemade software. The idea of the algorithm was to find the parameters of random disorder of individual filaments distinct from macroscopic disorder induced by squashing of the fiber due to deformation by the jaws of the CryoSnapper (13). Areas of reasonably extensive hexagonal lattice were identified. Up to six such areas could be selected within a micrograph where individual thin and thick filaments were defined as spots with the electron density above a background level selected by eye for each micrograph (Fig. 1). Then the positions of the centers of each thin and thick filament within the selected area were determined by the software as the centers of mass of the spots. In the regular actin-myosin lattice each thin filament lies at a trigonal point formed by three nearest thick filaments and each thick filament lies in the center of a hexagonal super-lattice unit cell formed by six nearest thick filaments (Fig. 1).

Figure 1.

A fragment of an electron micrograph of a transverse section of a muscle fiber in the low temperature, relaxed state. Thick and thin spots correspond to myosin and actin filaments, respectively. Examples of elementary unit cells for individual filaments are shown: a hexagonal myosin-centered super-lattice cell (on the left) and a triangular actin-centered cell (on the right). Open circles show the software calculated positions of the centers of mass of myosin filaments in the cells. Black solid circles cover the central filaments in the cells.

In the first step, all neighboring myosin filaments (three for an actin or six for a myosin filament, respectively) were detected (Fig. 1). Then the expected position of a thin or a thick filament in a real cell was determined as the center-of-mass of a triangle or a hexagon formed by neighbor thick filaments. Then the deviation of an actin (Δa) or a myosin (Δm) filament from the expected position was calculated as the distance between its actual and expected positions (Fig. 2).

Figure 2.

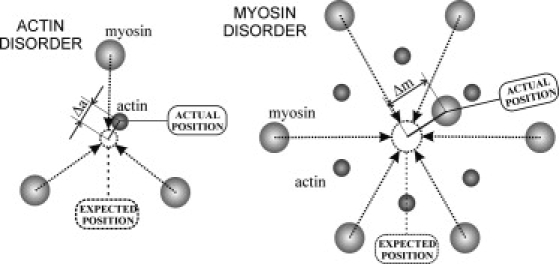
An illustration of the method of disorder analysis. (Small and large circles) Actin and myosin filaments, respectively. Disorder of a filament is a displacement Δa and Δm for actin and myosin filaments, respectively, between expected and actual position in a cell.

Finally, the mean deviations from expected lattice positions were calculated separately for the thin (Δa) and thick (Δm) filaments for each fiber and for all fibers in the same conditions (rigor, cold relaxed and hot relaxed states). This method allowed us to avoid the possible influence of lattice squashing on estimated disorder. For some micrographs in all three states, the root-mean-square deviations (RMSD) of the filament positions from their expected lattice positions were calculated. It was found that RMSD of the thin and thick filaments is ∼1.13 (∼$2/\sqrt{\pi }$) times higher than their average deviations, Δa and Δm, respectively, as would be expected if the distribution of filament positions was Gaussian.

Modeling of equatorial reflections

A model suggested by Malinchik and Yu (26) was used with slight modifications concerning the modeling of filament disorder to calculate the equatorial diffraction pattern. The backbones of the thick filaments and thin filaments were approximated by cylinders of uniform electron density and of 16- and 11-nm diameter, respectively. The distance between the centers of the thick and thin filaments was set to 23.5 nm as in our x-ray diffraction experiments. Detached and weakly attached myosin heads were modeled by two halos with uniform electron densities that surround the backbones of thick and thin filaments, respectively. The relative diffracting powers of the filaments and heads were assumed to be proportional to their molecular weights. The relative weights of the halos for detached and attached heads were proportional to their fractions in the model: from 1 to 0.95 for detached and from 0 to 0.05 for weakly attached heads. The outer diameter of the halo of detached myosin heads was varied according to whether they were more or less helically ordered on the surface of the thick filaments; the outer diameter of the halo of attached myosin heads was set to 10 nm. Varying of this parameter from 5 to 12 nm did not result in visible changes in the calculations. The equatorial intensity was calculated, taking lattice disorder into account (27,28). Values of actin and myosin disorder found in the analysis of electron micrographs were taken as parameters of the lattice disorders of the first and second kind, respectively. Visual inspection of the micrographs (see Fig. 1 as an example) shows that the thick filaments obey local neighbor-to-neighbor order probably due to elastic forces in the M-lines of sarcomeres, i.e., their disorder is of the second kind (27). In contrast, the thin filaments do not show any short-range order and their position is somewhere within a triangle formed by three thick filaments. For this reason, actin disorder was described as the disorder of the first kind (i.e., thermal disorder).

Results

X-ray diffraction

The x-ray diffraction patterns of relaxed rabbit psoas muscle before and after a ∼30°C T-jump is shown in Fig. 3. The previously reported differences between the two temperatures (1–7) are well seen. The intensity profiles of the off-meridional reflections at low and high temperatures are shown in Fig. 4 A.

Figure 3.

X-ray diffraction patterns of hot and cold relaxed muscle (right) and their difference (left). Mirrored patterns (right lower and upper quadrants) taken at 5–6°C and at 34–37°C, respectively, that was achieved by a ∼30°C T-jump. White: higher intensity. Patterns in the two right quadrants are shown on a logarithmic scale to depict weak and strong layer lines simultaneously. The equator is vertical and attenuated 20-fold. The patterns were obtained from five muscle bundles of 3–5 fibers each during 0.2-s-long exposures before each T-jump at ∼5°C and after it at ∼35°C. The total exposure in each state was 65 s. X-ray reflections of interest are labeled.

Figure 4.

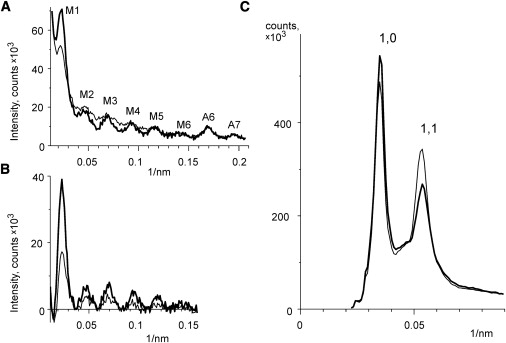
Meridional (A and B) and equatorial (C) intensity profiles from x-ray diffraction patterns from cold (thin lines) and hot (thick lines) relaxed muscle. (A) Off-meridional integration from 0.02 nm⁻¹ to 0.087 nm⁻¹ in the equatorial direction. The positions of myosin layer lines, M1–M6, and of two actin layer lines, A6 and A7, are marked. (B) Same as A, but with subtracted background. (C) Integration in the meridional direction in the range of ±0.0014 nm⁻¹. Positions of the 10 and 11 equatorial reflections are marked. The same diffraction patterns as those shown in Fig. 3 with no background subtraction.

At the higher temperature (∼35°C), the intensity of the first myosin layer line is brighter than that at the lower temperature (5°C). The ratio of the M1 intensity at 5°C to that at 35°C was 0.46 in our experiments (Fig. 4 A). The higher order myosin reflections behave in the same way, although it is less obvious because their intensity is only 10–15% of that of the first layer line. On the other hand, the actin layer lines, A6 and A7, are unaffected by temperature. No measurable change in stiffness of relaxed bundles upon the T-jumps was found, suggesting that the contribution of attached heads to the diffraction patterns was small at both the pre- and post-T-jump temperatures. In addition, no force generation upon T-jump was observed (which was in agreement with previous findings at the same sarcomere length and temperature range (29)).

A change in the relative intensities of the equatorial reflections, I₁₀ and I₁₁ is also seen after a temperature jump (Fig. 3 and Fig. 4 B). In particular, the 11 reflection at the higher temperature is much weaker while the 10 reflection is somewhat brighter. The radial width of the equatorial reflections (especially of the 11) in the hot relaxed muscle is greater than that at low temperature (Fig. 4 B). This observation supports the assumption made in the modeling that disorder of the thick filaments is of the second kind. Quantitative determination of the changes in width of the equatorial reflections was not possible because the size of the x-ray beam on the detector was comparable with that of the reflections. There was also some lattice shrinkage at the higher temperature which appears as a change in spacing of the equatorial reflections (Fig. 4 B).

While it is possible that the equatorial and layer line changes are due to the same structural change, no evidence for this possibility was available. Evidence can be provided by determining the time course of these changes. To do this we investigated the rate of intensity change of the equatorials and the first layer line after a T-jump. The time course for the change in the intensity of the first myosin layer line is shown in Fig. 5 A for a T-jump from 5°C to 34–37°C. The rate constant describing the intensity change is 380 ± 130 s⁻¹.

Figure 5.

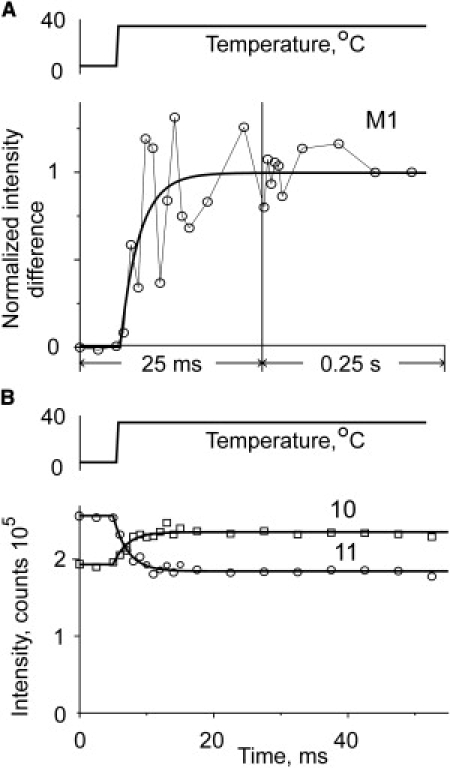
(A and B) Time course of changes in the intensity of the first myosin layer line and in equatorial 11 and 10 x-ray reflections in relaxed muscle fibers induced by a T-jump from 5°C to 35°C. (A, circles and solid line) Experimental data and exponential fit through the data, respectively. (B, circles and squares) Experimental data for the intensity of 11 and 10 reflections, respectively; (solid lines) exponential fits through the data. Intensities were calculated after background subtraction.

The data could alternatively be expressed as an amplitude calculated as the square-root of the intensity (not shown), which is proportional to the number of diffractors—in this case, the number of ordered myosin heads. The apparent rate constant of the increase in amplitude of the first myosin layer line is somewhat faster than the intensity change, ∼410 ± 110 s⁻¹.

The time course for the change in the intensity of equatorials is seen in Fig. 5 B. Both equatorials change with similar rate constant, 550 ± 100 s⁻¹ for the 10 and 460 ± 50 s⁻¹ for the 11 reflections, consistent with the original observation that the changes occurred on a millisecond timescale and have a high Q₁₀ (11). Within the experimental scatter, these rates are the same as that of the change in the layer line, suggesting that a common process is responsible for the change in the layer line and in the equatorial intensities.

Electron microscopy

The increase in intensity of the myosin layer lines at higher temperatures and the change in relative intensities of the equatorial reflections were confirmed by electron microscopy of muscle fast-frozen before and after a T-jump (13). We also noted that in the hot muscle the thin filaments seemed more disordered in the lattice than in the cold. An increase in the disorder could substantially affect the equatorial intensities while having little effect on the meridional and layer line reflections. To test this, we used electron micrographs of transverse sections of rapidly frozen muscle to determine the amount by which the thin and thick filaments deviate from their ideal positions in hot and cold relaxed muscle. We compared these deviations to those in rigor muscle where the filaments are held more firmly in place by the crossbridge. The mean distance of the thin filament from the center-of-mass of its three nearest-neighbor thick filaments, Δa, and the mean distance of each thick filament from the center-of-mass of six nearest-neighbor thick filaments, Δm, were determined for each thick and thin filament in regions where the hexagonal lattice was clear. Table 1 gives the values for the three states of the muscle.

Table 1.

Calculated lattice disorder in different physiological states for muscle fibers

State	Actin disorder, Δa, nm	Myosin disorder, Δm, nm
5°C relaxed	3.67 ± 0.4 (3034)	2.79 ± 0.41 (1072)
35°C relaxed	4.26 ± 0.65 (2868)	3.24 ± 0.61 (1047)
5°C rigor	2.9 ± 0.39 (2464)	2.11 ± 0.33 (937)

Values are mean ± SD. Figures in parentheses represent the number of elementary cells analyzed. The difference for Δa and Δm between the cold and hot relaxed states was statistically significant (p < 0.001).

The table shows that in all states the filaments deviate from their ideal positions by 2.1–4.3 nm. The deviation in rigor is smallest, as expected, because cross-bridge attachment maintains the spacing between the filaments. In cold relaxed muscle, the disorder of both thick and thin filaments is less than at the higher temperature. Disorder of the thin filaments in each of the three states is 1.3–1.4 times higher than that of the thick filaments. It should be noted that average distance between the centers of the thin and thick filaments estimated from the spacing of 11 equatorial reflection is, in our experiments, 23.5 nm while the distance between neighbor thick filaments is ∼41 nm, so that the average deviation of the thick filaments from their ideal position is <8% of the myosin-to-myosin distance while the deviation of the thin filaments is up to 18% of the actin-to-myosin distance. To interpret the changes in the x-ray pattern when the temperature is raised, the increased disorder in the filament positions must be taken into account as well as the increase in helical order.

Modeling

Fig. 6 shows the results of modeling of the equatorial reflections using different assumptions for changes in myosin-head packing and the extent of filament disorder. Packing of myosin heads on the backbone of the thick filaments at different temperatures was modeled by varying the width of the halo of myosin heads around a thick filament from 9 nm at 5°C to 6 nm at 35°C. This led to a dramatic increase in the 10 intensity without a significant change in the 11 intensity if the disorder of the thin and thick filaments remained unchanged (Fig. 6). This is different from what is seen on the x-ray diffraction pattern where the decrease in the 11 intensity after the T-jump is more pronounced than the increase in the 10 intensity (Figs. 3–5). However, if the temperature-induced change in the degree of filament disorder revealed by electron microscopy is incorporated into the model, the observed changes are well reproduced (Fig. 6). Only marginal, <5% changes in calculated equatorial intensities were observed when 5% of myosin heads were assumed to be weakly bound to actin.

Figure 6.

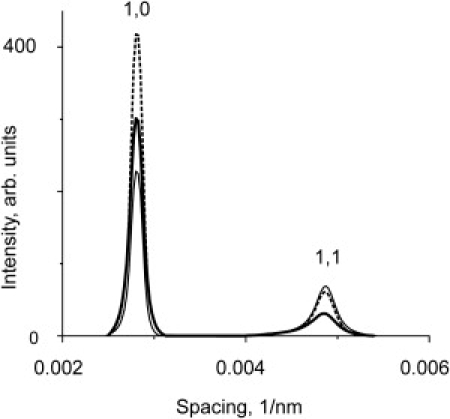
Results of modeling of the equatorial intensity using disorder parameters obtained from electron microscopy: RMSD for the thin and thick filaments were taken as their average deviations, Δa, Δm (Table 1) multiplied by a factor of 1.13. Model of cold relaxed state (thin line) was obtained using cold relaxed disorder parameters (Table 1) and by assuming that the width of the myosin head halo is 9 nm. The hot state (thick line) was modeled using a 6-nm halo and hot disorder parameters. The dashed line corresponds to a state where myosin heads are closely packed (6-nm halo), but the disorder parameters are the same as those for the cold state.

Discussion

Changes in the myosin layer lines as a result of a rise in temperature

Variations in the myosin layer lines in x-ray diffraction patterns of rabbit muscle as a result of temperature changes was first described by Wray (1) and subsequently by other authors (2–6). In addition, the temperature effect on the order in thick filaments from rabbit and chicken has also been observed by electron microscopy (30,31). Wray suggested that it was correlated with the changes in the state of nucleotide bound to the myosin heads (1). Myosin.ATP (M.ATP) favors the disordered state of the myosin filaments while myosin.ADP.P_i (M.ADP.P_i) populates the helically ordered state.

Recently it has been suggested that, irrespective of nucleotide, myosin can exist in at least two states. Two of these have been identified with the closed and open structural conformations identified by x-ray crystallography. The distribution of the two at any temperature depends on the nucleotide, and the closed state is more favored at higher temperatures (8). M.ATP is biased toward the open state and is more plentiful at lower temperatures, while the transition to the closed state and subsequent hydrolysis to M.ADP.P_i are accelerated at higher temperatures where the closed state is the major species. Xu et al. (7) have used these data to show that the myosin layer line x-ray data is consistent with the idea that the heads in the closed conformation are the helically ordered heads. Further evidence for this interpretation comes from experiments where blebbistatin stabilized helical order of the thick filaments in the presence of ADP (10).

If this concept is correct, then there are two processes to be considered to determine the rate of development of myosin layer line after a T-jump—the transition of the ATP species to a closed state, and the hydrolysis of ATP. Kinetic experiments using T-jumps and pressure jumps on solutions of myosin S1 give equilibrium and rate constants which we can use to determine the rate of development of the closed conformation (8,32). The experiments with ATP show three transients. At 20°C, the first is very rapid (≥1000 s⁻¹) and corresponds to the rate of change seen with nonhydrolyzable ATP analogs to the change in equilibrium between open and closed states brought about simply by the rise in temperature. The second has a rate constant of ∼100 s⁻¹. This corresponds to the hydrolysis of ATP. The third component is small and much slower than our experiments would detect. We can extrapolate to 35°C the rate constants used by Urbanke and Wray (32) in their model calculations based on experiments with rabbit muscle myosin: in a T-jump from 5°C to 35°C, more than one-half of the response would be the rapid temperature transition of the M.ATP state from open to closed with the rate constant of >3000 s⁻¹. This is followed by the slower hydrolysis step with the rate constant of ∼400 s⁻¹. Although our data is quite noisy, we did not see a significant component with the rate constant >1000 s⁻¹. Clearly, as discussed above for the earlier model, our data are consistent with the major phase arising from the ATP cleavage step. Another possible explanation for the absence of the fast components is that helical packing of myosin heads on the backbone of the thick filaments is not instantaneous, and instead, takes some processing time.

In rabbit muscle fibers when conditions favor the ordered state of the thick filaments, the ATPase rate per myosin head was shown to decrease to 1:230 s⁻¹ (33), i.e., to a value approximately an order-of-magnitude slower than the ATPase rate of isolated myosin molecules or their subfragments. We believe this so-called super-relaxed state is a true relaxed state providing significant economy of ATP energy in resting muscle under physiological conditions. This explains why, in muscles of cold-blooded animals where the muscles operate over a wide range of temperatures (34), the ordered helical packing of the heads on the backbone of the thick filaments is always observed. In warm-blooded animals the ordered state is only required over the narrower but higher physiological range of temperature.

Changes in the equatorial reflections as a result of increase in temperature

Rapp et al. (11) first showed that the ratio of intensities of the 10 and 11 equatorial reflections was affected by temperature and that they changed after a T-jump from 15°C to 22°C with a half-time of 5 ms. In line with this, we have shown here that the rate of change of the equatorial reflections after T-jumps from ∼5°C to ∼35°C is 450-550 s⁻¹. The myosin layer line intensity increases with the rate of ∼400 s⁻¹ and so the rate is the same as those for the equatorials within the experimental error. This suggests that the equatorial changes come about as a result of the helical ordering and occur essentially at the same time. The relative intensity of the equatorial reflections has generally been used to monitor the movement of the myosin heads within the lattice. In this case, the I₁₁/I₁₀ ratio falls as the temperature increases, consistent with a movement of the myosin heads toward the thick filament backbone as they become more ordered. However, this simple model is not enough to explain the observed changes in the intensities of the equatorial reflections. We have seen that the 10 reflection increases only slightly while the 11 reduces in intensity more markedly (Fig. 4 B). Our calculations show that there should be a substantial increase in the 10 while the 11 remains little changed (Fig. 6). This agrees with earlier modeling results of Malinchik and Yu (26), but is in contradiction to other experimental observations. One possible explanation is an increase in the disorder of the position of the filaments in the lattice. We previously noted that in electron micrographs of cryofixed fibers the filament lattice in the relaxed fibers at high temperature appeared more disordered than that in fibers at a lower temperature (13). In agreement with this, analysis of the filament positions showed that the degree of disorder about their ideal positions is greater for the relaxed muscle at high temperatures compared to the low temperatures. Furthermore, the thin filaments have a greater disorder than the thick filaments. Applying these experimentally obtained disorder parameters to the calculations of the equatorial intensities shows that the disorder reduces the intensity of the 11 reflection more than the 10 and the observed changes in the intensities can be reproduced (Fig. 6).

The thick filaments are much less flexible than the thin ones and essentially behave as rigid unbendable rods. Their good lattice order with small deviations in relaxed muscle is probably mainly determined by the elasticity of the M-band connections (38). On the other hand, the thin filaments exhibit disorder of the first kind which, at least partially, results from their bending flexibility and thermal fluctuations. The persistence length of an actin filament with troponin and tropomyosin is L_p = 20 μm (39). Gittes et al. (40) give an equation for the variance (root-mean-square amplitude) of an n^th mode of vibration in terms of persistence length

$$L_{\text{p}}=L^2/n^2{\pi }^2.\mathrm{var}\left(a_{\text{n}}\right).$$

The RMSD of a thin filament can be calculated as

$$\sqrt{\mathrm{var}{\left(a_1\right)}^2+\mathrm{var}{\left(a_2\right)}^2+\dots }$$

because the vibration modes are independent. For a thin filament with L = 1 μm, the variance for n = 1 is ∼5 nm, for n = 2 it is ∼1.25 nm, etc., and hence the RMSD is ∼5 nm. This number is similar to the actin disorder parameter we have found from analysis of micrographs of the hot relaxed state, i.e., 4.3 nm (Table 1). Interestingly, relaxed muscle from cold-blooded animals such as frog, fish, and tarantula, which show a highly ordered helical myosin structure even at low temperatures, also have a disordered filament lattice (30,34,41,42).

In the cold relaxed state, disorder of the actin filaments is significantly smaller, probably because they are constrained by myosin heads. This constraint could be either specific or nonspecific. We have no evidence for a major contribution from bound heads from force or stiffness measurements either before or after a T-Jump. However, Kraft et al. (35) have described a population of weakly bound heads at both high and low temperatures. They show that the relative stiffness of relaxed rabbit muscle fibers at μ = 0.17 M is 7–8% of its rigor value at 5°C and 5–6% at 20°C. Corresponding figures at μ = 0.12 M were 12–13% at 5°C and 7% at 20°C (35). An earlier report (36) gives even smaller values for stiffness of relaxed fibers. Interpolation of the above values for μ = 0.15 M used in our experiments gives a normalized stiffness of 10% at 5°C and 6% at 20°C. If we assume that 75% of a half-sarcomere compliance in rigor is accounted for by the thin and thick filaments (37) and that the weakly bound head has the same stiffness as a rigor one, we can calculate that 2.5% and 1.8% of the total number of myosin heads are weakly bound to actin at the low and higher temperatures. Addition of 2.5% or 1.8% of weakly bound heads to our model of the equatorial x-ray reflections leads to a <2% change in the calculated values of I₁₁ and I₁₀. Doubling the contribution of weakly attached heads to stiffness to values of 5% and 3.6% did not change the calculated I₁₁ and I₁₀ by >5%. Our modeling results agree with those of Malinchik and Yu (26), who also found similar changes in calculated 10 and 11 intensities upon binding of a small fraction of myosin heads to actin (see Fig. 5 A in Malinchik et al. (26)).

The observation that both equatorial and M1 layer line intensity changes occur with a similar rate constant suggests that the changes are concomitant. That is, as the myosin heads become more ordered it allows the filaments, particularly the thin filaments, to become more disordered. While the weak binding heads will contribute to this process, it is unlikely that they have a major role in ordering the thin filaments because they should operate at both low and high temperatures. We suggest that at the lower temperatures the major contribution is from the unbound disordered heads that box-in the thin filaments. These heads having a large radial and azimuthal freedom of movement collide with the thin filaments. The time- and space-averaged effect of these collisions emanating from all surrounding thick filaments, constrain the thin filaments toward their trigonal lattice point. At the higher temperatures, the ordered heads are more closely apposed to the thick filament backbone and leave more room for the thin filaments to flex and exhibit increased disorder.