Salt Concentration Effects on Equilibrium Melting Curves from DNA Microarrays

Abstract

DNA microarrays find applications in an increasing number of domains where more quantitative results are required. DNA being a charged polymer, the repulsive interactions between the surface of the microarray and the targets in solution are increasing upon hybridization. Such electrostatic penalty is generally reduced by increasing the salt concentration. In this article, we present equilibrium-melting curves obtained from dedicated physicochemical experiments on DNA microarrays in order to get a better understanding of the electrostatic penalty incurred during the hybridization reaction at the surface. Various salt concentrations have been considered and deviations from the commonly used Langmuir adsorption model are experimentally quantified for the first time in agreement with theoretical predictions.

Introduction

DNA microarrays are widely used in applied genomics, drug discovery, disease diagnosis or prognosis, and in the agricultural and food industries (1). Its principle is based on the hybridization of a mixture of DNA targets to probes grafted onto a surface. From the known sequences of the probes and their precise location on the surface, the composition of the target solution may be determined. Practical applications concern the determination of mRNA transcript concentrations from the entire genome as well as the detection of point mutations, especially single nucleotide polymorphisms (SNPs) that are responsible for many kinds of cancer. In both cases, the usual qualitative analyses are no longer sufficient and precise quantitative results are now necessary. The difficulty in quantitatively analyzing the data from microarrays comes from the large number of parameters entering their fabrication and their use (2). Starting from the biological problem at hand, the selection of pertinent probes (sequence, length, number per gene, etc.) is crucial to improve the selectivity and sensitivity in the detection of the targets (3). The grafting of the probes on the surface is usually done with an intercalated spacer chain to allow for a better accessibility of the probes (4). The nature, length, and flexibility of the spacer chains can affect the results (5). The grafting density is also crucial because it controls the distance between probes and their possible interactions (6). Finally, solution preparation will determine the concentrations and lengths of the targets whereas the hybridization protocol will set the temperature, incubation time, salt concentration, and possible buffer adjuvant like denaturants.

The target concentrations in samples are determined from the hybridization content on the array via a known relation, which strongly depends on the various parameters of the microarray fabrication. Some theoretical studies have recently tried to analyze their effects. The most commonly used model is the Langmuir adsorption, which considers probes as active sites and neglects all possible interactions (7). However, it is usually insufficient to correctly describe the DNA hybridization process at the surface. To begin with, the importance of thermodynamic equilibrium was recognized as a crucial point (8). The lack of equilibrium requires to take into account the convective and diffusive aspects of the hybridization protocol (9–11). Due to the phosphate charges along the DNA backbone, the effect of salt concentration and the electrostatic penalty for hybridization was considered (12,13). Furthermore, competitive hybridization on the surface and/or in solution is present due to the mixture of different targets affecting the hybridization kinetics and the available target concentrations (7,14–17). To test the different models, dedicated experiments are necessary for which the fabrication parameters are controlled and the target solutions well known (2). A few examples are present in the literature, including the competitive hybridization (18–20) and the dependency of hybridization on the grafting density and salt concentration (21–24).

In this article, we propose to go one step further in the analysis of the electrostatic penalty on hybridization. From dedicated physicochemical experiments, we measured the equilibrium melting curves on microarrays for a single target sample but with various salt concentrations. Different probes have been considered, such as using a perfectly matched sequence or using sequences including one or two point mutations to emphasize the potential applications of SNP detection. Knowing the importance of the grafting chemistry, two grafting procedures have been considered:

• 1.Electropolymerization of oligonucleotides modified with a pyrrole moiety.
• 2.Self-assembling of thiolated oligonucleotides on gold.

Procedure 2 is known to lead to higher grafting densities of probes. The effects of the electrostatic penalty on the DNA hybridization will be studied. In the next section, we will introduce the modified Langmuir model to account for the electrostatic interactions.

Langmuir Model with Electrostatic Interactions

Relevant length scales

An important length is the height H of the probe layer which is directly related to the size of the probes. If we consider N_p bases and the existence of a spacer chain consisting of N_s nucleotides to improve the accessibility of the probe, then the grafted chains comprise N = N_p + N_s charged monomers. In the nonhybridized state, the probes are present in a random coiled state with a size

$$L=N^{3/5}a,$$

where a ≃ 0.6 nm is the base size and 3/5 the Flory exponent. Usually probes are composed of 15 < N_p < 25, with as few as N_s ≃ 10 spacer monomers recognized as being sufficient to allow for a good accessibility of the probes (4). Thus, the size of the grafted chains is comprised between 4 and 6 nm. After hybridization with a target, the probe part of the grafted chain is in a helical state. Assuming for simplicity that the targets comprises N_t bases, with N_t ≃ N_p to avoid the complications due to the presence of long dandling ends (25), the length of the grafted duplex is bN_t with the helical length per base b = 0.34 nm. Furthermore, assuming that the grafting of the chains permits unperturbed rotation around the anchoring point in the rigid helicoidal state, the averaged height of the chain is one-half its length. In conclusion, for either state of the probes, hybridized or not, the height is similar and H ≃ 5 nm. Thus, the probe layer thickness is assumed to be independent of the fraction θ of hybridized probes, the temperature, and the salt concentration.

A second relevant length is the distance d between the probes. This distance is determined by the grafting density. In the mushroom region (Fig. 1), for d > L, the probes are distant from each other and do not feel excluded volume interactions. The thickness of the probe layer is H = L but the surface charge is inhomogeneous (Fig. 1). In the brush region, for d < L, the probes feel each other. The probe layer thickness is slightly increased and the charges may be considered as homogeneously distributed in the layer (7). We will focus later mainly on the brush region, which is the most relevant due to the grafting densities practically considered.

Figure 1.

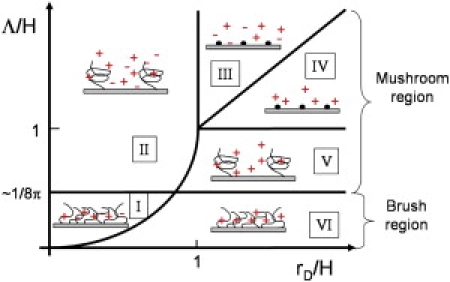
Schematic representation of the electrostatic regimes of hybridization on DNA microarrays. For the brush region, two electrostatic regimes I and VI exist, corresponding, respectively, to salt and counterion screening. For the mushroom region, we distinguish four different electrostatic regimes: II salt and V counterions screening of a two-dimensional array of penetrable charged spheres, and III salt and IV counterions screening of a two-dimensional array of pointlike charges.

The fact that the probes and targets are charged introduces two supplementary relevant lengths. For the case of the salt concentration, c_s, the charge screening by salt occurs on the Debye length

$$r_D=1/\sqrt{8\pi l_B{c}_s}$$

with l_B = 0.7 nm the Bjerrum length. For a salt-free solution, the probe layer charges are screened by counterions. For a uniformly charged surface, the screening length

$$\Lambda =1/2\pi l_B\sigma$$

is called the Gouy-Chapman length with σ the number charge density of the surface. However, Λ is not independent from d, because it is directly related to the grafting density. For example, the bare surface charge for unhybridized probes

$${\sigma }_0=\left(N_p+N_s\right)/d^2,$$

whereas for a fraction θ of hybridized probes,

$$\sigma =\left(N_p+N_s+N_t\theta \right)/d^2.$$

Overall, three independent lengths exist—H, Λ, and r_D. The first one, the probe layer thickness H, is determined by the length of the probes and is imposed by the biological problem at hand through the number of probe bases necessary for a good selectivity and sensitivity. The last two represent electrostatic lengthscales. The Gouy-Chapman length Λ, which depends on the surface charge and thus on the grafting density, is imposed by the microarray fabrication while the Debye length r_D, which depends on the salt concentration, is determined by the hybridization procedure. From those three lengths, two independent dimensionless parameters, Λ/H and r_D/H, allow us to determine different electrostatic regimes (Fig. 1). Typically, the charge layer is screened by the salt for Λ >> r_D and by the counterions for r_D >> Λ. Furthermore, the boundary between the brush and the mushroom region may be interpreted in terms of Λ/H. Because

$$\Lambda =d^2/2\pi l_B\left(N_p+N_s\right),$$

the condition d = H reduces to

$$\Lambda /H=H/2\pi l_B\left(N_p+N_s\right)\simeq 1/8\pi$$

$$\text{with}H=N_{t}b/2\text{.}$$

At last, when both Λ/H and r_D/H are >1, the probes may be considered as pointlike and the thickness of the layer may be neglected. The resulting phase diagram differs from Halperin et al. (13) because we consider explicitly the mushroom region where the probe charge layer is inhomogeneous.

Equilibrium melting curves

In the following, we consider the equilibrium melting curves for the competition free hybridization of a single target in solution at concentration c_t on a solid surface grafted with complementary probes (7,13). At equilibrium, the fraction θ of hybridized probes is determined from a modified Langmuir isotherm taking into account the electrostatic penalty incurred by a target with N_t charges during the hybridization process,

$$\frac{\theta }{1-\theta }=c_t{K}_0\exp \left[-\frac{N_t}{kT}\frac{\partial {\gamma }_{el}}{\partial \sigma }\right],$$ (1)

with the electrostatic free energy γ_el per unit surface and the reference state hybridization reaction constant K₀ = exp(–ΔG₀/RT). Because the effects of the charges from probes, targets, and salt are taken into account in γ_el, the reference state is the surface reaction without the electrostatic interactions or for uncharged chains like the peptide nucleic acids.

The electrostatic free energy γ_el may be determined in the brush region assuming a uniformly charged layer of thickness H at the surface (13). For the high salt regime I, the probe and target charges are mainly screened by the salt and

$${\gamma }_{el}=4\pi kT{\sigma }^2{l}_B{r}_D^2/H.$$

In the regime VI, the charges are screened by the counterions and

$${\gamma }_{el}=kT\sigma \ln \left(\sigma l_B{r}_D^2/H\right)\text{.}$$

The boundary between the two is given by Λ/H = (r_D/H)² (see Fig. 1). Those expressions have been determined within the box model assuming steplike concentration of the probe, target, salt, and counterion charges (13). From solutions of the Poisson-Boltzmann equation, expressions that are more rigorous lead to similar results up to numerical prefactors. In the mushroom region (Fig. 1), the approximation of a homogeneously charged layer as considered in Halperin et al. (13) breaks down and does not allow us to obtain simple expressions for γ_el because long-range interactions between probes may occur (26).

The hybridization reaction in solution would correspond to the limit of infinitely diluted grafting (Λ → ∞) while keeping the salt concentration (r_D) constant. However, because the expressions of the electrostatic penalty in the low grafting regimes (mushroom region) are not determined, the model does not predict the salt corrections for the reaction constant in solution. Generally, the free energy ΔG for the reaction constant of the hybridization in solution is obtained from nearest-neighbor (NN) models with simple salt corrections for the entropy (addition of a logarithmic term of the salt concentration) (27). The reference state in the NN model is the 1 M salt concentration. Thus, within the model presented, there is no obvious relation between both free energies ΔG and ΔG₀.

Experimental parameters

To test the model, it is important to know in which electrostatic regime the experiments are performed. The experimental conditions are detailed in the next section (see Materials and Methods below). However, the probes considered are N_p = 16 bases long with a spacer chain of N_s = 10 thymidines. The targets are N_t = 20 bases long chains. The grafting density from both chemistries is in the range 2–10 pmol of probes per cm² with higher densities for the thiols self-assembly. Thus, the distance between probes d ≃ 4–9 nm is comparable to their size, L ≃ 5 nm, placing the experimental points at the boundary between the brush and mushroom regions. The salt concentrations were varied from 157 to 620 mM, leading to r_D from 0.4 to 0.8 nm—that is, considerably smaller than the width of the probe layer H ≃ 5 nm. Thus, the experimental points lie in the salt screening regime I in the phase diagram (see Fig. 1). For this regime, Eq. 1 writes:

$$\log \left(\frac{\theta }{1-\theta }\right)+\Gamma \left(1+\mathit{\alpha \theta }\right)=\log c_t-\frac{\Delta H_0}{RT}+\frac{\Delta S_0}{R}.$$ (2)

The parameters are

$$\Gamma =8\pi l_B{\sigma }_0{N}_t{r}_D^2/H=N_t{r}_D^2/\mathrm{\Lambda }H$$

$$\text{and}\alpha =N_t/\left(N_p+N_s\right)\text{.}$$

The free energy

$$\Delta G_0=\Delta H_0-T\Delta S_0$$

of the reference state is expressed as a function of the enthalpy ΔH₀ and entropy ΔS₀. Whereas α is imposed by the lengths of the probe and target sequences, Γ reflects the modification from the Langmuir behavior due to the electrostatic penalty. A simple expression,

$$\Gamma =N_t{c}_p/c_s,$$

emphasizes the dependence on the salt concentration c_s and the number charge concentration in the probe layer c_p = σ₀/H before the hybridization of targets (13,23). The electrostatic effects are proportional to the target charge through N_t and proportional to the ratio between the initial concentration of charges in the probe layer and the salt concentration. As expected, the electrostatic penalty is reduced by increasing the salt concentration while it is increased by a denser probe layer.

In the expression Eq. 2, we explicitly separate the dependence on the fraction of hybridized probes θ from the temperature dependence. Experimentally, we observe the equilibrium melting curves θ(T). Thus, we are able to plot the left-hand side of Eq. 2 as function of the inverse temperature for the various salt concentrations. Instead of fitting the three unknown parameters (c_p, ΔH₀, and ΔS₀) for each salinity, we separate the determination of c_p from the thermodynamical parameters. For an appropriate parameter c_p, all the curves should collapse on a single master curve because the enthalpy ΔH₀ and entropy ΔS₀ are independent of the salt concentration. The existence of the collapse using all the data (equilibrium melting curves for all salt concentrations) would be a strong evidence in favor of the theoretical model.

The corresponding value of c_p should be consistent with the expected one,

$$c_p={\sigma }_0/H\simeq 100-500\text{mM},$$

with

$${\sigma }_0=\left(N_p+N_s\right)/d^2\simeq 50-250\text{pmol}.{\text{cm}}^{-2}\text{and}H\simeq 5\text{nm}\text{.}$$

However, because the prefactors in the expression for γ_el are not obtained exactly, a difference by a factor 2–5 may also be expected. Comparison between grafting densities should still be pertinent and we thus expect a stronger electrostatic penalty (larger c_p) for thiols self-assembly than for pyrrole electropolymerization.

Furthermore, the model not only predicts the collapse onto a master curve but also a linear behavior of the master curve as function of the inverse temperature. From this linear behavior, it is possible to extract the thermodynamic parameters ΔH₀ and ΔS₀ of the reference state reaction from a linear fit. The slope is directly related to ΔH₀ and the intercept to ΔS₀. A decrease of the corresponding free energy ΔG₀ due to the presence of point mutations is expected.

Materials and Methods

The Materials and Methods used for this study are described in more detail in the Supporting Material.

DNA sequences and chip preparation

DNA sequences used are given in Table 1. The probes of 16 bases correspond to the SNP G/A A870G of codon 242 on exon 4 of the cyclin D1 gene. The analyzed mutation is placed in the middle of the probes to decrease the affinity for mismatched duplexes to a greater extent. A second mutation is placed adjacent to the analyzed SNP to enhance mutation detection (28).

Table 1.

Probe and target sequences

Probes	Sequences 5′ → 3′	# MM
G	(T)10 TGT GAC CCG GTA AGT G	PM
A	(T)10 TGT GAC CCA GTA AGT G	1 MM
TG	(T)10 TGT GAC CTG GTA AGT G	1 MM
TA	(T)10 TGT GAC CTA GTA AGT G	2 MM
PC	(T)10 TGG AGC TGC TGG CGT
Targets	Sequences 5′ → 3′
Gc	CTC ACT TAC CGG GTC ACA CT
PCc	ACG CCA GCA GCT CCA

PM, perfect match; MM, mismatch. Mismatches are represented in boldface. Note that, on the 5′ end, depending on the grafting procedure, either a pyrrole moiety or a thiol (SH(C)₆) is present on the probes.

The DNA chips are prepared on a gold-coated glass prism for surface plasmon resonance (SPR) applications purchased from GenOptics (Orsay, France). For immobilization purposes with electropolymerization, probes bear a 10-thymidine spacer chain and a pyrrole moiety on their 5′ end. The oligonucleotides are immobilized spot by spot (4,29). The poly-pyrrole spots have a diameter of ∼400 μm and a thickness of ∼5 nm. The probe density obtained is estimated to be ∼2–10 pmol.cm^–2 (29).

The procedure for thiols self-assembly was adapted from Malic et al. (30). The gold-coated prisms are spotted with 10 and 50 μM solutions of thiolated oligonucleotides using an OmniGrid automated spotter (GenOptics). A quantity of 6-mercapto-1-hexanol (MCH) serves to block the remaining gold surface thereby rendering it insensitive to nonspecific DNA adsorption. Successive temperature cycles up to 75°C have not shown any reduction of the hybridization performance except a 10% decrease after the first cycle.

For both chemistries, the amount of probes is very small compared to the targets in solution, thus, we can assume that the target DNA concentration is constant throughout the experiments. Spots bearing different DNA probes are grafted in multiples to control the reproducibility of the signal obtained by SPR imaging. On each prism, additionally to probes used in the analysis, a positive control sequence (PC) and a negative control (poly-pyrrole spots without DNA or MCH-covered gold for thiol chips) are considered. The chips are stocked desiccated under argon atmosphere at 4°C between experiments.

SPR imaging setup with temperature control

Interactions on the DNA spots coated on the gold surface of the prism can be detected using surface plasmon resonance imaging with a charge-coupled device camera (Pixelfly VGA; PCO, Kelheim, Germany) under fixed angle. In this way, local adsorption can be followed in real-time by image analysis (LabView software, GenOptics) without any need for target labeling.

All experiments are carried out on a home-made SPR imaging apparatus coupled to a temperature regulation system as described in Fiche et al. (31). Linear temperature scans are possible from 20 to 85°C with a precision of 0.05°C using a home-made LabView interface (National Instruments, Austin, TX).

DNA hybridization and melting curves

Experiments are carried out in buffer solutions based on phosphate-buffered saline prepared with ultrapure water. The salt concentration is adjusted with NaCl giving final concentrations of monovalent cations from 157 to 620 mM. All reagents were purchased from Sigma (St. Louis, MO).

The flow rate was set to 50 μL/min and DNA hybridizations are carried out for 10 min at 25°C with a target concentration of 250 nM. During hybridization, the absence of nonspecific signal on negative and positive control spots is controlled. Linear temperature scans are performed at 2°C/min while keeping the DNA concentration constant in the reaction cell (equilibrium DNA melting). The target solution is maintained in the hybridization chamber while pushing and aspiring alternatively to keep the liquid agitated.

Results

Equilibrium melting curves

In this study, we used the temperature-regulated SPR imaging system to acquire equilibrium melting curves on microarrays (28,31,32). To check that equilibrium is effectively obtained, we performed heating and cooling cycles at controlled temperature scan rate and check for DNA melting curves superposition without hysteresis. Experiments were first carried out using static conditions, i.e., no flow applied during the temperature scans. Under these conditions, the thermodynamic equilibrium was not reached. During cooling, the initial hybridization level was not regained and hysteresis was observed. As it turned out, the annealing process is penalized mainly by insufficient mass transport (11). To improve the situation without decreasing further the scan rate of 2°C/min, agitation of the solution was applied during temperature scans. The automated syringe pump pushes the liquid back and forth without any net flow. In this way, we were able to establish thermodynamic equilibrium over most of the temperature range considered. Only one region near the onset of annealing at high temperatures is perturbed; it shows a slight opening for the microarrays with probes grafted through electropolymerization of pyrrole (see Fig. 2). It must, however, be noted that this region is possibly affected by temperature hysteresis due to the fast change of the set point at T = 75°C. For microarrays with probes grafted through self-assembly of thiols, the higher grafting density increases the electrostatic penalty and slows down the kinetics of hybridization. In this case, equilibrium melting curves were obtained only for the higher salt concentrations (c_s ≥ 400 mM). Strong hysteresis was observed for low salt concentrations (see Fig. 3).

Figure 2.

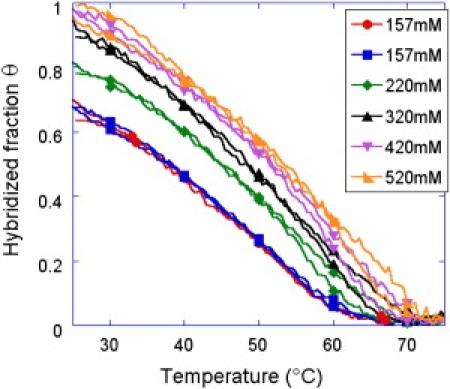
Equilibrium melting curves for various salt concentrations for the probe G grafted by electropolymerization of pyrrole. The reproducibility of the experiments is evident from the two cycles performed at c_s = 157 mM.

Figure 3.

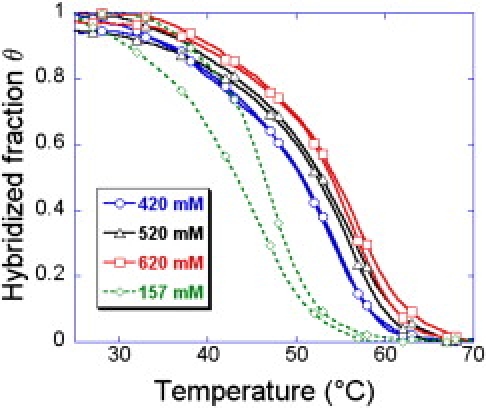
Equilibrium melting curves for various salt concentrations for the probe TG grafted through thiol self-assembling. The melting curve at low salinity c_s = 157 mM shows strong hysteresis.

The equilibrium melting curves show a good reproducibility as can be seen from the two different temperature scans at c_s = 157 mM in Fig. 2. The curves have been set to their hybridization fraction at the onset of the temperature scan with normalization applied to the whole heating and cooling cycle simultaneously, so that any differences in heating and cooling would be conserved.

For both chemistries (Figs. 2 and 3), the fraction of hybridized probes decreases with decreasing salt concentration of the buffer. Salt effects provoke strong variations in melting temperature and hybridization signal at low salt concentrations, but become insignificant at large salt concentrations of c_s ≥ 400 mM, in the case of pyrrole electropolymerization grafting (Fig. 2). This suggests that c_s = 400 mM is the ideal salt concentration to suppress electrostatic interactions without unnecessarily decreasing the specificity of the probe-target interactions in this case. For thiol self-assembly, the electrostatic interactions are sensible up to c_s = 620 mM, suggesting already a larger grafting density and charge surface. The presence of hysteresis at low salt concentration (example of c_s = 157 mM on Fig. 3) may also be explained by those increased electrostatic interactions. It is clear that an increased surface charge reduces the kinetics of hybridization of the targets due to the increased repulsion.

Another difference in the equilibrium melting curves obtained with the two grafting chemistries concerns the width of the transition. While the melting spans nearly 30°C for the grafting by electropolymerization of pyrrole, the thiols self-assembly shows a reduced span of 20°C. For practical applications, we may expect to detect more easily a difference in melting temperature and thus detect a point mutation with the later grafting chemistry (28).

Collapse onto a master curve

Those equilibrium melting curves for various salt concentrations allow us to test the extended Langmuir model incorporating the electrostatic interactions. For hybridization in solution, salt effects are assumed to modify only the entropy of the reaction in a logarithmic way (ΔS + δ log c_s with δ proportional to the charges in the formed duplex) (27). In the case of hybridization with one of the strands grafted to a surface, the correction is also mainly entropic but linear in the fraction of hybridized probes θ and inversely proportional to the salt concentration (ΔS₀ – RN_tc_p(1 + αθ)/c_s with Γ = N_tc_p/c_s from Eq. 2). To test the theoretical predictions, it is possible to plot the left-hand side of Eq. 2 versus the inverse of the temperature for each salt concentration. All the curves should collapse for one particular value of c_p corresponding to the number charge concentration of the probe layer before hybridization. Furthermore, the corresponding collapsed master curve should be linear with the inverse temperature so that we are able to obtain the corresponding thermodynamic parameters ΔH₀ and ΔS₀ by linear regression. This procedure allows us to separate the determination of the parameter c_p from the thermodynamic parameters ΔH₀ and ΔS₀. Furthermore, all the experimental data are used for the determination of c_p, which imposes strong constraints on the model.

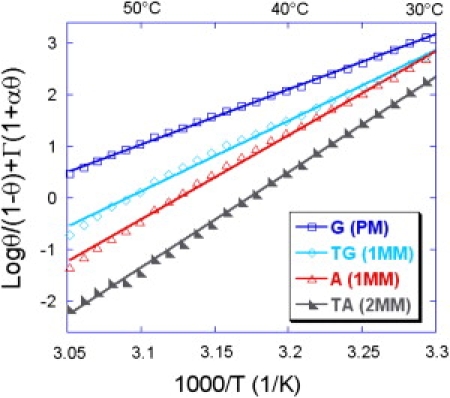
To obtain the best value for c_p, the left-hand side of Eq. 2 is calculated for the normalized reflectivity data that reflects θ at each temperature (Figs. 2 and 3). The regions with θ ≃ 0 and θ ≃ 1 are excluded because the logarithm term enhances the experimental errors. The value of c_p is chosen to minimize the standard deviation between the curves for the different salinities yielding the best collapse. With this value of c_p, the collapse of the different curves is optimized and leads to a sensible test of the theoretical predictions. By this method, we obtained a parameter c_p = 13 ± 5 mM for the poly-pyrrole electropolymerization grafting (Fig. 4). The good collapse confirms the validity of the model we applied. From this value and assuming a constant height H ≃ 5 nm for the probe layer, we obtain a grafting density of 0.3 pmol.cm^–2, which is one-order-of-magnitude lower than expected. However, despite possible crude estimate of the experimental parameters, it has to be noted that the prefactors have been neglected in the model, which may explain part of the discrepancy. Another possibility concerns the grafting chemistry itself. The electropolymerization of pyrrole leads to the presence of a small cushion of poly-pyrrole of height 5 nm that may enhance the effective probe layer thickness by a factor two, reducing by the same factor the charge concentration c_p. Residual positive charges in the poly-pyrrole film may also explain the apparent reduction of the charge concentration of the probe layer.

Figure 4.

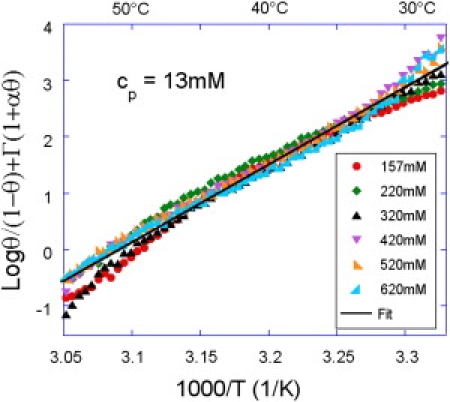
Collapse of the equilibrium melting curves onto a master curve for the probe TG grafted by electropolymerization of pyrrole with a concentration c_p = 13 mM of charges in the probe layer.

The thiols self-assembly was realized with two different concentrations of thiolated oligonucleotides (10 μM and 50 μM), yielding c_p = 39 mM and 53 mM, respectively. These parameters are obtained only from salinities c_s ≥ 420 mM, because lower salinities displayed hysteresis and thermodynamic equilibrium is thus not reached. The three curves can, however, be considered as relevant because the melting temperature still increases significantly when passing from c_s = 520 mM to 620 mM. The c_p values are consistent with higher charge densities on thiol-modified DNA surfaces than for poly-pyrrole grafting. Furthermore, a higher concentration of thiols also leads to an increased grafting density ranging from 0.75 to 1 pmol.cm^–2.

Finally, the parameter c_p should only depend on the microarray preparation (grafting density and probe layer thickness) but not on the sequence of the probes. This is confirmed by the fact that for each grafting chemistry considered, the same value for c_p was able to collapse the equilibrium melting curves for the different probes. This suggests that the probe density is mainly dependent on the grafting chemistry but not on the probe sequences, especially when these present the same length but only differ by point mutations.

Thermodynamic parameters

The master curves obtained after rescaling with the appropriate value of c_p are averaged and presented on Figs. 5 and 6 for both grafting chemistries for the different probes considered in this study. First of all, it is clear that the linear part is larger for the poly-pyrrole grafting chemistry than for the thiols self-assembly, similarly to the temperature span of the melting transition. From a linear fit (minimization of the mean-square difference), it is possible to extract the enthalpy ΔH₀ and the entropy ΔS₀ of the reference state reaction directly from the slope and intercept. Those data are presented in Table 2 with the corresponding free energy ΔG₀ calculated at 37°C. These parameters reflect the different duplex stabilities for complementary and mismatched duplexes. As can be seen from Table 2, the single-point mismatch reduces the free energy by nearly 0.3–0.5 kcal/mol whereas two successive mutations have a stronger effect of nearly 1 kcal/mol. This difference may be used to detect single-point mutations from temperature scans (28).

Figure 5.

Collapsing master curves for all probes grafted by electropolymerization of pyrrole. Enthalpy ΔH₀ and entropy ΔS₀ are extracted from linear fits.

Figure 6.

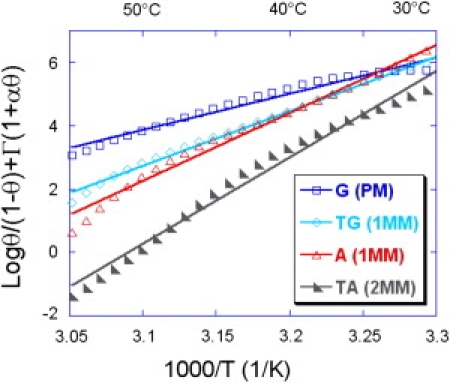
Collapsing master curves for all probes grafted by self-assembling of thiols. Enthalpy ΔH₀ and entropy ΔS₀ are extracted from linear fits.

Table 2.

Enthalpy ΔH₀ in kcal/mol and entropy ΔS₀

For target Gc		Poly-pyrrole grafting			Thiols self-assembly
Probes	#MM	ΔH0	ΔS0	ΔG0	ΔH0	ΔS0	ΔG0
G	PM	–21.2	–33.4	–10.9	–22.6	–32.1	–12.7
A	1 MM	–32.6	–71.7	–10.4	–42.9	–98.3	–12.4
TG	1 MM	–27.2	–54.0	–10.5	–34.4	–71.1	–12.4
TA	2 MM	–36.8	–86.6	–10.0	–54.4	–138.0	–11.6

Measured in cal/mol/K from linear fits of the collapsed master curves for the different probes and grafting chemistry (errors from the fits are ∼1%). Corresponding free energy ΔG₀ in kcal/mol calculated at 37°C.

As expected, those thermodynamic parameters differ from the ones calculated with the NN model (27) for the same reaction in solution. As already discussed in Langmuir Model with Electrostatic Interactions, this is not surprising because ΔH₀ and ΔS₀ correspond to the thermodynamic parameters of the reference state reaction (without electrostatic interactions) and not to the parameters of the reaction in solution. To compare the parameters, we would need to know the thermodynamic parameters for uncharged chains in solution.

More surprising is their evolution with an increasing number of mutations. ΔH₀ and ΔS₀ decrease whereas their analogs for the reaction in solution are increasing. This may not be explained by the fact that they apply to the reference state. We could expect some grafting modifications to be the origin of this phenomenon. For example, similar results were obtained when studying the effects of probe lengths on the thermodynamic parameters (31). The origin of the problem was believed to be the entrapment of the probes in the polymer matrix of the poly-pyrrole. However, in this study, we considered two different grafting chemistries and in the case of thiol self-assembling microarrays, the entrapment of the probes may not be an explanation. Probe-probe interactions were suggested recently to affect importantly the thermodynamic parameters (24). This may be the explanation for our results. Possibility for interchain hybridization of four consecutive GC pairs was detected for the perfect match probes. Only two GC and two AT pairs or four GC and two AT pairs with an internal mismatch for the single-mismatch probes and two GC pairs and two AT pairs for the double-mismatch probes were detected. The probe-probe interactions are decreasing with the number of mismatches. Thus, we may expect that the perturbation due to those probe-probe interactions (not considered in the model) may explain the effects on the thermodynamic parameters.

More interesting is the fact that the difference in the thermodynamic parameters between the two grafting chemistries is low, ∼20% and within the experimental errors, and increases with the number of mutations present in the sequence. Those parameters were not expected to be dependent on the grafting chemistry, but more-precise experiments may be necessary to determine whether this difference is relevant or mainly due to experimental errors.

Discussion and Conclusions

Fundamental studies on DNA duplex stability with free DNA in solution are common. Systematic melting analysis of a huge number of oligonucleotides permitted to establish the NN parameters for all possible combinations of basepairs in the double-helix including mismatches, dangling ends, and salt corrections (27). Those data are at the basis of steadily improved predictions for melting temperatures, secondary structures, etc., for any possible DNA sequence. They are often used for microarray applications even though the validity of those parameters in such conditions has not been demonstrated. This issue has been critically noted by Levicky and Horgan (2), who solicited further experiments on solid phase hybridization to gain insight and control for microarray applications.

Today several integrated heating or denaturing systems are available that permit us to obtain melting profiles on DNA microarrays. To date, most experiments studying melting curves on microarrays use fluorescence analysis. Polyacrylamide gel pads are used to immobilize DNA in a three-dimensional matrix and fluorescent labeling is then used as a signal transducer (33,34). In those cases, the probes are in a three-dimensional environment and the effects of the surface are reduced. Because main applications are using probes grafted directly to the surface, it would be interesting to obtain melting curves in those conditions. In fact, there exist some experimental techniques to detect the hybridization fraction for probes directly grafted to the surface. Recently, Genewave (Palaiseau, France) proposed a new product, hybLIVE, allowing the real-time measurement of hybridization and melting on standard microarrays using fluorescence but with probes grafted directly on glass slides (35). Previously, Krull et al. (36) grafted the probes to an optical fiber to study the solid-phase melting curves in combination with fluorescent labeling. They compared bulk and surface hybridization for different grafting densities and at different salinities. In both cases, because many fluorophores are less efficient at elevated temperatures, the signal needs to be corrected. Moreover, it has been shown that fluorescent labeling, depending on the dyes and spacer chains employed, may alter the free energy associated to DNA duplex formation (37). Thus, investigation of DNA melting curves for on-chip experiments should also use label-free techniques in order to study exclusively the thermodynamic changes due to the interactions between the DNA and its support. As a rare exception, Biswal et al. (38) proposed a label-free melting curve detection system based on the deflection of microcantilevers, and Peterlinz et al. (21) obtained melting curves by washing the biosensor surface with heated buffers using SPR detection. Our temperature scan method coupled to SPR imaging presents a novel, simple, and direct solution to obtain information on the DNA hybridization at surfaces from equilibrium melting curve analysis (28,31).

First of all, we have seen that mass transport to and from the surface plays a crucial role for establishing favorable conditions for equilibrium hybridization (11). This is not only true in the case of equilibrium melting curves of short targets, but can be generalized for microarray hybridization experiments which need a constant flow of targets to the surface to achieve optimum hybridization kinetics.

Furthermore, we have seen that the electrostatic interactions are essentially linked to the grafting density of the probes and depend strongly on the salt concentration, the effects being observed up to very high concentrations (c_s > 0.5 M). Our modified Langmuir model, which incorporates the electrostatic penalty occurring during the target hybridization, seems to reproduce correctly the experimental data for various salt concentrations, as well as for the presence or absence of mutations in the probe sequences and for two different grafting chemistries. At this point, it is important to notice the influence of the grafting chemistry which seems to extend farther than to the grafting density of the probes alone. The lack of a universally recognized grafting chemistry for DNA microarray fabrication is evident when considering the list of all possible alternatives developed. It seems that each has its own advantages and drawbacks. In our case, the small cushion of pyrrole formed by electropolymerization renders the grafting dispersed on a height of 5 nm while the temperature resistance of the grafting is excellent (temperature scans up to 85°C without affecting the hybridization properties). The thiols self-assembly seems to produce a more homogeneous probe layer directly grafted on the gold; however, the stability is reduced, especially for temperatures higher than 75°C, and the conservation of the microarrays over a long period is critical.

Only few previous studies were concerned by the effects of the salt concentration on the hybridization of DNA to microarrays. Peterlinz et al. (21) compared the salt effects for tethered DNA and free DNA in solution. There, the melting temperatures for tethered strands seemed to follow the logarithmic dependence observed for the same reaction in solution. We observed similar results for the melting temperatures in our experiments. However, when applied to the whole equilibrium melting curves, this simple model failed to collapse the curves appropriately. It seems that the electrostatic penalty explicitly depends on the fraction of hybridized probes as proposed by the modified Langmuir model. The simple explanation is that the surface is increasingly charged as soon as the target hybridization occurs. The electrostatic penalty is thus increasing upon hybridization. More-recent experiments at room temperature and for various grafting densities also confirmed the presence of different hybridization regimes related to the ratio c_p/c_s between the charge concentration in the probe layer and the salt concentration (23,24). The most recent study (24) directly compared experiments and theory, which also serve to validate the extended model presented here. In our experiments, the good collapse of the equilibrium melting curves for all the salt concentrations gives a strong validation of the model. As expected, the only adjustable parameter, c_p, suggests a stronger grafting density for the thiols self-assembling compared to the poly-pyrrole electropolymerization grafting chemistry. An important point is the lack of grafting-chemistry dependence of the thermodynamic parameters. For the future, another possible test for the modified Langmuir model would consist in varying the target's lengths. Because σ₀ and H only depend on the probes, the curves should collapse for the same value of c_p. However, possible steric interactions of dangling ends from longer targets upon hybridization to shorter probes could also affect the results (25).

In conclusion, the effects of the electrostatic penalty on the DNA hybridization on solid support have been shown to be relevant up to salinity as high as 0.5 M for the monovalent salts currently used in practical applications. Furthermore, the melting curves at different salt concentrations present an electrostatic penalty, in agreement with the theoretical predictions that differ from the solution phase reaction. A useful expression for the practitioners of microarrays relates the hybridization content to the salt concentration and grafting density:

$$\frac{\theta }{1-\theta }=c_t{K}_0\left(t\right)\exp \left(-\frac{c_p}{c_s}{N}_t\left(1+\alpha \mathit{\theta }\right)\right)\text{.}$$ (3)

The salt concentration c_s appears explicitly with the concentration of charges in the probe layer

$$c_p=\left(N_p+N_s\right)/d^{2}H,$$

which involves not only the grafting density 1/d² (or probe distances d) but also the height H of the probe layer and the number N_p + N_s of charges in the probes (plus spacers if any). This concentration may generally be estimated for each microarray fabrication protocol. The expression

$$\alpha =N_t/\left(N_p+N_s\right)$$

is the experimentally known ratio between the numbers of target charges and probe (plus spacer) charges. Finally, the reaction constant K₀(T) is sequence- and temperature-dependent. Dedicated studies comparable to those performed to determine the NN parameters for the DNA hybridization in solution could be considered to obtain the NN parameters for the reaction constant K₀(T). The fact that both chemistries lead to similar thermodynamical parameters suggests that the NN parameters may be universal for the hybridization of DNA at the surface.

Finally, we consider that the effort for a better understanding of the mechanisms of DNA hybridization on a solid support should be continued. It should bring a sufficient background that will be useful for practical applications in order to improve the microarray fabrication and the choice of the protocol parameters.