Laser-Assisted Single-Molecule Refolding (LASR)

Abstract

To assemble into functional structures, biopolymers search for global minima through their folding potential energy surfaces to find the native conformation. However, this process can be hindered by the presence of kinetic traps. Here, we present a new single-molecule technique, termed laser-assisted single-molecule refolding (LASR), to characterize kinetic traps at the single-molecule level. LASR combines temperature-jump kinetics and single-molecule spectroscopy. We demonstrate the use of LASR to measure single-molecule DNA melting curves with ∼1°C accuracy and to determine the activation barrier of a model kinetic trap. We also show how LASR, in combination with mutagenesis, can be used to estimate the yields of competing pathways, as well as to generate and characterize transient, unstable complexes.

Introduction

To become active, biological macromolecules (e.g., proteins, RNA, and DNA) must fold from a linear chain into a native three-dimensional structure following pathways determined by their folding potential energy surfaces. However, these potential energy surfaces can be rugged and rife with local energy minima that confine the biopolymer into long-lived intermediate states called kinetic traps (1). Kinetic traps can impede biological function because they prevent the formation of the native state. In vivo, kinetic traps can be resolved by refolding the biopolymer with the help of chaperones, helicases, and other cellular folding cofactors (2–5). To understand the macromolecule refolding problem, it is necessary to characterize kinetic traps by determining their activation barriers, but this can be very challenging because the barrier may be significantly higher than thermal energy at room temperature (k_BT).

Single-molecule microscopy-based approaches are ideally suited to study kinetic traps because they enable such traps to be identified even in the presence of other conformations in solution. Single-molecule Arrhenius and Eyring analyses of folding rate constants can be used to determine energy barriers but for technical reasons are limited to temperatures below ∼50°C, (J. Fiore and D. Nesbitt, JILA/NIST Quantum Physics Division, University of Colorado, personal communication, 2010), which may not be high enough to melt many nucleic acid folds. Furthermore, Mg²⁺ ions, which play an important role in RNA folding (7,8), can cleave the backbone of RNA molecules at high temperatures (>50°C), making it impractical to study deep kinetic traps in their presence.

Here, we report a new single-molecule technique, termed laser-assisted single-molecule refolding (LASR), that enables characterization of the activation barriers of deep kinetic traps by combining traditional single-molecule detection with infrared (IR) laser-induced temperature jumps (T-jumps) (9–12). An IR laser is used to excite the second overtone of the water OH stretch (∼1400 nm) (13) and thus rapidly increase the solvent temperature. As a result, kinetically trapped biopolymers in solution receive sufficient thermal energy to overcome the refolding activation barrier. Our T-jumps are transient (but reversible) temperature increases, and thus differ from traditional ones. We demonstrate the application of LASR to measure single-molecule melting curves of double-stranded DNAs (dsDNAs) and to characterize a model kinetic trap comprised of two complementary hairpin RNAs that can form a stable loop-loop interacting complex (kissing complex).

Materials and Methods

DNA labeling and purification

DNA samples were purchased from Sigma (St. Louis, MO) with no modifications or with a 3′-biotin, 5′-Cy3, and internal amino-modified dT for Cy5 labeling (for sequences see Table S1 in the Supporting Material). Modified DNAs were purified and Cy5-labeled as previously described (15). Unmodified DNAs were used without further purification.

RNA labeling and purification

RNA samples were purchased from the W.M. Keck synthesis facility at Yale University with a 5′-biotin (B) and 3′-amino linker for Cy3 labeling (HP1 and HP3; Table S1) or with a 5′-Cy5 (HP2 and HP4; Table S1). All RNA samples were purified and labeled as described previously (15).

Ultraviolet melting experiments

Ultraviolet (UV) melting experiments for the DNA duplexes were carried out on a Beckman Coulter spectrophotometer (DU800; Beckman Coulter, Brea, CA). Equal amounts (2 μM) of two complementary DNA strands (Table S1) were mixed in standard buffer (50 mM TRIS-HCl, pH 7.5, 10 mM Mg²⁺, total volume 100 μL), heated to 90°C for 2 min, and then cooled at room temperature for >15 min. The duplex absorbance at 260 nm (1 cm light path) was measured at room temperature. The solution was then diluted in standard buffer until the absorbance reached ∼1 OD. The sample absorbance at 260 nm (0.5 s averaging time) was monitored as temperature was increased from 15°C to 95°C at 1°C/min rate to generate melting curves (see black curves in Fig. 3). Experimental data were then analyzed with the use of the Melt Curve Processing Program (MeltWin V3.5 build 010401) to obtain melting temperatures.

Figure 3.

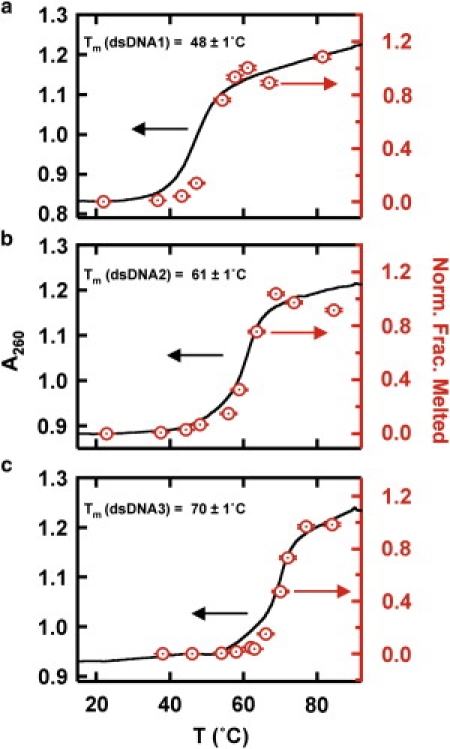
Validation of LASR. UV melting curves (black) for DNA duplexes (a,b, and c, as indicated) and corresponding normalized single-molecule melting curves (red). Single-molecule melting curves are obtained by calculating the fraction of molecules that transition from low to high FRET after a LASR T-jump, and normalizing the high-temperature fraction to one. Error bars were calculated as $1/\sqrt{n}$, where n is the number of molecules observed.

LASR experiments

T-jumps were generated using a broadband supercontinuum fiber laser (SC450; Fianium, Eugene, OR). IR radiation was selected using a long-pass filter (RG665; Schott, Cambridge, UK) and introduced through the total internal reflection prism, but at an angle more acute than the total internal reflection angle. A small portion of red light was kept for alignment purpose. When not used, the IR laser was blocked using a computer-driven shutter. The shutter was opened for 1 s for heating. Neutral density (ND) filters were used to attenuate the IR laser power and control the jump temperature. The CCD camera was blocked during heating to avoid damaging the CCD chip. Multiple experiments at various jump temperatures were performed to obtain the LASR curves (see Fig. 5), and then fit to the following hyperbolic equation:

$$f\left(T\right)=f_0+\left(f_{\text{max}}-f_0\right)\frac{T^n}{T_C^n+T^n}$$ (1)

where f(T) is the fraction reacted at a temperature T; f₀ and f_max are the initial and final fractions reacted, respectively; T_c is the critical temperature (refolding or dissociation); and n is a cooperativity factor.

Figure 5.

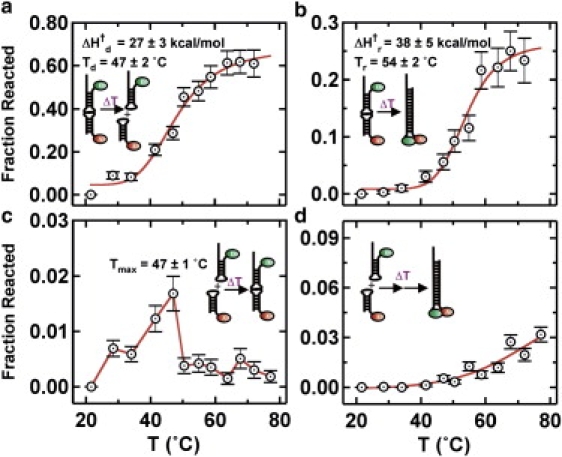
Temperature-dependent LASR curves. (a) Temperature dependence of LASR-induced kissing complex dissociation. (b) Temperature dependence of LASR-induced extended duplex formation. (c) Temperature dependence of LASR-induced kissing complex formation. (d) Temperature dependence of LASR-induced extended duplex formation from free hairpins.

Temperature calibration

The jump temperature was calibrated using an in-house-built, micrometer-sized gold sensor. The sensor was fabricated on a microscope slide and assembled into a microfluidic channel in standard buffer (Fig. S1). The experimental geometries for the gold wire and the sample were maintained almost identical, and therefore only small differences in thermal properties are expected. IR laser radiation was introduced through the total internal reflection prism, but at an angle more acute than the total internal reflection angle. The sensor's electric resistance was measured with a multimeter (34401A; Agilent, Santa Clara, CA). With the sensor on top of the microscope objective, the laser was aligned by maximizing the sensor's electrical resistance using a fine-tuned translation stage with micrometer accuracy. The IR laser was then blocked using a computer-driven shutter. The shutter was opened for 1 s to heat the sensor, and its electrical resistance was recorded. Different ND filters were used to attenuate the IR laser power and control the jump temperature. The IR laser intensity in the H₂O absorption bands was determined by measuring the laser intensity before and after a 1 cm water cuvette. The sensor's electrical resistance increase was then converted to temperature with the use of Fig. S1. The jump temperature should be calibrated before each LASR experiment.

Results and Discussion

Description of the method and temperature calibration

To image single molecules, we used an in-house-built, prism-based total internal reflection fluorescence microscope with laser excitation at 532 nm, as described previously (16). To generate T-jumps, we used an IR laser source that could be absorbed by water molecules in the sample (see Materials and Methods). To monitor the T-jump, we first measured the emission from single, surface-immobilized, fluorescent beads, the intensity of which decreased with increasing temperature. The normalized fluorescence intensity from a single bead at room temperature (T = 22°C) exhibited a stable emission before the jump (t < 10 s; Fig. 1 a). In the presence of IR radiation (Fig. 1 a, purple), the bead fluorescence decreased rapidly, indicating an increase in the bead's surrounding temperature. When the IR laser was turned off (t = 14 s; Fig. 1 a), the bead fluorescence intensity recovered exponentially, indicating that the bead's surrounding temperature returned to its initial value. An exponential fit to the fluorescence recovery curve (Fig. 1 a, inset) revealed a time constant of 110 ± 10 ms.

Figure 1.

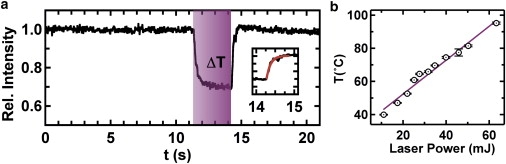
Principle of LASR. (a) T-jump profile. Normalized emission time trajectory of a single fluorescent bead. The heating period is highlighted in purple. During heating, the bead's fluorescence emission intensity decreases and then recovers rapidly after the T-jump. Inset: Exponential fit to the fluorescence emission recovery. (b) T-jump calibration curve. Jump temperatures are controlled by ND filters. Temperature is calibrated with a micrometer-sized gold sensor.

To calibrate the temperature reached during the jump, we used a micrometer-size gold sensor whose electrical resistance was linearly dependent on temperature (Fig. S1). The sensor was positioned on the slide surface in standard buffer (50 mM TRIS-HCl, pH 7.5, 10 mM MgCl₂) and exposed to IR radiation for 1 s. An increase in electrical resistance was recorded during the T-jump, consistent with a temperature increase in the sensor surroundings (Fig. S1). The wire resistance was so much larger than the resistance of the rest of the circuit that the temperature dependence of the rest of the circuit did not make any significant impact on the calibration. ND filters were used to adjust the IR laser power and the final jump temperature (T_jump). The resulting calibration curve (Fig. 1 b) shows that T_jump increased linearly with IR laser power, as expected. This curve enabled us to control T_jump with ∼1°C accuracy, demonstrating that LASR provides an accurate means to control temperature increases in a range that is useful for biopolymer folding studies (20–90°C).

LASR validation by dsDNA melting

To validate this technique, we used LASR to melt DNA duplexes with varying lengths and melting temperatures. Three DNA duplexes with 18, 21, and 24 basepairs (dsDNA1–3, respectively; Table S1) were designed to melt between 50°C and 70°C. The DNA sequences were engineered to form stable heteroduplexes, to prevent formation of homodimers, and to form stable DNA hairpins in the absence of the complementary strand (Fig. 2 a). We determined their melting temperatures (T_m = 48 ± 1, 61 ± 1, and 70 ± 1°C, respectively; Fig. 3, black curves) by ensemble-averaged UV-melting experiments that monitored the oligonucleotides' absorbance change at 260 nm as a function of temperature, as described previously (17). For the single-molecule LASR experiments, we labeled one of the DNA strands with a 5′-Cy3, a Cy5 near the 3′ end, and a 3′-biotin for surface immobilization (Fig. 2 a, Table S1). In the heteroduplex conformation, the fluorophores are far from each other, resulting in low fluorescence resonance energy transfer (FRET; Fig. 2 a). The FRET ratios reported here are apparent FRET efficiencies calculated as I_a/(I_a + I_d), where I_a and I_d are the acceptor and donor fluorescence intensities. Single-molecule FRET time trajectories of the surface-immobilized, fluorophore-labeled dsDNA1 show a stable ∼0.15 FRET before the T-jump (Fig. 2 b). Exposing this DNA to IR radiation for 1 s (T_jump = 60°C; Fig. 2 b, purple) results in a FRET increase to ∼0.95. This result is consistent with DNA duplex melting, diffusion of the unlabeled strand away from the surface, and refolding of the surface-immobilized strand into a DNA hairpin that brings the 5′ and 3′ ends into close proximity (Fig. 2 a). The extremely small concentrations in solution prevent the two strands from reannealing and forming duplex DNA. To rule out temperature-induced chemical instability of the fluorophores, we performed control experiments with donor-only labeled DNA and found that the fluorophore behaved similarly before and after the T-jumps (not shown). Note that all of the FRET ratios reported here are calculated at the same temperature, and therefore temperature-induced changes in fluorescence efficiency are not critical here. An analysis of >900 time trajectories yielded the fraction of DNA duplexes that melt at a given T_jump (Fig. 3 a, red). We then varied the jump temperature between 40°C and 84°C by adjusting the IR laser power (Fig. 1 b) to obtain a single-molecule melting curve (Fig. 3 a, red). The LASR single-molecule melting curves for all three dsDNAs clearly overlap with the ensemble-averaged UV-melting curves, validating both the temperature calibration and the LASR method for measuring single-molecule melting curves. Of interest, the T-jump experiments are nonequilibrium experiments, and the extent of dissociation may change with time and may not be linear with time or temperature. However, we overcome this issue by 1), averaging many hundreds of single-molecule trajectories; and 2), heating on a timescale (1 s) much longer than the expected DNA melting timescale (microseconds to milliseconds). One might expect complete and irreversible melting of all duplexes; however, the maximum melting observed at the highest temperatures is ∼34%, due in part to photobleaching and donor-only labeled molecules.

Figure 2.

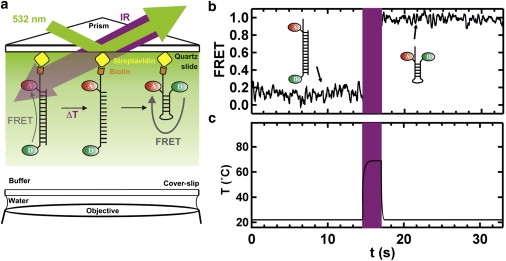
Single-molecule DNA melting. (a) Schematic diagram of LASR applied to DNA melting. A dsDNA is surface-immobilized and fluorophore-labeled. The FRET donor is excited with a 532 nm green laser using total internal reflection fluorescence. The sample is exposed to an IR laser beam for 1 s to generate a T-jump (ΔT), which causes the dissociation of the duplex, and the immobilized DNA folds back to form a hairpin. (b) Single-molecule melting of a DNA duplex using LASR. FRET changed from ∼0.15 (duplex) to ∼0.95 (hairpin) after the T-jump (purple). Experiments were carried out in 50 mM TRIS pH 7.5 and 10 mM Mg²⁺. The dsDNA was immobilized at 25 pM concentration and excess DNA was washed out. (c) Idealized temperature profile.

LASR applied to study a model kinetic trap

We then sought to apply LASR to study the dimerization reaction of two complementary hairpin RNAs that can form a stable kinetic trap, known as the kissing complex (Fig. 4 a). Loop-loop (or kissing) interactions are ubiquitous tertiary structure stabilizing elements in RNA (18–22). Two RNA hairpins (HP1 and 2; Table S1) were designed to have complementary loops that form stable hairpins, to form stable extended duplexes, and to prevent formation of homodimers (N. Salim and A. Feig, Wayne State University, personal communication, 2010). HP1 was labeled with a 3′-Cy3 and a 5′-biotin for surface immobilization, and HP2 was labeled with a 5′-Cy5. The labels are designed to yield zero FRET for the free hairpins, intermediate FRET when the kissing complex forms, and high FRET in the extended duplex conformation (Fig. 4 a). This kissing complex behaves as an ideal model for kinetic traps because formation of the extended duplex is very slow compared to formation of the kissing complex (16). Before a LASR T-jump, surface-immobilized HP1 can readily bind and dissociate HP2 in solution (35 nM HP2, 50 mM TRIS-HCl, 10 mM MgCl₂) to form the kissing complex, as evidenced by the presence of random excursions to 0.45 FRET in the single-molecule time trajectories (Fig. 4, b–e). We previously determined the kissing complex formation and dissociation rate constants at room temperature (k_on and k_off) to be 0.12 and 0.17 s⁻¹, respectively (16). Only three out of >600 observed trajectories exhibit a transition to the extended duplex conformation in the absence of T-jumps as expected for this model kinetic trap.

Figure 4.

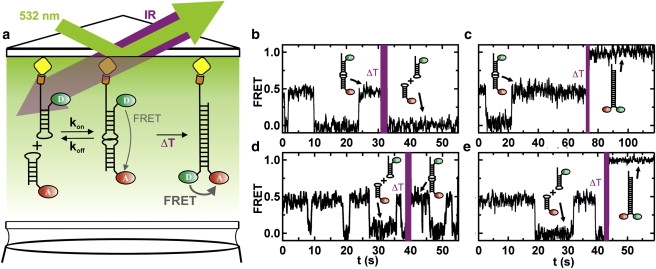
LASR applied to a model kinetic trap. (a) Donor-labeled RNA hairpin (HP1 or HP3) was surface-immobilized on the quartz slide in the presence of an acceptor-labeled complementary RNA hairpin (HP2 or HP4). The kissing complex forms and dissociates at room temperature, but extended duplex formation is slow. LASR causes a T-jump (ΔT) that induces extended duplex formation. (b–e) Characteristic single-molecule time trajectories of LASR-induced kissing complex dissociation, extended duplex formation, kissing complex formation, and extended duplex formation from free hairpins, respectively.

After a T-jump to 67°C, we observed four distinct behaviors (Fig. 4, b–e). Of the 212 molecules in the kissing complex conformation immediately before the jump, 25 ± 3% refold into the extended duplex conformation (high FRET; Fig. 4 c), whereas 62 ± 5% dissociate to the free hairpin conformation (0-FRET; Fig. 4 b), and the remaining molecules stay in the kissing complex conformation. We then varied T_jump from 28°C to 72°C to determine the temperature dependence of the kissing complex dissociation and refolding reactions (Fig. 5, a and b). Our data show that the fraction of molecules that dissociate or refold increases with increasing T_jump, as expected. A hyperbolic fit to the resulting refolding curves (see Materials and Methods) yields dissociation and refolding temperatures T_d = 47 ± 2°C and T_r = 54 ± 2°C, respectively. The refolding temperature is higher than the dissociation temperature because the activation barrier to form the extended duplex is higher than that for dissociation. It is noteworthy that the refolding curve is more cooperative (i.e., with a steeper slope near the transition temperature) than the dissociation curve. This likely indicates that more hydrogen bonds are broken and formed during extended duplex formation than during dissociation.

During the T-jump, a small fraction (1–2%) of the molecules initially in the free state (FRET = 0) form the kissing complex (0.5 FRET; Fig. 4 d). This fraction increases between 28°C and 47°C, and decreases to <1% at higher temperatures (Fig. 5 c). Of interest, the maximum of this refolding curve (T_max) coincides with the dissociation temperature (T_d) because above this temperature, kissing complex dissociation is predominant (Fig. 5 a).

During T-jumps above 40°C, we also observe a small fraction of molecules (≤3%) that transition from the free state (FRET = 0) to the extended duplex (high FRET; Fig. 4 e), and this fraction increases with T_jump (Fig. 5 d). These molecules may reach the extended duplex conformation by two competing pathways that we cannot distinguish (Fig. 6 c): 1), through the kissing complex intermediate; or 2), by melting and annealing HP1 and HP2 during the 1-s T-jump. To test these two possible pathways, we designed an RNA hairpin (HP3; Table S1) that cannot form the kissing complex with HP2 (noncomplementary loops) but is still capable of forming the extended duplex, albeit with a 3 nucleotide internal bulge. Before the LASR T-jump (t < 30 s; Fig. 6 a), single-molecule trajectories of surface-immobilized HP3 in the presence of HP2 in standard conditions show no evidence of kissing complex formation, as expected. After the LASR T-jump (t > 30 s, T_jump = 70°C; Fig. 6 a), however, a small fraction of molecules transition to the extended duplex conformation (high FRET). Because HP2 and HP3 cannot form the kissing complex, these molecules can only reach the extended duplex through pathway 2 (Fig. 6 c). Therefore, the fraction of HP3 molecules that forms the extended duplex represents an estimate of HP1 molecules that form the extended duplex through the melting pathway. The fraction of HP1 molecules that reach the extended duplex is larger than HP3 at all temperatures (compare Figs. 6 b and 5 d), and their difference represents an estimate for HP1 molecules that form the extended duplex through pathway 1. This enables determination of the fraction of HP1 molecules that react through pathway 1 at each temperature (Fig. 6 d). Between 40°C and 80°C, this fraction is constant at ∼80%, indicating that the kissing complex pathway is largely favored over the melting pathway over this temperature range. This result shows that LASR can be used to estimate the yields of competing reaction pathways, a quantity that would be challenging to measure otherwise.

Figure 6.

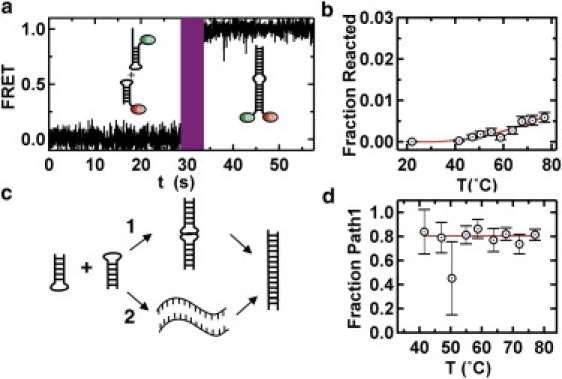
Temperature-dependent refolding reaction pathways. (a) FRET time trajectory of the dimerization reaction of two nonkissing hairpin RNAs with complementary stems. (b) LASR melting curve of the dimerization reaction of two nonkissing hairpin RNAs with complementary stems. (c) Two distinct reaction pathways for hairpin RNAs dimerization reaction. Reaction pathway 1 goes through the kissing complex intermediate structure. Reaction pathway 2 goes through unfolded hairpin structures. (d) Ratio of yields of both reaction pathways.

A fourth RNA hairpin (HP4; Table S1) was designed to form a kissing complex with HP1 (complementary loops) but not to form a stable extended duplex (noncomplementary stems). Before the LASR T-jump, single-molecule trajectories of surface-immobilized HP1 in the presence of HP4 in standard conditions clearly show the formation of the kissing complex, as expected (t < 30 s; Fig. S2 a). After a T-jump to 75°C, we observed that 25% of the molecules in the kissing complex immediately before the jump refolded into a high-FRET conformation. However, this conformation differs from the extended duplex (Fig. 4, c and e) in two ways. First, its average FRET ratio is slightly lower than that of the extended duplex (0.95 vs. 1.0; compare Fig. S2 a and Fig. 4 e). Second, its FRET ratio drops to zero after a few seconds, whereas the extended duplex remains stable in the high FRET for the duration of the experiment. Based on these observations and the sequences of HP1 and HP4, we assigned this new species to a transient RNA duplex that is stabilized by up to 9 basepairs from the loops of HP1 and HP4 (Fig. S2 and Table S1). This experiment enables us to determine the stability of this transient RNA duplex by measuring the dwell-time distribution in the high-FRET state (Fig. S2 b). An exponential fit to this distribution reveals a dissociation rate constant k_diss = 0.07 ± 0.01 s⁻¹. These results show that LASR can be used to generate and characterize transiently stable RNA species that cannot be observed otherwise. This may be useful for studying short RNA duplexes, such as the 7 nt seed regions of micro RNAs that are important for micro RNA target recognition (23).

Transition-state analysis using LASR

To obtain transition-state parameters for the kissing complex dissociation and refolding reactions, we derived an expression based on transition-state theory and the Gibbs-Helmotz equation (see Supporting Material). This expression was used to fit the LASR dissociation and refolding curves (Fig. 5, a and b, red curves) to obtain the activation energy barrier (ΔH^‡). For the dissociation reaction, we obtain ΔH^‡_d = 27 ± 3 kcal/mol, which is in excellent agreement with previous bulk studies (N. Salim and A. Feig, Wayne State University, personal communication, 2010). To further validate this analysis, we determined ΔH^‡_d, by single-molecule Eyring analysis. We measured k_on and k_off at temperatures ranging from 15°C to 23°C using a temperature-controlled microscope stage (Fig. S3). At higher temperatures k_on and k_off could not be determined because the number of kissing complexes observed decreased with temperature. A linear fit to an Eyring plot of k_off as a function of temperature yields a dissociation activation energy barrier ΔH^‡_d = 29 ± 7 kcal/mol, which is in excellent agreement with the value obtained with LASR.

For the refolding reaction, a fit to the LASR data results in ΔH^‡_r = 38 ± 5 kcal/mol (Fig. 5 b), which is higher than ΔH^‡_d, as expected. However, because the kissing complex is a deep kinetic trap, most molecules dissociate before forming the extended duplex, and thus ΔH^‡_r cannot be readily determined by other methods, including single-molecule Eyring analysis. Therefore, LASR presents a unique opportunity to determine transition-state parameters that cannot be measured otherwise.

Conclusions

The ability to characterize folding kinetic traps is critical for understanding the refolding mechanisms of biological macromolecules. However, this can be challenging because of the high-energy barriers involved. Here, we have demonstrated how a new single-molecule technique, LASR, can be used for this purpose. By combining T-jump kinetics with single-molecule spectroscopy, we are able to drive refolding reactions that would otherwise be hindered by large kinetic barriers. We first showed how LASR could be used to study DNA melting at the single-molecule level for three dsDNAs with melting temperatures ranging from 48°C to 70°C. A comparison with an ensemble averaged DNA melting assay confirms the accuracy of the LASR measurement. We then used LASR to study the refolding reaction of a model kinetic trap, an RNA kissing complex, into an extended duplex. From the resulting LASR temperature curves we obtain quantitative energy barriers for the kissing complex reactions that we validate against two other measurements at the single-molecule level and in bulk. The primary advantage of LASR is that it enables us to study reactions that would otherwise be very challenging with other methods. We also demonstrate how LASR combined with mutagenesis can be used to estimate the relative yields of competing reaction pathways, as well as to generate and characterize transiently stable RNAs that cannot be formed otherwise.