The Biophysical Origin of Traveling-Wave Dispersion in the Cochlea

Abstract

Sound processing begins at the peripheral auditory system, where it undergoes a highly complex transformation and spatial separation of the frequency components inside the cochlea. This sensory signal processing constitutes a neurophysiological basis for psychoacoustics. Wave propagation in the cochlea, as shown by measurements of basilar membrane velocity and auditory nerve responses to sound, has demonstrated significant frequency modulation (dispersion), in addition to tonotopic gain and active amplification. The physiological and physical basis for this dispersion remains elusive. In this article, a simple analytical model is presented, along with experimental validation using physiological measurements from guinea pigs, to identify the origin of traveling-wave dispersion in the cochlea. We show that dispersion throughout the cochlea is fundamentally due to the coupled fluid-structure interaction between the basilar membrane and the scala fluids. It is further influenced by the variation in physical and geometrical properties of the basilar membrane, the sensitivity or gain of the hearing organ, and the relative dominance of the compression mode at about one-third octave beyond the best frequency.

Introduction

Hearing relies on the coding of intensity, frequency, and timing of acoustic signals. In mammals, sound processing begins at the outer and middle ear, which improves the efficiency of the delivery of vibrations to the cochlea. The cochlea spatially and temporally separates various frequencies, which are encoded by activity at the auditory nerve (1). Except in the outer and middle ear, the encoding and transfer of sound information is a highly nonlinear process. These nonlinearities are important to perception.

The fundamental mechanism of wave propagation in the cochlea, the slow basilar membrane (BM) displacement waves, was discovered by Von Bekesy in human cadavers (2). In the context of mammalian cochlear physiology, the term traveling waves refers to these displacement or pressure waves, which are slower by orders of magnitude than ordinary acoustic pressure waves that propagate in the cochlear fluids at nearly 1500 m/s and traverse the entire cochlea in just a few microseconds (3). Measurements of BM motion using a laser Doppler velocimeter and other in vivo methods in the sensitive cochleae of many species have further confirmed Von Bekesy's traveling-wave theory (4–6), including its spatial representation (7). It is little appreciated that one of the fundamental nonlinearities is obvious in the measurements of BM velocity and auditory nerve responses to broadband acoustic input, where the derived impulse responses show that the instantaneous frequency of the waveform reaching the measured location changes with time. This behavior is sometimes referred to as frequency modulations (8) or glides (5,8,9), which is a manifestation of the traveling-wave dispersion in the cochlea.(The BM response to acoustic stimulation demonstrates spatial dispersion in addition to frequency dispersion. Unless specifically mentioned, the terms dispersion and glides in this article refer to frequency dispersion.) De Boer and Nuttall (9) observed glides in the BM velocity impulse response at the 4-mm tonotopic (basal) location in the guinea pig cochlea. Similar glides have also been reported at basal locations in other species (e.g., at 3.5 mm in Chinchilla (5)). In the apical region with best frequency (BF) below 1.5 kHz, the instantaneous frequency has sometimes been observed to decrease with time (10). Glides have been observed in passive as well as in active responses, and in many species. Further, glides have been found to be nearly invariant until the passive BF with stimulus intensity, which is also seen in the near-invariance of the phase with level (9). These observations suggest that glides are not the consequence of physiologically active processes. However, glides change with stimulus level beyond the passive BF, thus demonstrating nonlinear behavior.

Both linear and nonlinear aspects of traveling-wave dispersion are important to auditory perception, affecting masking (11–13) and loudness (14). The dispersion influences monaural and binaural encoding of complex sounds (15–17) and has been incorporated into auditory filterbank models, such as the so-called gammachirp (18), for speech processing. In addition, in clinical practice, traveling-wave velocities derived from auditory-evoked brainstem response recordings could be used for diagnosis of Meniere's disease in humans (19). It is also crucial to be able to infer the wave-propagation paths involved in spontaneous and evoked sound emissions from the cochlea to utilize them as tools for studying the biomechanical feedback process known as the cochlear amplifier.

Although substantial theoretical and modeling work on hydrodynamics has supported the existence of cochlear traveling waves (20–22), the physiological basis of active and passive traveling-wave dispersion in the cochlea remains obscure (9). Wave dispersion could be influenced by many factors, such as the nature of elastic coupling and forcing (e.g., beam versus bar or plate versus membrane), acoustic-elastic coupling, geometry and frequency (e.g., nonplanar acoustic modes propagating in a semi-infinite rigid duct), as well as by variations in physical properties, making it difficult to unravel in a complex system such as the cochlea. Using the cochlear model from Zweig (23), Shera (24) proposed that the glides observed in BM velocity responses arise out of glides in the pressure response, and that they result therefore from the global dispersive character of wave propagation in the cochlea. However, the origin of glides in pressure or BM velocity is not explained.

In this article, traveling-wave dispersion is explored in depth by making new physiological measurements in the passive guinea pig cochlea to determine the phase of the BM velocity relative to the stapes to about one octave above the BF. A simple analytical model is presented to explain the observed dispersion in the cochlea. We first show that the basic phenomenon of glides is a fundamental property of any coupled system, where a flexible plate interacts with fluid (even air) in a duct. Spatially varying properties are not necessary to demonstrate the basic frequency dispersion phenomenon. More important, however, we then show how the dispersion in the cochlea is unique and different from the generic coupled plate-duct system. In conclusion, we show how the same analytical model also elucidates traveling-wave dispersion in the active response from a sensitive cochlea.

Materials and Methods

Surgical preparation

Young, pigmented guinea pigs weighing 250–400 g were used in this study. To focus on the basic underlying biomechanical properties for wave dispersion, only postmortem animals were used. This avoided any contribution from active mechanics of the organ of Corti. An opening ∼300 μm wide was made on the scala tympani side of the cochlear basal turn to allow for measurement of BM velocity in anesthetized animals. To avoid optical distortions and fluid vibrations affecting the optical path length, a glass coverslip was placed over the opening. Other surgical details are the same as described previously (25). The experimental protocols used were in accordance with the rules established by the Committee on Use and Care of Animals at the Oregon Health and Science University.

Instrumentation

Acoustic stimuli were generated using a ½-inch condenser microphone (model 4134, Bruel & Kjaer, Norcross, GA) operated as a speaker with a +200-V bias. The condenser microphone was coupled to the external ear of the animal with a plastic speculum, creating a closed sound field. Voltage control to the speaker via an amplifier was from the oscillator output of a lock-in amplifier (model SR830, Stanford Research Systems, Sunnyvale, CA). Individual tones were presented as tone bursts in the frequency range from 1 kHz to 40 kHz in 100-Hz steps. BM velocity measurement was accomplished by directing a laser beam (model 1102, Polytec OFV, Irvine, CA) through a compound microscope at a gold-plated glass bead of diameter 10–30 μm placed onto the basilar membrane. The LDV microscope design is described in a previous article (25). A 100-μm glass bead was used to measure stapes velocity at the incus-stapes joint. The voltage output of the velocimeter was directed to the input of the lock-in amplifier.

Dispersion curves

Dispersion phenomena can be represented as changes in instantaneous frequency with time, as typically used in discussing glides in the BM and auditory nerve responses in the cochlea (5,9,10). In this article, for ease of comparison with the model, an analogous representation of phase speed versus frequency is used. Phase speed is the speed at which the wave front propagates. The effective phase speed, c_p, is derived from velocity measurements simply as c_p = x/t_p, where t_p = −ϕ/ω is the phase delay, x is the effective distance between the stapes and the BM location in the measurement, ϕ is the measured BM phase referenced to the stapes, and ω is the radian frequency of excitation. The effective distance from the stapes to the BM location measured is ∼1 mm smaller than the tonotopic distance along the BM. This is due to the bending of the BM profile in the hook region. The phase speed derived from published data for BM velocity referenced to stapes glides down with frequency until above the BF, analogous to the instantaneous frequency glide from low to high as a function of time.

Results

New measurements of BM and stapes velocities were made in postmortem animals to determine the phase speed of the traveling wave to at least one octave above the BF. To ensure the passive condition, seven guinea pigs were sacrificed after surgery and before data recording. In two of these animals, velocity recordings from both BM and stapes were obtained. Both animals had similar responses, and just one is shown here. We used high sound levels around 85–115 dB sound pressure level (SPL) to measure BM and stapes velocities. This enabled a high signal/noise ratio up to more than one octave above the passive BF.

The measured gain and phase of BM velocity normalized to stapes is very similar to other measured data in the published literature, except that our data extend to higher frequencies (Fig. 1 left). At all the four beads shown in the figure (within 200 μm longitudinal spacing), the amplitude increased up to the passive BF and decreased steeply immediately above the BF and at a slower rate at very high frequencies. The phase showed traveling-wave delay increasing to above the BF; the phase remained nearly flat above one-third octave beyond the BF, at a frequency we refer to as the crossover frequency (COF). At the COF, a notch in magnitude can be observed in the measured data. Both the notch and the nearly flat phase at high frequencies have been attributed to the relative dominance of the compression mode beyond the COF (26–28). It has been speculated that the notch at the COF arises from canceling of the traveling-mode component by the compression-mode component (27,28).

Figure 1.

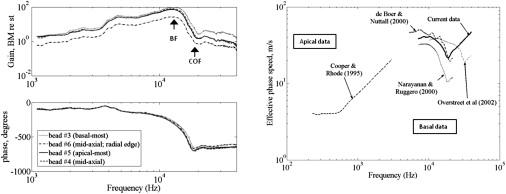
(Left) Our measurements of passive BM velocity toward scala vestibuli referenced to stapes. Magnitude (upper) and phase (lower) at multiple beads located within 200 μm tonotopic spacing. Multiple beads used in the same experiment demonstrated tonotopicity (a bead 200 μm apical has BF smaller by ∼700 Hz) and larger delay with increasing tonotopic distance. In addition, it formed a test for robustness of the data. (Right) Effective coupled phase speeds derived from published data in different species at the base (4,50,51) and at the apex (6). All data are for BM motion toward scala vestibuli; basal data are referenced to the stapes, whereas apical data are referenced to the incus. The effective distance from the stapes to a measured location for the apical data (BF ≈ 250 Hz) is 16 mm (the apical data from Khanna and Hao (52) are very similar and not shown); for current measured data, the distance is 2.3 mm; for the data from Narayanan and Ruggero (50), it is 1.7 mm; for the data from Overstreet et al. (51), it is 1.2 mm; and for the data from de Boer and Nuttall (4), it is 2 mm.

The effective phase speed at the measured location (Fig. 1 right, Current data, derived from the phase shown at lower left) decreases from around the BF (13 kHz) to 18.5 kHz (the COF). Beyond the COF, the effective phase speed increases quite rapidly, approximately linearly with frequency. The phase speeds derived from four other published reports in various species (guinea pigs, gerbils, and chinchilla (Fig. 1)) for BM velocity toward scala vestibuli relative to stapes show a similar trend at the base, although this trend appears to have been disregarded by earlier investigators. At the apex, the phase speed has a different characteristic—it is almost flat or only slightly decreases around the BF, but increases at high frequencies, similar to basal data. The physical basis for these observed trends is not immediately apparent, and it is explored here. The effective phase speed at the basal locations is not shown at low frequencies, because small deviations in the low-frequency measured phase could lead to large deviations in the corresponding phase speeds.

Traveling-wave dispersion in the cochlea

If coiling is neglected, the mechanics of the passive cochlea is similar to that of the two fluid-filled ducts scala vestibuli (SV) and scala tympani (ST) separated by a flexible plate, the BM. Even though the BM interacts with both fluid-filled ducts, the dispersion behavior is similar for BM interaction with only one, owing to the nearly symmetric geometry. The slow forward propagating wave in the cochlea along the BM faces negligible reflection from the apex, as the wave nearly perfectly cuts off at its frequency-dependent best place along the BM. Therefore, the dispersion of the wave propagating along the BM can be approximated by that for a semi-infinite plate-duct system.

Dispersion in a uniform plate-duct system

The coupled phase speeds due to fluid-structure interaction between a flexible plate and fluid in a duct (Fig. 2, inset) can be approximated analytically. For a wave propagating along the longitudinal (x) direction in an isotropic plate interacting with fluid in a single duct, the governing differential equations are

$$g\left[{\left(\frac{d^2}{d{z}^2}\mathrm{-}{k}_x^2\right)}^2\mathrm{-}{k}_B^4\right]U=P_p\text{on}\text{the}\text{plate}\text{surface};$$

$${\nabla }^{2}P+\left(k^2\mathrm{-}{k}_x^2\right)P=0\text{in}\text{the}\text{fluid}\text{.}$$ (1)

Here, U is the outward plate displacement, P is the acoustic pressure in the fluid, P_p is the pressure on the plate surface, k_x is the coupled wavenumber for propagation along the plate, $k=\omega /c$ is the acoustic wavenumber, b is the plate width, k_B = (mω²/g)^1/4 is the plate-bending wavenumber in vacuum, m = ρ_ph is the mass/unit area of the plate, g = Eh³/12(1 − v²) is the flexural rigidity of the plate, E is the Young's modulus of the plate, h is the plate thickness, ρ is the fluid density, c is the speed of sound in the fluid, and ${\nabla }^2$ is the Laplacian operator in two dimensions (y and z). In addition, the plate displacement and fluid normal displacement are equal at the interface.

Figure 2.

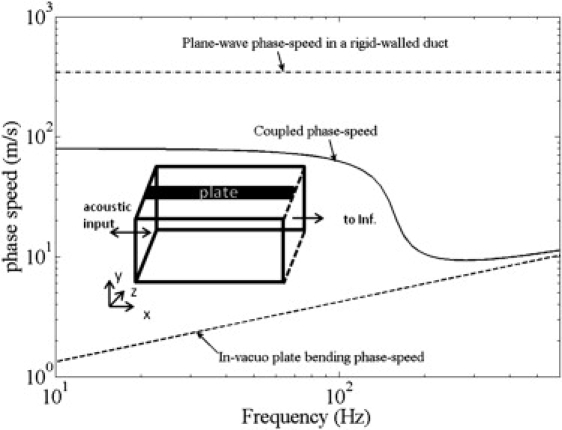
First coupled mode in a uniform thin brass plate clamped along the lateral edges and forming one side wall of an otherwise rigid, air-filled rectangular duct (see inset). The duct is acoustically excited at one end. In general, the plate width could be less than or equal to the duct width, although in this example the width of the plate is the same as that of the duct.

In this article, a variational (or integral) formulation of the governing equations shown in Eq. 1 is adopted from Martin et al. (29) by defining the variational functional

$$\Psi =\rho {\omega }^2{\int }_{\mathcal{C}}\left\{\left(\frac{g}{2}\right)\left[{\left(\frac{d^{2}U}{d{z}^2}\right)}^2+2k_x^2{\left(\frac{dU}{dz}\right)}^2+\left(k_x^4\mathrm{-}{k}_B^4\right)U^2\right]-U{P}_p\right\}dz+\frac{1}{2}{\iint }_{\mathcal{R}}\left[\nabla P·\nabla P-\left(k^2-k_x^2\right)P^2\right]dR,$$ (2)

where the region within the duct cross section is denoted R; C represents the flexible plate portion in the cross section and ∇ is the gradient operator in two dimensions. Here, Ψ can be interpreted as an error function to be minimized with respect to the pressure and displacement degrees of freedom. At low frequencies, a simple 2 degrees of freedom Rayleigh-Ritz formulation could be used by taking a uniform amplitude trial function for the sound pressure and a simple trial function for the plate displacement to approximate its first radial mode shape. The stationary values of the variational functional Ψ with respect to the plate displacement and the acoustic pressure degrees of freedom lead to the approximate coupled dispersion relation for a uniform isotropic plate coupled to fluid in a single duct. For a plate with clamped boundary condition at the lateral (radial) edges vibrating only in the first lateral mode, assuming a squared half-sine radial mode shape for the plate displacement, the dispersion equation is

$$k_x^6+\left[\frac{8}{3}{\left(\frac{\pi }{b}\right)}^2-k^2\right]k_x^4+\left[\frac{16}{3}{\left(\frac{\pi }{b}\right)}^4-\frac{8}{3}{k}^2{\left(\frac{\pi }{b}\right)}^2-k_B^4\right]k_x^2+\left[k^2{k}_B^4-\left(\frac{16}{3}\right)k^2{\left(\frac{\pi }{b}\right)}^4-\frac{\left(\frac{2}{3}\right)\rho {\omega }^{2}b}{gR}\right]=0.$$ (3)

Here, R is the duct cross-sectional area. This equation, which implicitly assumes that the pressure field in the duct is nearly planar, is valid only at low frequencies until the cut-on frequency of the first higher cross mode in the equivalent rigid-walled duct (30), and for the first structural cross mode only. For these low-frequency conditions, it has been verified numerically and experimentally (29,30). The dispersion curves are determined as roots of the dispersion equation. Of the three roots (the other three are for waves in the opposite direction viz. reflected waves), only the propagating wavenumber whose imaginary part is significantly less than its real part is used. The coupled phase speed ($c_p=\omega /k_x$) changes with frequency in a plate-duct system, showing that it is a dispersive system. It can be shown from Eq. 3 that the low- and high-frequency asymptotes of the phase speed of the first coupled mode for a clamped plate are

$$c_p^L=\frac{1}{\sqrt{\frac{1}{c^2}+\frac{\frac{\rho b}{R}}{8g{\left(\frac{\pi }{b}\right)}^4}}}$$

$$c_p^H=\frac{\omega }{k_B}={\sqrt{\omega }}^4\sqrt{\frac{g}{m}}.$$ (4)

This equation shows why the low-frequency phase speed, $c_p^L$, in a duct with a flexible wall is smaller than the speed of sound in the fluid, c, and it describes the parameters on which this depends. The phase speed is smaller for a denser fluid, wider plate, lower plate modulus, lower duct cross section, and thinner plate. Above the resonance frequency, the phase speed asymptotes to $c_p^H$, the in vacuo bending phase speed of the plate. Depending on the parameters, the phase speed of the first coupled mode may or may not decrease near the coupled resonance frequency of the system. The decrease in phase speed around the resonance will be seen only if the low-frequency phase speed is higher than the plate in vacuo bending phase speed near the resonance frequency. As an example, consider a rigid-walled air-filled duct of rectangular cross section 0.0254 m × 0.0254 m with one of the walls replaced by a 25.4-μm-thick brass plate. The first coupled-mode dispersion curve for wave propagation along the length of the plate is determined using Eq. 3 coded in MATLAB (The MathWorks, Natick, MA) and shown in Fig. 2. In this system, the low frequencies propagate at a speed ∼4.25 times smaller than the speed of sound in air until the first coupled plate resonance at 135 Hz. This resonance frequency is analogous to the BF of the BM response. The phase speed decreases further around the resonance frequency, and at higher frequencies, it asymptotes to the in vacuo plate-bending phase speed (according to Eq. 4) over the frequency range shown. At even higher frequencies, higher duct cross modes and higher plate modes contribute to the dispersion curve, and this effect is not shown here. This example demonstrates that frequency dispersion and glides occur even in a uniform duct with air coupled to a flexible plate.

Adopting the variational method from Martin et al. (29) for a plate with simply supported edges (assuming half-sine radial mode shape), the coupled dispersion relation can be derived as

$$\eta k_x^6+\eta \left[2{\left(\frac{\pi }{b}\right)}^2-k^2\right]k_x^4+\left[{\left(\frac{\pi }{b}\right)}^4-2\eta k^2{\left(\frac{\pi }{b}\right)}^2-k_B^4\right]k_x^2+\left[k^2{k}_B^4-k^2{\left(\frac{\pi }{b}\right)}^4-\frac{\left(\frac{8}{{\pi }^2}\right)\rho {\omega }^{2}b}{gR}\right]=0.$$ (5)

In addition to the simply supported boundary condition, Eq. 5 also includes the effect of plate orthotropy by introducing the parameter η, which is the ratio of longitudinal to radial Young's modulus; η = 0 for a strongly orthotropic plate (no longitudinal coupling) and η = 1 for an isotropic plate. The low-frequency dispersion relation for an orthotropic plate is derived by replacing the isotropic plate structural operator with its orthotropic counterpart. From Eq. 5, for a simply supported isotropic plate (η = 1), the high-frequency asymptote of the phase speed is the same as for a clamped isotropic plate (Eq. 4) and the low-frequency asymptote is similar to that for a clamped plate (Eq. 4) with 8g in the denominator replaced by (π²/8)g. The second term in the denominator of $c_p^L$ in Eq. 4 can be seen as the ratio of mass loading of the fluid to stiffness of the plate. For an orthotropic plate (η < 1), the low-frequency asymptote of the phase speed does not depend on η, but the high-frequency asymptote is smaller in proportion to the fourth root of η, which leads to a steeper drop in the phase speed around the coupled resonance frequency. This is consistent with the observations of Naidu and Mountain (31), who estimate that the BM longitudinal coupling cannot be neglected when the wavelength is small, especially near the BF, and that it is negligible for frequencies less than the BF.

Dispersion for uniform BM

Using local tonotopic BM properties for the plate, the coupled dispersion curves for a hypothetical uniform BM interacting with scala fluids are shown in Fig. 3. In the cochlea, because there are two ducts, the total pressure acting on the BM exciting the traveling wave mode is two times that in a single duct. To take this into account, the Young's modulus and plate density used in the single-duct equations (Eq. 5) are half of the actual values. Up to the BF, the predicted phase speed for a uniform BM at a 4-mm tonotopic basal location is qualitatively similar to that of the effective phase speeds from measured data (Fig. 3). Beyond the BF, the uniform BM model shows that phase speed tends to the in vacuo bending phase speed of the plate (as shown in Fig. 2), whereas the measured data are significantly higher, especially above the COF. At a more apical location (not shown), the predicted dispersion curves retain the same basic character but shift to lower resonance frequency and smaller phase speed due to lower flexural rigidity (Eq. 4).

Figure 3.

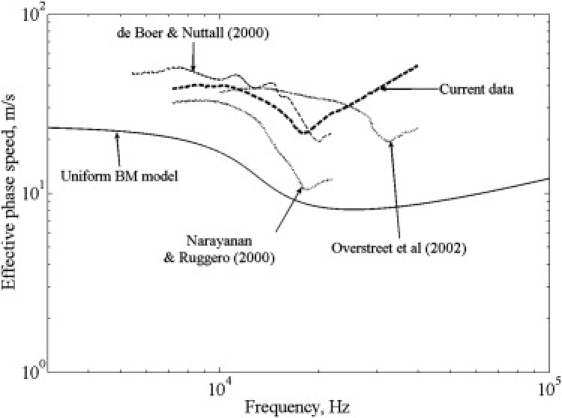
Measured phase speeds at the base (see Fig. 1 for references) are compared with the phase speed predicted for a uniform plate with BM local tonotopic properties (4 mm tonotopic location) coupled to fluid-filled ducts representing scala vestibuli and scala tympani. Model parameters: the boundary condition at the two radial edges of the BM is assumed to be simply supported (clamped does not change the qualitative results, but increases the quantitative phase speeds (not shown)). Fluid and duct properties: ρ = 1000 kg/m³ and c = 1500 m/s, R = 1 mm². BM properties: density accounting for effective additional mass from other Organ of Corti structures is 2000 kg/m³; Young's modulus decreases exponentially from base to apex: E = 1.5e7 (base)–1.55e6 (apex). The hysteretic plate damping factor is 0.05; thickness decreases exponentially from 20 μm (base) to 1 μm (apex); width increases exponentially from 140 μm (base) to 210 μm (apex) and length is 17 mm. BM is assumed to be isotropic for these results; the effect of longitudinal coupling is discussed later.

Effect of varying BM properties

At any frequency, the local phase speed of the traveling wave varies along the cochlea due to varying properties of the BM. To incorporate the decrease in the local phase speed along the BM, its 17-mm length is numerically subdivided into hundreds of sections, each with different BM properties. At each frequency, the net delay experienced by the traveling wave to reach a given location is calculated as the sum of the delays in the basal sections. The effective phase speed incorporating the varying BM properties is then given as the ratio of the effective distance from the stapes to the net phase delay. Because basal regions have higher local phase speeds, the effective phase speed for propagation to the apex is higher than if the BM were uniform with apical properties. This brings the predicted effective phase speeds closer to the measured phase speeds up to the COF, but there is significant discrepancy above the COF.

Traveling-wave cut-off

In the cochlea, the coupled traveling wave is nearly extinguished at and around the best place corresponding to each frequency. At a location apical to the best place, referred to as the crossover place (COP), the coupled traveling wave has negligible energy. The compression-wave magnitude is therefore relatively larger, and the little energy beyond the COP would possibly propagate as a compression wave (26–28) (Fig. 4, inset). Note that the COP is more basal at higher frequencies because the best place is more basal. Likewise, at any given location along the BM, for frequencies greater than the COF (approximately one-third octave above the best frequency), the compression mode may be dominant.

Figure 4.

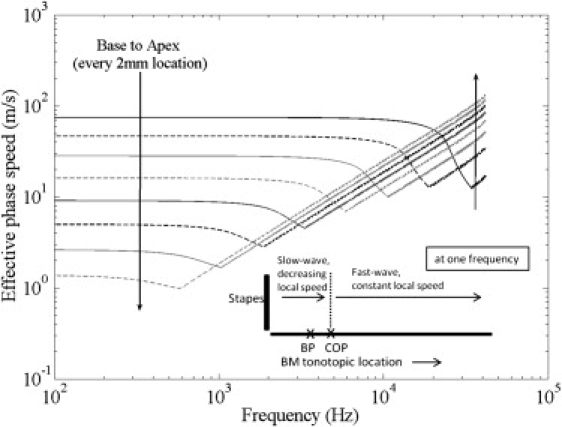
Predicted effective phase speeds at multiple tonotopic locations along the BM. This result includes fluid-structure coupling, varying plate properties, plate orthotropy of 1:10 (the trends are similar for other orthotropy values), and compression mode above the COF. It has been estimated that the orthotropy could vary from base to apex (31) and could be up to ∼1:100 (53) at the base. (Inset) Spatial variation of the phase speed of a single frequency component.

When the speed of propagation at frequencies beyond the COF for each location is set as 1500 m/s (the speed of sound in water) to incorporate the compression mode, the predicted effective phase speeds increase more rapidly beyond the COF at basal and apical locations, as shown in Fig. 4. The effective phase speed at low frequencies decreases from base to apex, whereas it increases at high frequencies. The higher effective phase speed at the apex compared to the base at high frequencies comes from contributions over a longer stretch of the BM from fast-wave (Fig. 4, inset). The effective phase speeds predicted by including all three factors (fluid-structure coupling, variation in BM properties, and compression mode beyond the COF) and for a plate orthotropy of 1:10 (η = 0.1) are very similar to the measurements at the base, as well as qualitatively at the apex, as shown in Fig. 5. The quantitative difference at the apex could be due to a different boundary condition (clamped instead of simply supported) along the BM radial edges in that region. Even though we have considered only passive responses so far, the model also agrees with the measured phase speeds in the active response, as discussed in the next section.

Figure 5.

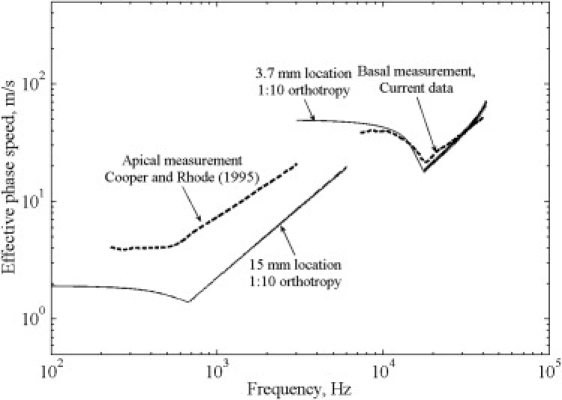
Effective phase speeds (two solid curves) predicted for varying BM and assuming compression mode for frequencies greater than the COF matches the measured data (dashed curves) quantitatively at base and qualitatively at apex.

Dispersion in a sensitive cochlea

It is well known that the active response magnitude of the BM velocity is higher than the passive response (5), particularly above the passive BF. The current understanding is that the higher magnitude comes from the energy added to the traveling wave by the hypothetical active amplification mechanism termed the cochlear amplifier (3). Therefore, in the active response, the traveling wave continues to dominate until a higher frequency. In other words, the COF would be higher for an active cochlea at low sound levels, presumably proportional to the increase in the BF. In a more sensitive response, the compression-wave contribution would therefore be significant beyond a higher COF. The phase speeds thus predicted for sensitive (higher COF) and insensitive responses are compared with published experimental data from Ren and Nuttall (32) in Fig. 6. The effective phase speed in response to lower SPL continues to drop further than the response to higher SPL, because the former has a higher COF owing to higher traveling-wave magnitude. However, beyond its COF, the sensitive (lower-SPL) effective phase speed increases at nearly the same rate as the insensitive (high-SPL) effective phase speed.

Figure 6.

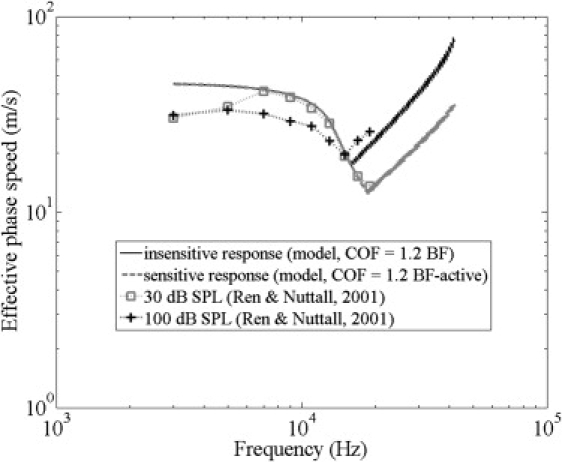
Predicted phase speeds for sensitive response (COF = 1.2 times the active BF, which is equal to 1.4 times the passive BF in this case) and insensitive response (COF = 1.2 times the BF) with η = 0.1 are compared with gerbil data published in Ren and Nuttall (32).

Discussion

Physiological origin of traveling-wave dispersion

We show that the dispersion of the stapes-induced traveling wave in the cochlea, and as measured in BM velocity, scala pressure adjacent to the BM (26), and auditory nerve fibers, is fundamentally due to the fluid-structure coupling between the scala fluids and the BM. A somewhat similar dispersion and frequency glides occur even in a generic uniform plate coupled to fluid (even air) in a duct. However, there are some unique features to the traveling-wave dispersion observed in the cochlea. The tonotopic variation in BM properties causes the local phase speeds at a given frequency to decrease with increasing distance from the stapes until the COP, which increases the effective phase speed of the traveling wave up to the COP. In addition, in the cochlea, traveling waves almost completely lose their energy to damping, and there is negligible energy beyond the COP. The little energy that reaches the more apical regions is likely due to the fast wave, which travels at 1500 m/s (27,28) (Fig. 4 right). These three factors all contribute to the overall traveling-wave dispersion (note that the overall phenomenon is collectively referred to as traveling-wave dispersion, although strictly speaking, the terminology may be imprecise, because of the fast-wave contribution) seen in the cochlea (Fig. 5). The analytical model discussed in this article also suggests that the drop in active phase speed around the BF is steeper than that of its passive counterpart because the COF for active response is higher owing to a larger traveling-mode component and higher BF (Fig. 6).

Coupled fluid-structure waves

Unlike earlier analytical models of cochlear hydrodynamics, the formulation presented here was adopted to satisfy the governing equations of the coupled plate-duct system in an integral or variational form. Fluid compressibility is also included so that the same formulation can be used to demonstrate dispersion even in air-filled ducts with a flexible plate. Furthermore, BM longitudinal coupling is also included here. In some earlier models of passive cochlear hydrodynamics, concern was raised regarding the validity of the long-wave model (which assumes that the wavelength is long compared to the duct height (23)) in the vicinity of the BF (33,34). These earlier analytical models represented the BM mass and stiffness as lumped quantities, a representation that neglects the BM longitudinal coupling, which causes the coupled phase speed to drop very steeply to nearly zero around the BF (Eq. 5 and Fig. 7). Some of the questions regarding these long-wave models, such as a sharper jump in phase around the BF compared to experiment (see, e.g., Fig. 2 in Zweig (23)) could be attributed to neglecting the BM longitudinal coupling. The predicted effective phase speed drops more steeply around the BF for smaller BM longitudinal coupling (smaller η in Fig. 7). Although the variational formulation presented here is different from the earlier long-wave models, it is worth reviewing one relevant point here. In a coupled duct, the pressure-mode shape along the height is of the form exp(−α × y′), exponentially decreasing from the surface of the BM. Here, y′ is the distance from the BM along the duct height. The pressure-mode shape deviates from being planar for large α, but note that it is confined to the near field at the BM surface. In coupled acoustic ducts, including the cochlea, such an evanescent mode along the height (but propagating longitudinally) is associated with subsonic longitudinal phase speed that is smaller than the speed of sound in the fluid. Capturing the near field requires higher-order pressure modes along the height, but the energy in the fluid pressure is carried mainly by plane waves at these frequencies. At these subsonic phase speeds, significant energy is coupled to the structure, which thereby enables the dissipation of that energy. (This phenomenon is used to design engineered biomimetic silencers (35).) The current variational formulation, which satisfies the governing equations in the integral form using nearly planar pressure field, is a good approximation for predicting the dispersion even around the BF region, as is clear from the results presented in this article. Based on their analysis of an isotropic plate, Cummings et al. (30) showed that their variational formulation, which is adopted in this article, compares very well with the dispersion curves predicted by finite element analysis, even where the subsonic waves occur, including the resonance-frequency region (BF in the cochlear terminology), and up to the cut-on frequency of the higher-order pressure mode in an otherwise rigid-walled duct (which is ∼750 kHz in the 1-mm-sized cochlear ducts).

Figure 7.

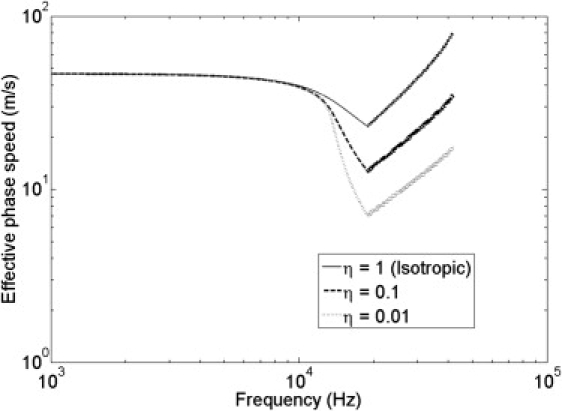
Predicted phase speeds at the 4-mm tonotopic location (using Eq. 5), including the varying BM and transition to fast wave above the COF, for three different values of the BM longitudinal coupling factor (η = 1, 0.1, and 0.01).

Relevance of dispersion to diagnosis and perception

The passive and active coupled dispersion described in this article has broad significance to the research on wave propagation in the cochlea. In particular, the physiological origin of the fundamental phenomenon discussed here will help us differentiate the forward traveling wave from other waves that might arise in an active cochlea, such as during stimulated or spontaneous emissions. The origin of the dispersion phenomenon in the cochlea could help explicate the debate on qualitative differences between species (36), such as, for example, directing the focus to their relative geometry and quantitative differences in the relevant physical properties. In humans, the traveling-wave velocities derived from auditory-evoked brainstem response could be used to diagnose Meniere's disease (19).

The latency behavior of the cochlear traveling wave could provide the means through which different components of the acoustic signal are placed into appropriate temporal register for the central brainstem and cortex to code and analyze (17,37). Using controlled chirp signals, which attempt to compensate for the traveling-wave delay, it has been shown that the neural synchrony increases due to synchronized contributions from apical regions (38–40) and influences our perception. Pitch is one of the primary attributes of auditory sensation, playing a crucial role in music and speech perception and in analyzing complex auditory scenes, but our perception of pitch is not well understood (41). In particular, the use of envelope information and the relevance of phase information are still widely debated. Better representation of pitch and temporal fine structure in cochlear implants and hearing aids remain important goals. The importance of phase- or frequency-modulation information for cochlear implant users to perceive pitch under background noise has been shown recently (42). Utilizing synthesized stimuli with the envelope of one sound and the fine structure of another, Smith et al. (43) conducted psychoacoustic experiments to show that the envelope of the speech signal is important for its reception, whereas the fine structure (which has phase information) is essential for pitch perception and sound localization. Conveying fine-structure information to implant users would require novel processing schemes that attempt to simulate some of the properties of the mechanical traveling wave that propagates along the BM of the normal cochlea (44), because the dispersion changes the internal representation of the sound before the information is sent to higher levels of the auditory nervous system (45). Such an internal representation could be predicted using the analytical model presented in this article. According to the place-time theory of pitch perception (45,46), the patterns of phase differences along the BM could be used by the auditory system to derive the frequency of a pure tone. Recently, Smith and Lewicki (47) have suggested that the acoustic composition of speech might be adapted to the auditory system, as indicated by the striking similarity between the auditory filters based on efficient coding theory and the measured auditory nerve revcor (approximate impulse response) data in the cat (10). Psychoacoustic experiments adopting harmonic complexes, such as Schroeder-phase waveforms, have shown that the traveling-wave dispersion may be perceived as masking (11–13) by ∼20 dB and loudness (14) of ∼10 dB. The neurophysiological connection between traveling-wave dispersion and higher levels of auditory processing in humans has been discovered at the brainstem level (38) and even at the level of the auditory cortex (48,49). Our understanding of pitch perception and design of speech processors for auditory prostheses and speech-recognition systems could benefit from the physiological basis for dispersion in the inner ear elucidated in this article.