Toward a Consensus View of Duplex RNA Flexibility

Abstract

The structure and flexibility of the RNA duplex has been studied using extended molecular dynamics simulations on four diverse 18-mer oligonucleotides designed to contain many copies of the 10 unique dinucleotide steps in different sequence environments. Simulations were performed using the two most popular force fields for nucleic acids simulations (AMBER and CHARMM) in their latest versions, trying to arrive to a consensus picture of the RNA flexibility. Contrary to what was found for DNA duplex (DNA₂), no clear convergence is found for the RNA duplex (RNA₂), but one of the force field seems to agree better with experimental data. MD simulations performed with this force field were used to fully characterize, for the first time to our knowledge, the sequence-dependent elastic properties of RNA duplexes at different levels of resolutions. The flexibility pattern of RNA₂ shows similarities with DNA₂, but also surprising differences, which help us to understand the different biological functions of both molecules. A full mesoscopic model of RNA duplex at different resolution levels is derived to be used for genome-wide description of the flexibility of double-helical fragments of RNA.

Introduction

Nucleic acids exist in nature as two main polymers (DNA and RNA), which despite having quite similar chemical composition display quite different structure and very different biological function. While DNA carries genetic information and is usually found as a right-handed double helix, RNA is much more versatile and can display very different secondary and tertiary structures, allowing it to engage in a very different range of biological functions, from carrying genetic information to gene regulation or catalysis (1–4). DNA is synthesized to define a perfectly paired self-complementary duplex (DNA₂), where one strand recognizes the other by means of A·T and G·C Watson-Crick pairings (5). RNAs, in developed organisms, exist mostly as single strands which adopt compact structures where the strand recognizes itself to maximize the amount of duplex, which (when possible) will be formed by Watson-Crick A·U and G·C pairings. For some cases, as in that of microRNA, such hairpins are processed to generate pure antiparallel duplexes—which are then recognized by microRNA processing proteins (6) in having a key role in the control of cell function.

It has been known since the 1950s that a right-handed duplex with 10 basepairs per turn (known as the “B-form”) is the most stable conformation for DNA₂ under physiological conditions, and that a more compact ,11 basepairs per turn, right-handed duplex (known as the “A-form”) is the preferred conformation for the RNA duplex (RNA₂). RNA₂ is more stable than DNA₂, except in the case of sequences very rich in A and T(U) pairings, where it has been shown (7) that DNA₂ can be more stable. Structural analysis shows that DNA₂ can display a large variety of structures close to the B-form (8), which combined with the larger polymorphism of the DNA backbone (S↔E repuckering or BI↔BII transitions) has been traditionally used to support the idea that canonical B-DNA duplex is more flexible than RNA₂ (and A-DNA₂). However, as already discussed elsewhere (9), flexibility is a quite dangerous concept with little meaning when disconnected from the geometrical perturbation used to define it, and certainly this interpretation of experimental data is not unique (see below).

Molecular dynamics (MD) simulations using state-of-the-art simulation conditions and last-generation force fields are a perfect complement to experimental techniques in the definition of nucleic acids flexibility (9,10). Thus, different groups (11) have made extensive analysis of the flexibility properties of DNA₂ (12–14), which has provided very valuable descriptors to help us understand not only gene structure, but also regulatory mechanisms or chromatin organization (15–18). These studies have provided detailed information on fine details of DNA₂ deformability, such as the sequence- (at the basepair step level) and perturbation-dependent stiffness of DNA₂ (19,20). Massive multigroup projects are currently under development (11) to obtain a refined database of the stiffness of the DNA duplex considering the local helical deformations at the tetramer level, which can yield refined parameters for mesoscopic modeling of DNA. In comparison with the large amount of information for DNA₂ flexibility derived from MD simulations, little is known for RNA₂ (9,10,21–24). Recently, using the AMBER force field, our group studied a 12-mer sequence of DNA₂ and RNA₂, finding that in global terms, RNA₂ was more rigid than DNA₂—mostly due to a higher backbone flexibility for DNA (9,25,26). However, that situation reverses when only the very first deformation modes were considered. Findings supported by a parallel database analysis (23) suggest that the DNA₂ deformation space is wide and complex, while that of RNA₂ is narrow and simple, becoming dominated by a very few numbers of very low-frequency movements.

These conclusions have been challenged in an even more recent work by Priyakumar and MacKerell (22), who presented carefully analyzed CHARMM-based data pointing in an opposite direction: i.e., that RNA₂ is in global terms more flexible than DNA₂. To clarify this issue and, for the first time to our knowledge, obtain a full characterization of the sequence-dependent properties of RNA₂, we decided to perform a CHARMM27 (27,28) and AMBER-ff99/Parmbsc0 (29–31) study of several long and representative RNA and DNA duplexes to derive the corresponding flexibility descriptors. The desired objective of our work was the derivation of a consensus picture of RNA duplex flexibility, as we did previously for proteins (32,33) and DNA duplex (34). Unfortunately, results reported here show that, contrary to the situation with parent DNA₂s, no convergence between force fields has been reached and that extra caution is required when deriving conclusions from MD simulations on RNA duplexes. Analysis of long trajectories (150 ns) for four 18-mer duplexes containing a variety of sequences (18,34) reinforce our confidence in the results obtained with the Parmbsc0 revision of the AMBER ff99/Parmbsc0 force field (in the following noted simply as Parmbsc0), while some aspects of the structural and flexibility patterns reported by CHARMM27 simulations seem difficult to fit to available experimental data—supporting previous claims of different groups on CHARMM27-based simulations of RNA duplexes (35,36). After a careful study of all trajectories and extensive comparison with available experimental data, a first atlas of the flexibility of RNA₂ is derived. Such an atlas can be used to describe the flexibility of RNA duplexes as well as to understand and quantify, in a fast and efficient way, important aspects of RNA biology, such as the indirect-recognition mechanisms for protein binding.

Methods

System selection

To make conclusions as general as possible, and following previous works (34), four sequences of DNA₂ and RNA₂ were selected, namely,

• SEQ1: x(GCCYAYAAACGCCYAYAA)·x(YYAYAGGCGYYYAYAGGC),

• SEQ2: x(CYAGGYGGAYGACYCAYY)·x(AAYGAGYCAYCCACCYAG),

• SEQ3: x(CACGGAACCGGYYCCGYC)·x(GACGGAACCGGYYCCGYG),

• SEQ4: x(GGCGCGCACCACGCGCGG)·x(CCGCGCGYGGYGCGCGCC),

where x stands for ribo (r) or deoxyribo (d) backbones and Y stands for either U (RNA) or T (DNA)). These four sequences are sufficiently long to reduce the importance of end-effects in simulations and contain many copies of the 10 unique base steps, namely,

• (x(GG)·x(CC),

• x(GC)·x(GC),

• x(GA)·x(YC),

• x(GY)·x(AC),

• x(AG)·x(CY),

• x(AA)·x(YY),

• x(AY)·x(AY),

• x(CG)·x(CG),

• x(CA)·x(YG),

• x(YA)·x(YA),

where x is equal to r or d and Y equal to T or U, making possible a statistically reliable analysis of the sequence-dependence in duplex flexibility.

System preparation and production runs

Following the protocol described elsewhere (37–39), all the systems were neutralized by adding a suitable number of Na⁺ ions to be surrounded by ∼9200 TIP3P water molecules. Solvent boxes were manipulated to guarantee that an equal number of water molecules exist for DNA and RNA duplexes of the same sequence. All the systems were partially optimized, thermalized, and equilibrated using a standard multistep procedure (38,40). RNA₂ simulations were equilibrated by 10 ns before the 150-ns production runs, while DNA₂ simulations started from the end of previous 100-ns trajectories (34) and were extended for an additional 50 ns to complete 150 ns trajectories, which, based on our experience with microsecond-long simulations (39), should be large enough as to capture well the near-equilibrium dynamic properties of the different duplexes. All simulations were performed in the isothermal-isobaric ensemble (T = 298 K, P = 1 atm) using periodic boundary conditions and particle-mesh Ewald treatments to account for long-range electrostatic effects (41). SHAKE (42) was used to maintain all bonds involving hydrogen atoms at their equilibrium values, which allowed the use of a 2-fs integration step. Simulations were carried out with NAMD (43) and PMEMD (44) computer programs (see details in the Supporting Material) after checking carefully (see Fig. S1 in the Supporting Material) that no differences can be expected from the use of these two different MD codes.

Analysis of trajectories

The 150-ns-long trajectories of the four DNA and four RNA duplexes were processed to obtain information on the structural and flexibility properties of both nucleic acids at global and local levels. Structural analysis was performed using standard procedures (45) on the central 14-mer portion using CURVES+ (46) for the helical analysis, the ptraj module of AMBER9 for energetic analysis, and VMD (47), as well as in-house programs. The expected pattern of interaction of the average DNA and RNA duplexes was determined from classical molecular interaction potentials (48). The global deformability of DNA and RNA duplexes was characterized by means of entropy calculations using pseudoharmonic modes (49,50) (see Methods in the Supporting Material). The global patterns of deformation of duplexes were studied by means of essential dynamic algorithms adapted to nucleic acids (14,37) using the same atom-compression rules as for entropies when different duplex types of different sequences were compared. The essential dynamic analysis processes the Cartesian coordinates compiled from the dynamics into a set of eigenvectors ({υ_i}) and eigenvalues ({λ_i}); the first provides information on the nature of the essential deformation movements, while the second informs on the stiffness associated with such deformations (K_i),

$$K_i=\frac{k_{\text{B}}T}{{\lambda }_i},$$ (1)

where k_B is the Boltzmann's constant and T is the temperature.

Comparison between the essential deformation modes in two trajectories (A and B) was performed using similarity indexes (14) (see the Supporting Material) that were computed for a common set of atoms.

The stiffness associated to pure global deformations (Θ) was determined by inversion of the associated variance,

$$K_{\Theta }=\frac{k_{\text{B}}T}{\langle {\left(\Theta -{\Theta }_{\text{0}}\right)}^2\rangle },$$ (2)

where 〈…〉 stands for a Boltzmann's averaging and the index 0 refers to the equilibrium value of the global coordinate. Four global helical values were considered (tilt, roll, stretch, and twist) for all the possible fragments of the central 14-mer of the four DNA and RNA duplexes. These descriptors were combined to get the most commonly used global stiffness parameters: the stretch modulus (C), the twisting (T), and the bending (B) persistence lengths. For bending (which has roll and tilt contributions), both isotropic and anisotropic persistence lengths were computed. Additional technical details on the methodology used to derive global stiffness indexes can be found in Lankas et al. (20).

The analysis of local helical flexibility was carried out from the study of the stiffness matrix (∈) associated to helical deformations (twist (w), roll (r), tilt (t), rise (s), slide (l), and shift (f)) at the dinucleotide level, and determined by inversion of the MD-associated covariance matrix (⊂),

$$\Xi =E{\left(\Delta X\right)}^{-2}=k_{\text{B}}T{\subset }^{-1}=\left(\begin{array}{cccccc}{k}_w& k_{wr}& k_{wt}& k_{ws}& k_{wl}& k_{wf}\\ k_{wr}& k_r& k_{rt}& k_{rs}& k_{rl}& k_{rf}\\ k_{wt}& k_{rt}& k_t& k_{st}& k_{tl}& k_{tf}\\ k_{ws}& k_{rs}& k_{st}& k_s& k_{ls}& k_{lf}\\ k_{wl}& k_{rl}& k_{tl}& k_{ls}& k_l& k_{lf}\\ k_{wf}& k_{rf}& k_{tf}& k_{lf}& k_{lf}& k_f\end{array}\right),$$ (3)

where E is the energy associated to the deformation ΔX and k stands for the different stiffness constants defining the 36 elements of the stiffness matrix.

Stiffness parameters for a given dinucleotide step were computed individually for each sequence and averaged later to avoid the derivation of artifactual soft parameters due to nonneighbor effects on equilibrium geometry (11,34). By using this procedure, the stiffness parameters for a given step agree well independently of the dinucleotide environment, suggesting that stiffness parameters are less dependent on remote neighbors than equilibrium geometry parameters.

Analysis of structural databases

The structures of all DNA and RNA duplexes deposited on the 2009 version of NDB (23,34,51) were filtered to define a set of naked DNA₂ and RNA₂ from which we derived dinucleotide structural data. Thus, we eliminated from the database all oligos bound to proteins or drugs as well as those containing mismatchings and noncoding nucleobases or those solved with poor quality (resolution <3.5 Å). To reduce the impact of packing effects, all oligos shorter than eight basepairs were also eliminated. The remaining duplexes were studied using helical descriptors at the dinucleotide level identical to those used in trajectory analysis, as suggested by Olson et al. (15). Dinucleotide steps showing extreme helical values (outside three standard deviations from the average of any of the six helical parameters) were excluded from the analysis, because these deformations cannot be explained with the harmonic model considered here (a very small number of cases were eliminated due to these criteria). Note that the experimental data derived in this way can be reasonably accurate in terms of average values, but caution is necessary with the standard deviations (from which stiffness parameters are derived). This is due to scarcity of experimental data for several dinucleotide steps and additional errors in experimental estimates that are expected from systematic biases in refinement used considering simple force fields with reduced rough experimental information.

Results and Discussion

Reliability of RNA trajectories

A crucial point in any MD study is the validation of the trajectories in terms of their ability to reproduce known experimental data. The 8 × 150 ns RNA₂ trajectories studied here were stable, sampling in all cases helical (or pseudohelical) structures. However, contrary to the situation found in the DNA duplex, where small deviations from the canonical helical conformation were found (Fig. S2 and Fig. S3) and excellent convergence between Parmbsc0 and CHARMM27 simulation was achieved, nonnegligible differences are found here between both RNA force fields. Significant structural alterations are evident in some of the CHARMM27 simulations (specially for seq2 and seq4), whose root-mean-square deviation (RMSD), with respect to canonical A-form, becomes very large (Fig. 1), even when the floppy ends are eliminated from the RMSD calculation (Fig. 1 and Fig. S4). Graphical analysis of the structure evolution clearly illustrates that CHARMM27 leads to local unfoldings of the helix, which are reversible in some cases but irreversible in many others (see Figs. 2 and 3 and Fig. S5, Fig. S6, and Fig. S7). The distortions detected in these simulations are very large in terms of twist for some steps, which take often completely artifactual values (Fig. S7), leading to a complete lost of helicity in some fragments of the structure (see Fig. 2) and dramatic changes in the major groove geometry (see Fig. S5). Local base geometry is largely altered in CHARMM27 RNA₂ simulations, affecting both r(A·U) and r(G·C) pairs with either temporary or permanent losses of interstrand hydrogen bonds (see examples in Fig. 3 and Fig. S6), which leads to major losses of helicity in the opening region (something that is not detected in Parmbsc0 simulations). It is worth noting here that reversible base opening is not necessarily an artifactual behavior, but the process is experimentally known (7,52) to happen in the millisecond (and not in the nanosecond) timescale, and the population of opened conformations is expected to be very small at room temperature. Finally, it must be noted that, while severe distortions happen in some parts of the helix, other regions with similar composition remain close to the expected conformation—indicating the stochastic nature of the distortion process found in these calculations, and the fact that, for some small regions, CHARMM27 results could be used to derive local helical parameters.

Figure 1.

Smoothed RMSD (in Å) from A-RNA fiber conformation (in gray) and average structure (in black) for RNA/Parmbsc0 (on the left) and CHARMM27 simulations (right) for the central 14-mer of the four RNA sequences.

Figure 2.

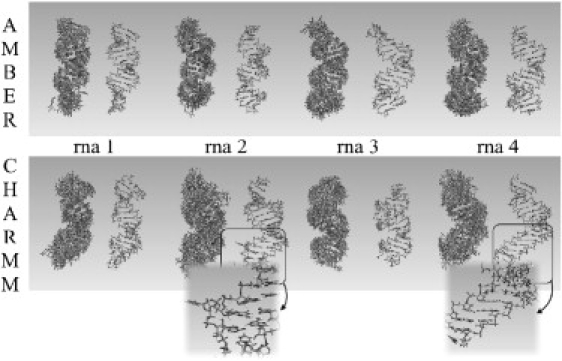
Ensemble at different times of simulation (on the left) and final (on the right) structures of the four RNA sequences for Parmbsc0 (at the top) and CHARMM27 (at the bottom) simulations. In the case of CHARMM27 simulations, some fragments undergo irreversible nonhelical transition. (Insets) Detailed images of some of the major distortions.

Figure 3.

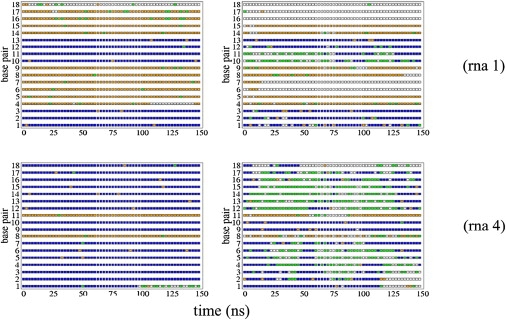
Comparison of averaged interstrand hydrogen-bonding interactions for every basepair along sequences 1 (on the top) and 4 (at the bottom) and along the time of simulation for Parmbsc0 (on the left) and CHARMM27 trajectories (right) for RNA. (Blue means three standard Watson-Crick hydrogen bondings; orange stands for two of them; green means only one hydrogen interaction; and white, no standard interaction between one base and its complement.)

The four 150-ns trajectories of RNA₂ done with the Parmbsc0 force field yield very stable trajectories, with sampling conformations close to the expected A-form (Figs. 1 and 2 and Fig. S4). Hydrogen-bond pattern is strictly maintained (Fig. 3), with the exception of some fraying movements at the ends (especially in r(A·U) steps), agreeing with experimental findings on the stability of RNA₂ hydrogen bonds and on the very slow kinetics of basepair opening (7,52). No local unfolding, untwisting, or any other artifactual distortion of the helix is detected during the four simulations reported here (Fig. 2). In summary, all our analysis suggest that Parmbsc0 simulations of RNA duplexes sample near-equilibrium geometries close to those expected for the corresponding sequences based on the known experimental evidence, and can be used safely to derive mechanical descriptors of RNA₂.

General structure of the RNA duplex

The four Parmbsc0-derived trajectories were analyzed to obtain a representation of the average structural properties of the RNA duplex in solution. The RNA₂ helix appears as a compact structure, with helical parameters very close to those of crystal structures (see Fig. S8 and Table S1), except for twist—where the force field underestimates experimental values at ∼3° (as happens for DNA₂ with the same force field). Analysis of backbone conformations reports results similar to those expected for an A-duplex as found in experimental structures (Fig. S9). Sugar puckering is strictly fixed in the North region for the four RNA/Parmbsc0 duplexes, agreeing well with available experimental data (see Fig. S9). Very interestingly, the variability in backbone conformation obtained in RNA₂ simulations seems smaller than that detected during equivalent DNA₂ simulations (see Fig. S9), mainly due to the restricted sampling around the δ-, ζ/ɛ-, and α/γ-torsions, pointing to the higher rigidity in the RNA backbone. Clearly, CHARMM27 structures should be taken with caution due to the existence of abnormal distortions. However, if the dinucleotide analysis is performed using CHARMM27 trajectories from which all the steps affected by base opening (i.e., those losing hydrogen bonds and their neighbors during at least 50% of the time of simulation) are removed, the helical equilibrium results are indistinguishable from the Parmbsc0 ones (see Table S1), reinforcing the confidence in our theoretical results.

Di-nucleotide equilibrium geometries

Despite the uncertainties implicit with the use of the nearest-neighbor model (11), dinucleotide equilibrium helical parameters appear as a simple and intuitive approach to roughly characterize sequence-effects on duplex geometry. Analysis of Parmbsc0 trajectories allowed us to derive average helical equilibrium geometries for each of the 10 unique RNA₂ dinucleotide steps in 3–8 different sequence environments (see Fig. 4). With the data presented here is not possible to perform a systematic evaluation of nonneighbor effects (4- or 6-mer) in di-nucleotide geometry, as done for DNA in a recent article (11). However, analyses of data suggest that the influence of the environment on the equilibrium geometry of di-nucleotides is moderate. For example, no bimodal distributions are found in any of the cases, and for the analysis of the four-dinucleotide step where we have at least four different environments, standard deviations in average are very small, even for twist (standard deviations range between 0.4 and 0.7°; AC: ± 0.5; CG: ± 0.4; CC: ± 0.7; GA: ± 0.5°).

Figure 4.

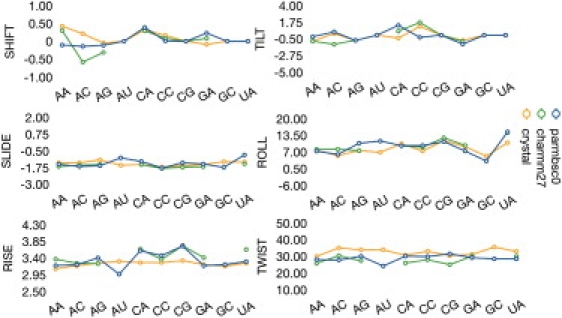
Average helical parameters for RNA for the 10 unique representative basepair steps for translational (shift, slide, and rise; in Å) and rotational (tilt, roll, and twist; in degrees) parameters. The CHARMM27 values were taken after removing open steps.

Analysis of Fig. 4 strongly suggest that sequence effects even smaller that in DNA₂ (see Fig. S10), are still quite significant for RNA₂, as shown in ranges of sequence-dependent variability of 6° or 11° in twist and roll. Profiles obtained with Parmbsc0 agree pretty well with data derived from structures solved experimentally, even though caution is needed with the latter because some of the steps are poorly represented in the experimental databases (for example, AU average was taken from only 15 steps extracted from only 13 different duplexes; see Table S1). Also interestingly, CHARMM27 results also agree well with Parmbsc0 data—provided open steps are neglected from the analysis, reinforcing the hypothesis that opening is the main reason for structural distortion in CHARMM27 simulations of RNA duplexes. Finally, it is worth noting that some sequence-dependent geometry profiles (like twist and roll) are similar in DNA₂ and RNA₂, but most of them are clearly different, suggesting that backbone restrictions influence significantly the arrangement of nucleotide pairs in the duplexes and that sequence-effects are not orthogonal to backbone effects.

Molecular interactions

Classical molecular interaction potentials (48) (see Fig. S11) allowed us to trace the different interaction properties of DNA₂ and RNA₂ for a common sequence. As expected from previous studies (9) a dramatic change in preferred interaction sites is detected in RNA₂ compared to DNA₂, probably due to the different geometries of the grooves (Fig. S11). Such a change is reflected in a complete alteration of the pattern of hydration. Thus, the central 14-mer RNA duplex binds (see Table S2), on average, ∼13 water molecules more than the equivalent DNA duplex; 26.6 water molecules per basepair in DNA₂ and 27.6 for RNA₂. The presence of the polar 2′ hydroxyl group and the large electronegative cloud in the major groove are the main factors responsible for the higher hydrophilicity of RNA₂.

Global flexibility

The concept of flexibility is not well defined at either the global or the local levels, but a reasonable approach is to consider that one duplex (of a given length) is more flexible than another one when, for a common set of atoms, it shows higher intramolecular entropy. Parmbsc0 results in Table 1 clearly demonstrate that DNA₂ is more flexible than RNA₂ due to the greater deformability of its backbone, something that could already be expected from the dihedral analysis noted above (see Fig. S9). Analysis of the frequencies associated with each deformation movement (see Fig. S12) reveals that the larger flexibility of DNA₂ is due to the higher order deformation modes, because the lower modes, those explaining a larger percentage of variance, are in fact very similar for RNA₂ and DNA₂ (a result already found in previous simulations (9) and which is also clear from the inspection of the stiffness associated to the different deformation modes (Fig. S12)). These findings confirm our previous claims that while RNA₂ has a quite simple dynamics and explores very deeply only a small number of modes, the DNA₂ explores a much larger number of deformation modes.

Table 1.

Intramolecular entropies (in kcal/mol·K) for DNA and RNA (italics)

	Schlitter and Klähn method	Andricioaei and Karplus method
Seq 1	3.35	3.07
	2.82	2.54
Seq 2	3.31	3.03
	2.90	2.62
Seq 3	3.37	3.09
	2.93	2.65
Seq 4	3.33	3.05
	2.95	2.66
Averages	3.34	3.06
	2.90	2.62

Performed for 150-ns simulation time computed with the Schlitter and Klähn (49) and Andricioaei and Karplus (50) methods, taking into account the all common atoms of the central 14-mer for the four sequences considered.

According to Parmbsc0 calculations, major deformability of RNA₂ is dominated by twisting and bending motions, which are similar, but not identical to those of the corresponding DNA duplexes as noted in similarity indexes (see Table S3). Contrary to the situation in DNA₂, where similarity between Parmbsc0 and CHARMM27 was very high (similarity indexes at ∼0.9), there is a mediocre correspondence between both force fields for most RNA₂ duplexes considered here (see Table S4). Clearly the large distortions in some CHARMM27 trajectories are responsible for the reduced similarity between the flexibility patterns computed from the two force fields.

As an additional analysis of the global flexibility of RNA duplexes, we derived global helical stiffness parameters from the oscillation of helical parameters (for the 14-mer central duplex (see Methods)). The parameters obtained by this analysis are quite robust to the length of the oligo considered (see Fig. S13) and provides quite intuitive information on the global helical flexibility, which can be directly compared with experimental measures of stress. The results (again only Parmbsc0 results make sense here) shown in Table 2 indicate that the deformations of the global roll, tilt, and twist for RNA₂ are more difficult than for DNA₂. This is in agreement not only with previous theoretical suggestions (9) but with experimental results (53–55) suggesting a bending persistence length at ∼54 ± 2 nm for DNA and 20–30% higher in the case of RNA duplex, which confirms the reliability of our results on short oligos. However, it is also worth noting that DNA₂ becomes stiffer than RNA₂ for global stretch deformations, which again warns against a too-simplistic or too-general use of the concept “flexibility.”

Table 2.

DNA and RNA (in italics)

	Bending (nm)			Stretching (pN)	Twisting (nm)
	Roll	Tilt	Isotropic
Seq 1	64.99	55.67	59.97	2318.36	86.38
	77.45	71.74	74.49	1662.39	177.19
Seq 2	71.83	46.38	56.37	2540.19	93.05
	102.13	62.32	77.40	1745.22	191.66
Seq 3	74.35	37.11	49.51	2262.47	90.93
	105.67	67.57	82.43	1860.05	198.35
Seq 4	66.49	57.83	61.86	2475.36	81.34
	99.67	71.42	83.21	1448.42	195.18
Averages	69.42 ± 4.41	49.25 ± 9.49	56.93 ± 5.45	2399.09 ± 30.27	87.93 ± 5.20
	96.23 ± 12.76	68.26 ± 4.39	79.38 ± 4.16	1679.02 ± 173.79	190.60 ± 9.35

Bending (anisotropic and isotropic) (B) and twisting (C) persistence lengths (in nanometers) and stretch modulus (S, in picoNewtons) for every sequence, and the corresponding averages and standard deviations from Parmbsc0 simulations. Analysis done by taking the values from sequences of 11 basepairs.

Sequence-dependent flexibility

The analysis of trajectories by basepair step resolution harmonic models (see Methods) provides very useful descriptors of local flexibility which can be integrated so as to derive complete pictures of flexibility of long DNA fragments (14,56–58). As noted above, we cannot reach consensus values here due to the distortions detected in CHARMM27 trajectories, but it is worth noting that if snapshots with open steps are eliminated from CHARMM27 trajectories (see above), the derived stiffness parameters are not far from those obtained with Parmbsc0 simulations (see Fig. 5). This, and the good agreement with the few stiffness parameters that can be derived, with statistical significance, from the geometrical variability in experimental structure (only steps with at least 40 structures were used here), allows us to conclude that even without fill consensus, our Parmbsc0-derived stiffness parameters are likely to be very reliable descriptors of RNA duplex flexibility. Note that local flexibility descriptors presented here are based in the nearest-neighbor approximation, and accordingly might be contaminated by nonneighbor effects (4- or 6-mer). However, analysis of our data show that:

• 1.No sequence-dependent bimodality as that found in DNA₂ is detected in RNA duplex, and
• 2.Di-nucleotide force constants (stiffness parameters) are rather robust (in general <9% variation) to change 4- or 6-mer effects (as in fact happens for DNA₂ where the 4- or 6-mer effects are focalized in the equilibrium values rather than in the stiffness parameters).

Figure 5.

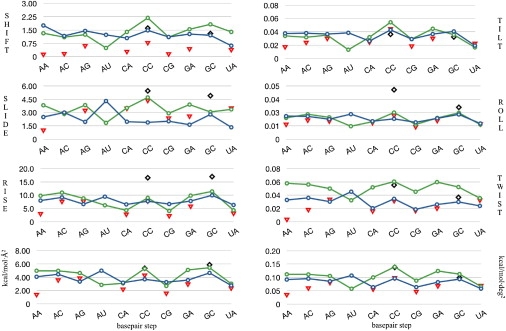
Stiffness constants (translational ones in kcal/mol·Å² and rotational ones in kcal/mol·deg²) for the 10 representative dinucleotide steps associated to the different deformation modes comparing DNA/Parmbsc0 (in blue), RNA/Parmbsc0 (in green with lines), RNA/CHARMM27 (in red triangles), and derived for analysis of x-ray structural data (in black diamonds) values. (Bottom) Summation of stiffness constants for translational helical parameters (left), and the same for rotational helical parameters (right).

Accordingly, with all the required cautions, we believe that Parmbsc0 estimates of the stiffness parameters can be used to describe RNA₂ deformability.

Stiffness parameters (Fig. 5, original numerical data in Table S5 and Table S6) derived from Parmbsc0 trajectories reveal the large sequence-dependence of local flexibility in RNA₂, as noted in variation of up to 400% in local helical stiffness parameters. Certain steps are intrinsically rigid (like GC or CC), while others seem very flexible (like AU and UA), but in general, the concept of rigid and flexible steps should be taken with extreme caution, because the relative deformability depends dramatically on the nature of the deformation considered. For example, AC is stiffer than CC for rise deformation but simultaneously much softer for tilt deformation (see Fig. 5 and Table S5). Once again, the concept of flexibility and rigidity without link to the nature of the deformation movement is meaningless. It is worth noting that the relative ordering of stiffness for the different steps in RNA₂ is very similar to that found previously for DNA₂ (see Fig. 5), with the exception of r(A·U) steps, which are unexpectedly soft in RNA₂, probably due to the lack of the 5-Me group. For all the steps (except in the d(AT)/d(AU) pair), RNA₂ is stiffer than DNA₂ both in terms of rotational and translational deformations, in agreement with the results found in global helicity and entropy analysis. However, the analysis of Fig. 5 reveals that the difference in DNA₂ versus RNA₂ stiffness is smaller than the sequence-related variability, which implies that it could be possible to design sequences of RNA₂ with softer than average DNA₂ sequences.

Intrapair flexibility

An important, but often neglected pattern of flexibility is related to the relative movement of paired nucleobases. This is defined by three relative translations (stagger, stretch, and shear) and rotations (propeller twist, opening, and buckle). Of particular interest is the analysis of opening for two reasons:

• 1.Most of Parmbsc0 versus CHARMM27 differences arise from massive openings when the latter force field is used; and
• 2.NMR data (7,52) suggest that opening is often easier for RNA₂ than for DNA₂, which could be interpreted as a support to claims that RNA₂ is more flexible than DNA₂.

Results in Table 3, which are integrated for all the A·T / A·U and G·C steps, indicates that while CHARMM27 and Parmbsc0 opening force-constants are reasonably close for DNA₂ (especially for d(A·T) steps), they are completely different for RNA₂. This reflects the tendency of CHARMM27 simulations to open the pairs in the multi-nanosecond timescale, something that contrasts with NMR-measured average base opening times (∼1 ms; (7,51)). Clearly in this case, analysis should be restricted to Parmbsc0 values, which shows very clearly that in any sequence, environment openings of basepairs is easier (by ∼10%) for RNA₂ than for DNA₂. Note that this finding seems counterintuitive, because RNA helices are generally more stable than DNA₂, but agrees well with previous quantum mechanical calculations (23,59), which suggested that the general conformation of the RNA duplex induces a slight reduction in stability of the purine·pyrimidine hydrogen bonding compared with DNA₂. There is also beautiful agreement with NMR data (7,52), which points toward an easier opening in RNA than in DNA duplex, despite the globally larger stiffness of RNA₂. Our simulations are underlying again the complexity and richness of the concept of flexibility and the danger of making general claims about flexibility based on a single physical descriptor.

Table 3.

Opening force constants and their averages

	Seq 1		Seq 2		Seq 3		Seq 4		Averages
d(A·T)	0.017	0.015	0.017	0.016	0.020	0.019	0.022	0.022	0.019	0.018
r(A·U)	0.016	0.005	0.017∗	0.003	0.019	0.003	0.015	0.004	0.017	0.003
d(G·C)	0.068	0.051	0.063	0.047	0.059	0.044	0.064	0.048	0.063	0.047
r(G·C)	0.062	0.003	0.057	0.007	0.052†	0.006	0.056	0.003	0.058	0.005

Measured in kcal/mol deg² for d(A·T), r(A·U), d(G·C), and r(G·C) for the four sequences. The ending two basepairs have been removed for the analysis. Values corresponding to Parmbsc0 simulations are in roman style while those corresponding to CHARMM27 are in italics.

^∗Basepair 3 was removed due to fraying effects.

^†Basepair 16 was removed due to fraying effects.

Conclusions

Contrary to the situation in DNA duplex, where the two most widely used force fields provide similar structural and mechanical information, no general consensus picture of RNA₂ can be reached (to our knowledge), because of the large distortions occurring in RNA duplexes simulated with the CHARMM27 force field (which seems to be related to the loss of hydrogen bonding during simulations). It is, however, worth noting that if corrupted segments are eliminated from the analysis, reasonable agreement is found between CHARMM27 and Parmbsc0 simulations—pointing to a potential convergence between force fields in the near future.

Extreme caution is required when talking about flexibility, because this depends on the sequence and the level of resolution considered (global structure, base steps, or basepairs). However, if entropy or global stiffness parameters are accepted as global measures of flexibility, the DNA duplex appears clearly as an overall more flexible structure. At the basepair step level, the situation becomes more complicated, because even if DNA₂ is in general more flexible, sequence-dependent variability can induce larger changes in flexibility/rigidity than those originated by the nature of the oligonucleotide considered. Very interestingly, upon examining this at the basepair level, some deformation movements, such as opening, can be more difficult for DNA₂ than for RNA₂. Such finding is in excellent agreement with experimental and high level QM data. However, it is also quite counterintuitive, when one considers the overall larger rigidity and stability of the RNA duplex.

Parmbsc0 simulations allowed us to derive (to our knowledge), for the first time, not only global helical stiffness parameters (which agree well with experimental data), but sequence-adapted stiffness (and equilibrium) parameters for the RNA duplex. Results reveal a dependence of physical deformability with the sequence, which is similar, but not identical to that found in DNA₂. The apparently minor change T→U from DNA₂ to RNA₂ leads to major changes in the relative flexibility of the A·X step (X = T or U) between the two nucleic acids, which raises an interesting hypothesis on the motivations of nature for use different pyrimidines in DNA and RNA and suggest intriguing hypothesis on the physical mechanisms of epigenetic gene control mechanisms. Mesoscopic parameters presented here for the first time can be used to describe near-equilibrium geometric deformations of any RNA structure showing double-helix fragments, as is the case of interference RNA binding to the RISC complex. This opens the field for correlation of sequence effects with biological properties of RNA duplexes.