Metabolic Profiling And The Metabolome-Wide Association Study: Significance Level For Biomarker Identification

Abstract

High throughput metabolic profiling via the metabolome-wide association study (MWAS) is a powerful new approach to identify biomarkers of disease risk, but there are methodological challenges: high dimensionality, high level of collinearity, the existence of peak overlap within metabolic spectral data, multiple testing and selection of a suitable significance threshold.

We define the metabolome-wide significance level (MWSL) as the threshold required to control the family wise error rate through a permutation approach. We used ¹H NMR spectroscopic profiles of 24 hour urinary collections from the INTERMAP study. Our results show that the MWSL primarily depends on sample size and spectral resolution. The MWSL estimates can be used to guide selection of discriminatory biomarkers in MWA studies.

In a simulation study, we compare statistical performance of the MWSL approach to two variants of orthogonal partial least squares (OPLS) method with respect to statistical power, false positive rate and correspondence of ranking of the most significant spectral variables. Our results show that the MWSL approach as estimated by the univariate t-test is not outperformed by OPLS and offers a fast and simple method to detect disease-related discriminatory features in human NMR urinary metabolic profiles.

Introduction

The use of post-genomic technologies in large-scale molecular epidemiology is proving fruitful in detecting associations between molecular markers (genes, proteins, metabolites, etc.) and disease. For example, genome-wide association studies (GWAS) have found associations between genotype variation and disease phenotypes,^1,2 and analogously, the metabolome wide association study (MWAS) has revealed associations of metabolic phenotypes with disease risk.^3,4 In such studies, many hundreds to tens of thousands of molecular markers are assayed for each individual, leading to data which are highly multivariate, noisy and collinear. A key difficulty is the detection of statistically significant relationships between molecular variables and phenotype, while minimising risk of false positive associations at adequate power. The problem has received considerable attention in the statistical genetics and genomics literature,^5,6 but has not been the subject of detailed investigation in metabolic profiling and MWAS, where the level of collinearity within data is much higher.

Arguably the most popular and conservative approach is to control the family wise error rate (FWER), which is the probability of one or more significant results under the null hypothesis of no association. For a test applied at each of n molecular variables simultaneously, the simplest way to control the FWER is to apply the Bonferroni or Šidák correction. These set the significance level for the entire family of n hypotheses equal to α by taking the significance level for each comparison as α′ = α/n for Bonferroni correction or α′ = 1 − (1 − α)^1/n for Šidák correction. Less conservative FWER procedures are also available.^7–9 A popular approach in genomics is to estimate and control the false discovery rate (FDR), i.e., the expected proportion of falsely rejected null hypotheses.¹⁰ The FDR has been successfully applied to the analysis of gene expression data, for which many true positive associations are typically expected, but it has been less successful in the context of GWAS due to the small number of true positive associations and the presence of linkage disequilibrium with flanking SNPs.

Metabolic profiling employs spectroscopic techniques such as nuclear magnetic resonance (NMR) spectroscopy and mass spectrometry (MS) to measure hundreds or thousands of metabolites in cells, biofluids or tissues. Metabolic profiling at the epidemiological scale requires optimization of experimental protocols to maximize reproducibility, sensitivity, accuracy and to reduce analytic drift.⁴ When complex metabolic spectra are analyzed, control for false positive associations is essential for effective data exploitation and biomarker discovery. Permutation procedures can yield the correct FWER even when the tests are dependent. However, they are computationally intensive and their application has been limited by the large size of data sets typical of GWAS, and are problematic also for MWAS, although the number of variables is an order of magnitude lower. This has led to approximations to reduce the computational effort,^11–13 although such approximations are still problematic when dealing with multiple molecular variables. Moreover the results of permutation procedures apply only to the data set under investigation and must be recomputed when the data set is altered.

In modelling spectroscopic data, two complementary approaches can be taken: direct modelling of the raw spectral profiles, or estimation and modelling of individual compound concentrations. Both approaches often use multivariate projection methods such as principal components analysis (PCA) and partial least squares (PLS) regression because of their ability to cope with highly multivariate, noisy, collinear and possibly incomplete data. Typically, the metabolic profiles of disease cases and non-disease controls are compared with the aim of identifying spectral features, and ultimately metabolites, which discriminate the classes. With PLS-discriminant analysis (PLS-DA), identification of discriminatory variables proceeds from an analysis of the PLS weights or regression coefficients. Orthogonal PLS (OPLS and O2PLS)^14,15 improves interpretability of models by removing variation uncorrelated to the response variable and reducing the complexity of the model. Methods of interpreting the weights and coefficients vary, and despite some attempts to assess loading significance levels,¹⁶ probabilistic measures of significance or association are not frequently used.

As a fast and simple alternative to the OPLS-DA approach, we estimate metabolome-wide significance levels (MWSLs) to control the FWER, where two-sample t-tests are used for detection of associations between metabolic variables and phenotype. We adopt an approach similar to the genome wide significance level recently introduced in GWAS.⁵

To assess the accuracy of the MWSL approach, we then compare the results it provides with those obtained from two variants of the O2PLS algorithm, which have already been applied to data from the INTERnational study of MAcro nutrients and blood Pressure (INTERMAP).¹⁷ Specifically, we perform a simulation study using spectroscopic data from the INTERMAP study in which 24 hour urinary collections were obtained and profiled by ¹H NMR spectroscopy for 4,630 free-living individuals from 17 population samples in four countries (China, Japan, UK, US). We compare the statistical performance of (i) univariate t-tests with MWSL and (ii) O2PLS-DA procedures with p-values calculated using either bootstrap resampling (O2PLS-Bootstrap), or a standard permutation test (O2PLS-Permutation).

Materials and Methods

Definition of the Metabolome-Wide Significance Level (MWSL) and Effective Number of Tests (ENT)

We propose a metabolome wide significance level approach to identify association between metabolic variables and disease status. Analogous with the genome wide significance level, we define the MWSL (α′) as the per-test significance level to be considered for each univariate two-sample t-test, to reach the target overall significance level FWER α.⁵ Its calculation relies on n permutations of the case-control status (here n = 50,000). For each permutation we draw a sample of N cases and N controls from our reference population, we then calculate the p-value for each spectral variable, using a univariate t-test and record q, the minimal p-value calculated over all variables. The per-variable significance level α′ that corresponds to a FWER α satisfies α = Pr(min{p_i} < α′), where p_i denotes the p-value from the i-th variable. Point estimates for α′ are defined as α′ = q_nα, where q_nα denotes the n × α^th smallest value for q, among its n realizations. Continuing with this notation, the 95% confidence limits for α′ can be deterministically approximated by $q_{n\alpha \pm \sqrt{n\alpha (1-\alpha )}}$.

The effective number of tests ENT_B and ENT_S are defined as the number of independent tests that would be required to obtain the same significance level using Bonferroni or Šidák corrections respectively: ENT_B = α/α′ and ENT_S = log(1 − α)/log(1 − α′). The ENT implicitly quantifies the level of dependency within the data.

Results corresponding to the Šidák correction were calculated but are not reported as they were qualitatively similar to those obtained using Bonferroni correction.

The Use of INTERMAP Data

To determine the MWSL, based on real-world data, we exploited the rich variety of human metabolic phenotypes available in the INTERMAP dataset; a unique resource providing a large-scale standardized set of urinary metabolic profiles which captures variation within and between human populations in China, Japan, UK and US.

Two timed 24 h urine specimens were obtained from each individual according to a standard protocol described elsewhere.¹⁷ Only data from the first collection are used here. Metabolic profiles were acquired by ¹H NMR spectroscopy at 600 MHz and automatically phased, baseline corrected and chemical shift referenced using an in-house MATLAB script.³ Spectra were normalized to unit integrated intensity to account for large variations in overall urinary dilution between participants.

We chose the Chinese (N = 836 spectra) sample as a reference population. We investigated the influence of the spectral digital resolution, i.e., the number of variables in the spectrum, by considering both high and medium resolution representations of the NMR spectra (16,118 and 7,100 variables respectively). The high resolution corresponds to the native digital resolution of the acquired spectra. The medium resolution data were obtained by integrating the NMR signal intensities in adjacent bins of width 0.001 ppm (0.6 Hz), for the regions δ0.5–9.5 (excluding δ4.5–6.4 containing the residual water and urea resonances). Since the typical peak width at half height is 1 Hz, this corresponds approximately to two intensity variables per peak, thus retaining the majority of information in the spectra. We also examined population heterogeneity by repeating the analysis using the US population (N = 2,164 spectra) at medium resolution (7,100 variables).

Disease Model Simulations

To assess their reliability, results from the MWSL approach are compared, by means of a simulation study, to those provided by two variants of the O2PLS algorithm, which is well established in metabolic profiling.¹⁵

Disease Model

From the reference population we randomly sampled a set of N cases and N controls, assigning case/control status according to a logistic (multiplicative) disease model, which was chosen, for its simplicity and flexibility. Specifically, let X_{i j} be the peak intensity at location j for individual i. The probability that individual i is a case given a subset of m peaks (one peak for each metabolite) is given by

$$\text{P}(Y_i=1\mid X_{ij},j=1,\dots ,m)=\frac{exp\left\{{\beta }_0+{\sum }_{j=1}^m{\beta }_j{X}_{ij}\right\}}{1+exp\left\{{\beta }_0+{\sum }_{j=1}^m{\beta }_j{X}_{ij}\right\}},$$ (1)

where Y_i denotes the case/control indicator for individual i and each peak intensity is standardized to have unit variance in the reference population.

The intercept β₀ relates to the underlying risk in the population and the slope β _j mimics a form of metabolite (log) relative risks for each individual. Note that in the disease model defined in eq. (1), to create association between the disease and a particular metabolite, we use just one of the spectral variables from one of its NMR resonances. In our simulations we vary the following parameters: the sample size of cases and controls N (N = 50,100,200); the number m of metabolites associated with the disease (m = 0,1,3) and prevalence of disease K in the population (K = 10,30,50%). For m = 1, association strength was defined by β₁ = logit(K) − β₀ and for m = 3, we chose |β₁| = 1, |β₂| = 2, and |β₃| = 4 to examine a range of association strengths. In both cases β₀ was set such that the disease probability within the population ranged from 0 to 1.

When m = 0, there is no metabolite-disease association, therefore any peak estimated as significantly associated with disease is a false positive. In this setting, case/control status was randomly assigned to each individual with a probability of being a case equal to 0.5.

Furthermore, as the spectral fingerprint of a metabolite may be represented by more than one spectral variable, and some NMR resonances are subject to small variations in chemical shift (caused by differences in sample pH or ionic concentration), we consider as a true positive any significant variable which is located in a range Δ of any of the reference peaks of the ‘causal’ metabolite. For a metabolite with several multiplets, Δ consists of several separate ranges of chemical shift. The width of ‘true positive’ range Δ is influenced by the spectral line width and multiplicity of each resonance, here computed from the mean spectrum for the whole Chinese sample (SI Table 1).

We define statistical power as the proportion of the 50 replicates yielding at least one significant association within the range Δ. Additionally, we define the false positive rate as the mean ratio of the number of significant peaks outside the range Δ to the total number of significant associations.

Assessing Significance in the O-PLS-DA Approach

We fitted the O2PLS model using an in-house O-PLS-DA code in MATLAB, and obtained estimates of the regression coefficients b _j, which represent the contribution of the jth spectral variable to case-control discrimination. We first used a bootstrap resampling technique to estimate the uncertainty of each regression coefficient (O2PLS-bootstrap). Based on the bootstrap samples we then used the estimates of the standard deviation of each regression coefficient b_j to perform an approximate t-test and determine p-values for each b_j as described previously.16 A second variant of the O2PLS-DA approach, based on permutation tests, was also implemented (O2PLS-permutation). As for O2-PLS-bootstrap, we fitted the O2PLS model using an in-house O-PLS-DA code in MATLAB to obtain estimates of the regression coefficients b_j. To estimate the p-value associated with each regression coefficient, we performed a standard permutation test by taking permutations of the case/control indicator for each data set.

Results and Discussion

Metabolome-Wide Significance Level and Effective Number of Tests

We considered three sample sizes: 50, 100 and 200 cases, with equal numbers of controls, typical of sample sizes reported in metabolic profiling studies.^18,19 For the larger US sample, it was also possible to consider 500 cases and controls. For each statistic, mean and 2.5^th and 97.5^th percentiles were calculated over 50,000 re-samplings. Table 1 gives estimates of the per-spectral variable significance level α′ for the corresponding FWER α of 1 or 5% for the Chinese and US populations.

Table 1.

Significance threshold α′ (×10⁻⁵) and effective number of tests (×10³) based on Bon-ferroni correction (ENT_B). 95% confidence intervals are given in parentheses. Bold figures are the proportion of Effective/Actual number of tests. Figures are based on 50,000 re-samples of the disease indicator under the null hypothesis.

Dataset	Sample size #Cases/controls		Overall error rate α =
			1%		5%
Chinese population High resolution 5 × 10−4 ppm 16,118 variables 836 spectra	50/50	α′	0.48 (0.45;0.52)	13%	2.12 (2.03;2.19)	15%
		ENTB	2.08 (1.92;2.24)		2.36 (2.28;2.46)
	100/100	α′	0.35 (0.33;0.39)	17%	1.64 (1.58;1.70)	19%
		ENTB	2.82 (2.58;3.05)		3.06 (2.95;3.16)
	200/200	α′	0.25 (0.23;0.27)	25%	1.24 (1.19;1.31)	25%
		ENTB	3.96 (3.69;4.26)		4.02 (3.83;4.19)
Chinese population Medium resolution 10−3 ppm 7,100 variables 836 spectra	50/50	α′	0.87 (0.82;0.94)	16%	3.81 (3.68;3.92)	18%
		ENTB	1.14 (1.06;1.23)		1.31 (1.27;1.36)
	100/100	α′	0.66 (0.61;0.72)	21%	3.22 (3.09;3.36)	22%
		ENTB	1.51 (1.40;1.64)		1.55 (1.49;1.62)
	200/200	α′	0.50 (0.46;0.54)	28%	2.48 (2.37;2.58)	28%
		ENTB	2.00 (1.84;2.16)		2.02 (1.93;2.11)
US population Medium resolution 10−3 ppm 7,100 variables 2164 spectra	50/50	α′	1.04 (0.95;1.14)	14%	4.43 (4.28;4.59)	16%
		ENTB	0.97 (0.88;1.05)		1.13 (1.09;1.17)
	100/100	α′	0.81 (0.73;0.86)	17%	3.61 (3.46;3.74)	20%
		ENTB	1.24 (1.16;1.37)		1.39 (1.34;1.44)
	200/200	α′	0.65 (0.60;0.71)	22%	2.98 (2.84;3.07)	24%
		ENTB	1.54 (1.41;1.68)		1.68 (1.63;1.75)
	500/500	α′	0.46 (0.44;0.51)	30%	2.41 (2.31;2.51)	29%
		ENTB	2.15 (1.95;2.30)		2.07 (1.99;2.16)

In all scenarios considered, our estimate of α′ is larger than that estimated from a metabolome-wide Bonferroni correction. The corresponding ENT is always less than the actual number of tests, due to dependence between variables.

As expected α′ increases with α, while ENT_B seem insensitive to the overall error rate for given population and sample size, since their values depend mainly on the extent of correlation within the data. Typically α′ decreases as the case-control sample size increases. For example, an increase in sample size from 50 to 500 cases and controls in the US population resulted in α′ decreasing by almost a factor of two, and an approximate doubling of the ENT.

Comparing high and medium resolution data, roughly halving the number of spectral variables approximately doubles the MWSL. The proportion of effective/actual tests is slightly higher for the medium resolution data, suggesting that, as expected, the lower resolution decreases the correlation between spectral variables.

When comparing the results obtained from the Chinese and US populations at the lower resolution, we note that the MWSLs are fairly close, although slightly higher ENT (and correspondingly more stringent MWSL) is found for the Chinese population, possibly reflecting the larger population size in the US dataset and/or a country-specific patterns in the spectral data.

Stability of these estimates was investigated further by calculating the MWSL based on all 4,630 metabolic profiles available within the INTERMAP study, i.e. pooling individuals from China, Japan, UK and US samples (SI Table 2). Results confirm that, for given FWER level, sample size and spectral resolution, estimates of the MWSL are stable regardless of the population on which estimates are based. As a general rule, assuming 35% independent tests, regardless of spectral resolution and sample size, conservative but credible values for MWSL are 9 × 10⁻⁶ and 1.5 × 10⁻⁶ for FWERs of 0.05 and 0.01 respectively, at a resolution of 16,118 spectral variables; and 2 × 10⁻⁵ and 4 × 10⁻⁶ at a resolution of 7,100 variables.

Performance Comparison

Here we assess and compare the performance of (i) independent t-test with Bonferroni correction or MWSL, (ii) O2PLS-bootstrap and (iii) O2PLS-permutation methods. P-value calculations for the O2PLS methods are based on 1,000 bootstrap samples and 1,000 permutations respectively. For both O2PLS methods, a Bonferroni correction was used to correct significance levels. We used the Chinese sample from the INTERMAP database as the reference population, and used high resolution spectral data. The following results are averaged over 50 replicates of the disease model.

Assessing False Positive Rates

Table 2 shows the estimates of the false positive rates under the scenario of no association (null hypothesis). The t-test, corrected for multiple testing, performs better than the multivariate methods in terms of false positive rates. Over 50 replications, the t-test with either Bonferroni correction or exact MWSL does not detect any significant association.

Table 2.

Mean number of false positive associations under the null hypothesis of no association. The results shown are averages over 50 replicates (minimum and maximum values over the replicates are given in parentheses). Both O2PLS approaches are based on a Bonferroni corrected threshold. T-test results are reported uncorrected, Bonferroni corrected, using the exact metabolome-wide significance level (MWSL), and using the general MWSL we estimated. Estimates of the MWSL are based on a FWER α of 1%.

# Cases/Controls	50/50	100/100	200/200
O2PLS - Bootstrap	40.3 (4–163)	48.5 (4–526)	25.0 (0–128)
O2PLS - Permutation	16.1 (1–65)	15.9 (0–49)	14.9 (0–48)
T-test uncorrected	104.4 (17–322)	173.1 (35–921)	139.5 (33–424)
T-test Bonferroni	0.0 (0–0)	0.0 (0–0)	0.0 (0–0)
T-test exact MWSL	0.0 (0–0)	0.0 (0–0)	0.0 (0–0)
T-test general MWSL α′ = 1.5 × 10−6	0.0 (0–0)	0.0 (0–1)	0.0 (0–0)

O2PLS with permutation tests picks on average less than 20 false positive associations. This is an over-estimation of the number of significant associations found by the O2PLS-permutation method since (i) with 1,000 permutations, p-values are estimated with a precision 10⁻³, and (ii) the Bonferroni corrected threshold to which p-values are compared is approximately 3 × 10⁻⁶ (based on 16,118 variables).

The O2PLS-bootstrap procedure seems to detect a larger number of false positive associations than the other two approaches (mean number of false positive associations > 25), for all sample sizes. This might be because the Gaussian assumption for the distribution of the test statistic underlying the bootstrap estimation method is not a good approximation of the true distribution.

When the FWER is set to 5%, regardless of the sample size, the mean number of false associations under the null is > 45 for O2PLS-bootstrap. For O2PLS-permutation, due to estimation precision, numbers remain unchanged. No false positive associations are found under the null hypothesis for t-test with Bonferroni correction, while there are no more than 2 false positive findings when the exact MWSL is applied (SI Table 3).

Statistical Power

We first consider the scenario in which m = 1, i.e., only one metabolite associated with disease. We chose hippurate as the associated metabolite, in particular the peak at 7.846 ppm. Results are summarized in Table 3.

Table 3.

Per-metabolite statistical power, calculated over the 50 replications of the disease model, for the single (Table 3-a) and the multi-metabolite models (Table 3-b). False positive (FP) rate is defined as the mean number of false positive associations as a proportion of the number of significant variables. Population size did not allow investigation of sample sizes >50 at a prevalence of 10%. FWER is set to 1%.

Table 3-a One disease associated metabolite (hippurate).

Prevalence	Sample Size	10%		30%		50%
		Power	FP Rate	Power	FP Rate	Power	FP Rate
O2PLS Bootstrap	50/50	100%	33.4%	100%	29.1%	100%	30.1%
	100/100	N.A.	N.A.	100%	36.7%	100%	53.1%
	200/200	N.A.	N.A.	100%	50.9%	100%	69.8%
O2PLS Permutation	50/50	98%	9.3%	98%	9.2%	100%	3.5%
	100/100	N.A.	N.A.	100%	6.1%	100%	4.7%
	200/200	N.A.	N.A.	100%	4.9%	100%	6.0%
T-test Bonferroni	50/50	68%	0.4%	66%	0.3%	94%	0.4%
	100/100	N.A.	N.A.	100%	2.1%	100%	4.7%
	200/200	N.A.	N.A.	100%	9.9%	100%	28.6%
T-test exact MWSL	50/50	84%	1.4%	86%	0.8%	98%	1.3%
	100/100	N.A.	N.A.	100%	3.8%	100%	8.2%
	200/200	N.A.	N.A.	100%	14.8%	100%	35.9%
T-test general MWSL α′ = 1.5 × 10−6	50/50	72%	0.8%	74%	0.4%	96%	0.6%
	100/100	N.A.	N.A.	100%	2.7%	100%	6.1%
	200/200	N.A.	N.A.	100%	12.7%	100%	33.2%

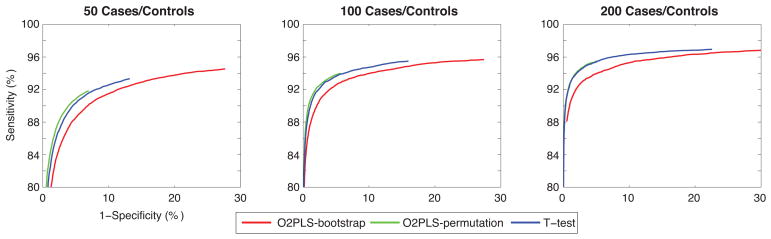
Both O2PLS approaches yield a power > 98% in all scenarios, while for the univariate analysis the power is > 65% (and > 80% when the exact MWSL is used). As expected power increases with sample size, and for the largest sample sizes, all the methods perform equally regardless of disease prevalence. The O2PLS-bootstrap approach has high false positive rates (ranging from 30 to almost 70%), while false positive rates for O2PLS-permutation are < 10% and appear unaffected by sample size. False positive rates for O2PLS-bootstrap and univariate t-test appear to increase as sample size and disease prevalence increase. We conclude that, although there is a slight advantage in terms of false positive rates for O2PLS-permutation in large samples, both t-test and O2PLS-permutation offer a satisfactory and comparable solution for the single metabolite model. This is confirmed by the receiver-operator curves (ROC) in Figure 1 (for K=30%), and SI Figures 1 (for K = 10%) and 2 (for K = 50%). When setting α to 5%, false positive rates and power are both similar, although slightly higher (SI Table 4).

Figure 1.

ROC curves for the single metabolite model, prevalence is set to 30%. Figures are based on 500 data points corresponding to α ∈ [10⁻¹⁰;10⁻¹].

Next we considered a multi-metabolite association model, in which m = 3 metabolites (hippurate, alanine and formate) are assumed to be associated with the disease. We chose these three metabolites as examples as each was found to be associated with blood pressure in previous analyses of INTERMAP data³. The prevalence was set close to 50% (K = 45.6%), with different relative risks for each metabolite (|β₁| = 1, |β₂| = 2, and |β₃| = 4 for hippurate, alanine and formate respectively) to assess performance over a range of signal strengths.

Although similar trends to the single metabolite disease model are seen in Table 3-b for the multi-metabolite model, there is a trade-off between power and false positive rate. For all three metabolites, O2PLS approaches result in high false positive rates (> 68 and 46% for O2PLS-bootstrap and permutation, respectively), while this proportion is < 14% for the t-test with exact MWSL. Per spectral variable statistical power reflects the absolute value of the logistic coefficient that measures the strength of the association between peak intensity and disease. Statistical power for formate (the metabolite which was set to have the strongest disease association), is always high and reaches 100% for all methods when sample size exceeds 50 cases/controls. For hippurate and alanine, power is < 10% for the t-test. For both O2PLS approaches, statistical power is higher and peaks at 60% for O2PLS-bootstrap when N = 200 (corresponding value for the O2PLS-permutation is 34%). In most scenarios, despite its stronger association with disease, statistical power for alanine is lower than for hippurate, which might reflect the smaller number of alanine peaks.

Table 3-b.

Three disease associated metabolites (hippurate, alanine and formate)

Metabolite	Logistic coefficient (|β|)	Power			FP rate
		Hippurate 1.0	Alanine 2.0	Formate 4.0
O2PLS Bootstrap	50/50	18%	12%	94%	79.6%
	100/100	36%	26%	100%	73.2%
	200/200	60%	46%	100%	68.8%
O2PLS Permutation	50/50	14%	8%	92%	65.9%
	100/100	26%	22%	100%	49.8%
	200/200	34%	28%	100%	46.9%
T-test Bonferroni	50/50	0%	0%	38%	2.0%
	100/100	0%	2%	100%	0.5%
	200/200	2%	4%	100%	9.3%
T-test exact MWSL	50/50	0%	0%	70%	1.2%
	100/100	4%	4%	100%	2.5%
	200/200	4%	10%	100%	13.5%
T-test general MWSL α′ = 1.5 × 10−6	50/50	0%	0%	54%	1.0%
	100/100	0%	2%	100%	1.3%
	200/200	4%	8%	100%	11.7%

From a computational perspective, the multivariate methods are more demanding than univari-ate analysis: for S bootstrap or permutation re-samples, the t-test is over 3S times faster than either O2PLS approaches. This may become rate-limiting for large sample sizes.

The MWSL is designed to control the number of false positive associations under the null hypothesis of no association, i.e. to control the type I error. In practice, high levels of correlation within the data can yield a large number of positive signals, as variables correlated with the causal metabolites will likely also be significantly associated with the outcome (see for example false positive rates in Table 3). Therefore, it is essential to develop methods accounting for the correlation structure: as a first approach, we estimated here the independent number of tests. In GWAS, it is common practice to replicate positive findings in different cohorts to guard against false associations. A similar strategy was adopted for the INTERMAP MWAS: two urine collections were available per person, and only metabolites that were significantly associated with the outcome in both specimens were declared true positives.³ An extension of our simulation study showed that in that situation, for a FWER of 1%, the O2PLS-bootstrap method would yield a power of 100% and false positive rates <7%, and the MWSL approach, a power of 100%, and false positive rates <0.4%, regardless of sample size and prevalence.

Ranking of Variables

One important goal of MWAS is to rank metabolites in terms of their strength of association with disease, in order to improve detection of biologically meaningful metabolites and reduce the false positive rate.

In SI Figures 4–5 we show the mean spectrum with each variable colored according to median p-value over the 50 replicates for the single metabolite model. The figures show that the ‘true positive’ ranges are associated with lower p-values (colored green), suggesting that the three methods (t-test, O2PLS-bootstrap, O2PLS-permutation) are able to correctly locate the causal metabolites; including when metabolite signals comprise different multiplets across the spectrum, as in the case of hippurate. The bootstrap approach detects more variables with low p-values, consistent with the higher false positive rate associated with this method. The p-value distributions across the spectrum seem comparable for the permutation and t-test, consistent with their similar performance (Figure 1, and SI Figures 1 and 2). The plot for the multi-metabolite disease model is presented in SI Figure 6. The p-values corresponding to hippurate and alanine spectral variables are large, reflecting the low power of all methods for correspondingly low association strengths. On the other hand, all methods were successful in detecting formate (which corresponds to a strong association signal) and this is reflected by the concentration of low p-values in the formate region (8.46 ppm). In the plot, high false positive rates correspond to a large number of variables with low p-values outside the true positive range and SI Figure 6 confirms the poor performance of O2PLS-bootstrap in terms of false positive rate.

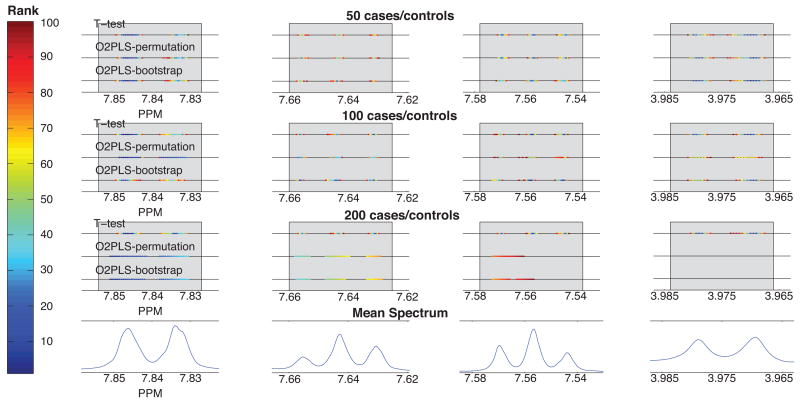
We now consider how the different methods rank the metabolites in order of strength of association with disease. In Figure 2 the top 100 variables for each method and sample size are colored according to their ranking for the single metabolite model at a prevalence of 30%.

Figure 2.

Location of the 100 metabolites with the lowest mean p-values using the three methods, single metabolite model (hippurate). For all simulations, none of the top 100 metabolites were found outside the ‘true positive’ range (represented in light grey in the figure). Points are colored according to their rank. Results are provided for a prevalence set to 30%

Regardless of method or simulation parameters, the top 100 variables (i.e., the variables with lowest p-values whether significant or not) all correspond to the hippurate reference peak. The variables with the lowest p-values are located mainly in the [7.827 – 7.854] region (corresponding to the reference peak used in the disease model). Some of the top 20 variables are also located in the [3.966 –3.984] region which corresponds to the aliphatic doublet of hippurate, while most of the variables ranked between 20 and 100 are located in the remaining three hippurate regions. The sample size clearly affects the distribution of the top ranked variables. For all three methods, the top 100 variables are distributed across all four regions at sample sizes of n = 50 and n = 100, but at n = 200 none are found in the aliphatic doublet region [3.966 – 3.984] for either O2PLS approach. Additionally, with increased sample size, the top ranked variables are found more towards the low field (high ppm) regions; this is more apparent for the O2-PLS based methods than for the t-test. For example, based on n = 50, the top 20 variables are found in all four regions while for n = 200, they are located exclusively in the region of the reference peak. Similar behavior is seen at a prevalence of 50% (SI Figure 7). Results for the multi-metabolite model are shown in SI figure 8. All methods have a similar performance in terms of ranking metabolites in order of strength of association with disease.

Conclusion

Identification of metabolites that contribute significantly to discrimination between classes in MWAS is problematic. We find that the MWSL accounts appropriately for the high degree of correlation in spectral data, and provides a practical threshold that can be used as a benchmark for future MWAS of human urine. A conservative estimate of the independent number of tests is 35% regardless of spectral resolution and sample size. This leads, for example, to an estimated MWSL of 2 × 10⁻⁵ and 4×10⁻⁶ for a FWER of 0.05 and 0.01 respectively, at medium spectral resolution (7,100 variables). While the work presented here focuses on NMR metabolic profiles, our method may be applied to other metabolic profiling technologies such as liquid/gas chromatography-MS.

It is well known that spectral variables from metabolic profiles exhibit a high degree of collinearity, and this is supported by our finding that the computed MWSL greatly exceeds the Bonferroni or Šidák corrected value across all three data sets. The extent of collinearity is summarized by the ratio of effective to actual number of tests which varies between 15 and 30% across diverse spectral resolutions, sample sizes and populations. The number of independent variables might give an indication of the number of independent metabolic processes exhibited by the system, since each independent process might be expected to manifest itself through multiple metabolic variables. If the data are interpreted this way, our analysis suggests that there are between one and four thousand separate metabolic processes being captured by NMR metabolic profiles of urine among free living humans in these two populations.

The univariate approach with MWSL seems to perform satisfactorily in the task of discovering features discriminating case-control samples when compared to multivariate methods in terms of false positive rates and statistical power. Both the t-test and O2-PLS-permutation methods had comparable sensitivity and specificity for the populations tested. However, the multivariate approaches may have other benefits such as the ability to detect and remove outliers, rejection of noise, dimension reduction, intuitive visualizations, and construction of a predictive framework which allows a train/test set validation of the resulting model. In addition, orthogonal filtering methods, such as those examined here, enable greater interpretability of the models by partitioning the variance according to its correlation with the response, allowing, for example, the filtering out of potential confounding effects. In this paper we focused on a two-class response, and it is possible that multivariate methods may show an improved relative performance when applied to multi-class or continuous outcomes. Furthermore, due to our simple disease model, we were restricted to a limited number of causal metabolites. It is possible that multivariate models may show improved performances in more complex situations where many metabolites are responsible for the discrimination between case and control samples. Nonetheless, for detection of discriminatory features in NMR metabolic profiles of human urine, univariate methods such as the t-test used with an appropriate MWSL, may be recommended as a fast and simple alternative to the more complex and computationally intensive multivariate approaches.