Abstract
Currently the Protein Data Bank (PDB) contains over 18,000 structures that contain a metal ion including Na, Mg, K, Ca, V, Cr, Mn, Fe, Co, Ni, Cu, Zn, Pd, Ag, Cd, Ir, Pt, Au, and Hg. In general, carrying out classical molecular dynamics (MD) simulations of metalloproteins is a convoluted and time consuming process. Herein, we describe MCPB (Metal Center Parameter Builder), which allows one, to conveniently and rapidly incorporate metal ions using the bonded plus electrostatics model (Hoops et al., J. Am. Chem. Soc. 1991, 113, 8262–8270) into the AMBER Force Field (FF). MCPB was used to develop a Zinc FF, ZAFF, which is compatible with the existing AMBER FFs. The PDB was mined for all Zn containing structures with most being tetrahedrally bound. The most abundant primary shell ligand combinations were extracted and FFs were created. These include Zn bound to CCCC, CCCH, CCHH, CHHH, HHHH, HHHO, HHOO, HOOO, HHHD, and HHDD (O = water and the remaining are 1 letter amino acid codes). Bond and angle force constants and RESP charges were obtained from B3LYP/6-31G* calculations of model structures from the various primary shell combinations. MCPB and ZAFF can be used to create FFs for MD simulations of metalloproteins to study enzyme catalysis, drug design and metalloprotein crystal refinement.
Introduction
There are currently over 66,000 structures in the Protein Data Bank (PDB) and searching for “metal” results in over 25,000 hits with an approximate break down shown in Table 1. Metal ions play a vital role in protein function, structure, and stability, with zinc, iron, manganese, and copper transition metals being the most represented in the PDB (see Table 1). It is desirable to model metalloprotein systems using MM models because one can carry out simulations to address important structure/function and dynamics questions that are not currently attainable using QM and/or QM/MM based methods due to unavailability of parameters or simply due to system size.
Table 1.
Metals in the Protein Data Bank (July 2010).
| Metal | Hits | Metal | Hits | Metal | Hits |
|---|---|---|---|---|---|
| Na | 2701 | V | 59 | Pd | 8 |
| Mg | 5384 | Cr | 7 | Ag | 10 |
| K | 965 | Mn | 1412 | Cd | 521 |
| Ca | 5030 | Fe | 1403 | Ir | 2 |
| Co | 337 | Pt | 44 | ||
| Ni | 463 | Au | 30 | ||
| Cu | 763 | Hg | 343 | ||
| Zn | 5854 | ||||
| Total = 25336 | |||||
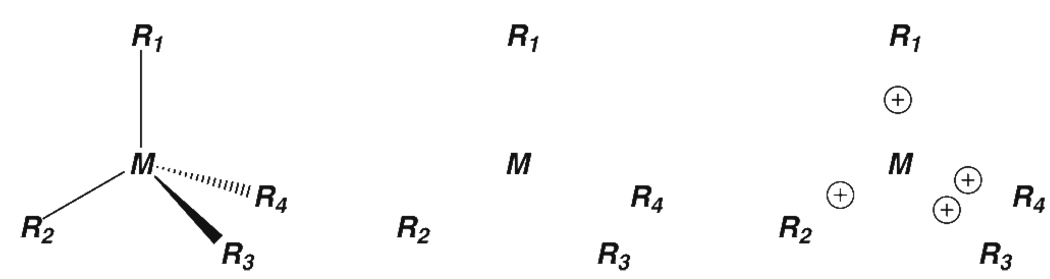
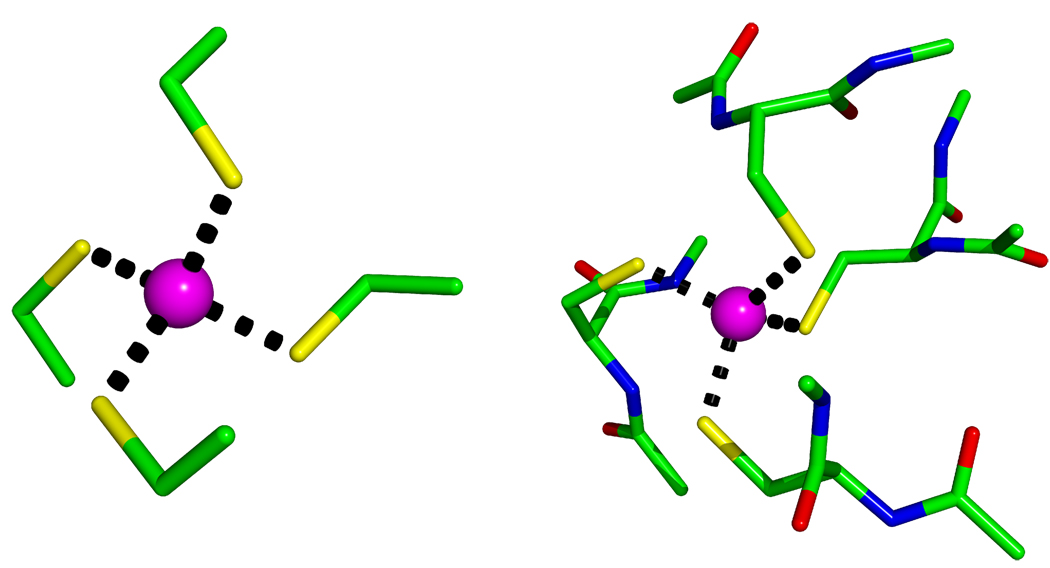
There are a number of approaches to incorporating metal ions into FFs. The Bonded Model defines bonds, angles, and torsions between the metal ion and its ligand, which are added to the FF plus the van der Waals component of the non-bonded function. Hancock1,2 used this approach to study systems including copper and nickel. The Bonded plus electrostatics Model3 defines bonds and angles between the metal ion and its ligand as well as electrostatic potential (ESP) charges (Fig. 1a). This method attempts to define the correct electrostatic representation of the metal active site because simply assigning a plus two formal charge to a divalent metal ion would not describe the reality of the electronic structure of a metal/ligand complex even though formally correct. The partial atomic charges can be calculated using the RESP approach4 or the CMX models of Truhlar and Cramer5. The bond and angle force constants are derived from experiment or calculated using ab initio or DFT methods while the torsion term has so far been neglected. The Non-Bonded Model does not define any extra bonds and places integer charge on the metal ion6. Electrostatic and Lennard-Jones terms describe the interactions. Modifications to this model to include polarization and charge transfer effects have been developed (Fig. 1b)7. The Cationic Dummy Atom Model is related to the non bonded method where it places dummy atoms (cations) to mimic valence electrons around the metal ion8. Electrostatic and Lennard-Jones terms between the dummy atoms and ligating residues describe the metal-ion interactions (Fig. 1c)9,10. Other methods include those of Vedani et al. which is a compromise between the bonded and non-bonded methods and is implemented in the YETI program11,12, the SIBFA of Gresh and co-workers13,14 and the Universal Force Field (UFF) of Goddard and Rappe and co-workers15–17. These methods do not use a pairwise additive potential or are not readily available in typical biomolecular modeling packages.
Figure 1.
Three Approaches to Incorporate Metal Atoms into Molecular Mechanics Force Fields. The bonded model (left) defines bonds, angles, and dihedrals between the metal and ligands, while the non-bonded model (middle) does not and uses electrostatics and van der Waals to model the interactions. The cationic dummy atom model (right) is a derivative of the non-bonded model where cations are placed near the metal center to mimic valence electrons around the metal.
Carrying out MM modeling or MD simulations of metal containing proteins is a complicated procedure using the bonded plus electrostatics model. Incorporating metals into protein force fields is a convoluted process due to the plethora of QM Hamiltonians, basis sets and charge models to choose from. Also it has generally been carried out by hand without extensive validation for specific metalloproteins. Some of the published force fields for zinc, copper, nickel, iron, and platinum containing systems using the bonded plus electrostatics model are listed in Table 2. There have been numerous other FFs containing various metals published including ruthenium(II)-polypyridyl18, cobalt corrinoids19–22, Staphylococcal Nuclease23, alcohol dehydrogenase24,25, and metalloporphyrins26–30.
Table 2.
Published Metalloprotein Force Fields Using the Bonded Plus Electrostatics Model.
Automated procedures for the parameterization of MM functions for inorganic coordination chemistry have been developed over the last number of years by Norrby and co-workers31,32. Their attempts have focused on generating parameters using experimental, structural data from databases such as the Cambridge Structural Database (CSD) and quantum mechanical reference data using a version of the MM3 force field33. Recently, we used the approach described herein to build a FF for the Ni contain metal center in NikR34, but the full computational details were not presented. Herein, we present these details in the context of a Zn FF. We note that a similar approach was published after our NikR work by Lin and Wang35, but a program or framework with which people can easily and consistently build parameters for metal containing protein systems was not fully developed. The advantage of a program, like the one reported here, is it possible to quickly build a metal ion FF for the typically troublesome metal sites that are common in naturally occurring biological systems.
Herein we describe an approach to rapidly build, prototype and validate MM based FFs for metalloprotein systems using the AMBER FF. The base approach will be the bonded plus electrostatics model, as we have the most experience and are most comfortable with this approach. However, the tools created can be readily utilized to develop other class of metal ion FF models including non-bonded models.
Implementation
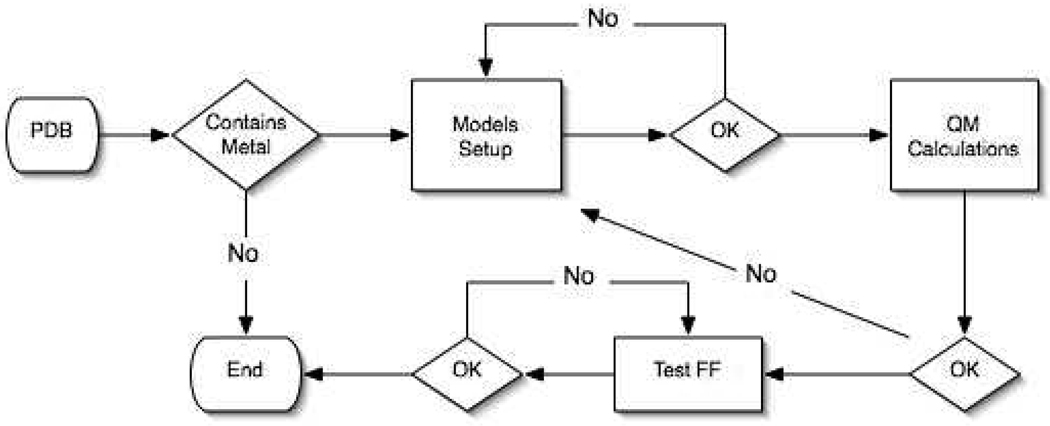
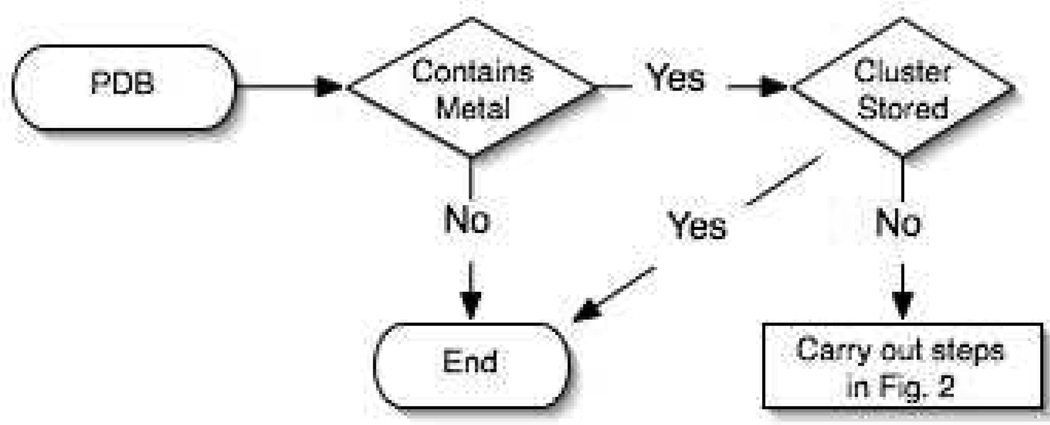
The goal of this research was to provide a platform to rapidly build, prototype, and validate MM models of metalloproteins using the bonded plus electrostatics model for the AMBER suite of programs53. The bonded plus electrostatics model was chosen over the other approaches as the resulting parameters fit the FF functional forms used in AMBER54 and CHARMM55 which are two widely used biomolecular simulation packages. Additionally, the functions used in these programs are pairwise additive meaning there are no cross-terms and are thus easier to parameterize and less computationally expensive. The latter is a key point when considering fully solvated metalloproteins in MD simulations can have many hundreds of thousands of atoms. A computer program, MCPB (Metal Center Parameter Builder), to generate FF parameters for metalloproteins was developed to this end. MCPB was not built to supersede the approaches developed by Norrby described above but instead to incorporate a realistic bonded and electrostatic model of the metallocenter into the AMBER FF. The MCPB program was built using the MTK++ Application Program Interface (API), which was developed as an in-house modelling platform for metalloproteins. A complete workflow of MCPB can be seen in Figure 2. The MCPB program carries out the following steps after a structure is downloaded from the Protein Data Bank (PDB). First the program checks whether the structure contains a transition metal. If the structure does not contain a metal then the program terminates. Otherwise MCPB attempts to determine the primary and secondary ligands of the metal using rules described by Harding56–61, which will be described in more detail below. Once a metal site is found, MCPB creates model structures of the metal's first coordination sphere with which ab initio calculations can be performed on to generate AMBER-like FF parameters. These models include one to generate charges, qi, and another to determine bond, Kr, and angle, Kθ, force constants. The AMBER function includes bond, angle, torsion, improper, van der Waals and electrostatic terms; however, only bond, angle and electrostatic terms are parameterized under the assumption made by Hoops et al. that dihedral terms can be ignored.3 Lennard-Jones parameters are also not parameterized here due to the fact that most metals are buried and that van der Waals interactions are not as important as the electrostatics32. Lennard-Jones parameters for the most common metal ion in biology were taken from the literature62–66. The methods of incorporating the bond, angle and charge parameters are outlined below. Once a FF is produced it is tested using minimization techniques to observe its stability. Further validation tools such as comparing the frequencies from both ab initio and the resulting FF could be used as well67.
Figure 2.
MCPB Flow Diagram.
Equilibrium Bond Lengths and Angles
Equilibrium values for bonds, req, and angles, θeq, can be determined through ab initio calculations or taken directly from the crystal structure in the PDB. There are pros and cons for using values from both methods. Ab initio calculations are generally carried out in the gas phase but solvent effects can be incorporated with, for example, PCM but with an added cost. Crystal structures may contain spurious values and may not be representative of all structures with this bond or angle type. Therefore the values from ab initio calculations were used here. Alternatively, data from the CSD could be utilized as well, but as with the approaches described above this method has pros and cons as well. Given our focus on metalloproteins and not solid-state metal clusters we have not compared with or used CSD derived information in the present article.
Force Constants
The force constants, Kr, and Kθ, were obtained by first creating a model (model 1) of the metal site, adding hydrogen atoms using the functionality within MTK++ and then optimizing it in the gas phase. The residues bound to the metal were approximated, for example, cysteine by a thiolate or histidine by a methyl-imidazole, to reduce the computational cost of the minimization. However, all bonds and angles missing from the FF were accounted for. Once a minimum was found the second derivatives were determined. The Cartesian Hessian matrix is shown in Eq. 1, which is the second derivative of energy with respect to coordinates. The eigen-analysis of k provides the force constants, λi, and the normal modes, ν̂i, as shown in Eq. 2. The interatomic force constant, KAB, between atoms A and B is required to determine the force on atom A by displacing atom B as shown in Eq. 3 which is required for a MM function.
| (1) |
| (2) |
| (3) |
From the minimized structure of model 1 the metal-Ligand bond and angle force constants were evaluated. The force constants were converted from Cartesian into internal coordinates using the Gaussian program68 providing the following keyword (iop(7/33=1)). Force constants were also determined using a method described by Seminario69 and mathematical details can be found in the supplementary material. Briefly the force constants are calculated from sub matrices of the Cartesian Hessian matrix. This method has the advantage over the “Traditional” method of determining force constants as it avoids defining internal coordinates. The MCPB program then reads either the internal force constant matrix or the Seminario derived parameters and assigns the values to the appropriate bonds and angles.
Point Charges
The atom centered partial charges were derived using the Merz-Singh-Kollman (MK)70 and the Restrained Electrostatic Potential (RESP)4,71,72 schemes using a second model (model 2) of the metal center. This model included all atoms of a bound residue, which were capped with acetyl (ACE) and N-methylamine (NME) residues. If two ligating residues were less than five residues apart then they were tethered with glycine residues and the chain capped with ACE and NME. Again hydrogen atoms were added using MTK++. This model was not allowed to relax to save computational expense and to keep the crystallographic geometry. The van der Waals radii for the metals used in the MK scheme were taken from the literature.3 The MK/RESP scheme was favored over other charge model schemes because its ability to adjust the charge of the capped or linking residues to an integer value, thus allowing the formal charge of the cluster to disperse over the metal and the bound ligands.
In this work, four different methods to develop charges were implemented. The first method allows all atoms of the bound residue to change (ChgModA), the second technique restrains the backbone heavy atoms (CA, N, C, O) to those values found in the AMBER parm94 force field (ChgModB), the third one restrains all the backbone atoms (CA, H, HA, N, HN, C, O) to the AMBER parm94 force field values (ChgModC) while the fourth one (ChgModD) also adds carbon beta (CB) into the restraint list.
Zinc AMBER Force Field
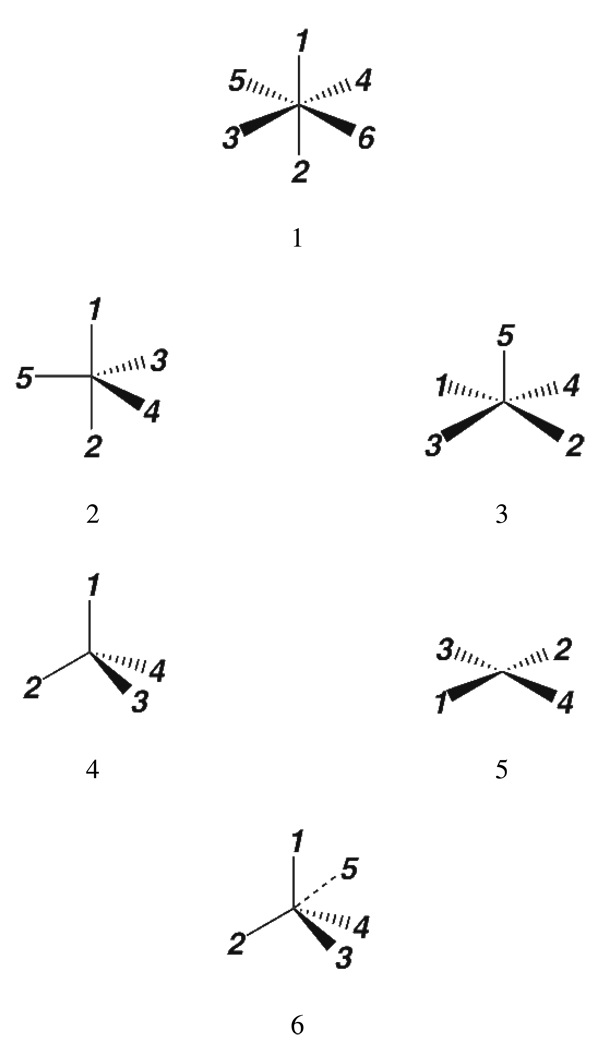
With the ability to build metal FFs established, the task of generating a FF that facilitates simulations for the majority of Zn proteins was initiated. Zinc was chosen because a considerable number of proteins contain that metal as highlighted in Table 1, while also being computationally well behaved. Metalloproteins containing zinc are both structural and functional proteins and in general Zn is four coordinate, although sometimes five or six coordinate when multiple ASP/GLU residues or water molecules bind. It was then necessary to determine all Zn environments that exist in proteins. This was carried out using a program called pdbSearcher to analyze all structures currently in the PDB. Again pdbSearcher was developed using the API provided by MTK++. All X-ray crystal structures with a resolution below 3.0 Å were extracted from a local mirror of the PDB for further analysis. For each metal site the primary and secondary shell ligands were determined using Harding's bond cut-off values as shown in Table 356–61. These values were determined from a series of papers describing metal coordination in the CSD. A donor atom is considered to be in the primary coordination shell of a metal ion if it is within the target distance as shown in Table 3 plus some tolerance (0.5 Å was used). Metal-donor distances lying between the target distance plus the tolerance and the target distance plus a second tolerance (1.0 Å was used) were defined as secondary shell ligands. For example, if a Zn atom is less than 2.53 Å from a Histidine ND1 or NE2 atom then it is considered a primary ligand. If it was less than 3.03 Å away then that ligand is labeled as secondary, otherwise it is unbound. Once the number of primary and secondary shell ligands was determined, the geometry of the metal centers was evaluated. The coordination states allowed include octahedral, Fig. 3.1, Trigonal bipyramid, Fig. 3.2, Square Pyramid, Fig. 3.3, tetrahedral, Fig. 3.4, square planar, Fig. 3.5, and tetrahedral plus a non-bonded contact, Fig. 3.6. From Fig. 3 we can see that the coordination number alone is not enough to assign a metal geometry. Thus the root mean square deviation (RMSD) of the metal coordination sphere angles from those found in a regular polyhedron was calculated. Equation 4 was used to distinguish between square planar and tetrahedral geometries with the ideal angles used in Table 4. Likewise, equations 5 and 6 were used for five and six coordinate metals respectively. The atom indices in Table 4 correspond to those atoms in Fig. 3. This indexing is useful to differentiate between axial/equatorial and cis/trans ligands. The coordination state with the lowest RMSD was assigned to the metal and its ligands.
| (4) |
| (5) |
| (6) |
Table 3.
Metal-Donor Bond Target Lengths in Å. The following donor atoms of residues are implied: HOH@O, ASP@OD1/OD2, GLU@OE1/OE2, HIS@ND1/NE2, CYS@SG, MET@SG, SER@O, THR@O, TYR@O and the amino acid backbone carbonyl oxygen atom CRL. If a metal-donor distance is within these target distances plus some tolerance (0.5Å) it is considered a primary interaction.
| Metal | HOH | ASP/GLU | HIS | CYS/MET | SER/THR | TYR | CRL |
|---|---|---|---|---|---|---|---|
| Na | 2.41 | 2.41 | 2.38 | ||||
| Mg | 2.07 | 2.07 | 2.10 | 1.87 | 2.26 | ||
| K | 2.81 | 2.82 | 2.74 | ||||
| Ca | 2.39 | 2.36 | 2.43 | 2.20 | 2.36 | ||
| Mn | 2.19 | 2.15 | 2.21 | 2.35 | 2.25 | 1.88 | 2.19 |
| Fe | 2.09 | 2.04 | 2.16 | 2.30 | 2.13 | 1.93 | 2.04 |
| Co | 2.09 | 2.05 | 2.14 | 2.25 | 2.10 | 1.90 | 2.08 |
| Ni | 2.09 | 2.05 | 2.14 | 2.25 | 2.10 | 1.90 | 2.08 |
| Cu | 2.13 | 1.99 | 2.02 | 2.15 | 2.00 | 1.90 | 2.04 |
| Zn | 2.09 | 1.99 | 2.03 | 2.31 | 2.14 | 1.95 | 2.07 |
Figure 3.
Metal Ligand Geometries Perceived Using Harding's Rules.
Table 4.
Ideal angles used to calculate root mean square deviations for tetrahedral, square planar, trigonal bipyramidal, square pyramid and octahedral geometries. The notation a12 describes the angle between atom 1, the metal and atom 2. The atom indices correspond to Fig. 3. bm is the mean of the four angles between the apical bond and the basal bonds in square pyramid geometries.
| Type | Coordination | Angle | Atoms | |
|---|---|---|---|---|
| ML4 | Tetrahedral | 109.5° | ||
| Square Planar | 180.0° | a12, a34 | ||
| 90.0° | All others | |||
| ML5 | Trigonal Bipyramidal | 180.0° | a12 | |
| 120.0° | a34, a45, a35 | |||
| 90.0° | All others | |||
| Square Pyramid | a15, a25, a35, a45 | |||
| (360.0 − 2bm ) | a12, a34 | |||
| 2sin−1(2−½[sin(180.0 − bm)]) | a13, a23, a14, a24 | |||
| ML6 | Octahedral | 180.0° | a12, a34, a56 | |
| 90.0° | All Others | |||
Protein Data Bank Survey Zinc Containing Proteins
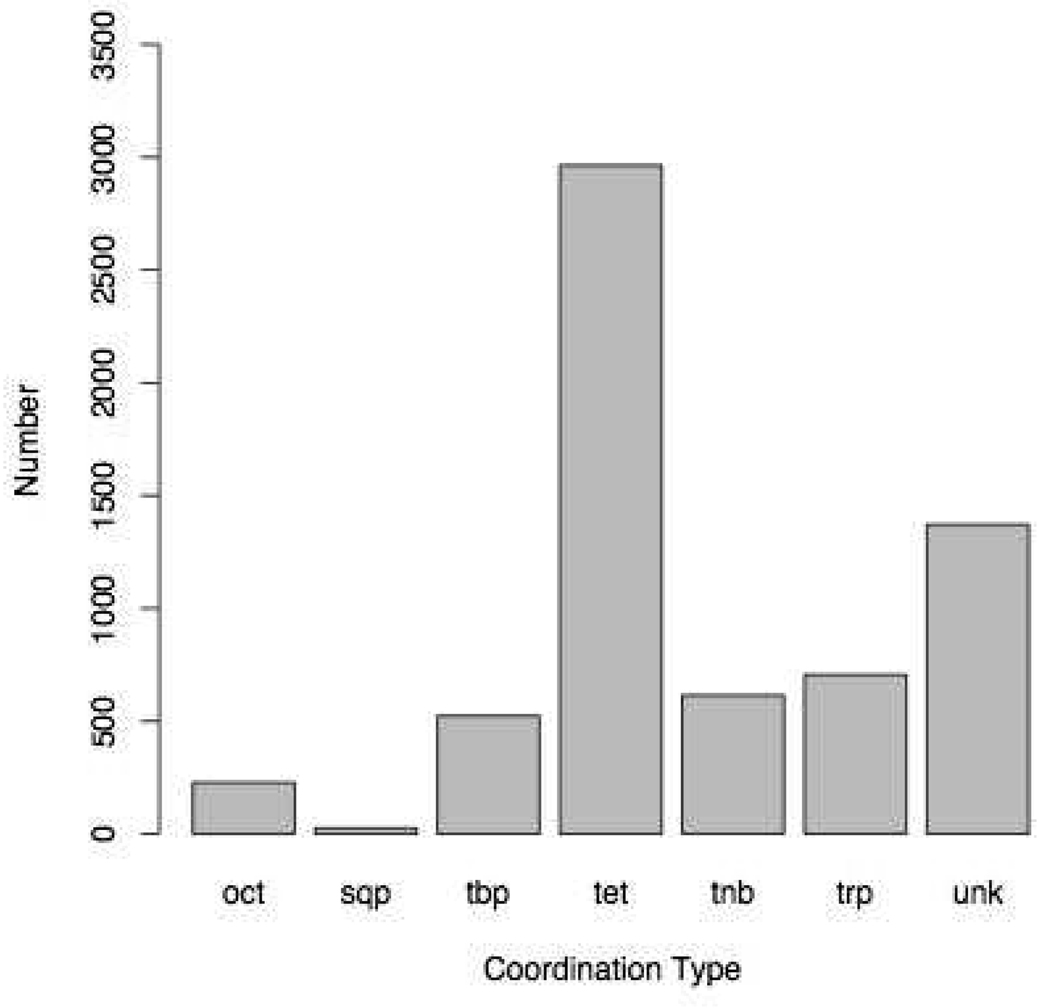
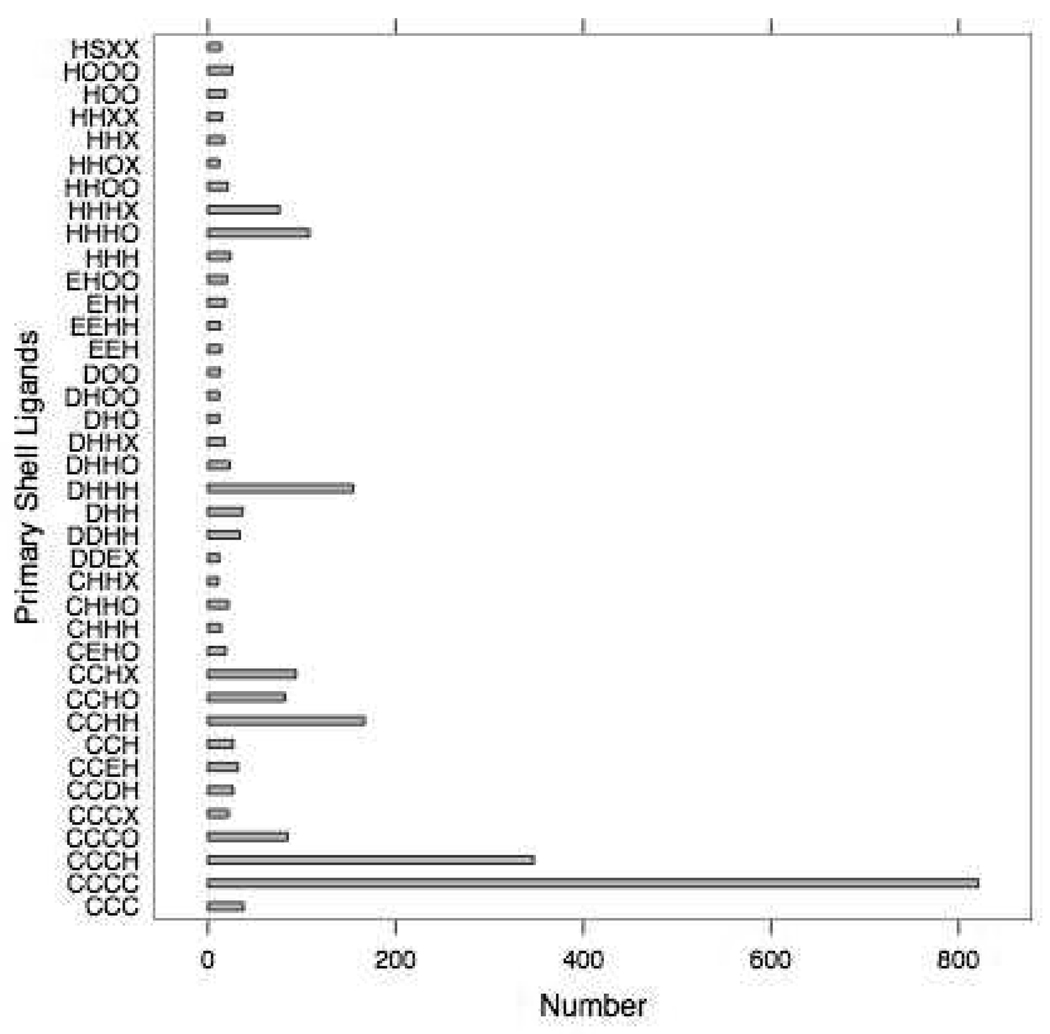
The results of searching the PDB (accessed on the 5th of April 2007) for zinc metalloproteins using the rules above are shown in Figure 4. There are 524 cases of trigonal bipyramidal (tbp) and 706 cases of square pyramid (trp) and 228 instances of octahedral (oct). 615 metal centers are found as tetrahedral with a non-bonded contact (tnb) and 1372 are ill defined using the current definitions (unk). 2964 out of 6435 total observations or 46.1% of zinc atoms in protein structures are found to be tetrahedral (tet), and, hence, the results and discussion will focus on them. The most common Zn coordinating ligands in tetrahedral environments are shown in Figure 5. Here the 1 letter amino acid codes are used with X describing an unknown ligand such as a non-standard amino acid or drug molecule.
Figure 4.
Zinc Coordination Geometry Distribution from the PDB.
Figure 5.
The Most Common Tetrahedral Zinc Coordinating ligands Combination Distribution. Three lettered environments also contain a secondary ligand not shown.
The most common tetrahedral Zn environment is CCCC with four coordinating cysteines, followed by CCCH, CCHH, DHHH, HHHO, HHHX, CCHX, and CCHO as shown in Figure 5. This data led the research in a direction to investigate the relationship between Zinc coordination environment and geometric parameters such as bond lengths and angles. The bonds between Zinc and Sulfur, Nitrogen and Oxygen from 11 unique primary shell environments are shown in Table 5.
Table 5.
Tetrahedral Zinc Primary Ligating Residues. Bond Lengths are in Å. 1 Letter amino acid codes are used; C:CYS, H:HIS, O:HOH, D:ASP. N is the number of Bond instances. Min and Max are the minimum and maximum bond lengths respectively. The 1st Q, 3rd Q, mean, median, and standard deviation are statistical parameters to describe the bond length distribution.
| N | Bond | Min | 1st Q | Median | Mean | 3rd Q | Max | Std Dev | |
|---|---|---|---|---|---|---|---|---|---|
| CCCC | 3284 | Zn-S | 1.424 | 2.294 | 2.338 | 2.338 | 2.389 | 2.805 | 0.1218 |
| CCCH | 1041 | Zn-S | 1.448 | 2.284 | 2.332 | 2.332 | 2.382 | 3.047 | 0.1089 |
| CCHH | 334 | Zn-S | 1.908 | 2.234 | 2.295 | 2.301 | 2.361 | 2.795 | 0.1289 |
| CHHH | 14 | Zn-S | 2.18 | 2.27 | 2.296 | 2.344 | 2.39 | 2.608 | 0.1364 |
| CCCH | 347 | Zn-N | 1.833 | 2.056 | 2.124 | 2.132 | 2.2 | 2.525 | 0.1157 |
| CCHH | 334 | Zn-N | 1.716 | 2.023 | 2.078 | 2.088 | 2.149 | 2.465 | 0.1188 |
| CHHH | 42 | Zn-N | 1.778 | 1.964 | 2.034 | 2.056 | 2.113 | 2.486 | 0.1403 |
| HHHH | 12 | Zn-N | 1.935 | 2.006 | 2.04 | 2.049 | 2.107 | 2.129 | 0.0627 |
| HHHO | 108 | Zn-O | 1.359 | 2 | 2.252 | 2.185 | 2.362 | 2.518 | 0.2218 |
| HHOO | 42 | Zn-O | 1.866 | 2.092 | 2.268 | 2.233 | 2.384 | 2.543 | 0.1816 |
| HOOO | 78 | Zn-O | 1.611 | 2.006 | 2.143 | 2.115 | 2.241 | 2.495 | 0.1914 |
| OOOO | 12 | Zn-O | 1.781 | 2.004 | 2.158 | 2.135 | 2.3 | 2.428 | 0.1917 |
| HHHO | 324 | Zn-N | 1.872 | 2.044 | 2.098 | 2.116 | 2.176 | 2.757 | 0.114 |
| HHOO | 42 | Zn-N | 1.85 | 2.06 | 2.143 | 2.161 | 2.26 | 2.453 | 0.1455 |
| HOOO | 26 | Zn-N | 1.836 | 2.041 | 2.089 | 2.102 | 2.121 | 2.459 | 0.1295 |
| HHHD | 155 | Zn-O | 1.688 | 1.914 | 2 | 2.007 | 2.086 | 2.457 | 0.1425 |
| HHDD | 68 | Zn-O | 1.805 | 2.053 | 2.148 | 2.166 | 2.262 | 2.938 | 0.184 |
| HHHD | 465 | Zn-N | 1.604 | 2 | 2.064 | 2.077 | 2.144 | 2.499 | 0.1275 |
| HHDD | 68 | Zn-N | 1.959 | 2.101 | 2.184 | 2.192 | 2.302 | 2.46 | 0.128 |
| ASP | 460 | Zn-O | 1.688 | 1.958 | 2.044 | 2.077 | 2.165 | 2.988 | 0.1899 |
| GLU | 227 | Zn-O | 1.462 | 1.996 | 2.102 | 2.134 | 2.265 | 2.823 | 0.2276 |
| HIS | 825 | Zn-ND | 1.716 | 2.03 | 2.096 | 2.107 | 2.181 | 2.525 | 0.1256 |
| HIS | 1768 | Zn-NE | 1.604 | 2.031 | 2.093 | 2.108 | 2.177 | 2.757 | 0.1228 |
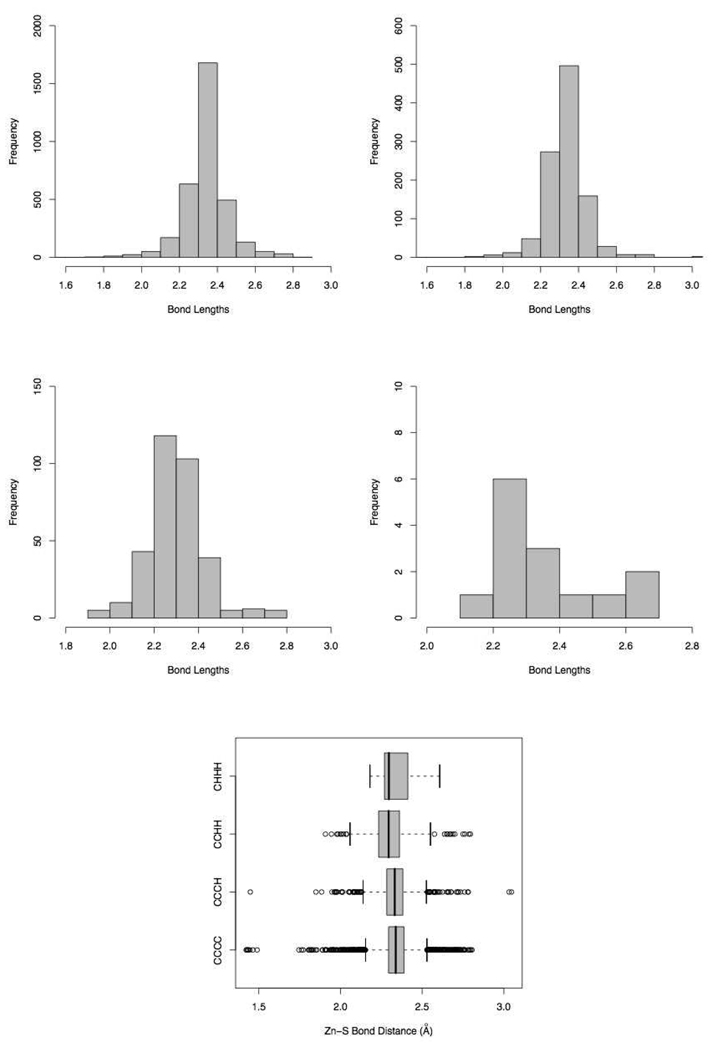
The distribution of Zinc-Sulfur bonds in proteins that contain environments such as CCCC, CCCH, CCHH, and CHHH are shown Figure 6. The four distributions are also summarized as a box plot (max and min values, the lower and upper quartiles and the median of data is plotted) in Fig. 6. The Box plots of Zn-N bonds can be found in the supporting material available online.
Figure 6.
Zn-S Bond Length distributions in CCCC (top left), CCCH (top right), CCHH (middle left), and CHHH (middle right) Tetrahedral Environments and a Box Plot summarizing all four environments (bottom).
The peaks of the Zn-S bond length distributions in the CCCC and CCCH environments lie between 2.3 and 2.4 Å, while for CCHH and CHHH systems it occurs between 2.2 and 2.3 Å. There are only 14 instances of CHHH and the Zn-S and Zn-N bonds have large standard deviations of 0.1364 and 0.1403 respectively. Also in the case of the Zn-S bonds the median differs from the mean considerably (2.296 compared to 2.344), thus suggesting unreliability of this data. The Box plots also point to some outliers in the data, for example there are Zn-S bonds in the PDB below 1.5 Å that upon visual inspection are clearly crowded and poorly resolved.
The distribution of Zinc-oxygen, and -nitrogen bonds are shown in Fig. S1 and S2. Zinc bonded to glutamic and aspartic acid oxygen atoms (GLU@OE1/OE2 or ASP@OD1/OD2) or histidine nitrogen atoms (HIS@ND1/NE2) all show similar behavior with bonds lengths around 2.1 Å being most common. In spite of this similarity the standard deviations of ASP and GLU bonds are greater than those of HIS. Also it is worth nothing that the majority of Zn histidine bonding is through the epsilon nitrogen.
Tetrahedral Zn Environment Force Field Parameterization
Metal-ligand bonds are softer than those of organic molecules; however, there are obvious trends in the data presented above. These findings encouraged us to build a FF that facilitates simulations for the majority of Zn proteins, which we termed the Zinc AMBER Force Field or ZAFF. A concept key to this approach is “plug-and-play” where a researcher can download a metalloprotein structure from the PDB and run dynamics using predefined parameters as illustrated in Figure 7. To this end FFs for the 12 unique environments shown in Table 6 were built using MCPB in order to validate the basic approach. A single structure from the PDB representative of each environment was chosen. FFs were built using the B3LYP DFT method with the 6-31G* basis set73. The resulting FFs were stored in xml format for later use within MTK++. For each environment a new Zn residue type was created while new 28 amino acid residues were also added. The atom type of the bonding atom within the residue was also changed as shown in Table 6.
Figure 7.
ZAFF Flow Diagram. This illustration demonstrates when a metalloprotein structure is downloaded from the PDB and an equivalent metal site is stored the MTK++ package has the ability to assign parameters to carry out MD simulations.
Table 6.
List of PDB codes, Zn environments, residue and atom type names that was used to create ZAFF.
| PDB | Environment | Residue/Type | ||||
|---|---|---|---|---|---|---|
| 1A5T | Zn-CCCC | ZN1 | CY1/S1 | |||
| 1A73 | Zn-CCCH | ZN2 | CY2/S2 | HE1/N1 | ||
| 2GIV | Zn-CCCH | ZN3 | CY3/S3 | HD1/N2 | ||
| 1A1F | Zn-CCHH | ZN4 | CY4/S4 | HD2/N3 | ||
| 1CK7 | Zn-CHHH | ZN5 | CY5/S5 | HD3/N4 | ||
| 1CA2 | Zn-HHHO | ZN6 | HD4/N5 | HD5/N6 | HE2/N7 | WT1/O1 |
| 1CA2 | Zn-HHHO | ZN7 | HD6/N8 | HD7/N9 | HE3/N0 | OH1/O2 |
| 1U0A | Zn-HHDD | ZN8 | HE4/E1 | AP1/D1 | ||
| 2USN | Zn-HHHD | ZN9 | HD8/NQ | HD9/NP | HE5/E2 | AP2/D2 |
| 1PB0 | Zn-HHHH | Z10 | HDD/NR | |||
| 1VLI | Zn-HHOO | Z11 | HDA/NT | WT2/O3 | ||
| 1L3F | Zn-HOOO | Z12 | HE6/NY | WT3/O4 | ||
Two models of each representative Zn cluster were generated. For example the two models of ZN-CCCC from PDB ID 1A5T are shown in Fig. 8 (All other models are displayed in the supplementary material.
Figure 8.
Zn-CCCC Cluster Models (PDB ID: 1A5T).
The average optimized Zn-S bond length within Zn-CCCC was 2.43 Å that is higher than the mean value from the survey of the PDB but it is within one standard deviation. The corresponding mean bond force constant is 100.7 (71.3) kcal/(mol Å2) calculated using the “Traditional” and Seminario methods respectively. The mean S-Zn-S and C-S-Zn angles are 109.1° and 101.8° with an average force constants of 15.0 (73.52) and 81.5 (113.5) kcal/(mol rad2) respectively.
The structures 1A73 and 2GIV from the PDB were used as representative structures of the Zn-CCCH cluster. The delta nitrogen of His is bound to the Zinc atom in 1A73 while the epsilon nitrogen is bound in 2GIV. The average Zn-S bond length was determined at 2.35 Å, which is in good agreement with the value determined from the PDB survey. The Zn-S bond lengths are shorter in Zn-CCCH than they are in the Zn-CCCC cluster and this corresponds to the change in force constant from 100.7 (71.3) to 143.3 (105.4) kcal/(mol Å2). The mean S-Zn-S, S-Zn-N, and C-S-Zn angles for 1A73 and 2GIV clusters are 115.2°/116.4°, 102.9°/101.3° and 102.5°/101.8° with an average force constants of 13.7 (80.0)/10.4 (72.2), 21.9 (75.7) /15.2 (70.96), and 78.6 (110.12) /65.2 (104.56) kcal/(mol rad2) respectively.
The 1A1F structure from the PDB was used as a representative structure for the Zn-CCHH cluster. The average Zn-S and Zn-N bond length are 2.31 Å and 2.09 Å with corresponding force constants of 181.5 (143.0) and 147.1 (100.8) kcal/(mol Å2) respectively. The average value of the Zn-S bond length from the PDB is 2.301 Å while the mean Zn-N value is 2.088 Å which are in excellent agreement with the calculated values. Both the Zn-S and Zn-N bonds are shorter than the previous clusters and this is reflected by the fact that stronger force constants been observed computationally. The mean S-Zn-N, C-S-Zn, and C-N-Zn, angles for the 1A1F cluster are 103.2°, 105.1°, and 126.6° with average force constants of 12.5 (78.3), 69.3 (87.7), and 34.5 (111.22) kcal/(mol rad2) respectively.
The final Zn center considered in this study which contains a cysteine residue was Zn-CHHH. The 1CK7 structure from the PDB was used to model the Zn-CHHH cluster. Two models of this cluster were built using MCPB and the Zn-S bond length was determined as 2.26 Å with a force constant of 186.2 (168.6) kcal/(mol Å2). The mean Zn-N bond length is 2.05 Å with a force constant of 146.2 (127.8) kcal/(mol Å2). The mean N-Zn-N and S-Zn-N angles are 105.8° and 113.0° with force constants of 2.8 (75.4) and 3.3 (75.8) kcal/(mol rad2) respectively.
There is a very small number of Zinc ions surrounded by four histidine residues in the PDB. But to complete this computational study the bond and angle force constants were determined using 1PB0 as a starting geometry. The average Zn-N bond distance was determined at 2.01 Å with a force constant of 217.6 (157.0) kcal/(mol Å2). The angles of the Zn center are 109.5° with a force constant of 6.1 (70.5) kcal/(mol rad2).
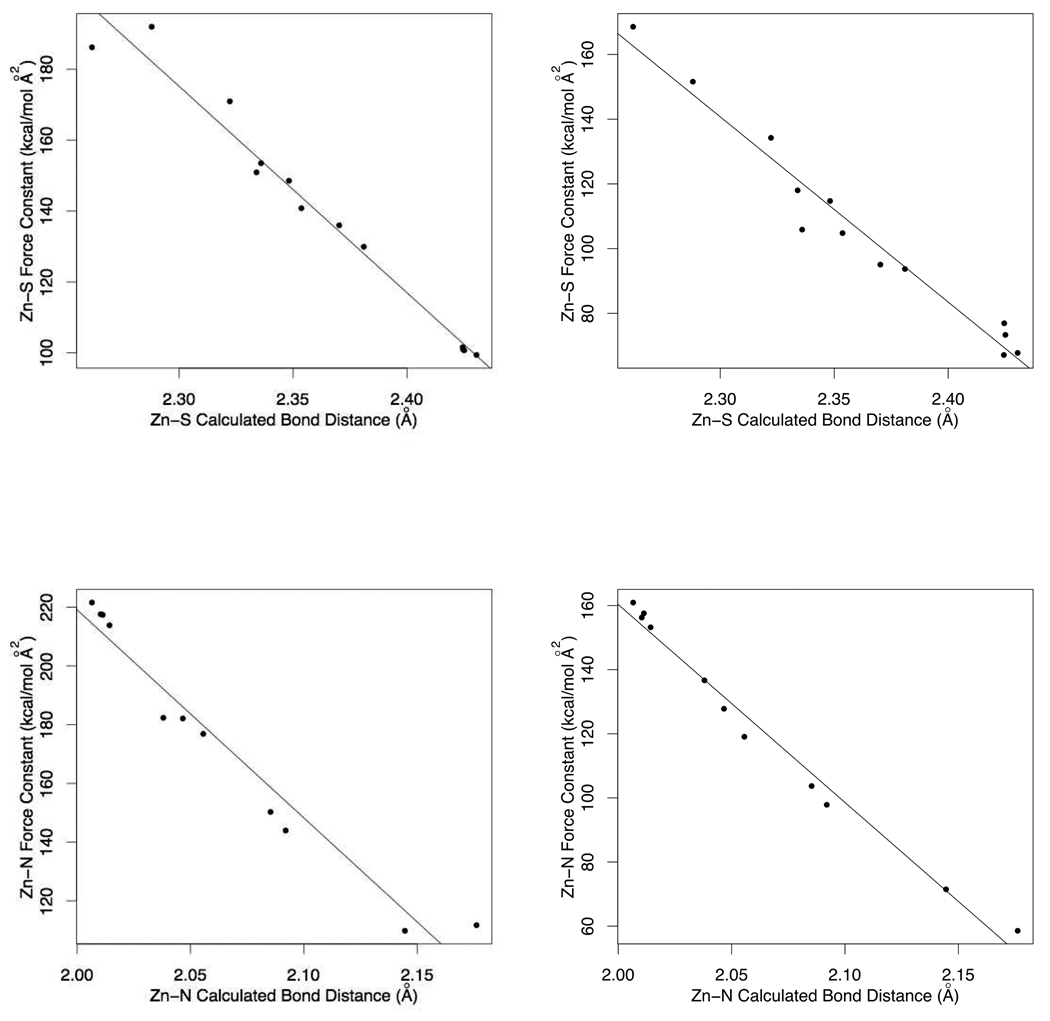
It is evident there are clear trends in the calculated bond lengths and force constants described above. The bond lengths of Zn-S through the series CCCC, CCCH, CCHH, and CHHH correlate with the calculated force constants with an R2 value of 0.97 (0.96) as seen in Figure 9 (top). The Zn-N bond lengths and force constants correlate with an R2 of 0.95 (0.98) as shown in Figure 9 (bottom). It is worth noting here that Zn donor bond lengths differ within the various environments. Thus having a single Zn-S or Zn-N bond equilibrium and force constant value will not work appropriately. The proposed solution to this problem is to store all Zn bond types and assign the parameters in an automatic manner within the metal center perception algorithm of MTK++.
Figure 9.
The Correlation between (top) Zn-Cys@S and (bottom) Zn-His@N Bond Lengths and Calculated Force Constants through the Series CCCC, CCCH, CCHH, CHHH, and HHHH using the “Traditional” and Seminario methods.
The average angle size and force constants of S-Zn-S are smaller and stronger, 109.5°/15.0 (73.5) kcal/(mol rad2) in the CCCC cluster compared to those of the CCHH cluster where values of 135.0°/9.7 (104.4) kcal/(mol rad2) were determined. The N-Zn-N angles of the CCHH, CHHH, and HHHH clusters lie between 105.8° and 109.5° with force constants between 2.8 (75.4) and 8.4 (58.0) kcal/(mol rad2). The experimental force constant of the N-Zn-N was reported to be approximately 5.0 kcal/(mol rad2) which is in good agreement with those calculated by the “Traditional” method.3 It has been reported that this angle force constant is too weak to prevent the angle opening beyond the ideal tetrahedral angle in MD simulations and in the past arbitrary scaling factors have been applied to prevent this from occurring3,41. However this does not seem to be the case for the Seminario method and so the need to arbitrary scale values is negated.
The variation of bond distances and angles of Zinc clusters containing histidine residues and water molecules were determined. The 1CA2 structure was used to represent the Zn-HHHO cluster which is a structure of human Carbonic Anhydrase II (HCA II). HCA II is a catalytic center for the conversion of CO2 into bicarbonate. Therefore to account for both the water and hydroxyl states two FFs were evaluated. It is of no surprise that the bond lengths and associated force constants of the two systems are different. The Zn-O bond is longer in the case of water binding while the Zn-N bonds are shorter due to the strength of the hydroxyl bond. The accompanying force constants are also considerably different. The Zn-O bond force constants changes from 120.3 (82.86) to 394.7 (303.6) kcal/(mol Å2) upon removal of a proton while the Zn-N force constant becomes weaker from 248.4 (184.4) to 194.4 (131.3) kcal/(mol Å2). These calculated equilibrium bond lengths and force constants are different from those published by Hoops et al.; however, the QM methods used to generate the numbers also differ. The Zn-O bond lengths of the HHHO clusters in the PDB have a large standard deviation of 0.22 Å with a mean value of 2.19 Å confirming that both states exist. The calculated angles and force constants for this cluster are in good agreement with those published previously, except for the H-O-Zn angle force constant that was scaled to a higher value to insure trajectory stability during MD simulation.
The 1VLI structure from the PDB was used to investigate the strength of bond and angle force constants of the Zn-HHOO cluster. Again the MCPB program was used to build the models required for parameterization. The equilibrium bond length of Zn-O was calculated as 1.95 Å which is approximately 0.4 Å shorter than the bond length for the Zn-HHHO cluster. This contradicts the trend from the PDB survey. Plausible reasons for this discrepancy include the small number of data points for the Zn-HHOO cluster in the PDB and the large standard deviation value of 0.15 Å. The angle force constants calculated for this cluster are of similar magnitude to those calculated for the Zn-HHHO cluster.
The final tetrahedral environment containing histidine residues and water molecules was the HOOO cluster from PDB ID 1L3F. The average Zn-O and Zn-N bond lengths are 2.01 Å and 1.93 Å respectively which are shorter distances than those in the Zn-HHHO and Zn-HHOO clusters, agreeing with the experimental means from the PDB.
Two clusters containing histidine and aspartate residues were considered in this study. The 2USN and 1U0A were chosen as characteristic structures of the Zn-HHHD and Zn-HHDD environments. The PDB survey showed that the bond lengths of Zn-O bonds in H/D systems changed from 2.007 Å to 2.166 Å going from HHHD to HHDD and this trend is also seen in the calculated values of these clusters.
Molecular Dynamics Validation
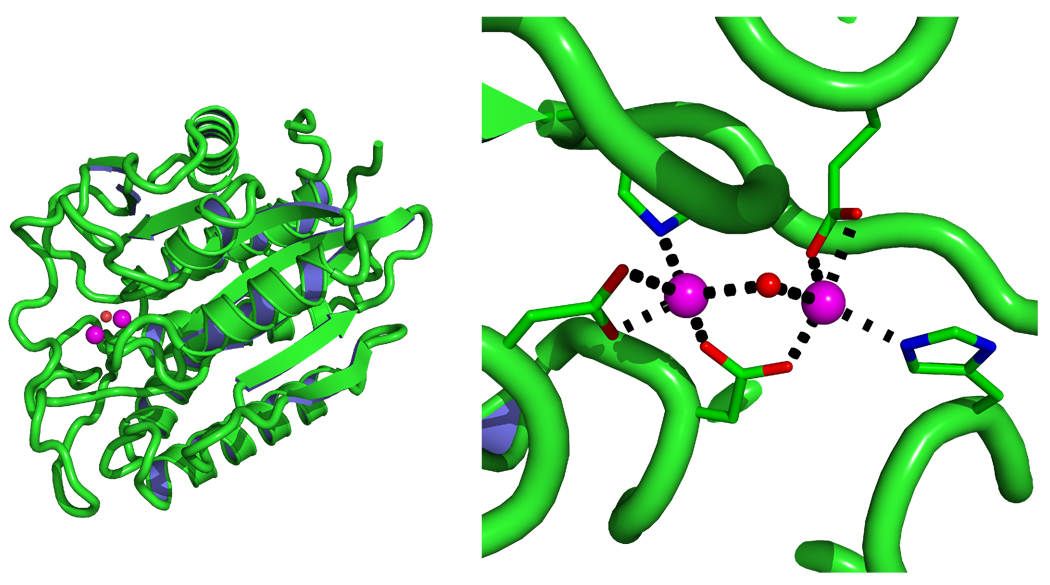
The partial charges of the Zinc clusters were determined applying four different methods using the larger models as described above. It was difficult to determine, a priori, which method would out perform the others. Thus MD simulations and normal mode analysis were used to determine which combination of force constant approach (Traditional and Seminario) and partial charge model (ChgModA, B, C, D) was most appropriate. With this in mind, we carried out MD simulations on two different systems, one of which was a zinc finger complex (PDB ID 1A5T) and the other was a di-zinc system (PDB ID 1AMP) as shown in Fig. 10. The zinc finger system was used to compare the difference between different charge models, while the di-zinc system was chosen to further evaluate the feasibility of our approach on a di-metal cluster.
Figure 10.
Cartoon Representation (left) of the dizinc Protein (PDB ID 1AMP) and its metal sites (right).
In each of the eight simulations of 1A5T, the system was solvated in a rectangular periodic box with each side of the box having a distance of at least 8.0 Å from the closest atom from the enzyme. The TIP3P water model was used and sodium ions were added to neutralize the system. The AMBER FF ff99SB was used to model the enzyme while the zinc complex was modeled with the parameters generated using the MCPB package. The Particle Mesh Ewald (PME) method was applied to handle the long-range electrostatic interactions and the default setting of an 8.0 Å cutoff for the real-space nonbond interactions and 1.0 Å grid spacing for the reciprocal space was used. All bonds with hydrogen atoms were constrained using SHAKE. The whole system was first fully minimized with a weak positional restraint in order to eliminate any close contacts. Then the temperature was slowly increased to 300 K during a 100 ps, 0.5 fs time step canonical ensemble simulation with the restraint force being gradually removed. This was followed by 3 ns NPT production runs at 1atm with a 2 fs time step.
The results from eight sets of simulations with different set of parameters were collected and carefully compared by four criteria (Table 7): 1) Average δtet/sqp by using equation 4, 2) average mean Zn-S bond lengths, 3) Average RMSD of zinc complex and 4) Average RMSD of the backbone of the enzyme. In general the simulation which used the Seminario force constants outperformed those from the “Traditional” method mainly due to the fact the force constants of zinc containing angles are smaller in the latter approach. The Seminario/ChgModB combination gave the most impressive performance while Seminario/ChgModD also showed promising results. This is in keeping with the fact that the backbone atoms were used in the fitting of the torsional parameters of the FF.
Table 7.
Comparison of the performance from MD simulations using eight sets of parameters.
| Seminario | Traditional | |
|---|---|---|
| Average δtet/sqp | ||
| ChgModA | 4.64 | 8.45 |
| ChgModB | 4.37 | 9.27 |
| ChgModC | 4.59 | 9.06 |
| ChgModD | 4.42 | 8.33 |
| Average mean Zn-S bonds lengths (Å) | ||
| ChgModA | 2.33 | 2.35 |
| ChgModB | 2.40 | 2.41 |
| ChgModC | 2.41 | 2.42 |
| ChgModD | 2.43 | 2.43 |
| Average RMSD of zinc complex (Å) | ||
| ChgModA | 4.62 | 8.47 |
| ChgModB | 4.35 | 9.29 |
| ChgModC | 4.58 | 9.08 |
| ChgModD | 4.41 | 8.34 |
| Backbone RMSD (Å) | ||
| ChgModA | 1.63 | 1.96 |
| ChgModB | 1.44 | 1.64 |
| ChgModC | 1.68 | 1.53 |
| ChgModD | 1.31 | 2.04 |
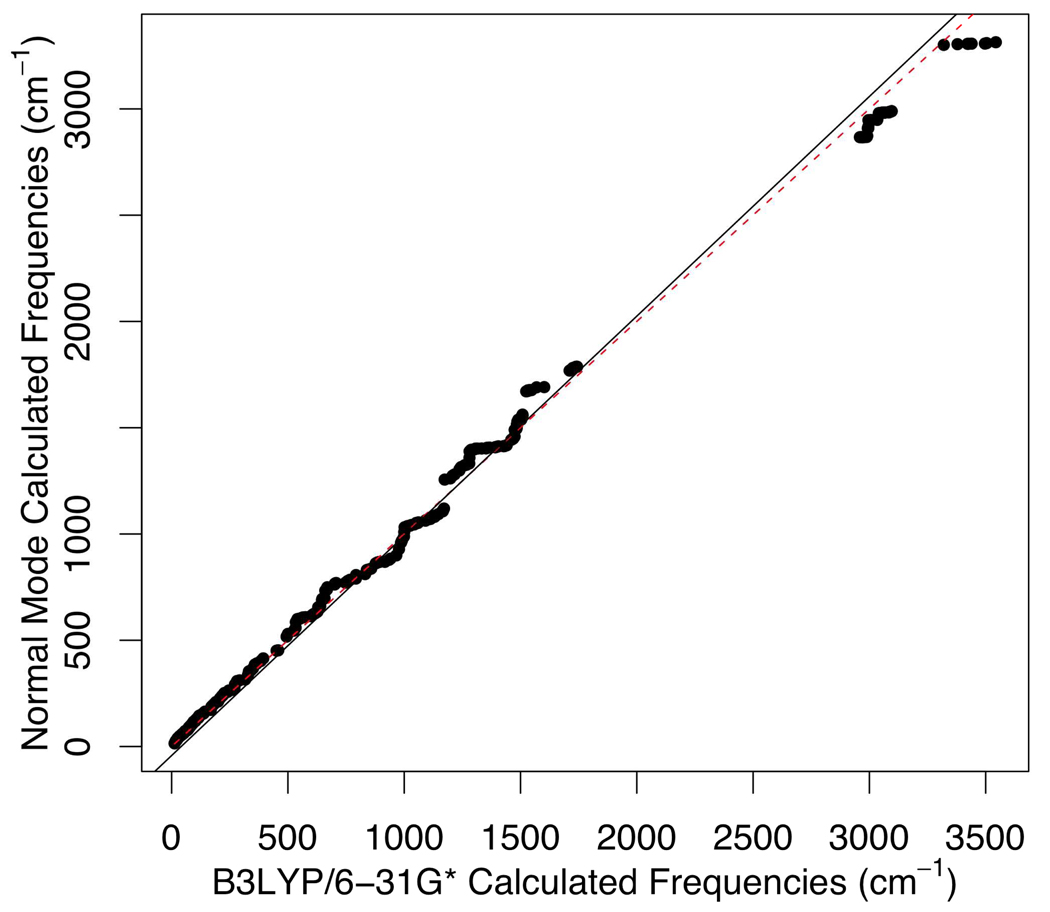
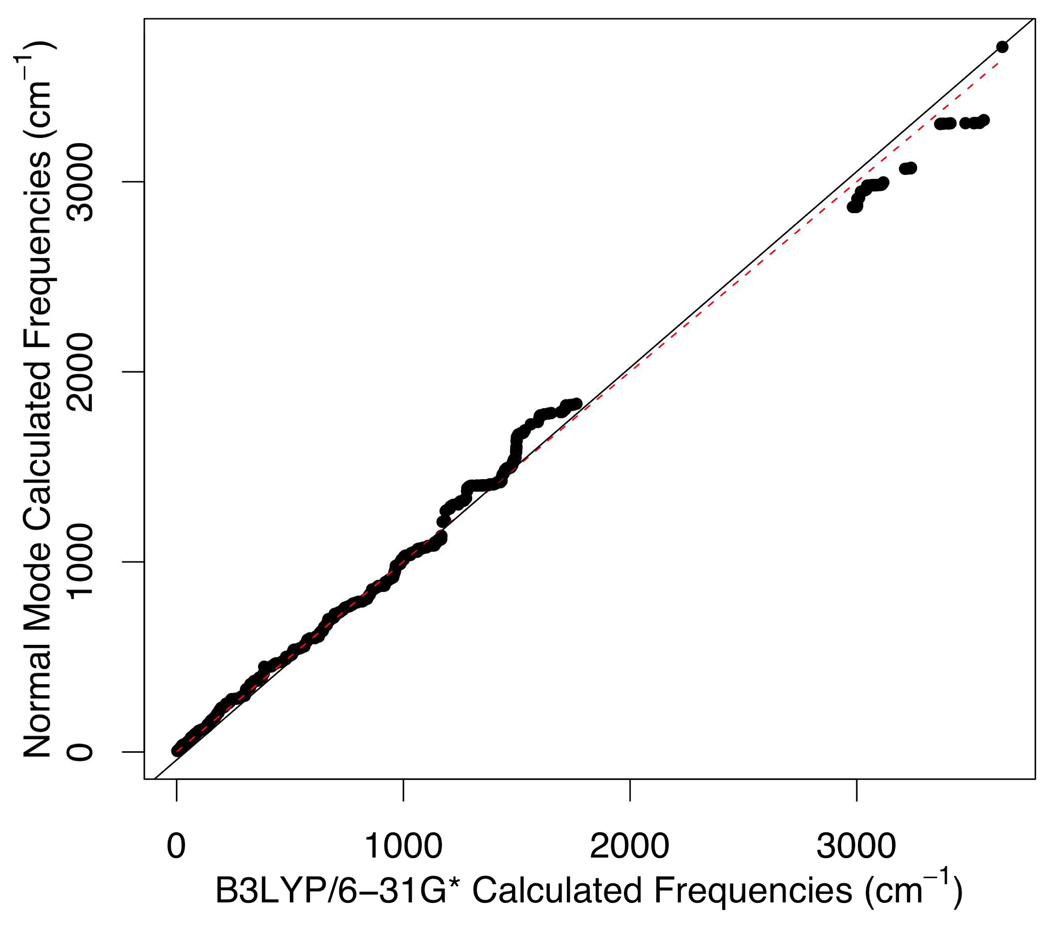
We also carried out normal mode calculations on the second model of 1A5T, as shown in Figure 8, with different sets of parameters to check if the MCPB built parameters reproduce B3LYP/6-31G* computed results. Figure 11 shows the fitting results of frequencies calculated from normal mode calculation with the Seminario/ChgModB set of parameters to those from QM calculation. The matching between MM normal modes and the QM ones is good despite discrepancies above 3200 cm−1, which corresponds to X-H bond (X = heavy atom) stretching.
Figure 11.
Correlation from 1A5T normal mode calculation with parameters built from the Seminario model to the B3LYP/6-31G* computed frequencies (R2=0.99).
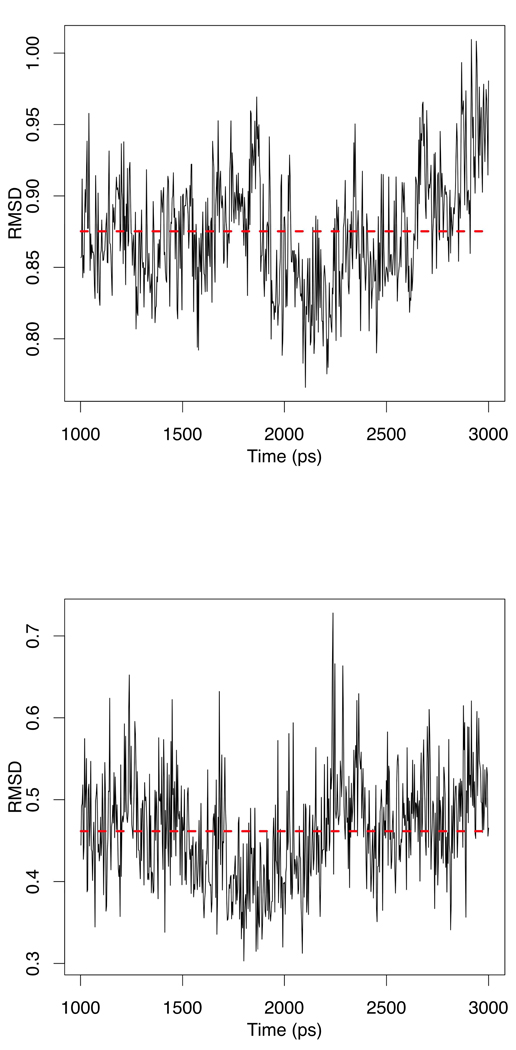
Despite the fact that around 46% of zinc structures are found to be tetrahedral, we felt it was necessary to further validate our program and strategy on a less common zinc complex, for instance, a di-zinc system. As a prototypical member of the di-zinc enzyme family, Aeromonas proteolytica aminopeptidase (PDB ID 1AMP) featured a di-zinc binding pocket offers a good choice. The same procedure as applied on 1A5T (see above) was followed, with the only difference being that only Seminario/ChgModB set of parameters, which gave the best performance in the 1A5T case, were built. Results from both MD simulations and normal mode calculations were collected and examined. From Figure 12, the RMSD of the backbone and the zinc active site complex (Residues: HID97, ASP117, GLU152, ASP179, HID256, OH294, ZN292, ZN293) are stable throughout the simulation. Moreover, the MM normal mode results showed a very good agreement with the QM results except in the >3200 cm−1 region, as shown in Figure 13. Thus, our conclusions from the 1A5T test are confirmed in that MCPB provides a reliable parameter set for, at least, zinc containing metal systems.
Figure 12.
RMSD (in Å) of the 1AMP backbone heavy atoms (above) and the RMSD of the zinc complex (bottom) over the final 2 nanoseconds.
Figure 13.
Fitting results from 1AMP normal mode calculation with parameters built from Seminario model coupled with restraint scheme 1 to B3LYP/6-31G* computed frequencies (R2=0.99).
Conclusions
This research describes the design, development, and implementation of two programs called pdbSearcher and MCPB. The former carries out metalloprotein data mining of the Protein Data Bank. Results focused on zinc metalloproteins as a large number of proteins contain this element. We present a concept of a “cluster parameterization” where a metal ion and its coordination environment are treated as a single unit. The majority of Zn metalloproteins are tetrahedrally coordinated to histidine, cysteine, aspartate, glutamate residues, or water molecules. Thus, cluster models of each of these environments have been built. The distribution of bond lengths between Zn and the donor atoms of these residues was investigated, with some short Zn-S bonds highlighted which may be due to errors during crystal structure refinement. Not unexpected periodicities of Zn-S and Zn-N bonds were observed (bond lengths change as a function of coordination environment) highlighting the need for a detailed analysis of a metallocluster behavior before assigning force constants and equilibrium bond lengths. The notion of a standard Zn-N or Zn-S force constant, for example, within the AMBER FF is not supported by this work.
The MCPB program was used to build, prototype, and validate AMBER-like force fields using the bonded plus electrostatics model for metalloproteins that can be added to the AMBER suite of programs. MCPB was used to investigate the environmental effects on bond lengths, angles, plus bond and angle force constants using 10 unique metal coordination environments. These included Zn bound to CCCC, CCCH, CCHH, CHHH, HHHH, HHHO, HHOO, HOOO, HHHD, and HHDD clusters. A Zinc AMBER Force Field (ZAFF) library was created to store these FF parameters in a convenient way as to allow later use with different metalloproteins than those used in the parameterization.
This work has many current and future uses. The equilibrium bond lengths and angles can be used to aid the refinement of Zn metalloprotein X-ray crystal structures. The models developed can be used by non-experts in studies of zinc metalloproteins for the coordination environments examined. The present work also provides the foundation to develop new approaches to the accurate model of metalloproteins using non-diagonal force fields along with advanced electros sic modeling. The MCPB program allows for rapid development, limited by the cost of the ab initio or DFT calculations, of FF parameters for metalloproteins which could have many uses in drug design projects for example where the target structure contains a metal ion; the feasibility of building parameters with this program has been tested via extensive MD simulations. This program also provides a platform where non-expert users can develop metalloprotein FF parameters which until now was not available. We are currently using the approaches outlined herein to explore next generation force fields for a number of metalloprotein systems.
Supplementary Material
Acknowledgments
We thank the NIH (GM044974 and GM066859) for financial support of this research.
Footnotes
Supporting Information Available
The equations used to determine the Seminario force constants are outlined. A graphical representation of the Zn cluster models used in this study is provided. The Zn-N and Zn-O bond distributions and box plots are presented. The ZAFF xml parameter files (Seminario/ChgModB) that can be used with MTK++/AMBER are provided. This information is available free of charge via the Internet at http://pubs.acs.org. Additionally, the source code of MTK++, pdbSearcher, and MCPB are available from the authors upon request at http://www.qtp.ufl.edu/~kmmprogs/.
References
- 1.Hancock RD. Acc. Chem. Res. 1990;23:253. [Google Scholar]
- 2.Hancock RD. Prog. Inorg. Chem. 1989;37:187. [Google Scholar]
- 3.Hoops SC, Anderson KW, Merz KM., Jr J. Am. Chem. Soc. 1991;113:8262. [Google Scholar]
- 4.Bayly CI, Cieplak P, Cornell WD, Kollman PA. J. Phys. Chem. 1993;97:10269. [Google Scholar]
- 5.Li JB, Zhu TH, Cramer CJ, Truhlar DG. J. Phys. Chem. A. 1998;102:1820. [Google Scholar]
- 6.Stote RH, Karplus M. Proteins. 1995;23:12. doi: 10.1002/prot.340230104. [DOI] [PubMed] [Google Scholar]
- 7.Sakharov DV, Lim C. J. Am. Chem. Soc. 2005;127:4921. doi: 10.1021/ja0429115. [DOI] [PubMed] [Google Scholar]
- 8.Aqvist J, Warshel A. J. Mol. Biol. 1992;224:7. doi: 10.1016/0022-2836(92)90572-2. [DOI] [PubMed] [Google Scholar]
- 9.Pang YP. Proteins. 2001;45:183. doi: 10.1002/prot.1138. [DOI] [PubMed] [Google Scholar]
- 10.Pang YP, Xu K, Yazal JE, Prendergas FG. Protein Sci. 2000;9:1857. [PMC free article] [PubMed] [Google Scholar]
- 11.Vedani A, Huhta DW. J. Am. Chem. Soc. 1990;112:4759. [Google Scholar]
- 12.Vedani A, Huhta DW, Jacober SP. J. Am. Chem. Soc. 1989;111:4075. [Google Scholar]
- 13.Gresh N. Curr. Pharm. Des. 2006;12:2121. doi: 10.2174/138161206777585256. [DOI] [PubMed] [Google Scholar]
- 14.Gresh N, Piquemal JP, Krauss M. J Comput Chem. 2005;26:1113. doi: 10.1002/jcc.20244. [DOI] [PubMed] [Google Scholar]
- 15.Rappe AK, Casewit CJ, Colwell KS, Goddard WA, Skiff WM. J. Am. Chem. Soc. 1992;114:10024. [Google Scholar]
- 16.Rappe AK, Colwell KS, Casewit CJ. Inorg. Chem. 1993;32:3438. [Google Scholar]
- 17.Sirovatka JM, Rappe AK, Finke RG. Inorg. Chim. Acta. 2000;300:545. [Google Scholar]
- 18.Brandt P, Norrby T, Akermark E, Norrby PO. Inorg. Chem. 1998;37:4120. doi: 10.1021/ic980021i. [DOI] [PubMed] [Google Scholar]
- 19.Marques HM, Brown KL. THEOCHEM. 1995;340:97. [Google Scholar]
- 20.Brown KL, Zou X, Marques HM. J. Mol. Struc-Theochem. 1998;453:209. [Google Scholar]
- 21.Marques HM, Brown KL. Coord. Chem. Rev. 1999;192:127. [Google Scholar]
- 22.Marques HM, Ngoma B, Egan TJ, Brown KL. J. Mol. Struct. 2001;561:71. [Google Scholar]
- 23.Aqvist J, Warshel A. J. Am. Chem. Soc. 1990;112:2860. [Google Scholar]
- 24.Ryde U. Protein Sci. 1995;4:1124. doi: 10.1002/pro.5560040611. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Ryde U. Proteins: Struct., Funct., Genet. 1995;21:40. doi: 10.1002/prot.340210106. [DOI] [PubMed] [Google Scholar]
- 26.Hancock RD, Weaving JS, Marques HM. J. Chem. Soc., Chem. Commun. 1989:1176. [Google Scholar]
- 27.Marques HM, Brown KL. Coord. Chem. Rev. 2002;225:123. [Google Scholar]
- 28.Marques HM, Cukrowski I. PCCP. 2002;4:5878. [Google Scholar]
- 29.Skopec CE, Robinson JM, Cukrowski I, Marques HM. J. Mol. Struct. 2005;738:67. [Google Scholar]
- 30.Skopec CE, Cukrowski I, Marques HM. J. Mol. Struct. 2006;783:21. [Google Scholar]
- 31.Norrby PO, Liljefors T. J. Comput. Chem. 1998;19:1146. [Google Scholar]
- 32.Norrby PO, Brandt P. Coord. Chem. Rev. 2001;212:79. [Google Scholar]
- 33.Allinger NL, Yuh YH, Lii JH. J. Am. Chem. Soc. 1989;111:8551. [Google Scholar]
- 34.Sindhikara DJ, Roitberg AE, Merz KM. Biochemistry. 2009;48:12024. doi: 10.1021/bi9013352. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Lin F, Wang R. J. Chem. Theory. Comput. 2010 doi: 10.1021/ct900454q. [DOI] [PubMed] [Google Scholar]
- 36.Merz KM., Jr J. Am. Chem. Soc. 1991;113:406. [Google Scholar]
- 37.Merz KM, Jr, Murcko MA, Kollman PA. J. Am. Chem. Soc. 1991;113:4484. [Google Scholar]
- 38.Diaz N, Suarez D, Merz KM., Jr J. Am. Chem. Soc. 2001;123:9867. doi: 10.1021/ja0113246. [DOI] [PubMed] [Google Scholar]
- 39.Suarez D, Brothers EN, Merz KM., Jr Biochemistry. 2002;41:6615. doi: 10.1021/bi0121860. [DOI] [PubMed] [Google Scholar]
- 40.Suarez D, Diaz N, Merz KM., Jr J. Comput. Chem. 2002;23:1587. doi: 10.1002/jcc.10157. [DOI] [PubMed] [Google Scholar]
- 41.Cui GL, Wang B, Merz KM., Jr Biochemistry. 2005;44:16513. doi: 10.1021/bi051020m. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Ullmann GM, Knapp EW, Kostic NM. J. Am. Chem. Soc. 1997;119:42. [Google Scholar]
- 43.De Kerpel JOA, Ryde U. Proteins: Struct., Funct., Genet. 1999;36:157. doi: 10.1002/(sici)1097-0134(19990801)36:2<157::aid-prot3>3.0.co;2-y. [DOI] [PubMed] [Google Scholar]
- 44.Olsson MHM, Ryde U. J. Biol. Inorg. Chem. 1999;4:654. doi: 10.1007/s007750050389. [DOI] [PubMed] [Google Scholar]
- 45.Remenyi R, Comba P. J. Inorg. Biochem. 2001;86:397. doi: 10.1016/j.jinorgbio.2003.12.004. [DOI] [PubMed] [Google Scholar]
- 46.Comba P, Remenyi R. J. Comput. Chem. 2002;23:697. doi: 10.1002/jcc.10084. [DOI] [PubMed] [Google Scholar]
- 47.Estiu G, Merz KM., Jr Biochemistry. 2006;45:4429. doi: 10.1021/bi052020p. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Estiu G, Suarez D, Merz KM., Jr J. Comput. Chem. 2006;27:1240. doi: 10.1002/jcc.20411. [DOI] [PubMed] [Google Scholar]
- 49.Collins JR, Camper DL, Loew GH. J. Am. Chem. Soc. 1991;113:2736. [Google Scholar]
- 50.Collins JR, Du P, Loew GH. Biochemistry. 1992;31:11166. doi: 10.1021/bi00160a030. [DOI] [PubMed] [Google Scholar]
- 51.Yao SJ, Plastaras JP, Marzilli LG. Inorg. Chem. 1994;33:6061. [Google Scholar]
- 52.Branco RJF, Fernandes PA, Ramos MJ. J. Phys. Chem. B. 2006;110:16754. doi: 10.1021/jp056855l. [DOI] [PubMed] [Google Scholar]
- 53.Case DA, Darden TA, Cheatham ITE, Simmerling CL, Wang J, Duke RE, Luo R, Merz KM, Jr, Pearlman DA, M. Crowley M, R.C. Walker RC, W. Zhang W, Wang B, Hayik S, Roitberg A, Seabra G, Wong KF, Paesani F, Wu X, Brozell S, Tsui V, Gohlke H, Yang L, Tan C, Mongan J, Hornak V, Cui G, Beroza P, Mathews DH, Schafmeister C, Ross WS, Kollman PA. San Francisco: University of California; 2006. [Google Scholar]
- 54.Cornell WD, Cieplak P, Bayly CI, Gould IR, Merz KM, Jr, Ferguson DM, Spellmeyer DC, Fox T, Caldwell JW, Kollman PA. J. Am. Chem. Soc. 1995;117:5179. [Google Scholar]
- 55.Brooks BR, Bruccoleri RE, Olafson BD, States DJ, Swaminathan S, Karplus M. J. Comput. Chem. 1983;4:187. [Google Scholar]
- 56.Harding MM. Acta Crystallogr. Sect. D. Biol. Crystallogr. 1999;55:1432. doi: 10.1107/s0907444999007374. [DOI] [PubMed] [Google Scholar]
- 57.Harding MM. Acta Crystallogr. Sect. D. Biol. Crystallogr. 2000;56:857. doi: 10.1107/s0907444900005849. [DOI] [PubMed] [Google Scholar]
- 58.Harding MM. Acta Crystallogr. Sect. D. Biol. Crystallogr. 2001;57:401. doi: 10.1107/s0907444900019168. [DOI] [PubMed] [Google Scholar]
- 59.Harding MM. Acta Crystallogr. Sect. D. Biol. Crystallogr. 2002;58:872. doi: 10.1107/s0907444902003712. [DOI] [PubMed] [Google Scholar]
- 60.Harding MM. Acta Crystallogr. Sect. D. Biol. Crystallogr. 2004;60:849. doi: 10.1107/S0907444904004081. [DOI] [PubMed] [Google Scholar]
- 61.Harding MM. Acta Crystallogr. Sect. D. Biol. Crystallogr. 2006;62:678. doi: 10.1107/S0907444906014594. [DOI] [PubMed] [Google Scholar]
- 62.Bondi A. J. Phys. Chem. 1964;68:441. [Google Scholar]
- 63.Aqvist J. J. Phys. Chem. 1990;94:8021. [Google Scholar]
- 64.Babu CS, Lim C. Chem. Phys. Lett. 1999;310:225. [Google Scholar]
- 65.Babu CS, Lim C. J. Phys. Chem. B. 1999;103:7958. [Google Scholar]
- 66.Babu CS, Lim C. J. Phys. Chem. A. 2006;110:691. doi: 10.1021/jp054177x. [DOI] [PubMed] [Google Scholar]
- 67.Vaiana AC, Schulz A, Wolfrum J, Sauer M, Smith JC. J. Comput. Chem. 2003;24:632. doi: 10.1002/jcc.10190. [DOI] [PubMed] [Google Scholar]
- 68.Frisch MJ, Trucks GW, Schlegel HB, Scuseria GE, Robb MA, Cheeseman JR, Montgomery JJA, Vreven T, Kudin KN, Burant JC, Millam JM, Iyengar SS, Tomasi J, Barone V, Mennucci B, Cossi M, Scalmani G, Rega N, Petersson GA, Nakatsuji H, Hada M, Ehara M, Toyota K, Fukuda R, Hasegawa J, Ishida M, Nakajima T, Honda Y, Kitao O, Nakai H, Klene M, Li X, Knox JE, Hratchian HP, Cross JB, Bakken V, Adamo C, Jaramillo J, Gomperts R, Stratmann RE, Yazyev O, Austin AJ, Cammi R, Pomelli C, Ochterski JW, Ayala PY, Morokuma K, Voth GA, Salvador P, Dannenberg JJ, Zakrzewski VG, Dapprich S, Daniels AD, Strain MC, Farkas O, Malick DK, Rabuck AD, Raghavachari K, Foresman JB, Ortiz JV, Cui Q, Baboul AG, Clifford S, Cioslowski J, Stefanov BB, Liu G, Liashenko A, Piskorz P, Komaromi I, Martin RL, Fox DJ, Keith T, Laham MAA, Peng CY, Nanayakkara A, Challacombe M, Gill PMW, Johnson B, Chen W, Wong MW, Gonzalez C, Pople JA. [Google Scholar]
- 69.Seminario JM. Int. J. Quantum Chem. 1996;60:1271. [Google Scholar]
- 70.Singh UC, Kollman PA. J. Comput. Chem. 1984;5:129. [Google Scholar]
- 71.Besler BH, Merz KM, Jr, Kollman Pa. J. Comput. Chem. 1990;11:431. [Google Scholar]
- 72.Cieplak P, Cornell WD, Bayly C, Kollman PA. J. Comput. Chem. 1995;16:1357. [Google Scholar]
- 73.Siegbahn PEM, Borowski T. Acc. Chem. Res. 2006;39:729. doi: 10.1021/ar050123u. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.