Postural Constraints on Movement Variability

Abstract

Movements are inherently variable. When we move to a particular point in space, a cloud of final limb positions is observed around the target. Previously we noted that patterns of variability at the end of movement to a circular target were not circular, but instead reflected patterns of limb stiffness—in directions where limb stiffness was high, variability in end position was low, and vice versa. Here we examine the determinants of variability at movement end in more detail. To do this, we have subjects move the handle of a robotic device from different starting positions into a circular target. We use position servocontrolled displacements of the robot's handle to measure limb stiffness at the end of movement and we also record patterns of end position variability. To examine the effect of change in posture on movement variability, we use a visual motor transformation in which we change the limb configuration and also the actual movement target, while holding constant the visual display. We find that, regardless of movement direction, patterns of variability at the end of movement vary systematically with limb configuration and are also related to patterns of limb stiffness, which are likewise configuration dependent. The result suggests that postural configuration determines the base level of movement variability, on top of which control mechanisms can act to further alter variability.

INTRODUCTION

Over the past decade, a great deal of research in the field of motor control has examined the problem of how the nervous system controls variability in movement (Gribble et al. 2002; Harris and Wolpert 1998; Lametti et al. 2007; Osu et al. 2003; Selen et al. 2009; Todorov et al. 2002; van Beers et al. 2004). Indeed, it is very difficult to make exactly the same movement twice; when humans make movements to a particular point in space, one readily finds that, not one end position, but instead a cloud of end positions is generated around the target (Gordon et al. 1994b; Laboissière et al. 2009; Shiller et al. 2002; van Beers et al. 2004). Motor commands, it seems, are hard to precisely replicate, perhaps because of noise in the command introduced both centrally (Churchland et al. 2006) and by the firing of motor neurons at the periphery (Fitts et al. 1954; Harris and Wolpert 1998; Jones et al. 2002).

Regardless of the source of movement variability, it is frustratingly present and the nervous system must deal with it. Some have argued that movements are planned specifically to minimize endpoint variability (Harris and Wolpert 1998). More recently, optimal control theory (Todorov 2009; Todorov et al. 2002) has been used to model motor behavior (Diedrichsen 2007; Haruno et al. 2005). In this context, it has been suggested that the nervous system corrects only for variability—movement errors—in directions that are relevant to the goals of the movement. Others have demonstrated empirically that movement variability can be constrained by increasing the mechanical stiffness, or resistance to displacement, of the moving limb (Burdet et al. 2001; Gribble et al. 2002; Laboissière et al. 2009; Lametti et al. 2007; Osu et al. 2003; Wong et al. 2009).

In Lametti et al. (2007) we showed that when moving into targets of different shape, variability at the end of movement, which we referred to as endpoint variability, was low in directions where limb stiffness was high and was high in directions where limb stiffness was low. Despite this correlation, patterns of endpoint variability generally conformed to the shape of the target. There was, however, one exception: when subjects moved into a circular target, patterns of endpoint variability within the circle were elliptical and, on average, had an orientation that was approximately perpendicular to the direction of maximum limb stiffness. In that case, limb stiffness at the end of movement appeared to be a better predictor of the resulting pattern of endpoint variability than the shape of the target itself. The result suggests that geometrical and mechanical factors may play a larger role in patterns of movement variability than previously thought. In the present study we examine these factors in greater detail.

Using a robotic device, subjects made movements into a circular target and movement variability and limb stiffness were measured at movement end just as the hand came to rest in the target zone. A unique visuomotor transformation was used to experimentally alter patterns of limb stiffness. The visuomotor shift systematically changed the configuration of the limb (Mussa-Ivaldi et al. 1985), but held visual feedback constant in the center of the workspace such that the visual goals of the task were unaltered across limb configurations. We found that, regardless of movement direction, patterns of endpoint variability were related to limb configuration. This finding suggests a significant role for posture in the regulation of movement variability.

METHODS

In all, 14 subjects participated: 8 in experiment 1 (4 males) and 6 in experiment 2 (3 males). Subjects were right handed, had normal or corrected vision, and were between the ages of 18 and 30 yr. The McGill University Research Ethics Board approved the experimental procedures.

Apparatus

In both experiments, subjects used their right hand to grasp the handle of a two-joint robotic manipulandum (Interactive Motion Technologies, Cambridge, MA) and move it in a horizontal plane. A computer program compensated for the inertial anisotropy of the manipulandum so that its behavior was effectively that of an isotropic 600-g object irrespective of where in the workspace the handle was moved. A semisilvered mirror positioned immediately above the robot's handle blocked vision of the arm; a flat-panel TV projected a cursor and target onto the mirror from above. Subjects sat in a chair with a harness that restrained shoulder movement. An air sled supported the arm and allowed subjects to make nearly frictionless movements of the handle. A six-axis force torque transducer (ATI Industrial Automation, Apex, NC), mounted below the handle, sensed subject-generated forces. Optical encoders (16-bit, Gurley Precision Instruments, Troy, NJ) recorded the robot's joint angles. Force and position data from the robot were sampled at 400 Hz.

Experimental task

In both experiments, subjects moved the handle from different starting points on a circle (12.5 cm radius) to put a cursor (0.5 cm radius) into a circular target (2 cm radius). The position of the target on the mirror was determined for each subject separately and corresponded to a shoulder angle of 45° relative to the frontal plane and an elbow angle of 90° relative to the upper arm (Fig. 1A, center trace). The position of the visual target was the same in both experiments. In experiment 2, the configuration of the limb changed between conditions, whereas the visual target position remained constant (see following text).

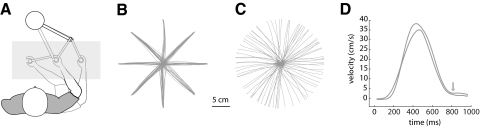
Fig. 1.

Subjects moved the handle of a manipulandum into a circular target in 3 different postures. Visual feedback was held constant at the central location, that is, as if the subject were moving the robot's handle with their limb in the central posture (darkest trace in A). In experiment 1, subjects made movements to a single target at the central location from 8 discrete starting positions centered on the target (B); in experiment 2, subjects made movements from random starting positions centered on the target (C) in each of the 3 limb configurations shown in A. D shows tangential velocity for a representative subject. The area bounded by the curve represents ±1SE. Limb stiffness and movement variability were measured at the end of movements (approximate location of the gray arrow).

Subjects were instructed to start each movement when the target was illuminated, to enter the target zone within 350 ms (±50 ms) of leaving the start zone, and to come to a complete stop within the boundaries of the target. Figure 1D shows the average velocity profile for a representative subject who participated in the experiment. Changes in target color signaled successful or unsuccessful trials. If the target was not entered within the allotted time, or if the hand left the target zone after entering, one point was added to an error counter displayed on the mirror. Subjects were instructed to minimize errors. After feedback was given, the robot moved the subject's hand to the next start location.

Experiment 1

We examined both stiffness and movement variability at movement end, as the hand came to rest within the target zone. To assess the dependence of stiffness and variability on movement direction, movements were made in random order from eight equidistant starting positions about a circle into the target (Fig. 1B). Subjects were given 100 to 150 practice movements. After a short break, subjects then made between 150 and 200 movements and patterns of limb stiffness and kinematic variability were measured at the end of movement. The number of trials differed for different subjects because of differences in the number of movements required to satisfy the timing and accuracy requirements of the task.

Experiment 2

Subjects made movements into the target from random starting positions around a circle (Fig. 1C). To examine how changes in posture affect patterns of movement variability and limb stiffness, subjects were tested in separate blocks of trials with three different limb configurations (Fig. 1A). Importantly, the position of the visual target and cursor remained fixed in the center position throughout the experiment and only the handle of the robot, invisible to the subject, was shifted. For example, in the center configuration, with the cursor in the target, the robot's handle was positioned under the target; in the rightward configuration, however, with the cursor in the target zone on the display, the robot's hand was some distance to the right of the target, a distance defined on a per subject basis based on the joint angles specified by the new limb configuration. Thus the visual location of the target on the display was never changed from the central configuration. The visual motor transformation kept the axes of movement and the visual feedback of movements aligned across limb configurations, allowing us to alter posture without altering the visual goals of the task.

The three postural configurations used were as follows: in the central location—the location where the handle and the cursor were aligned—with the cursor in the target, the angle at the shoulder was 45° and the angle at the elbow was 90° (Fig. 1A, center trace); at the left, the angle at the shoulder was 90° and the angle at the elbow was 135° (Fig. 1A, left trace); at the right, the angle at the shoulder was 0° and the angle at the elbow was 90° (Fig. 1A, right trace).

In all, 100 practice movements were given in each location to allow subjects to adapt to the visuomotor transformation, especially those involving the left and right postural configurations. We quantitatively assessed practice effects by dividing the data from the practice phase into bins of 5 movements. A short break followed the completion of the practice phase. Subjects then made between 150 and 200 movements in each limb configuration and patterns of limb stiffness and kinematic variability were measured at the end of movement. Five-minute breaks were given between limb configurations and the order in which the three different postures were experienced was counterbalanced across the six subjects that participated in experiment 2—that is, each of the six subjects got one of the six possible orderings of limb configurations (left then center then right, center then left then right, and so forth) such that every possible ordering of limb configuration was examined.

Measuring limb stiffness

In both experiments, limb stiffness was measured at the end of some movements as in Lametti et al. (2007): on 32 randomly selected movements in which subjects met the timing and accuracy requirements of the task, position servocontrolled displacements of the handle were applied at the end of movement, when hand velocity had dropped to <2% of peak (approximate location of black arrow in Fig. 1D). The 0.6 cm displacement was built up over 75 ms and held the limb in position for 250 ms. Four perturbations were delivered in each of eight directions (0, 45, 90, 135, 180, 225, 270, and 315°) for a total of 32 perturbations per stiffness estimate.

When the limb is displaced from a static position, the relationship between change in force and change in position can be modeled as

$$\mathrm{d}F=K\mathrm{d}P$$ (1)

In two dimensions, the equation can be written in matrix notation

$$\left[\begin{array}{c}\mathrm{d}{F}_x\\ \mathrm{d}{F}_y\end{array}\right]=\left[\begin{array}{cc}{K}_{xx}& K_{xy}\\ K_{yx}& K_{yy}\end{array}\right]\left[\begin{array}{c}\mathrm{d}{P}_x\\ \mathrm{d}{P}_y\end{array}\right]$$ (2)

In Eq. 2, dF is change in force in N due to the perturbation, dP is change in position in m, and K is stiffness in N/m. K_xx gives the resistive force of the limb in x per unit displacement in x; K_xy is the resistive force of the limb in x per unit displacement in y, and so on. dF and dP were calculated using a 10 ms window immediately prior to the displacement and a 30 ms window during the hold phase of the displacement, 270 ms after the start of the perturbation.

Using the stiffness matrices, limb stiffness at the hand was represented graphically for each subject as an ellipse; the major axis of the ellipse gives the direction of maximum stiffness and the minor axis gives the direction of minimum stiffness (Burdet et al. 2001; Darainy et al. 2004, 2006, 2007; Gomi and Kawato 1997; Gomi and Osu 1998; Hogan et al. 1985; Mussa-Ivaldi et al. 1985). Singular value decomposition of the stiffness matrix was used to obtain values for the magnitude and orientation of the axes of the ellipse (Lametti et al. 2007; Shiller et al. 2002; van Beers et al. 2004). For purposes of statistical analysis, we used ellipse orientations in the second and third polar quadrants (90–270°) to account for the circular nature of the data.

Measuring kinematic variability

Measured hand position was low-pass filtered at 30 Hz and then numerically differentiated to calculate velocity. Movement start and end were scored at 5% of peak velocity. Movements with multiple peaks in tangential velocity (<2.5% of movements, on average) were discarded. From movements that were retained, 150 final limb positions were chosen from each condition semirandomly—in particular, all 32 trials in which limb stiffness was estimated were included in an otherwise random sample to give a total of 150 observations. From these endpoints, covariance matrices were calculated and, from these, the distribution of 150 endpoints for each subject was displayed as a 95% confidence ellipse (van Beers et al. 2004). Singular value decomposition was used to determine the size and orientation of each ellipse (Shiller et al. 2002; van Beers et al. 2004). As with the stiffness ellipses, values for variability ellipse orientations were always taken in the second and third quadrants (90–270°).

In experiment 1, from the 150 endpoints selected for each subject, endpoints from each of the eight movement directions were binned. Covariance matrices were calculated for each bin and, from these, the distribution of endpoints for each movement direction was displayed as a 95% confidence ellipse (Fig. 2C). Singular value decomposition was used to determine the size and orientation of each ellipse. Ellipse orientations for each movement direction were then compared using repeated-measures ANOVA.

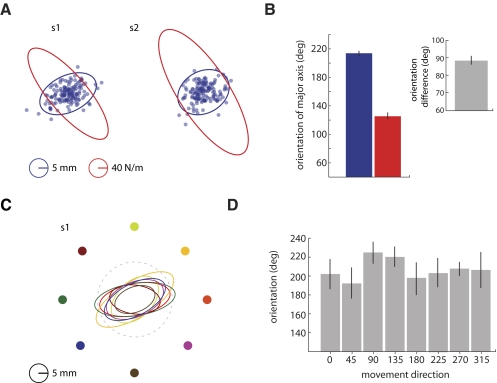
Fig. 2.

Experiment 1. A shows data from 2 subjects (s1 and s2). Patterns of limb stiffness (red) are related to patterns of movement variability (blue); the difference in average ellipse orientation (B) between stiffness and variability was about 90° (gray bar, B). C shows variability ellipses for each of the 8 movement directions (represented by 8 colors) constructed from s1's end position data. The dashed line represents the target. End position variability was elliptical in shape. The mean orientation of the variability ellipse (D) did not change with movement direction. Error bars represent ±1SE.

RESULTS

The aim of this study was to understand the contribution of geometrical and mechanical factors to patterns of movement variability. The work was motivated by a surprising finding that patterns of movement variability at the end of movements into a circular target were, on average, not circular, but elliptical in shape and systematically related to the direction of maximum limb stiffness (Lametti et al. 2007).

In both experiments, limb stiffness was measured at the end of movement just as subjects had come to a stop in the target. The degree to which the stiffness ellipse represents the limb's restoring force in response to a perturbation was calculated by correlating the magnitude of the measured restoring force with the restoring force predicted by the stiffness matrix (Franklin et al. 2007). In the present data, on average, the stiffness matrix accounted for 92% (SD 8%) of the variance in the measured restoring force.

In experiment 1, the average stiffness matrix in N/m (±1SE) was

$$\left[\begin{array}{cc}-177\pm 22& 79\pm 13\\ 87\pm 13& -235\pm 27\end{array}\right]$$

In experiment 2, the average stiffness matrix for the three postures (from left to right) in N/m (±1SE) was

$$\left[\begin{array}{cc}-187\pm 17& 85\pm 6\\ 89\pm 11& -166\pm 18\end{array}\right]$$

$$\left[\begin{array}{cc}-83\pm 12& -46\pm 10\\ -7\pm 11& -217\pm 32\end{array}\right]$$

$$\left[\begin{array}{cc}-125\pm 16& 69\pm 9\\ 68\pm 10& -206\pm 20\end{array}\right]$$

The average stiffness matrices were typically symmetrical; the off-diagonal terms of the matrices were similar in magnitude. One exception was the stiffness matrix at the right in which the off-diagonal terms differed [t₍₁₀₎ = 0.38, P > 0.70, at the left; t₍₂₆₎ = 0.24, P > 0.80, at the center; t₍₁₀₎ = 5.07, P < 0.05, at the right]. For individual subjects, the average SD of the K_xx component of the stiffness matrix was 16.21 N/m; for K_xy the average SD was 16.10 N/m; for K_yx the average was 17.54 N/m; and for K_yy the average was 19.15 N/m.

In experiment 1, subjects made movements from eight starting positions into a circular target; patterns of movement variability and limb stiffness were measured at the end of movement. Figure 2A shows patterns of limb stiffness (red ellipses) and movement variability (blue ellipses) at the end of movement for two representative subjects. On average, patterns of limb stiffness and patterns of movement variability were perpendicular [t₍₁₄₎ = 0.59, P > 0.5]. The orientation of the major axis of the variability ellipse was 213 ± 3.19° (mean ± 1SE, Fig. 2B, blue bar); the orientation of the major axis of the stiffness ellipse was 125 ± 4.39° (Fig. 2B, red bar); and the mean difference in orientation between the major axes was 88 ± 3.62° (Fig. 2B, gray bar).

Patterns of variability at the end of movement were examined in each of the eight movement directions. Figure 2C shows patterns of movement variability from a representative subject (subject S1 in Fig. 2A) at the end of movement in each of the eight movement directions used in experiment 1. For this subject, it can be seen that, regardless of movement direction, the pattern of endpoint variability was similar. Across subjects a similar result was observed; the orientation of major axis of the variability ellipse did not differ across the eight movement directions [Fig. 2D: F_(7,56) = 0.57, P > 0.75].

In experiment 2, posture was systematically varied using a visuomotor transformation that kept the location of the visual target constant but shifted the handle and arm. At each location, subjects were required to move to a central target from random locations about a circle. Movements for each of the three limb configurations were displayed visually at a single location in the center of the workspace. Patterns of movement variability and limb stiffness were then measured at the end of movement.

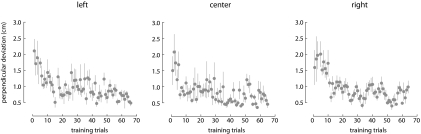
Figure 3 shows the maximum perpendicular deviation of the hand from a straight-line path during the practice phase of experiment 2. For purposes of analysis, we divided the practice phase data into bins of five movements. ANOVA showed that there were no differences in mean movement curvature due to the postural configuration of the limb [F_(2,10) = 0.13, P > 0.90]. Movement curvature did change, however, over the course of movement [F_(11,59) = 34.14, P < 0.001]. Bonferroni-corrected comparison showed that perpendicular deviation in the first bin of five movements was significantly greater than that in the final bin (P < 0.05). Moreover, after 35 practice movements, perpendicular deviation did not change for the remainder of the practice phase (P > 0.05 in all cases). This suggests that subjects successfully adapted to the visuomotor transformation associated with each postural configuration and had reached asymptotic levels of performance by the start of the main experimental manipulation.

Fig. 3.

Experiment 2. The perpendicular deviation from a straight-line path decreased over the course of training in each of 3 postures. Individual points represent perpendicular deviation averaged over the 6 subjects that participated in experiment 2. Error bars represent ±1SE.

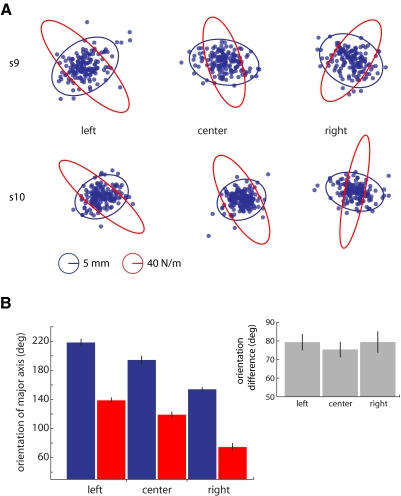
Figure 4A shows patterns of limb stiffness (red) and movement variability (blue) for two representative subjects in the left, center, and right limb configurations. Changes in posture were observed to cause changes in the orientation of the major axis of the stiffness ellipse [red bars in Fig. 2B; F_(2,10) = 65.25, P < 0.001 with a repeated-measures ANOVA]. The stiffness orientations at the three locations each differed reliably from one another by Bonferroni-corrected comparisons (P < 0.05 in each case). The major axis of the stiffness ellipse was 139° (SE = 3.33°) at the left, 119° (SE = 3.69°) in the center, and 75° (SE = 5.03°) at the right. This result replicates the finding of Mussa-Ivaldi et al. (1985): patterns of limb stiffness are systematically related to differences in limb geometry.

Fig. 4.

Experiment 2. A: shows stiffness (red) and variability ellipses (blue) from 2 subjects, s9 and s10, who made movements in the 3 postures (left, center, right) used in experiment 2. As posture was altered the direction of maximum limb stiffness and movement variability changed systematically (B). The relationship between the 2 did not change (C). Error bars represent ±1SE.

Altering posture also caused systematic changes in the orientation of the variability ellipse even though the visual target was circular and fixed in position in the center of the workspace. Repeated-measures ANOVA indicated that differences in the testing posture resulted in reliable differences in the orientation of the major axis of the variability ellipse [blue bars in Fig. 4B: F_(2,10) = 51.27, P < 0.001]. Variability orientations each differed reliably from one another (P < 0.05 in each case with a Bonferroni correction). The orientation of the major axis of the variability ellipse was 218° (SE = 4.81°) at the left, 195° (SE = 5.10°) in the center, and 154° (SE = 2.50°) at the right.

Changes in posture altered patterns of both limb stiffness and movement variability, but did not change the relationship between variability and stiffness (gray bars in Fig. 3B). The angle between the major axis of the variability ellipse and the major axis of the stiffness ellipse—78° (SE = 2.57°), on average—did not differ reliably between postures [F_(2,10) = 0.35, P > 0.70, repeated-measures ANOVA]. This suggests that, at the end of movement, patterns of movement variability and limb stiffness are both linked to posture. Moreover, in each case, we observe a systematic relationship between stiffness and variability such that in directions where stiffness is high, variability is low, and vice versa.

In experiment 1, subjects made movements from eight starting positions about a circle into a circular target. In experiment 2, in the center posture—the same posture used in experiment 1—subjects made movements from random starting positions around a circle into the same circular target. Although the sample sizes varied slightly between these two conditions (eight subjects in experiment 1 vs. six in experiment 2), the results for movements to the central target can be compared (with caution) to examine the effect that introducing random starting positions had on the relationship between limb stiffness and endpoint variability.

The difference between the orientation of the major axis of the stiffness ellipse and the major axis of the variability ellipse in experiment 1 was closer to 90° than that observed in the same posture in experiment 2 (88 vs. 75°, respectively). An analysis revealed that no difference in orientation of the major axis of the stiffness ellipse between the two experimental conditions [Student's t-test for unpaired samples: t₍₁₂₎ = 1.06, P > 0.30], but there was a difference in the orientation of the major axes of the variability ellipse [Student's t-test for unpaired samples: t₍₁₂₎ = 3.30, P < 0.01]. Having subjects start movements from random starting locations thus led to a decrease in the extent to which directions of maximum stiffness and directions of maximum variability were orthogonal.

DISCUSSION

In the present study, we found that regardless of movement direction, patterns of both endpoint variability and limb stiffness are related to limb configuration. In each case, in directions where limb stiffness was high, endpoint variability was low; in directions where limb stiffness was low, endpoint variability was high.

The design of the task per se did not result in the fact that patterns of variability were related to patterns of limb stiffness; that is to say, subjects could have come to a stop anywhere within the circular target. Indeed, one would have predicted that when moving into a circular target the pattern of endpoint variability produced would be, on average, circular in shape. Consistently, though, patterns of movement variability were elliptical in shape no matter which direction the movement was made from. When posture was altered, patterns of movement variability were also altered and the relationship between limb stiffness and movement variability was maintained.

It seems likely that limb configuration determined the patterns of both limb stiffness and movement variability observed in these experiments. In Lametti et al. (2007) we compared limb stiffness measured at the end of movement to limb stiffness measured at the same position with the arm at rest. We found that the two ellipses had similar orientations. Thus limb stiffness measured at the end of movement largely reflects limb geometry; there is little effect on the orientation of the ellipse due to the actual level of muscle contraction or cocontraction. Here, without changing the visual goals of the task, we directly manipulated posture and found systematic changes in both limb stiffness and movement variability, suggesting that both depend on posture. The result, however, does not mean that limb stiffness has no role in the regulation of movement variability. Many studies have previously shown that when the task demands an increase in limb stiffness, movement variability is subsequently reduced (Gribble et al. 2002; Lametti et al. 2007; Selen et al. 2005; Wong et al. 2009). The task used in this experiment was relatively easy and subjects likely did not need to use a strategy of stiffening up their limb to achieve the goals of the task. In fact, it could be argued that it would be energy efficient to ignore variability in directions of low stiffness since these end positions still generally fell within the boundaries of the target (Todorov 2009; Todorov et al. 2002). When moving into a space, posture, it seems, is a primary determinant of movement variability, but if the task demands it, limb stiffness can be used to make movements even more accurate.

A number of studies have examined patterns of end position variability when reaching toward a target. Gordon et al. (1994a) and van Beers et al. (2004) both found that endpoint variability is oriented along the direction of movement. In these studies, subjects had to move without visual feedback of hand position toward a small circle (0.06 cm in van Beers et al. 2004; 1.28 cm in Gordon et al. 1994a) and stop as close to the circle as they possibly could. Gordon et al. (1994b) concluded that limb inertia was a major determinant of patterns of endpoint variability.

Compared with the studies conducted by Gordon and van Beers, a different pattern of end position variability was observed here and in Lametti et al. (2007): variability patterns at movement end are configuration dependent. We believe that the difference in these reports lies in the specifics of the task. Here, and in Lametti et al. (2007), subjects had to make movements toward a circle with a 2 cm radius and come to a complete stop within the boundaries of the circle. We also note that our results suggest a lesser role for limb inertia in determining the shape of the variability ellipse. In Mussa-Ivaldi et al. (1985) limb inertia in postures similar to those used here was estimated based on the weight and limb-segment length of subjects who participated in the experiment. They report that inertia ellipses were consistently 30° counterclockwise (closer to the x-axis) than stiffness ellipses measured for the same subjects (see Fig. 10 in Mussa-Ivaldi et al. 1985). Assuming this angular difference between the directions of maximum stiffness and inertia is similar in the present study, it suggests that the angular difference of about 50° between the direction of maximum limb inertia and maximum endpoint variability is a weaker relationship than that observed between the direction of maximum stiffness and maximum variability. Indeed, given full visual feedback during movements the nervous system might be better at compensating for the inertial properties of the limb.

Last, we noted, with some caution due to the small sample size, that having subjects make movements from random positions into the target, as opposed to eight, discrete positions, led to a decrease in the angular difference between the variability ellipse and the stiffness ellipse: 75° for movements from random positions versus 88° for movements from discrete positions. Although this result is presently unexplainable, it is worth noting that in Lametti et al. (2007), in which subjects also made movements from random starting positions into a circular target, the angle between stiffness and variability at the end of movement was 75°. At the least, our result thus agrees with that of a previous report.

GRANTS

This research was supported by the National Institute of Child Health and Human Development Grant HD-048924, Natural Sciences and Engineering Research Council, Canada, and Fonds Québécois de la Recherche sur la Nature et les Technologies, Quebec.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).