Abstract
Visual memories of landmarks play a major role in guiding the habitual foraging routes of ants and bees, but how these memories engage visuo-motor control systems during guidance is poorly understood. We approach this problem through a study of image matching, a navigational strategy in which insects reach a familiar place by moving so that their current retinal image transforms to match a memorized snapshot of the scene viewed from that place. Analysis of how navigating wood ants correct their course when close to a goal reveals a significant part of the mechanism underlying this transformation. Ants followed a short route to an inconspicuous feeder positioned at a fixed distance from a vertical luminance edge. They responded to an unexpected jump of the edge by turning to face the new feeder position specified by the edge. Importantly, the initial speed of the turn increased linearly with the turn's amplitude. This correlation implies that the ants’ turns are driven initially by their prior calculation of the angular difference between the current retinal position of the edge and its desired position in their memorized view. Similar turns keep ants to their path during unperturbed routes. The neural circuitry mediating image-matching is thus concerned not only with the storage of views, but also with making exact comparisons between the retinal positions of a visual feature in a memorized view and of the same feature in the current retinal image.
Keywords: view-based-homing, snapshot, memory-retrieval, insect
Visual landmarks play a major role in guiding the foraging routes of some ants and bees (1–4). Landmarks both set the shape of the route that an ant follows and specify the position of the route's endpoint. Ants, far from the goal, approach landmarks as beacons, or detour round them, or use them for directional information (5–8). When close to the goal, ants and other insects move as if they are trying to improve the fit of their current 2D image of the goal's surroundings to their stored view of those surroundings and search for the goal where the two images coincide (9–14).
Here, we ask how image-matching operates over a route segment that covers the last meter to a feeding site. In dense vegetation, with rapidly changing views, a single view stored at the goal can only guide an ant accurately within a small catchment area around the goal. The range of image-matching can be elongated by employing a sequence of views stored along the final route segment (15, 16). The use of multiple snapshots allows ants to approach the goal in a standard direction and more easily pinpoint its location. But how does an ant use a snapshot to correct its path?
Results
Corrective Turns During Normal Approaches.
In these experiments, ants approached a sucrose reward from a starting point about 1 m away. For some ants, the inconspicuous feeder lay directly below, and for other ants to one side of the base of a vertical, luminance edge displayed on a large LCD screen (see Materials and Methods, SI Text, and Fig. S1). Ants accustomed to one route or the other took a slightly sinuous path that went almost directly from the starting point to the feeder (Fig. 1A), so that on average the angle between the ant's longitudinal axis and the feeder (the feeder-angle) was about 0° (cf. 16).
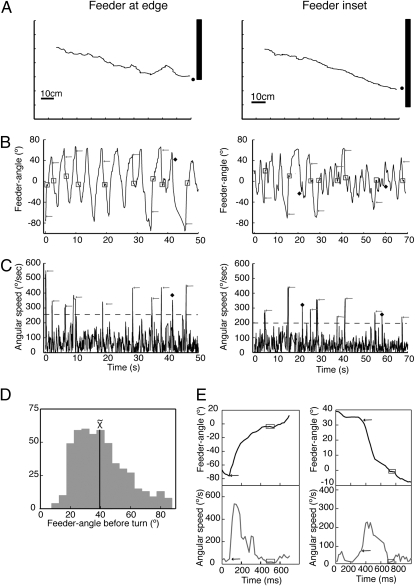
Fig. 1.
Approaches to a feeder defined by a luminance edge. (A) Two sample paths. (B and C) Plots of feeder-angle and angular speed during the course of these paths. Horizontal dashed line in C shows threshold for measuring turns at 2 SD above the mean angular speed (mean speed with feeder at edge is 120° per s−1 ± 75° per s−1 SD; mean with feeder inset is 107° per s−1 ± 45° per s−1 SD). Note that the onset of the rapid turn often occurs after the feeder-angle has peaked. Arrows show the onset of turns and the boxes their end. Filled diamonds show peaks that did not correspond to identifiable turns (see Materials and Methods). (A–C) (Left) Data from routes with the feeder at the base of the edge; (Right) Routes with feeder inset. (D) Distribution of absolute values of feeder-angles before a turn. Data come from 495 approaches. (E) Plots of turns at high resolution. The start of a turn is specified by the sudden increase in angular velocity and its end by at least three frames over which the ant's body orientation changes by <1°. Boxes and arrows defined as above.
Ants are able to continue to the goal after such an edge has been made to vanish (17), showing that their overall straight path does not require continuous visual feedback from the edge. Every so often they turn rapidly to face the feeder (Fig. 1B) (mean interval between detected turns is 9.6 s ± 6.9 s SD, n = 287). The time-course of the feeder-angle during a route shows that this angle tends to rise gradually and is corrected rapidly (Fig. 1B).
The ants’ speed of walking was quite variable (mean 2.16 cm per s−1 ± 2.32 cm per s−1 SD), but sufficiently slow to imply that these changes in feeder-angle are dominated by rotational movements. Occasional spikes, corresponding to the corrective turns, are seen in the accompanying plot of the ant's rotational velocity (Fig. 1C). Turns occur most often when the feeder-angle lies between 20 and 40° (Fig. 1D).
Because turns start and stop cleanly (Fig. 1E), their size can be measured reliably. Turn-size (see Materials and Methods) is related linearly to the feeder-angle before the turn with a slope close to unity (Fig. 2A), both with the feeder at the base of the vertical edge and with it inset by 15 cm. The distribution of errors at the end of a turn is centered on 0°, whether the ant began the turn facing the light or the dark side of the edge (Fig. 2B). The periods of feeder fixation after the turn are brief, lasting on average 0.19 s ± 0.13 s SD (n = 495, mode = 0.08 s).
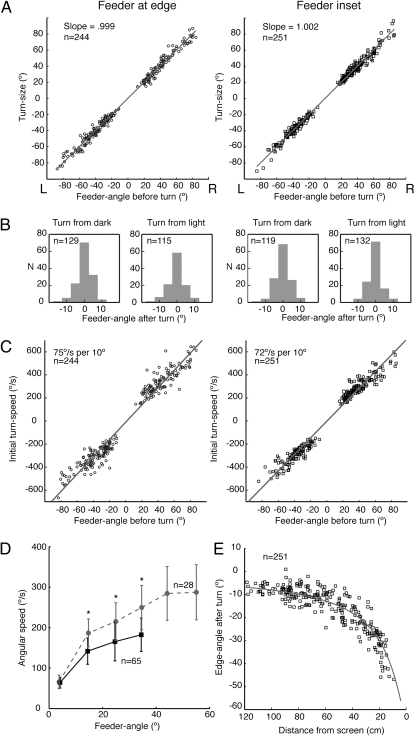
Fig. 2.
Turn-sizes and speeds. (A) Plot of turn-size against feeder-angle before turn with linear fits to these data (r2 feeder at base = 0.991; r2 feeder inset = 0.991). Here and throughout the article, negative angles indicate turns to the ant's left and positive to its right. (B) Distribution of feeder-angles after the turn, separated according to whether ants face the dark or the light side of the edge at the onset of the turn. (C) Plots of initial turn-speed against feeder-angle before the turn with linear fits to these data (r2 feeder at edge = 0.959; r2 feeder inset = 0.970). (A–C) (Left) Data from routes with the feeder at the base of the edge; (Right) Routes with feeder inset. (D) Plots of angular speed against feeder-angle during turns of two size ranges. As the turns progress, the feeder-angle falls, accompanied by a drop in angular speed. Speeds between the two size ranges differ until the feeder-angle is less than 20°. Dashed line: starting feeder-angle lies between 60 and 70°, solid line feeder-angle lies between 40 and 50°. Angular speed is averaged over 10° bins of feeder-angle within each size range. To pool data from turns of both directions, anticlockwise turns are reflected. Data points showing mean values and error bars (±1 SD) are placed at the center of each bin. Asterisk (*) indicates difference between speeds is significant at P < 0.01 (t test). (E) For routes with inset feeder, edge-angle after a turn is plotted against the ants’ distance from the screen. Data cluster around the calculated solid line that gives the edge-angle corresponding to 0° feeder-angle along the route.
The angular speed of the turn, measured over the initial 0.06 s (initial turn-speed), is strongly related to the feeder-angle before the turn (Fig. 2C), which tells us that the ant knows right at the start how large a turn is needed. In the the SI Text and Figs. S2 and S3, we analyze this relationship further and present an additional experiment to confirm that the relation between initial turn-speed and feeder-angle before the turn is similar when the feeder is far from a visual edge. Plots of angular speed against feeder-angle during turns of different sizes (Fig. 2D) show that differences in angular speed between larger and smaller turns are sustained over much of the turn (see Fig. S4 for examples of a small and a large turn) Thus, ants correct their course with intermittent, preprogrammed turns, but it is unclear whether turns terminate through visual feedback.
Because an ant does not detect the feeder until it has almost stumbled over it, it must compute the feeder-angle from the retinal position of the edge just before the turn. As a proxy for retinal position, we use the angle between the edge and the ants’ longitudinal axis (the edge-angle, see Materials and Methods). The data of Fig. 2 A and B imply that a corrective turn places the edge in a retinal position corresponding to a feeder-angle of 0° (the desired edge-angle). When the feeder is inset from the edge, the desired edge-angle increases as the ant approaches the feeder. That the ants’ orientation at the end-points of the corrective turns matches the increasing desired edge-angle during the approach (Fig. 2E) is strong evidence that ants store a sequence of retinal edge positions (16) along the route and that their corrective turns eliminate the difference between the currently viewed and desired edge positions.
The increasingly eccentric desired retinal position of the edge during the route seems to be controlled primarily by the apparent width of the black side of the edge (16), which grows during the ant's approach (see Fig. S1 for luminance profile of edge). But it is unknown whether ants learn a discrete series of desired edge positions, each linked to a different angular width of the landmark, or if there develops a continuous mapping between landmark width and desired edge position. We use the terms “sequence of stored images” or “multiple snapshots” without prejudging this issue.
Corrective Turns Induced by Landmark Perturbations.
By making the edge jump during the ant's approach, we can ask whether similar turns correct errors that are imposed and unpredictable, rather than self-induced. Water striders, which use landmarks to maintain station in fast-running streams, stop rowing with their legs if an imposed error in the retinal position of a landmark can be corrected by moving downstream, and row more vigorously if the error is in the opposite direction (12). They know at least the direction of imposed errors. Do wood ants correct both the amplitude and direction of an imposed error?
Ants familiar with the route received tests with three training trials between each test. The edge was made to jump when the ant reached a preset distance from the screen, with the direction (left or right) and amplitude of the jump varying from test to test, so that the edge-angle changed by 18° or 30°. On most tests (see Materials and Methods) the jump of the stimulus evoked a saccade-like body turn with a mean latency of 0.35 s ± 0.31 s SD (n = 415). See Fig. 3C for distribution of latencies. As with spontaneous turns, the size of evoked-turns is matched to the feeder-angle before the turn, causing ants to face the feeder (Fig. 3A). The evoked-turns also resembled spontaneous turns in the relation between initial turn-speed and feeder-angle before the turn (Fig. 3B and Fig. S2).
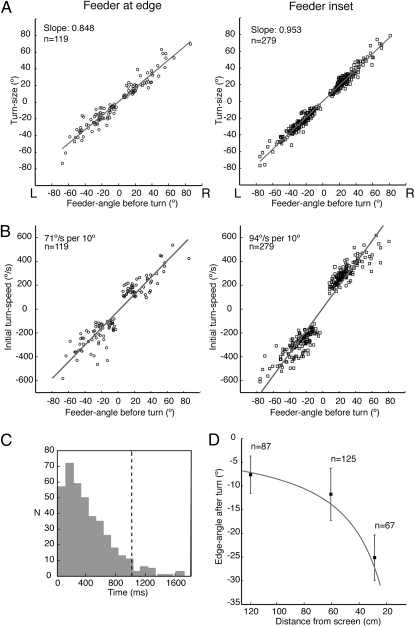
Fig. 3.
Turns induced by jumps of the edge. (A) Plots of turn-size against feeder-angle before turn with linear fits to the data (r2 feeder at edge = 0.865; r2 feeder inset = 0.928). (B) Plots of initial turn-speed against feeder-angle before turn with linear fits to the data (r2 feeder at base = 0.898; r2 feeder inset = 0.919). (C) Delay between edge-jump and turn combining all tests. Turns with delays beyond the dashed line at ∼2 SD were not analyzed. (D) For routes with inset feeder, mean and SD of edge-angle after turn are plotted against distance from screen at onset of turn. The solid line shows calculated edge-angle for 0° feeder-angle.
Ants trained with the feeder inset from the edge were tested with stimulus jumps when they were at 120, 60, or 30 cm from the screen. The edge-angles at the end of these evoked-turns (Fig. 3D) fall close to the predicted edge-angle vs. distance curve for a feeder-angle of 0°. This relationship shows again that the ant places the edge on the retina in a manner that is consistent with route guidance by a sequence of stored images.
Corrective Turns in Ants Trained to Two Routes.
The ability to correct errors through preprogrammed turns suggests that ants recognize a landmark feature stored in one retinal position when it appears at other retinal positions. To examine whether ants distinguish between different features, we trained individuals to follow two edge-defined routes (Fig. 4A). On some trials, ants approached a light-dark edge with the sucrose placed on the light side and set 5 cm to the left of the edge. On others, the same ants approached a dark-light edge with the sucrose on the dark side and placed 15 cm from the edge. Ants could follow both routes and generated the appropriate spontaneous fixation-turns for each one (Fig. 4A). Thus, the ants identified which feature they faced and placed it in the retinal position corresponding to that feature and the ants’ position along the route.
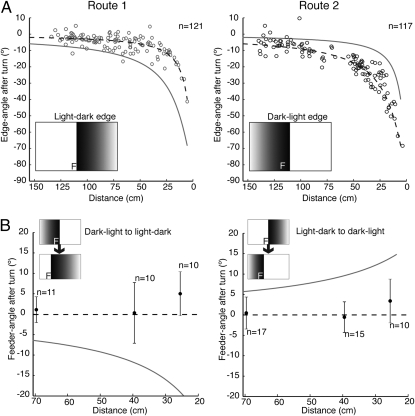
Fig. 4.
Ants trained to two routes. (Left) Route 1. (Right) Route 2. (A) Turns during training runs. Edge-angle after a turn is plotted against the ant's distance from the screen for the two routes. Dashed curve shows edge-angle corresponding to 0° feeder-angle along the currently appropriate route. Ants follow this dashed curve significantly better than the solid curve for the alternate route (paired t test on the distance of each point from predicted curve, P < 0.0001 in both cases). (Insets) Position of feeder (F) relative to edge. (B) Turns induced by edge jumps. Data show mean (± SD) feeder-angle at the end of turns, which were evoked when ants were 70, 40, or 26 cm from the screen. Horizontal dashed line represents 0° feeder-angle for the replacement edge. Solid curve gives the predicted 0° feeder-angle for the same sized stimulus jump, but without switch of edge polarity. Insets show display on LCD screen before and after stimulus jump.
Ants trained to both routes were tested in two ways. To check that the induced turns were appropriate for each tested route, the position of the light-dark or the dark-light edge simply jumped 30° during the route. In most tests, two things happened at the perturbation. The light-dark edge replaced the dark-light edge, or vice-versa, and the position of the edge jumped so as to shift the expected feeder-angle by 30°. These tests demand that the ant suddenly change the route memory that it is using. Does it still recognize the edge away from its desired retinal position and make appropriate corrective turns?
The relation between the feeder-angle immediately after this perturbation and the amplitude of the corrective saccade is shown with the ant at 70, 40, or 26 cm from the LCD screen (Fig. 4B). The data fit the dashed line of 0° feeder-angle better than they fit a prediction that is based on the same-sized edge jump, but with no change in edge polarity (curved lines). The latency of the corrective saccades (mean = 0.35 s, SD = 0.27 s, n = 73) did not differ significantly from those of ants trained to a single route with an inset edge (mean = 0.31 s, SD = 0.28 s, n = 279). When the polarity of the edge is switched, ants seem to be guided immediately by the new edge. Thus, like Drosphila (18), ants can identify a feature at retinal positions that are remote from the learned position of that feature. The additional contribution is that they compute the angular difference between the two positions. For simplicity, we have limited this study to the ants’ responses when following a route controlled primarily by a single feature. But by combining the angular differences generated by several features within a stored view, insects might obtain richer guidance information, such as their proximity to a goal.
Discussion
These data show that ants calculate the difference between the desired and current position of a visual feature, like an edge, and that their turning velocity when correcting their path is related precisely to this difference. Additional experiments are needed to test whether there is an accurate computation of turn-amplitude. The preprogramming of amplitude may well be crude with the precision of the turn's endpoint reliant on visual feedback. The use of such turns to correct errors during landmark guidance gives insects flexibility. It means that they need not allocate all their attention to following a route. They can drift off route a little, while scanning the environment, and now and then make a rapid turn to regain the correct path.
The same general strategy may operate in flying insects in which image-matching can be achieved through changes in flight direction, but with body orientation kept constant (19). The ability to calculate the difference between the desired and current retinal position of a visual feature may be exploited in a variety of ways by different insects. The apparent simplicity of image-matching as a guidance mechanism has provoked a number of computational models of the process (e.g., 11, 20–22). It will be interesting to see how the performance of such models changes if the present findings are incorporated.
Materials and Methods
Insect Handling.
A group of about 40 foragers from laboratory-maintained colonies of Formica rufa L. was marked individually with dots of paint for each experiment. About half the group survived to give useful data. Ants were collected from the nest, placed in the experimental arena for a foraging run, and returned to the nest after each run.
Experimental Set-Up.
A rectangular arena (165 × 390 cm) surrounded by white curtains was positioned in the center of a windowless room lit by high-frequency, fluorescent lamps. The floor of the arena was covered with A0-sized white paper that was frequently rotated, turned over, or changed to minimize the use of odor cues. The arena was placed next to a high-resolution (1,920 × 1,080 pixels) LCD monitor (120 × 67 cm) and raised to be level with the bottom of the screen. A camera above the arena (Sony EVI-D30, Sony Corp.) tracked the movements of individual ants. Data from the camera were captured at 50 Hz and sent to a computer which for each frame extracted the ant's position and orientation of its longitudinal axis (Trackit, Biobserve GmbH). This output controlled the visual display on the LCD screen according to the ant's position in the arena. In all experiments, the LCD screen displayed a vertical dark-light or light-dark edge that extended from the top to the bottom of the screen (SI Text). The approximate horizontal intensity profile of the edge is shown in Fig. S1.
Training Procedure.
Ants learned to approach a microscope slide with a drop of sucrose solution in its central well. In some experiments the well was at the base of the edge and in others it was inset 15 or 5 cm from the edge. Previous experiments (14, 16) show that trained ants follow the same route, whether this inconspicuous feeder is present or absent. In each trial, ants were released into a cylindrical pot (7 cm in diameter) with an exit slit directed toward the LCD screen. The position of this start pot was changed from trial to trial. Training began with approximately 50 trials in which groups of 5 to 10 ants learned to approach the feeder from various start positions. Between each trial, the slide and the edge were shifted in concert to different screen positions. Thus, the starting point, the direction of the route and the endpoint varied with respect to fixed room cues and the edges of the screen. As training progressed, the size of the groups was reduced until ants were trained singly and the approaches of individual ants were recorded and tests introduced. The consistency of the results in Figs. 1 to 4 indicates that the edge was the major determinant of the ants’ behavior and that other visual cues in the room had little influence.
Analysis.
Recorded trajectories were analyzed with Matlab (The Mathworks Inc.). Turns were picked out by eye from plots of the angular velocity of the ants’ longitudinal axis against the ants’ distance from the LCD screen. The start of each turn was identified by a sudden spike in the velocity trace that was greater than 2 SD above the mean (Fig. 1C). The endpoint of the turn (e.g., Fig. 1E) was defined as the moment when the angular velocity fell below 50° per second for at least three frames with < 1° change in orientation. Turn-size is defined as the angular difference in the orientation of the ant's body axis between the turn's start and endpoint. About 10% of the spikes (71 out of 733) did not correspond clearly to identifiable turns and had to be excluded. Either there was no clear drop in angular velocity, or the recording system was noisy. Of the 665 completed test runs with ants trained to a single route, 415 yielded usable saccades; 173 tests failed because the stimulus jumped to a position where the new feeder-angle was < 5° so that no saccade could be detected; on 77 tests there were tracking errors or the end of the turn was ill-defined. We ignored turns that occurred more than 1 s (∼2 SD longer than the mean latency) after the jump (Fig. 3C).
The other variables to be extracted from the data were the horizontal positions of significant features—the edge and the feeder—on the retina. As head movements could not be resolved, the retinal position of the edge was taken as the angle between the ant's longitudinal axis and the edge (the edge-angle). The position of the feeder was given by the angle between the ant's longitudinal axis and the feeder (the feeder-angle). In the SI Text we present data on head movements during turns (Fig. S4). These data suggest that errors introduced by using body orientation to calculate edge-angle or feeder-angle before and after turns reach about 5°.
Supplementary Material
Acknowledgments
We thank Matthew Collett and Mike Land for discussion and comments on an earlier draft, Andy Philippides for Matlab code, and the Engineering and Physical Sciences Research Council Engineering Instrument Pool for the loan of a high-speed camera. Financial support came from the Biotechnology and Biological Sciences Research Council.
Footnotes
The authors declare no conflict of interest.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1006021107/-/DCSupplemental.
References
- 1.von Frisch K. The Dance Language and Orientation of Bees. London: Oxford University Press; 1967. [Google Scholar]
- 2.Menzel R, et al. The knowledge base of bee navigation. J Exp Biol. 1996;199:141–146. doi: 10.1242/jeb.199.1.141. [DOI] [PubMed] [Google Scholar]
- 3.Collett TS, Collett M. Memory use in insect visual navigation. Nat Rev Neurosci. 2002;3:542–552. doi: 10.1038/nrn872. [DOI] [PubMed] [Google Scholar]
- 4.Kohler M, Wehner R. Idiosyncratic route-based memories in desert ants, Melophorus bagoti: How do they interact with path-integration vectors? Neurobiol Learn Mem. 2005;83:1–12. doi: 10.1016/j.nlm.2004.05.011. [DOI] [PubMed] [Google Scholar]
- 5.Collett TS, Collett M, Wehner R. The guidance of desert ants by extended landmarks. J Exp Biol. 2001;204:1635–1639. doi: 10.1242/jeb.204.9.1635. [DOI] [PubMed] [Google Scholar]
- 6.Graham P, Fauria K, Collett TS. The influence of beacon-aiming on the routes of wood ants. J Exp Biol. 2003;206:535–541. doi: 10.1242/jeb.00115. [DOI] [PubMed] [Google Scholar]
- 7.Graham P, Cheng K. Ants use the panoramic skyline as a visual cue during navigation. Curr Biol. 2009;19:R935–R937. doi: 10.1016/j.cub.2009.08.015. [DOI] [PubMed] [Google Scholar]
- 8.Collett M. How desert ants use a visual landmark for guidance along a habitual route. Proc Natl Acad Sci USA. 2010;107:11638–11643. doi: 10.1073/pnas.1001401107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Collett TS, Land MF. Visual spatial memory in a hoverfly. J Comp Physiol. 1975;100:59–84. [Google Scholar]
- 10.Wehner R, Räber F. Visual spatial memory in desert ants, Cataglyphis bicolor. Experientia. 1979;35:1569–1571. [Google Scholar]
- 11.Cartwright BA, Collett TS. Landmark learning in bees. Experiments and models. J Comp Physiol. 1983;151:521–543. [Google Scholar]
- 12.Junger W. Waterstriders (Gerris paludum F) compensate for drift with a discontinuously working visual position servo. J Comp Physiol. 1991;169:633–639. [Google Scholar]
- 13.Åkesson S, Wehner R. Visual navigation in desert ants Cataglyphis fortis: Are snapshots coupled to a celestial system of reference? J Exp Biol. 2002;205:1971–1978. doi: 10.1242/jeb.205.14.1971. [DOI] [PubMed] [Google Scholar]
- 14.Durier V, Graham P, Collett TS. Snapshot memories and landmark guidance in wood ants. Curr Biol. 2003;13:1614–1618. doi: 10.1016/j.cub.2003.08.024. [DOI] [PubMed] [Google Scholar]
- 15.Judd SPD, Collett TS. Multiple stored views and landmark guidance in ants. Nature. 1998;392:710–714. [Google Scholar]
- 16.Harris RA, Graham P, Collett TS. Visual cues for the retrieval of landmark memories by navigating wood ants. Curr Biol. 2007;17:93–102. doi: 10.1016/j.cub.2006.10.068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Lent DD, Graham P, Collett TS. A motor component to the memories of habitual foraging routes in wood ants? Curr Biol. 2009;19:115–121. doi: 10.1016/j.cub.2008.11.060. [DOI] [PubMed] [Google Scholar]
- 18.Tang S, Wolf R, Xu S, Heisenberg M. Visual pattern recognition in Drosophila is invariant for retinal position. Science. 2004;305:1020–1022. doi: 10.1126/science.1099839. [DOI] [PubMed] [Google Scholar]
- 19.Dale K, Collett TS. Using artificial evolution and selection to model insect navigation. Curr Biol. 2001;11:1305–1316. doi: 10.1016/s0960-9822(01)00418-3. [DOI] [PubMed] [Google Scholar]
- 20.Lambrinos D, Moller R, Labhart T, Pfeifer R, Wehner R. A mobile robot employing insect strategies for navigation. Robotics Autonomous Systems. 2000;30:39–64. [Google Scholar]
- 21.Zeil J, Hofmann MI, Chahl JS. Catchment areas of panoramic snapshots in outdoor scenes. J Opt Soc Am A Opt Image Sci Vis. 2003;20:450–469. doi: 10.1364/josaa.20.000450. [DOI] [PubMed] [Google Scholar]
- 22.Möller R, Vardy A. Local visual homing by matched-filter descent in image distances. Biol Cybern. 2006;95:413–430. doi: 10.1007/s00422-006-0095-3. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.