Guidance for Data Collection and Computational Modelling of Regulatory Networks

Abstract

Many model regulatory networks are approaching the depth of characterisation of bacteriophage λ, wherein the vast majority of individual components and interactions are identified, and research can focus on understanding whole network function and the role of interactions within that broader context. In recent years, the study of the system-wide behaviour of phage λ’s genetic regulatory network has been greatly assisted by the combination of quantitative measurements with theoretical and computational analyses. Such research has demonstrated the value of a number of general principles and guidelines for making use of the interplay between experiments and modelling. In this chapter we discuss these guidelines and provide illustration through reference to case studies from phage λ biology.

In our experience, computational modelling is best facilitated with a large and diverse set of quantitative, in vivo data, preferably obtained from standardised measurements and expressed as absolute units rather than relative units. Isolation of subsets of regulatory networks may render a system amenable to ‘bottom-up’ modelling, providing a valuable tool to the experimental molecular biologist. Decoupling key components and rendering their concentration or activity an independent experimental variable provide excellent information for model building, though conclusions drawn from isolated and/or decoupled systems should be checked against studies in the full physiological context; discrepancies are informative. The construction of a model makes possible in silico experiments, which are valuable tools for both the data analysis and the design of wet experiments.

1. Introduction

In our studies of small gene regulatory networks, our model organisms are two temperate bacteriophages, lambda (λ) and the unrelated P2-like phage 186. Both phage make a decision between lysis and lysogeny upon infection of their host Escherichia coli, and contain within their genetic circuitry a module that operates as a bistable genetic switch when isolated and inserted into E. coli. Phage λ’s bistable switch is a paradigm for the molecular basis of epigenetics, and the lysis-lysogeny decision is the most thoroughly characterised model system of developmental decision-making. Both phage λ and 186 are sufficiently well characterised that most key components of the lysis-lysogeny decisions have been identified, allowing research to extend to both the smaller and larger scales, respectively, to detailed characterisation of the molecular mechanisms and to the role of an interaction within the context of a larger network.

Phage allows us to study the organism on all scales, from atomic resolution of proteins to behaviour of the whole organism. We observe the basis of information processing and decision-making at the level of protein–protein and protein–nucleic acid interactions, which often converge at transcription regulation. However, the behaviour of a subset of a genetic regulatory network, even as small as two promoters and two regulatory genes, can display the complexity of behaviour beyond the ability of intuition or qualitative description to fully appreciate. Therefore, our studies of phage frequently require us to apply quantitative experimental methods and mathematical and/or computational modelling in the interpretation of data.

A minority of biochemical and genetic experiments provide data with the qualities necessary for mathematical modelling; a change in the character of experimental data is being advocated by those who see molecular biology progressing to a stage where quantitative and systems-level understanding will be a central component of future progress (1, 2). This lab’s 35 years of experience in phage λ and 186 can testify that as the identification of key components in a system draws to completion, quantitative studies and theoretical analyses are necessary to assemble the data provided by reductionist experiments into a coherent picture of the whole network and to guide future experiments into network function.

2. Data Collection for Modelling

Production of experimental data suitable for mathematical modelling is challenging; for a majority of applications, a large set of highly quantitative data is a must. Furthermore, although data are usually obtained as relative units, expression in absolute units is often valuable, potentially requiring an entirely different experiment for calibration, which again requires quantitative techniques.

We find the following guidelines useful in the production of experimental data suitable for computational modelling.

2.1. Use Quantitative Techniques

Models based upon purely qualitative descriptions of interacting systems will possibly have different solutions capable of describing the same data, and are likely to suffer from a lack of detail and accordingly a lack of predictive power. With quantitative data, the process of fitting a model to the data provides estimates of relevant parameters, sometimes providing information that may not be at all accessible to direct experimental measurement. Production of reliably quantitative data requires replicate experiments, especially when working in vivo.

2.2. Acquire a Large and Diverse Data Set

For a mathematical model to be held in confidence, it must have fewer parameters than the number of independent data points; a large and diverse data set has the greatest chance of delivering an accurate model. Data particularly amenable to modelling include measurements of concentrations or reaction rates, as a function of either time or concentration of a regulatory molecule. Such concentration or time series appear frequently in biological literature, but usually with sparse data, adequate to prove a qualitative point. The inclusion of more frequent or more densely spaced measurements in these studies can easily make data more amenable to computational modelling, from which much more may potentially be learnt about the system.

The ‘diversity’ of a data set is a trait distinct from size, and is also valuable. While it is useful to measure, for example, a time series with many data points, there is a different advantage in measuring that time series under different circumstances, such as with certain components of the system altered or removed. Such changes, particularly mutations, are routine in most biochemical experiments, and they are no less useful when acquiring data for the purposes of computational modelling, as the acquisition of a new data set with one or two parameters altered can be extremely useful for fitting a model to the data.

2.3. Keep Conditions as Close to Physiological as Possible

In attempting to model a process inside a cell, it is of course important that any quantitative measurements needed for the model be performed under conditions as close to physiological as possible. In vivo experiments are ideal, but for many measurements only in vitro techniques are available; in these cases, in vitro experiments performed under conditions most similar to in vivo are most useful. This can be accomplished by the use of physiologically realistic salt concentrations and pH, with the inclusion of macro-molecular crowding agents, and by working at the same temperature as any in vivo experiments.

2.4. Measure Absolute Units or Use Standardised Measurements

Even using quantitative techniques, measurements often only provide relative units, e.g. a fold change is provided in protein concentration or promoter activity. Quantitative techniques may provide only enough data to draw qualitative conclusions. For the construction of a computational model, it is much more desirable to obtain absolute units, e.g. number of proteins per cell, or promoter initiations per minute. Calibration against a known standard will provide this information, which can be immensely valuable in modelling. Beyond assisting your model, providing absolute units provides a reliable way to make quantitative comparisons of data obtained from different laboratories. Such calibrations themselves require quantitative techniques and may require substantial effort; if calibrations are not possible or simply low priority, the use of standardised measurements may at least assist the comparison of data from different laboratories, the difficulty of which has been lamented by the researchers interested in modelling (1).

3. Case Study: Measurement of Prokaryotic Promoters

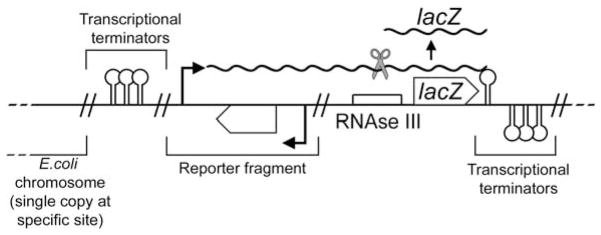
Current techniques for the measurement of prokaryotic promoters provide a good example of the efforts that can be taken to acquire the highest quality of data for computational modelling. Promoter regulation is amenable to quantitative measurement by the placement of a ‘reporter’ gene downstream of a promoter, whose product is easily measurable, and demonstrates minimal interference with cellular behaviour. In E. coli the leading example is the lacZ gene, whose product β-galactosidase is measured in the Miller LacZ assay by the rate of enzymatic cleavage of a chromogenic substrate (3). This assay has been refined to automated kinetic lacZ assays, which provide a highly quantitative technique for the measurement of promoter activity, with sensitivity spanning 4 orders of magnitude (4). Chromosomal single-copy reporters are used to avoid noise due to plasmid copy number variability, by the use of reporters integrated into the E. coli chromosome at a specific phage attachment site, using either phage themselves or a system of plasmids that exploits the integration machinery of temperate phage (5, 6). Transcriptional terminators isolate the region of interest from read-through effects from the surrounding E. coli chromosome (Fig. 15.1). When combining a LacZ reporter with a lactose / IPTG-inducible expression system, lacY (permease) should be deleted to avoid feedback from transcription (output) to transport of the inducer (input) (7). It is worth noting that chromosomal single-copy reporters, long used in E. coli, have recently been implemented in mammalian cell lines (8).

Fig. 15.1.

Schematic diagram of chromosomal single-copy lacZ reporter. Double slashes indicate junctions between DNA of different origin.

Transcriptional fusions to lacZ are used to enable the placement of an RNAseIII site preceding the lacZ gene, such that all lacZ transcripts are cleaved between their start sites and the LacZ coding sequence (Fig. 15.1). This yields a standardised measurement, as lacZ transcripts of identical length and sequence are produced from any promoter, providing mRNA translation efficiencies and half-lives, which are promoter and context independent(9). By using a standardised assay, promoter activities measured by this assay are directly comparable to any prokaryotic promoter assayed, provided the host strain and its growth conditions are kept constant. Translation regulation can be studied by LacZ assays through the use of translational fusions to lacZ (5). Translational fusions to lacZ also can provide information on the efficiency of translation from a given message and ribosome-binding site, subject to the limitation that fusion of a protein to LacZ may alter its activity and fusion of a transcript to the lacZ coding sequence may alter mRNA stability.

For the purposes of computational modelling, LacZ units can be converted into the absolute units of RNA polymerase initiations / minute, by the work of (10), whose exhaustive study of constitutive promoters in E. coli characterised the RNA polymerase initiation rate from a range of promoters, as a function of growth rate. Any given quantitative assay of promoter activity can be calibrated with the measurement of one or more of the promoters studied by (10).

In cases where an inducible promoter provides a variable supply of protein, quantitative western blotting allows for the conversion of inducer concentration to protein concentration (an absolute unit), given knowledge of the cells’ internal volume and a protein standard of known concentration. A protein standard can be obtained from purified protein or from some fixed internal supply of protein, such as is common in measurements of the λ lysogenic repressor CI, where the steady concentration present in a lysogen (Wild-type Lysogenic Unit = W.L.U.) is taken as a point of reference.

4. Experiment Design for ‘Bottom-Up’ Modelling

Molecular biology has made enormous strides with the reductionist approach: ‘The idea is that you could understand the world, all of nature, by examining smaller and smaller pieces of it. When assembled, the small pieces would explain the whole’ (11). ‘Bottom-Up’ modelling is the technique of assembling these small pieces of information into the whole, and accordingly for the typical molecular biology laboratory, this is the most useful way to incorporate theoretical methods into an experimental program. In contrast, ‘top-down’ modelling involves models based on global data sets such as whole genome or proteome expression profiles, for which theoretical analyses are an absolute necessity. A general investigative procedure that may be of assistance to experimentalists considering the incorporation of bottom-up modelling follows (Fig. 15.2).

Fig. 15.2.

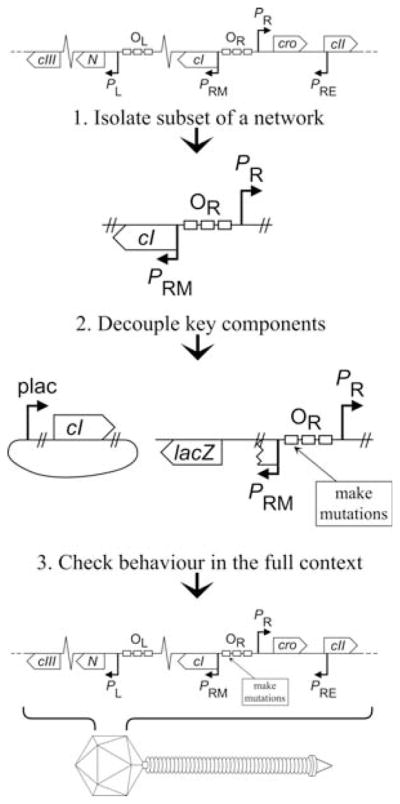
Generalised experimental procedure facilitating bottom-up modelling. Illustrations are derived from the case study of 5.1.

4.1. Isolate Subsets of a Network

While not always possible, if a small subset of a network can be identified and studied in isolation from its full natural context, detailed characterisation of components and their interactions is greatly assisted. Though this does not provide all physiologically relevant information about the isolated components, such as their responses to now absent inputs, the more thorough characterisation that can be achieved with a smaller and less complex system provides an excellent foundation for subsequent expansion to a larger system. A subset of a network need not necessarily be a ‘module’ in the sense of an independently functioning unit: there may be value even in dissecting the system beyond the point of functionality.

Studies of temperate bacteriophage have the rare privilege of being able to isolate components, e.g. the bistable switch, and express them within their usual cytoplasmic environment, e.g., E. coli, in the absence of any other transcribed phage genes. For many areas of research, the techniques for isolation of a system while remaining in vivo do not yet exist, making in vitro reconstitution the best procedure available. It is reasonable to expect though that in time the technologies will be developed which will allow for subsets of biochemical networks to be isolated and studied under in vivo conditions; the history of phage λ research demonstrates the value of these technologies.

4.2. Decouple Key Components

Where a complex system is able to settle into one or more stable states, probing the conditions of these states provides much less information than can be obtained with a method of probing the full continuum of states, which exist when the system displays dynamic behaviour or switches between stable points. An experimental approach to achieve this is to decouple key regulatory components, i.e., remove them from the context of their usual control mechanisms, and make their concentration or activity an independent experimental variable.

With regulatory proteins or stimuli controlled experimentally, they can be varied independently over the physiologically relevant scope, potentially spanning the entire range from ‘knock-out’ to overexpression. Detailed measurements over this range will be much more informative than the measurement of stable states or extremes only. In particular, this approach is an ideal way to succeed in the advice mentioned in Section 2.2.

Finally, feedback is a common theme in dynamical systems of sufficient complexity to justify a modelling approach; gene regulatory networks and signal transduction pathways have shown themselves to be prime examples. Even small systems may exhibit complex behaviour specifically due to feedback, which can complicate the interpretation of experimental results. Removal of feedback mechanisms by decoupling of a feedback-regulated component may both simplify data analysis and expose the purpose of feedback when compared to the non-decoupled behaviour.

4.3. Check Behaviour in the Full Context

It is in vivo behaviour that we ultimately aim to understand, and all interactions observed in a smaller subsystem exist to serve a greater purpose within an entire cell or organism. Therefore, it is of critical importance that any conclusions drawn from studies of isolated and/or decoupled systems be checked against the behaviour observed in the full physiological context. The return to wild-type can be taken in steps, beginning with the restoration of regulatory links that may have been removed in the process of decoupling (as described above in investigating feedback), prior to returning to the study of the subsystem within its full physiological context.

We find it highly productive to characterise the effects of mutations upon both the isolated subset and the whole organism. If the effect of a mutation on the isolated subset does not explain the mutation’s phenotype in the physiological context, a clue is provided to the discovery of new components or interactions that were excluded from the previously chosen subset. The physiological role of long-range DNA looping in phage λ was found by just such an observation; this example is detailed in Section 5.1.

A noteworthy alternative is the ‘module-replacement’ approach developed by Little and Atsumi, wherein a regulatory factor and the cis-acting sites to which it binds (collectively a module) are replaced by an equivalent exogenous factor and its cognate binding sites (12, 13). The module-replaced system can in principle be characterised both as an isolated subset and in the whole organism. Firstly, this technique will check assumptions about the properties and functions of the regulatory module, by assessing whether the replacement module indeed provides functionality; failure may indicate that more has been removed than is appreciated. Secondly, the inserted module can be engineered to exclude one or more features, such as a specific binding site, much more easily than its wild-type counterpart; all that is necessary is to not add a feature, rather than removing a pre-existing feature.

4.4. Model Building

When a molecular system is characterised to the extent that most components have been identified and hypotheses have been developed about interactions between components, bottom-up models can be built by assembling the known or suspected interactions into a deterministic or stochastic model. Competing models can be built containing different sets of interactions or molecular mechanisms, and their ability to explain the quantitative experimental data will assist in the discrimination between models.

4.4.1. Modelling Techniques

The choice of modelling technique is of significance to both the accuracy and the educational value of the model. For relatively simple systems, an analytic model can be constructed, that is, a simple set of descriptive equations, while increasingly complex systems will require such approaches as the use of the partition function from statistical thermodynamics, or modelling with ordinary differential equations (ODEs). In our experience, time-series data is best described by ODEs, and the partition function is most useful for explaining data expressed as a function of the concentration of some component. All these techniques are deterministic: they do not account for statistical fluctuations in concentrations and rates, or ‘molecular noise’, which is increasingly appreciated as an important factor in the behaviour of biochemical systems (14). Therefore, even where modellers provided with perfect and complete information about a system, a stochastic simulation would be the only way to produce accurate data. However, deterministic methods remain very worthwhile due to their greater educational value: inspection of analytic equations can make immediately clear the relevance of parameters and can highlight important relationships between components, and deterministic models can easily produce graphical comparisons of parameters, e.g. oscillation frequency versus half-life of an mRNA, through the use of mathematical computing packages. Stochastic simulations are in general computationally demanding, and parametric plots will require a simulation at every desired point on the graph, which may be simply too time-consuming. We find a combination of deterministic and stochastic modelling to be most useful, initially modelling with deterministic techniques to gain insight into the system’s behaviour and the underlying principles of the model, and finally turning to stochastic simulation for accuracy in the final stages of parameter and data fitting. To give a specific example, our laboratory and colleagues developed a mathematical model of transcriptional interference in E. coli, which contains three implementations: analytic, ‘mean-field’ (probabilistic), and stochastic, the three techniques producing similar but not identical output (15). The development of this model benefited greatly from the combination of approaches, each providing unique contributions to our understanding of the system.

4.4.2. Level of Detail

The level of detail included heavily influences the educational value of a model. A model with an excessive number of parameters might be able to be made to fit any data set, destroying the ability to discriminate between alternative hypotheses. Conversely, it is important for all biologically relevant behaviour to be included; the dismissal of one seemingly unimportant feature may render a model irredeemably inaccurate. In an interdisciplinary team, proficient communication between modellers and experimental biologists is necessary for the important decisions of which features are of relevance to the model, and which can be discarded. The choice of detail is especially significant to modellers of biology, as here we face a problem: biochemical systems feature an extraordinarily large number of parameters relative to most physical or chemical systems, thus the inclusion of exhaustive detail in a model may require impossibly extensive experimental investigation to provide the necessary parameters. Much may be omitted without a loss of validity, e.g. a promoter could be characterised in terms of protein production rate, without including mRNA production, translation, and degradation; but if mRNA regulation is a significant feature of the system, this detail may be vital.

4.4.3. Parameter Fitting

Given the number of parameters that are likely to exist in any biological model, it is unlikely that each one has been experimentally measured, requiring parameters to be selected on the basis of those values that allow the model to reproduce experimental data: the process of parameter fitting. This is a procedure performed more easily with deterministic than stochastic models, though it may be found that parameters selected to fit a deterministic model may require adjustment when shifting to stochastic simulation (16). If data have been obtained from replicate experiments, the knowledge of confidence limits at each point is of assistance to the fitting process, as individual data points can be weighted according to the precision of their measurement, by minimising

$${\chi }^2=\sum _i{\left[\frac{{(\text{experimental}\text{value})}_i-{(\text{model}\text{value})}_i}{{(\text{experimental}\text{confidence}\text{limit})}_i}\right]}^2.$$

A model may be held in greater confidence when only a small number of parameters need be fitted to the data. Indeed, with many fewer parameters than data points and a conceptually sound model, the process of fitting the model to the data can itself constitute an accurate method of measuring those parameters. The process of parameter fitting can be assisted by the examination of literature for other measurements or estimates of your parameters, and by checking that fitted parameters produce biologically reasonable values. The process of parameter fitting can itself be an investigative tool: fits that produce unreasonable values may need adjustment, or may in fact be highlighting failures in the model or mistaken assumptions. Biological systems have demonstrated clever techniques to circumvent physical laws, such as the use of dual operators in the lac operon, providing the Lac repressor with an effective association rate to a single operon that is apparently faster than diffusion (17); a fit that provides a physically or biologically unreasonable value just might be a clue to an exciting discovery.

4.4.4. Discrimination Between Alternative Hypotheses

After the construction of a basic framework for a model, a large number of alternative hypotheses can be incorporated into the model and assessed by their ability to fit experimental data while selecting realistic parameters. This may highlight some hypotheses as worthy of direct experimental investigation, while hypotheses incapable of satisfactory fits can be ostensibly discarded, until such time as new data are acquired or the model is revised.

4.4.5. Long-Term Development of a Model

Over the course of a prolonged investigation into a system, the data available for modelling gradually builds, which places an increasing demand on the accuracy of the model: it should be fully consistent with all relevant data. Successfully obtaining a precise match between theory and experiment will become increasingly challenging, but correspondingly the confidence that a successful fit reflects on an accurate model will also increase. With more data to place constraints on a model and fewer parameters in need of fitting, the ability to discriminate between alternative hypotheses improves, increasing the educational value of the model.

4.5. Make Predictions with In Silico Experiments

Theorists may be content to have produced a model that adequately explains all data available for a given system, but for the experimentalist the principal value of a model lies in the ability to guide the choice and design of future experiments. A model can be altered to include whatever changes to the system may be planned for future experiments, such as the introduction of mutations or additional components, or if appropriate a model may be applied to a new system. The predictions of the model constitute an in silico experiment; and if the investigators have adequate confidence in the accuracy of the model, based on fits to past data, then the most interesting of these predictions can make excellent targets for wet experimental investigation.

Provided a respectable model is available, in silico experiments are well worth the effort, especially given how little effort they take: typically orders of magnitude less time and money than the identical wet experiment. In silico experiments can suggest which future experiments are likely to reveal the most useful information; when working quantitatively, in silico experiments may demonstrate that a particular perturbation to the system is unlikely to produce a sufficiently large change in the measured variable(s) to answer a question. This may guide the experimentalists to an improved choice of perturbation, potentially saving much time and effort. When a model contains ambiguity, i.e., two or more theories of significant difference that equally explain previous data, it may be valuable to design experiments that distinguish between these alternatives: here in silico experiments, performed with competing models, are invaluable. Finally, certain changes to the system under study may produce emergent behaviour that would elude the intuition: in silico experiments can reveal such features and direct the investigator to experiments that may otherwise have been discarded as uninteresting.

A large pool of possible wet experiments can therefore be assessed by in silico experiments to select the most promising and make predictions about results. These results are then almost certain to be very interesting: should the model’s prediction be correct, there is value in both the result itself and in the predictive power of the model. Should a model fail to anticipate the experimental findings, the previous theoretical understanding of the system has been challenged, and new hypotheses need be incorporated into models in the effort to explain these results. In silico experimentation is a good way to identify the wet experiments most likely to refute an accepted hypothesis and ‘prove yourself wrong’, to drive the development of new theories.

4.6. Introduce New Components

A reasonable benchmark for understanding of the chosen subsystem is the ability of a model to quantitatively explain all available data, preferably including ‘diverse’ data such as the behaviour of mutants in addition to the wild-type system. Having elucidated the roles of components and their interactions in a chosen subsystem, the system of study can be enlarged to include more components or more inputs / outputs. A quantitatively characterised and understood subsystem provides a theoretical framework of great value to subsequent expansion of the system under study, which is likely to make the identification of new components and new interactions easier than was the initial characterisation of a subsystem.

5. Case Study: Promoter Regulation in Phage λ

In this section we use phage λ research to illustrate the principles of experimental design that facilitate the incorporation of ‘bottom-up’ modelling into an investigative program, and to provide examples where modelling has provided information inaccessible by other means. In particular, we focus on research into promoter regulation, which we find to be a nexus of decision-making, the product of numerous inputs, and thus a valuable position to probe the behaviour of a system.

5.1. Design of Experiments

In our studies of transcription regulation in temperate bacterioph-age, thorough quantitative characterisation of interactions is instrumental in understanding network function. Therefore, we typically aim to measure the response of each promoter to the full physiological range of all components relevant to its regulation. However, there are too many interacting components to deconstruct behaviour within the whole organism into knowledge of individual interactions, and it is therefore necessary to isolate subsystems of interest.

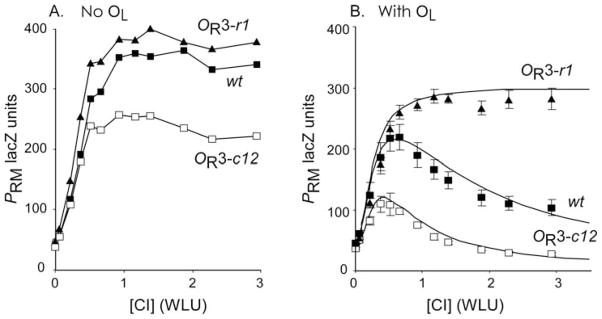
An example of such a subsystem that has been studied by many labs including our own is the autoregulation of the P_RM promoter by its own product CI. P_RM is part of the Right Operator (O_R) of phage λ, which contains three adjacent CI dimer-binding sites, O_R1, O_R2, and O_R3, with decreasing affinity for CI dimers. At the strongest binding site O_R1, CI represses P_R; at O_R2 CI also represses P_R, and activates P_RM by cooperative binding to RNA polymerase; at the weakest binding site O_R3, CI represses P_RM. Within the whole phage, the positive and negative feedback of this small system is complicated by the many other features, such as transcription of cI from P_RE, and Cro, which also binds to O_R1, 2, and 3. Therefore, to quantitatively investigate this autoregulation, the cI gene and O_R with its promoters P_R and P_RM need to be examined in isolation. This can be accomplished by placing the relevant region of phage λ into the E. coli chromosome as a single-copy reporter (isolation of a subsystem; Fig. 15.2, Step 1). Furthermore, to study the response of P_R and P_RM to a range of CI concentrations, cI is not placed downstream of P_RM, subject to autoregulatory control, but placed on a plasmid under the control of an inducible promoter (decoupling key components; Fig. 15.2, Step 2), with lacZ replacing cI downstream of P_RM. By varying the concentration of inducer, the response of P_RM to a wide range of CI concentrations can be examined in detail. To further understand the properties of CI autoregulation, measurements of P_RM activity were also performed in the presence of mutations to O_R3, which strengthen (c12) or abolish (r1) CI binding (acquiring a diverse data set). These experiments showed that P_RM was not repressed even at high CI concentrations, and that the r1 and c12 mutations had very little impact on P_RM activity (Fig. 15.3), indicating that CI association to O_R3 and repression of P_RM was not influential to this system (4).

Fig. 15.3.

(A) Activity of wild-type and mutant P_RM promoters in the absence of O_L. Reproduced from (4). (B) As (A) but in the presence of O_L. Points with error bars show 95% confidence limits of experimental measurements. Solid lines represent the result of physicochemical modelling of CI regulation, incorporating O_R–O_L long-range interactions. Reproduced from (19).

These findings in the isolated system were compared with results obtained in the whole phage, by introducing the r1 and c12 mutations to λ phage (checking behaviour in the full context; Fig. 2, Step 3). These mutations revealed phenotypic changes in the process of UV induction of lysogens, wherein CI is degraded in response to UV-induced DNA damage resulting in lysis of the host and release of phage. The r1 mutation, which makes little change to Cro association to O_R3 but substantially weakens CI binding, produced defective UV induction, while the c12 mutation, which strengthens CI association and weakens Cro binding to O_R3, induced more readily. This suggested higher [CI] in the r1 lysogen and lower [CI] in the c12 lysogen, subsequently confirmed by experiment, indicating that these mutations did indeed alter P_RM activity, despite the apparent lack of effect on isolated P_RM (4).

Drawing on previous observations that CI can mediate DNA loops between O_R and the Left Operator (O_L) (18), it was reasoned that the discrepancy between studies of whole phage (as lysogens) and of isolated P_RM was the presence of O_L. The introduction of O_L to the isolated P_RM lacZ reporters revealed substantial repression of P_RM at physiological CI concentrations, confirmed by enhancement of repression in a c12 mutant and lack of repression in an r1 mutant (4) (Fig. 15.3). This experimental procedure was able to extract from a complex network that O_R to O_L DNA looping plays a critical role in the regulation of P_RM, and produced data of a quality enabling a thorough statistical mechanical model of this process. Subsequent work not detailed here confirmed a model in which CI bound to O_R1 and O_R2 forms an octamer with CI at O_L1 and O_L2, forming a long-range DNA loop, allowing a CI tetramer to form from dimers at O_R3 and O_L3, stabilising occupation of O_R3 and P_RM repression (19) (Fig. 15.4).

Fig. 15.4.

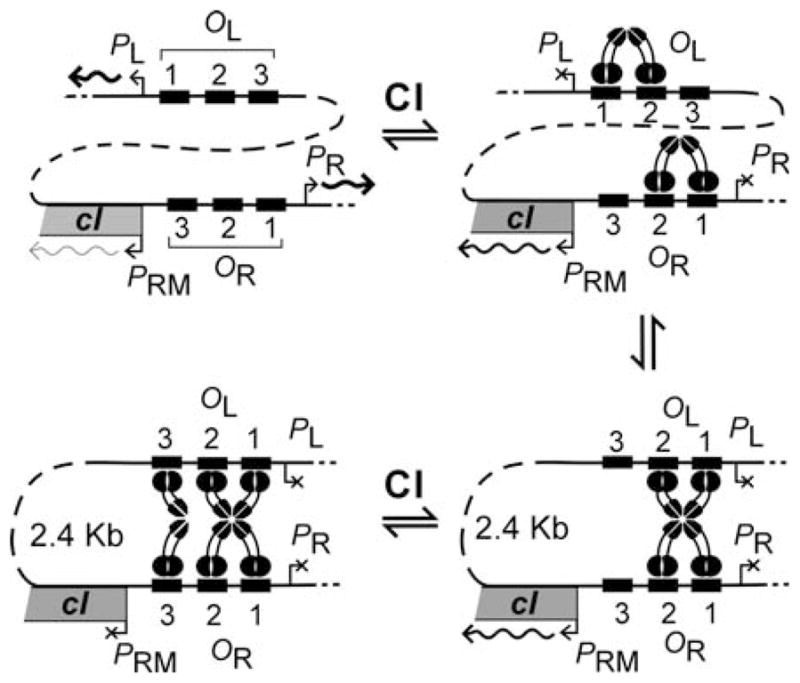
Model of CI regulation with long-range DNA looping. Cartoon depicting the major predicted CI: DNA complexes at O_R and O_L on the λ chromosome and their effects on transcription as CI concentration increases. Reproduced from (19).

5.2. Computational Modelling of Data

The wealth of thermodynamic data on CI association to operators in O_R and O_L permitted the description of the system by the partition function, which relates the probability of a system to exist in state ‘i’, P_i, to the standard free energy of that state, ΔG_i, through

$$P_i\propto exp\left(\frac{-\mathrm{\Delta }{G}_i}{RT}\right),$$

where R is the gas constant and T is the temperature in Kelvin. Degeneracy must be explicitly accounted for, e.g. when modelling the binding of repressors to operators, a state containing ‘n’-bound repressors requires an additional factor of (number of repressors)ⁿ, as the same state can be composed in this number of different ways, each known as a microstate. Hence

$$P_i=\frac{{[\text{repressor}]}^{n_i}exp\left(\frac{-\mathrm{\Delta }{G}_i}{RT}\right)}{Z},$$

where Z is a normalisation factor known as the partition function:

$$Z=\sum _i{[\text{repressor}]}^{n_i}exp\left(\frac{-\mathrm{\Delta }{G}_i}{RT}\right)$$

Previous measurements of CI affinity for all six operators at O_R and O_L, as well as cooperative CI interactions between adjacent dimers, permitted the creation of a partition function describing all possible combinations of CI binding, as well as long-range DNA looping between O_R and O_L. By detailing the prevalence of each species present at any [CI], it is possible to fully describe P_R and P_RM activities as a function of [CI]. The experimental data to be fitted by this model were measurements of P_R and P_RM activities as a function of [CI], with and without O_L, and also with r1 or c12 mutations at O_R3. Out of 29 parameters in this model (free energies of CI association / cooperativity, and basal / activated / repressed promoter activities), 26 had been explicitly measured, leaving only 3 degrees of freedom with which to fit the model to data. These three parameters were the strength of non-specific DNA binding by CI, the free energy of formation of a long-range DNA loop maintained by a CI octamer bound to O_R1, O_R2, O_L1, and O_L2 (ΔG_oct), and the free energy of formation of a CI tetramer across O_R3 and O_L3 (ΔG_tet), which is reasoned to only form once the DNA loop has been stabilised by octamer formation. This model was able to accurately reproduce all data, but for an overestimate of P_R repression at low [CI], lending strong support to the model of O_R-O_L DNA looping and its role in pRM autoregulation (19).

The full implications of this research are discussed in more detail elsewhere (4, 19–21); here is described two key conclusions that were provided solely by the thermodynamic model. Describing the prevalence of each species as a function of [CI] demonstrated that the lysogenic CI concentration lies precisely at the point of the sharpest transition between states of active P_RM and of repressed P_RM; therefore, the lysogenic state appears poised to produce the most sensitive response in P_RM activity to dampen fluctuations in [CI], providing optimum stability and resistance to molecular noise. Computational modelling thus provided the means to make this striking observation of network architecture, which could not have been directly acquired from the experimental methods of this study: it was necessary though to acquire data of a quality enabling modelling. By fitting ΔG_oct and ΔG_tet to P_RM activities (Fig. 15.3), it was possible to estimate the in vivo free energy of DNA looping between operators 3.8 kb apart. This combination of quantitative experimental data and a partition function to produce a thermodynamic model is the only technique that has yet produced in vivo measurements of the energetics of DNA looping. This technique has been used to probe the in vivo mechanical properties of DNA in work, which challenges prevailing models of DNA (22).

The same approaches to experimental design and data collection described in this case study do not necessarily require a system as extensively characterised as λ in order to facilitate computational modelling. Similar approaches were applied to the study of transcriptional interference between two promoters in phage 186, for the purpose of characterising the molecular mechanisms of interference (23, 24). On the basis of the diverse set of standardised, quantitative, in vivo data collected, a general mathematical model of transcriptional interference by RNA polymerase traffic in E. coli was developed (15). This model was able to accurately explain all data in the studies of (23), and further enhanced our understanding of the mechanisms of interference observed in this and other studies. Our laboratory is currently using a combination of in vivo and in silico experiments to discriminate between different hypotheses for the transcriptional interference observed in other systems, where the model is demonstrating significant predictive power. As demonstrated, a variety of experimental programs in our laboratory have benefited from bottom-up computational modelling, whose application has been facilitated by the approach to experimental design and data collection described here. We therefore expect that these principles can find widespread utility in the study of regulatory networks, in enabling the construction of bottom-up computational models and their use as experimental tools.