A device for the measurement of residual chemical shift anisotropy and residual dipolar coupling in soluble and membrane-associated proteins

Abstract

Residual dipolar coupling (RDC) and residual chemical shift anisotropy (RCSA) report on orientational properties of a dipolar bond vector and a chemical shift anisotropy principal axis system, respectively. They can be highly complementary in the analysis of backbone structure and dynamics in proteins as RCSAs generally include a report on vectors out of a peptide plane while RDCs usually report on in-plane vectors. Both RDC and RCSA average to zero in isotropic solutions and require partial orientation in a magnetic field to become observable. While the alignment and measurement of RDC has become routine, that of RCSA is less common. This is partly due to difficulties in providing a suitable isotopic reference spectrum for the measurement of the small chemical shift offsets coming from RCSA. Here we introduce a device (modified NMR tube) specifically designed for accurate measurement of reference and aligned spectra for RCSA measurements, but with a capacity for RDC measurements as well. Applications to both soluble and membrane anchored proteins are illustrated.

Introduction

Residual anisotropic interactions, such as residual dipolar coupling (RDC) and residual chemical shift anisotropy (RCSA), contain rich structural and dynamic information (Bax 2003; de Alba and Tjandra 2004; Prestegard et al. 2004). RDC is usually manifested as a small perturbation upon a much larger scalar (J) coupling. Since the J coupling is relatively insensitive to chemical environmental factors such as pH, buffer compositions and temperature, RDC can be reliably extracted from differential line-splitting in isotropic and anisotropic media. RCSA is measured as the resonance frequency shift between isotropic and anisotropic conditions. Unfortunately, the chemical shielding tensor is very sensitive to environmental conditions, and therefore it is difficult to distinguish the RCSA shift due to weak alignment from shifts due to slight variations in the chemical environment. The key to accurate RCSA measurement is conducting shift measurements under isotropic and anisotropic conditions while keeping other environmental conditions as identical as possible. There are several existing ways of achieving this but each has certain limitations. Most common RCSA measurements have relied on the temperature-dependent phase transition of certain lipid-based liquid crystals. Lack of order at a lower temperature provides for a measurement under isotropic conditions and field induced order at a higher temperature provides for measurement under aligned conditions (Cornilescu et al. 1998; Cornilescu and Bax 2000; Lipsitz and Tjandra 2001; Wu et al. 2001; Bryce et al. 2005; Burton and Tjandra 2006; Hansen and Al-Hashimi 2006; Ying et al. 2006; Yu et al. 2007). Here inherent variations of chemical shifts with temperature present a referencing problem, although the fact that elements of the chemical shielding tensor have a simple linear temperature dependence can provide a correction. Another approach for RCSA measurement is to tune the amplitude of alignment by varying the concentration of alignment agents such as phage and or alkyl polyethylene glycol detergents (Burton and Tjandra 2006). In this case, measurements can be conducted at the same temperature, but the chemical shift changes due to solvent effects need to be corrected. The extraction of RCSA has also been achieved using magic-angle spinning (Grishaev et al. 2009). In this case, rotation at the magic angle removes the anisotropic shift and provides an isotropic reference, but special magic angle spinning hardware is required. An ideal RCSA measurement is also possible for molecules that exhibit significant field-dependent alignment (Ottiger et al. 1997), such as DNA/RNA and paramagnetic-ion binding proteins. In these cases the magnetic field can be changed to scale the effects of RCSA, but the resulting changes in chemical shift can be quite small. Here we show that RCSA and RDC can be conveniently and accurately measured using two states of a stretched polyacrylamide gel, an alignment medium that is widely applicable to both soluble and membrane proteins (Sass et al. 2000; Tycko et al. 2000; Cierpicki and Bushweller 2004; Cierpicki et al. 2006). Variations in solvent and temperature conditions are minimal, and only a specially modified NMR tube is required. With this device isotropic and anisotropic experiments can be conducted on a single sample under virtually identical conditions.

The utility of the device is demonstrated through the measurement of C’, N, and HN RCSA and N-HN RDC for the myristoylated yeast ARF1·GDP protein (~21 kDa) and the myristoylated yeast ARF1·GTP·bicelle complex (~70 kDa). The ARF1 protein (ADP ribosylation factor 1) is an N-myristoylated GDP/GTP switch protein that plays important roles in membrane trafficking (D’Souza-Schorey and Chavrier 2006; Kahn 2009). The tendency of this protein to interact with lipids limits choices of alignment media, making polyacrylamide gels one of a few possible selections. Polyacrylamide gels can be cast at densities that provide open aqueous cavities in which macromolecular assemblies can tumble isotropically. When the gel is stretched these cavities become asymmetric and collisions with the boundaries impart the low level of molecular alignment needed for RCSA and RDC measurement. The size of the ARF1·GTP·bicelle complex also dictates per-deuteration of the protein and a need to optimize collection of data at backbone sites using measurements such as RCSA and RDC.

The value of complementary measurement of RCSAs and RDCs is clear. RDCs are most commonly measured from the additional splittings in doublets produced by directly bonded and coupled pairs of ¹⁵N and ¹H nuclei in amide bonds of proteins and polypeptides. The observables are interpreted in terms of an angular restraint of the N–H bond relative to the magnetic field, more specifically, a sum of products of direction cosines relative to a molecular frame and an order tensor for that frame (Prestegard et al. 2004). Additional RDCs are available from coupling of other nuclear sites in the amide plane. However, it is very important to generate constraints on vectors perpendicular to the amide plane. RCSAs can provide these constraints (Sitkoff and Case 1998). They in fact display very similar angle dependence to an RDC, but the constraint is on a CSA principal axis system, with respect to a molecular fixed frame, rather than a single bond with respect to that frame. The device presented, and the application protocols described, can provide these valuable constraints.

Materials and methods

NMR tube design and sample preparation

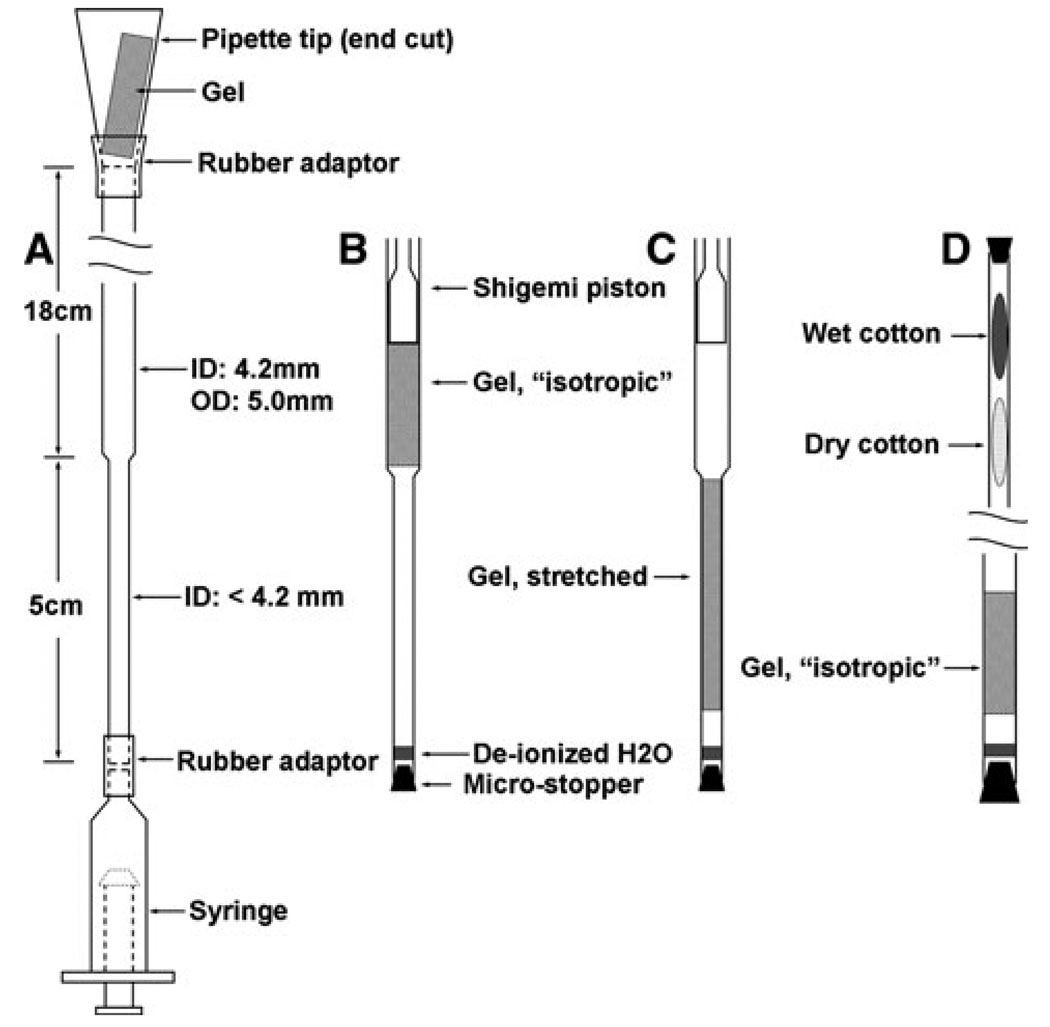
Casting a polyacrylamide gel with a diameter slightly larger than that of an NMR tube, swelling the dried gel in a buffer solution containing protein, and squeezing the gel into an NMR tube is one of the most commonly used procedures for achieving partial alignment of proteins for NMR measurements (Chou et al. 2001). The isotropic reference is usually provided through observation of the protein in buffer, but in the absence of polyacryamide. This procedure is adequate for RDCs, but not for RCSA measurement in the following cases: (1) the protein has a tendency to interact with the gel; (2) chemical shifts are sensitive to protein concentration (such as in weak oligomers) or buffer concentration, since the gel matrix will alter these concentrations; (3) gels, particularly charged gels, can affect local buffer pH. Our device builds on previous polyacrylamide gel procedures, but incorporates a two stage tube that allows both isotropic and aligned measurement on the same polyacrylamide sample. The NMR tube design is shown in Fig. 1a. The salient feature is that it contains an upper portion and a lower portion with different inner diameters. The upper portion has an i.d. of 4.2 mm while the lower portion has a smaller i.d. for gel stretching. The protein sample absorbed in a polyacrylamide gel is sucked in from the upper opening using a 10 ml syringe connected to the lower opening through a rubber tube. A 1 ml pipette tip is used as a funnel to deliver the gel through the upper opening. The sharp end of the pipette tip is cut off so that the diameter of the tip opening roughly matches that of the upper opening of the NMR tube, i.e. 4.2 mm. A short rubber tube is used to connect the tip funnel to the upper portion of the NMR tube.

Fig. 1.

The two-stage NMR tube for RDC and RCSA measurement and accessories for sample loading. The inner diameter of the lower portion can be adjusted during the manufacture stage according to the size of the molecule to be aligned

The gel sample is first situated right above the narrow portion for “isotropic” measurement (Fig. 1b). Afterwards, the gel is sucked into the narrow portion for anisotropic measurement (Fig. 1c). RCSAs and RDCs are extracted from the chemical shift differences and resonance splittings (or intensity modulation), usually measured from positions of cross-peaks in HSQC and/or TROSY spectra, under these two conditions. It should be mentioned that mild gel stretching may be encountered for the initial “isotropic” measurement and therefore the “isotropic” values obtained may not reflect the real J couplings or isotropic chemical shifts due to small contributions from anisotropic interactions. However, this background alignment is harmless for RDC and RCSA measurement because one is only concerned that all molecular sites reflect the same alignment tensor, and the difference of two traceless and symmetric alignment tensors produces a third tensor of equal utility in this respect.

Proper tube sealing is important to prevent evaporation during NMR experiments, particularly for the lower opening which faces the air-flow for temperature control. The lower end is sealed with a small amount of de-ionized water to prevent sample evaporation and then a micro-rubber stopper (Fig. 1a). To seal the upper opening, a 5 mm Shigemi piston is inserted and fastened with Teflon tape. The susceptibility-matched Shigemi piston can also be used to facilitate shimming if sample length is limited. For this purpose, the piston should be inserted until its bottom surface completely contacts the upper surface of the gel. Sample length is not a problem during the anisotropic measurement since the gel is stretched in the lower portion.

It must be pointed out that measurement in the isotropic state requires positioning the tube with the narrow portion extending well beyond the normal tube insertion limits of some NMR probes. Some cold probes and probes that accommodate flow cells allow this, but probes with temperature sensors or other components directly below the sample may be damaged by exceeding insertion limits. For those probes, an alternative mode of “isotropic” data acquisition can be utilized as depicted in Fig. 1d. The NMR tube is placed “upside down” with the gel located near the end of the wide opening. Deionized water and a micro-rubber stopper are used to seal the end. If the gel length is shorter than 2.3 mm, a susceptibility matched plug can be stuck in from the bottom of the gel to facility shimming. The total length of the wide portion is long (18 cm) so that a regular 5 mm spinner can be used to hold the NMR tube in the magnet. The narrow opening is first filled with a piece of dry cotton and then a piece of wet cotton. The wet cotton prevents the gel from drying during the “isotropic” measurement, and the dry cotton prevents water from leaking onto the gel. The very end is also sealed with a micro-rubber stopper. Before the gel is sucked into the narrow portion for the aligned measurement, the cotton is removed by a syringe needle. Residual water on the inner wall is automatically removed as the dry cotton is taken out.

There may also be a concern about a potential sample temperature difference between the “isotropic” and aligned conditions, since the temperature controlling air flow can be affected by the NMR tube position which is different for the two measurements. To examine sample temperature stability, we filled the NMR tube with ethylene glycol and recorded temperatures with the upper and lower portions centered in the probe coil, respectively. The temperature differences between the two configurations are 0.20, 0.14, and 0.05°C with sample temperatures at 11, 24, and 32°C, respectively. Using a 0.14°C temperature change, upper limits for temperature induced H and N chemical shift variations are estimated at 1.54 and 3.36 bbp, respectively (Ottiger et al. 1997). A temperature uncertainty of this order is not expected to significantly affect RCSA measurement by our device.

To prepare the polyacrylamide gel, a mixture of 5% acrylamide (or mixture of acrylamide and its charged derivative)/ N,N′-methylenebisacrylamide (19:1), 0.1% freshly made ammonium persulfate (APS, (NH₄)₂S₂O₈), and 0.5% tetramethylethylenediamine (TEMED) diluted in 10 9 TBE buffer (0.9 M TRIS, 0.9 M borate, 0.02 M EDTA, pH 8.4) for a total volume of 490 µL is injected into a glass tube of 4.5 mm inner diameter and a length of 40 mm. Polymerization is complete over night and the gel is removed from the mould under hydraulic pressure using a 1 ml pipetter with the sharp end of the pipette tip cut off. The gel is then washed in deionized water four times over a period of 2 days. The diameter of a 5% gel reaches 5 mm after washing. The gel is then cut with a razor blade to a diameter: length ratio of 1:5.7. Finally the gel is placed on a Teflon coated baking plate at ambient temperature until it dehydrates completely. Due to the time involved in such preparations, it is advisable to make several gels at one time. The dried gels can be kept at ambient temperature for later use.

To make the NMR sample, the gel is soaked in 400 µl of protein solution at ambient temperature until the final gel length reaches 23 mm or greater. The process takes 1–2 days depending on the buffer conditions. For high salt or lipid/detergent containing buffers, gel swelling can be hindered. Polyacrylamide doped with charged derivatives, such as 2-acrylamido-2-methyl-1-propanesulfonic acid, can be used to enhance osmotic swelling; in these cases the total content of acrylamide can be lowered to from 5 to 4% to facilitate gel expansion.

The utility of the device was tested with two different forms of the myristoylated yeast ARF1 protein, the GDP-bound form (myr-yARF1·GDP) and the GTP-bound form (myr-yARF1·GTP). Both proteins were prepared in per-deuterated, ¹⁵N, ¹³C, labeled forms as previously described (Liu et al. 2009, 2010). The myristoylated yARF1·GDP is soluble with a molecular size of about 21 kDa. The NMR buffer for yARF1·GDP contained 10 mM K₂HPO₄ (pH = 7), 50 mM NaCl, 10 mM K₂SO₄, 2 mM MgCl₂, 5 mM DTT, and 5% D₂O. The protein was absorbed in a gel polymerized from 5% acrylamide. The myristoylated yARF1·GTP is soluble only as a membrane associated complex (bicelle complex with an effective size of 70 kDa in the case presented). The NMR buffer was similar to that used for myr-yARF1·GDP, but with an additional component of 6% lipids ([DMPC]:[DHPC] = 0.25). Preparation of the bicelle-containing sample follows a previously described procedure (Liu and Prestegard 2009). Efficient protein absorption was achieved with a gel polymerized from 3.92% acrylamide and 0.08% of a negatively charged acrylamide-derivative, 2-acrylamido-2-methyl-1-propanesulfonic acid. To introduce a charge in the gel, other derivatives, such as (3-acrylamideopropyl)-trimethylammonium chloride, can be used (Cierpicki and Bushweller 2004). Due to the size difference between the two protein systems, two different NMR tubes were employed to produce an alignment amplitude within an acceptable range. The inner diameters of the lower portions are 3.2 and 3.6 mm for myr-yARF1·GDP and myr-yARF1·GTP·bicelle, respectively.

Data acquisition

All experiments were conducted at 25°C on a 900 MHz Varian VNMRS spectrometer equipped with a triple resonance, z-axis gradient, cold probe. The N-HN RDCs were measured with pairs of HSQC-TROSY experiments (Kontaxis et al. 2000). ¹⁵N acquisition times of 52 and 40 ms were employed for the myr-yARF·GDP and myr-yARF·GTP·bicelle samples, respectively. A direct ¹H acquisition time of 85 ms was employed for both samples. The ¹⁵N and ¹HN RCSAs were derived from HSQC spectra under isotropic and stretched conditions. The ¹³C’ RCSAs were determined from the H-C’ 2-D plane of a TROSY-based HNCO experiment (Yang and Kay 1999). A ¹³C’ acquisition time of 42 and 30 ms was used for myr-yARF·GDP and myr-yARF·GTP·bicelle samples, respectively. To improve digital resolution, the ¹H, ¹³C, and ¹⁵N dimensions were zero-filled to 1.7, 0.8, and 2.6 Hz/point, respectively. Peak positions were further derived from line-shape fitting to Gaussian functions. It is worth pointing out that chemical shift changes due to temporal instabilities of the buffer, or the protein itself, are not easily corrected for in the current experimental design, because the acquisitions of isotropic and anisotropic data cannot be interleaved. Therefore, when signal to noise is not a limiting factor, shorter experiments that are less susceptible to such changes are preferable.

Data analysis

The measured RCSAs and RDCs of myr-yARF1·GDP and myr-yARF1·GTP were fit, respectively to the crystal structures of the non-myristoylated yeast ARF2·GDP (Amor et al. 2001) (PDB: 1MR3) and the GTP-bound mouse ARF1 protein without the N-terminal 17 residues (Shiba et al. 2003) (mARF1-GTP-Δ17) (PDB: 1o3y), by the Singular Value Decomposition (SVD) method as suggested by Losonczi et al. (1999). Both RCSA and RDC are described by the following set of linear equations:

$$\left(\begin{array}{ccccc}\hfill {\mathrm{C}}_{\text{yy}}^1\hfill & \hfill {\mathrm{C}}_{\text{zz}}^1\hfill & \hfill {\mathrm{C}}_{\text{xy}}^1\hfill & \hfill {\mathrm{C}}_{\text{xz}}^1\hfill & \hfill {\mathrm{C}}_{\text{yz}}^1\hfill \\ \hfill {\mathrm{C}}_{\text{yy}}^2\hfill & \hfill {\mathrm{C}}_{\text{zz}}^2\hfill & \hfill {\mathrm{C}}_{\text{xy}}^2\hfill & \hfill {\mathrm{C}}_{\text{xz}}^2\hfill & \hfill {\mathrm{C}}_{\text{yz}}^2\hfill \\ \hfill ·\hfill & \hfill ·\hfill & \hfill ·\hfill & \hfill ·\hfill & \hfill ·\hfill \\ \hfill ·\hfill & \hfill ·\hfill & \hfill ·\hfill & \hfill ·\hfill & \hfill ·\hfill \\ \hfill {\mathrm{C}}_{\text{yy}}^{\mathrm{n}}\hfill & \hfill {\mathrm{C}}_{\text{zz}}^{\mathrm{n}}\hfill & \hfill {\mathrm{C}}_{\text{xy}}^{\mathrm{n}}\hfill & \hfill {\mathrm{C}}_{\text{xz}}^{\mathrm{n}}\hfill & \hfill {\mathrm{C}}_{\text{yz}}^{\mathrm{n}}\hfill \end{array}\right)\left(\begin{array}{c}\hfill {\mathrm{S}}_{\text{yy}}\hfill \\ \hfill {\mathrm{S}}_{\text{zz}}\hfill \\ \hfill {\mathrm{S}}_{\text{xy}}\hfill \\ \hfill {\mathrm{S}}_{\text{xz}}\hfill \\ \hfill {\mathrm{S}}_{\text{yz}}\hfill \end{array}\right)=\left(\begin{array}{c}\hfill {\mathrm{V}}^1\hfill \\ \hfill {\mathrm{V}}^2\hfill \\ \hfill ·\hfill \\ \hfill ·\hfill \\ \hfill {\mathrm{V}}^{\mathrm{n}}\hfill \end{array}\right)$$ (1)

Here the ${\mathrm{C}}_{\text{ab}}^{\mathrm{i}}$ terms stem from the molecular frame descriptions of the i-th dipolar interaction or CSA tensor chemical shift contribution, and the order tensor elements S_ab (a,b = x,y,z) weight these descriptions. Due to the traceless nature of the order tensor, one of the three diagonal elements (arbitrarily S_xx) is dropped from (1). Vⁱ represents a RDC or RCSA value associated with the i-th anisotropic tensor. For a rigid body, the order tensor S is only governed by the molecular alignment relative to the B₀ field and therefore all residual anisotropic observables, including RCSAs and RDCs, are related by the same order tensor.

${\mathrm{C}}_{\text{ab}}^{\mathrm{i}}$ in (1) is more precisely described by:

$${\mathrm{C}}_{\text{ab}}^{\mathrm{i}}=\{\begin{array}{cc}\hfill {\mathrm{\Delta }}_{\text{ab}}·\frac{2}{3}{\displaystyle \sum _{\mathrm{i}=\mathrm{x},\mathrm{y},\mathrm{z}}{\delta }_{\text{ii}}({\text{cos}}^2{\theta }_{\text{ai}}-{\text{cos}}^2{\theta }_{\text{xi}})+(1-{\mathrm{\Delta }}_{\text{ab}})·\frac{4}{3}{\displaystyle \sum _{\mathrm{i}=\mathrm{x},\mathrm{y},\mathrm{z}}{\delta }_{\text{ii}}\text{cos}{\theta }_{\text{ai}}\text{cos}{\theta }_{\text{bi}}}}\hfill & \hfill \text{RCSA}\hfill \\ \hfill {\mathrm{\Delta }}_{\text{ab}}·({\text{cos}}^2{\varphi }_{\mathrm{a}}^{\mathrm{i}}-{\text{cos}}^2{\varphi }_{\mathrm{x}}^{\mathrm{i}})+(1-{\mathrm{\Delta }}_{\text{ab}})·2\text{cos}{\varphi }_{\mathrm{a}}^{\mathrm{i}}\text{cos}{\varphi }_{\mathrm{b}}^{\mathrm{i}}\hfill & \hfill \text{RDC}\hfill \end{array}$$ (2)

Here θ_ai is the angle between the i-th principal axis of the chemical shift anisotropy (CSA) tensor and the a-th axis of an arbitrary molecular frame, ϕ_a is the angle between the dipolar axis and the a-th axis of the molecular frame, δ_ii is the principal value of the i-th CSA axis, and Δ_ab is the delta function (its conventional symbol δ is not used here to avoid confusion with the symbols for CSA principal values). Eigen values of the CSA tensor are related to those of the chemical shift (CS) tensor by: δ_ii = δ_jj − δ_iso, where i = x, y, or z, and j = 1, 2, or 3, and δ_iso = (δ₁₁ + δ₂₂ + δ₃₃)/3. The CSA tensor is clearly traceless by this definition.

For a known structure, the C matrix in (1) can be straightforwardly calculated based on (2). The dipolar tensor is symmetric with the principal axis parallel to the inter-atom vector. The chemical shift tensors of ¹H, ¹³C’, and ¹⁵N atoms on the peptide plane were taken from solution NMR studies based on an extensive set of cross-correlated relaxation measurements (Loth et al. 2005). The V vector of (1) contains the experimental observables and therefore is also known. Thus the order tensor elements contained in the S vector can be determined in the least squares sense by SVD with a program written in house. The residual anisotropic observables are back-calculated as the product of the C matrix and the S vector, and the agreement between the experimental and back-calculated values can be examined.

Results and discussion

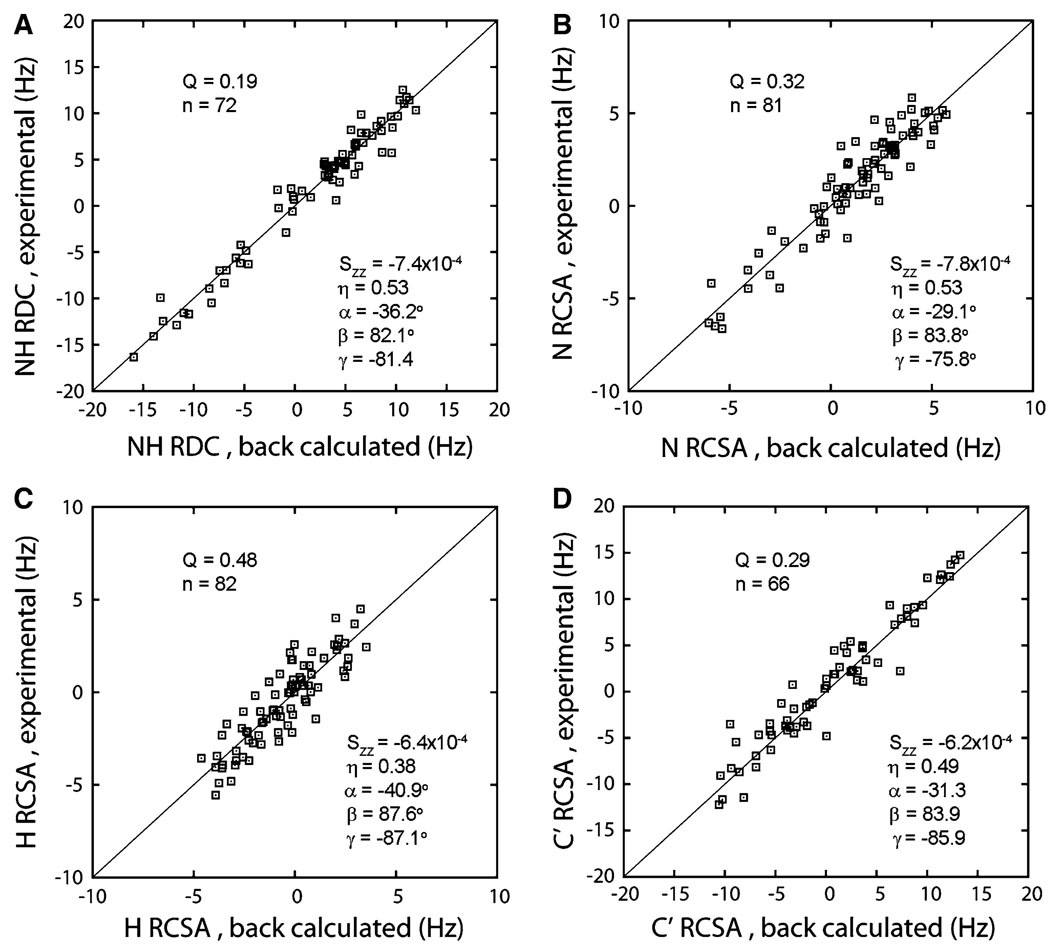
The utility of RDC and RCSA measurements using the described alignment device was first evaluated using the medium-sized soluble protein, myr-yARF1·GDP. The agreement between experimental and back-calculated N–H RDCs is shown in Fig. 2a. The NH RDC has a span of about 28 Hz and clearly represents a useful source of information.

Fig. 2.

Best fits of NH RDC (a), N RCSA (b), H RCSA (c), and C’ RCSA (d) to the crystal structure of non-myristoylated yeast ARF2·GDP (PDB: 1MR3) by singular value decomposition. The order tensor parameters are provided, including the principal and asymmetrical parameters ${\mathrm{S}}_{\text{zz}}^{\prime }$ and η, and the Euler anges (by z-y’-z”, all counter clockwise) α, β, and γ for transforming the PDB molecular frame into the order tensor principal axis frame

The N, H, and C’ RCSAs from the same sample are shown in Fig. 2b–d. The CSA tensors of all 3 atoms are assumed to have one axis perpendicular to the peptide-bond plane, leaving only a single angular variable, θ, to describe rotation about this axis. The definitions of θ for N, H, and C’ CSA tensors are described in the literature (Loth et al. 2005). This angle varies from site to site to some extent but a uniform value, optimized through a simple grid search across the usual ranges, was used in the back-calculation. The final values used were: θ_N = 19°, θ_H = 17°, and θ_C = 40°, each with respect to the H–N (θ_N and θ_H) or C–N (θ_C) bond. Besides the orientation of the CSA tensor, the CSA principal values have site-specific variations. Interestingly, the 3 CSA principal values for each atom type display linear relationships with respect to the isotropic chemical shift (Loth et al. 2005; Wylie et al. 2007; Yao et al. 2010). The CSA principal values as functions of the isotropic chemical shift as shown by Loth et al. were employed in our study to determine the site-specific CSA principal values.

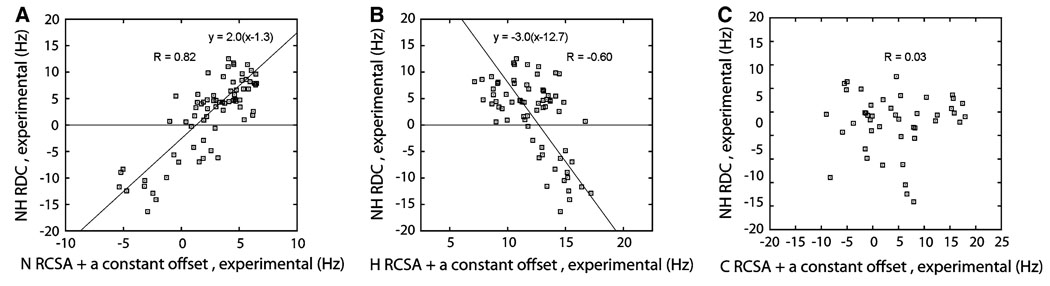
During data fitting, a constant offset was noticed between the experimental and back-calculated RCSA values. This offset is 14 ppb for all three types of RCSAs (1.3, 12.7, and 3.2 Hz for N, H, and C’, respectively), indicating a change of B_o field strength between the “isotropic” and “stretched” measurements. This change can be related to lock signal splitting in the stretched sample due to quadrupolar coupling and preferential locking to one side of the water deuterium doublet. Direct measurements of deuterium splittings on similar samples support this explanation. For this reason, a 14 ppb constant has been removed from all experimental RCSA data in Fig. 2b–d. When such direct splitting measurements cannot be made another procedure can be followed. Due to the nearly axial N CSA tensor and the fact that the unique axis of the N CSA tensor is nearly co-axial with the N–H dipolar vector, the scatter plot of N RCSA and NH RDC shows some linear correlation (Fig. 3a) and thus can be used to estimate this frequency offset.

Fig. 3.

Correlation plots between NH (i) RDC and N (i) RCSA (a), H (i) RCSA (b), and C’ (i−1) RCSA (c). The theoretical correlation lines for N and H RCSAs are derived as described in the main text

As shown in Fig. 2b–d, the C’ RCSA has a span of −11 to 15 Hz, which is close to that of the NH RDC at −16 to 12 Hz, while the spans of N and H RCSAs are considerably smaller at approximately −6 to 6 Hz and −5 to 4 Hz, respectively. All three types of RCSAs fit reasonably well to the crystal structure, with the fitting quality reflected in the Q factors. In many cases quality improves with data span. Of course, fitting quality and the correlation between quality and span can be lost for larger molecules due to different sensitivities and measurement errors of HSQC and HNCO experiments. It is also evident from parameters shown in Fig. 2 that the order tensors determined from RDCs and RCSAs are numerically similar, as they should be, since these observables are averaged by the same molecular tumbling process.

Data presented in Fig. 2 suggest the potential utility of RCSAs in structural and dynamical studies. RCSAs are known to provide information complementary to the more regularly used RDC data. This fact is illustrated in Fig. 3 which shows the scatter plots of NH RDCs versus N, and H RCSAs for each residue. For the C’ RCSA, plots are made comparing the (i − 1)-th residue RCSA to the i-th residue NH RDC, since these atoms are on the same peptide plane and consequently correlation between these values is more likely to be detected if present. The extent of scatter is an indication of the independence of the data, with a linear correlation indicating lack of independence. The linear correlation is the strongest for the N RCSA versus RDC plot (Fig. 3a). H RCSA also displays a noticeable level of (anti-)correlation (Fig. 3b), although to a lesser extent. However, no correlation or anti-correlation is observed between C’ RCSAs and NH RDCs as shown in Fig. 3C. Comparison of Figs. 2 and 3 indicates that all 3 types of RCSAs can provide complementary information to NH RDC, but to varying extents. This can be anticipated based on the principal axes of the chemical shift tensors. The C’ RCSA is the most sensitive to a direction that is perpendicular to the peptide plane, and is the least sensitive to a direction that is roughly parallel to the NH vector. As a result, a C’ RCSA is most complementary to an NH RDC. The H RCSA is equally sensitive to a direction that has a small angle to the NH vector and a direction that is perpendicular to the peptide bond plane, but is indifferent to the third direction of its tensor axis lying within the plane. The significant correlation observed between N RCSA and NH RDC is due to the fact that the N CSA tensor is nearly axial and its unique axis has a small angle relative to the N–H bond vector.

The previously described 14 ppb frequency offset contained in the crude RCSA data is manifest in Fig. 3 a and b, as revealed by the intersection of the best correlation lines (constrained to a theoretical slope relating RCSAs and RDCs as detailed in the “Appendix”) and the y = 0 line (1.3 Hz for N and 12.7 Hz for H). The signs of the slopes are related to the relative geometry of the CS tensor and the NH dipolar vector. The NH vector is nearly co-linear with the least shielded axis of the N CS tensor but with the most shielded axis of the H CS tensor. Consequently the slopes for N and H are of opposite signs (Fig. 3a and b).

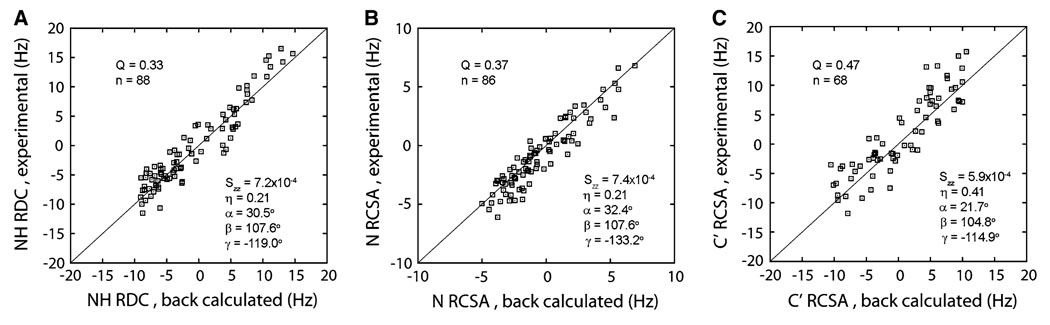
The constrained polyacrylamide gel is particularly suitable for aligning transmembrane proteins and membrane-anchored proteins in that polyacrylamide has no significant interactions with the detergents or lipids that are required to solubilize these proteins. To explore the utility of this device in the measurement of RDC and RCSA on membrane containing systems, we carried out similar experiments on the membrane-anchored myr-yARF1·GTP protein. The agreements between experimental and back-calculated values for NH RDC, N RCSA, and C’ RCSA are shown in Fig. 4. The mouse protein mARF1-GTP-Δ17 used for back-calculation shares 76% sequence identity with the yeast ARF1 protein. In our initial trial using an NMR tube with an upper:lower i.d. ratio of 4.2:3.2 mm and a total acrylamide concentration of 5%, a RDC span of around 65 Hz was obtained, which is large enough to adversely affect INEPT transfer and cause significant line-broadening. Increasing the lower i.d. to 3.6 mm and lowering the total acrylamide concentration to 4% reduces the RDC span to about 25 Hz, which allows collection of a larger amount of data. A 4.3 ppb offset was removed from the N and C’ RCSA data shown in Fig. 4b and c. The H RCSA shows poor correlation to the structure with a Q factor of 0.8 (data not shown), but the fitting qualities of NH RDC, and N & C’ RCSAs, although degraded compared to those from the much smaller GDP-bound ARF protein, do suggest utility in structure determination. For ARF·GDP, a better agreement was observed for C’ RCSA compared to N RCSA (Fig. 2 b and d). As the size of the protein goes up, this relationship is reversed. This change is most likely due to the differential sensitivities of the HSQC and HNCO experiments to molecular sizes.

Fig. 4.

Best fits of NH RDC (a), N RCSA (b), and C’ RCSA (c) to the crystal structure of mARF1-GTP-Δ17 (PDB: 1o3y) by singular value decomposition. The order tensor parameters indicates are defined by the same convention as in Fig. 2

Conclusion

Thus, we have introduced a simple device that can produce the molecular alignment needed for RDC and RCSA measurements by stretching polyacrylamide gels. More importantly, the device provides for accurate referencing of RCSA measurements. Validation data on soluble myr-yARF1•GDP and membrane associated myr-yARF1•GTP sets of data show that this device can produce RDC and RCSA data of sufficient quality to allow structure determination of soluble and membrane-associated proteins. The complementarity of RDC and RCSA data, and the ability to collect these data simultaneously for multiple nuclear sites in a single amide plane will become very important as backbone data begins to play a larger role in structure determination of proteins (Raman et al. 2010).

There are also potential applications beyond structure determination. For example, CSA tensors carry information about the chemical environment of specific amide planes, including the strength and direction of hydrogen bonds (Sitkoff and Case 1998). In principle, five independent alignments are required to fully determine the traceless and symmetric CSA tensor. However, some of the tensorial variables have small fluctuations and can be assigned values fixed at an “average” value. Also, molecular geometry can fix certain parameters. For example, with N, H, and C’ atoms assumed to be on the peptide bond plane, one of the principal CSA axes is expected to be perpendicular to the plane. This simplification leaves room for better characterization of parameters having larger variations and allows meaningful interpretation based on a limited set of RCSAs. The device we introduce here can potentially be used to collect multiple alignments. The device works with both neutral gels and gels modified to carry positive or negative charges. These often give independent alignments allowing potential application in determination of site specific CSA tensors.

Appendix

The RCSA span is an important consideration in terms of its practical application. Generally a larger span allows more room for measurement errors and therefore is preferable. Here we derive the relationship between the upper and lower bounds of RCSAs and the order tensor. We use the symbol δ⌢ for the chemical shift tensor as suggested by Mason (1993).

RCSA, in ppm, is described by the following equation in an arbitrary reference frame:

$$\text{RCSA}=\langle {\mathrm{B}}^{\mathrm{T}}·\stackrel{⌢}{\delta }·\mathrm{B}\rangle -{\delta }_{\text{iso}}$$ (A1)

where B is a column vector representing the direction of the B₀ field in the reference frame and B^T is the transposed row vector. The chemical shift (CS) tensor δ̑ is also expressed in the same reference frame. The isotropic chemical shift δ_iso is a constant that equals the average of the 3 eigen values of the CS tensor, (δ₁₁ + δ₂₂ + δ₃₃)/3. The bracket represents averaging by molecular reorientation. Written in the principal axis frame (PAF) of the CS tensor, (A1) becomes:

$$\text{RCSA}={\delta }_{11}\langle {\text{cos}}^2\alpha \rangle +{\delta }_{22}\langle {\text{cos}}^2\beta \rangle +{\delta }_{33}\langle {\text{cos}}^2\gamma \rangle -{\delta }_{\text{iso}}$$ (A2)

where α, β, and γ are the angles between B₀ and the x, y, and z axis of the CS PAF. By convention, the eigen values of the CS tensor are ordered so that δ₁₁ ≥ δ₂₂ ≥ δ₃₃ (This originates from the ordering convention for chemical shielding tensor that σ₃₃ ≥ σ₂₂ ≥ σ₁₁). Notice that in (A2), 〈cos²θ 〉 (θ = α, β, or γ) can be regarded as weights for the eigen values, based on the fact that 0 ≤ 〈cos²θ 〉 ≤ 1 and 〈cos²α〉 + 〈cos²β〉 + 〈cos²γ〉 = 1. Therefore, the upper bound of RCSA occurs when the largest eigen value δ₁₁ gets the largest weight and the smallest eigen value δ₃₃ gets the smallest weight. Similarly, the lower bound of RCSA occurs when the largest eigen value gets the smallest weight and the smallest eigen value gets the largest weight.

Next we examine the largest and smallest possible weights in terms of their relationships to the Saupe order matrix. The order matrix element in an arbitrary molecular frame is given by:

$${\mathrm{S}}_{\text{ij}}=\frac{1}{2}(3\langle \text{cos}{\theta }_{\mathrm{i}}\text{cos}{\theta }_{\mathrm{j}}\rangle -{\mathrm{\Delta }}_{\text{ij}})$$ (A3)

where θ_i is the angle between the B_o field and the i-th axis of the molecular frame, and Δ_ij is the delta function. If the molecular frame is chosen to be a CS PAF, then obviously the weights in (A2), namely 〈cos²α〉, 〈cos²β〉, and 〈cos²γ〉, are directly related to the diagonal elements (i = j) of the order matrix in the CS PAF. Clearly, the largest and smallest weights are associated with the largest and smallest diagonal elements, respectively. Note that for the diagonal elements, comparison is by the numerical value but not by the absolute value, i.e. a negative value of a high magnitude is smaller than a positive number of a low magnitude. It is easy to show that the diagonal elements of the order matrix in the CS PAF (or any other frame) can be expressed as a weighted average of the diagonal elements in the order tensor’s PAF:

$${\mathrm{S}}_{\text{ii}}={\mathrm{U}}_{\text{xi}}^2{\mathrm{S}}_{\text{xx}}^{\prime }+{\mathrm{U}}_{\text{yi}}^2{\mathrm{S}}_{\text{yy}}^{\prime }+{\mathrm{U}}_{\text{zi}}^2{\mathrm{S}}_{\text{zz}}^{\prime }(\mathrm{i}=\mathrm{x},\mathrm{y},\mathrm{z})$$ (A4)

where ${\mathrm{S}}_{\text{xx}}^{\prime }$ is the diagonal element of the order matrix in its PAF (principal value), and U_ij is an element of the rotation matrix that relates the order tensor PAF and the CS PAF. The orthogonality of the axis systems related through the rotation matrix U requires that ${\mathrm{U}}_{\text{xi}}^2+{\mathrm{U}}_{\text{yi}}^2+{\mathrm{U}}_{\text{zi}}^2=1$. Therefore, for a diagonal element S_ii in an arbitrary frame, the relation holds that ${\mathrm{S}}_{\text{min}}^{\prime }\le {\mathrm{S}}_{\text{ii}}\le {\mathrm{S}}_{\text{max}}^{\prime }$, where ${\mathrm{S}}_{\text{max}}^{\prime }$ and ${\mathrm{S}}_{\text{min}}^{\prime }$ stand for the maximal and minimal principal values. According to (A3), the following relation is derived: $(2{\mathrm{S}}_{\text{min}}^{\prime }+1)/3\le \langle {\text{cos}}^2\theta \rangle \le (2{\mathrm{S}}_{\text{max}}^{\prime }+1)/3$, where θ = α, β, or γ.

The order matrix is traceless, i.e., S_xx + S_yy + S_zz = 0. By convention, the principal values are ordered so that |S_zz| ≥ |S_yy| ≥ |S_xx|. Therefore if ${\mathrm{S}}_{\text{zz}}^{\prime }\ge 0,{\mathrm{S}}_{\text{max}}^{\prime }={\mathrm{S}}_{\text{zz}}^{\prime }$ and ${\mathrm{S}}_{\text{min}}^{\prime }={\mathrm{S}}_{\text{yy}}^{\prime }$; otherwise, ${\mathrm{S}}_{\text{max}}^{\prime }={\mathrm{S}}_{\text{yy}}^{\prime }$ and ${\mathrm{S}}_{\text{min}}^{\prime }={\mathrm{S}}_{\text{zz}}^{\prime }$. Going back to (A1), after some straightforward reorganization, gives the following result for ${\mathrm{S}}_{\text{zz}}^{\prime }\ge 0$:

$$\{\begin{array}{c}{\text{RCSA}}_{\text{max}}=\frac{2}{3}\left({\delta }_{11}{\mathrm{S}}_{\text{zz}}^{\prime }+{\delta }_{22}{\mathrm{S}}_{\text{xx}}^{\prime }+{\delta }_{33}{\mathrm{S}}_{\text{yy}}^{\prime }\right)\hfill \\ {\text{RCSA}}_{\text{min}}=\frac{2}{3}\left({\delta }_{11}{\mathrm{S}}_{\text{yy}}^{\prime }+{\delta }_{22}{\mathrm{S}}_{\text{xx}}^{\prime }+{\delta }_{33}{\mathrm{S}}_{\text{zz}}^{\prime }\right)\hfill \end{array}$$ (A5)

The upper bound occurs when the (x, y, z) axes of the CS tensor are collinear with the (z, x, y), (z, −x, −y), (−z, x, −y), or (−z, −x, y) axes of the order tensor, respectively, and the lower bound occurs when the (x, y, z) axes of the CS tensor are collinear with the (y, x, −z), (y, −x, z), (−y, x, z) or (−y, −x, −z) axes of the order tensor, respectively. If ${\mathrm{S}}_{\text{zz}}^{\prime }<0$, the relationships in (A5) for RCSA_max and RCSA_max are simply swapped, and so are relationships between the CS tensor and the order tensor. Clearly, independent of the sign of ${\mathrm{S}}_{\text{zz}}^{\prime }$, the RCSA span is given by:

$$|{\text{RCSA}}_{\text{max}}-{\text{RCSA}}_{\text{min}}|=\frac{2}{3}({\delta }_{11}-{\delta }_{33})\left|{\mathrm{S}}_{\text{zz}}^{\prime }-{\mathrm{S}}_{\text{yy}}^{\prime }\right|$$ (A6)

Or using the asymmetry parameter, η, of the order tensor defined as $\eta =({\mathrm{S}}_{\text{xx}}^{\prime }-{\mathrm{S}}_{\text{yy}}^{\prime })/{\mathrm{S}}_{\text{zz}}^{\prime }$, (A6) is re-written as:

$$|{\text{RCSA}}_{\text{max}}-{\text{RCSA}}_{\text{min}}|=({\delta }_{11}-{\delta }_{33})\left|{\mathrm{S}}_{\text{zz}}^{\prime }\right|\left(1+\frac{\eta }{3}\right)$$ (A7)

This result suggests that the RCSA span is basically the full chemical shift span scaled down by the order tensor. The RDC span is well known:

$$|{\text{RDC}}_{\text{max}}-{\text{RDC}}_{\text{min}}|=|{\text{DC}}_{\text{max}}|\left|{\mathrm{S}}_{\text{zz}}^{\prime }\right|\left(1+\frac{\eta }{3}\right)\frac{3}{2}$$ (A8)

Therefore the ratio between RDC and RCSA spans is given by:

$$\mathrm{k}=\frac{3}{2}\frac{|{\text{DC}}_{\text{max}}|}{{\nu }_0({\delta }_{11}-{\delta }_{33})}$$ (A9)

where ν₀ is the Larmor frequency of the atom in MHz. This ratio depends only on the relative sizes of the spin interactions, but not on molecular alignments. Typical ratios for NH RDC over RCSAs of N, H, and C’ atoms on the peptide bond plane are 2.0, 3.0, and 0.9 on a 900 MHz spectrometer.