Abstract
The acquisition of high quality MR images of neonatal brains is largely hampered by their characteristically small head size and low tissue contrast. As a result, subsequent image processing and analysis, especially for brain tissue segmentation, are often hindered. To overcome this problem, a dedicated phased array neonatal head coil is utilized to improve MR image quality by effectively combing images obtained from 8 coil elements without lengthening data acquisition time. In addition, a subject-specific atlas based tissue segmentation algorithm is specifically developed for the delineation of fine structures in the acquired neonatal brain MR images. The proposed tissue segmentation method first enhances the sheet-like cortical gray matter (GM) structures in neonatal images with a Hessian filter for generation of cortical GM prior. Then, the prior is combined with our neonatal population atlas to form a cortical enhanced hybrid atlas, which we refer to as the subject-specific atlas. Various experiments are conducted to compare the proposed method with manual segmentation results, as well as with additional two population atlas based segmentation methods. Results show that the proposed method is capable of segmenting the neonatal brain with the highest accuracy, compared to other two methods.
1. Introduction
Tissue segmentation, which partitions brain magnetic resonance (MR) images into gray matter (GM), white matter (WM), and cerebrospinal fluid (CSF), is a crucial step for subsequent volumetric and cortical surface analysis. However, effective segmentation of neonatal brain images still remains a great challenge in many emerging neonatal studies, which have the potential of revealing interesting brain development patterns and also neurodevelopmental disorders. In particular, two major factors confound neonatal tissue segmentation: 1) the inability of current imaging techniques to acquire images with a sufficiently high resolution and signal-to-noise ratio (SNR) for tissue segmentation, and 2) the lack of prior knowledge for a more informed and guided segmentation. In this paper, we address both of these issues. First, a dedicated neonatal phased array coil is devised to improve the SNR as well as spatial resolution. Second, a hybrid atlas combining both cortical enhanced subject-specific characteristics and population probability maps is constructed to improve the accuracy of tissue segmentation. Both of these two novel developments will be discussed in greater details in the following sections.
The brain size of a neonate is typically about one half of an adult. As a result, spatial resolution of neonatal brain images has been substantially limited, particularly under the constraint of data acquisition time. Moreover, rapid dynamic WM changes due to ongoing myelination process in the neonatal brain [2] further complicated the contrast between gray and white matter; GM and WM tissue contrast manifests in an inverted fashion when compared with that of adults. All these factors confound the effectiveness of brain tissue segmentation, and hence the accuracy of subsequent image processing and analysis. To improve MR image quality without lengthening data acquisition time, a dedicated phased array neonatal head coil is devised. In a conventional MR imaging session, a volume coil (independent of age) covering the whole brain is utilized. However, it is a known fact that a surface coil with a smaller diameter and thus a smaller sensitivity region can achieve higher signal-to-noise ratio (SNR) in comparison to a volume coil. It is hence a sensible approach that multiple small coils can be arranged in such a way to cover a large region of interest (ROI). In so doing, the phased array coil technology capitalizes the advantages of surface coil in improving SNR while covering a large ROI. In addition, coupling with the parallel imaging technologies, it yields images with significantly higher quality compared to images acquired using conventional techniques, which essentially translates to a better head start for tissue segmentation. But it should be pointed out that, despite the improved image quality, a dedicated algorithm for neonatal brain segmentation is still crucial.
Numerous brain image segmentation methods have been proposed, but they were mainly developed for adult brains [3]. In the case of neonatal brains, existing methods include clustering [4] and population-atlas based [5–7] segmentation approaches. Affected by low image quality and also large intensity variability between non-myelinated and myelinated WM, clustering-based methods relying solely on image intensities are very limited in terms of segmentation performance. In light of this, atlas-based methods employ population atlases as spatial priors for segmentation guidance. The existing atlases are usually built by averaging a group of spatial normalized segmented images. This approach is straightforward and easy to implement, but has several inherent drawbacks. First, the atlases are generally fuzzy and fall short in providing sufficient prior information especially when fine tissue structures are concerned. Second, the atlases are often aligned to the subjects utilizing only affine transform, which cannot guarantee topological correspondences and thus jeopardizes the segmentation accuracy. In general, a good atlas for guiding segmentation should have the following two properties: 1) Contains a wide range of coarse-to-fine structural information to maximize guidance capacity, and 2) Capable of achieving sufficient homology with respect to the subject in order to minimize guidance errors. To meet these requirements, we construct a subject-specific atlas, in contrast to the conventional population atlases, capable of capturing major subcortical information of a population of subjects and also unique subject-specific cortical information.
To construct a subject-specific atlas, a two-phase strategy is proposed. First, the cortical folding pattern is enhanced. It can be observed from the acquired neonatal images (as shown in Fig. 6) that the fine structures of the cortical folding pattern are well delineated and can hence be effectively enhanced using a modified vessel-tracking motivated method [8]. The enhanced cortical folding pattern is subject-specific and characterizes GM spatial distribution in the cortical region. Second, a population atlas is constructed to provide global tissue spatial information and to mitigate bias when only a specific prior is used. Combining the results from these two phases, a final hybrid atlas, namely a subject-specific atlas, can be constructed.
Fig. 6.
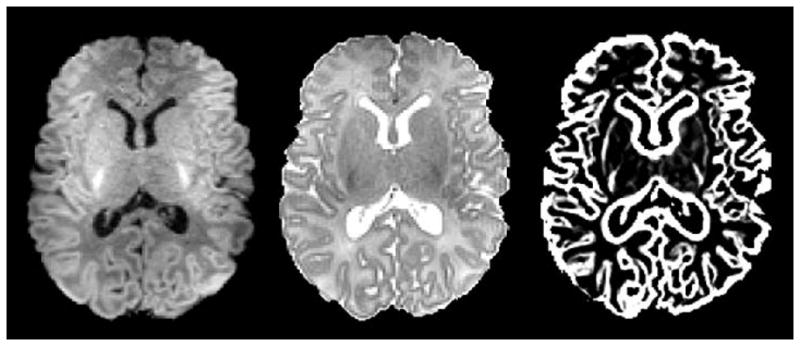
Original T1 image, T2 image, and the enhanced GM structures.
The atlas-to-subject registration problem is solved by a simultaneous registration and segmentation scheme. At each iteration, atlas-to-subject registration is refined by the availability of a better segmented subject image. On the other hand, the segmentation is also refined by a better registration of the atlas onto the subject.
In this paper, we aim to construct a subject-specific atlas for tissue segmentation of the neonatal images acquired using a dedicated neonatal phased array coil. By enhancing image acquisition and atlas building, neonatal segmentation accuracy is improved. Results are also validated by visual inspection and also by quantitative comparison with manual segmentations. The rest of the paper is organized as follows. Section 2 introduces the phased array coil imaging technique, and Section 3 details the proposed tissue segmentation scheme. Experimental results are provided in Section 4. Section 5 concludes this paper.
2. Imaging with Phased Array Coil
In MR imaging, the sensitivity volume of a coil is proportional to its diameter. A volume coil provides uniform coverage of a large region of interest with a price of lowering SNR. On the other hand, while a small surface coil can only cover a small anatomical region, i.e., field of view (FOV), the signal acquired generally has higher SNR compared to a volume coil. By arranging multiple mutually decoupled surface coils surrounding the brain and imaging simultaneously, this composed phased array coil can obtain higher resolution images with higher SNR at a sufficiently short acquisition time as widely demonstrated in [9, 10].
After acquiring a series of images by a number of coil elements (such as 8 coil elements in Fig. 1), now the question of how to combine these images needs to be addressed. Due to the limited reachable volume of each surface coil, the voxels close to the coil yield better SNR and better tissue contrast, comparing to those farther away. To take full advantage of each image in generating a final single combined image, a proper weighting scheme is necessary. For this purpose, the coil profile, which can be obtained concurrently in the same scanning session by taking a low-resolution scan of the whole brain, can be used as reference images to generate a sensitivity map for each coil.
Fig. 1.
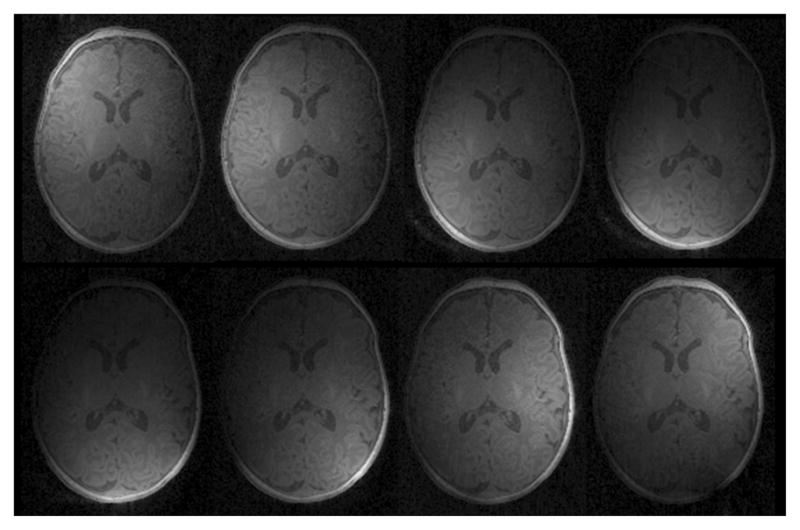
Eight T1 MR images obtained from the eight phased array coil elements. Each image has different sensitivity region, corresponding to the individual location of each coil.
In our study, the phased array coil consists of 8 receiving channels (see Fig. 1). Their acquired images, denoted as Ci, i = 1,…, 8, are accompanied by their respective sensitivity profiles, denoted as Pi, i = 1, …,8, respectively. Although the resolution of the coil profile images is low, they still contain too much structural information to be used as sensitivity maps. To estimate a sensitivity map from the respective coil profile Pi, a low-pass filter [11] is employed (Fig. 2). For simplicity, Pi is used also to denote the generated sensitivity map for each coil. Based on the sensitivity maps, a high-quality image I can be reconstructed from all the acquired images using the sum-of-squares metric:
| (1) |
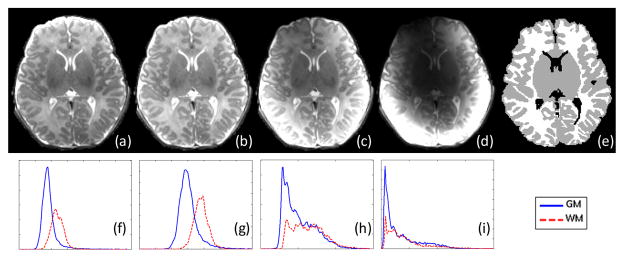
where N is the number of coils, which is equal to 8 in this study. As we can see from this equation, the image Ci is first corrected via inverse weighting by Pi, which is effectively an intensity equalization process, and is then further weighted by the sensitivity map with exponent raised to q, i.e. . The parameter q reflects the weight assigned to each of the sensitivity maps in the reconstruction. For example, when q is 0, the 8 intensity-corrected images are combined in a spatially uniform manner. When q is 1, the uncorrected images are combined directly (as used in [12]). As q decreases or increases, the voxels farther from the coils will be increasingly emphasized or suppressed, respectively. It is hence crucial to determine a suitable q value that will give us a balanced image with good tissue contrast in the whole brain. Sample results with q = 0,0.3,1,2, are shown in Fig. 3(a)–(d). With the help of a manually segmented image, shown in Fig. 3(e), the intensity distributions of GM and WM can be computed, as shown in Fig. 3(f)–(i). These distributions are indicative of how well GM and WM can be separated. Generally, the farther the GM and WM peaks are, the easier the segmentation will be. We employ a symmetric Kullback-Leibler (KL) divergence to measure the difference between the GM and WM distributions. We experimented q value from (−1) to 2 with a 0.1 interval, and the KL divergence is shown in the right panel of Fig. 4 for the global region, region A, and region B, which are shown in the left panel of Fig. 4. The peaks of KL divergence for these regions fall the interval of 0 to 0.5. In particular, the choice of q = 0.3, which is used in this study, gives us a optimal separation compared to other q values.
Fig. 2.
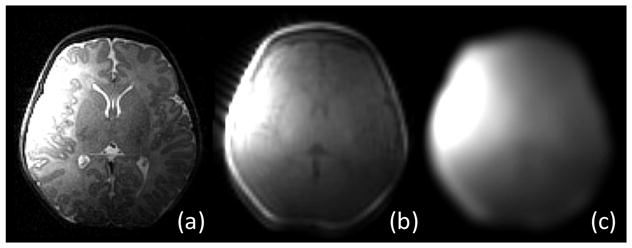
Illustrations of (a) coil image, (b) coil profile image, and (c) estimated sensitivity map. Note that, to reach (c), non-brain tissues are first removed to better concentrate on the brain parenchyma.
Fig. 3.
Image reconstruction results with different q values. (a)–(d) show the results when q is set as 0, 0.3, 1, 2, respectively. (f)–(i) are the GM and WM intensity distributions corresponding to (a)–(d), obtained with the help of a manually segmented image (e).
Fig. 4.
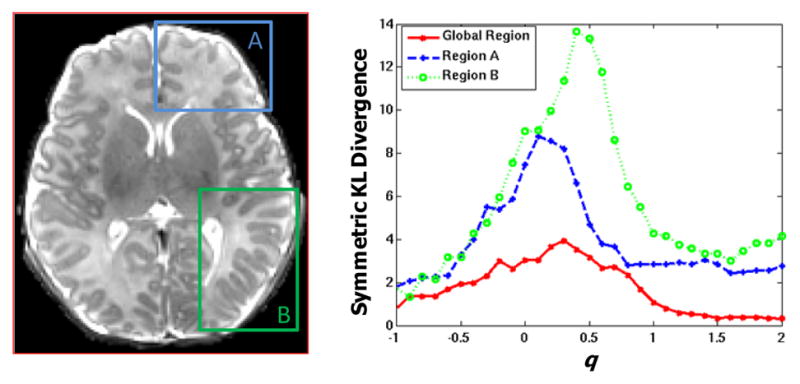
Symmetric KL divergence between GM and WM histograms with different q values in global region, region A, and region B.
3. Subject-specific Atlas Construction and Tissue Segmentation
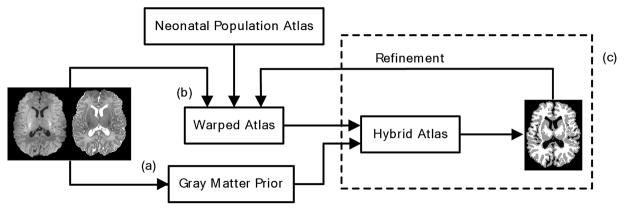
Due to low tissue contrast and large overlapping of GM and WM intensity distributions in neonatal brain images, additional tissue priors can be employed to provide helpful cues in tissue segmentation. Unlike conventional population atlases, a hybrid atlas approach is proposed in this paper. In particular, our atlas incorporates subject-specific cortical GM distribution with a neonatal population atlas. Neonatal tissue segmentation problem is formularized as an iterative hybrid atlas construction and segmentation. The segmentation framework consists of three major steps, shown as steps (a)–(c) in Fig. 5. The first step involves the enhancement of the cortical GM sheet, which is the characteristic of each neonatal image and which can serve as a cortical GM prior. This can be achieved via a second-order geometric structure identification approach [8]. The second step involves the construction of neonatal population atlas by nonlinear registration [13] of a large group of pre-segmented neonatal images. Finally, the neonatal population atlas is warped to a neonatal subject, and the cortical GM prior of this subject is combined with the neonatal population atlas, resulting in a subject-specific atlas. The registration accuracy between the warped atlas and the neonatal subject is refined by a simultaneous registration and segmentation process, which will be explained in greater detail in subsection 3.3.
Fig. 5.
The schematic diagram of the proposed neonatal segmentation framework. (a)–(c) are the three major steps. The T1 and T2 images on the left are the inputs, and the segmented image on the right is the output.
Before segmentation, all images are preprocessed. Specifically, non-brain tissues (such as skulls) are stripped with Brain Surface Extractor (BSE) [14], and the cerebellum is removed semi-automatically so that more focus can be placed for the tissue segmentation of the cerebrum region.
3.1. Cortical Gray Matter Prior
Brain cortical convolution pattern is unique to each individual. It is hence desirable that this pattern can be enhanced to formulate a more informed segmentation algorithm especially when the cortical region is questioned. The segmentation of cortical region is often the weak spot of population-based atlases, since fine details in this region is often smoothed out by the averaging process in constructing the atlases due to large inter-subject variability. Approaches based on intensities alone are quite limited in revealing the cortical pattern, since the intensity distributions of GM and WM are often overlapping. One way of revealing this pattern is by utilizing geometric measurements [15]. Geometric measurements reflect the spatial relationship of the anatomical structures and not solely the intensity differences. They can delineate fine structures with seemingly similar intensities and can hence enhance local GM/WM intensity contrast especially in the cortical region where we can often find rapid changes of geometric patterns. The first-order intensity derivative, i.e., gradient, gives us information on the major local direction of intensity change, and can only be used to detect whether or not there is structure. The second-order derivative, as is encapsulated in the Hessian matrix, can furnish further information such as the curvature of the local structure. In human brain, GM covers the WM in a sheet-like fashion with a typical thickness of 1.5–5 mm. We employ the Hessian matrix to build structural filters for delineating the cortical structures in brain images. The filters are modified from a vessel-tracking method [8] by fine-tuning the filter response to sheet-like structures of specific width (we choose 3.5 in this paper), and by combining them with Gaussian smoothing to reduce the effect of noise.
In particular, for each voxel x in an Gaussian smoothed image I, its local structure can be analyzed with Taylor approximation up to the second order in a neighbor defined by scale s:
| (2) |
where ∇ is the gradient vector, and H the Hessian matrix. H can be decomposed in the form of:
| (3) |
where and λk are the k-th eigenvector and eigenvalues, respectively, and k = 1,2,3. The three eigenvectors can be used to form an ellipsoid, which describes the local structures. Several structures can be defined and identified by the relative amplitudes of the eigenvalues, namely line-, plate-, and ball-like structures. If the three eigenvalues are comparable, the local structure around x is similar to a ball. Assuming |λ1| ≤ |λ2| ≤ |λ3|, if |λ1| ≪ |λ2|, |λ3|, local intensities change significantly in two directions and so it is a line-like structure. If |λ1|, |λ2|≪ |λ3|, the local structure is plate-like. Because the cortical folding curvature is sharp at gyri and sulci, but flat at locations between them, both line- and plate-like local structures exist in the cortical GM sheet. Hence, for each point x, we compute the structureness measures of both structures and the larger value determines whether the point is line- or plate-like. We define two geometric ratios ℜB and ℜA:
| (4) |
where ℜB is minimized for plate and line structures, and ℜA is minimized when detecting a line structure. Because we aim to extract brighter structures from a darker background in the T1-weighted image (Fig. 5; note that the intensity is inverse in the T2-weighted image), λ2 and λ3 should be negative for line structure, and λ3 should be negative for plate structure. The line and plate filters are given by:
| (5) |
| (6) |
| (7) |
where D is the dimension of the image, and S is the second-order structureness measurement defined to constrain the magnitudes of the derivatives. α, β, and c are the parameters which control the structure sensitivity of the filters. In this paper, α, β are fixed at 0.5, and c is set as half the value of the maximum Hessian norm value. The equations above are applied to each voxel and the probability maps returned by them indicate the degrees of structureness of each voxel. It is worth noting that by using only the plate filter, there will be some discontinuities in the detected cortical GM structures. Hence, we employ both the line and plate filters, and determine the structure at each voxel based on the maximal value between the two values given by the two filters. The cortical GM enhanced by the proposed method is shown in Fig. 6. The GM folding probability map is enhanced entirely based on the subject image and this cortical GM prior will be combined with a population atlas (described below) into a hybrid atlas for guiding the segmentation.
3.2. Construction of Neonatal Population Atlas
Due to the rapid development of neonatal brains especially during the first year of life, adult atlases, or even those constructed from pediatric brains, are not directly applicable for segmentation of neonatal brain images due to large anatomical differences. Here we use a dataset collected in one of our longitudinal studies, involving 68 neonatal subjects (38 male and 30 female) with first scan at neonate (1.3±0.7 months) and second scan at one-year-old (13.5±0.9 months). These neonatal images were segmented with the aid of longitudinal information with the method presented by Shi et al. in [16]. Note that only segmented neonate data is used in this paper for generating neonatal population atlas purpose.
Numerous approaches for atlas construction have been proposed [1, 17]. Some earlier approaches involve the registration of all images onto a template (usually chosen from one of the subjects) and average the warped results [18]. Approaches as such are bias prone, since the chosen template will often have dominance over the final created atlas. A better alternative is to construct a representative atlas, to which all subjects can be warped with a minimum amount of transformation [17]. In the process of creating such atlas, all subject images are maintained unchanged, and the atlas is progressively refined, as detailed below.
To construct a neonatal atlas from N tissue-segmented neonatal subjects, all subjects are first affine registered to a standard ICBM atlas space [19] and averaged to obtain an initial atlas T0. Then, at each iteration t, each subject i is registered to the previous atlas Tt−1 with a deformation field estimated by nonlinear elastic registration algorithm HAMMER [13]. The estimated deformation field is pointing from the atlas Tt−1 to the subject i. The new atlas Tt can be constructed by averaging all warped subject images. Moreover, by averaging deformation fields from the atlas to all subjects, i.e., , the center of these subjects can be estimated. Thus, with this average deformation field, atlas Tt can be transformed to the center of subjects as a new refined atlas, also denoted as Tt. By repeating the above process, an increasingly refined atlas Tt can be obtained. Once the algorithm converges, a final neonatal atlas can be constructed, as the one shown in the middle row of Fig. 7. It can be observed that, compared with the other atlas such as that shown in the first row of Fig. 7, our atlas is sharper and preserves more subtle structures of GM and WM.
Fig. 7.
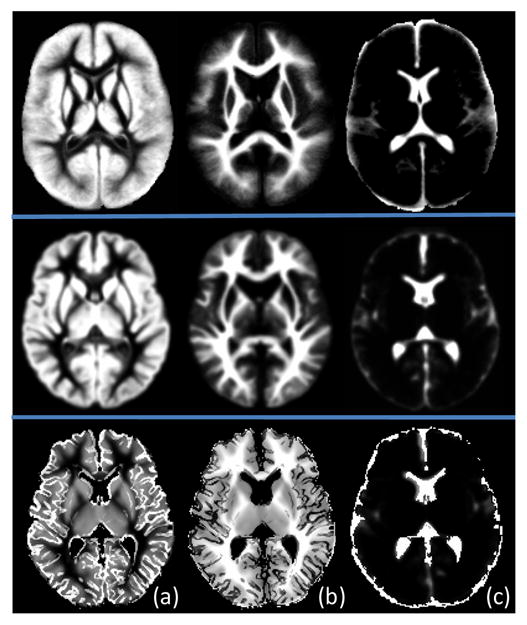
Illustration of prior probability maps from a population atlas in [1], our generated neonatal atlas, and the proposed subject-specific atlas, from top to bottom. (a)–(c) are the GM, WM, and CSF priors, respectively.
3.3. Joint Registration and Segmentation
During the tissue segmentation of neonatal brain image, the neonatal atlas is first registered onto the neonatal subject by an affine registration. The warped neonatal atlas is then integrated with the cortical GM prior computed from the neonatal subject as follows:
| (8) |
where PGM is the GM prior of the warped neonatal atlas, CGM is the cortical GM prior from the neonatal subject, and γ is a parameter controlling the ratio between two priors in producing the final (hybrid) GM prior P̃GM. We set γ to 0.5 so that the two priors are weighted equally. The final GM prior is then combined with the WM and CSF priors to form a hybrid atlas, i.e., the subject-specific atlas, as shown in the last row of Fig. 7.
After obtaining the subject-specific atlas, an atlas-based segmentation algorithm [20] is applied to perform tissue segmentation of neonatal subjects. In brief, the algorithm involves alternating among bias correction, tissue classification, and atlas-to-subject registration steps. In particular, a mixture of Gaussians is used to model the distribution of each brain tissue. The hybrid atlas represents the prior probabilities of different tissues being found at each location of an image. Bayes rule is used to combine these priors with tissue probabilities derived from voxel intensities to provide the posterior probability, thus giving the tissue membership probabilities of each voxel. Based on the segmentation results, the registration between the atlas and the neonatal subject is refined by the HAMMER registration algorithm [13], to further reduce registration error and thus bring the atlas much closer to the neonatal subject for guiding more accurate segmentation of neonatal brain tissues, as most joint registration and segmentation algorithms do [21]. The steps of bias correction, tissue segmentation, and atlas-to-subject registration are iterated until convergence.
4. Experimental Results
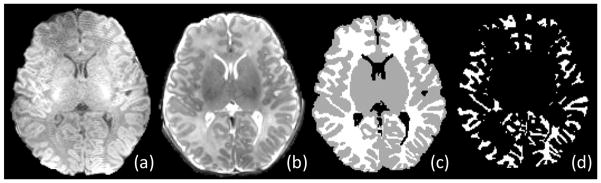
A total of 10 neonates (5 males and 5 females), with postnatal age range of 0.5–1.9 months, are used in this paper for performance evaluation of our proposed neonatal brain segmentation method. MR images of these 10 neonates were acquired using a 3T head-only MR scanner. The overall shape of the dedicated neonatal phased array coil was designed according to the average brain shape estimated from 60 normal pediatric subjects. The phased array coil consists of 8 receiving channels (Fig 1). T1-weighted images were acquired using a MP-RAGE sequence with imaging parameters: TR=1820ms, TE=4.38ms, Flip Angle=7, resolution=0.79×0.79×0.8 mm3, and 2 average and acceleration factors (AF=2). T2-weighted images were acquired with imaging parameters: TR=9280ms, TE=119ms, Flip Angle=150, resolution =1×1×1.3 mm3, and AF=2. In addition, a low-resolution spin density weighted 3D FLASH sequence was employed to obtain eight coil sensitivity profiles. Typical acquired T1- and T2-weighted neonatal brain images are shown in Fig. 8(a)–(b).
Fig. 8.
Illustration of (a) T1, (b) T2, (c) manual segmentation, and (d) cortical WM images.
To evaluate the performance of our segmentation method, two other population atlas based segmentation methods are also included for comparison. In the first method (which we refer to as Method A below), a population atlas obtained from 76 infants ranging in age from 9 to 15 months [1] is used to directly guide the tissue segmentation of neonatal brains. In the second method (which we refer to as Method B below), our generated neonatal atlas in section 3.2 (Fig. 7 middle row) is used to directly guide the brain tissue segmentation of neonates. An example of the prior probability maps used in these three methods (Method A, Method B, and Proposed method) is shown in Fig. 7. Fig. 9 shows the corresponding segmentation results of these three methods on the neonatal brain image given in Fig. 8. Visually, the segmentation results obtained by our proposed method provide more detailed segmentations in coarse and fine structures, compared to those produced by the other two population atlas based methods.
Fig. 9.
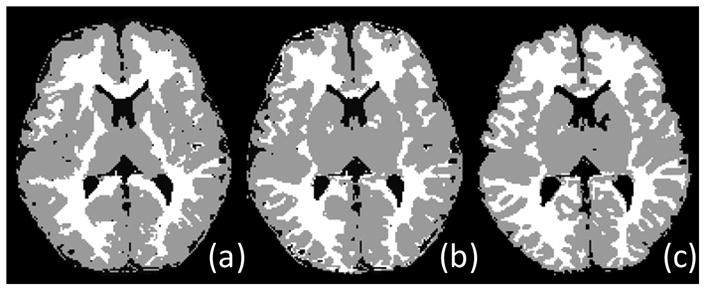
Segmentation results of (a) Method A, (b) Method B, and (c) our proposed method.
To quantitatively evaluate the performance of our proposed segmentation method, manual segmentation (using ITK-SNAP [22]) was performed on all 10 neonates, and the obtained results are used as a ground truth for evaluation of the tissue segmentation results. For quantitative comparison, the Dice ratio (DR) [23] is employed as DR = 2|A ∩ B|/(A + B) to measure the overlap rate between manually segmented images and those produced by Method A, Method B, and Proposed method. The Dice ratio ranges from 0 to 1, corresponding to the worst and the best segmentation results. The Dice ratios of the three methods for GM and WM are shown in Table 1, respectively. As we can observe from this figure, the proposed subject-specific atlas based segmentation method produced results which agrees best with the manual segmentation results for both GM and WM. The volume errors (VE) for the segmentation results of each of three methods are also provided for GM and WM in Table 1. Volume error is computed as VE = |VA − VB|/VA (VA is manual segmentation), ranging from 0 to 2. A similar conclusion can be made that the proposed method yields the least error among the three methods.
Table 1.
The Dice ratios and volume errors for the segmentation results obtained by Method A, Method B, and Proposed method. The results of GM, WM, and cortical WM are provided.
| Dice Ratio | Volume Error | |||||
|---|---|---|---|---|---|---|
| GM | WM | Cortical WM | GM | WM | Cortical WM | |
| Method A | 0.81+0.02 | 0.74+0.05 | 0.63+0.06 | 0.34+0.06 | 0.29+0.08 | 0.54+0.06 |
| Method B | 0.82+0.02 | 0.77+0.05 | 0.65+0.05 | 0.32+0.06 | 0.29+0.06 | 0.51+0.06 |
| Proposed | 0.89+0.01 | 0.89+0.01 | 0.85+0.03 | 0.12+0.05 | 0.14+0.04 | 0.26+0.04 |
Besides comparing global volumes of segmented GM and WM as described above, the segmentation performance is further evaluated in the cortical WM, with an example shown in Fig. 8(d). The Dice ratios and volume errors are both computed for each of three methods, with results given in Table 1. Again, the proposed method achieves the best agreement with manually segmented images, compared to the two population atlas based segmentation methods. Accordingly, both visual inspection and quantitative evaluation results confirm the advantages of using the proposed subject-specific atlas for neonatal brain image segmentation.
5. Conclusion
Tissue segmentation of neonatal brain images has been a daunting task, largely due to their poor spatial resolutions and low signal-to-noise ratio. With a system of phased array coils dedicated for neonatal brains, image quality can be significantly improved by combining a set of images with better quality. The coils, operating in a parallel fashion, make acquisition with a sufficiently low amount of time possible – especially crucial for the acquisition of neonatal brain images. By utilizing these images with improved quality, better segmentation results can be obtained. To this end, a novel subject-specific atlas based MRI segmentation method is developed. This atlas combines the benefits given by the subject-specific cortical GM folding pattern and the neonatal population atlas. The results, compared with two population atlas based segmentation methods, demonstrate that the proposed approach is capable of achieving higher accuracy in neonatal brain segmentation, especially in the cortical regions.
Acknowledgments
This work was supported in part by grants 1R01EB006733, 1R03EB008760 and R01EB008374.
References
- 1.Altaye M, Holland SK, Wilke M, Gaser C. Infant brain probability templates for MRI segmentation and normalization. Neuroimage. 2008;43:721–730. doi: 10.1016/j.neuroimage.2008.07.060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Connors SL, Levitt P, Matthews SG, Slotkin TA, Johnston MV, Kinney HC, Johnson WG, Dailey RM, Zimmerman AW. Fetal mechanisms in neurodevelopmental disorders. Pediatr Neurol. 2008;38:163–176. doi: 10.1016/j.pediatrneurol.2007.10.009. [DOI] [PubMed] [Google Scholar]
- 3.Pham DL, Xu C, Prince JL. A survey of current methods in medical image segmentation. Annual Review of Biomedical Engineering. 2000;2:315–337. doi: 10.1146/annurev.bioeng.2.1.315. [DOI] [PubMed] [Google Scholar]
- 4.Anbeek P, Vincken KL, Groenendaal F, Koeman A, van Osch MJ, van der Grond J. Probabilistic brain tissue segmentation in neonatal magnetic resonance imaging. Pediatr Res. 2008;63:158–163. doi: 10.1203/PDR.0b013e31815ed071. [DOI] [PubMed] [Google Scholar]
- 5.Xue H, Srinivasan L, Jiang S, Rutherford M, Edwards AD, Rueckert D, Hajnal JV. Automatic segmentation and reconstruction of the cortex from neonatal MRI. Neuroimage. 2007;38:461–477. doi: 10.1016/j.neuroimage.2007.07.030. [DOI] [PubMed] [Google Scholar]
- 6.Prastawa M, Gilmore JH, Lin W, Gerig G. Automatic segmentation of MR images of the developing newborn brain. Medical Image Analysis. 2005;9:457–466. doi: 10.1016/j.media.2005.05.007. [DOI] [PubMed] [Google Scholar]
- 7.Weisenfeld NI, Mewes AU, Warfield SK. Highly accurate segmentation of brain tissue and subcortical gray matter from newborn MRI. MICCAI 2006. 2006:199–206. doi: 10.1007/11866565_25. [DOI] [PubMed] [Google Scholar]
- 8.Frangi AF, Niessen WJ, Vincken KL, Viergever MA. Medical Image Computing and Computer-Assisted Interventation (MICCAI) Springer; 1998. Multiscale Vessel Enhancement Filtering; pp. 130–137. [Google Scholar]
- 9.Roemer PB, Edelstein WA, Hayes CE, Souza SP, Mueller OM. The NMR phased array. Magnetic Resonance in Medicine. 1990;16:192–225. doi: 10.1002/mrm.1910160203. [DOI] [PubMed] [Google Scholar]
- 10.Wald LL, Carvajal L, Moyher SE, Nelson SJ, Grant PE, Barkovich AJ, Vigneron DB. Phased array detectors and an automated intensity-correction algorithm for high-resolution MR imaging of the human brain. Magnetic Resonance in Medicine. 1995;34:433–439. doi: 10.1002/mrm.1910340321. [DOI] [PubMed] [Google Scholar]
- 11.Lin FH, Chen YJ, Belliveau JW, Wald LL. A wavelet-based approximation of surface coil sensitivity profiles for correction of image intensity inhomogeneity and parallel imaging reconstruction. Human Brain Mapping. 2003;19:96–111. doi: 10.1002/hbm.10109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P. SENSE: Sensitivity encoding for fast MRI. Magnetic Resonance in Medicine. 1999;42:952–962. [PubMed] [Google Scholar]
- 13.Shen D, Davatzikos C. HAMMER: hierarchical attribute matching mechanism for elastic registration. IEEE Transactions on Medical Imaging. 2002;21:1421–1439. doi: 10.1109/TMI.2002.803111. [DOI] [PubMed] [Google Scholar]
- 14.Shattuck DW, Leahy RM. Automated graph-based analysis and correction of cortical volume topology. IEEE Transactions on Medical Imaging. 2001;20:1167–1177. doi: 10.1109/42.963819. [DOI] [PubMed] [Google Scholar]
- 15.Kirbas C, Quek F. A review of vessel extraction techniques and algorithms. ACM Computing Surveys. 2004;36:81–121. [Google Scholar]
- 16.Shi F, Fan Y, Tang S, Gilmore JH, Lin W, Shen D. Neonate brain MRI segmentation using subject-specific probabilistic atlas. SPIE Medical Imaging 2009; Florida. 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Joshi S, Davis B, Jomier M, Gerig G. Unbiased diffeomorphic atlas construction for computational anatomy. Neuroimage. 2004;23:151–160. doi: 10.1016/j.neuroimage.2004.07.068. [DOI] [PubMed] [Google Scholar]
- 18.Warfield SK, Zou KH, Wells WM. Validation of Image Segmentation and Expert Quality with an Expectation-Maximization Algorithm. MICCAI 2002. 2002:298–306. [Google Scholar]
- 19.Ca C, Kwan K, Evans R. BrainWeb: online interface to a 3-D MRI simulated brain database. NeuroImage. 1997;5 [Google Scholar]
- 20.Ashburner J, Friston KJ. Unified segmentation. Neuroimage. 2005;26:839–851. doi: 10.1016/j.neuroimage.2005.02.018. [DOI] [PubMed] [Google Scholar]
- 21.Yezzi A, Zollei L, Kapur T. A variational framework for integrating segmentation and registration through active contours. Med Image Anal. 2003;7:171–185. doi: 10.1016/s1361-8415(03)00004-5. [DOI] [PubMed] [Google Scholar]
- 22.Yushkevich PA, Piven J, Hazlett HC, Smith RG, Ho S, Gee JC, Gerig G. User-guided 3D active contour segmentation of anatomical structures: Significantly improved efficiency and reliability. Neuroimage. 2006;31:1116–1128. doi: 10.1016/j.neuroimage.2006.01.015. [DOI] [PubMed] [Google Scholar]
- 23.Dice LR. Measures of the Amount of Ecologic Association Between Species. Ecology. 1945;26:297–302. [Google Scholar]