PET imaging for the quantification of biologically heterogeneous tumours: measuring the effect of relative position on image-based quantification of dose-painting targets

Abstract

Quantitative imaging of tumours represents the foundation of customized therapies and adaptive patient care. As such, we have investigated the effect of patient positioning errors on the reproducibility of images of biologically heterogeneous tumours generated by a clinical PET/CT system. A commercial multi-slice PET/CT system was used to acquire 2D and 3D PET images of a phantom containing multiple spheres of known volumes and known radioactivity concentrations and suspended in an aqueous medium. The spheres served as surrogates for sub-tumour regions of biological heterogeneities with dimensions of 5–15 mm. Between image acquisitions, a motorized-arm was used to reposition the spheres in 1 mm intervals along either the radial or the axial direction. Images of the phantom were reconstructed using typical diagnostic reconstruction techniques, and these images were analysed to characterize and model the position-dependent changes in contrast recovery. A simulation study was also conducted to investigate the effect of patient position on the reproducibility of PET imaging of biologically heterogeneous head and neck (HN) tumours. For this simulation study, we calculated the changes in image intensity values that would occur with changes in the relative position of the patients at the time of imaging. PET images of two HN patients were used to simulate an imaging study that incorporated set-up errors that are typical for HN patients. One thousand randomized positioning errors were investigated for each patient. As a result of the phantom study, a position-dependent trend was identified for measurements of contrast recovery of small objects. The peak contrast recovery occurred at radial and axial positions that coincide with the centre of the image voxel. Conversely, the minimum contrast recovery occurred when the object was positioned at the edges of the image voxel. Changing the position of high contrast spheres by one-half the voxel dimension lead to errors in the measurement of contrast recovery values which were larger than 30%. However, the magnitudes of the errors were found to depend on the size of the sphere and method of image reconstruction. The error values from standard OSEM images of the 5 mm diameter sphere were 20–35%, and for the 10 mm diameter sphere were 5–10%. The position-dependent variation of contrast recovery can result in changes in spatial distribution within images of heterogeneous tumours. In experiments simulating random set-up errors during imaging of two HN patients, the expectation value of the correlation was ~1.0 for these tumours; however, Pearson correlation coefficient values as low as 0.8 were observed. Moreover, variations within the images can drastically change the delineation of biological target volumes. The errors in target delineation were more prominent in very heterogeneous tumours. As an example, in a pair of images with a correlation of 0.8, there was a 36% change in the volume of the dose-painting target delineated at 50%-of-max-SUV (ROI_50%). The results of these studies indicate that the contrast recovery and spatial distributions of tracer within PET images are susceptible to changes in the position of the patient/tumour at the time of imaging. As such, random set-up errors in HN patients can result in reduced correlation between subsequent image-studies of the same tumour.

1. Introduction

Molecular imaging modalities, such as positron emission tomography (PET), have great potential to detect and measure tumour-specific characteristics in vivo and to be used to guide cancer therapies. For example, it has been shown that the preferential retention of specific PET radiopharmaceuticals within tumours correspond to increased metabolic function (Reivich et al 1979, Rohren et al 2004), proliferation (Shields et al 1996, Buck et al 2003), angiogenesis (Cai et al 2006) and low oxygen concentration or hypoxia (Fujibayashi et al 1997, Dehdashti et al 2003). In radiation oncology, it has been suggested that the spatial distribution of PET radiotracers can be used to conform the radiotherapy dose distributions to target sub-volumes of biological activity within tumours, and treatment fields could be adapted to maximize the local response of tumours. Biologically targeted radiotherapy to tumour sub-volumes has been termed ‘dose-painting’ (Ling et al 2000, Bentzen 2005, Thorwarth et al 2007). However, a number of object and imaging-system specific factors limit the ability of PET to provide absolute quantification of the spatial and functional heterogeneities of tumours. These include the spatial resolution, sampling interval (Hoffman et al 1979, Huang et al 1980, Kessler et al 1984, Bendriem et al 1989, Miller et al 1990), temporal resolution of the detectors (Bailey et al 2005, Lewellen 2008), the dimensions, shape and contrast of the object (Hoffman et al 1979, Mazziotta et al 1981), the position (Bendriem et al 1989, 1991) and motion of the object (Nehmeh et al 2002, Pevsner et al 2005) during image acquisition.

In the three decades since the invention of PET imaging, the quantitative accuracy of PET imaging systems has vastly improved through developments in detector materials and advances in detector-system designs (Lewellen 2008). Additionally, CT-based attenuation correction (Huang et al 1979, Burger et al 2002) and iterative reconstruction methods (Miller and Wallis 1992, Hudson and Larkin 1994, Gutman et al 2003) have improved image quality (Tarantola et al 2003). However, limited spatial resolution is inevitable in all imaging systems due to finite detector size, and so it remains a source of error in the quantification and delineation of small objects (dimensions smaller than twice the FWHM image resolution). This impact within images is termed the partial volume effect (PVE) and quantified by the recovery coefficient (RC)—a ratio of the maximum activity concentration measured in a reconstructed image (contrast recovery) divided by the actual specific activity at the time of imaging (Hoffman et al 1979, Soret et al 2007). The PVE is a composite effect of the three-dimensional blurring from the system response function and the discrete sampling process or tissue fraction effect (Aston et al 2002), which sums the activity of all structures that fall within an image voxel. Due to the fixed sample separation and discrete nature of block detector systems, RC values vary systematically with the position of the object relative to the face of the detector crystals. This position-dependence was discussed by Hoffman et al (1982) when they calculated and measured the intrinsic spatial resolution of coincidence detectors (Hoffman et al 1982). Because discretization of the continuous tracer distribution occurs during both the image acquisition and reconstruction processes, PVE depends on both the detector system and the reconstruction method.

A number of subsequent studies have evaluated the position dependence along the axial direction of multi-slice PET systems (Kessler et al 1984, Bendriem et al 1989, Miller et al 1990, Pevsner et al 2005). In the axial direction, the peak observed activity occurs when the object is located at the axial centre of the plane, and observed activity falls off toward the intersection of adjacent imaging planes (Bendriem et al 1989, Miller et al 1990). Miller et al (1990) measured the recovery coefficient errors along the z-axis of a multislice PET scanner and defined a unique metric, E_rc, to quantify these errors. In their work, the single largest, and single smallest, measurements were used to calculate the error metric, and E_rc was defined as the difference between the largest and smallest measured RC values normalized by the largest RC measurement.

Like Miller, most studies have focused on the variations in contrast recovery and RC values due to displacement in the axial direction (Bendriem et al 1989, Miller et al 1990, Pevsner et al 2005, Hoffman et al 1982), and little work has been done to investigate RC variations along the radial direction. In the radial direction, there is finer sampling and peak activity is no longer located at a fixed physical point relative to a coincident pair of detectors. Even so, significant variation in RC can be expected due to the tissue-fraction effect that occurs as an object is moved between and across the discrete transverse pixels. In this study, we have characterized the systematic axial and radial variation in contrast recovery for objects with dimensions of one to four times the axial sampling interval of a whole-body PET system, and investigated the effect of this uncertainty for the quantitative imaging of head and neck tumours.

2. Methods and materials

2.1. Image acquisition and reconstruction

An experiment was designed and conducted to investigate the limitations of a commercial whole-body PET imaging systems to quantify activity within sub-tumour volumes. We specifically measured the sensitivity of measurements to small changes in position. The GE Discovery VCT, a multi-slice PET/CT system, was used to repeatedly acquire images of a phantom, while the position of the phantom was incrementally changed between each image acquisition. For both 2D and 3D acquisition mode, the nominal resolution (provided by the manufacturer) was 5.0 cm (full width half maximum (FWHM) of point-spread function) at a 1 cm off-axis, for both transverse and axial measurements, with the FWHM increasing to 5.4 cm (transverse) and 5.6 cm (axial) at a 10 cm off-axis. Published reports on the spatial resolution of this model of PET scanner also showed this region of fairly uniform and isotropic resolution (Teraas et al 2007). As the majority of tumours fall inside this central region during imaging studies, all measurements were made within a radial distance of 10 cm off the centre of the scanner bore. 2D and 3D PET image acquisitions of a unique PET phantom set-up were performed, and the images were reconstructed with reconstruction parameters used in typical clinical PET imaging.

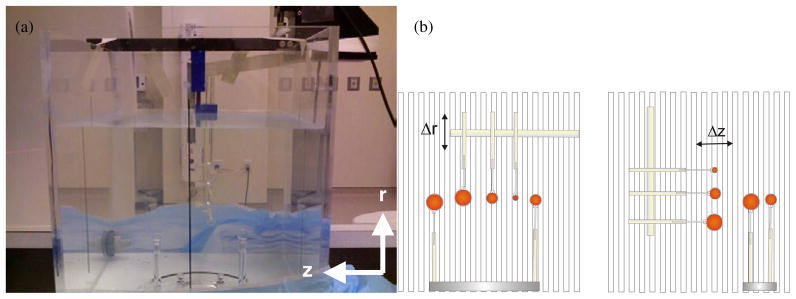
The phantom consisted of small acrylic spheres, which were filled with identical activity concentrations of ¹⁸F radionuclide and placed in a 15 L water bath. The spheres were surrogates for sub-tumour regions of biological heterogeneities with the diameters of 5 mm, 10 mm and 15 mm, where these dimensions were on the same order as and up to 4.5 times the axial sampling interval of the PET scanner (Teraas et al 2007). The water bath provided a medium for attenuating and scattering of the emitted photons. Three spheres were arranged on a rigid acrylic rod such that the centres lay along a single plane, where this plane was perpendicular to the direction of motion (see figure 1). Between image acquisitions, a motorized-arm, the Standard Imaging 1D controller arm (Standard Imaging, Inc.), was used to shift these three spheres sequentially, with a positioning accuracy of ±0.05 mm. A total of 15 discrete radial positions and 15 axial positions were sampled, where each position of the phantom was 1 mm apart from the prior position.

Figure 1.

Picture (a) and illustration (b) of the phantom used to investigate the precision of a PET imaging system, specifically the quantitative errors associated with the relative position of an object. (a) The phantom consisted of spheres of radioactivity submerged in a water bath. This phantom was repeatedly imaged with identical acquisition and reconstruction parameters. Between each acquisition, three spheres were repositioned at 1 mm increments along either the radial direction (Δr) or the axial direction (Δz). These three spheres were arranged as shown in the illustrations (b), where their centres lay along a single plane and perpendicular to the direction of motion. Vertical lines in the illustration depict axial slice separation as defined by the orientation of the detector rings. Two additional spheres were also present in the phantom; however, these were fixed to a stationary base and their position kept constant for all images.

Because of the Poisson nature of photon imaging, there is some intrinsic variability between subsequent images, even if all physical factors were kept constant. This statistical variation is especially noticeable in single voxel measurements such as contrast recovery. As such, two additional spheres were placed within the imaging field of view (FOV) but were kept stationary during all image acquisitions. The diameters of these stationary spheres were equal to the diameter of the larger moving spheres and mid-way between that of the two smaller spheres (i.e. 15 mm and 7 mm respectively). We would use the contrast recovery values from these stationary spheres to assess the intrinsic variations associated with our measurements and determine if observed fluctuations are above the ‘noise’ background of our measurement technique, and so truly position-dependent.

Axial and radial measurements were performed separately, but similar techniques of image acquisition and analysis were employed. 2D and 3D images were acquired for each position of the phantom. In 2D acquisition mode, coincident photon counts were acquired for 4 min; however, with the increased sensitivity and higher count rate of 3D mode, the acquisition time was reduced to 3 min per position. The PET images, which corresponded to each position of the spheres, were reconstructed over a 50 cm radial FOV using a grid of 128 × 128 × 47 yielding the voxels of 3.9 × 3.9 × 3.3 mm³. Clinical reconstruction protocols were used to generate these images. This included ordered subset expectation maximization (OSEM) with the reconstruction parameters set at 28 subsets of projection data (counts) per iteration for two iterations, and post-reconstruction smoothing filters of 3 mm (FWHM) were applied in the transverse plane, with no smoothing along the z-axis. Alternate reconstruction methods were also investigated, including filtered back-projection (FBP) with a noise-reducing Hann filter with a cut-off width of 7 mm, and OSEM images reconstructed using wider smoothing filters (7 mm FWHM).

2.2. Quantifying the variation in contrast recovery, Ê_M

The Miller et al (1990) recovery coefficient error metric, E_rc, was adapted for the analysis of position-dependent variations of contrast recovery. However, we modified the definition of the metric to reduce the effect of Poisson noise and extended the original definition to include variations measured along any path and relative to any sampling interval of the PET imaging system. In this way, a single error metric was used to describe the measurements along any axis of the PET scanner.

The original definition of the Miller et al error metric used recovery coefficients or RC values, where RC = M/true activity and M is the contrast recovery or the maximum observed activity in a PET representation of the object. However, during data analysis, all images were decay corrected to a common reference time. Because of these corrections for radioactive decay, the common factor of ‘true activity’ could be eliminated and decay-corrected M values used in place of RC values in the definition of the error metric. To reflect these changes, the adapted Miller et al metric was now denoted by Ê_M and defined by

$${\widehat{E}}_M\equiv \frac{({\widehat{M}}_{\text{peak}}-{\widehat{M}}_{\text{trough}})}{\overline{M}}$$ (1)

where M̂_peak and M̂_trough were the expectation value (mean) of the maximum and minimum contrast recovery of an arbitrary voxel, respectively. The constant, M̄, is the normalizing factor or mean contrast recovery, becoming $\overline{M(z)}$ for measurements along the axial direction (z-axis) and $\overline{M(r)}$ along the radial direction (either the x- or y-axis).

The error metric, Ê_M, describes the variability of contrast recovery within reconstructed PET voxels and is linked to the magnitude of change from M_peak to M_trough values. However, for this investigation, the Ê_M error values were not calculated, but were derived from empirical fits of the measurements of contrast recovery (within the image of the spheres) versus position. The cyclical patterns of the measurements were modelled to first-order periodic functions as

$$\left(\frac{M(r)}{\overline{M(r)}}\right)-1=\left(\frac{{\widehat{E}}_M}{2}\right)cos\left(2\pi \frac{(r-r_0)}{{\lambda }_M}\right)$$ (2)

where r represents the radial position of the object at the time of measurement and r₀ is a reference position. For axial measurements, these symbols were replaced by z and z₀. These reference positions can be arbitrarily assigned; however, for the phantom experiments, r₀ and z₀ referred to the initial position of the spheres and corresponded to points near the centre of the scanner bore. The cycle length, λ_M, of the fitted functions represented a distance twice the displacement between consecutive maximum and minimum contrast recovery along a direction of motion. Likewise, Ê_M was the peak-to-trough amplitude of the corresponding empirical function.

It should be noted that with coincident detector systems, the shape of the response functions becomes flatter and wider at radial positions closer to either face of the coincident detectors (DeGrado et al 1994), and the magnitude of the Ê_M would depend on the width of the response function. However, these experiments were designed to collect data on contrast recovery over multiple voxels, while ensuring that any changes in resolution and sensitivity would be small and so not reflected in the results. To accomplish this, the spheres were arranged in a single plane that was perpendicular to the direction of displacement. The ‘in-plane’ design ensured that the spheres moved through similar changes of intrinsic resolution along the radial direction, and similar changes in sensitivity along the axial or radial directions. Additionally, measurements, which would be directly compared to each other, were made within a maximum distance of 1.5 cm of all other measurements.

In addition to fitting empirical functions in the spatial domain, the contrast recovery values from 2D and 3D images were further analysed in the spatial frequency domain. The discrete Fourier transforms of the normalized contrast recovery values, M/M̄, were calculated for each sphere and each direction of motion. This analysis separated any unique frequency components of the M/M̄ values from the inherent noise in our measurements. Unique frequencies were recognized as distinct peaks in power spectrum plots of the squared Fourier transform versus spatial frequency. Any dominant spatial frequencies identified using this Fourier analysis technique were compared to the cycle length of the sinusoidal fits, and also to the sampling interval of the PET imaging system.

2.3. Implication for imaging heterogeneous tumours

A computer simulation study was conducted to investigate the effect of positioning errors on the reproducibility of quantitative PET imaging of biologically heterogeneous head and neck tumours. The models of contrast recovery versus relative displacement, as described in equation (2), were used to calculate the changes in the image intensity of each voxel (voxel value) within PET images that occur due to differences in the position of a patient at the time of acquisition. PET images of two head and neck cancer (HN) patients were used for this study. These images were sampled from a database of anonymized PET/CT studies conducted at the PET Imaging Center and were selected as representative examples of a highly heterogeneous tumour (many distinct sub-regions) and a more biologically uniform (few sub-regions) tumour. Here, individual sub-regions within the tumour were identified based on the gradient or relative difference in intensity values between adjacent voxels. Using a gradient analysis method, two adjacent voxels with intensity values within ±50% of each other were assigned to a single contiguous sub-region. This ±50% gradient criterion was a semi-arbitrary choice; however, the voxels with intensity values within ±50% were considered to either contain cancer tissue with similar biological function, or contain individual sub-regions of biological activity that were too close together to be resolved by the imaging system.

The two HN cancer patients selected for this retrospective investigation had similar tumour histology but different tumour appearances. Both patients had been previously diagnosed with squamous cell carcinoma of the base of the tongue and had a second larger mass of involved lymph nodes in the neck. These patients had been imaged on a clinical PET/CT scanner using [¹⁸F] FDG, a PET radiotracer that is preferentially retained within tissue with high rates of metabolism. However, the tumour (primary and involved node) of patient #1 was considered very heterogeneous, and the initial FDG PET image showed many distinct sub-regions of proliferative activity, surrounding a central region of low tracer-uptake. Additionally, the region of interest (ROI) where the voxel values exceeded 50% of the maximum standard uptake value (SUV_max) occupied 413 voxels or approximately 27 cm³. Conversely, the initial FDG PET image, of the tumour in patient #2, showed a uniform tracer distribution with larger contiguous regions of proliferative activity, and fewer distinct sub-regions of high and low tracer uptake. The ROI_50% (ROI where voxels value ≥ 0.5*SUV_max) within this tumour was also smaller and occupied approximately 12 cm³. The distributions of radiotracer in PET/CT images provide a qualitative appreciation of the distinction in heterogeneity between the two tumours.

The PET images of the HN tumours were segmented into sub-regions of contiguous voxels with values within ±50% of each other. The centre of activity of each sub-region was then randomly assigned an initial position relative to the centre of each of its constituent voxels. This randomization was implemented to account for the fact that the exact position of the centre of activity in the initial PET voxels was not known. As such, the probability distribution functions of initial position (xyz_initial) were 3D Rect functions with widths equal to the voxel dimensions.

Subsequent images were then simulated to incorporate random set-up errors or changes in the positioning of the patient within the scanner. No comprehensive studies have been published on the day-to-day positioning of patients for PET/CT imaging studies. However, in the oncological setting where head and neck patients are typically imaged in the treatment position, the positioning errors in multi-day imaging studies would be expected to be similar to those that occur during fractionated radiotherapy. The day-to-day random set-up error seen during fractionated radiotherapy would be perceived as discrete displacements of the patient/tumour between image acquisitions. As such, the positioning errors used for this study were the typical random set-up errors associated with fractionated radiation therapy of HN cancer patients. Set-up errors of the HN tumours were simulated as combinations of linear shifts along the x-, y- and z-axes. The magnitude of the randomized displacements, between the initial position of a sub-region (xyz_initial) and its final position (xyz_final), was sampled from Gaussian distributions with standard deviations of σ(Δx) = 4.4 mm, σ(Δy) = 5.1 mm and σ(Δz) = 3.4 mm and based on the study of random set-up errors published by Hong et al (2005). Only rigid displacements were simulated and the entire tumours (and all sub-regions) were assumed to move along the same paths, and all dimensions were defined within the reference frame of the PET scanner.

The changes in voxel values, which occur when the patient position is varied, were calculated by scaling each voxel value in the images by the ratio of the contrast recovery values at the initial position, M(xyz_initial), and the final position, M(xyz_final), of the centre of activity within that voxel. If the simulated set-up error moved the centre of activity towards the peak of the response function, then the voxel value was increased in the subsequent image. Alternatively, if the centre of activity of the voxel moved towards the edge of the image plane, then the value of that voxel decreased. M(xyz) values were calculated as the product M(x) × M(y) × M(z), where these M values were interpolated from the empirical functions of contrast recovery versus position described in equation (2). The Ê_M values used for these functions depended on the dimension of the sub-region and corresponded to the contrast-recovery error measured in spheres of diameter similar to that of sub-region. One thousand random set-up errors were simulated for each HN patient, and Pearson’s correlation coefficient was used to assess the resulting changes in the spatial distribution within the images.

3. Results

3.1. Position-dependent changes in contrast recovery, M

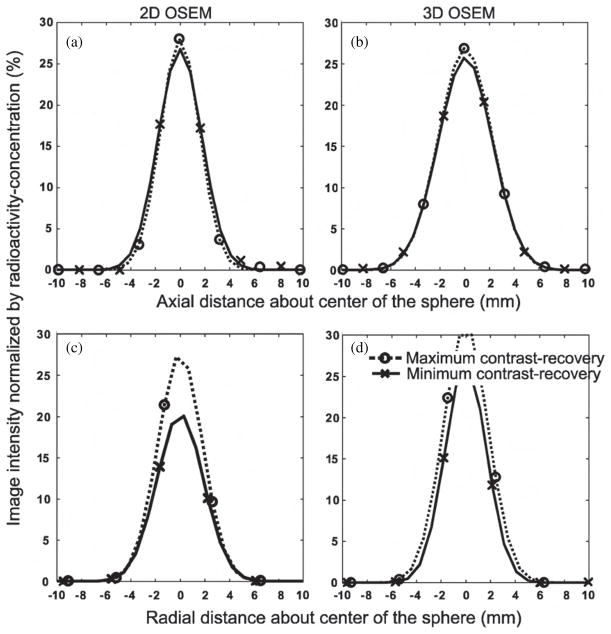
The ability to use PET imaging to quantify activity within small objects showed strong dependence on their position relative to the centre of the voxel in both the axial and radial directions. Figure 2 plots the image intensity value along line profiles through a central axis of the 5 mm sphere. These plots show the changes in image intensity, seen in 2D and 3D reconstructed images, which occur as the position of the sphere was altered at the time of acquisition. Figures 2(a) and (b) show line profiles generated from axial repositioning of the sphere, and figures 2(c) and (d) correspond to radial repositioning. The dotted and solid lines respectively indicate these maximized and minimized line profiles and the x and o symbols correspond to individual voxels that contributed to the line profiles.

Figure 2.

Line profiles from OSEM reconstructed images of the 5 mm diameter sphere. Abscissas of all plots were calculated about the centre of the sphere. Profile points (O and X) were the image intensity values (voxel values) in PET images where the contrast recovery was maximized (O) or minimized (X) due to the position of the sphere relative to the voxel separation (i.e. relative to the detector rings and/or reconstruction grid). Profile points were fitted to a Gaussian curve to create line profiles as shown. Dotted curves are line profiles corresponding to maximum contrast recovery and solid curves correspond to minimum contrast recovery. The line profiles shown in plots (a) and (c) were sampled from 2D images where the (a) axial or (c) radial position corresponded to an extremum of the contrast recovery. Profiles (b) and (d) represent voxel values from the corresponding 3D images.

The line profiles of figure 2 show that the ability to use imaging to quantify activity within the spheres has a strong dependence on the position relative to the boundaries of the voxel (or reconstruction grid). These plots also show that the decrease in observed activity of the sphere was accompanied by an increase of its apparent diameter. When the sphere was positioned at the centre of the voxel, the observed activity within the reconstructed image was focused within a single image voxel, as indicated by a prominent o symbol. At this position, the contrast recovery was maximized and a M_peak value was found. However, when the sphere was positioned at the abutment of voxels, the image intensity was no longer focused. In the representative line profiles, we saw two voxels with similar intensities, and these were indicated by the x symbols. Because the observed activity was distributed and the contrast recovery was minimized to M_trough, which was as low as 65% of the value from the centrally located sphere.

3.2. Dependence on image reconstruction

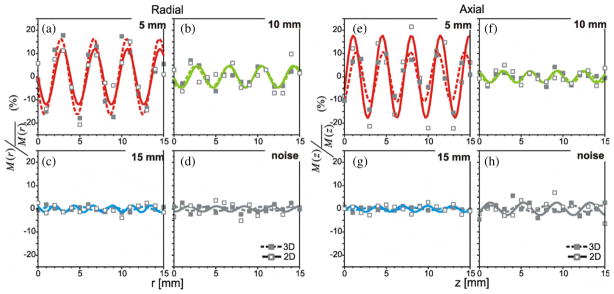
The differences in image intensity described above were part of a systematic trend observed between the position of the spheres and the normalized contrast recovery, M/M̄. This position dependence was associated with well-defined periodic patterns of M/M̄ versus position as shown in figures 3 through 6, where each plot represents changes in the contrast recovery as the spheres were incrementally repositioned along the radial (a), (b), (c), (d) or axial (e), (f), (g), (h) directions. Figure 3 plots the normalized contrast recovery values, from PET data of the phantom acquired in 2D mode (solid lines) and 3D mode (dashed lines), and derived from images reconstructed with a standard OSEM algorithm. Figures 3(a) and (e) show the contrast recovery in OSEM images of the 5 mm diameter sphere corresponding to incremental positions of the sphere along the radial and axial directions respectively. Figures 3(b) and (f) are the plots of contrast recovery in OSEM images versus incremental position for the 10 mm diameter sphere; figures 3(c) and (g) were equivalent plots for the 15 mm diameter sphere. Figure 3(d) is the contrast recovery in OSEM images of a stationary sphere. The two stationary spheres were kept at the same position between image acquisitions, while the other three spheres present in the phantom were moved. As such, the variations observed in measurements of the two stationary spheres represent an approximation of image noise or the intrinsic uncertainty associated with repeated measurements of contrast recovery.

Figure 3.

Relative change in observed activity (normalized by mean) versus position for OSEM reconstructed images that were acquired in 2D (–□–) and 3D (–■–) mode. Images were reconstructed on 3.9 × 3.9 × 3.3 mm³ voxels and a 3 mm (FWHM) post-reconstruction filter applied in the transverse plane. Plots (a), (b) and (c) show 5 mm, 10 mm and 15 mm diameter spheres, as they were moved in 1 mm intervals along the radial direction. Plots (e), (f) and (g) show 5 mm, 10 mm and 15 mm diameter spheres, as they were moved in 1 mm intervals along the axial direction. Figures (d) and (h) show random variations within the normalized M values for the stationary spheres. The sinusoidal functions, which were fitted to the data, are also shown.

Figure 6.

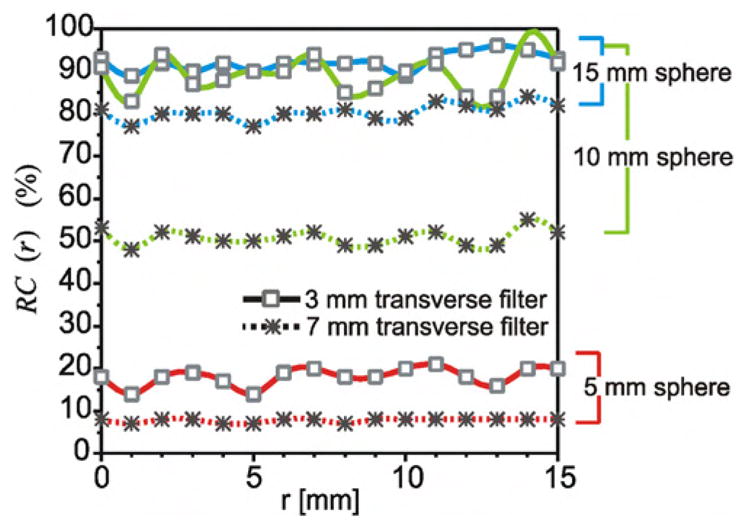
Absolute change in recovery coefficients versus position for OSEM reconstructed images of 2D acquisition PET acquired with the spheres at intervals along the radial direction. Plots show recovery coefficients (max voxel value expressed as a per cent of activity) of the 5 mm, 10 mm and 15 mm diameter spheres from images reconstructed on 3.9 × 3.9 × 3.3 mm³ voxels, with post-reconstruction smoothing filters of FWHM widths of 3 mm (–□–) and 7 mm (–*–).

From these figures, we observed that the contrast recovery in OSEM images of the 10 mm and 5 mm spheres shows sequential patterns of increases then decreases in contrast recovery as these spheres were moved within and across voxels. The data points from both the 2D and the 3D images of these spheres were well fitted to sinusoidal functions of position. For the 5 mm diameter sphere the goodness of fit was above r² = 0.8 for all reconstructions (figures 3(a) and (e)), and the goodness of fit for the 10 mm diameter sphere in OSEM reconstructed images ranged from 0.5 (in 2D images) to 0.8 (in 3D images). This cyclical behaviour was not detected in the contrast recovery from the OSEM images of the 15 mm diameter sphere, and the data points could not be fit to the sinusoidal model (r² < 0.4). It is likely that any variations observed were on the same magnitude as the intrinsic fluctuations of contrast recovery of the OSEM images. This intrinsic fluctuation for repeated contrast-recovery measurements, which occur due to ‘noise’ in the OSEM images, can be seen in figures 3(d) and (f).

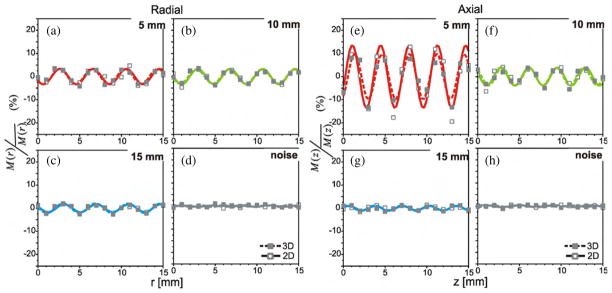
The λ_M values derived from the fitted sinusoidal functions of M/M̄ versus position for the 5 mm diameter spheres showed cycle lengths that correspond to the dimension of the voxels (sample separation). Further frequency-domain analyses confirm these findings; Fourier analysis of the 2D and 3D images showed distinct spatial periodicity among the contrast recovery values of the two smaller spheres. For those values, measured as the spheres were incrementally displaced along the axial direction, distinct spectral peaks were seen at 3.0 cycles cm⁻¹ (λ_M = 3.3 mm). Similarly, a dominant spatial frequency of 2.5 cycles cm⁻¹ (λ_M = 4.0 mm) was observed in the contrast recovery measured along the radial direction. This periodicity coincides with the radial and axial voxel dimensions of 3.9 mm and 4.3 mm. However, distinct spectral peaks were not observed for the 15 mm diameter sphere, in 2D and 3D acquired data. From these results, we saw that for the standard OSEM images, the cyclical pattern of contrast recovery versus position appeared to be limited to the objects smaller than 15 mm in diameter. However, this may be because the magnitude of the noise associated with repeat measurements with OSEM image-derived values exceeds any position-dependent variation that may or may not have occurred for this sphere. With the much lower intrinsic fluctuations, of the contrast recovery values derived from FBP images, we did observe distinct cyclical trends of position-dependent recovery even for the largest diameter sphere.

The plots of figure 4 describe this systematic trend in contrast recovery as observed in the FBP reconstructed images. These plots were derived from reconstructions of the same PET acquisition datasets as used for the standard OSEM reconstruction, and so the sub-plots (a), (b), (c) and (d) each represent the contrast recovery values for a particular sphere, as detailed in the preceding description of figure 3. Figures 4(d) and (h) show the negligible intrinsic variations in the contrast recovery derived from the FBP images. Because of the low noise in the data derived from FBP images, the systematic variations could be observed for the 15 mm sphere. In fact, the contrast recovery values were well fit to the same type of empirical model that governed the position dependence of the smaller diameter spheres. The sinusoidal fits of M/M̄ versus axial and radial positions were well above r² = 0.6 for all sphere diameters and all acquisition modes. Spectral analysis of the contrast recovery data from the 2D and 3D FBP images confirmed the spatial periodicity for all three spheres diameters; again distinct spectral peaks were observed at frequencies corresponding to the voxel dimensions.

Figure 4.

Relative change in observed activity (normalized by mean) versus position for FBP reconstructed images of 2D (–□–) and 3D (–■–) acquisition PET. Images were reconstructed on 3.9 × 3.9 × 3.3 mm³ voxels using a 7 mm Hann filter. Plots (a), (b) and (c) show contrast recovery of the 5 mm, 10 mm and 15 mm diameter spheres at intervals along the radial direction. Plots (e), (f) and (g) show normalized values measured along the axial direction. Plots (d, h) were obtained from analysis of the stationary spheres. Sinusoidal functions, which were fitted to the data, are also shown.

As expected from the plots of contrast recovery versus position, the contrast recovery error values, Ê_M, depend on the diameter of the sphere and methods of image reconstruction. The full list of the Ê_M values is detailed in table 1. The Ê_M values from standard OSEM images of the 5 mm diameter sphere were 20–35%, and for the 10 mm diameter sphere were 5–10%. When a reliable functional fit was not available for spheres of larger diameters, then the Ê_M value could not be calculated. However, the mean amplitude of change in the contrast recovery of OSEM images for the 15 mm diameter sphere was less than 3%, where this error was calculated as the difference between the mean of all contrast recovery values greater than M̄ and the mean of all values less than or equal to M̄.

Table 1.

Ê_M values derived from the empirical sinusoidal model of contrast recovery versus position, where the cycle length approximated the voxel dimension. Error bars (± 1 standard deviation) are included in parentheses. The contrast recovery error metric was not derived where there was a poor fit to the model, i.e. r²≤0.40.

Direction of displacement	Reconstruction method	Sphere diameter (mm)	ÊM (±std)%
			2D	3D
Radial	OSEM 3 mm transverse filter without axial smoothing	5	24 (4)	33 (3)
		10	10 (3)	9 (1)
		15	–	–
	FBP 7 mm Hann window without axial smoothing	5	7 (1)	7 (1)
		10	7 (1)	6 (1)
		15	3 (0)	4 (0)
	OSEM 3 mm transverse filter with axial smoothing	5	26 (4)	33 (4)
		10	10 (2)	10 (1)
		15	–	–
	OSEM 7 mm transverse filter with axial smoothing	5	11 (2)	15 (2)
		10	8 (2)	8 (1)
		15	3 (1)	4 (1)
Axial	OSEM 3 mm transverse filter without axial smoothing	5	36 (4)	22 (2)
		10	5 (0)	5 (1)
		15	–	–
	FBP 7 mm Hann window without axial smoothing	5	27 (2)	20 (2)
		10	8 (1)	8 (1)
		15	2 (0)	2 (0)
	OSEM 3 mm transverse filter with axial smoothing	5	24 (3)	15 (2)
		10	5 (1)	6 (1)
		15	4 (1)	2 (1)
	OSEM 7 mm transverse filter with axial smoothing	5	25 (3)	14 (2)
		10	7 (1)	7 (1)
		15	3 (1)	2 (0)

For the FBP reconstructed images, the Ê_M values were 20–25%, 8% and 2% for the 5 mm, 10 mm and 15 mm diameter spheres respectively. Even though the cyclical patterns of M versus position were well defined for all sphere diameters in FBP images, the peak-to-trough amplitudes were smaller for this method of reconstruction. We also saw that, with the FBP method used, the Ê_M values were larger for displacements along the axial direction. This difference occurred because noise reduction and smoothing were applied in the transverse plane only; there was no axial component to the filter used during FBP image reconstruction.

Additional analysis also confirmed this observed dependence between the Ê_M values and the amount of filtering applied during image reconstruction. Figures 5 and 6 illustrate the effect of post-reconstruction smoothing on the pattern and magnitude of contrast recovery. Figure 5 is a plot of the corresponding contrast recovery values versus radial position as derived from the heavily smoothed 2D OSEM images, and figure 6 plots the magnitude of the recovery coefficients from these images. The Ê_M values were largest within images reconstructed using the OSEM algorithm with minimal smoothing (3 mm FWHM post-filter), and the magnitudes of these position-dependent variations were reduced by increasing the width of the smoothing filters used during image reconstruction. In figure 5(d), we see that smoothing did not reduce the intrinsic fluctuations of contrast recovery and as such, cyclical behaviour of the 15 mm sphere, as seen in FBP images, was not revealed. In fact, the contrast recovery for all sphere diameters lost some of their cyclical nature as the magnitude of peak-to-trough variation was decreased. For example, increasing the OSEM filter to 7 mm (FWHM) decreased the radial positioning error for the 5 mm sphere to 10%, while the 10 mm sphere showed a smaller change as Ê_M were reduced to a value of 8%, and these changes could be seen in figures 5(a) and (b) respectively.

Figure 5.

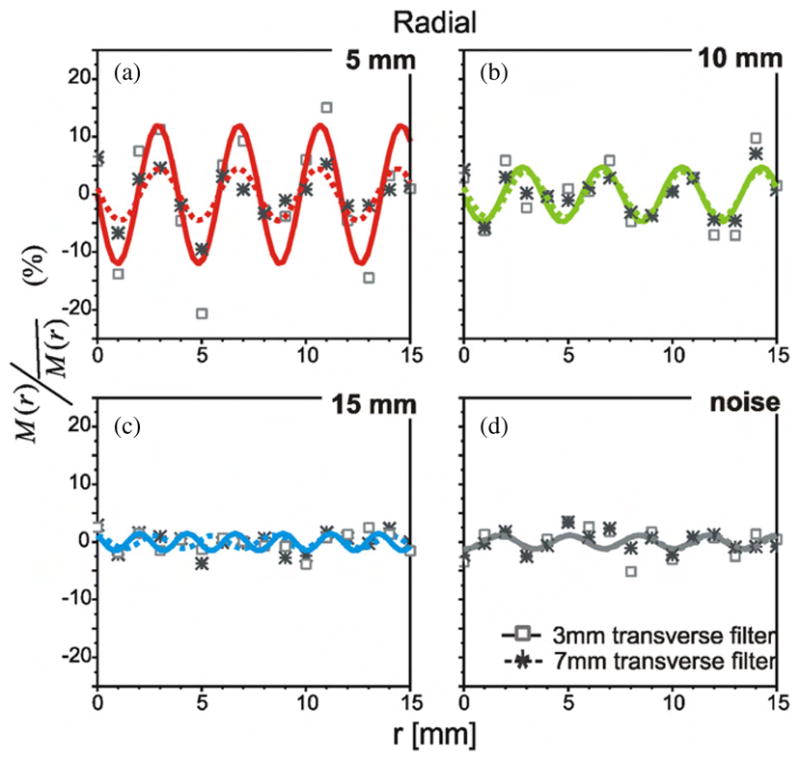
Relative change in observed activity (normalized by mean) versus position for OSEM reconstructed images of 2D acquisition PET with the post-reconstruction smoothing filters of 3 mm (–□–) and 7 mm (–*–) FWHM. Images were reconstructed on 3.9 × 3.9 × 3.3 mm³ voxels, and post-reconstruction smoothing filters were applied in the transverse plane. Plots show contrast recovery and the sinusoidal functions, which were fitted to the data. Plots (a), (b) and (c) show the 5 mm, 10 mm and 15 mm diameter spheres at intervals along the radial direction, respectively, and plots in (d) were obtained from analysis of the stationary spheres. Note that the plots and fitted functions for the 3 mm smoothing filter (–□–) are the same as shown in figure 3, where the effects of 2D versus 3D acquisition were compared.

Post-reconstruction filtering reduced the position-dependent variations observed in contrast recovery of the smallest spheres; however, this excessive smoothing also severely decreased the ability to detect the spheres. As such, the RC values of these spheres were reduced to less than one-half of the value seen in the unsmoothed images. This loss of quantitative accuracy due to smoothing, and the associated reduction of RC values, was shown in figure 6. In the same way, reconstruction with the FBP algorithms resulted in smaller Ê_M error values, but lower RC values. As such, there is an unfortunate trade-off between imaging accuracy (large RC values) and precision (the magnitude of variation of these RC values).

However, the patterns of contrast recovery versus position were independent of the acquisition method. This conclusion was based on the large p-values (>0.05) obtained in Kolmogorov–Smirnov statistical tests on the normalized contrast recovery from the 2D images and corresponding 3D images for OSEM and FBP. Here, the null hypothesis of the statistical tests was that the M/M̄ values, from the 2D and corresponding 3D image sets, were sampled from some common continuous function of position. In fact, for OSEM images of the 10 mm and 5 mm diameter spheres, the p-values were all well above 0.3 for radial displacement, and above 0.6 for axial displacements.

The amplitude of this peak-to-trough variation depends on the diameter of the sphere and the method of image reconstruction. However, there was a trade-off between quantitative accuracy and quantitative precision. The OSEM reconstruction method, with minimal post-reconstruction smoothing, generated voxel values that better estimated the ‘true activity’ within even the smallest diameter spheres of the phantom. However, this method of reconstruction would be more affected by changes in the patient positioning, as the contrast recovery had strong dependence on the position of the sphere relative to the voxel separation employed.

3.3. Implication for imaging heterogeneous tumours

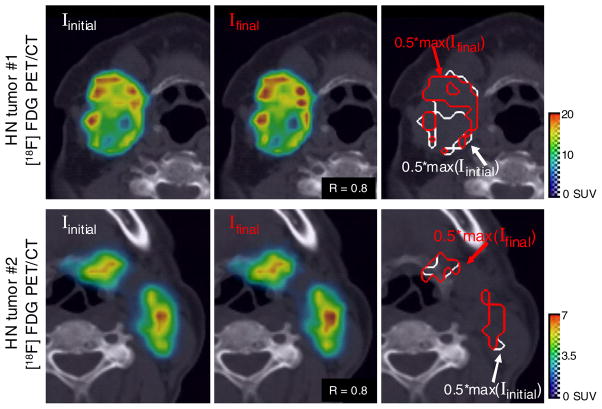
The spatial distribution of tracer in the PET images of heterogeneous tumours depends on the relative position of the patient at the time of imaging. Examples of the variation in spatial distribution with patient position are demonstrated in figure 7, which shows images of heterogeneous HN tumours before and after a simulated set-up error. In figure 7, the images across each row are of the same patient and show a cross-section through identical transverse planes of that patient’s tumour. The initial image (I_initial) of the tumour is shown to the far left, and the central images show images generated after a randomized set-up error (I_final). The Pearson correlation coefficient (calculated for voxels of a ROI_50% defined in the initial tumour) between each pair of images was 0.8. However, in the very heterogeneous tumour of patient #1, the presence of new ‘hot spots’ and ‘cold spots’ is visible in a visual comparison of I_initial and I_final, while differences in the appearance of the images of patient #2 are more difficult to discern visually.

Figure 7.

[¹⁸F] FDG-PET tracer distribution in heterogeneous HN tumours, and the apparent redistribution and quantitative errors that would occur if this patient were subsequently scanned; however, the patient was placed at a slightly different position in the scanner bore (due to a random set-up error). Set-up errors were modelled as rigid translations along six degrees of freedom, where the magnitude and the direction of motion were randomly sampled from Gaussian distributions with standard deviations of σ(Δx) = 4.4 mm, σ(Δy) = 5.1 mm σ(Δz) = 3.4 mm. All images show identical cross-sectional slices through the tumour. Images to the far left show that the clinical reference PET and images in the central column are the resulting images created by calculating the changes in voxel values that occur with the relative position of the tumour. The Pearson correlation coefficient between the initial and final PET images shown here was 0.8. The isolines shown in the images to the far right demonstrate the effect of the variations in voxel values on the delineation of targets volumes.

The distribution of correlation values that resulted from all the simulated set-up errors is shown in figure 8. These correlation values are Pearson’s correlation coefficients calculated between the initial and simulated images, and calculated using the voxels that correspond to a reference region, ROI_50%. ROI_50% was defined as all voxels of the initial image with values ≥ 0.5*SUV_max. The region corresponding to ROI_50% is illustrated by the white isolines of figure 7. The expected values of the changes in tracer distribution due to random set-up errors for these patients were assessed by calculating the population correlation coefficient (ρ) (Soper et al 1917), and for both patients ρ approaches the ideal value 1. However, for both patients, individual set-up errors resulted in a broad distribution of correlation values of ranging from R = 0.8 through R = 1.0.

Figure 8.

Distribution of correlation coefficients within ROI_50% and the expected value of the correlation coefficient (ρ) due to random set-up errors during repeated imaging studies. One thousand random set-up errors were simulated for each patient.

Position-dependent variation of contrast recovery and the changes in spatial distribution within images of heterogeneous tumours can also lead to quantitative errors when voxel values are used to define ‘target volumes.’ The effect of set-up errors on delineation of target volumes can be observed by the isolines of figure 7. Here the target volume is defined for each image as those voxels within the top 50th percentile of SUVs (i.e. greater than 50% of the maximum voxel value for that image). For the heterogeneous tumour of patient #1, large variations in voxel values from one scan to the next led to dissimilar target volume being delineated. In the heterogeneous tumour of patient #1, the initial target consisted of 413 voxels; however, the target within the subsequent image was only 265 voxels. Correlation between the images was 0.8 indicating good agreement between images; however, there was a 36% change in the volume of the target regions. However, the uniformity within the tumour of patient #2 makes it less susceptible to position-dependent uncertainties, and ultimately, to reproducible target delineation. For patient #2, the PET-based target-volumes derived from the final images were within 2% of the initial volume (181 voxels versus 177 voxels). Correlation between these images was also 0.8.

4. Discussion and conclusion

Due to finite sampling spacing, the uptake values and spatial distributions of tracer observed with PET images of small objects are susceptible to changes in the position of the patient/tumour at the time of imaging. While the magnitude of the Ê_M reported here is specific to the experiment set-up and reconstruction parameters, similar position-dependent variations in RC can be expected for all multi-slice PET systems (Miller et al 1990, Hoffman et al 1982). Therefore, the systematic uncertainty in the PET measurements should be taken into account when designing acquisition and/or reconstruction protocols for quantitative PET and when using PET voxel values during quantitative analysis of uptake within tumours. A number of alternative acquisition and post-processing methods have been proposed and published for the detection and correction of tumour displacement in tomographic imaging (Livieratos et al 2005, Lu and Mackie 2002, Reyes et al 2007, Kennedy et al 2006). Of note are sinogram-based methods where the patient or the reconstruction grid could be shifted by one-half of the FWHM to generate an interpolated PET image (Senda et al 1985, Kennedy et al 2006). This method may correspond to a more reproducible value, M_mean, and would allow reliable cross-comparison between images and facilitate accurate corrections to recover the true activity within heterogeneous tumours.

Alternative acquisition and reconstruction methods may decrease the magnitude of position-dependent variations in recovered activity within images. However, we found that 3D acquisition was not a useful method to mitigate the position-dependent changes. 3D acquisition increases the number of accepted lines of response; however, the sampling interval is not improved above that of 2D acquisition. As such, similar position-dependent changes in contrast recovery were observed in the phantom studies acquired in both 2D and 3D mode.

Reproducibility should be a necessity for quantitative PET imaging. Precise voxel-based values would allow for a reliable comparison of tumour heterogeneities during longitudinal image studies, and stable RC values would facilitate PVE corrections to recover the true activity within sub-tumour volumes. However, our phantom measurements showed systematic variations in the ability to recover the activity of small objects, where variations were observed to coincide with changing the positioning between subsequent image acquisitions.

These imaging uncertainties can result in the misidentification of target volumes for radiation oncology when relative image values are used to define and delineate radiotherapy targets (e.g. boost region at ROI_50%), or when the absolute values of image voxels are to be used to define non-uniform dose distributions (e.g. voxel-based dose-painting). From the simulation study, we saw that small errors in patient positioning can alter the spatial distribution observed within images and reduced the correlation between subsequent image studies of the same tumour. Moreover, the volume of target regions identified in the two simulation images differed by as much as one-third, indicating that position-dependent variations of the voxel values can drastically change the delineation of biological targets for radiotherapy.