On the Optimal Design of Genetic Variant Discovery Studies

Abstract

The recent emergence of massively parallel sequencing technologies has enabled an increasing number of human genome re-sequencing studies, notable among them being the 1000 Genomes Project. The main aim of these studies is to identify the yet unknown genetic variants in a genomic region, mostly low frequency variants (frequency less than 5%). We propose here a set of statistical tools that address how to optimally design such studies in order to increase the number of genetic variants we expect to discover. Within this framework, the tradeoff between lower coverage for more individuals and higher coverage for fewer individuals can be naturally solved.

The methods here are also useful for estimating the number of genetic variants missed in a discovery study performed at low coverage.

We show applications to simulated data based on coalescent models and to sequence data from the ENCODE project. In particular, we show the extent to which combining data from multiple populations in a discovery study may increase the number of genetic variants identified relative to studies on single populations.

Introduction

New developments in sequencing technologies have brought along substantial reductions in cost and increases in genomic throughput by more than three orders of magnitude (Shendure and Ji, 2008; Tucker et al., 2009; Metzker, 2010). These improvements have in turn contributed to the launch of the 1000 Genomes Project (http://www.1000genomes.org/page.php), and to an increasing number of smaller scale sequencing studies. These studies have as one of their goals the identification of the genetic variation in the region under study, mostly low frequency variants, with the ultimate goal of performing association testing between rare variants and complex diseases (Li and Leal 2008, Madsen and Browning 2009).

The number of genetic variants identified in these studies depends on several factors. Among these the most important are the number of individuals sequenced, and the sensitivity to call variants present in a sequenced individual. With the new sequencing technologies the sensitivity to detect a variant is influenced directly by the depth of coverage at the variant position. Therefore when designing a variant discovery study researchers need to decide the number of individuals that can be sequenced, and the average depth of coverage to be used for each individual given a fixed study cost in order to maximize the expected number of variants to be discovered. The natural tradeoff is between lower depth of coverage for more individuals, and higher coverage depth for fewer individuals. In this paper, we propose analytical methods that allow estimation of the number of genetic variants we expect to identify in sequencing studies performed at reduced coverage, and that provide a natural solution to this tradeoff.

We frame the problem of estimating the genetic variation in a population as a species problem in ecology, where one is interested in estimating the number of species in a closed population (Sekar and Deming, 1949; Efron and Thisted, 1976; Bunge and Fitzpatrick, 1993). Here we extend the approach in Ionita-Laza et al. (2009) to account for imperfect probability of variant detection in an individual, and this extension allows us to address the optimality issue of the current sequencing studies. The approach is appealing in that it makes few and reasonable assumptions, and it makes use of already generated sequence data in the region of interest to empirically estimate the underlying distribution of the variant frequency. In the remaining of the paper we present details of the approach and show applications to simulated data based on a coalescent model and to the ENCODE data.

Methods

We present here a statistical framework for estimating the number of genetic variants we expect to identify in a fixed number of individuals. We start by introducing several assumptions on the underlying frequency distribution of variants in the population, and on the process of calling variants in a set of sequenced individuals. We assume here that variants are in linkage equilibrium, and that their population frequencies follow a Beta distribution (Wright, 1959), and hence the observed frequency counts follow a Beta-Binomial distribution. This assumption in addition to theoretical justification has also proved to work well in practice.

In the context of current sequencing technologies, the probability of calling a truly present variant is a function that depends on several factors, including the number of reads observed at the variant location (i.e., the coverage depth) and the number of reads consistent with the non-reference allele at the location (we assume that the reference allele is known). We focus here on the discovery of true variants, and assume that the probability of calling a non-existent variant is negligible. Note that this latter probability can be made as small as desired by imposing a more stringent variant calling rule.

Expected number of variants to be identified

We assume that the average depth of coverage across the genome is denoted by λ (per base), which means that each variant position is sequenced λ times on average; the value of λ is known. Accordingly, the number of reads, say m, at a given location (i.e., the coverage depth) is approximately Poisson(λ). The number of reads at a location is an important covariate as it affects the probability that a truly present variant in an individual is detected. In general, the higher the number of reads at a location, the greater the probability of making a call at a variant position. The specific algorithm for calling variants can vary from study to study. For our purposes we assume that a variant is called whenever at least k copies of the same (non-reference) allele are detected among all the reads at a position; however other calling procedures can be accommodated as well, but require more specific information about the sequencing technology used. If we let p_err be the error probability for a single read per base (assume the errors are independent), m be the total number of reads at a location, and m_noerr be the number of reads without error, then the calling probability can be modeled using a binomial distribution, as follows:

$$\begin{array}{l}{C}_{m,k}=P(\text{call}\hspace{0.17em}\text{a}\hspace{0.17em}\text{variant}\hspace{0.17em}\text{in}\hspace{0.17em}\text{an}\hspace{0.17em}\text{individual}|\#\text{reads}\hspace{0.17em}\text{at}\hspace{0.17em}\text{a}\hspace{0.17em}\text{location}\hspace{0.17em}\text{is}\hspace{0.17em}m)\\ =P(m_{\text{noerr}}\ge k),\end{array}$$ (1)

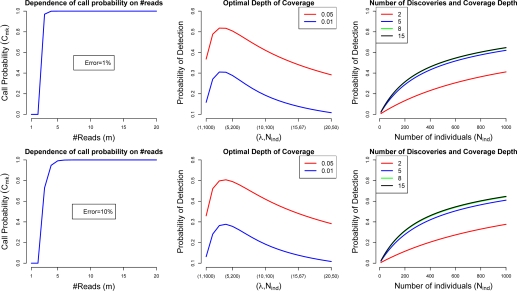
where m_noerr is approximately Binomial(m, 1–p_err). A plot of C_m,k as a function of m when k = 3 is shown in Figure 1 for two different values of the error probability p_err, 1% and 10%.

Figure 1:

Optimal design of variant discovery studies. The error probability per base, p_err, is 0.01 (upper panel), and 0.10 (lower panel). The first column shows the probability of calling a variant, C_m,k, when the number of reads at a location is m and the number of reads needed without error, k, is 3. The middle column shows the expected proportion of rare variants (frequency less than 0.01 or 0.05) to be discovered as a function of mean depth of coverage, λ (and, implicitly, number of individuals, N_ind), when the cost of the study is fixed, and assumed to be equal to λ· N_ind. The third column shows the expected proportion of rare variants (frequency less than 0.01) to be discovered as a function of the number of individuals sequenced, for various levels of the average coverage depth (λ = 2, 5, 8, 15) and assuming a cost function that increases linearly with the number of individuals.

The expected number of variants with frequencies between f₁ and f₂ to be discovered in N_ind individuals is given by the following formula:

$$\begin{array}{l}{E}_{N_{\text{ind}},f_1,f_2,\lambda }=M{\int }_{f_1}^{f_2}P(\text{detect}\hspace{0.17em}\text{a}\hspace{0.17em}\text{variant}\hspace{0.17em}\text{with}\hspace{0.17em}\text{frequency}\hspace{0.17em}\theta )f(\theta )d\theta \\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=M{\int }_{f_1}^{f_2}[1-P(\text{do}\hspace{0.17em}\text{not}\hspace{0.17em}\text{detect}\hspace{0.17em}\text{a}\hspace{0.17em}\text{variant}\hspace{0.17em}\text{with}\hspace{0.17em}\text{frequency}\hspace{0.17em}\theta )]\hspace{0.17em}f(\theta )d\theta \\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=M{\int }_{f_1}^{f_2}\left[1-{\left(1-\sum _m{C}_{m,k}\theta \hspace{0.17em}{f}_{\lambda }(m)\right)}^{2N_{\text{ind}}}\right]\hspace{0.17em}f(\theta )d\theta ,\end{array}$$ (2)

where M is the total number of variants (unknown), f₁ and f₂ are bounds on the frequencies of variants, λ is the mean depth of coverage across the genome,

$$f_{\lambda }(m)=\frac{e^{-\lambda }{\lambda }^m}{m!}(\text{Poisson}\hspace{0.17em}\text{distribution}\hspace{0.17em}\text{function}),$$

and

$$f(\theta )=\frac{{\theta }^{a-1}{(1-\theta )}^{b-1}}{B(a,\hspace{0.17em}b)}(\text{Beta}\hspace{0.17em}\text{distribution}\hspace{0.17em}\text{function}).$$

Parameters a and b of the Beta distribution can be estimated from available data using maximum likelihood estimation (see Appendix).

Optimal coverage depth in order to maximize the expected number of discoveries

For a fixed study cost we are interested in maximizing the number of variants we expect to discover. Therefore an important aspect in the design of new sequencing studies is choosing the average depth of coverage that one should use per individual, and the number of individuals to sequence. In our framework, this can be rephrased as maximizing the expected number of variants we expect to discover at a given coverage λ and for a given number of individuals N_ind, i.e.:

$$\underset{\lambda ,\hspace{0.17em}{N}_{\text{ind}}}{\text{max}}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{E}_{N_{\text{ind}},f_1,f_2,\lambda }$$ (3)

with the constraint that the cost of the study is fixed. With the current sequencing technologies, it is reasonable to assume that the cost of the study is linear in the number of individuals, i.e. Cost = cN_ind · Cost(λ), where c is a constant, and Cost(λ) is the cost of sequencing an individual at an average coverage depth of λ. We assume here that Cost(λ) is linear in λ, although other cost functions can be accommodated as well.

Number of variants missed in a discovery study

We assume now that we have already performed a variant discovery study at average depth λ in N_ind individuals, and we are interested in estimating the number of genetic variants that we missed in the study. The number of unseen genetic variants can then be decomposed into two separate components: the number of variants missed in the N_ind individuals due to the depth of coverage used (denoted here by M₁), and the number of variants missed due to our sampling only N_ind individuals from the entire population (M₂). The first component (M₁) can be estimated as follows:

$$M_1=E_{N_{\text{ind}},f_1,f_2,\infty -E_{N_{\text{ind}},f_1,f_2,\lambda }},$$

where E_{Nind,f1,f2,∞} is the number of variants that we expect to discover in N_ind individuals with perfect coverage.

The second component (M₂), i.e. missing variants due to our sampling of only N_ind individuals, can be estimated as follows. Let Δ_{Nind,f1,f2,∞} (t) be the expected number of new variants to be discovered if we were to do a new discovery study in an additional t·N_ind individuals with perfect coverage. Then

$${\Delta }_{N_{\text{ind}},f_1,f_2,\infty }(t)=E_{(t+1)·N_{\text{ind}},f_1,f_2,\infty }-E_{N_{\text{ind}},f_1,f_2,\infty }.$$ (4)

Note: Estimating the number of variants to be identified in future sequencing studies at the same depth of coverage λ as used in the initial discovery study follows easily using the above notations, i.e.

$${\Delta }_{N_{\text{ind}},f_1,f_2,\lambda }(t)=E_{(t+1)·N_{\text{ind}},f_1,f_2,\lambda }-E_{N_{\text{ind},}{f}_1,f_2,\lambda }.$$

Replication probability for variants in the discovery study

Once a discovery study has been performed it is often of interest to assess the chance that we will see a variant detected in the discovery study in other independent datasets. This replication probability depends on estimating the posterior frequency distribution for such a variant. The information about the frequency of each variant detected in the discovery study is given by x, the number of times it appears in the study. Given x, we can estimate the posterior frequency distribution for a variant, i.e.

$$P_x(f\le p)=P(f\le p|\text{variant}\hspace{0.17em}\text{is}\hspace{0.17em}\text{observed}\hspace{0.17em}x\hspace{0.17em}\text{times}\hspace{0.17em}\text{in}\hspace{0.17em}\text{our}\hspace{0.17em}\text{study}),$$

as follows:

$$P_x(f\le p)=\frac{{\int }_0^p{({\sum }_m\theta ·C_{m.k}·f_{\lambda }(m))}^x{(1-{\sum }_m\theta ·C_{m,k}·f_{\lambda }(m))}^{2N_{\text{ind}}-x}f(\theta )d\theta }{{\int }_0^1{({\sum }_m\theta ·C_{m,k}·f_{\lambda }(m))}^x{(1-{\sum }_m\theta ·C_{m,k}·f_{\lambda }(m))}^{2N_{\text{ind}}-x}f(\theta )d\theta }$$ (5)

where f(θ) is the distribution function for the beta distribution. The probability of replicating a variant seen x times in N_ind individuals in an additional tN_ind individuals can then be calculated using (5). We now show applications to simulated examples, and to real data from the ENCODE project.

Results

Optimal design

In a first set of examples we show applications to the optimal design of variant discovery studies. In particular we show how the expected proportion of rare variants to be discovered in a study varies as a function of the mean coverage depth if we assume a fixed study cost and various values for the error probability, p_err, in equation (1). As shown in Figure 1 (second column), for a fixed cost, a mean coverage depth below or above the optimal depth level may lead to substantial reductions in the expected number of discoveries. Also shown is that, using the reasonable assumption that the cost function is linear in both the number of individuals and the average coverage depth, a larger number of individuals at a lower coverage is preferable to a lower number of individuals at higher coverage, if the goal is to maximize the number of variants detected.

On the other hand, if our goal is to discover as many variants as possible in a fixed number of individuals and the cost is not fixed, then a larger coverage depth will naturally result in a larger number of discoveries. However, there are diminishing returns as the coverage increases; and after a certain level is reached, each additional level of coverage leads to only a small increase in additional discoveries (Figure 1, third column).

Probability of replication

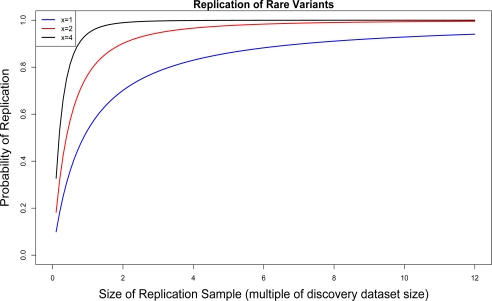
Once a discovery study has been performed in a number of individuals, N_ind, it is of interest to inquire about the probability of replicating a particular variant in future datasets. In Figure 2 we show the probability of replicating a variant that was seen in only a few individuals in a discovery study (i.e. singletons, doubletons etc.). As shown, for singletons many more individuals than present in the original study are needed in order to achieve a high probability of replication (e.g. 10 times more the discovery dataset size for a replication probability of 93%). In contrast, for variants that occur twice or more the number of individuals required for replication is substantially smaller (e.g. 3 times more the discovery dataset size for a replication probability of 95%).

Figure 2:

Probability of replicating a variant in a new set of individuals, given its observed frequency count (x = 1, 2, 4) in the original discovery dataset of size 50 individuals; p_err = 0.10 and λ = 20.

In addition, we have used the sequence data on 16 CEU individuals that are part of the ENCODE project1, to show that the estimates for the replication probability are sensible in a real study. To achieve this, we split the dataset on 16 individuals into two datasets, a discovery dataset and a replication dataset, with 8 individuals each, and compare the actual number of replicated discoveries with the estimated one for several classes of variants, e.g. singletons (variants that occur once in the discovery samples). As shown in Table 1, our predictions are fairly accurate in this application.

Table 1:

Accuracy for the Probability of Replicating Variants detected in a Discovery Study: application to the CEU ENCODE data on 16 individuals. The discovery dataset and the replication dataset each contain 8 individuals. n_x is the number of variants that occur x times in the discovery dataset.

	n1	n2	n3	n4	n5
Discovery Dataset	1,855	925	859	763	532
true #replications	993	812	826	711	526
estimated #replications	1, 020	725	774	729	522

Number of genetic variants missed from a discovery study

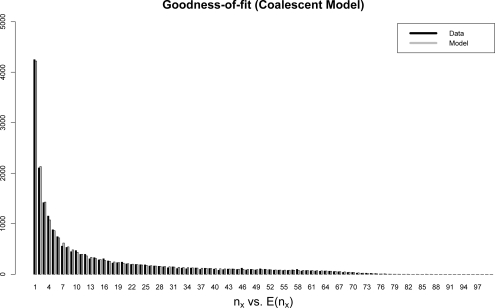
We use the software package Genome (Liang et al. 2007) to simulate sequence data on 10, 000 haplotypes according to a coalescent model (Hudson 1990), resulting in a total of 43, 305 SNVs (single-nucleotide variants) in a large genomic region on a single chromosome. We form datasets of N_ind individuals (in our examples N_ind = 50, or 100 haplotypes) by randomly sampling from the generated haplotypes. For each haplotype the number of reads at a single location is Pois(λ), and the probability that we call a truly present variant depends on the actual number of reads at a location and on the number of reads without error, as explained before in (1). In Figure 3 we show that the beta-binomial model fits the observed frequency counts very well.

Figure 3:

Coalescent-based simulated data with reduced coverage. Fit of the beta-binomial model to the observed frequency counts (n_x). The mean coverage depth is λ = 8, and the model relating the probability of calling a variant given the number of reads at a location (eq. 1) is specified by p_err = 0.1 and k = 3.

With simulated data we are in the unique position to be able to assess the accuracy of the estimates produced by our model. In particular, we use our approach to estimate the number of missing variants in the random sample of 100 haplotypes, and compare it with the true number of missing variants that can be directly assessed based on the remaining 9, 900 haplotypes. As shown in Table 2 the estimates on the missing variation are fairly accurate even if they are based on a sample of only 100 haplotypes.

Table 2:

Accuracy of the estimates of missing genetic variation. T is the true number of remaining variants, i.e. present in the 10, 000 haplotypes and not seen in the 100 haplotypes in the discovery dataset; E is the estimated number of remaining variants. λ = ∞ corresponds to a perfect sensitivity case. Mean and SD are calculated based on 100 independent samplings of 100 haplotypes; p_err = 0.1 and k = 3.

λ	#Missing Variants (T/E)	#Missing Variants f ≥ 0.01 (T/E)
4	22, 187 ± 104/21, 508 ± 454	1, 602 ± 52/1, 714 ± 24
∞	20, 604 ± 117/19, 961 ± 549	917 ± 71/939 ± 26

Rare variants and coverage

An important class of variants is those that have low observed frequency count (i.e. singletons, doubletons) in a study, since they contain many of the rare variants (population frequency less than 1%) identified in a study. This is especially true with low coverage design and small discovery studies. In Table 3 we report for various values of λ, i.e. the coverage parameter, the proportion of (true) rare variants identified in 100 – 600 chromosomes that have a small frequency count in the study, e.g. P(x = 1|f ≤ 0.01 AND identified in the study). As shown, for low coverage, 68% – 93% of the rare variants identified in a reasonably sized study are expected to be singletons; for a higher coverage study only 39% – 78% of rare variants identified appear as singletons. Singletons, together with other variants with low frequency count, are therefore important to ascertain if the main goal is to identify rare variants. Such variants can be validated by subsequent genotyping in the discovery study.

Table 3:

The proportion of rare variants detected in a study which have a small frequency count: x = 1 – 4 as a function of the coverage parameter λ (i.e. P(x = 1|f ≤ 0.01 AND identified in the study)).

Nind	λ	x = 1	x = 2	x = 3	x = 4
50	8	0.78	0.17	0.03	0.01
50	4	0.84	0.14	0.02	0.00
50	2	0.93	0.06	0.01	0.00
300	8	0.39	0.22	0.14	0.09
300	4	0.46	0.24	0.14	0.08
300	2	0.68	0.22	0.07	0.02

Discovery studies in multiple populations

We have applied the methods here to the ENCODE data2 to investigate how combining different populations in a discovery study affects the overall number of discoveries. Sequence data in ten 500-kilobase regions of the genome were available for 39 unrelated DNA samples: 8 Yoruba (YRI), 16 CEPH European (CEU), 7 Han Chinese (CHB), and 8 Japanese (JPT). These regions were chosen to be representative of the genome in general, including various chromosomes, recombination rates, gene density and values of non-transcribed conservation with mouse.

We have compared the observed number of variants identified by combining individuals from any two populations at a time (shown here are CEU and YRI; CEU and CHB; CHB and JPT) with the estimated number of discoveries, if the discovery dataset consisted of the same number of individuals from only one of the two populations. To estimate the number of new variants we expect to find if we had additional individuals from the same population we used Δ_Nind,0,1,∞(t) (eq. (4)). In Table 4 we show that, as expected, adding more individuals from a different population (rather than the same population as in the discovery study) may lead to an increase in the overall number of discoveries. This is particularly striking when combining individuals from CEU and YRI, and comparing with only CEU individuals. More precisely, the observed number of discoveries in the combined CEU and YRI datasets is 13, 968 compared to only 10, 766 estimated in the same number of CEU individuals. While many of the additional discoveries may be specific to the YRI population, some will also be polymorphic in the CEU population.

Table 4:

Discovery Studies with individuals from multiple populations. Data on 8 YRI, 16 CEU, 7 CHB and 8 JPT individuals is available.

Datasets	16 CEU	8 YRI	16 CEU + 8 YRI	16 CEU + 8 CEU	8 YRI + 16 YRI
#discoveries	10, 119	10, 315	13, 968	10, 766a	13, 479a
Datasets	16 CEU	7 CHB	16 CEU + 7 CHB	16 CEU+ 7 CEU	7 CHB + 16 CHB
#discoveries	10, 119	7, 802	11, 466	10, 700a	9, 278a
Datasets	7 CHB	8 JPT	7 CHB + 8 JPT	7 CHB + 8 CHB	8 JPT + 7 JPT
#discoveries	7, 802	7, 804	8, 613	8, 790a	8, 425a

^aEstimated

Discussion

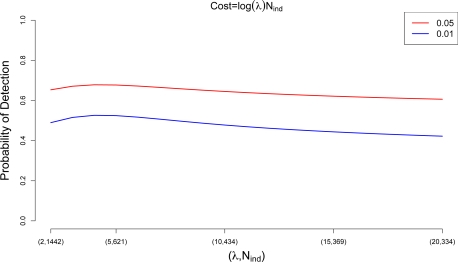
Variant discovery studies using the new sequencing technologies are now underway. Such studies aim to identify low frequency variants that may explain the yet unaccounted for genetic variance (Manolio et al., 2009) for complex diseases. The amount of the underlying variation identified in such studies is influenced directly by the sensitivity to detect variants present in an individual, and the number of individuals sequenced. In this paper we proposed statistical approaches that can be useful in the context of such studies. In particular, we have been concerned with the optimal design of variant discovery studies, i.e. how does one choose the optimal depth of coverage for a given study cost in order to maximize the expected number of discoveries. Such a choice inevitably depends on the sequencing technology employed, but we show here that, assuming a cost function linear in both the number of individuals and the coverage depth, sequencing a larger number of individuals at lower coverage depth will generally lead to more discoveries than sequencing a smaller number of individuals at deeper coverage. The assumptions we made on the cost function are reasonable at this time. It is however possible that in the future the cost of sequencing will increase slower than linearly as a function of λ. In Figure S1, we illustrate the case of a logarithmic cost function in λ, and show that the same overall conclusion still holds.

Our approaches are based on several reasonable model assumptions (e.g. linkage equilibrium, Beta-binomial model), and as such results may be sensitive to deviations from these assumptions. Therefore we sought it was important to apply the proposed methods to both coalescent-based simulated data and real sequence data from the ENCODE project. We showed in our applications that the proposed methods work well, and in particular that the predicted number of missing variants is very close to the true number.

With low coverage many of the rare variants will tend to appear as singletons. Since singletons are also enriched for sequencing errors it is important that such variants discovered in a study be confirmed by subsequent genotyping of the discovery data. Discovery studies with individuals in multiple populations can be useful as well. Having data from multiple populations in a discovery study not only ensures a more representative study of the global human variation, but may also increase the overall number of discoveries compared with individual populations. Therefore when there is population stratification, and thus individuals from several subpopulations are included in a study, more genetic variants may be discovered than for the same number of individuals in a single subpopulation.

We have focused here on the estimation of the number of true variants to be identified in a sequencing study, and have assumed that the probability of calling non-existent variants is small. This latter probability can be made arbitrarily small by adopting a more stringent variant calling rule, for example, by requiring a large number of the non-reference allele, k, to be observed at a variant position. Having fixed such a rule, the same methods we already described apply.

Current sequencing studies focus on sequencing each individual at a time at an expected coverage, λ. An alternative design, suitable mostly when the sequencing error is low, is to sequence pools of DNA samples together (Futschik et al. 2010). DNA pooling could prove more cost-effective for variant detection in the future, and the methodology described here can be adapted easily to accommodate such a design.

The approach we proposed is appealing since it makes few and reasonable model assumptions, is flexible enough to take into account important covariates that influence variant detection (in this case the coverage depth), and at the same time provides fast and accurate estimates for the number of missing variants from a discovery study.

Software R code implementing these methods is freely available on the first author's webpage.

Appendix. Fitting the Beta-Binomial model

We assume that the observed frequency counts can be modeled using a Beta-Binomial model. The probability that at a position the frequency count is x is given by:

$$P_x={\int }_0^1\left(\begin{array}{c}2N_{\text{ind}}\\ x\end{array}\right){(\sum _m\theta ·C_{m,k}·f_{\lambda }(m))}^x{(1-\sum _m\theta ·C_{m,k}·f_{\lambda }(m))}^{2N_{ind}-x}f(\theta )d\theta$$

for x ≥ 0. Since we only observe those variants that have frequency count 1 or above, the truncated probabilities are:

$$P_x^t=\frac{P_x}{{\sum }_{x=1}^{2N_{\text{ind}}}{P}_x}$$

for x ≥ 1. The likelihood function can then be written as:

$$L(a,\hspace{0.17em}b)=\prod _{x=1}^{2N_{\text{ind}}}{(P_x^t)}^{n_x}$$

and the log-likelihood function is:

$$LL(a,\hspace{0.17em}b)=\sum _{x=1}^{2N_{\text{ind}}}{n}_x\text{log}(P_x^t),$$

where we assume that the variants are in linkage equilibrium. We maximize LL(a, b) to obtain the maximum-likelihood estimators (MLEs) for a and b. The maximization is carried out through the Newton-Raphson method.

Figure S1:

Cost function is logarithmic in λ (the average coverage depth). Shown is the expected proportion of rare variants (frequency less than 0.01 or 0.05) to be discovered as a function of mean depth of coverage, λ (and, implicitly, number of individuals, N_ind), when the cost of the study is fixed, and assumed to be equal to log(λ) · N_ind.