Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2011 Sep 17.
Published in final edited form as: J Biomech. 2010 Jun 9;43(13):2548–2553. doi: 10.1016/j.jbiomech.2010.05.015

CONTROL OF CENTER-OF-MASS MOTION STATE THROUGH CUING AND DECOUPLING OF SPONTANEOUS GAIT PARAMETERS IN LEVEL WALKING

D D Espy 1,2, F Yang 1, Y-C Pai 1,2
PMCID: PMC2942766  NIHMSID: NIHMS208521  PMID: 20542513

Abstract

Can the center of mass (COM) motion state, i.e., its position and velocity relative to the base of support (BOS), which dictate gait stability, be predictably controlled by the global gait parameters of step length and gait speed, or by extension, cadence? The precise relationships among step length and gait speed, and the COM motion state are unknown, partially due to the interdependence between step length and gait speed and the difficulty in independent control of both parameters during spontaneous level walking. The purposes of this study were to utilize simultaneous audio-visual cuing to independently manipulate step length and gait speed, and to determine the extent to which the COM position and velocity can be subsequently controlled. Fifty-six young adults trained at one of three gait patterns in which both the step length and gait speed were targeted simultaneously. The results showed that the cuing could successfully “decouple” gait speed from step length. Although this approach did yield reliable control of the COM velocity through manipulation of gait speed (R2 = 0.97), the manipulation of step length yielded less precise control of COM position (R2 = 0.60). This latter control appears to require manipulation of an additional degree of freedom at the local segment level, such that the inclusion of trunk inclination with step length improved the prediction of COM position (R2 =0.80).

Keywords: audio-visual cue, speed, step length, stability limits, gait training, trunk inclination

INTRODUCTION

With aging, preferred walking speed becomes slower with shorter step lengths (Laufer, 2005). It is unclear whether these result from the aging process or from a fear of falling, or both (Chamberlin et al., 2005). Equally controversial is whether either, a slower gait or shorter step lengths, contributes to fall risk or is a useful adaptation against falls. Slower gait has been shown to be associated with an increased risk of falls directly (Cromwell and Newton, 2004; Ness et al., 2003) and is correlated with lower scores on clinical balance scales (Rogers et al., 2005). Some have found that decreased gait speed led to decreases in local stability of various joint kinematics (Dingwell and Marin, 2006). In contrast, improved local stability has also been found at slower gait velocities (England and Granata, 2007; Li et al., 2005). For both young and older subjects, the natural response to a known slippery floor is to shorten the step length (Cham and Redfern, 2002), and increased step length has been associated with a greater slip probability (Moyer et al., 2006). Paradoxically, fear related step length shortening was considered maladaptive by some (Menz et al., 2007). Whether the slower gait and shorter step length seen with aging are to be encouraged, or if they contribute to the risk of falling, remains controversial.

A recently developed conceptual framework for investigating gait stability simultaneously takes into consideration both the center of mass (COM) position (which relates to step length) and its velocity (which relates to gait speed), both relative to the base of support (BOS). The COM velocity in the anteroposterior (AP) direction, VCOM/BOS, normalized as a dimensionless fraction of the square root of the acceleration due to gravity times body height (bh), and the position of the COM in the AP direction, XCOM/BOS, expressed relative to the rear of the heel, and normalized to foot length, are the variables which characterize the motion state of the COM (Pai and Patton, 1997; Yang et al., 2007; Yang et al., 2008a). In this model, the shortest distance from the instantaneous COM motion state to the mathematically derived limits of stability quantifies a person’s stability at that instant, in walking and other activities (Bhatt et al., 2005; Pai et al., 2000; Pai et al., 1998; Pai et al., 2003; Patton et al., 1999). A negative stability value (i.e., an instantaneous COM motion state below these stability limits) results in backward loss of balance (Bhatt et al., 2006) and is a key factor in falls in response to slipping during various daily activities (Yang et al., 2009).

Theoretically, either increasing VCOM/BOS and/or XCOM/BOS can move the COM motion state above the stability limits, so that either change should improve stability and perhaps ameliorate balance loss or falls in incidents such as a slip (Pai and Patton, 1997; Pai and Iqbal, 1999; Yang et al., 2007; Yang et al., 2008a). The XCOM/BOS can be shifted forward by shortening the step length and/or by altering the body segment configuration (i.e., posture); in fact though, over adaptation to repeated slip trials, XCOM/BOS was shifted primarily through step length shortening (Bhatt et al., 2006). To the extent that XCOM/BOS is determined primarily by step length and VCOM/BOS by gait speed (Bhatt et al., 2006), the gait alterations that typically accompany aging must cause conflicting consequences on the likelihood of balance recovery following a slip. Shorter steps may in fact provide greater stability, but this benefit may be offset by the accompanying slowness in gait speed.

Increases in gait speed (presumably in VCOM/BOS as well) are naturally achieved through corresponding increases in cadence and step length (presumably leading to a posterior shift in XCOM/BOS relative to the forward heel), and vice versa. Because of this inherent coupling in spontaneous gait patterns, the theoretically more stable, faster speeds are coupled with the theoretically less stable, longer step lengths. Hence, in spite of the fact that stability during walking is strongly related to gait speed and step length, without empirically decoupling these parameters, the true impact of each on the control of stability cannot be revealed. Moreover, while there is ample precedence for modulating one gait parameter at a time during gait training (Bonnard and Pailhous, 1993; Zijlstra et al., 1995), it is rare that two parameters are controlled simultaneously (Roerdink et al., 2007).

Furthermore, if separate cuing or modulation could simultaneously control gait speed and step length, or the 3rd parameter, cadence (Danion et al., 2003), it remains unclear whether the motion state components VCOM/BOS and XCOM/BOS can be controlled in this manner. For instance, a moderately strong relationship between step length and XCOM/BOS has been found across self-selected fast, natural and slow gait (Bhatt et al., 2005). However, the head and trunk carry nearly 60% of the body’s weight, so the inclination of the trunk could introduce another degree of freedom to the relationship between step length and XCOM/BOS. The relationship between gait speed and step length and their corresponding COM state variables is not well understood.

The purposes of this study were to show that a decoupling paradigm would allow us to manipulate step length and gait speed independently, and to determine whether this would lead to the direct and predictable control of the XCOM/BOS and VCOM/BOS. The first hypothesis was that the subjects could experimentally follow specific audio-visual cues, resulting in simultaneous control of the primary variables of targeted speed and targeted step length in level walking. The subsequent hypothesis was that this manipulation of the primary gait parameters would result in direct control of the secondary variables, XCOM/BOS and VCOM/BOS, because a presumed direct and predictable relationship exists between these primary and secondary variables. Specifically, we expected that two gaits of different speeds, but a common step length, would both produce the same resultant XCOM/BOS, and two gaits of different step lengths, but a common gait speed, would both produce the same resultant VCOM/BOS. Alternatively, we expected that trunk inclination may play a role in the control of XCOM/BOS, especially if the strength of the relationship between step length and XCOM/BOS cannot match that of gait speed and VCOM/BOS.

METHODS

Subjects

Fifty-six subjects, 19 to 45 years old, participated in the experiment (Table 1). Subjects were screened for any systemic disorders which might affect their participation. Each subject gave informed consent prior to participation, as approved by the local Institutional Review Board.

Table 1.

Mean (SD) of subject demographics; target step length (SLtarget) and gait speed (Starget); and resultant step length (SL) and gait speed (S), by group.

Group N Female Age (yrs) Height (m) Mass
(kg)		 SLtarget§
(m/bh)		 SL§
(m/bh)		 Starget§§ S §§
A 18 8 28.9 (5.9) 1.7 (0.1) 68.3 (14.7) .43 0.43 (0.04) 0.40§§§ 0.37 (0.04)
B 18 11 24.3 (4.9) 1.7 (0.1) 65.4 (13.5) .30 0.31 (0.03) 0.20 0.20 (0.02)
C 20 14 24.9 (5.1) 1.7 (0.2) 68.0 (12.6) .43 0.42 (0.03) 0.20 0.20 (0.01)
Open in a new tab

bh is the subject's body height.

§

These are normalized to bh.

§§

This is a dimensionless measure: sacral velocity normalized by the square root of the acceleration due to gravity times the subject's body height.

§§§

Target for the initial 7 subjects was 0.47; analysis revealed that the subjects could not consistently reach this target, so the target was adjusted to 0.40 for the remaining 11 subje

Experimental set up and protocol

The experimental manipulation was designed to control gait speed and step length simultaneously. A visual gait speed target was provided by small flags, evenly spaced along a rope loop driven at the target gait speed by a DC motor (Model 4Z248D, Dayton Electric, Niles, IL), one meter lateral to the subjects and parallel to the length of the 7-m walkway, with the top of the loop between their shoulder and eye level (Figure 1). Subjects matched their gait speed to that of the nearest target flag while simultaneously matching their footsteps to an audible metronome at the target cadence. Because gait speed is the product of step length and cadence, this controlled step length by extension.

Figure 1.

Figure 1

Open in a new tab

Experimental set up for target presentation during walking. Subjects matched velocity (V) and step frequency (SF) targets simultaneously while walking along a 7-m walkway. Velocity target was provided by flags attached to a rope loop running parallel to the length of the walkway and being driven at a constant velocity by a motor. Step frequency was provided by an audible metronome. Step length (SL) was also constrained because V = SL*SF.

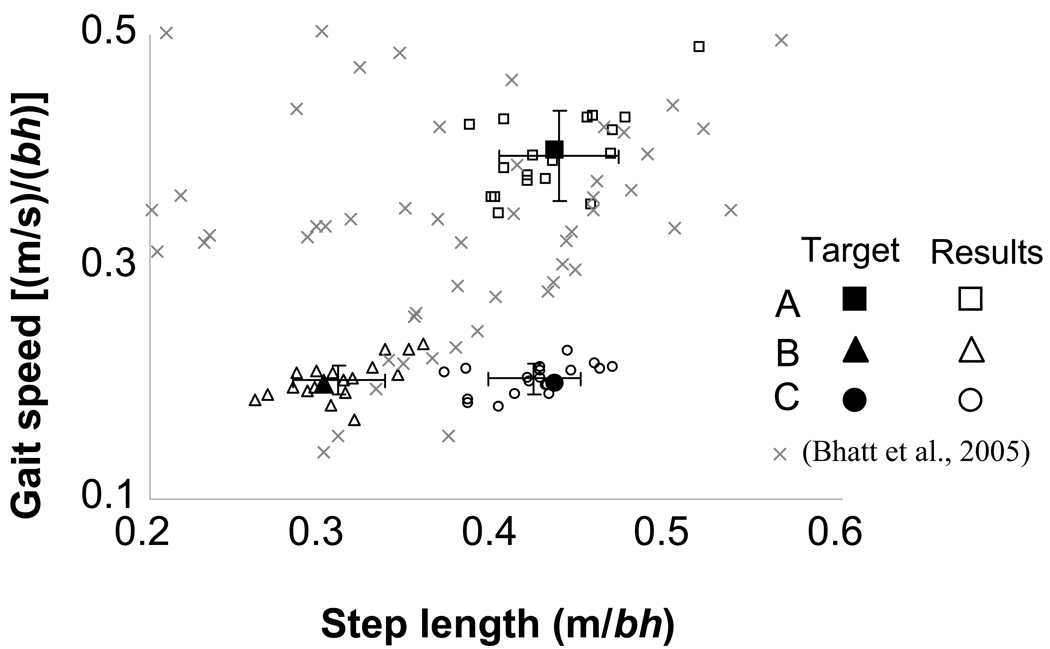
The subjects were randomly assigned to one of three target groups (Table 1). These COM motion state targets (X’COM/BOS and V’COM/BOS) were originally designed for a companion study to lie below the model predicted stability limits against backward balance loss after a slip. Two groups (B and C) had the same V’COM/BOS but different X’COM/BOS, while two groups (A and C) had the same X’COM/BOS but different V’COM/BOS. Based on the hypothesized predictability and linear correlation between the gait parameters and the COM motion state components, we also expected groups B and C to have a similar gait speed but different step lengths and groups A and C to have a similar step length but different gait speeds. These individualized step length (SLtarget) and gait speed (Starget) targets were selected to reflect the full range of those of spontaneous gait patterns (Figure 2).

Figure 2.

Figure 2

Open in a new tab

Gait parameter targets A, B, and C (filled shapes) and individual resultant gait parameters for each subject (open shapes), error bars represent ± 1 SD centered on the group mean (group mean not shown); light gray X’s represent parameters from self-selected fast, natural, and slow gait (Bhatt et al., 2005). bh is the subject’s body height. * Target for the initial 7 subjects was 0.47; analysis revealed that the subjects could not consistently reach this target, so the target was adjusted to 0.4 for the remaining 11 subjects.

To set these targets for each subject, regression equations (1 and 2) converting the preset V’COM/BOS to Starget and the preset X’COM/BOS to SLtarget, respectively, were derived from the data of a previous study in which young subjects were asked to walk at a self-selected fast, natural or slow pace for a number of trials, with no further instructions as to specific speed or other parameters given (Bhatt et al., 2005); along with the subject’s body height (bh):

SLtarget=[−(X’COM/BOS+0.1285)/2.2509]×bh  (in m) (1)
Starget=0.8028[V’COM/BOS×sqrt(g×bh)]+0.1449  (inm/s) (2)

Here, g is the acceleration due to gravity and X’COM/BOS is normalized to a foot length measure from the leading heel. The cadence for the metronome was set by dividing the Starget by the SLtarget.

At right step touchdown (TD), the sacral marker velocity was obtained in real time from the motion capture system described below and taken as gait speed, and the AP distance between the two heel markers was taken as SL. These estimates were used immediately after the trial to assess target matching (S − Starget and SL − SLtarget), provide feedback, and if necessary, to fine tune the rope speed or the metronome frequency. The subjects were instructed that their goal was to match both the rope speed and the metronome beats, as consistently as possible, throughout the experiment. After an initial unstructured practice, they were given verbal error feedback as to target matching, which was deemed successful (“on target”) if subjects were within 10% of the target value. The trial immediately after two consecutive “on target” trials was analyzed.

Data collection and analysis

The 26 motion markers applied to each subject at body segment landmarks were recorded by a passive motion capture system at 120 Hz (Motion Analysis Corporation, Santa Rosa, CA). Cutoff frequencies were determined for each marker through a residual analysis (Winter, 2005; Pavol et al., 2002) and each marker path was low-pass filtered at its specific cut-off frequency (range: 4.5–9 Hz) using zero lag, fourth-order Butterworth filters. Force plate data were collected at 600 Hz using a 64 channel, 16-bit A/D converter. Ground reaction force (GRF) and motion data were time synchronized at the time of collection.

Locations of joint centers were computed from the marker paths using transformations derived from anthropometric measurements and kinematic data. Right step TD of the analyzed trial was identified from vertical GRF, and verified from foot kinematic data. Each segment position and joint angle of a 13-segment, 3-dimensional representation of the body was determined. The trunk inclination was analyzed as a separate variable in order to evaluate its impact on the relationship between step length and the COM position. The actual (resultant) relative COM position and velocity, used to calculate XCOM/BOS and VCOM/BOS as above, were computed in post hoc processing, using sex- and age-dependent segmental inertial parameters (de Leva, 1996).

Statistics

To test the first hypothesis, the resultant gait speed and step length were assessed for target matching through paired t-tests (normalized resultant value compared to normalized target value). To test the second hypothesis, the extent to which these resultant gait parameters and the resultant XCOM/BOS and VCOM/BOS, were matched for each group as designed was tested using one way ANOVA with post hoc Tukey’s HSD. In the follow up study, one way ANOVA was used to compare trunk angles among groups. To establish predictive models, linear regression equations relating gait speed to VCOM/BOS and step length to XCOM/BOS were derived, both by group and across the combined data of all subjects. Linear regression was also used to relate XCOM/BOS to both step length and trunk angle across groups. Multiple regression analyses were used to compare the slopes of the within group regressions to assess group differences in the relationship between XCOM/BOS and step length, and between VCOM/BOS and gait speed. All statistics were performed with SPSS, version 17.0 (Chicago, IL) with α level of 0.05.

RESULTS

Each group was successful in following the cues: the resultant step lengths and gait speeds matched simultaneously the SLtarget and Starget, respectively (all P > .05, Table 1). There were significant between-group differences in gait speed (F2,55 = 283.607, P < .001) and step length (F2,55 = 98.435, P < .001) (Figure 2) as well as in VCOM/BOS (F2,55 = 340.851, P < .001) and XCOM/BOS (F2,55 = 55.574, P < .001).

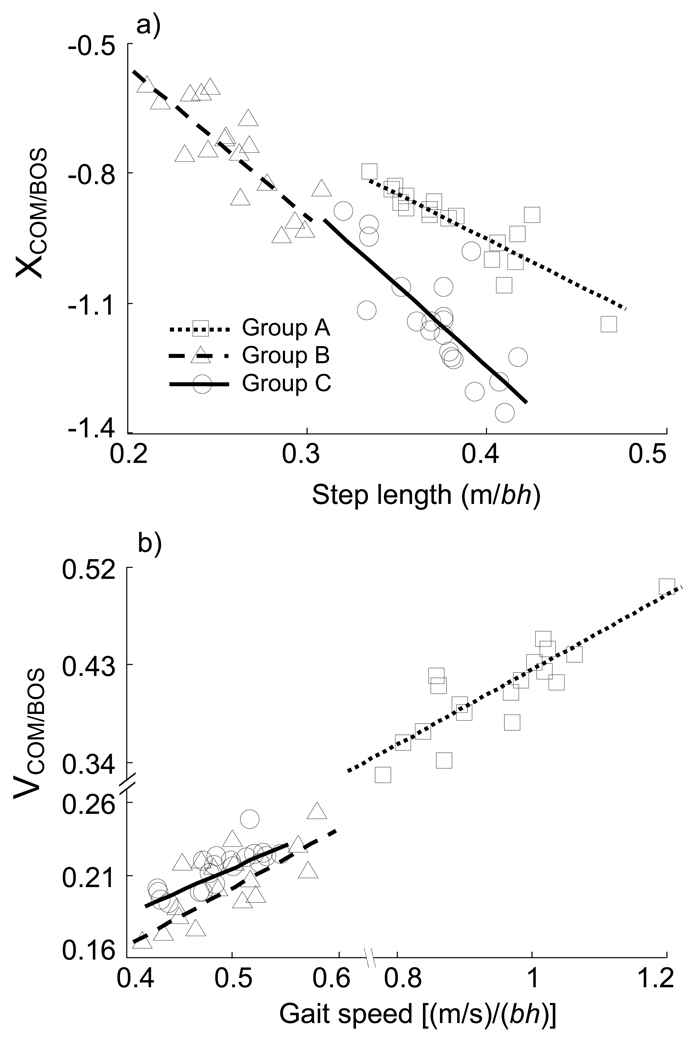
The gait speed of groups B and C were not different and were each significantly slower than group A (Table 2). Likewise, VCOM/BOS of groups B and C were not different and were each significantly lower than group A (Table 2). However, where the step lengths of groups A and C were the same, their XCOM/BOS were significantly different (Table 2). The overall (pooled from all groups) correlation was strong between gait speed and VCOM/BOS (R2 = 0.97, P < .001, Table 3). The slopes correlating gait speed to VCOM/BOS for individual groups were not different (all P > .05, Table 4, Figure 3). In contrast, the overall correlation between step length and XCOM/BOS was moderately strong (R2 = 0.60, P < .001, Table 3). The individual slopes correlating step length to XCOM/BOS were not different between groups A and B or between B and C (both P> .05), but were different between groups A and C (P< .05, Table 4, Figure 3).

Table 2.

Mean (SD) global gait parameters, including step length (SL) and gait speed (S), And center of mass (COM) position and velocity at right foot touchdown (TD), and results of post-hoc Tukey HSD statistics.

Variable Group A
Mean (SD)		 Group B
Mean (SD)		 Group C
Mean (SD)		 A vs. B
P value		 B vs. C
P value		 C vs. A
P value
S [(m/s)/(bh)] 0.95 (0.10) 0.49 (0.05) 0.49 (0.04) < 0.001 0.993 < 0.001
SL (m/bh) 0.43 (0.04) 0.31 (0.03) 0.42 (0.03) < 0.001 < 0.001 0.446
VCOM/BOS 0.41 (0.04) 0.20 (0.02) 0.21 (0.01) < 0.001 0.397 < 0.001
XCOM/BOS −0.92 (0.08) −0.76 (0.12) −1.14 (0.13) < 0.001 < 0.001 <0.001
Open in a new tab

S is the anteroposterior (AP) velocity of the sacral marker.

bh is the subject's body height.

SL is the AP distance from the left heel to the right heel.

VCOM/BOS is the COM velocity in the AP direction, normalized as a dimensionless fraction of the square root of the acceleration due to gravity times bh.

XCOM/BOS is the position of the COM in the AP direction, expressed relative to the rear of the forward heel, and normalized to foot length.

Table 3.

Parameters of the overall regression equations (all subject data together) relating gait speed (S) to VCOM/BOS; step length (SL) to XCOM/BOS, and to XCOM/BOS + trunk angle (T).

Across Groups Regressions a b c R2 P
VCOM/BOS = a×S + c 0.43 --- −0.01 0.97 <.001
XCOM/BOS = a×SL + c −2.37 --- −0.02 0.60 <.001
XCOM/BOS = a×SL + b×T + c −2.63 −0.02 0.06 0.80 <.001
Open in a new tab

Table 4.

Within group parameters of regression equations relating step length (SL) to XCOM/BOS, and gait speed (S) to VCOM/BOS; and parameters of the multiple regressions used to compare the slopes of the simple regression equations between pairs of groups.

Step Length and XCOM/BOS XCOM/BOS = a×SL + b×group# + c×(group×SL) + d
a b c d P+
      Group A vs. B −2.22 0.27 −1.24 0.04 0.066
      Group B vs. C −3.46 0.13 −0.28 0.31 0.771
      Group C vs. A −3.73 −0.40 1.51 0.44 0.049
Gait Speed and VCOM/BOS VCOM/BOS = a×S + b×group# + c×(group×S) + d
a b c d P+
      Group A vs. B 0.34 0.06 −0.01 0.09 0.956
      Group B vs. C 0.34 0.05 −0.07 0.03 0.349
      Group C vs. A 0.27 −0.05 0.07 0.08 0.478
Open in a new tab

The coefficients (a) and (d) apply also for the simple regression for the group listed first in the comparison. The significance of all the simple regressions was P<0.001.

#

(group) is a dummy variable.

+

P value corresponding to the interaction item, when this is less than 0.05, the slope is significantly different between the two groups.

Figure 3.

Figure 3

Open in a new tab

Regression lines by group for (a) step length predicting XCOM/BOS, and (b) gait speed predicting VCOM/BOS. VCOM/BOS is the COM velocity in the anteroposterior direction, normalized as a dimensionless fraction of the square root of the acceleration due to gravity times the height of the subject. XCOM/BOS is the position of the COM in the anteroposterior direction, expressed relative to the forward heel and normalized to foot length; a more negative value indicates a more posterior COM relative to the forward heel (BOS).

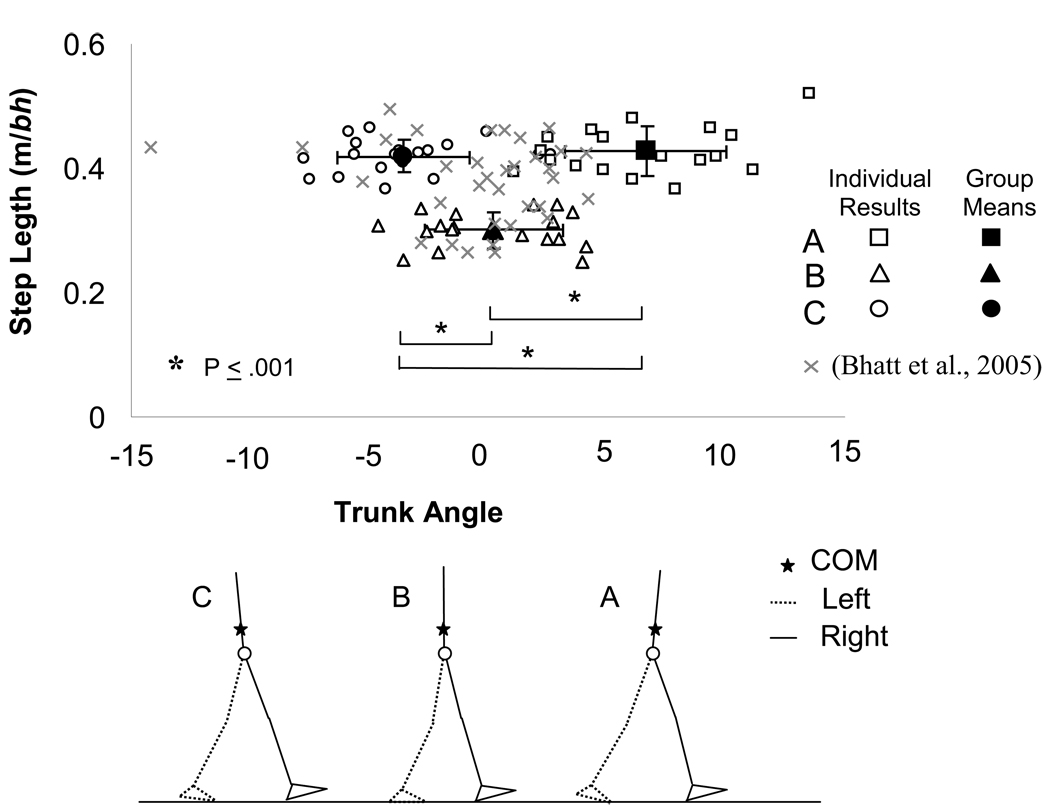
The average trunk angles were different among groups (F2,55 = 48.821, P < .001, Figure 4). Group A (6.40 degrees forward of vertical) was more forwardly inclined than B (0.23 degrees forward; P < .001), while C (3.53 degrees backward from vertical) was more backwardly inclined than B (P = .001). The linear regression model predicting XCOM/BOS from both step length and trunk angle for all groups together (R2 = 0.80, P < .001) was stronger than that of the equation which included only step length (Table 3).

Figure 4.

Figure 4

Open in a new tab

(a) Trunk angle (in degrees) and corresponding step length (m/bh) by group, at right TD; light gray X’s represent data from self-selected fast, natural, and slow gait (Bhatt et al., 2005). Note, negative values for trunk angles indicate that the line between the hips and shoulders lies posterior to vertical. (b) Schematic representation of average body orientation by group, at right TD.

DISCUSSION

The “decoupling” of gait speed from step length was effective. The subjects were able to follow their cadence (or by extension, step length) and speed cues simultaneously, resulting in a good match of each group’s targeted step length and speed in level walking. This learned control of their gait parameters allowed the subjects to modulate their VCOM/BOS more predictably than it did XCOM/BOS. Contrary to its presumed direct relationship with step length, the control over XCOM/BOS was rather imprecise and was influenced by the orientation of the trunk.

The findings of the present study lend support to the first hypothesis, that application of an audio-visual cue could simultaneously and independently control gait speed and cadence, whereby step length, perforce, would be determined. Specifically, because gait speed is the product of step length and cadence, we expected that following the audio-visual speed cues would result in a gait of the targeted speed and step length. In unconstrained walking, people maintain a preferred relationship among step length, frequency, and gait speed across a range of speeds (Zijlstra et al., 1995). The ratios of gait speed to step length of the decoupled gait patterns in this study were 2.18, 1.59, and 1.16 in groups A, B, and C, respectively, in comparison to 1.96 among healthy young subjects during unconstrained walking (McGibbons and Krebs, 2004). The subjects of the present study were able to override their natural tendency to successfully match the gait speed and step length targets simultaneously.

Although these gait parameters could be successfully and simultaneously manipulated in level walking, the findings do not fully support the second hypothesis. The XCOM/BOS and VCOM/BOS were not both directly controlled by altering gait speed and step length. Gait speed measured by the sacrum marker was consistent with the VCOM/BOS. The two groups who were able to match their targets at the same speed but with different step lengths did have the same resultant VCOM/BOS values. Further, the within group regression equations relating the VCOM/BOS to gait speed were not different among the three groups, indicating that the relationship between gait speed and VCOM/BOS was similar across groups. Overall, the speed of the sacrum marker explained 97% of the variability in VCOM/BOS.

On the other hand, step length modulation did not in itself translate into predictable control of XCOM/BOS as hypothesized. Two groups were able to match their targets to produce gaits of the same step length but at different speeds. However, contrary to expectation, the resultant XCOM/BOS of each was different. The subjects in each group appear to have applied different approaches to control their COM position, further evidenced by the difference in the slopes of the equations relating XCOM/BOS to step length between these two groups. Overall, the gait speeds and step lengths accomplished by the subjects, and the trunk angles observed in the slower two groups, fell within the range of values for self selected fast, natural, and slow gait (Figures 2 and 4); however, the trunk angles observed in the faster group were somewhat more forward than those observed during spontaneous gait.

Trunk angle varied significantly by group, and step length and trunk inclination together accounted for 80% of the variability in XCOM/BOS across all subjects, as opposed to only 60% accounted for by step length alone. A study of gait stability across a range of self-selected speeds found a similar moderate correlation between XCOM/BOS and step length (R2 = 0.58 without considering the trunk angle in Bhatt et al., 2005). The sagittal plane position of the COM relative to the BOS (i.e., XCOM/BOS) is, by definition, influenced by step length, but the trunk and head contribute nearly 60% of the body mass, thus their orientation would substantially influence the COM position. The prospect that the requirement to simultaneously match two gait parameter targets may alter a person’s spontaneous control of COM position cannot be completely ruled out. In studies of the kinetics and kinematics of subjects who were required to shorten or lengthen their step length for one gait cycle, step shortening resulted in forward displacement of the head-arms-trunk at touchdown (Varraine et al., 2000). Taken together, it is evident that changing one’s step length also changes the relationship of the trunk to the lower extremities.

In the present study, step lengthening resulted in opposite trunk postures depending on the gait speed: the slower group with very long steps had a backward leaning trunk at touchdown. In contrast, the fast group, whose step lengths were equally long, had a slightly forward leaning trunk. Both slow groups also had different trunk orientations. In this regard, a faster speed or a shorter step length would more likely lead to forward leaning of the upper body. Overall, trunk inclination appears to be jointly influenced by gait speed and step length, as well as being an additional degree-of-freedom in controlling the COM motion state.

The findings of the present study further underscore the complexity inherent in the control of COM stability. This stability, which is determined by the XCOM/BOS and VCOM/BOS, has been shown to be predictive of loss of balance in the face of slips under various circumstances (Bhatt et al., 2006), and is associated with falls in response to slip during various activities (Yang et al., 2009). It was unclear whether or how control of the COM motion state could be accomplished simply through modulating the global gait parameters. The results of the present study indicate that such attempts must be more complex than simply altering the global gait parameters, especially for XCOM/BOS. The orientation of the body, particularly the trunk angle, should also be considered. Further investigation focusing on the independent control of the global gait parameters and local body segment configuration would likely be valuable for gait stability training.

Acknowledgements

This work was funded by NIH 2R01-AG16727 (YCP). The authors thank Junyi Sun and Ting-yun Wang for assisting in data collection and processing, and Edward Wang, PhD, for statistical consultation.

Footnotes

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

Conflict of interest statement None of the authors has any conflict of interest related to this work. The study sponsors had no involvement in the study design, execution or manuscript preparation.

REFERENCES

  1. Bhatt T, Wening JD, Pai YC. Influence of gait speed on stability: recovery from anterior slips and compensatory stepping. Gait Posture. 2005;21:146–156. doi: 10.1016/j.gaitpost.2004.01.008. [DOI] [PubMed] [Google Scholar]
  2. Bhatt T, Wening JD, Pai YC. Adaptive control of gait stability in reducing slip-related backward loss of balance. Exp Brain Res. 2006;170:61–73. doi: 10.1007/s00221-005-0189-5. [DOI] [PubMed] [Google Scholar]
  3. Bonnard M, Pailhous J. Intentionality in human gait control: modifying the frequency-to-amplitude relationship. J Exp Psychol Hum Percept Perform. 1993;19:429–443. doi: 10.1037//0096-1523.19.2.429. [DOI] [PubMed] [Google Scholar]
  4. Cham R, Redfern MS. Changes in gait when anticipating slippery floors. Gait Posture. 2002;15:159–171. doi: 10.1016/s0966-6362(01)00150-3. [DOI] [PubMed] [Google Scholar]
  5. Chamberlin ME, Fulwider BD, Sanders SL, Medeiros JM. Does fear of falling influence spatial and temporal gait parameters in elderly persons beyond changes associated with normal aging? J Gerontol A Biol Sci Med Sci. 2005;60:1163–1167. doi: 10.1093/gerona/60.9.1163. [DOI] [PubMed] [Google Scholar]
  6. Cromwell RL, Newton RA. Relationship between balance and gait stability in healthy older adults. J Aging Phys Act. 2004;12:90–100. doi: 10.1123/japa.12.1.90. [DOI] [PubMed] [Google Scholar]
  7. Danion F, Varraine E, Bonnard M, Pailhous J. Stride variability in human gait: the effect of stride frequency and stride length. Gait Posture. 2003;18:69–77. doi: 10.1016/s0966-6362(03)00030-4. [DOI] [PubMed] [Google Scholar]
  8. de Leva P. Adjustments to Zatsiorsky-Seluyanov's segment inertia parameters. J Biomech. 1996;29:1223–1230. doi: 10.1016/0021-9290(95)00178-6. [DOI] [PubMed] [Google Scholar]
  9. Dingwell JB, Marin LC. Kinematic variability and local dynamic stability of upper body motions when walking at different speeds. J Biomech. 2006;39:444–452. doi: 10.1016/j.jbiomech.2004.12.014. [DOI] [PubMed] [Google Scholar]
  10. England SA, Granata KP. The influence of gait speed on local dynamic stability of walking. Gait Posture. 2007;25:172–178. doi: 10.1016/j.gaitpost.2006.03.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Laufer Y. Effect of age on characteristics of forward and backward gait at preferred and accelerated walking speed. J Gerontol A Biol Sci Med Sci. 2005;60:627–632. doi: 10.1093/gerona/60.5.627. [DOI] [PubMed] [Google Scholar]
  12. Li L, Haddad JM, Hamill J. Stability and variability may respond differently to changes in walking speed. Hum Mov Sci. 2005;24:257–267. doi: 10.1016/j.humov.2005.03.003. [DOI] [PubMed] [Google Scholar]
  13. McGibbon CA, Krebs DE. Discriminating age and disability effects in locomotion: neuromuscular adaptations in musculoskeletal pathology. J Appl Physiol. 2004;96:149–160. doi: 10.1152/japplphysiol.00422.2003. [DOI] [PubMed] [Google Scholar]
  14. Menz HB, Lord SR, Fitzpatrick RC. A structural equation model relating impaired sensorimotor function, fear of falling and gait patterns in older people. Gait Posture. 2007;25:243–249. doi: 10.1016/j.gaitpost.2006.04.005. [DOI] [PubMed] [Google Scholar]
  15. Moyer BE, Chambers AJ, Redfern MS, Cham R. Gait parameters as predictors of slip severity in younger and older adults. Ergonomics. 2006;49:329–343. doi: 10.1080/00140130500478553. [DOI] [PubMed] [Google Scholar]
  16. Ness KK, Gurney JG, Ice GH. Screening, education, and associated behavioral responses to reduce risk for falls among people over age 65 years attending a community health fair. Phys Ther. 2003;83:631–637. [PubMed] [Google Scholar]
  17. Pai YC, Iqbal K. Simulated movement termination for balance recovery: Can movement strategies be sought to maintain stability in the presence of slipping or forced sliding? J Biomech. 1999;32:779–786. doi: 10.1016/s0021-9290(99)00074-3. [DOI] [PubMed] [Google Scholar]
  18. Pai YC, Maki BE, Iqbal K, McIlroy WE, Perry SD. Thresholds for step initiation induced by support-surface translation: a dynamic center-of-mass model provides much better prediction than a static model. J Biomech. 2000;33:387–392. doi: 10.1016/s0021-9290(99)00199-2. [DOI] [PubMed] [Google Scholar]
  19. Pai YC, Patton J. Center of mass velocity-position predictions for balance control. J Biomech. 1997;30:347–354. doi: 10.1016/s0021-9290(96)00165-0. [DOI] [PubMed] [Google Scholar]
  20. Pai YC, Rogers MW, Patton J, Cain TD, Hanke TA. Static versus dynamic predictions of protective stepping following waist-pull perturbations in young and older adults. J Biomech. 1998;31:1111–1118. doi: 10.1016/s0021-9290(98)00124-9. [DOI] [PubMed] [Google Scholar]
  21. Pai YC, Wening JD, Runtz EF, Iqbal K, Pavol MJ. Role of feedforward control of movement stability in reducing slip-related balance loss and falls among older adults. J Neurophysiol. 2003;90:755–762. doi: 10.1152/jn.01118.2002. [DOI] [PubMed] [Google Scholar]
  22. Patton JL, Pai Y, Lee WA. Evaluation of a model that determines the stability limits of dynamic balance. Gait Posture. 1999;9:38–49. doi: 10.1016/s0966-6362(98)00037-x. [DOI] [PubMed] [Google Scholar]
  23. Pavol MJ, Runtz EF, Edwards BJ, Pai YC. Age influences the outcome of a slipping perturbation during initial but not repeated exposures. J Gerontol A Biol Sci Med Sci. 2002;57(8):M496–M503. doi: 10.1093/gerona/57.8.m496. [DOI] [PubMed] [Google Scholar]
  24. Roerdink M, Lamoth CJ, Kwakkel G, van Wieringen PC, Beek PJ. Gait coordination after stroke: benefits of acoustically paced treadmill walking. Phys Ther. 2007;87:1009–1022. doi: 10.2522/ptj.20050394. [DOI] [PubMed] [Google Scholar]
  25. Rogers HL, Cromwell RL, Newton RA. Association of balance measures and perception of fall risk on gait speed: a multiple regression analysis. Exp Aging Res. 2005;31:191–203. doi: 10.1080/03610730590915434. [DOI] [PubMed] [Google Scholar]
  26. Varraine E, Bonnard M, Pailhous J. Intentional on-line adaptation of stride length in human walking. Exp Brain Res. 2000;130:248–257. doi: 10.1007/s002219900234. [DOI] [PubMed] [Google Scholar]
  27. Winter DA. Biomechanics and Motor Control of Human Movement. Hoboken, NJ: Wiley; 2005. [Google Scholar]
  28. Yang F, Anderson FC, Pai YC. Predicted threshold against backward balance loss in gait. J Biomech. 2007;40:804–811. doi: 10.1016/j.jbiomech.2006.03.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Yang F, Anderson FC, Pai YC. Predicted threshold against backward balance loss following a slip in gait. J Biomech. 2008a;41:1823–1831. doi: 10.1016/j.jbiomech.2008.04.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Yang F, Bhatt T, Pai YC. Role of stability and limb support in recovery against a fall following a novel slip induced in different daily activities. J Biomech. 2009;42:1903–1908. doi: 10.1016/j.jbiomech.2009.05.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Zijlstra W, Rutgers AWF, Hof AL, T.W V. Voluntary and involuntry adaptation of walking to temporal and spatial constraints. Gait and Posture. 1995;3:13–18. [Google Scholar]

RESOURCES