Abstract
Ultra-short echo time (UTE) imaging is a technique that can visualize tissues with sub-millisecond T2 values that have little or no signal in conventional MRI techniques. The short-T2 tissues, which include tendons, menisci, calcifications, and cortical bone, are often obscured by long-T2 tissues. This paper introduces a new method of long-T2 component suppression based on adiabatic inversion pulses that significantly improves the contrast of short-T2 tissues. Narrow bandwidth inversion pulses are used to selectively invert only long-T2 components. These components are then suppressed by combining images prepared with and without inversion pulses. Fat suppression can be incorporated by combining images with the pulses applied on the fat and water resonances. Scaling factors must be used in the combination to compensate for relaxation during the preparation pulses. The suppression is insensitive to RF inhomogeneities because it uses adiabatic inversion pulses. Simulations and phantom experiments demonstrate the adiabatic pulse contrast and how the scaling factors are chosen. In vivo 2D UTE images in the ankle and lower leg show excellent, robust long-T2 suppression for visualization of cortical bone and tendons.
Keywords: Ultra-short Echo Time (UTE) Imaging, long-T2 suppression, short-T2 imaging, adiabatic pulses
Introduction
Ultra-short echo time (UTE) imaging is a magnetic resonance imaging (MRI) technique that can image tissues with very short T2 relaxation times (1). These tissues normally have little or no signal in conventional MRIs, and there are many potential in vivo applications of imaging short-T2 species (2, 3). These species are found in structured and connective tissues where strong dipolar couplings lead to short transverse relaxation times. Examples of such tissues include collagen-rich tissues such as tendons, ligaments and menisci, as well as calcifications, myelin, periosteum, and cortical and trabecular bone.
Conventional imaging methods have difficulty imaging species with T2 values smaller than a few milliseconds because of constraints on the minimum echo time (TE). UTE imaging captures much shorter T2 species because the TE is only limited by MR system switching times and coil ring down time. Most clinical MR systems can achieve a minimum TE of 40 to 200 μs, and the shortest reported is 8 μs (4).
There have been multiple studies published exploring possible clinical applications for UTE imaging. These include imaging calcifications, cavernomas, and metastases in the brain (5,6), hemochromatosis and cirrhosis in the liver (7), the periosteum (8), cortical bone (9), lung parenchyma (10, 11), and tendon, menisci and articular cartilage (12-14). Recent studies have also investigated using gadolinium for contrast enhancement (15), as well as short-T2 phosphorus and sodium imaging in vivo (16, 17). Imaging connective structures such as myelin, capsules, and falx are other potential applications.
Long-T2 component and fat suppression are widely used in UTE imaging to enhance the contrast of short-T2 components. Long-T2 components at both the fat and water resonances often have higher signal and also decay slower, overwhelming and obscuring the quickly decaying short-T2 components. There are various long-T2 suppression methods, each with their own advantages and disadvantages.
There are primarily two groups of long-T2 suppression methods. The first group uses T2 information gained from later echo times to suppress long-T2 species. Subtracting a later echo image, containing signal only from long-T2 species, is the most common method (2, 5, 18). Combining multiple different TE images can also create highly T2 selective images (19). Since later TE images have no short-T2 signal, the combination decreases short-T2 signal-to-noise ratio (SNR). Off-resonance and artifacts can be a problem too, especially for fat suppression. These techniques are simple to implement and provide useful reference images.
The second group of long-T2 suppression methods are based on RF saturation pulses. These are long π/2 pulses that do not excite short-T2 species for whom their decay rate exceeds the pulse excitation rate (20, 21). Long-T2 species are saturated by the pulse and subsequently dephased. This technique produces images with good short-T2 contrast, but is sensitive to off-resonance and inhomogeneous B1 fields. The off-resonance sensitivity can be improved by interrupting the long saturation pulse with short refocusing pulses (22). This method was designed for imaging longer short-T2 species (≈ 10 ms), and its performance varies with T1/T2.
Inversion recovery (IR) can also be used to selectively null long-T2 components with a particular T1 (2). Longer inversion pulses can be used to preserve more short-T2 signal, but are more sensitive to off-resonance.
In this article we introduce a new method for suppressing long-T2 components that is robust to B1 field variations because it is based on adiabatic inversion pulses. It involves combining two images in which the magnetization has been prepared by adiabatic inversion pulses that create T2 contrast. The pulses only invert long-T2 species, not short-T2 species, and the pulse bandwidth determines the contrast. Long-T2 species are removed by combining an image with inverted long-T2 species and an image without inversion preparation. Fat can also be suppressed by combining an image where fat is inverted and an image with inverted water long-T2 species. Phantom and in vivo experiments presented confirm that the suppression is precise and insensitive to B1 field variations while preserving short-T2 signal.
Theory
T2 Contrast
The T2 contrast of an RF pulse is primarily determined by the spectral bandwidth of the pulse. For a pulse with a bandwidth that is much greater than 1/T2, the longitudinal magnetization after a pulse, neglecting T1, will be approximately:
| (1) |
| (2) |
where ω1(t) is the RF pulse amplitude and Ω1(f) is its Fourier transform (21). Equation 1 shows that the change in MZ is proportional to T2 and the RF power, irrespective of the pulse shape, and Eq. 2 shows how this is related to the approximate pulse bandwidth.
Intuitively, the RF pulse T2 contrast comes from the idea that it is easy to excite long-T2 species but difficult to excite short-T2 species. Short-T2 species will decay faster than excited if the pulse amplitude is low enough, while longer T2 species will still be excited by the pulse.
Adiabatic Pulses
Adiabatic RF pulses are advantageous because of their insensitivity to inhomogeneities in the B1 field (23). They are characterized by amplitude and frequency modulation functions that define frequency sweeps, during which the magnetization is kept either aligned or perpendicular to the effective RF field provided that the RF amplitude is greater than the adiabatic threshold. It has been previously shown through Bloch equation simulations that T2 relaxation during the adiabatic hyperbolic secant (sech) pulse can prevent complete inversion of the magnetization (24), suggesting that T2 contrast can be generated by adiabatic pulses. They demonstrated how the net magnetization is smaller due to relaxation and also lies partially in the transverse plane.
It was also shown in (24) that increases in RF amplitude reduced the magnitude of the resulting short-T2 magnetization while the response of long-T2 components is invariant to RF amplitude variations above the adiabatic threshold. As B1 increases, the short-T2 magnetization is tipped more into the transverse plane, causing more T2 relaxation to occur. This result is consistent with Eq. 1. Adiabatic pulses for T2 contrast in UTE imaging should therefore be power efficient to preserve the most short-T2 signal.
The bandwidth of adiabatic pulses also affects the short-T2 response. Figure 1 demonstrates that, for an adiabatic sech pulse at the adiabatic threshold, the inversion is more effective with increasing bandwidth. This relationship is similar to Eq. 2, which was derived for non-adiabatic pulses (21). Shorter T2 species are tipped less than longer T2 species, as expected from (24).
Figure 1.
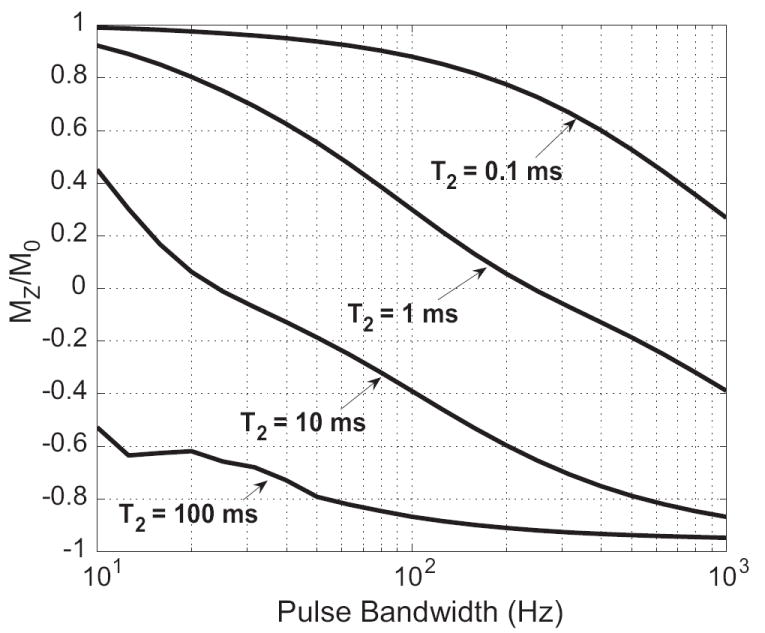
Plot of the simulated longitudinal magnetization remaining after 100 ms adiabatic sech inversion pulses with different bandwidths for various T2 values. As the pulse bandwidth increases, MZ decreases and the inversion is more complete. Longer T2 species also are more inverted than shorter T2 species, although they are still not fully inverted because of transverse relaxation during the pulse.
Adiabatic pulses for selective long-T2 inversion should be power efficient with a narrow bandwidth and a flat spectral profile across the inversion band. Offset independent adiabaticity (OIA) pulses have such a flat spectral profile across which they efficiently distribute their power (25). Of the OIA inversion pulses in (25), the sech and Lorentz modulation functions have the best spectral profiles with comparable power efficiency. They have the highest peak amplitudes, but this is not an issue for selective long-T2 inversion pulses which are long-duration and low-power to preserve short-T2 signal, and will not approach the peak amplitude limitations. Lorentz pulses have slightly less required power and a better profile than the sech pulse, but a higher peak amplitude.
Both T2 and T1 relaxation during selective long-T2 adiabatic inversion pulses have a non-negligible effect on the inversion because longer pulse durations are required for narrow bandwidth pulses. The pulse response in the presence of relaxation can be predicted accurately with full Bloch equation simulations, as done in (24).
Methods
Long-T2 Suppression
Our method for long-T2 suppression uses the pulse sequence shown in Fig. 2. It consists of two interleaved UTE acquisitions with adiabatic inversion magnetization preparation pulses applied immediately before one or both of the acquisitions. The 2D UTE acquisition uses summed half-pulse acquisitions with alternating slice select gradients to create a good slice profile, followed by a projection-reconstruction (PR) readout (10).
Figure 2.
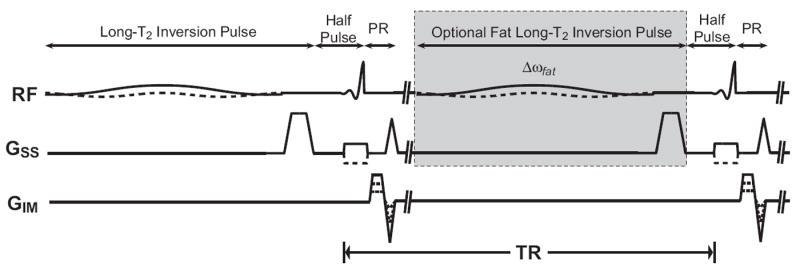
Inversion combination 2D UTE pulse sequence. An inversion pulse with a crusher gradient is applied before a standard UTE pulse sequence to create a long-T2 inverted image. This is interleaved with the second acquisition to minimize differences from T1-weighting and motion between the resulting images. A second inversion pulse centered on the lipid resonance can be applied (gray box) to additionally suppress fat long-T2 species.
Long-T2 suppression is achieved by combining the two acquisitions. The adiabatic inversion preparation pulse inverts only the long-T2 magnetization and the contrast is stored in MZ by the accompanying crusher gradient. The resulting long-T2 inverted image is summed with an image acquired without inversion preparation to suppress the long-T2 signal. This summation is complex to preserve the polarity of the signal. As shown in Fig. 2, the two image acquisitions are interleaved. This is done to minimize T1-weighting effects and potential motion artifacts when combining the images.
This method can be modified to also suppress long-T2 components in fat by applying a second inversion preparation pulse centered at the lipid resonance (gray box in Fig. 2). Long-T2 components at both resonances will be inverted only in their respective inversion-prepared images and can each be suppressed by combining the images, as shown in Fig. 3. Short-T2 species are attenuated by both pulses because of their broad spectrum.
Figure 3.
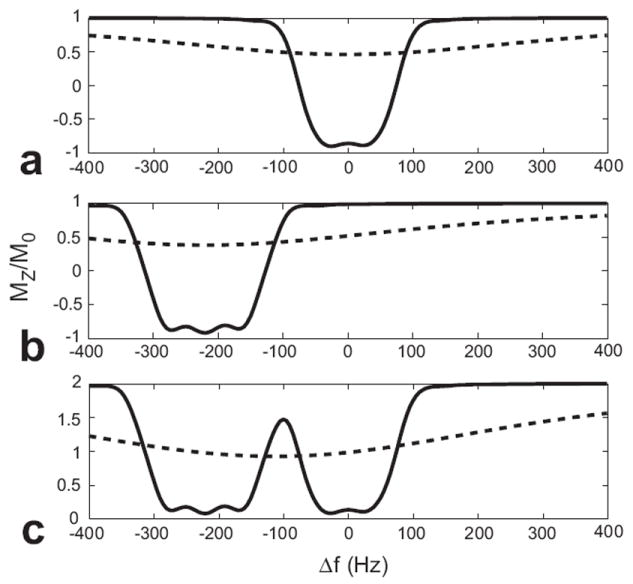
Adiabatic inversion pulse off-resonance profiles for T2 = 100 ms (solid line) and T2 = 500 μs (dashed line). (a) 30 ms Lorentz pulse (FWHM bandwidth = 135 Hz) applied at the water resonance. (b) 30 ms Lorentz pulse (FWHM bandwidth = 170 Hz) applied at the fat resonance. (c) Profile of combined water- and fat-inverted images. When the two images are combined, the long-T2 species at both resonances are suppressed. The short-T2 species, while attenuated, will have significantly improved contrast. For the values shown, the short-T2 to long-T2 contrast is increased by a factor of ten.
Summing the two images will improve short-T2 contrast but not completely suppress long-T2 components because relaxation during the preparation pulses decreases the total magnetization. For example, the inverted magnetization in Fig. 3, simulated with T2 = 100 ms and T1 = 1 s, is at MZ ≈ −0.9M0, indicating a 10% attenuation during the 30 ms inversion pulses. To compensate for this and improve the suppression, a scaling factor is applied when the images are combined.
This scaling factor can be predicted based on the steady-state magnetization and Bloch equation simulations. The non-inverted and inversion-prepared signal, S and Sinv, respectively, in the interleaved acquisitions are
| (3) |
| (4) |
where θ is the half-pulse flip angle, E1 = exp(−TR/T1), Ê1 = exp(−(TR −Tinv)/T1), Tinv is the inversion pulse duration, and Cprep is the factor by which the inversion pulse scales the longitudinal magnetization (Cprep = −1 for a complete inversion). Cprep is a function of T1, T2, and the inversion pulse, and is calculated with Bloch equation simulations.
The predicted scaling factor is the ratio of these two signals:
| (5) |
This can be simplified by using a half-pulse flip angle of θ = π/2. This reduces T1-weighting by putting the long-T2 magnetization in transverse plane after each excitation, reducing Eq. 5 to
| (6) |
Phantom experiments are compared to this result later in this paper. Multi-exponential relaxation can also be incorporated into this analysis, which is described in the Appendix.
Two scaling factors are required to completely suppress long-T2 species at both the water and lipid resonances because they are inverted in separate images. The model in Eq. 6 is used in conjunction with a phase separation process so only the inverted components are scaled in their respective images, which is illustrated in Fig. 4. The phase separation begins with removal of the estimated linear phase from each image. The linear phase is estimated by a least-squares fit of the phase in the object. This is followed by the addition of a constant phase shift to unwrap phase discontinuities. The separation is then performed by thresholding the difference between the corrected phases. Taking the phase difference removes any additional baseline phase. After the phase separation, the two scaling factors are applied only to the inverted components in their respective images, canceling out long-T2 species at both the water and lipid resonances.
Figure 4.
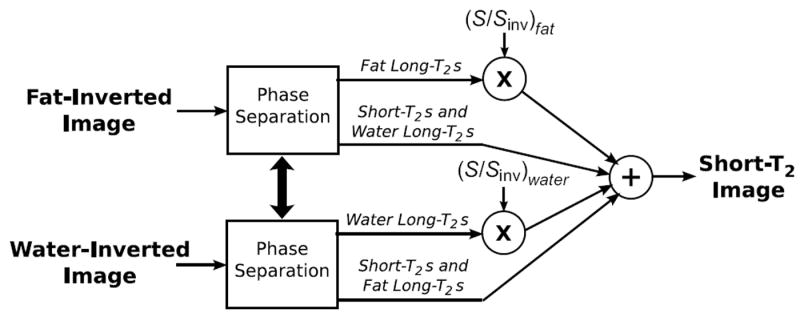
Method for fat and water long-T2 suppression. Fat-inverted and water-inverted images are acquired, and then separated into inverted and non-inverted components based on the corrected phase. The inverted components are scaled in their respective images, which are then combined.
Simulations
Simulations were used to validate the performance of the RF pulses as well as estimate the scaling factors. We used a Bloch equation simulation that calculates the precession and both T1 and T2 decay matrices using the RF waveforms for each of a set of resonant frequencies. This Bloch simulation was coded in Matlab (The Mathworks, Natick, MA, USA), and is available at http://www-mrsrl.stanford.edu/~brian/blochsim. The off-resonance frequencies used are relative to water protons at 1.5 T. When estimating the in vivo scaling factors, Cprep was averaged over ±50 Hz across the inversion band to account for small resonance shifts.
Experiments
A GE Excite 1.5T scanner with gradients capable of 40 mT/m amplitude and 150 T/m/s slew rate (GE Healthcare, Milwaukee, WI) was used for all experiments. Figure 2 shows the 2D UTE pulse sequence with inversion preparation pulses and interleaved half-pulse excitations. The half-pulses were designed for a 90° flip angle (26). This leaves the magnetization is in the transverse plane after each excitation, and was used to simplify Eq. 5 to Eq. 6.
We used a PR readout gradient with ramp sampling and an acquisition time of 1 ms, which is similar to the T2 values of interest (18). The maximum slew rate was used on the ramp, and the readout gradient amplitude was determined based on the resolution and the fixed acquisition time. The minimum TE of our configuration was 80 μs, limited by the coil ring down time and hardware switching times.
The acquisitions were oversampled in the radial direction, supporting a region larger than the desired field-of-view (FOV). This oversampling comes at no cost because the extra samples are averaged out in the gridding reconstruction. The in vivo acquisitions were undersampled in the angular direction to reduce the scan time. Angular undersampling is common in PR MRI because the diffuse aliasing of the trajectory produces tolerable aliasing artifacts (27-30).
The images were reconstructed using the gridding algorithm to resample the radial k-space data onto a uniform grid with a minimal oversampling ratio (31). The gridding was done on a matrix with an oversampling ratio of 1.25 using a Kaiser-Bessel kernel with a width of 6 grid samples and β calculated as described in (31). The kernel was presampled and then linearly interpolated to find the desired kernel value. Prior to gridding, a radial density compensation factor was applied. This factor was calculated based on the trajectory geometry and accounts for the ramp sampling. In the angularly undersampled acquisitions, it was made constant beyond the k-space radius for which the data was undersampled to increase the SNR efficiency (32).
Phantoms with various T1 and T2 values were created by doping distilled water with Manganese Chloride (MnCl2). They were imaged using TE = 220 μs, flip angle = 90°, 5 mm slice thickness, 3 mm in-plane resolution, and a transmit/receive head coil. TRs of 200 and 400 ms were used in scaling factor experiments, which had a maximum SAR of 0.1 W/kg.
In vivo experiments were performed on healthy volunteers. All subjects gave informed consent in accordance with Stanford University policy after they were screened for possible MRI risk factors. Axial images in the lower leg were acquired for imaging cortical bone in the tibia, which has a reported of 420-500 μs and T1 of 140-260 ms (9), using imaging parameters of TE = 80 μs, TR = 300 ms, flip angle = 90°, 5 mm slice thickness, 0.73 mm in-plane resolution, a 12 cm FOV with an angular undersampling factor of 2.0, a 3-inch receive-only surface coil, and 5 min 20 s total time for both the fat-inverted and water-inverted images. 30 ms Lorentz adiabatic pulses were used with a full-width half-maximum (FWHM) bandwidth of approximately 130 Hz on-resonance and 160 Hz at -220 Hz off-resonance. A wider bandwidth was used off-resonance for more robust inversion of fat. In the fat-inversion only experiment, a 30 ms, 200 Hz bandwidth Lorentz pulse at -220 Hz was used. Each inversion pulse amplitude was set at 20% above the adiabatic threshold to support up to 20% variation in the B1 field. The maximum SAR of this sequence was approximately 0.08 W/kg.
Images of the ankle were also acquired to visualize the Achilles’ tendon, which is reported to have two short- components of 0.53 ms (88%) and 4.80 ms (12%) posteriorly, and 0.60 ms (70%) and 4.20 ms (30%) anteriorly (33). The imaging parameters were TE = 80 μs, TR = 300 ms, flip angle = 90°s, 5 mm slice thickness, 0.73 mm in-plane resolution, a 10 cm FOV with an angular undersampling factor of 1.7, a 5-inch receive-only surface coil, and 5 min 20 s total time for both the fat-inverted and water-inverted image. 30 ms Lorentz adiabatic pulses were used with a FWHM bandwidth of approximately 160 Hz on-resonance and 200 Hz at -220 Hz off-resonance, and amplitudes 20% above the adiabatic threshold. Again, a wider bandwidth fat inversion pulse was used for more robust fat suppression. The maximum SAR of this sequence was approximately 0.08 W/kg.
Scaling factors based on Bloch simulations of the adiabatic pulses and Eq. 6 were initially applied to the acquired images. These values were then manually adjusted to give the most complete cancellation of fat and muscle in regions known to contain these long-T2 tissues.
Results
Simulations
An adiabatic sech inversion pulse is compared to rectangular and Shinnar-Le Roux (SLR) (34) inversion pulses in Fig. 5. All three pulses were designed to have the same FWHM bandwidth, thus they have similar on-resonance T2 profiles (Fig. 5d,e, and f). The rectangular pulse has a very poor off-resonance profile (Fig. 5g), but the SLR and sech pulses have flat off-resonance profiles (Fig. 5h, i). Changes in RF amplitude, indicated by the gray lines, severely degrade the rectangular and SLR pulse spectral profiles, while the adiabatic pulse profile is nearly invariant to these changes (Fig. 5i).
Figure 5.
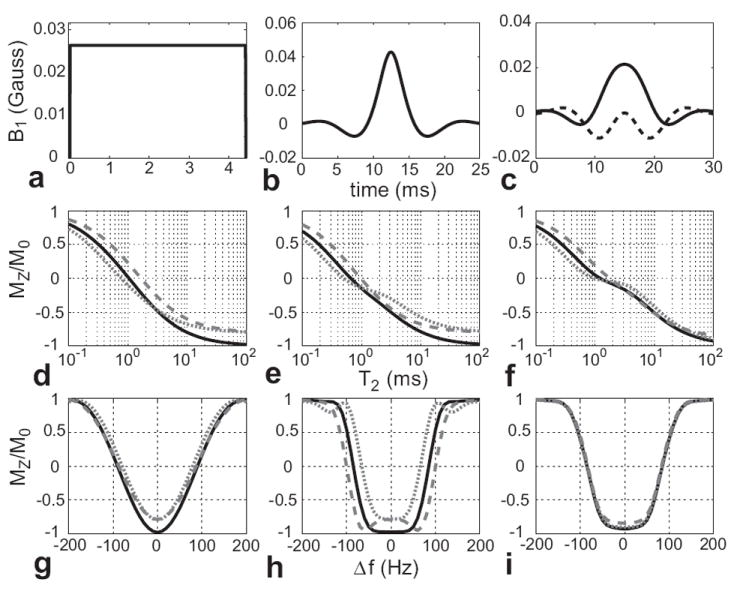
Bloch simulations of (a) 4.4 ms rectangular inversion pulse, (b) 25 ms SLR inversion pulse, and (c) 30 ms adiabatic sech inversion pulse with the amplitude at 20% above the adiabatic threshold (dashed line is imaginary component). (d), (e), and (f) are the corresponding T2 profiles on-resonance, where the solid, black lines were calculated using the desired B1 amplitude. The short-dash gray lines used 80% of the desired amplitude and the long-dash gray lines used 120%. (g), (h), and (i) are the off-resonance profiles for T2 = 100 ms for varying B1 amplitudes. The pulses were designed to have the same FWHM bandwidth, resulting in similar T2 profiles. The non-adiabatic pulse profiles suffer as the amplitude varies, while the adiabatic inversion pulse response for longer T2 values is practically insensitive to the changes in B1.
The sech pulse T2 profile in Fig. 5f shows less complete inversions than the rectangular and SLR pulses for T2 values greater than 1 ms. This is because the magnetization spends more time in the transverse plane during the frequency sweep of the 30 ms adiabatic sech pulse, resulting in more T2 decay than during the rectangular and SLR pulses. However, the sech pulse response for the longer T2 values does not change much with the ±20% RF amplitude variations, especially in comparison to the rectangular and SLR inversion pulses (Fig. 5d and e). There is substantial variation in shorter T2 response to amplitude modulations for all pulses, as expected from Eq. 1.
Experiments
Figure 6 shows a comparison of the predicted scaling factor (Eq. 6) and phantom imaging results. The predicted and experimental values agree very well.
Figure 6.

Simulated and measured scaling factors, S/Sinv, for various relaxation parameters, TRs, and adiabatic pulses. The squares were calculated using the Bloch equation and Eq. 6. The range of scaling factors and the mean (x’s) are shown for the experimental data, obtained using MnCl2-doped water phantoms. Each of the adiabatic pulses was 30 ms long. The results show that the scaling factors can be predicted with reasonable accuracy.
Figure 7 shows results of imaging the cortical bone in the tibia. In the phase of the image acquired with the inversion pulse centered at the water resonance (Fig. 7c), only the muscle is inverted, indicated by the dark shading. Similarly, only the fat near the skin and in the bone marrow is inverted in the phase of the image acquired with the inversion pulse centered at the fat resonance (Fig. 7d). In both images, the inverted components are not fully inverted, as shown by their reduced signal in the magnitude images (Fig. 7a, b - identically windowed). While the unscaled sum (Fig. 7e) provides better cortical bone contrast than the UTE image (Fig. 7i), the scaled sum (Fig. 7f), created using the process shown in Fig. 4, improves the contrast significantly and has better fat suppression. In addition to the cortical bone in the tibia and fibula (long, thin arrows), signal also remains in the skin, around the vessels, and between the muscles and also their fascicles. This may be from short-T2 components, such as collagen or other connective tissues, but could also be due to the off-resonance sensitivity of the inversion pulses or partial volume artifacts from the phase separation.
Figure 7.
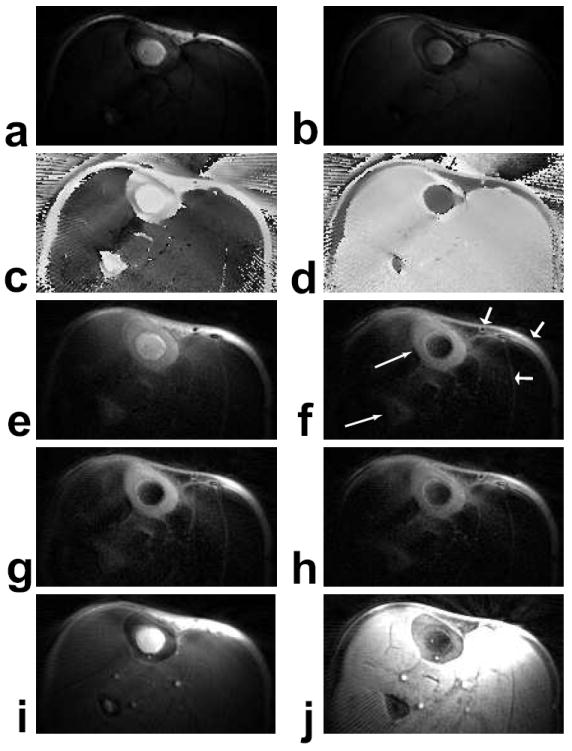
Axial images at the middle of the lower leg. (a) Water-inverted magnitude image. (b) Fat-inverted magnitude image. (c) Water-inverted phase image, corrected. (d) Fat-inverted phase image, corrected. (e) Sum of (a) and (b). (f) Scaled sum of (a) and (b). (g,h) Scaled sums with 80 % and 120 %, respectively, of the desired RF amplitude, windowed the same as (f). (i) UTE image (TE = 80 μs). (j) Scaled sum of a non-inverted and a fat-inverted image (not shown), also windowed the same as (f). The scaled sums of water-and fat-inverted images (f,g,h) show excellent contrast for the cortical bone in both the tibia and fibula (long, thin arrows). The signal in the skin, around the vessels, and between the muscles and fascicles (short, fat arrows) may be from short-T2 components, or suppression failures due to off-resonance and/or partial volume effects.
This suppression is still effective with the 20% variations in the B1 field artificially induced to produce the images in Fig. 7g and h. The cortical bone signal is proportional to the RF amplitude, as expected from Eq. 1, and the scaling factors used are slightly different across the images (see Table 1). Figure 7j shows the scaled sum result using a non-inverted and a fat-inverted image for just long-T2 fat suppression. While cortical bone contrast is improved, there is very high signal from the surrounding muscle and vessels. This large signal difference causes streaking artifacts, which are also seen in the UTE image (Fig. 7i) because of the angular undersampling. The result of suppressing only fat, windowed identically to the other scaled sums, shows no substantial gains in short-T2 signal.
Table 1.
Comparison of scaling factors estimated from Eq. 6 and applied to in vivo data for maximum suppression.
| Skeletal Muscle T2, T1 = 50, 870 ms | Blood T2, T1 = 50, 1200 ms | Fat T2, T1 = 80, 260 ms | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0.8 B1 | 1.0 B1 | 1.2 B1 | 0.8 B1 | 1.0 B1 | 1.2 B1 | 0.8 B1 | 1.0 B1 | 1.2 B1 | ||
| Lower leg (Fig. 7f,g,h) | Predicted S/Sinv | 1.50 | 1.39 | 1.47 | 1.49 | 1.38 | 1.46 | 1.48 | 1.38 | 1.44 |
| Applied scaling factor | 1.5 | 1.4 | 1.5 | 1.5 | 1.4 | 1.5 | 1.7 | 1.7 | 1.8 | |
| Ankle (Fig. 8j,k,l) | Predicted S/Sinv | 1.42 | 1.36 | 1.44 | 1.41 | 1.35 | 1.43 | 1.47 | 1.36 | 1.40 |
| Applied scaling factor | 1.5 | 1.4 | 1.5 | 1.5 | 1.4 | 1.5 | 1.8 | 1.6 | 1.6 | |
The predicted T1 and T2 values are from (37). For skeletal muscle and blood, the predicted scaling factors are very close to the actual scaling factors used. The fat scaling factors, however, are consistently underestimated.
A high-resolution ankle scan, taken at the distal tibia above the ankle joint, is shown in Fig. 8. The short-T2 tissues, such as the tendons and cortical bone, are visible in the unsuppressed UTE image (Fig. 8a), but have poor contrast. The effectiveness and spectral selectivity of the water and fat adiabatic inversion pulses is shown in the corrected phase images (Fig. 8g, h). The muscle and vessels have the opposite phase of the fat and tendons in the water-inverted acquisition while the fat has the opposite phase of the muscle, vessels, and tendons in the fat-inverted acquisition. When the difference of the phases is taken (Fig. 8i), the water long-T2 tissues, the fat long-T2 tissues, and the short-T2 tissues (arrows) can all be distinguished, and this map is used for segmentation. Figure 8d and e are identically windowed so the attenuation due to the inversion pulses can be seen.
Figure 8.
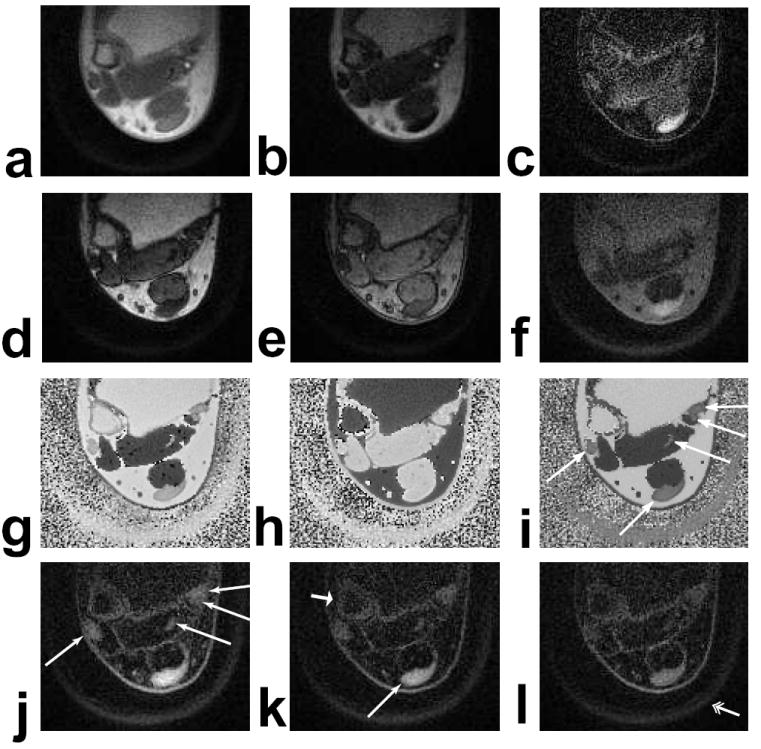
Axial ankle images at the distal tibia above the ankle joint. (a) UTE image (TE = 80 μs). (b) TE = 4.6 ms. (c) Difference of (a) and (b). (d) Water-inverted magnitude image. (e) Fat-inverted magnitude image. (f) Sum of (d) and (e). (g) Water-inverted phase image, corrected. (h) Fat-inverted phase image, corrected. (i) Difference between (g) and (h). (j,k,l) Scaled sums of water- and fat-inverted images with 80 %, 100 %, and 120 %, respectively, of the desired RF amplitude, all identically windowed. The Achilles’, peroneal, flexor hallucis longus, flexor digitorum longus, and tibialis posterior tendons have significantly improved contrast in the scaled sum images (long, thin arrows), and are also distinguishable in the phase difference (i). The cortical bone of the fibula (short, fat arrow) and the plastic boot stabilizing the foot (double arrow) are also very visible.
A simple sum of the fat- and water-inverted images yields reasonable suppression of long-T2 tissues (Fig. 8f). Without scaling, many of the tendons and the cortical bone are difficult to distinguish because they are surrounded by fatty tissue and muscle. The suppression is substantially improved by using a scaled sum (Fig. 8j, k, l). These images have signal in the skin and also at fat-water interfaces around the muscles and vessels which may be from short-T2 components in connective tissues or collagen but could also be the result of partial volume effects and off-resonance that prohibit accurate phase separation and appropriate scaling.
The short-T2 signal is proportional to the RF amplitude, which can be seen in Fig. 8j, k, l, particularly in the Achilles’ tendon. This relationship is expected from Eq. 1 and Fig. 5f. The suppression of the surrounding fat and muscle does not suffer from these changes in RF amplitude.
Combining the TE = 4.6 ms image (Fig. 8b) and the UTE image (Fig. 8a) eliminates most of the fat signal but not all of the muscle signal (Fig. 8c). Most of the short-T2 components are enhanced by the subtraction but the flexor hallucis longus tendon is completely obscured by the remaining flexor digitorum muscle signal. The muscle signal can also be suppressed by altering the scaling of the combination, but the fat signal will then be unsuppressed and other tendons will be obscured.
The scaling factors used for all in vivo suppression images are compared to the predicted scaling factors in Table 1. These agree well for skeletal muscle and blood, for which the same scaling factor is applied to the water-inverted images. For fat, however, there is a consistent underestimation of the required scaling factor. Varying the RF amplitude results in some fluctuation of both the predicted and actual scaling factors, but these are small relative to the variations that would arise from rectangular or SLR inversion pulses, as is shown in Fig. 5.
Discussion
Our method produces long-T2 suppressed images by combining two images which have different magnetization preparation schemes to distinguish various T2 values. This technique is B1 insensitive because adiabatic inversion pulses are used for the magnetization preparation. It is useful for imaging species with T2 values less than a few ms. Longer T2 species will be more affected by the inversion pulse and their SNR will suffer. There is some short-T2 signal attenuation from the inversion pulses in our technique.
This technique has some advantages and disadvantages when compared with the previous methods of subtracting a late echo and RF suppression pulses (21). This method is very similar to the RF suppression pulses in terms of contrast, SNR efficiency, and off-resonance sensitivity because they share the same RF pulse T2-bandwidth tradeoff. The advantage of this method is that it is B1-insensitive and also provides reference images. Subtracting a later TE image is also B1-insensitive, and is more robust to off-resonance. The resulting images appear noisy because the later TE images only add noise. Subtraction has been shown to be more SNR efficient than suppression pulses (35), and has less restrictions on the TR and flip angle than our method. The subtraction result shown in Fig. 8c doesn’t suppress all tissues well, but has good signal in the Achilles’ tendon.
The adiabatic inversion pulses must be designed for B1 insensitivity and minimization of off-resonance artifacts. Their amplitude must be set such that the maximum expected RF attenuation will result in an amplitude that corresponds to the adiabatic threshold. In Figs. 7 and 8, this was chosen to accommodate 20% RF attenuation. Other adiabatic inversion pulse shapes besides the sech and Lorentz could also be used, but will likely not significantly alter the performance of the technique because, regardless of the modulation functions, the bandwidth of the adiabatic pulse will primarily determine the T2 contrast. A shorter adiabatic pulse could potentially improve performance by reducing the relaxation effects for long-T2 components, thereby reducing the magnitude of the scaling factor.
There is a fundamental tradeoff in the inversion pulse design between bandwidth and short-T2 attenuation, which is described in Eq. 2 and shown in Fig. 1. In order to preserve short-T2 signal, narrow bandwidth pulses are used, which makes the suppression sensitive to off-resonance. This tradeoff is best managed by adjusting the pulse bandwidth for the application. For example, wider bandwidth pulses were used in the ankle (Fig. 8) because of the susceptibility near air-tissue interfaces. A field map can be used to best match the inversion pulse bandwidths and center frequencies to preserve the most short-T2 signal.
We do not anticipate that these pulses will introduce any significant T1ρ- weighting. This type of weighting requires large-amplitude, long-duration spin-locking pulses. Our T2-selective adiabatic inversion pulses have low amplitudes, and thus we do not anticipate any difference due to T1ρ.
The pulse sequence was designed to balance the magnetization between the two acquisitions, although scaling factors are still required for complete suppression. The acquisitions are interleaved to reduce differences in the steady-state magnetization and prevent motion artifacts. Half-pulses with 90° flip angles put the magnetization in the transverse plane after every excitation, resulting in nearly identical T1 relaxation between acquisitions and allowing for the use of Eq. 6. Other half-pulse flip angles could also potentially be used for greater SNR efficiency. The required scaling factors would be predicted by Eq. 5 and would have have more complicated dependencies on T1, TR, and the flip angle. The TR and the readout duration can also be adjusted for the optimal short-T2 SNR if the T2 and T1 are known.
In our experiments, we found the scaling factors predicted by Eq. 6 had to be adjusted slightly for complete long-T2 suppression, and especially for fat suppression. The underestimation has multiple possible causes, the most likely of which we believe to be either the broad range of resonances found in fat or a short-T2 component in fat, which has been previously suggested (35). Off-resonance decreases Cprep and thus increases the scaling factor, as would the presence of a short-T2 component. The Appendix characterizes some potential sources of variation in the scaling factor.
The fat and water long-T2 suppression technique requires accurate separation of the inverted and non-inverted components which is done using the phase of the images. Additional phase accumulation due to resonance shifts is nearly negligible because of the ultra-short TE. Taking the difference of the image phases also removes any baseline phase. The linear phase correction assists with phase unwrapping. We have found this separation to be reasonably robust, even in vivo. However, partial volume effects are problematic in voxels that contain both long-T2 fat and water. These voxels cannot be appropriately scaled to suppress both tissues. The partial volume effects can be reduced by using high resolution acquisitions.
Voxels with a short-T2 species and only one long-T2 species do not suffer from partial voluming provided the long-T2 magnetization exceeds the short-T2 magnetization. In this case the voxels are designated as inverted. The long-T2 components will be suppressed by the scaled sum and the short-T2 components will remain. Partial voluming is also not a problem for long-T2 suppression around one resonance because no phase separation is necessary.
Conclusion
We have introduced a new method for long-T2 suppression that is robust to variations in the B1 field by using adiabatic inversion pulses to create T2 contrast. These inversion pulses selectively invert long-T2 species, which can be suppressed by also acquiring an image where they are not inverted and then combining these images. This method can also include fat suppression by combining an image prepared with the inversion pulse on the water resonance and an image with the inversion pulse on the lipid resonance.
The phantom experiments presented confirmed the T2 contrast of the adiabatic inversion pulses and the effects of interleaved acquisitions. The images in the lower leg and ankle using long-T2 suppression at both resonances show excellent visualization of the cortical bone and tendons, and the suppression was robust to variations in B1.
Acknowledgments
We would like to thank Dr. Garry Gold for reviewing the images and assistance with the anatomical details.
This work was supported by GE Medical Systems and NIH grant number R01 EB002524.
Appendix
Scaling Factor Variations
The scaling factor derived in Eqs. 5 and 6 has been shown to match well with experimental results in phantoms (Fig. 6) and for muscles and vessels (Table 1), but there is consistent underestimation for fat. The in vivo predicted scaling factors use estimates of the relaxation parameters, the RF amplitude, and the resonance frequency, all of which are potential sources of error.
Table 1 shows the effect of RF amplitude variations on the predicted scaling factors. The 20% B1 variations result in less than 10% of variation in S/Sinv. Changes in the relaxation parameters of ±20%, shown in table 2, result in only up to 5% variation in the scaling factor. Table 2 also shows how off-resonance can have a very substantial effect on the scaling factor. This difference is greater for skeletal muscle because the water-inversion pulse used has a narrower bandwidth than the fat-inversion pulse.
Table 2.
Simulated effects of variations in the relaxation values and off-resonance on the scaling factor.
The scaling factor model can be modified to incorporate multi-exponential relaxation which exists in most tissues. This is done by modifying the relaxation terms, e−t/T1 and e−t/T2, to model multi-exponential decay and recovery. These terms, which are used to calculate E1, Ê1, and Cprep, are replaced with summed relaxation terms:
| (7) |
| (8) |
where and are the relaxation times of the different components which have respective relative concentrations of and Equations 5 and 6 can then be used following these modifications.
Simulated results using multi-exponential relaxation are shown in table 2. The resulting scaling factors are practically identical to simulations using the effective mono-exponential relaxation values of
| (9) |
| (10) |
There may also be additional short-T2 components with T2 < 2 ms in many tissues (36). They have not been included in this analysis, but their presence would cause the scaling factor to increase.
References
- 1.Pauly JM, Conolly SM, Nishimura DG, Macovski A. Slice-selective excitation for very short T2 species. Proc., SMRM, 8th Annual Meeting; Amsterdam. August 1989; p. 28. [Google Scholar]
- 2.Gatehouse PD, Bydder GM. Magnetic resonance imaging of short T2 components in tissue. Clin Radiol. 2003;58:1–19. doi: 10.1053/crad.2003.1157. [DOI] [PubMed] [Google Scholar]
- 3.Robson MD, Gatehouse PD, Bydder M, Bydder GM. Magnetic resonance: an introduction to ultrashort TE (UTE) imaging. J Comput Assist Tomogr. 2003;27:825–846. doi: 10.1097/00004728-200311000-00001. [DOI] [PubMed] [Google Scholar]
- 4.Brittain JH, Shankaranarayanan A, Ramanan V, Shimakawa A, Cunningham CH, Hinks S, Francis R, Turner R, Johnson JW, Nayak KS, Tan S, Pauly JM, Bydder GM. Ultra-short TE imaging with single-digit (8us) TE. Proceedings of the 12th Annual Meeting of ISMRM; Kyoto. 2004. p. 629. [Google Scholar]
- 5.Nayak KS, Pauly JM, Gold GE, Nishimura DG. Imaging ultra-short T2 species in the brain. Proceedings of the 8th Annual Meeting of ISMRM; Denver. 2000. p. 509. [Google Scholar]
- 6.Waldman A, Rees JH, Brock CS, Robson MD, Gatehouse PD, Bydder GM. MRI of the brain with ultra-short echo-time pulse sequences. Neuroradiology. 2003;45:887–892. doi: 10.1007/s00234-003-1076-z. [DOI] [PubMed] [Google Scholar]
- 7.Chappell KE, Patel N, Gatehouse PD, Main J, Puri BK, Taylor-Robinson SD, Bydder GM. Magnetic resonance imaging of the liver with ultrashort TE (UTE) pulse sequences. J Magn Reson Imaging. 2003;18:709–713. doi: 10.1002/jmri.10423. [DOI] [PubMed] [Google Scholar]
- 8.Reichert IL, Benjamin M, Gatehouse PD, Chappell KE, Holmes J, He T, Bydder GM. Magnetic resonance imaging of periosteum with ultrashort TE pulse sequences. J Magn Reson Imaging. 2004;19:99–107. doi: 10.1002/jmri.10432. [DOI] [PubMed] [Google Scholar]
- 9.Reichert IL, Robson MD, Gatehouse PD, He T, Chappell KE, Holmes J, Girgis S, Bydder GM. Magnetic resonance imaging of cortical bone with ultrashort TE pulse sequences. Magn Reson Imaging. 2005;23:611–618. doi: 10.1016/j.mri.2005.02.017. [DOI] [PubMed] [Google Scholar]
- 10.Bergin CJ, Pauly JM, Macovski A. Lung parenchyma: projection reconstruction MR imaging. Radiology. 1991;179:777–781. doi: 10.1148/radiology.179.3.2027991. [DOI] [PubMed] [Google Scholar]
- 11.Bergin CJ, Noll DC, Pauly JM, Glover GH, Macovski A. MR imaging of lung parenchyma: a solution to susceptibility. Radiology. 1992;183:673–676. doi: 10.1148/radiology.183.3.1584917. [DOI] [PubMed] [Google Scholar]
- 12.Gold GE, Pauly JM, Macovski A, Herfkens RJ. MR spectroscopic imaging of collagen: tendons and knee menisci. Magn Reson Med. 1995;34:647–654. doi: 10.1002/mrm.1910340502. [DOI] [PubMed] [Google Scholar]
- 13.Gold GE, Thedens DR, Pauly JM, Fechner KP, Bergman G, Beaulieu CF, Macovski A. MR imaging of articular cartilage of the knee: new methods using ultrashort TEs. AJR Am J Roentgenol. 1998;170:1223–1226. doi: 10.2214/ajr.170.5.9574589. [DOI] [PubMed] [Google Scholar]
- 14.Gatehouse PD, Thomas RW, Robson MD, Hamilton G, Herlihy AH, Bydder GM. Magnetic resonance imaging of the knee with ultrashort TE pulse sequences. Magn Reson Imaging. 2004;22:1061–1067. doi: 10.1016/j.mri.2004.08.018. [DOI] [PubMed] [Google Scholar]
- 15.Robson MD, Gatehouse PD, So PW, Bell JD, Bydder GM. Contrast enhancement of short T2 tissues using ultrashort TE (UTE) pulse sequences. Clin Radiol. 2004;59:720–726. doi: 10.1016/j.crad.2003.09.025. [DOI] [PubMed] [Google Scholar]
- 16.Robson MD, Gatehouse PD, Bydder GM, Neubauer S. Human imaging of phosphorus in cortical and trabecular bone in vivo. Magn Reson Med. 2004;51:888–892. doi: 10.1002/mrm.20055. [DOI] [PubMed] [Google Scholar]
- 17.Nielles-Vallespin S, Weber MA, Bock M, Bongers A, Speier P, Combs SE, Wöhrle J, Lehmann-Horn F, Essig M, Schad LR. 3D radial projection technique with ultrashort echo times for sodium MRI: Clinical applications in human brain and skeletal muscle. Magn Reson Med. 2007;57:74–81. doi: 10.1002/mrm.21104. [DOI] [PubMed] [Google Scholar]
- 18.Rahmer J, Börnert P, Groen J, Bos C. Three-dimensional radial ultrashort echo-time imaging with T2 adapted sampling. Magn Reson Med. 2006;55:1075–1082. doi: 10.1002/mrm.20868. [DOI] [PubMed] [Google Scholar]
- 19.Vidarsson L, Conolly SM, Lim KO, Gold GE, Pauly JM. Echo time optimization for linear combination myelin imaging. Magn Reson Med. 2005;53:398–407. doi: 10.1002/mrm.20360. [DOI] [PubMed] [Google Scholar]
- 20.Pauly JM, Conolly SM, Macovski A. Suppression of long-T2 components for short-T2 imaging. Proc., SMRI, 10th Annual Meeting; New York. April 1992; p. 330. [Google Scholar]
- 21.Larson PEZ, Gurney PT, Nayak K, Gold GE, Pauly JM, Nishimura DG. Designing long-T2 suppression pulses for ultrashort echo time imaging. Magn Reson Med. 2006;56:94–103. doi: 10.1002/mrm.20926. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Sussman MS, Pauly JM, Wright GA. Design of practical T2-selective RF excitation (TELEX) pulses. Magn Reson Med. 1998;40:890–899. doi: 10.1002/mrm.1910400615. [DOI] [PubMed] [Google Scholar]
- 23.Garwood M, DelaBarre L. The return of the frequency sweep: Designing adiabatic pulses for contemporary NMR. J Magn Reson. 2001;153:155–177. doi: 10.1006/jmre.2001.2340. [DOI] [PubMed] [Google Scholar]
- 24.Norris DG, Ludemann G, Leibfritz D. An analysis of the effects of short T2 values on the hyperbolic-secant pulse. J Magn Reson. 1991;92:94–101. [Google Scholar]
- 25.Tannus A, Garwood M. Improved performance of frequency-swept pulses using offset-independent adiabaticity. J Magn Reson A. 1996;120:133–137. [Google Scholar]
- 26.Pauly JM. Design of large-flip-angle half pulses. Proceedings of the 14th Annual Meeting of ISMRM; Seattle. 2006. p. 2997. [Google Scholar]
- 27.Scheffler K, Hennig J. Reduced circular field-of-view imaging. Magn Reson Med. 1998;40:474–480. doi: 10.1002/mrm.1910400319. [DOI] [PubMed] [Google Scholar]
- 28.Peters DC, Korosec FR, Grist TM, Block WF, Holden JE, Vigen KK, Mistretta CA. Undersampled projection reconstruction applied to MR angiography. Magn Reson Med. 2000;43:91–101. doi: 10.1002/(sici)1522-2594(200001)43:1<91::aid-mrm11>3.0.co;2-4. [DOI] [PubMed] [Google Scholar]
- 29.Barger AV, Block WF, Toropov Y, Grist TM, Mistretta CA. Time-resolved contrast-enhanced imaging with isotropic resolution and broad coverage using an undersampled 3D projection trajectory. Magn Reson Med. 2002;48:297–305. doi: 10.1002/mrm.10212. [DOI] [PubMed] [Google Scholar]
- 30.Peters DC, Rohatgi P, Botnar RM, Yeon SB, Kissinger KV, Manning WJ. Characterizing radial undersampling artifacts for cardiac applications. Magn Reson Med. 2006;55:396–403. doi: 10.1002/mrm.20782. [DOI] [PubMed] [Google Scholar]
- 31.Beatty PJ, Nishimura DG, Pauly JM. Rapid gridding reconstruction with a minimal oversampling ratio. IEEE Trans Med Imaging. 2005;24:799–808. doi: 10.1109/TMI.2005.848376. [DOI] [PubMed] [Google Scholar]
- 32.Pipe JG. Reconstructing MR images from undersampled data: Data-weighting considerations. Magn Reson Med. 2000;43:867–875. doi: 10.1002/1522-2594(200006)43:6<867::aid-mrm13>3.0.co;2-2. [DOI] [PubMed] [Google Scholar]
- 33.Robson MD, Benjamin M, Gishen P, Bydder GM. Magnetic resonance imaging of the Achilles tendon using ultrashort TE (UTE) pulse sequences. Clin Radiol. 2004;59:727–735. doi: 10.1016/j.crad.2003.11.021. [DOI] [PubMed] [Google Scholar]
- 34.Pauly J, Le Roux P, Nishimura D, Macovski A. Parameter relations for the Shinnar-Le Roux selective excitation pulse design algorithm. IEEE Trans Med Imaging. 1991;10:53–65. doi: 10.1109/42.75611. [DOI] [PubMed] [Google Scholar]
- 35.Rahmer J, Blume U, Börnert P. Selective 3D ultrashort TE imaging: comparison of “dual-echo” acquisition and magnetization preparation for improving short-T2 contrast. MAGMA. 2007;20:83–92. doi: 10.1007/s10334-007-0070-6. [DOI] [PubMed] [Google Scholar]
- 36.Brix G, Schad LR, Lorenz WJ. Evaluation of proton density by magnetic resonance imaging: phantom experiments and analysis of multiple component proton transverse relaxation. Phys Med Biol. 1990;35:53–66. doi: 10.1088/0031-9155/35/1/006. [DOI] [PubMed] [Google Scholar]
- 37.Bernstein MA, King KF, Zhou XJ. Handbook of MRI Pulse Sequences. Elsevier Academic Press; Boston, MA: 2004. [Google Scholar]
- 38.Bakker CJG, Vriend J. Multi-exponential water proton spin-lattice relaxation in biological tissues and its implications for quantitative NMR imaging. Phys Med Biol. 1984;29:509–18. doi: 10.1088/0031-9155/29/5/003. [DOI] [PubMed] [Google Scholar]


