Modeling the spatial and temporal dependence in fMRI data

Summary

Functional magnetic resonance imaging (fMRI) data sets are large and characterized by complex dependence structures driven by highly sophisticated neurophysiology and aspects of the experimental designs. Typical analyses investigating task-related changes in measured brain activity use a two-stage procedure in which the first stage involves subject-specific models and the second-stage specifies group (or population) level parameters. Customarily, the first-level accounts for temporal correlations between the serial scans acquired during one scanning session. Despite accounting for these correlations, fMRI studies often include multiple sessions and temporal dependencies may persist between the corresponding estimates of mean neural activity. Further, spatial correlations between brain activity measurements in different locations are often unaccounted for in statistical modeling and estimation. We propose a two-stage, spatio-temporal, autoregressive model which simultaneously accounts for spatial dependencies between voxels within the same anatomical region and for temporal dependencies between a subject’s estimates from multiple sessions. We develop an algorithm that leverages the special structure of our covariance model, enabling relatively fast and efficient estimation. Using our proposed method, we analyze fMRI data from a study of inhibitory control in cocaine addicts.

1. Introduction

Functional magnetic resonance imaging (fMRI) studies yield large data sets that contain temporal correlations from repeated scanning (within and between scanning sessions) and complex spatial correlations. Ignoring correlations affects the precision of estimates of model parameters and consequently may lead to inaccurate statistical tests. Spatio-temporal modeling may mitigate these shortcomings by incorporating more physiologically plausible assumptions and by borrowing strength across related measures of neural activity. One session of a typical fMRI neuroactivation study acquires 3-D scans every 2–3 seconds while the subject performs different experimental tasks. fMRI studies may also involve multiple sessions (e.g corresponding to pre- and post-treatment periods). Typical analyses investigating task-related changes in measured brain activity use a two-stage procedure in which the first stage involves subject-specific and voxel-specific models relating neural processing to experimental tasks. The second stage specifies voxel-specific models for group (or population) level parameters. The stage I analysis accounts for temporal correlations between serial scans within one session using variants of autoregressive models (Bullmore et al., 1996; Purdon et al., 2001; Friston et al., 2002). Despite addressing scan-to-scan correlations within a session, the stage I estimates for multiple sessions may also exhibit correlations, typically not accounted for at the second stage. Our focus is on modeling these latter correlations.

Some attempts have been made at modeling the repeated measures correlations and spatial correlations in fMRI data, though typically not in the same statistical model. Worsley et al. (2002) introduce a random effects analysis for combining sessions and the method removes trends in effects over time. Bowman and Kilts (2003) fit repeated measures covariance structures within a linear model to address between-session correlations in positron emission tomography (PET) neuroimaging data. Neither of these two approaches addresses the spatial correlations between localized brain activity measurements, and the method by Bowman and Kilts (2003) involves long computations for PET data, making it less suitable for higher dimensional fMRI data. Bowman (2005) presents a two-stage model in which the second stage accounts for spatial dependencies within brain regions or networks, and Bowman et al. (2008) give a more flexible Bayesian model to capture correlations both within and between brain regions. Neither of these approaches, however, accounts for temporal or repeated measures associations between the multiple experimental effects for a subject. There have been a few attempts to model both temporal and spatial correlations simultaneously, but these approaches are generally hampered by long computations. The computations generally involve inverting large covariance matrices, and separable models (over space and time) are often considered (Benali et al., 1997; Hartvig, 2002). Gössl et al. (2001) use a Bayesian approach to fit a semi-parametric spatial and temporal model for fMRI data. Their approach requires extensive computations, limiting its applicability in practice. Woolrich et al. (2004) propose a Bayesian framework to model the noise via a non-separable space-time, simultaneous autoregressive model. This approach is very time consuming for the fMRI datasets, taking roughly 6 hours for processing a single slice of 3-D fMRI data.

We propose a two-stage model that accounts for both spatial and temporal correlations in fMRI data, and our model leads to fast parameter estimation. In the second stage, we construct a simultaneous autoregressive model to capture spatio-temporal correlations between the multiple (session) effects at a given location and between pairs of voxels within defined anatomical regions. We use maximum likelihood (ML) methods to estimate parameters from our spatio-temporal model. We overcome computational challenges involved with estimation by deriving an algorithm that simplifies the calculations of inverses and determinants of large matrices, leading to fast estimation of the model parameters. Our spatio-temporal model provides a unified framework for both voxel-level and region-level inferences. Using our proposed model, we analyze fMRI data from a study of inhibitory control in cocaine addicts to evaluate the effects of behavioral therapy on neural processing related to inhibitory control. To further delineate benefits of our spatio-temporal model, we conduct two simulation studies: one to validate the accuracy of our estimation methods and the other to evaluate the relative efficiency of our proposed spatio-temporal model compared to the general linear model (GLM (not to be confused with generalized linear model)).

2. Experimental Data

To illustrate the use of our proposed model and to give motivation for its development, we apply it to data from an fMRI study evaluating the impact of cocaine addiction and treatment-related abstinence on neural responses to motor inhibition tasks. The sample included 12 cocaine addicts enrolled in an intensive outpatient behavioral treatment program and 15 healthy controls, matched by age, sex (all males), race, handedness, education and early life adversity. All the subjects were scanned while performing an inhibitory control task used to model a characteristic hallmark of drug addiction: an impairment in the ability to inhibit behaviors (e.g. drug-seeking behaviors). The cocaine addicts were scanned in two separate sessions, before and after treatment, and similarly control subjects had baseline and follow-up scans.

Experimental conditions

The inhibitory control task, referred to as the STOP-signal task, was designed to evaluate the ability to cancel a prepotent motor response (Aron and Poldrack, 2006). In this task, subjects are presented with visual GO-stimuli, consisting of uppercase alphabetical letters appearing on the screen for 0.5 seconds with an inter-stimulus interval of 2.3 seconds. They are instructed to respond to this signal by pressing a button as quickly as possible. An auditory STOP-signal (also lasting 0.5 seconds) appears randomly in 16% of the trials. The occurrence of the STOP-signal following a GO-stimulus is an indicator to refrain from pushing the button. Hence, a successful performance requires the inhibition of a prepotent behavior. The aim of our analysis is to identify brain locations where there are inhibitory control-related increases in brain activity following treatment for cocaine addiction.

3. Methods

We represent a single scan from a subject as a 53×63×46 3-D rectangular lattice consisting of volume elements (voxels) indexed by a mapping of coordinates (x, y, z) to v = 1, …, V (V > 150, 000 in our study). From one scanning session, each voxel contains serial measures of localized brain activity called Blood-Oxygen-Level Dependent (BOLD) fMRI responses. The number of intracranial voxels is too large to estimate a global spatial correlation matrix including all voxel pairs. While retaining the ability to address voxel-level inference, we partition the voxels into mutually exclusive neuroanatomical regions known as Brodmann areas (BA’s) (Brodmann, 1909), additionally separating BA’s in the left and right hemispheres. For broader coverage, we add several subcortical regions to the BA map, obtained from the Automated Anatomical Labeling (AAL) system (Tzourio-Mazoyer et al., 2002). Building our model based on well-established anatomical parcellations, rather than data-driven functional clusters aids interpretability.

3.1 Statistical Model

Following the conventional two-stage modeling approach for fMRI data, we fit a GLM at the first stage for each individual’s vector of serial BOLD responses, separately for each voxel. The GLM regresses each voxel’s BOLD responses for subject i (i = 1, …, K) on within-subject design variables (e.g. session or stimulus indicators) and on covariates that are not of intrinsic interest, such as high-pass filtering variables. The model accounts for short-range scan-to-scan correlations within a session using a first-order autoregressive process with white noise (Purdon et al., 2001; Friston et al., 2002). The regression coefficient, $B_{\mathit{igs}}^{(p)}(v)$, for voxel v represents a summary measure of an individual’s (mean) neural activity associated with session or stimulus p. We add a subscript g to denote the neuroanatomic region to which voxel v belongs (g = 1, …, G), with the region consisting of V_g voxels in total.

At the second stage, we propose a spatio-temporal (ST) autoregressive model to capture temporal correlations between the multiple sessions and spatial correlations between pairs of intra-regional voxels. We express the spatio-temporal model as follows:

$$B_{\mathit{igs}}^{(p)}(v)={\mathbf{x}}_i^{\prime }{\mathit{\beta }}_{gs}^{(p)}(v)+{\rho }_{gs}\frac{1}{V_g-1}\sum _{v^{\ast }\in {\mathcal{N}}_v}\left(B_{\mathit{igs}}^{(p)}(v^{\ast })-{\mathbf{x}}_i^{\prime }{\mathit{\beta }}_{gs}^{(p)}(v^{\ast })\right)+{\xi }_{gs}\frac{1}{q-1}\sum _{p^{\ast }\ne p}\left(B_{\mathit{igs}}^{(p^{\ast })}(v)-{\mathbf{x}}_i^{\prime }{\mathit{\beta }}_{gs}^{(p^{\ast })}(v)\right)+e_{\mathit{igs}}(v),$$ (1)

where x_i is a vector of between-subject design variables, ${\mathit{\beta }}_{gs}^{(p)}(v)$ are the group-level parameters, $e_{\mathit{igs}}(v)\sim N(0,{\phi }_{gs}^2)$ ( ${\phi }_{gs}^2$ is the between-subject variation), ρ_gs is a spatial dependence parameter, ξ_gs reflects the temporal dependence between sessions, is the set of all voxels within the same neuroanatomic region as v, and s denotes a subject group (e.g., patients, controls). When ρ_gs = ξ_gs = 0, model (1) resembles a typical stage II GLM from a random effects analysis of brain imaging data, with constant variances within each region.

3.2 Parametric Covariance Model

Our model involves three parameters defining the variance-covariance structure: the spatial (ρ) and temporal (ξ) dependence parameters and the variance parameter (φ²). In this section, we present details about the assumed covariance/correlation model. Let ${\mathbf{B}}_{\mathit{igs}}={\left({\mathbf{B}}_{\mathit{igs}}^{{(1)}^{\prime }},\dots ,{\mathbf{B}}_{\mathit{igs}}^{{(q)}^{\prime }}\right)}^{\prime }$, where each ${\mathbf{B}}_{\mathit{igs}}^{(p)}$ contains individualized parameters for all voxels in region g, and similarly ${\mathit{\beta }}_{gs}={\left({\mathit{\beta }}_{gs}^{{(1)}^{\prime }},\dots ,{\mathit{\beta }}_{gs}^{{(q)}^{\prime }}\right)}^{\prime }$. Model (1) implies that B_igs has the following multivariate normal distribution B_igs ~ MVN (β_gs, Ω_gs) (see Appendix), where ${\mathbf{\Omega }}_{gs}={\phi }_{gs}^2{\mathbf{\Psi }}_{gs}{\mathbf{\Psi }}_{gs}$, and Ψ_gs is a qV_g × qV_g matrix with

$${\mathbf{\Psi }}_{gs}^{-1}={\left[\begin{array}{cccc}{\mathbf{I}}_{V_g}-{\rho }_{gs}{\mathbf{W}}_g& -\frac{{\xi }_{gs}}{q-1}{\mathbf{I}}_{V_g}& \dots & -\frac{{\xi }_{gs}}{q-1}{\mathbf{I}}_{V_g}\\ -\frac{{\xi }_{gs}}{q-1}{\mathbf{I}}_{V_g}& {\mathbf{I}}_{V_g}-{\rho }_{gs}{\mathbf{W}}_g& \dots & -\frac{{\xi }_{gs}}{q-1}{\mathbf{I}}_{V_g}\\ ⋮& ⋮& \ddots & ⋮\\ -\frac{{\xi }_{gs}}{q-1}{\mathbf{I}}_{V_g}& -\frac{{\xi }_{gs}}{q-1}{\mathbf{I}}_{V_g}& \dots & {\mathbf{I}}_{V_g}-{\rho }_{gs}{\mathbf{W}}_g\end{array}\right]}_{{qV}_g\times {qV}_g}$$ (2)

(I_Vg and J_Vg denote identity and unity matrices of size V_g). In (2), W_g = [1/(V_g − 1)](J_Vg − I_Vg) specifies the neighborhood structure consisting of all voxels that fall in the same anatomical region. The blocks along the main diagonal of ${\mathbf{\Psi }}_{gs}^{-1}$ allow for spatial correlations between measures of task-related brain activity for voxels in region g, i.e. between elements of ${\mathbf{B}}_{\mathit{igs}}^{(p)}$. The off-diagonal blocks of ${\mathbf{\Psi }}_{gs}^{-1}$ capture correlations between the summary measures of brain activity associated with various scanning sessions. Our model assumes an exchangeable covariance structure between voxels in the same neuroanatomic region. Although the complexity of human brain function is likely to render departures from this assumption, the exchangeable structure provides an improvement over the often used independence assumption and seems reasonable for statistical modeling purposes based on descriptive empirical results (not shown here; see Web Appendix A).

Calculating the matrix Ψ_gs

Calculating Ψ_gs involves inverting a matrix of size qV_g × qV_g, which can become unwieldy for large regions, and this calculation is performed iteratively during estimation of the model. We derive an algorithm to facilitate calculations of inverses and determinants of our large highly structured covariance matrices, thereby enabling estimation of our model for fMRI applications. By recursive calculation on q, the number of blocks in ${\mathbf{\Psi }}_{gs}^{-1}$, we represent ${\mathbf{\Psi }}_{gs}^{-1}$ as follows

$${\mathbf{\Psi }}_{gs}={\left[\begin{array}{cccc}d{\mathbf{I}}_{V_g}+f{\mathbf{J}}_{V_g}& u{\mathbf{I}}_{V_g}+z{\mathbf{J}}_{V_g}& \cdots & u{\mathbf{I}}_{V_g}+z{\mathbf{J}}_{V_g}\\ u{\mathbf{I}}_{V_g}+z{\mathbf{J}}_{V_g}& d{\mathbf{I}}_{V_g}+f{\mathbf{J}}_{V_g}& \cdots & u{\mathbf{I}}_{V_g}+z{\mathbf{J}}_{V_g}\\ ⋮& ⋮& ⋮& \ddots \\ u{\mathbf{I}}_{V_g}+z{\mathbf{J}}_{V_g}& u{\mathbf{I}}_{V_g}+z{\mathbf{J}}_{V_g}& \cdots & d{\mathbf{I}}_{V_g}+f{\mathbf{J}}_{V_g}\end{array}\right]}_{{qV}_g\times {qV}_g}$$ (3)

Hence, Ψ_gs is determined by four functions: d(ρ_g, ξ_g, V_g, q), f (ρ_gs, ξ_gs, V_g, q), u(ρ_gs, ξ_gs, V_g, q), and z(ρ_gs, ξ_gs, V_g, q). The explicit formulas for d, f, u and z are quite lengthy and are given in the Web Appendix B. We employ (3) to circumvent issues of long computing times and excessive memory consumption.

Estimated spatial and temporal parameters are not directly interpretable as spatial and temporal correlations. The spatial and temporal correlations, denoted η_ρ and η_ξ, respectively, require calculation of the covariance matrix Ω_gs, i.e. of Ψ_gs Ψ_gs. Leveraging the special structure of Ψ_gs, we obtain Ψ_gs Ψ_gs as a partitioned matrix, with equal diagonal blocks AI_Vg + BJ_Vg, and off-diagonal blocks CI_Vg + DJ_Vg, where

$$\begin{array}{ll}A=d^2+(q-1)u^2\hfill & B=2df+V_g{f}^2+(q-1)(2uz+V_g{z}^2)\hfill \\ C=2du+(q-2)u^2\hfill & D=2(fu+dz+V_{g}fz)+(q-2)(2uz+V_g{z}^2).\hfill \end{array}$$ (4)

The expressions for the spatial correlation, η_ρ, and the temporal correlation, η_ξ, are then given by η_ρ = B/(A + B) and η_ξ = (C + D)/(A + B).

3.3 Estimation

We perform estimation of the second stage spatio-temporal model using ML methods. The log-likelihood function for model (1) is given by

$$ℒ(\mathit{\phi },\mathit{\rho },\mathit{\xi },\mathit{\beta }\mid \mathbf{B})\propto \sum _{s=1}^2\sum _{i\in K_s}\sum _{g=1}^G\left\{-\frac{{qV}_g}{2}ln({\phi }_{gs}^2)+ln(\text{abs}\mid {\mathbf{\Psi }}_{gs}^{-1}\mid )-\frac{1}{2{\phi }_{gs}^2}{({\mathbf{B}}_{\mathit{igs}}-{\mathbf{X}}_i{\beta }_{gs})}^{\prime }{\mathbf{\Psi }}_{gs}^{-1}{\mathbf{\Psi }}_{gs}^{-1}({\mathbf{B}}_{\mathit{igs}}-{\mathbf{X}}_i{\beta }_{gs})\right\},$$ (5)

where K_s denotes the number of subjects in subgroup s (cocaine addicts and controls). The ML estimator of the mean parameter vector β_gs is given by ${\widehat{\mathit{\beta }}}_{gs}=\frac{1}{K_s}{\displaystyle \sum _{i=1}^{K_s}}{\mathbf{B}}_{\mathit{igs}}$, g = 1, …, G. β̂_gs is unbiased (as is β̂_gs from a GLM analysis) and does not depend on the covariance parameters. Estimation of the covariance parameters, therefore, proceeds using the partially maximized likelihood function (φ, ρ, ξ, β̂|B). We use the Fisher scoring algorithm to estimate the covariance parameters ρ_s = (ρ_1s, …, ρ_Gs)′, ξ_s = (ξ_1s, …, ξ_Gs)′, and φ_g = (φ_1s, …, φ_Gs)′.

Note on the parameter space

To apply our model, the matrix ${\mathbf{\Psi }}_{gs}^{-1}$ must be nonsingular, or equivalently Ω_gs must be positive definite. In the context of our fMRI data, with V_g > 20, for all g, and q = 2, the resulting explicit parameter constraints are as follows:

$$\begin{array}{rr}\hfill {\rho }_{gs}+(V_g-1)(1+{\xi }_{gs})\ne 0& \hfill {\rho }_{gs}+(V_g-1)(1-{\xi }_{gs})\ne 0\\ \hfill {\rho }_{gs}-{\xi }_{gs}\ne 1& \hfill {\rho }_{gs}+{\xi }_{gs}\ne 1.\end{array}$$

We monitor these boundary constraints during our iterative estimation procedure.

Estimation involves iterative calculations of the determinant and the inverse of a qV_g × qV_g matrix (up to roughly 5,800×5,800 in our data application). Employing the simplifications discussed in Section 3.2 enables fast and efficient computations. Web Appendix C contains details regarding the score functions necessary for estimation.

3.4 Inferences

Inferences that are commonly sought in functional neuroimaging studies target the identification of differences in neural processing between experimental tasks, sessions (e.g. treatment periods), or groups. One may pursue these inferences at an extremely localized (voxel) level or at a more spatially coarse regional level. In either case, estimation and inferences in this setting produce maps of distributed brain activity and the corresponding thresholded maps showing statistically significant (or highly probable, in a Bayesian context) differences. We seek inferences about linear functions of ${\mathit{\beta }}_{gs}^{(p)}$, where for the inhibitory control study in cocaine addicts, p = 1 (baseline or pre-treatment) or p = 2 (follow-up or post-treatment) and s = 1 (cocaine addicts) or s = 2 (controls).

Voxel-level inferences

Following estimation using our spatio-temporal model, we obtain t-statistic images from the voxel-specific contrast estimates, then threshold the t-statistics to determine voxels exhibiting statistically significant changes (or differences) in brain activity. To adjust for typical changes observed with repeated scanning sessions in the inhibitory control study, we identify voxels for which the changes in brain activity following treatment are larger in cocaine addicts than the corresponding changes between follow-up and baseline activity in control subjects. Specifically, we estimate and test hypotheses about ${\mathit{\theta }}_g^{\ast }={\mathbf{C}}_g^{\ast }{\mathit{\beta }}_g$, where ${\mathbf{C}}_g^{\ast }={[-{\mathbf{I}}_{V_g}{\mathbf{I}}_{V_g}{\mathbf{I}}_{V_g}-{\mathbf{I}}_{V_g}]}_{(V_g\times 4V_g)}$ and ${\mathit{\beta }}_g={[{\mathit{\beta }}_{g1}^{{(1)}^{\prime }},{\mathit{\beta }}_{g1}^{{(2)}^{\prime }},{\mathit{\beta }}_{g2}^{{(1)}^{\prime }},{\mathit{\beta }}_{g2}^{{(2)}^{\prime }}]}_{(4V_g\times 1)}^{\prime }$. Each element of ${\mathit{\theta }}_g^{\ast }$ represents a voxel-specific parameter. We construct Wald-type statistics for hypothesis testing, with $\text{Var}({\widehat{\mathit{\theta }}}_g^{\ast })={\mathbf{C}}_g^{\ast }\text{Var}({\widehat{\mathit{\beta }}}_g){\mathbf{C}}_g^{{\ast }^{\prime }}$ and df = 2(n_p + n_c − 2), where n_p is the number of addicts, and n_c is the number of controls. We apply the stringent threshold of α = 0.005, which is one approach that has a strong precedent in the neuroimaging literature, but other thresholding approaches, such as false discovery rate (Benjamini and Hochberg, 1995) and random field theory (Friston et al., 1995) are also available.

Region-level inferences

Our spatio-temporal model also enables analyses targeting an entire anatomical brain region corresponding to the underlying anatomical parcellation. For inferences in region g, define θ_g = C_gβ_g, with ${\mathbf{C}}_g=\frac{1}{V_g}{[-{\mathbf{1}}_{V_g}^{\prime }{\mathbf{1}}_{V_g}^{\prime }{\mathbf{1}}_{V_g}^{\prime }-{\mathbf{1}}_{V_g}^{\prime }]}_{(1\times 4V_g)}$, and construct the t-statistic using $\text{Var}({\widehat{\theta }}_g)={\mathbf{C}}_g\text{Var}({\widehat{\mathit{\beta }}}_g){\mathbf{C}}_g^{\prime }$ and degrees of freedom df_r = 2V_g(n_p + n_c − 2). Combining both sessions for subgroups s, i.e., ${\mathit{\beta }}_{gs}={[{\mathit{\beta }}_{gs}^{{(1)}^{\prime }},{\mathit{\beta }}_{gs}^{{(2)}^{\prime }}]}^{\prime }$, the variance of β̂_gs is given by $\text{Var}({\widehat{\mathit{\beta }}}_{gs})=\frac{1}{n_p+n_c}{\phi }_{gs}^2{\mathbf{\Psi }}_{gs}{\mathbf{\Psi }}_{gs}$. A notable advantage of modeling spatial correlations using our model is that the resulting regional level analyses account for spatial dependencies between intra-regional voxel pairs, rather than implicitly assuming independence.

Statistical significance of spatial and temporal correlations

It is often informative to examine the magnitudes of spatial and temporal correlations as discussed in Section 3.2. Given the complexity of the estimators of these quantities, it is difficult to derive analytical expressions for the variances of these estimators. If one has inherent interest in testing hypotheses about these parameters, then standard bootstrapping methods are applicable. However, this approach may be computationally demanding. Given that testing hypotheses about correlations was not of chief interest in the inhibitory control study, we present estimates of correlations mainly for descriptive purposes. We estimate standard errors of the correlations using 30 bootstrap samples drawn (with replacement) from the subjects in our data, separately for controls and patients. We apply our model and estimate the spatial and temporal correlations for each sample, and then calculate the bootstrap standard errors as the standard deviations of the 30 estimated values for each parameter, which should provide reasonable estimates of variability (Efron and Tibshirani, 1998).

4. Application to Study of Inhibitory Control in Cocaine Addicts

We used our spatio-temporal model to analyze fMRI data from the inhibitory control study in cocaine addicts. We estimate separate spatial and temporal parameters for cocaine addicts and controls. We carry out image pre-processing (slice timing, realigning, normalizing, smoothing) and first level, single subject analyses in SPM5 (SPM5 is a MATLAB software package implementing Statistical Parametric Mapping for neuroimaging data available for download from the Wellcome Trust Centre for Neuroimaging web page http://www.fil.ion.ucl.ac.uk/spm/software/spm5/). To account for inter-subject neuroanatomic differences that may persist after spatial normalization, we apply very focal spatial smoothing (6 mm [2 voxels] full width at half maximum (FWHM) Gaussian kernel) rather than the more spatially expansive smoothing often applied in practice. Our smoothing should only have a small effect on subsequent spatial modeling, since most of the Brodmann areas (within which we model spatial correlations) are quite large, relative to the small size of the smoothing kernel. Our analysis includes 38 BA’s in each hemisphere, after excluding those with fewer than 20 voxels, and we supplement the BA’s with six subcortical regions, resulting in a parcellation consisting of 82 brain regions. We perform exploratory analyses, computing crude estimates of spatial and temporal correlations (Web Appendix A), which provide support for the existence of correlations from both sources as well as for the exchangeability assumption in our covariance model.

4.1 Voxel-level inferences

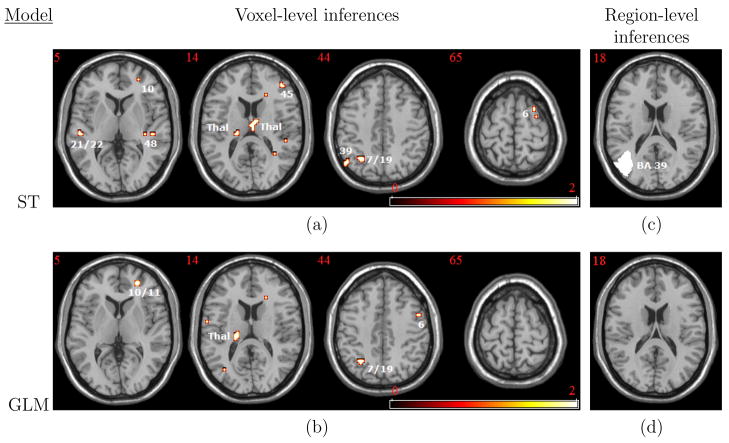
Figure 1(a) shows voxels that reveal statistically significant increases in inhibitory control-related brain activity following treatment at α = 0.005. The axial slices correspond to 5 mm, 14 mm, 44 mm, and 65 mm above the anterior-posterior commissural plane. The significant areas include the right frontopolar cortex (BA 10), left middle temporal gyrus (BA 21), and retrosubicular area (BA 48) in the 5 mm slice; left and right thalamus and the right inferior frontal cortex (BA 45) at 14 mm; left visual association cortex V3 (BA 19) and somatosensory association cortex (BA 7) and the left angular gyrus (BA 39) at 44 mm; and the right pre-supplementary motor area (pre-SMA, BA 6) at 65 mm. Other regions (not shown) exhibiting significant treatment-related increases in brain activity include the right inferior prefrontal gyrus (BA 47), left and right fusiforum gyrus (BA 37), and left primary auditory cortex (BA 41).

Figure 1.

Voxel-level and region-level inferences for two models: the proposed spatio-temporal (ST) model (top) and the GLM (bottom). (a): voxels that achieve statistical significance in the ST model analysis at α = 0.005 in favor of a one-sided alternative hypothesis of increased activity following treatment for cocaine addiction. Significant increases occur in the right frontopolar area (BA 10), left middle and superior temporal gyri (BA’s 21/22), right retrosubicular area (BA 48), right inferior frontal cortex (BA 45), left and right thalamus (Thal), left somatosensory and visual association cortices (BA’s 7 and 19), left angular gyrus (BA 39), and right BA 6 (pre-SMA); (b): voxel-level results from a GLM analysis; (c): region, left BA 39 (angular gyrus), that achieves significance in our ST model analysis at α = 0.05; (d): corresponding region-level results from the GLM. Slice labels denote the distance, in mm, above the anterior-posterior commissural plane.

Figure 1(b) shows results from the corresponding GLM–based analysis commonly used in the neuroimaging literature. Many of the areas showing statistical significance agree with the results from our approach (e.g. Brodmann areas 6, 7, 10, and 19 emerged in both analyses), but there are some differences. For example, our method identifies increased treatment-related brain activity in BA 48 and BA’s 21 and 22 (5 mm), which do not emerge from the GLM analysis. Also, both methods identify areas in the thalamus, but our method detects a large right thalamic activation not revealed by the GLM. Similarly, both methods identify voxels in BA’s 6 (pre-SMA) and 39, but our model yields more spatially extensive activations. Overall, our ST model produces more statistically significant voxels than the GLM. However, neither method produces significant voxels when applying more conservative family-wise error or false discovery rate multiple testing procedures. The differences between the two models become more apparent at larger significance levels (e.g. α = 0.01, not shown), suggesting that with a larger sample size and stronger activation signal, greater differences are likely to emerge. We provide interpretive remarks about our results in Section 4.4.

4.2 Region-level inferences

Our region-level analysis of treatment-emergent changes in neural processing, using methods described in Section 3.4, revealed only one region (left BA 39, angular gyrus) achieving statistical significance at α = 0.05, uncorrected (see Figure 1(c)). The comparative region-level GLM analysis (that implicitly assumes spatial and temporal independence) did not yield any statistically significant differences. Neither method reveals significant differences at more stringent thresholds such as α = 0.005 (uncorrected).

4.3 Spatial and temporal correlations

Figure 2 shows the model-based estimates of spatial and temporal correlations for both the cocaine addicts and control subjects in one axial slice of the brain. The color scale indicates the strength of correlations, with brighter shades indicating correlations of larger magnitude. For temporal correlations, positive values are shown in one color (top colorbar) and negative values are shown in a separate color (bottom colorbar). For clearer distinction, we add stripes to regions with negative correlations. All of the correlations in Figure 2 would have the value zero in a GLM analysis, signaling the need to account for them in our model.

Figure 2.

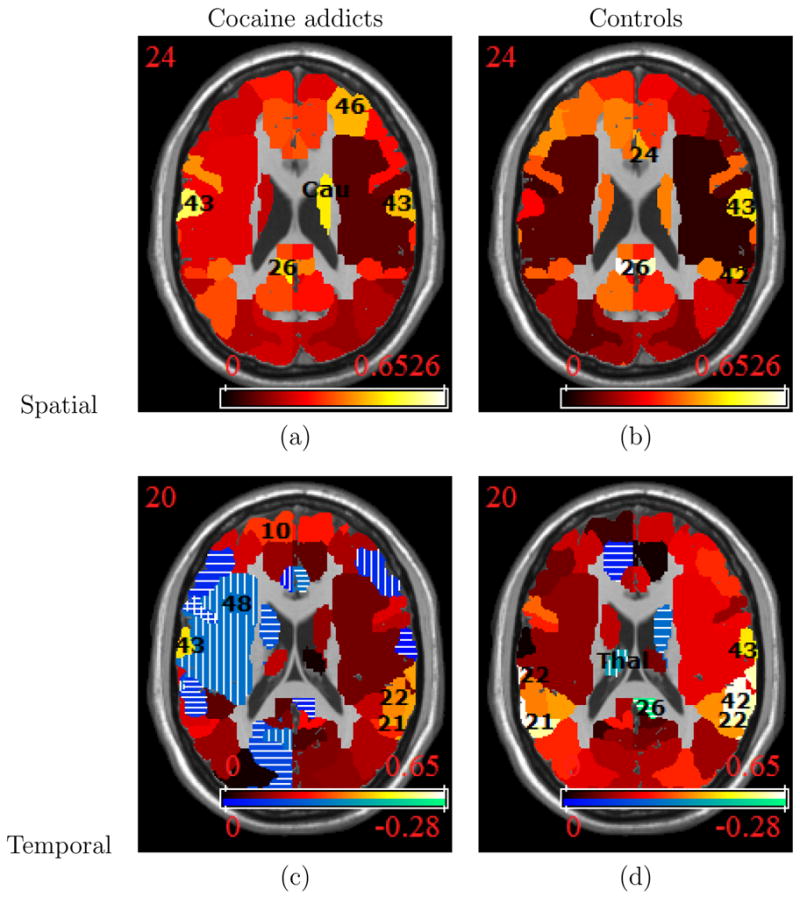
Model-based estimates of the spatial and temporal correlations for the inhibitory control study (a) addicts: spatial correlations, (b) controls: spatial correlations, (c) addicts: temporal correlations, (d) controls: temporal correlations. For (a) and (b), the darker to lighter intensities in the colorbar represent lower to higher correlations. For (c) and (d), the top colorbar represents positive correlations, again with lighter intensities reflecting higher correlations, and the bottom colorbar represents negative correlations (stripes added to maps) with brighter intensities indicating stronger negative correlations. The temporal correlations for control subjects range from −0.28 to 0.64 and are in general larger than those for the cocaine addicts, which range from −0.24 to 0.45. The regional spatial correlations are not consistently higher for either group, ranging from 0.08 to 0.54 among cocaine addicts and from 0.04 to 0.65 for healthy controls.

Table 1 gives the model-based estimates, along with bootstrap standard errors (in parentheses), of both temporal and spatial correlations for select regions in the inhibitory control study. The associated spatial (ρ) and temporal (ξ) dependence parameters achieve statistical significance for all regions at α = 0.01, except for BA 29 (L), which is significant at α = 0.05. The selected regions in Table 1 are those that have correlations with the largest magnitude. The temporal correlations for cocaine addicts range from −0.24 to 0.45 and tend to be larger in control subjects for whom they range from −0.28 to 0.64. The regional spatial correlations are not consistently higher for either group, ranging from 0.08 to 0.54 among cocaine addicts and from 0.04 to 0.65 for healthy controls.

Table 1.

Model-based estimates of spatial and temporal correlations and estimated bootstrap standard errors (in parentheses).

Group	Region	Temporal correlations (std. err.)	Region	Spatial correlations (std. err.)
Addicts
	BA 43 (L)	0.45 (0.19)	BA 43 (L)	0.54 (0.10)
	BA 22 (R)	0.39 (0.15)	BA 29 (L)	0.50 (0.12)
	BA 42 (R)	0.37 (0.18)	BA 3 (L)	0.47 (0.10)
	BA 3 (L)	0.37 (0.17)	caudate (R)	0.47 (0.10)
	BA 9 (R)	0.34 (0.28)	BA 43 (R)	0.43 (0.07)
	BA 35 (R)	−0.24 (0.06)	BA 48 (R)	0.08 (0.07)
Controls
	BA 22 (L)	0.64 (0.07)	BA 26 (L)	0.65 (0.05)
	BA 42 (R)	0.63 (0.09)	BA 26 (R)	0.60 (0.08)
	BA 22 (R)	0.60 (0.09)	BA 5 (R)	0.50 (0.12)
	BA 21 (L)	0.58 (0.10)	putamen (L,R)	0.50 (0.08, 0.06)
	BA 43 (R)	0.46 (0.10)	BA 38 (L)	0.47 (0.10)
	BA 26 (R)	−0.28 (0.11)	BA 48 (R)	0.04 (0.02)

The brain regions with highest temporal correlations differ between the two groups. For the controls, the highest temporal correlations (~ 0.6) are in right BA 42, partially covering the auditory association cortex, and in left BA 21, left BA 22, and right BA 22, regions in the temporal lobe which are also revealed by our voxel-level analysis. For the cocaine addicts, the highest temporal correlations are somewhat smaller (~ 0.4) and appear in left BA 43 and in right BA 22. Spatial correlations for the control group are highest (≥ 0.6) in left and right BA 26, a retrosplenial region in the cingulate cortex. For the cocaine addicts, the highest estimated spatial correlations (~ 0.5) are in left BA 29, also in the retrosplenial region, and in left BA 43. For both groups, the region with the lowest estimated spatial correlation (≤ 0.08) is the right BA 48, which is the second largest region (2,875 voxels). This suggests that it is the least spatially homogeneous region and that subdividing large BA’s may be warranted.

4.4 Implications of Results

The study on inhibitory control in cocaine addicts that is the subject of this novel image analysis approach is, to the best of our knowledge, the first to examine the changes in brain activity associated with an intensive addiction behavioral therapy. Inhibiting prepotent or automatic responses is critical to the organization of successful goal-directed behaviors. Aron et al. (2007) demonstrated that the ability to stop motor responses depends critically on a network of structures including the right inferior frontal cortex and the subthalamic nucleus, both of which are connected to the pre-SMA.

Our results agree, in several aspects, with the findings from these and other previous neuroimaging studies. Greater activation of the right orbitofrontal cortex is necessary for behavioral inhibition in impulsive individuals (Horn et al., 2003). Additionally, the right ventral prefrontal cortex has been selectively implicated in the neuropathophysiology of drug addiction (Volkow et al., 2005). Voxel-level analysis of our data reveals that an important effect of treatment is an enabling of the right inferior prefrontal gyrus (BA 47) and right orbitofrontal cortex (BA 11) responses to a demand for inhibition of habitual motor responses. Our findings are promising since they suggest a positive effect of the behavioral therapy on the neural processing deficits associated with cocaine-addiction, though we do not strictly regard these effects to be causal.

The pre-SMA is identified as a significant treatment-related area in our voxel-level analysis. The caudal pre-SMA is critical to controlled action selection (Nachev et al., 2007) and is functionally compromised in cocaine addicts (Kaufman et al., 2003). Enhancing the neural response of the pre-SMA to a demand for a shift from habitual responses to controlled response inhibition represents a plausible neural correlate of drug refusal skills acquired in behavioral therapies targeting relapse prevention. Our region level analysis identifies the angular gyrus (BA 39), which is important in visuospatial attention (Cattaneo et al., 2009).

In areas exhibiting significant voxel-level post-treatment increases in task-related brain activity, we observe distinct patterns of intra-regional correlations between patients and controls. Based on the estimates of the spatial correlations, the controls exhibit higher spatial coherence in, for example, right BA’s 11 (controls = 0.24(0.11), addicts = 0.14(0.04)) and 47 (controls = 0.28(0.13), addicts = 0.18(0.10)), which are frontal areas involved in executive functioning, planning and decision making, as well as in both left and right thalamus (e.g. in right thalamus, controls = 0.32(0.09), addicts = 0.17(0.07)), which play a central role in the flow of information to the cortex (Sherman and Guillery, 2002). Cocaine addicts showed more coherent functioning in left BA’s 19 (addicts = 0.16(0.02), controls = 0.09(0.07)) and 39 (addicts = 0.31(0.10), controls = 0.16(0.10)), which are involved in visual attention. The latter finding is particularly interesting since BA 39 was identified in our region-level analysis.

5. Simulations

We report results of two simulation studies but defer many of the details to Web Appendix D. The goal of the first simulation is to evaluate the accuracy of our estimation procedure. In the second simulation study, we evaluate the relative efficiency of our spatio-temporal model compared to the GLM, both for voxel-level and region-level estimators of secondary parameters of interest. Below we briefly summarize the main findings.

In the first simulation study, we find that estimates for both ρ_gs and ξ_gs (spatial and temporal parameters) are quite accurate, while the between subject variability ${\phi }_{gs}^2$ is slightly underestimated (roughly 6%), which likely stems from the well-known downward bias of ML estimates of variance components (Laird and Ware, 1998). Restricted ML estimation can be used for our model and would presumably mitigate the observed bias. We favor ML estimation in our context, however, because it substantially facilitates computations. The second simulation reveals that the GLM-based voxel-level variance estimates are on average higher than the corresponding estimates obtained from our spatio-temporal model. At the region level, our model also gives more precise estimates compared to GLM. The increased precision of our model estimates stems from the fact that we borrow strength across within region measures of neural activity, which will tend to yield gains in statistical power.

6. Discussion

We propose a novel spatio-temporal modeling framework for functional neuroimaging data, overcoming unsupported independence assumptions of standard GLM-based methods. We use Brodmann area templates to define neuroanatomic regions, but other maps are applicable. Our approach provides a unified framework for voxel-level and region-level inferences. An important contribution of our work is that we derive efficient computational solutions to facilitate implementation.

One limitation of our model is that it does not account for correlations between regions. Doing so within our current framework would lead to substantially increased, perhaps prohibitive, computations. Bowman et al. (2008) establish a Bayesian framework that models between-region correlations, in addition to within-region correlations, but the number of regions included in the analysis is consequently constrained by the sample size. An advantage of our proposed model is that the number of regions included is unconstrained. Our current ML estimation procedure requires close monitoring to ensure convergence and confinement within the parameter space.

In summary, our proposed spatio-temporal model provides an appealing, computationally efficient alternative to standard GLM-based methods for analyzing fMRI data. Our model is based on assumptions that are more neurophysiologically plausible, capturing correlations between different brain locations and between estimates of neural activity at different scanning sessions. These correlations lead to interpretive advantages over the GLM, e.g. revealing information about the degree of coherence in brain activity within defined neuroanatomic regions. Our simulation studies demonstrate that our model estimates are quite accurate and that the standard errors associated with estimates of our mean model parameters are on average smaller than those from a GLM. This increase in efficiency will often lead to more powerful statistical tests and the detection of more statistically significant voxels.

7. Appendix

Our stage-two model (1) can be written in matrix form as follows:

$${\mathbf{B}}_{\mathit{igs}}={\mathit{\beta }}_{gs}+{\rho }_{gs}{\mathbf{W}}^{\ast }({\mathbf{B}}_{\mathit{igs}}-{\mathit{\beta }}_{gs})+{\xi }_{gs}{\mathbf{M}}^{\ast }({\mathbf{B}}_{\mathit{igs}}-{\mathit{\beta }}_{gs})+{\mathit{e}}_{\mathit{igs}},$$

where ${\mathit{e}}_{\mathit{igs}}\sim \text{MVN}(\mathbf{0},{\phi }_{gs}^2\mathbf{I})$ and where W^* = I_q ⊗ W_g, M^* = 1/(q − 1)(J_q ⊗ I_Vg − Iq ⊗ I_Vg) and W_g = 1/(V_g − 1)(J_Vg − I_Vg). We can rewrite the above equation as

$${\mathbf{B}}_{\mathit{igs}}={\mathit{\beta }}_{gs}+{(\mathbf{I}-{\rho }_{gs}{\mathbf{W}}^{\ast }-{\xi }_{gs}{\mathbf{M}}^{\ast })}^{-1}{\mathit{e}}_{\mathit{igs}}={\mathit{\beta }}_{gs}+{\mathbf{\Psi }}_{gs}{\mathit{e}}_{\mathit{igs}}$$ (6)

Therefore, ${\mathbf{B}}_{\mathit{igs}}\sim \text{MVN}({\mathit{\beta }}_{gs},{\phi }_{gs}^2{\mathbf{\Psi }}_{gs}{\mathbf{\Psi }}_{gs})$.