Detecting genomic aberrations using products in a multiscale analysis

SUMMARY

Genomic instability, such as copy-number losses and gains, occurs in many genetic diseases. Recent technology developments enable researchers to measure copy numbers at tens of thousands of markers simultaneously. In this paper, we propose a non-parametric approach for detecting the locations of copy-number changes and provide a measure of significance for each change point. The proposed test is based on seeking scale-based changes in the sequence of copy numbers, which is ordered by the marker locations along the chromosome. The method leads to a natural way to estimate the null distribution for the test of a change point and adjusted p-values for the significance of a change point using a step-down maxT permutation algorithm to control the family-wise error rate. A simulation study investigates the finite sample performance of the proposed method and compares it with a more standard sequential testing method. The method is illustrated using two real data sets.

1. Introduction

The integrity and stability of chromosomes enable the cell to transmit accurately its genetic information and function properly physiologically. Aberrations in chromosomes such as rearrangements, deletions, amplifications and other types of copy number changes occur in many genetic diseases including, for example, Down syndrome which is a well-known developmental abnormality caused by trisomy (triplication) of the 21st chromosome. Studies of such aberrations, commonly referred to as genomic instability, can help understand the underlying mechanism of disease initiation and progression (Pinkel and Albertson, 2005).

A popular approach for assessing genomic instability is to measure genome-wide copy number variations using array-based comparative genomic hybridization (array CGH) (e.g., Snijders et al., 2001; Hodgson et al., 2001; Pollack et al., 2002). More recently, high-density single nucleotide polymorphism (SNP) arrays are used to genotype up to one million markers (e.g. Illumina Human 1M BeadChip). Although the two array technologies are different, data generated by them share common features. For these arrays, a set of genomic markers with known locations are chosen, and DNA copy numbers are measured as fluorescent intensity at each marker, so the data can be viewed as a sequence of copy number measurements ordered by the marker locations along the chromosome. With proper normalization (not the focus of this paper), an increase in the magnitude of positive or negative log ratios of test versus reference samples corresponds to possible copy number changes such as amplifications or deletions, respectively.

A variety of methods have been developed to segment chromosomes into regions of markers having the same underlying copy number. Although such a segmentation can also be used for identifying change points, little work has been done directly on the detection of change points and the corresponding statistical inference. This is the focus of our presentation.

A review of current approaches for copy number segmentation places them broadly into three main categories. The first category uses model-selection procedures, penalizing the number of segments (parameters) to avoid over segmenting an array CGH profile. These include Gaussian likelihood under a piecewise-constant model with various penalty parameters (Jong et al., 2003; Picard et al., 2007; Zhang and Siegmund, 2007), unsupervised Hidden Markov Models using Bayesian information criterion (BIC) or Akaike information criterion (AIC) (Fridlyand et al., 2004) and penalized least squares regression (Huang et al., 2005). More recently, Bayesian techniques have also been used in regularizing parameter estimation (Lai et al., 2008; Guha et al., 2008).

A second category consists of nonparametric function estimation to infer underlying true copy numbers, including a quantile smoothing method (Eilers and Menezes, 2005), a “fused lasso” method (Tibshirani and Wang, 2007) and a wavelet-based denoising method (Hsu et al., 2005). Wavelet methods and other nonparametric techniques are also suited to detect sharp changes as often observed in array CGH data, but to recover a piecewise constant function, an additional clustering of adjacent values may be needed.

A third category selects segments by controlling the overall type I error rate. For example, Olshen et al. (2004) proposed a circular binary segmentation (CBS) method using a sequential testing procedure. They considered all possible locations and widths of step functions and calculated the maximum t statistic for all combinations. The genome is then partitioned according to the maximum t statistic which exceeds the critical value at a pre-specified significant level. Each segment is then subjected to the same testing procedure. This procedure continues until no test statistic in each segment is significant. The approach of Wang et al. (2005) selects “significant” clusters formed along the chromosome by controlling false discovery rate (FDR). Cheng et al. (2003) proposed to detect copy number changes in a regression framework by pooling information across multiple samples.

Lacking among these methods are measures of significance for individual change points. The methods of Olshen et al. (2004) and Wang et al. (2005) provide some control on the overall type I error rate, although the latter requires an external set of normal samples to obtain the null distribution, and in the former, the false positive rate increases with the number of true change points. Both methods require one to pre-specify a level of significance. When individual change points are of interest, this is relatively inefficient as it requires one to re-run the segmentation procedures at different significant levels. We consider an alternative to this pre-specification of significance by estimating a p-value for each marker. This allows investigators to examine change points at their own significant levels without repetitive implementation of the same procedure. The method of Cheng et al. (2003) provides adjusted p-values by controlling family-wise error rate. However, it relies on multiple samples to estimate, and make inference about, the average intensity ratio for each marker. Like most literature in this field, our proposed method is designed to detect change points for each individual sample (i.e., in one array).

The paper is organized as follows. Section 2 describes the method for detecting change points which is based on a cross-scale product in a multiscale decomposition of the array signal. The wavelet transform used to produce this is introduced in 2.1. The test statistic and multiple comparison adjustment procedure are given in Section 2.2 and 2.3, respectively. Two real data sets are used to illustrate the proposed method and the results are shown in Section 3. Section 4 describes the results from a simulation study for examining the performance of the proposed approach and the method proposed by Olshen et al. (2004). Some final remarks are given in Section 5.

2. Detecting change points by multiscale products

Let Y_i be the observed log-relative intensity ratio for the ith marker location, x_i, for i = 1, …, n. Assuming additive measurement error for the log-relative intensities, the observed data can be modeled as

$$Y_i=f\left(x_i\right)+{\epsilon }_i,$$ (1)

where f is a piecewise constant function reflecting the discreteness in copy number; the ε_i, i = 1, …, n, are independent and identically distributed with mean 0 and variance σ².

Given R change points, there are R + 1 non-overlapping segments (0 ≤ R ≤ n − 1), each representing a region of amplification, deletion or no change in gene copy numbers. For the rth segment, let c_r denote the index of the end marker in the segment and μ_r be the corresponding copy number. Assume c₁ < c₂ < … < c_R and define c₀ = 0, c_R+1 = n. The collection {x_cr : r = 1, …, R} is the set of change point locations. Rewriting model (1) in these terms, Y_i = μ_r + ε_i for c_{r − 1} < i ≤ c_r. For identifiability of the change points, we assume μ_r ≠ μ_r+1. Under the null hypothesis of no change, f(x_i) = μ₀. Without loss of generality, we assume μ₀ = 0.

2.1 Multiscale wavelet products

We are interested in a test statistic that reflects significant step-like changes in copy number along the chromosome as modeled by f in (1). One way to focus attention on the step-like changes is to quantify the difference of adjacent averages in a neighborhood of each location x_i, such as ${\displaystyle {\sum }_{l=0}^{B-1}{Y}_{i+l}}-{\displaystyle {\sum }_{l=1}^B{Y}_{i-l}}$, where B is the number of markers in the neighborhood. Since the aberration size is unknown, it would be prudent to examine various neighborhood sizes.

A rigorous and efficient way to calculate these differences is by a wavelet transform of f: let $\psi \left(u\right)=-1/\sqrt{2}\text{ for }-1<u\le 0,\psi \left(u\right)=1/\sqrt{2}\text{ for }0<u\le 1$, and ψ = 0 otherwise. The collection of all translations and dilations, ${\psi }_{s,x}(u)≔\frac{1}{\sqrt{s}}\psi \left(\frac{u-x}{s}\right)$, forms a family {ψ_s,x : s ∈ ℝ⁺, x ∈ ℝ} of functions that define a wavelet transform of f defined as W f(s, x) ≔ ∫ ψ_s,x(u) f(u)du. Sampling at every marker location, x_i, i = 1, …, n, and at dyadic scales, s = 2^j, j = 1, …, J = ⌊log₂(n)⌋ (the greatest integer less than log₂(n)), gives coefficients W_j,i ≔ W f(2^j, x_i) of the maximal overlap discrete wavelet transform (MODWT). Of particular interest is the fact that $W_{j,i}\propto \left({\displaystyle {\sum }_{l=0}^{B-1}{Y}_{i+l}}-{\displaystyle {\sum }_{l=1}^B{Y}_{i-l}}\right)$, B = 2^{j − 1}, which quantifies the difference of adjacent averages in varying sized neighborhoods of x_i and reflects precisely-located changes in f that occur at scale 2^j. We use the terminology “level j” interchangeably with “scale 2^j”. In particular, let $W_j\equiv {\{W_{j,i}\}}_{i=1}^n=\mathit{W\; f}(2^j,\cdot )$ denote the level j coefficient function. See Percival and Walden (2000) regarding details of the MODWT.

We note that our use of a wavelet analysis differs from the more common goal of function estimation or denoising. In fact, we make no use of the inverse transform or thresholding techniques. Instead, our proposed test statistic is based on the coefficient functions W_j and whether, at a given location, they are more extreme than expected under the null (for a given amount of noise in the data). A useful property of these coefficient functions is that a change in f at a location x_i propagates across scales: the values |W_j,i′|, …, |W_j+k,i′| are increased for all i′ in some neighborhood of i, where j and k depend on the sharpness of the change and the width of the feature. We exploit this persistence across scales by considering the pointwise product W_j,i W_j+1,i of adjacent coefficient functions. This reinforces signal while canceling noise since coefficients related to high-frequency noise do not persist across scales and are diminished in the product.

A general multiscale product at the ith location is of the form Π_j∈D W_j,i, where D is a subset of all the possible levels {1, …, J}. If location i is indeed a change point, the wavelet coefficients at the adjacent levels are most correlated and so we focus attention on the product of two adjacent levels W_j,i W_j+1,i. We have restricted attention to two levels since for small aberrations and short segments, coarse levels that include markers not related to the aberration are less effective in detecting abrupt changes. We create, however, a test that is adaptive to varying sizes of aberration by considering the maximum of this product across levels at each location. That is, define M_i ≔ max_{j∈{2,…,J0}} {W_j,i W_{j + 1,i}} for some J₀ < J. Then the problem of detecting change points becomes one of testing

$$H_i^0:M_i=0\text{ versus }{H}_i^a:M_i>0$$

for each location i. Note that the test statistic M_i is always positive if location i is indeed a change point, so a one-sided test is used here.

For a genomic profile with different aberration sizes, the optimal scales used in M_i for detecting a change in copy number will depend on the properties of the chromosome aberrations and the density of markers. The choice of J₀ loosely depends on n since J₀ < J = ⌊log₂(n)⌋. However, averaging over long segments induces high spatial correlation among the M_i making it more difficult to precisely locate a true change point. Hence, when markers are sufficiently dense, J₀ is typically substantially less that J; setting J₀ = 6 or 7 generally provides adequate power for detecting change points.

Regarding the historical use of wavelet products, Bao and Zhang (2003) used two-scale products in a method for wavelet thresholding in signal recovery. In a work more closely related to ours, Sadler and Swami (1999) used two- and three-scale products aimed at detecting discontinuities. Their presentation considered theoretical and empirical distributions for these products, but failed to control an overall type I error rate and did not adjust for multiple comparisons. We are not aware of any work aimed at statistical inference based on multiscale products, one of the focuses of this presentation.

2.2 Local maximum

Given the two-scale product statistic at each marker, one might simply apply a multiple testing procedure to all n test statistics in an attempt to control the overall type I error rate. However, the MODWT coefficients within each level are locally correlated and elevated in an entire neighborhood surrounding a change point. The width of this neighborhood depends on the width of the aberration and the levels used in M_i. To circumvent this, we test only locations at which local maxima occur in M (as a function of i). Then for each local maximum, its location is designated to be a change point if the adjusted p-value is less than a pre-specified significance level. The notation i* is used to denote that a local maximum is detected at the ith location.

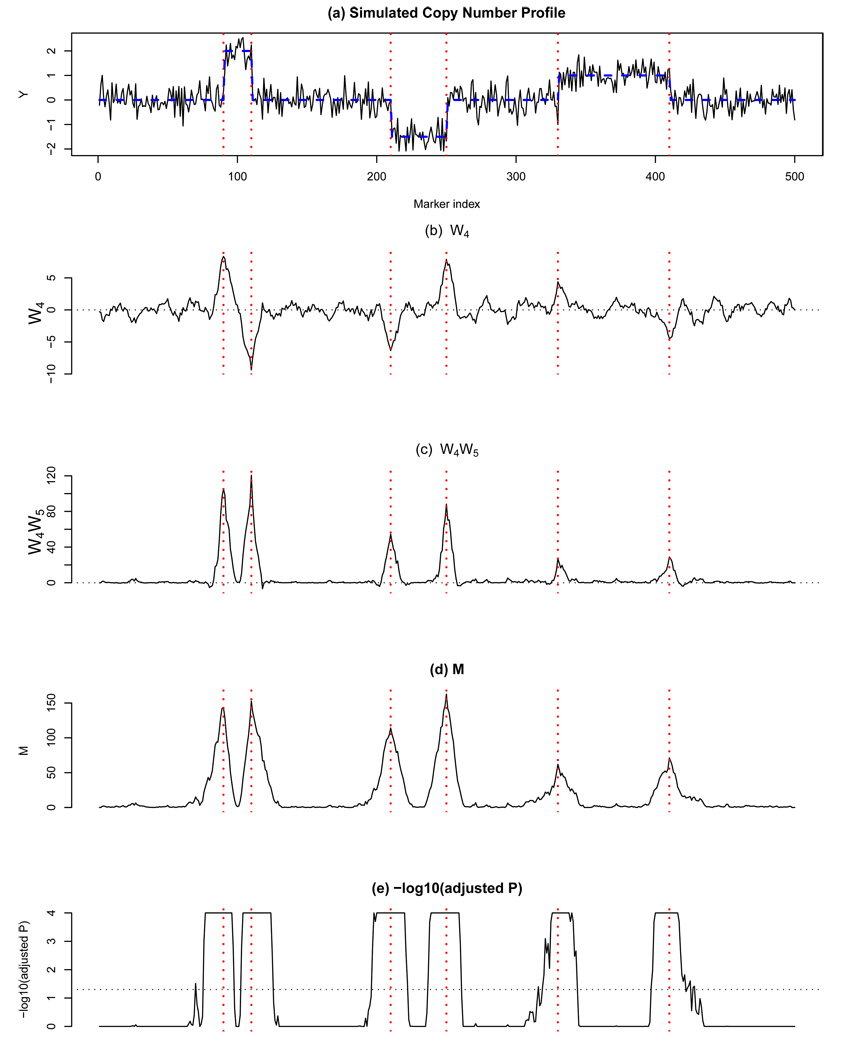
Figure 1 illustrates these ideas with a simulated copy number profile, the corresponding W₄, W₄W₅, M and the associated significance values, − log₁₀(p); each is plotted against i. We are only interested in the local maxima in M since they correspond to potential change points, yet as seen in Figure 1 the values of M_i tend to be elevated in an entire neighborhood of a change point since the W_j’s reflect neighborhood changes in f. It would be easy to obtain these if the copy number signal (hence M) was smooth, but any discrete noisy function will exhibit small local maxima that are not relevant since they don’t occur at a scale of interest. Although one could smooth M (say, with a kernel smoother using a particular bandwidth) and then seek local maxima, we have chosen to do this in one step through an efficient procedure based on the following fact: the level j transform of f is the first derivative of f after it has been smoothed with a kernel of scale 2^j (see Mallat, 1999). Therefore, the search for local maxima in M is achieved simply by performing a MODWT of M, at level j, and recording its zero crossings.

Figure 1.

Illustration of the proposed method. (a) A simulated copy number profile with 500 markers (f in a dotted line) and 6 change points (dotted vertical lines); (b) W₄; (c) W₄W₅; (d) M; (e) −log₁₀ of adjusted p-values truncated at 4. The horizontal dotted line indicates p = 0:05.

The locations of these local maxima in M are a small subset, {x_i* : i* ∈ K}, of the entire set of marker locations, where K is a set of indices for local maxima. A focus on only this subset of markers dramatically reduces the number of tests for change points. As a result, computing time for the proposed method does not substantially increase even as the number of markers increases to tens of thousands. We also show that the estimated change points converge to the true change point locations as the number of markers goes to infinity (see the Web Appendix).

2.3 Multiple testing

We describe a procedure for obtaining adjusted p-values at local maxima while accounting for multiple comparisons. We focus on controlling the family wise error rate (FWER) and note that the same test statistics can be used for obtaining other measures of statistical significance, such as q-values, using the algorithms described in Ge et al. (2003), which provides a comprehensive review of this topic.

Since both the marginal and joint distributions of the test statistics M_i* are unknown, we use resampling methods to estimate both raw and adjusted p-values. It is not obvious how to estimate a null distribution since the true function f is unknown. We consider two approaches for generating a null distribution.

The first approach is to permute ε̂_i = Y_i − f̂_i where f̂ s a robust estimator of f using lowess, a locally weighted regression (Cleveland, 1979). A simple permutation of the observed Y_i without subtracting f̂ would work if non-zero segments are only a small proportion of the whole region. Unfortunately the empirical distribution of errors is highly dependent on the estimated f̂. The key parameter in lowess smoothing is the width of the smoothing window; the larger the window size, the smoother f̂. We assessed the performance of the multiscale method by simulation using two different window sizes, 0.05 and 0.1, and found that the two sizes gave comparable results (results not shown). In the following sections, we used a window size of 0.1 and present results for window size 0.05 whenever a difference is observed.

The second approach is to permute the wavelet coefficients W₁ at the finest level. Since the W_1,i denotes the scaled difference Y_i − Y_i−1, this gives a close approximate estimation of the null distribution as R is relatively small compared to n. This approach, however, may overestimate R if the true error distribution is heavily tailed. To see this, let ε₁ and ε₂ be i.i.d. with mean 0 and variance σ², and W = ε₁ − ε₂. In general, W doesn’t have the same distribution as ε₁ and ε₂ unless ε₁ and ε₂ are normally distributed. To see the relationship between W and ε₁ (or ε₂), consider the first four moments: mean, variance, skewness and kurtosis for W and ε₁, one can show that the skewness of W is 0 and the kurtosis of W is one half of the kurtosis of ε₁ (or ε₂). For distributions with extremely heavy tails, permuting W₁ yields more false positives than expected. In this case, the first approach (permuting ε̂) is more appropriate.

After the null distribution of ε is estimated, the adjusted p-values can be computed using the step-down maxT permutation algorithm proposed by Westfall and Young (1993).

The following summarizes the proposed algorithm for detecting change points.

1. Compute the coefficient functions W_j for levels j = 1, …, J₀ + 1. Estimate the standard deviation σ using the MAD of W₁: $\widehat{\sigma }=\sqrt{2}\text{median}(|W_1|)/0.6745$ (the divisor provides asymptotically normal consistency). Standardize each level as $\sqrt{2^j}{W}_j/\widehat{\sigma }$.

2. Calculate point-wise products of standardized wavelet coefficients at all adjacent levels, W_jW_j+1, j = 2, … J₀. The test statistic for location i is M_i = max_{j∈{2,…,J0}} {W_j,i W_{j + 1,i}}.

3. Obtain the local maxima {M_i* : i* ∈ K} in M using level 4 wavelet transform.

4. Estimate the null distribution of M_i* by permuting W₁ (or ε̂) and obtain an adjusted p-value for each M_i* using the step-down maxT algorithm. Estimated change points are those whose corresponding adjusted p-values are smaller than a pre-specified threshold.

3. Results from real data

We illustrate the method using two real data sets: Coriel cell lines data (Snijders et al., 2001) and Illumina Human 1M SNP data (Peiffer et al., 2006). The proposed method is compared with the CBS method (Olshen et al., 2004). The CBS method is singled out because it performed consistently well based on a comprehensive comparison study by Lai et al. (2005). Since the CBS method detects change points by controlling the overall type I error rate, it makes the comparison with our proposed method more equitable than those based on model selection for which choosing tuning parameters is often an issue. The CBS method is used here without the extra preprocessing or pruning step because these steps are not part of the hypothesis testing and the number of estimated change points is very sensitive to the pruning parameters, the choice of which is rather subjective.

3.1 Coriel cell lines data

In 2001, Snijders et al. studied the DNA copy number changes for 15 Coriel cell lines using array CGH technology. Each array contained 2276 mapped BAC clones (markers) spotted in triplicate. The Coriel cell line data have been analyzed by many methods (e.g., Hsu et al., 2005; Olshen et al., 2004) and can be freely downloaded at http://www.nature.com/ng/journal/v29/n3/suppinfo/ng754_S1.html. This data is considered here primarily for proof-of-principle since the copy number alterations are known, having been identified by spectral karyotyping. Of 15 cell lines, six cell lines have whole chromosome amplifications only and nine cell lines have partial chromosome amplifications or deletions. We applied the proposed method and the CBS method to all 15 Coriel cell lines.

We analyzed the whole genome (all 23 chromosomes) simultaneously. The main consideration is that the total number of markers is 2276 and the density of markers varies greatly from chromosome to chromosome. For example, chromosomes 19, 21 and 22 have 35, 30 and 15 markers, respectively, and only seven chromosomes have more than 100 markers. The estimation of variance will be more accurate with the whole genome data than with each individual chromosome. In addition, it allows us to detect whole chromosome aberrations as the rest of the genome provides a good baseline reference. Finally, a genome-wide analysis allows us to control type I error rate for the whole genome, instead of at the chromosome level. A significance level of 0.01 was used.

The noise level of the Coriel data was very low with σ̂ ranging from 0.06 to 0.10 (a median of 0.07). The data appears approximately normally distributed based on Q-Q plots and histograms (results not shown), so both permutation procedures (W₁ and ε̂) were used to estimate the adjusted p-values and they gave the exactly same results for all cell lines except for GM02948, where permuting W₁ gave an additional false positive on Chromosome 20 at 65.3Mb. To save space only results from permuting ε̂ will be presented.

The Coriel data had strong signals and low background noise with median of the signal-to-noise ratio (SNR) 6.83 (first and third quantiles are 5.73 and 8.46, respectively). We observed that the CBS method detected many small segments for a total of 95 false positives. The multiscale method had no false positives (Table 1). Both methods missed the singleton on cell lines GM01535 in which only one altered marker exists on chromosome 12qtel. Note that by our convention in defining a change point in Section 2, the count of change points for a singleton is two. The adjusted p-values for the two false negatives on GM01535 are 0.231 and 1.000, respectively.

Table 1.

Summary of the number of false positives (FP) and false negatives (FN) on 15 Coriel cell lines using the multiscale and CBS methods. A significance level 0.01 was used for both methods.

	Multiscale		CBS
Cell line	FP	FN	FP	FN
GM00143	0	0	26	0
GM01524	0	0	11	0
GM01535	0	2	0	2
GM01750	0	0	2	0
GM02948	0	0	7	0
GM03134	0	0	0	0
GM03563	0	0	10	0
GM03576	0	0	1	0
GM04435	0	0	2	0
GM05296	0	0	0	0
GM07081	0	0	0	0
GM07408	0	0	2	0
GM10315	0	0	10	0
GM13031	0	0	0	0
GM13330	0	0	23	0
Total	0	2	95	2

3.2 Illumina’s Human 1M SNP data

The proposed method was also applied to detect copy number variation (CNV) using Illumina’s Human 1M SNPs data (http://www.illumina.com).To save space, we refer interested readers to Peiffer et al. (2006) for the normalization. The key point here is that, as in array CGH data, an increase in the magnitude of positive or negative log intensity ratios corresponds to possible insertion or deletion events, respectively. Therefore, segmentation methods developed for array CGH data would be applicable here.

The data here included 8 HapMap individuals whose high-resolution SNP intensity data, including normalized log intensity ratios, were freely available from Illumina web site. The reason we chose to work on these 8 HapMap individuals is that the CNV deletion events were detected and validated by two independent molecular experiments, fosmid-ESP assay and complete fosmid sequencing (Kidd et al., 2008). The data of the validated CNV events were downloaded from the supplementary material by Kidd et al. (2008) and Cooper et al. (2008).

We focused on deletion events that are covered by 10 or more SNPs to be consistent with Cooper et al. (2008)’s definition for detectable deletion events on the Illumina 1M array. This yielded 97 deletion events (i.e. 194 change points) which were twice validated experimentally and have sufficient probe coverage. We notice that the start and end locations of the selected 97 events detected by the two experiments were not identical, differing by up to 100K base pairs. Therefore, in the analysis we used the change point locations detected by complete fosmid sequencing as a gold standard and allowed for a 5-SNP difference on either side. Larger than 5 SNPs would cause ambiguity in the definition of change points for small-sized deletion events.

We analyzed one chromosome at a time due to the high-density markers. The number of SNPs per chromosome ranged from 15,408 to 98,752 with an average of 53,042. Two adjacent SNPs spanned on average 2.6kbp. The noise level of the SNP data was low with σ̂ ranging from 0.08 to 0.13 (a median of 0.09). We analyzed the data using a permutation of ε̂ because the error distribution was heavily tailed and permuting W₁ yielded more false positives (results not shown). We used a significance level 0.05, which differed from that used in the Coriel cell line data. This is because signals in the Illumina 1M SNP data are rather weak. A more relaxed significance level than 0.01 would allow us to detect more change points, and thus better discern the performance of the two approaches.

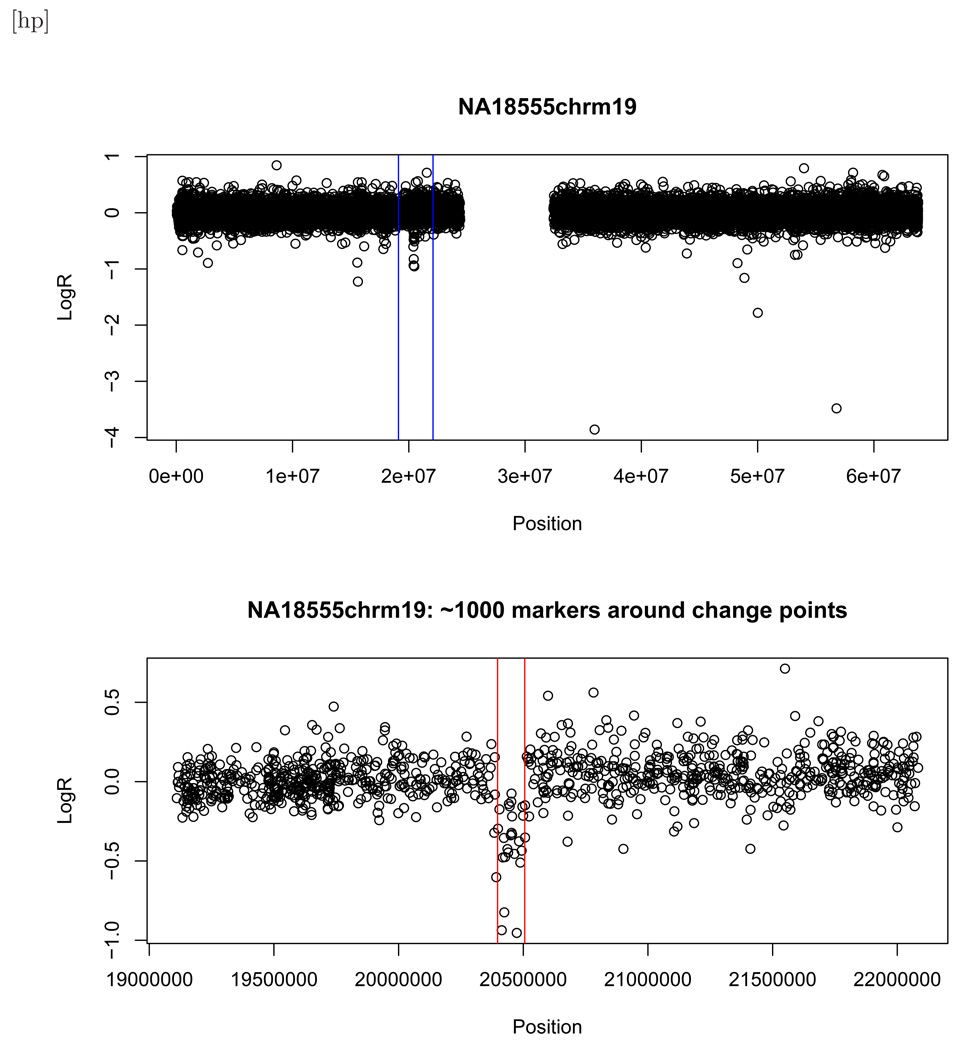
We observed that the CBS method falsely detected a total of 324 change points while the multiscale method had 217 false positives. The sensitivities were low for both CBS and multiscale methods. Of 194 change points which were twice validated by molecular experiments, the multiscale method detected 25 (12.9%) while CBS 19 (9.8%) (Table 2). All but two true change points detected by CBS were detected by the multiscale method. The two change points missed by the multiscale method were on chromosome 16 for NA19129 and had adjusted p-values 0.237 and 0.206 and raw p-values 0.003 and 0.002, respectively (see Web Figure 1). On the other hand, the CBS method missed eight change points that the multiscale method was able to detect. Figure 2 gives an example of a profile in which a deletion event is detected by the multiscale method but not by CBS. This is probably because the outliers in the data, as well as the large number of markers, increased the critical value for calling the significance of change points, which consequently reduced the power of CBS to detect these change points. In contrast, the multiscale method which is based on multiple scales and local maxima is more robust to outliers and more amenable to a large number of markers since the number of local maxima increases far less quickly than the number of markers.

Table 2.

Summary of the number of false positives (FP) and false negatives (FN) on 8 HapMap individuals using the multiscale and CBS methods. A significance level 0.05 was used for both methods.

	Multiscale		CBS		# change points
Cell line	FP	FN	FP	FN
NA12156	28	18	76	20	22
NA12878	52	33	66	35	38
NA18507	21	18	26	18	20
NA18517	14	11	16	12	12
NA18555	22	18	51	21	22
NA18956	19	17	27	17	22
NA19129	30	26	32	24	28
NA19240	31	28	30	28	30
Total	217	169	324	175	194

Figure 2.

Top panel: Scatter plot for NA18555 chromosome 19 (SNR = −3.71). The vertical lines indicate a small region that surrounds the validated change points. The blank spot is the centromere. Bottom panel: Zoomed-in scatter plot of the region that surrounds the change points. The vertical lines indicate the validated change points.

To understand why both methods had such low sensitivity we examined each profile manually. The reason appears to be that the signals for deletion events are weak for most profiles. The median SNR was −0.29 with first and third quartiles were −3.66 and 0.049, respectively; only one third (33) of 97 deletion events had SNR ≤ −1. Among the 64 events that had SNP > −1, 28 even had positive mean log intensity ratios and the maximum SNR was 1.24. This implies the measurement error, even though small in absolute value, is still quite large compared to the signal in the copy number data. For an example of a profile in which both methods failed see Web Figure 2.

It has been suggested that the use of genotyping information may help in detecting allele-specific CNV from these data (Dr. Adam Olshen, personal communications). Additional work along this line is clearly warranted, but is beyond the scope of this paper and not considered further.

4. A simulation study

This section discusses the finite-sample performance of the proposed method and contrasts it with the CBS method. Performance was measured by the number of estimated change points, true positive rate (TPR), false discovery rate (FDR) and number of exact detections. The TPR is the proportion of true change points rejected at a pre-specified significance level. The FDR is the proportion of false rejections among the total rejections. The number of exact detections is the number of simulated data sets in which all change points are correctly detected without any false positives and false negatives. Simulations were performed for both normally and non-normally distributed ε. For each simulation scenario, a total of 500 datasets were simulated with each dataset having 500 markers. A significance level 0.01 was used throughout, unless otherwise stated.

4.1 Simulation under normal distribution

Assume ε is normally distributed and consider data simulated according to the model (1). The performance of the proposed and CBS methods were evaluated under a variety of underlying mean functions, f, and noise levels, σ. For the complete null case, i.e., f = 0, the type I error rates were 0.008 and 0.002 for the proposed and CBS method, respectively. Permuting W₁ and ε̂ gave very comparable results.

Next, for the presence of change points, the data sets were generated from a model created by Olshen et al. (2004) as follows:

$$Y_i=f(i)+0.25\sigma \text{sin}(a\pi i)+{\epsilon }_i,$$

where ε_i are i.i.d. N(0, σ²), n = 500, and the second term is a sinusoid trend component to make the simulated data set more realistic and challenging. The noise parameter σ was set to be 0.1 or 0.2, and the trend parameter a was chosen to be 0, 0.01 or 0.025, corresponding to no trend and local trend with long and short periods, respectively. There were seven segments along the chromosome. The means of log intensity ratios within segments were given by:

i	1–130	131–220	221–240	241–300	301–310	311–350	351–500
f(i)	−0.40	0.08	1.20	−0.50	0.30	−0.70	−0.20

An example of a simulated data set using the trend model is given in Web Figure 3. We found that the proposed method using permutation of W₁ outperformed the CBS method in each of the no-trend, long- and short-period trend models (Table 3). The proposed method was robust to local trend in the sense that FDR, TPR and the number of exact detections did not appear to change with the trend parameter a. The CBS method tended to overestimate the number of change points in the presence of a local trend. The FDR increased with a and the number of exact change points detected decreased with a. However, permuting ε̂ was less powerful under the trend model because the default window size (0.1) over-corrected the trend. Therefore, under the normal (or near normal) situation, permuting W₁ is recommended because it is robust to trend and does not require any tuning parameter as for the approach based on ε̂.

Table 3.

Summary of results under the trend model. σ =noise level, a =trend parameter. FDR=# false rejections/# total rejections, TPR= # true rejections/R, Exact=# data sets with correct locations and number of estimated change points. A significance level 0.01 was used.

					R̂
σ	a	Method	4−	5	6	7	8+	FDR (%)	TPR(%)	#Exact
0.1	0	Permute W1	0	0	490	10	0	0.3	100	490
		Permute ε̂(0.10)	2	100	398	0	0	0	96.5	398
		CBS	0	0	472	11	17	1.2	100	472
	0.01	Permute W1	0	0	486	14	0	0.4	100	486
		Permute ε̂(0.10)	2	107	391	0	0	0	96.3	391
		CBS	0	0	407	35	58	4.1	100	407
	0.025	Permute W1	0	0	487	13	0	0.4	100	487
		Permute ε̂(0.10)	2	72	426	0	0	0	97.4	426
		CBS	0	0	394	22	84	5.1	100	394
0.2	0	Permute W1	0	0	436	57	7	2.3	99.7	428
		Permute ε̂(0.10)	0	85	410	5	0	0.8	96.6	405
		CBS	0	0	450	34	16	2.3	99.5	439
	0.01	Permute W1	0	6	437	52	5	2.2	99.3	423
		Permute ε̂(0.10)	5	150	343	2	0	0.8	94.0	328
		CBS	0	0	390	54	56	4.8	99.7	384
	0.025	Permute W1	0	7	432	54	7	2.2	99.4	422
		Permute ε̂(0.10)	2	75	413	10	0	0.5	97.1	408
		CBS	0	0	376	42	82	6.0	99.5	364

4.2 Simulation under non-normal distribution

In this section we contrast the performance of the proposed method with the CBS method when ε was not normally distributed. We evaluated both approaches of permuting W₁ and ε̂. We started with the complete null situation to examine the type I error rate and then followed with a power evaluation under an evenly-spaced change point model.

Under the complete null we generated the errors i.i.d. from t distributions with degrees of freedom (df) 1, 2, and 3, respectively. Web Table 1 shows the summary of simulation results. The CBS method performed consistently well and the family-wise type I error rates were below or close to the pre-specified level. The proposed method had the correct type I error rates when the null distribution was estimated by permuting ε̂. The null distribution estimated by permuting W₁ underestimated the tail probabilities and yielded increased type I error rates as the df for t distribution decreased, i.e., tails get heavier. However, the type I error rates were already below the pre-specified level when the df > 3 (results not shown).

To investigate the power of our method, we generated chromosome profiles with different numbers of evenly-spaced change points and aberration width under a t distribution with 3 degrees of freedom. The function f(i) was set to be either 0 or 1 corresponding to no change or copy number gains. The number of change points (R) varied among 2, 4, and 6. The width of each aberration region (width) increased from 20, 40 to 80 markers. Both the multiscale and CBS method were robust to this non-normal distribution and comparable under all but one setting examined (Table 4). This scenario, in which CBS appears more powerful, has only one large aberration segment: width = 80 and R = 2. As expected, permuting W₁ tended to overestimate the number of change points compared to permuting ε̂.

Table 4.

Summary of results for when ε is i.i.d. t(df=3). FDR=# false rejections/# total rejections, TPR= # true rejections/R, Exact=# data sets with correct locations and number of estimated change points. A significance level 0.01 was used.

R	Method	≤R−2	R−1	R	R+1	≥R+2	FDR(%)	TPR(%)	#Exact
						width=20
2	Permute W1	22	8	432	37	1	3.6	94.0	427
	Permute ε̂(0.10)	24	17	451	7	1	2.2	92.4	446
	CBS	40	0	449	5	6	1.4	91.5	445
4	Permute W1	27	7	433	32	1	3.5	94.1	419
	Permute ε̂(0.10)	28	14	444	13	1	2.8	93.6	430
	CBS	44	0	441	9	6	1.4	90.8	428
6	Permute W1	30	4	433	30	3	2.4	94.9	423
	Permute ε̂(0.10)	26	7	434	29	4	2.8	95.4	423
	CBS	48	0	438	10	4	0.7	90.6	432
						width=40
2	Permute W1	8	3	446	42	1	3.7	97.3	439
	Permute ε̂(0.10)	10	7	474	8	1	1.6	96.4	466
	CBS	13	0	479	3	5	1.6	96.5	470
4	Permute W1	12	4	456	27	1	2.1	97.1	442
	Permute ε̂(0.10)	12	0	473	14	1	1.8	97.2	458
	CBS	16	0	471	3	10	1.5	96.1	457
6	Permute W1	12	3	462	22	1	1.5	97.3	441
	Permute ε̂(0.10)	12	2	467	18	1	1.5	97.6	446
	CBS	25	0	458	11	6	1.1	94.8	444
						width=80
2	Permute W1	5	7	448	38	2	3.3	97.7	443
	Permute ε̂(0.10)	8	7	475	9	1	1.2	97.2	470
	CBS	5	0	492	1	2	0.9	98.4	486
4	Permute W1	10	1	458	29	2	2.1	97.4	442
	Permute ε̂(0.10)	9	5	473	12	1	1.6	97.4	456
	CBS	9	0	478	5	8	1.7	97.3	459
6	Permute W1	10	5	455	29	1	1.5	97.6	438
	Permute ε̂(0.10)	9	3	465	22	1	1.5	97.8	447
	CBS	15	0	453	16	16	2.1	96.2	428

We also examined a smaller window size, 0.05, and found that it was slightly more conservative and thus less powerful in detecting the change points than smoothing with window size 0.1 (results not shown). Based on the settings we examined here, a window size 0.10 for obtaining ε̂ appears to be a reasonable choice when ε is not normally distributed.

5. Discussion

We have proposed a non-parametric approach for detecting change points in genomic copy number data by seeking local changes that occur at multiple scales. We provide multiple comparison adjusted p-values for each potential change point. The p-values provide flexibility for investigators to call change points at their chosen level of significance. These p-values can be computed using re-sampling approaches by permuting either W₁ or ε̂. Which approach to use will depend on the error distribution, which, unfortunately, is not usually known. In practice, we suggest to visually examine the residuals from the lowess smoothing to determine if the errors are roughly normal or have heavy tails. Under the normal or near normal situation, permuting W₁ is recommended because it is robust to trend and does not require any tuning parameter as for permuting ε̂. For distributions with extremely heavy tails, permuting W₁ yields more false positives. In this case, permuting ε̂ is more appropriate than permuting W₁ and we recommend to use a smoothing window of width 0.1.

The proposed method performed well in most settings that we examined. It has the correct type I error rates under the null and is robust to background trend in the data and non-normal errors. However, because the test statistics are based on local variations the method has low power in detecting change points when the noise level is very high and the aberration region is narrow. This weakness may be overcome by improvements in array technologies, DNA extraction methods and increasing marker density. The CBS method, on the other hand, performs relatively well when the noise level is high and the aberration region is narrow. Like the proposed method, the CBS method also performs well when the error distribution is not normal. However, the CBS method tends to overestimate the number of change points when there exist multiple change points or when there is a background trend. This overestimation occurs even when the noise level is low, as shown in the Coriel cell line data and Illumina 1M SNP data.

All computations were done in R; the code is available from the authors upon request.