Matching ATP Supply and Demand in Mammalian Heart: In Vivo, In Vitro and In Silico Perspectives

Abstract

Although the heart rapidly adapts cardiac output to match the body’s circulatory demands, the regulatory mechanisms ensuring that sufficient ATP is available to perform the required cardiac work are not completely understood. Two mechanisms have been suggested to serve as key regulators: (1) ADP and Pi concentrations—ATP utilization/hydrolysis in the cytosol increases ADP and Pi fluxes to mitochondria and hence the amount of available substrates for ATP production increases; and (2) Ca2+ concentration—ATP utilization/hydrolysis is coupled to changes in free cytosolic calcium and mitochondrial calcium, the latter controlling Ca²⁺-dependent activation of mitochondrial enzymes taking part in ATP production. Here we discuss the evolving perspectives of each of the putative regulatory mechanisms and the precisemolecular targets (dehydrogenase enzymes, ATP synthase) based on existing experimental and theoretical evidence. The data synthesis can generate novel hypotheses and experimental designs to solve the ongoing enigma of energy supply–demand matching in the heart.

Introduction:The ATP supply and demand enigma

The core of any mechanism that performs work is the engine, but the control mechanisms must also be carefully engineered to maximize its performance in part by tuning its ability to match the supply of energy or fuel to the required output of work. Often ingenious control mechanisms are required to rapidly and adequately control the fuel utilization by the engine to match the demand. The heart, as an engine, can augment the cardiac output 7-foldwhile increasing the oxygen consumption (VO2), the fuel (i.e., ATP) consumption index, by 10-fold. Matching cardiac ATP supply to demand on a beat-to-beat basis is critical to ensure sufficient fuel availability to perform the required work. However, the identity of the mechanisms that control and regulate cardiac ATP supply and demand remains controversial. In this review, we shall examine and critique the major direct effectors and byproducts of cardiac work that have been suggested to serve as key regulators of these matching mechanisms and we shall discuss their molecular targets within the mitochondria. These mechanisms will be used together with certain key assumptions to describe mathematical models of matching supply to demand. Each model’s predictions will be explored and interpreted in light of existing in vivo and in vitro data.

Heart metabolism

The heart is capable of oxidizing fats, glucose, lactate, and/or ketones to produce ATP. In the cytosol, glucose is transformed to pyruvate and fatty acids are converted to fatty acyl-coenzyme A. Only diminutive amounts of ATP are created by metabolic reactions in the cytosol. On the other hand, the mitochondria are the primary supply source of ATP to match cellular demand. Mitochondrial ATP production is tightly controlled by several regulated and linked biochemical and molecular mechanisms, ¹ as illustrated in Figure 1. Pyruvate and fatty acyl-coenzyme A are transported across the inner mitochondrial membrane to the mitochondrial matrix. Pyruvate is transformed to acetyl-coenzyme A. Fatty acyl-coenzyme A is also converted to acetyl-coenzyme A while creating NADH and FADH₂. Acetyl-coenzyme A from both substrates is oxidized to carbon dioxide and water in the Krebs cycle, resulting in the formation of NADH and FADH₂. The redox-potential energy of these reducing equivalents is, in turn, harnessed by the electron transport chain. The energy released from this electron flow is used to transport protons across the inner mitochondrial membrane, out from the matrix. Under normal conditions, the electron transport chain flux is paralleled by the VO₂. The net result of this process is potential energy being stored in a large proton gradient (ΔpH) and electrical gradient (Δψm). Under actively respiring conditions, the mitochondrial proton concentration in the matrix is much lower (by ~1 pH unit) than in the intermembrane (IMM) space. Moreover, the IMM space is positively charged (by~ 180mV) with respect to the matrix. The proton concentration and membrane potential differences form an electrochemical gradient, responsible for the proton-motive force (PMF). The ability of the PMF from redox equivalents generated in the Krebs cycle to drive ATP synthesis was described as a “pushing” effect of respiration by O’Rourke.² This PMF drives ATP synthase (mitochondrial complex V) to make ATP. The ATP synthase consists of two main components, each made of a number of subunits: the F_o component has a ring structure and functions as a proton “channel”; the F₁ component forms the head of the enzyme complex for ATP generation and is coupled to F_o. The PMF drives protons through the ATP synthase back into the matrix in a process that creates ATP. Note that under certain conditions the ATP synthase (F₁F_o-ATPase) function can be reversed and the energy of ATP is then harnessed to pump protons out of the matrix. It was suggested that signals acting directly on ATP synthase might also facilitate the redox flux through the electron transport chain and increase ATP production.³ This phenomenon was termed by the O’Rourke lab as the “pull” effect on respiration.²

Figure 1.

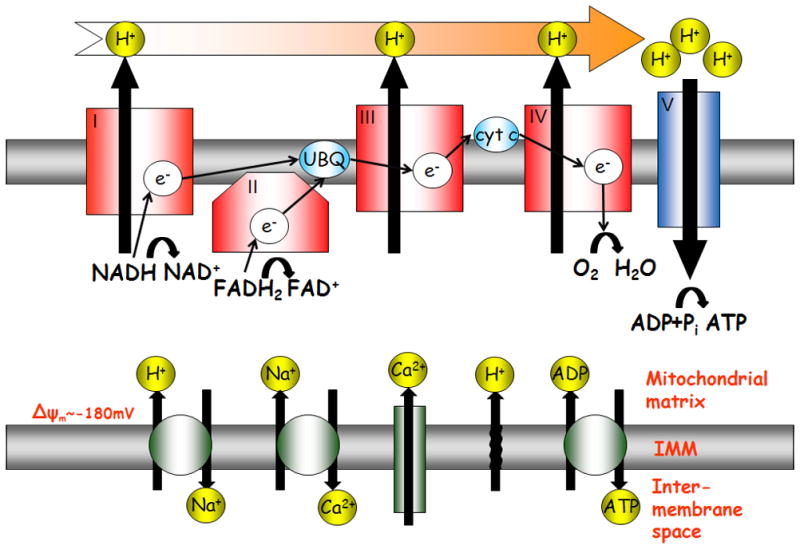
Bioenergetics scheme of mitochondrial membranes and matrix. The oxidative phosphorylation complexes are located in the inner mitochondrial membrane. The Krebs cycle produces a source of electrons whose redox-potential energy is, in turn, harnessed by the electron transport chain. The complement of ion channels that maintain the ionic gradients that establish the membrane potential ΔΨ_m, includine the Ca²⁺ uniporter, Na⁺/Ca²⁺ exchanger, Na⁺/K⁺ exchanger, adenine nucleotide translocator and proton leak.

Cytolsolic-mitochondrial metabolic feedback

In 1939, Vladimir Engelhardt discovered that muscle myosin hydrolyzes ATP, making a significant first step toward identifying one of the major consumers of ATP.⁴ Two years earlier, Herman Kalckar discovered the main source of ATP supply in highly aerobic tissues.⁵ He established that ATP synthase is linked with cell respiration and was the first to consider ATP to be final product of chain reactions. About the same time, Lipmann proposed that ATP functioned as a generalized energy carrier and is the main bearer of chemical energy in biological systems. ⁶ On the basis of these findings it was plausible to suggest that ATP supply and demand might be matched via some process that senses its hydrolysis byproducts, ADP and Pi. Studies have suggested that the ATP/ADP ratio determines the respiration rate of mitochondria.^7,8 In this scenario, an increase in workload would lead to an accumulation in cellular ADP, a decrease in cellular ATP due to myosin ATPase utilization, which would regulate downstream process by the “pushing” effect of the buildup of substrate gradients. Chance and Williams, however, in 1956 provided experimental evidence that the availability of ADP to F₁F_o-ATPase, and not the ATP/ADP ratio, controls the rate of respiration.⁹ It was suggested that ADP pushes the ATP synthase not only by its availability as a substrate, but also by activating the pyruvate dehydrogenase (PDH) complex, ^10,11 isocitrate dehydrogenase,^1,12 and the F₁F_o- ATPase.¹³ ATP is also produced by catalysis phosphocreatine (PCr) to creatine (Cr) by creatine kinase (CK). ADP and Pi are transferred to the mitochondria by a PCr shuttle. Thus, this PCr shuttle, which is controlled by ADP and Pi concentration, would be the regulator between supply and demand.^14,15 However, the heart has one of the lowest CK activities among different muscles. At this point, it is worth emphasizing several factors resulting from these regulatory mechanisms: First, if ADP or Pi are the main elements in the regulatory mechanism that matches ATP supply–demand, and assuming Michaelis–Menten kinetics between ATP synthase and its substrate, then a one-to-one relationship between the increase in ATP synthesis rate and ADP or Pi concentration should exist. Second, the conceptual basis of this regulatory mechanism has been based primarily upon data from isolated mitochondrial experiments. The temporal relationship between changes in VO2 by adding or consuming of ADP or Pi motivated the idea that ADP or Pi is the main regulatory mechanism.^1,10–12 However, these temporal relationships defined for mitochondrial suspensions have neither accurately predicted the mitochondrial behavior under in situ conditions,¹⁶ nor the time response of the mitochondria to cytosolic changes.¹⁷ Third, it is not trivial to evaluate the ADP effect in vivo because the ADP concentration in the cytoplasm is low and, therefore, difficult to measure. As a result, ADP concentration is typically calculated from the CK reaction kinetics at equilibrium.¹⁸

Constant ATP, ADP AND Pi

During the last three decades, it has been consistently demonstrated that over a wide working range and ATP demand, the levels of ATP, CrP, and other energy metabolites are maintained at essentially steady levels. By using the phosphorous NMR method, Katz and Balaban have found that in different species a linear relationship between VO₂ and cardiac work is not followed by changes in these energy metabolites.^19,20 Balaban has shown that increasing the ATP utilization by more than 10-fold is associated with only minor changes in ATP/ADP/Pi levels (i.e., not a one-to-one relationship).^20,21 It was also established that changing the perfusion metabolic-substrate species does not change the ATP metabolite concentrations.²² Moreover, Balaban emphasized that most experimental data are consist with metabolic homeostasis not only in the cytosol, but also in the mitochondrial matrix during a physiologic increase in workload.²³ Additionally, there is no significant change in cytochrome c redox state during work transitions.²⁴ If ADP or ATP were the rate-limiting steps, then the cytochrome c redox state would correspond to the mitochondrial flux. These data emphasize that other regulatory mechanisms must also exist controlling the matching of cardiac energy supply and demand (Fig. 2).

Figure 2.

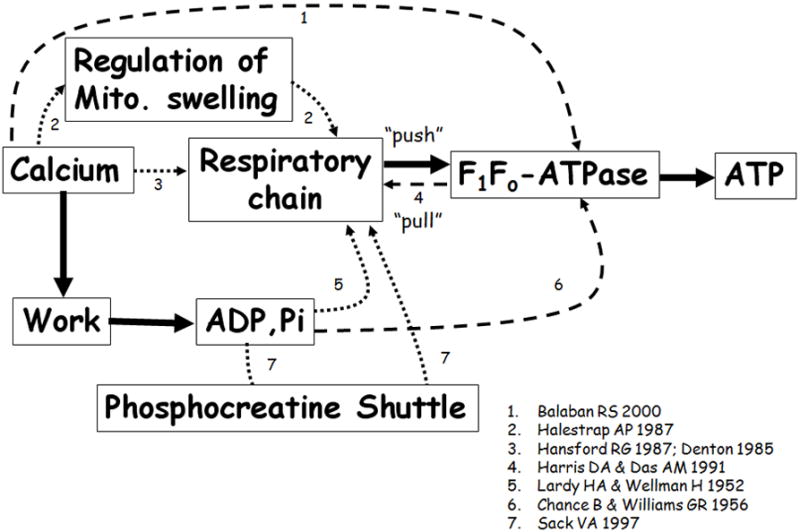
Proposed “push” and “pull” regulatory mechanisms. The solid lines represent connections that are well established. The dotted lines represent proposed “push” mechanisms, and the dashed lines represent the “pull” mechanisms. Appropriate citations are indicated adjacent to the connecting arrows.

Other regulation mechanisms

Several mechanisms have been suggested to serve as either direct or indirect regulatory control points to match energy supply with demand.²⁵ As described above, Δψ_m affects the PMF that controls the F1Fo-ATPase activity and it has therefore been suggested as a potential control mechanism.²⁵ It was postulated that under in vivo conditions, stimulation of the dehydrogenases increases the NADH level, which in turn is harnessed via the electron transport chain. As a consequence, both electron flux and Δψ_m would be increased. However, Wan and colleagues have shown in a perfused heart model using direct measurements of Δψ_m that increasing the work rate decreased the Δψ_m contrary to the expectation.²⁶ Thus, it seems unlikely that Δψ_m related–mechanisms are sufficient to explain the control of ATP supply–demand matching.

Although Δψ_m per se may not serve as this energy balance controller, the original idea was based on the fact that increases in NADH/NAD redox potential can promote respiration.²⁷ Therefore, the NADH/NAD ratio might serve as a controller. However, Hansford has found in mitochondrial suspensions that the magnitude of the changes in the NADH/NAD ratio which occurred as a consequence of varying Ca²⁺ or substrate availability in State 3 was not large.²⁸ Moreover, the NADH/NAD ratio in the whole heart remains constant.^29,30 Note, that under quiescent conditions, which are far from the physiologic range, the redox state is not constant.²¹

Halestrap has suggested thatmitochondrial Ca²⁺ can regulate and increase the mitochondrial matrix volume,³¹ which in turn can elevate respiration.³² Therefore, it was postulated that during electrical stimulation an increase in Ca²⁺ serves to facilitate this purpose. However, to date there are no direct measurements of in situ mitochondrial volume during electrical stimulation to confirm this theory.

O’Rourke and colleagues have described glycolytic and ADP oscillations driven by feedback loops in the regulation of key glycolytic enzymes.³³ Oscillations in ATP promoted electrophysiologic heterogeneity. Weiss’s lab explored the potential of the ADP oscillations to match ATP supply to demand.³⁴ However, they found that a high variation in ADP and CK levels would be needed to drive the oscillations, but these conditions are not seen under normoxic conditions. Nevertheless, glycolytic oscillations can play a role under ischemic conditions when the ATP reserve capacity is used up and the ADP level is high.

Ca²⁺ as a regulatory mechanism

ADP and Pi have been suggested as the natural regulatory mechanisms since they correlate with both ATP utilization and production. Another plausible mechanism that might control this nature is Ca²⁺. At high workloads more Ca²⁺ is bound to the contractile elements, causing a decrease in cytosolic Ca²⁺. The SR compensates for this decrease by releasing more Ca²⁺ to preserve systolic Ca²⁺ levels.^24,35 Therefore, from the demand point of view, Ca²⁺ is a direct effector that might be well positioned to play a role in the energy-matching regulatory mechanisms. A correlation was shown between cytosolic and mitochondrial Ca²⁺.^36,37 Ca²⁺ enters the mitochondria through the mitochondrial uniporter, which is sensitive to mitochondrial membrane potential, and is extruded by the mitochondrial Na⁺/Ca²⁺ exchanger.³⁸ Other plausible mechanisms for Ca²⁺ influx and efflux have been suggested (reviewed in Refs.^39–41). The kinetics of the two major pathways are different: Ca²⁺ uptake can occur rapidly during the cytosolic Ca²⁺ transient, but mitochondrial Ca²⁺ decay kinetics are slow. This results in mitochondrial Ca²⁺ accumulation in response to an increase in stimulation frequency or Ca²⁺ transient amplitude. Therefore, Ca²⁺ in the mitochondria reflects changes in demand. The first hint that Ca²⁺ may play a key role in controlling the ATP supply came from isolated mitochondria when PDH was shown to be stimulated by Ca^2+, with a concentration of 1 μM required to elicit the half-maximal response.¹² In myocyte suspensions⁴² and in perfused rat hearts⁴³ the increase in workload was correlated with the increase in PDH. Ruthenium red, an inhibitor of Ca²⁺ flux in isolated mitochondria, diminished the persistent elevations in dehydrogenase activity.¹² Ca²⁺ also activates other dehydrogenase mechanisms: isocitrate and α-ketoglutarate,^12,25 and the electron transport chain.⁴⁴ Whether Ca²⁺ directly activates adeninenucleotide transporters is controversial.⁴⁵ In the1990s Hajnoczky and colleagues demonstrated that NAD transients were synchronized to the individual spikes of the cytosolic Ca2+ oscillations.⁴⁶ Rizzuto established a sigmoidal relationship between [ATP] and Ca²⁺ in the mitochondria.⁴⁷ Recently, Jo and colleagues found that Ca²⁺ couples mitochondrial substrate dehydrogenation to cardiac workload in single guinea pig ventricular myocytes.⁴⁸ Hood and colleagues have shown using A-23178, a Ca²⁺ ionophore, that increased concentration of Ca²⁺ leads to activation of a number of nuclear genes encoding mitochondrial proteins, including F₁F_o- ATPase and cytocrome c.⁴⁹ Therefore, changes in mitochondrial Ca²⁺ during excitation–contraction coupling (i.e., caused by mitochondria taking up more Ca²⁺ in response to increased cytosolic Ca²⁺) are linked to changes in ATP supply and demand.

The “Pull” mechanism

We have summarized here experimental data where Ca²⁺ was found to stimulate the “push” mechanism. It has been postulated that Ca²⁺ might also serve as a control signal for the “pull” mechanism.²⁵ Balaban and his coworkers hypothesized that physiologic Ca²⁺ activates the ATP synthase in addition the dehydrogenase activities,³ in order to maintain a balance between supply and demand.¹⁹ Evidence for a role for Ca²⁺ in the pull mechanism was based upon their observation of a two-fold higher VO₂ than could be explained solely by the increase in NADH from the Krebs cycle.³ If the only role of Ca²⁺ was the push acting via the Krebs cycle, they should have observed a one-to-one relation between NADH and VO₂. However, the slope between VO₂ and NADH was different. Although Balaban raised the possibility of the involvement of Ca²⁺ in the pull mechanism, this important issue remains unresolved and the target of the pull mechanism has not been established.

In the next part of this review, we shall discuss different in silico perspectives, the assumptions behind the model, and its predictions.

Modeling Pi as a controller of supply and demand

Beard’s lab developed a comprehensive model for the biophysics of the respiratory system and oxidative phosphorylation⁵⁰ and applied it to normal and ischemic hearts.⁵¹ The model includes 17 differential equations of ionic flux and explicit equations for mitochondrial membrane potential and pH. Beard’s model is based on two assumptions: that dehydrogenase is activated by Pi and that the rate of F₁F_o-ATPase is controlled by ADP, ATP, and Mg²⁺. The first version of the model was fitted to NADH, VO₂, cytochrome c redox state, and matrix pH parameters obtained from experimental data on isolated rat cardiac mitochondria.⁵⁰ In order to obtain a better fit to the relationship between Δψ_m and buffer Pi, Beard incorporated phosphate-dependent control of complex III. The model faithfully describes the matrix NADH concentrations, Δψ_m, and mitochondrial VO2 as a function of buffer Pi concentration. However, the model parameters are solely based on steady-state data.

An improved version of the model extends the previous one by incorporating cardiac energy metabolism.⁵¹ This model simulates ⁵³ biochemical reactant concentrations. The model’s main assumption is again related to Pi (although the authors caution that ADP and Pi are too low to be directly observable under baseline conditions in normal hearts). Basing their conclusions on data with a large degree of scatter, they suggested that Pi increases with increasing workload. This analysis allows them to generate model-based predictions of the ATP hydrolysis potential and cytoplasmic free Pi and ADP concentrations as a function of VO2. Their steady-state analysis yields the hypothesis that the rate of ATP consumption of the heart is limited by the rate at which cardiac mitochondria can deliver ATP to the cytoplasm at the hydrolysis potential. On the basis of their results for the normal heart, the authors extend the model to the case of ischemia: the model predicts increased Pi concentrations during ischemia. These investigators concluded that Pi is the most significant product of ATP hydrolysis in limiting the capacity of the heart to hydrolyze ATP. The proposed role of Pi as a controller contradicts Balaban’s findings for metabolite homeostasis (discussed by Balaban²³), a conclusion that remains controversial because of the difficulty of measuring Pi in vivo under physiologic conditions.

Modeling CrP as a controller of supply and demand

Saks’s group has suggested that in the working heart the CK reaction in myocytes clearly operates far from equilibrium during most of the contraction cycle.^15,52 This hypothesis was derived from their former mathematical model of compartmentalized energy transfer.⁵³ Their new model is based on parameter estimation from working rat hearts. It predicts significant oscillations of the cytoplasmic ADP concentration in cells during the cardiac cycle. To model ATP supply and demand, a spatially inhomogeneous reaction-diffusion energy transfer system was developed in three compartments: the myofibrils together with the myoplasm, the mitochondrial IMM space, and the mitochondrial inner membrane-matrix space. ATP is hydrolyzed in the myofibrils, the mitochondrial CK reaction is coupled to the adenine nucleotide translocase (ANT) reaction in the IMM space, and ATP is produced in the reaction inside the mitochondria. Their equations were developed under the assumption that ATP synthase depended directly on Pi. As a result, this model predicts that ADP increases by three-fold when the workload increases from low to high levels. Over the same range of workloads, the model predicts that Pi increases by 25%. However, as determined by experimental evidence, over this range of workload, Pi actually remains constant.^19–21 Moreover, there is no direct evidence that effective bulk CK diffusion takes place in intact muscle.

Van Beek proposed that ADP and ATP are not directly transferred between cytosol and mitochondria under normal conditions.¹⁴ Instead a Pi group transfers from ATP to Cr and through the PCr shuttle into the IMM space. CK buffers the ADP in the cytosol, keeping ADP levels low and ATP levels high. This concept is similar to that of Saks’s group and, therefore, Cr may play an important role as a controller between supply and demand.^15,52 The van Beek model is based on Langendorff-model experiments, where CrP increases by 10% with a parallel increase in ATP synthase activity. However, this model is different from the in vivo model. For example, in the Langendorff-perfused heart the substrate affects the Pi levels. Glucose and insulin, compared to pyruvate, diminish the increase in ADP and CrP with the same increase in VO₂. Van Beek has suggested that there is a time delay until Ca²⁺ increases in the mitochondria and, therefore, ADP and Pi are responsible for the initial fast phase of activation of respiration.⁵⁴ However, the beat-to-beat regulation of Ca2+ might be different across different mammalian species (see review by Dedkova and Blatter⁴¹).

Bassingthwaighte⁵⁵ has chosen to use the van Beek model¹⁴ to link cellular energetics to abnormal routes of cardiac excitation. The amount of ATP consumed by the cross-bridges (XBs) is used to calculate the amount of ADP that controls ATP generation by oxidative phosphorylation. Our group estimated the amount of consumed ATP using the same method, but also examined its residual effect on cytosolic and mitochondrial Ca²⁺ and its control over the ATP synthase.⁵⁶ In mathematical simulations, both controllers can activate the metabolism to the same degree. In the ADP-controlled model, variability in ADP levels in the heart under normal conditions is inconsistent with experimental data.²⁰ Moreover, since ADP levels during abnormal cardiac excitation have not been determined, the role of ADP as a controller remains controversial.

Modeling Ca²⁺ as a controller of supply and demand

Korzeniewski was the first to mathematically formulate the activation of ATP synthesis by Ca2+ and named it “parallel activation”.^17,57 He based his assumption on the experimental findings that Ca2+ stimulates the tricarboxylic acid cycle dehydrogenases and ATP synthase. The model incorporates the major oxidative phosphorylation mechanisms: NADH production, the activity of complex I and III, oxygen consumption by complex IV, proton leak, ATP synthase, ANT, and the Pi carrier. On the basis of his model, parallel activation results in smaller changes in the ATP/ADP ratio for the same increase in VO₂ compared to direct activation of ATP production by ADP or Pi. The model also suggests that if NADH is the control mechanism, a significant increase (four-fold) in ATP/ADP ratio would occur with an 18-fold increase in VO₂ in contrast to Balaban’s finding that a five-fold increase in respiration increases ADP by only 0–20%. However, this model uses a phenomenologic description of ATP utilization and does not describe how Ca²⁺ is controlled by the demand. Korzeniewski designed an updated version that includes different ATP production regulators—ADP, CrP, and Ca²⁺ —and Ca²⁺ participating in a pull effect affecting both the dehydrogenases and F₁F_o-ATPase (thus incorporating both push and pull effects).¹⁷ He found that ATP levels alone cannot control respiration since there is no one-to-one relation between VO₂ and Pi. Regulation by CrP can explain theVO₂ Pi relation in isolated mitochondria, but fails to explain the contribution of proton leak to VO₂. The pull mechanism, controlled by Ca²⁺, cannot by itself fit the VO₂–Pi relationship, but can explain the tracking changes in NADH. On the other hand, the pull and push mechanisms controlled by Ca²⁺ acting together can explain the VO₂–Pi relation, as well as the contribution of proton leak to VO₂ and changes in NADH. However, Korzeniewski emphasized that theVO₂–Pi relation depends on the experimental model. For example, in Langendorff-perfused hearts, Pi increases in parallel with an increase in VO₂, while in the intact animal model Pi remains constant for the same increase in VO₂. Since Korzeniewski’s analysis to resolve the identity of the ATP regulator(s) was based on the in vivo VO₂–Pi relationship, different conclusions about the nature of this control mechanism to match supply and demand might be obtained using different model assumptions.

Noma’s lab⁵⁸ expanded Korzeniewski’s model¹⁷ of oxidative phosphorylation by adding ion channels, Ca²⁺ transients, and ATP consumption by several ATPases (troponin, SERCA, Na⁺/K⁺ pump). In this model, the total concentrations of adenine, Cr, and Pi in the cytoplasm are constant. The model was tested under conditions of anoxia, where the change in the ATP concentration fits experimental data. However, this model cannot differentiate between Ca²⁺ and Pi as regulators of ATP synthase and therefore lacks the ability to establish the identity of the supply and demand control mechanism.

Jafri’s lab has developed a mathematical model to explore the role of Ca²⁺ on energy production by the mitochondria.^59–61 Jafri combines a Ca²⁺ transient and metabolism model⁶¹ with Magnus and Keizer’s model of electron transport and ATP production.^62,63 While Ca²⁺ directly affects the dehydrogenases and F₁F_o-ATPase, it includes a phenomenologic description of ATP production by the F₁F_o-ATPase based on Balaban’s experiments.³ Furthermore, in Jaffry’s model the only source of ATP hydrolysis is the F₁F_o-ATPase. Although the model incorporates experimental Ca²⁺ transients and mitochondrial membrane potential, it predicts 5% changes in ATP and ADP during beat-to-beat regulation, which would be hard to detect experimentally. The current version of the model still lacks a physiologically relevant description of ATP utilization.⁵⁹

The O’Rourke lab has developed an extensive model integrating electrophysiology, contraction, and mitochondrial bioenergetics in ventricular myocytes and trabecula.^2,64 The model includes a description of the mitochondrial matrix and the cytosol. This work addresses two questions: Does Ca²⁺ affect both the “push” and “pull” mechanisms and can Pi regulate both mechanisms?² The model simulates experimental data of the response of NADH to the increase in stimulation frequency from 0.25 to 2 Hz in rat cardiac trabecula.⁶⁵ The NADH level is time-dependent and biphasic. When the stimulation frequency in the experiments increases, NADH levels display an initial transient undershoot followed later by an overshoot. Without the Ca²⁺ effect on respiration, NADH decreases, which is in contrast to published data.⁶⁵ By using only “push” theory, NADH levels produced by the model were lower than those determined experimentally.⁶⁵ By incorporating push and pull mechanisms, the mathematical model appears to be in better agreement with experimental data, although the authors admit that with an appropriately chosen set of parameter values they can produce the apparent results of matching supply and demand for either of the model cases. Therefore, they conclude that their model cannot strongly favor push-only over the push-and-pull mechanisms acting together. In an updated version of the model, O’Rourke suggests that the trend in NADH level depends on the identity of the controller of cardiac ATP supply–demand matching: if ATP is the controller, NADH decreased; if Ca²⁺ is the controller, NADH increased.² On the basis of the biphasic NADH response observed during electrical stimulation experiments (described above), because the simulation model shows that the Ca²⁺ control mechanism can explain only the increase in NADH level while the ATP control mechanism can produce only the decreasing phase, the authors conclude that a combination of both mechanisms is likely to exist in nature.⁶⁴

We have recently developed a model that couples cardiac metabolism with Ca²⁺ cycling and contractile myofilament energy utilization to emphasize regulation of both supply and demand by Ca²⁺.⁵⁶ The model incorporates the Zhou and colleagues model of cardiacmetabolism²⁹ with ATP consumption by the XBs,^66–68 the major ATP-consumer, and Ca²⁺ transients in the different compartments. It describes both a push and pull mechanism and explains the observed insignificant changes in Pi concentrations together with an increase in twitch force. Because of the lack of experimental data, the model uses phenomenologic equations to describe the synthesis of ATP by the F₁F_o-ATPase instead of separating the effect of push and pull by Ca²⁺ on F₁F_o-ATPase regulation. Further experimentation will permit us to more precisely separate push and pull effectors.

Summary

The heart, as an engine, has sophisticated mechanisms for converting fuel into mechanical work, that is, by the Ca²⁺-activated force-generation and shortening of contractile elements harnessing the energy of ATP to create the circulation of blood to supply oxygen to the organs. To maintain a constant energy supply to contract, the heart has local mechanisms that match supply to demand and the nature of these mechanisms was discussed in this review. While most evidence supports Ca²⁺ regulation of the push mechanism, predictions based on models without operational parallel pull mechanisms remain inadequate to explain key experimental findings. Thus, more experimental evidence will be necessary to establish whether or not the push and pull mechanisms work together to maintain the matching between ATP supply and demand in the working heart.