Carotid Bifurcation Hemodynamics In Older Adults: Effect Of Measured vs. Assumed Flow Waveform

Abstract

Recent work has illuminated differences in carotid artery blood flow rate dynamics of older vs. young adults. To what degree flow waveform shape, and indeed the use of measured vs. assumed flow rates, affects simulated hemodynamics of older adult carotid bifurcations has not been elucidated. Image-based computational fluid dynamics models of N=9 normal, older adult carotid bifurcations were reconstructed from magnetic resonance angiography. Subject-specific hemodynamics were computed by imposing each individual’s inlet and outlet flow rates measured by cine phase contrast MRI, or by imposing characteristic young and older adult flow waveform shapes adjusted to cycle-averaged flow rates measured or allometrically-scaled to the inlet and outlet areas. Despite appreciable differences in the measured vs. assumed flow conditions, the locations and extents of low wall shear stress (WSS) and elevated relative residence time (RRT) were broadly consistent; however, the extent of elevated oscillatory shear index (OSI) was substantially underestimated, more by the use of assumed cycle-averaged flow rates than the assumed flow waveform shape. For studies of individual vessels, use of a characteristic flow waveform shape is likely sufficient, with some benefit offered by scaling to measured cycle-averaged flow rates. For larger-scale studies of many vessels, ranking of cases according to presumed hemodynamic or geometric risk is robust to the assumed flow conditions.

INTRODUCTION

Studies over the past few decades have suggested that the genesis and progression of atherosclerosis are correlated with the wall biomechanical properties and hemodynamics. In particular, the disturbed flow environment, often characterized by low and oscillating wall shear stress, is thought to promote atherogenesis [1]. The carotid bifurcation is a widely studied vessel in this context, owing to its obvious clinical relevance and the relative ease of access by high-resolution medical imaging. In particular, the hemodynamics of carotid bifurcations are often now inferred from an image-based computational fluid dynamics (CFD) approach, whereby the lumen geometry is reconstructed from anatomic images [2]. In many cases, however, the individual flow rates are not available and so, typically, characteristic young adult flow waveforms, readily available in the literature [3–5] or easily acquired from volunteers, are commonly adopted as boundary conditions in these cases.

Recently, we demonstrated that blood flow rate waveform dynamics at the carotid arteries of older adults are significantly different than those of young adults [6]. The most evident difference is the presence, in the older adult case, of a strong secondary peak during early systolic deceleration, a phase typically associated with the formation of flow disturbances. In that large-scale studies of carotid atherosclerosis are beginning to focus on older subjects with early disease, it is reasonable to question the suitability of imposing a young adult flow waveform condition for the purposes of inferring an older individual’s exposure to disturbed flow. Moreover, such studies typically must make broad assumptions about the cycle-averaged flow rates in the absence of individual measurements. To what degree the assumed flow conditions affect the hemodynamic distributions in anatomically realistic carotid bifurcations is not clear. In the current study, we investigate whether a suitably-scaled representative young or older adult flow waveform can faithfully predict the disturbed flow in normal, older carotid bifurcations via image-based CFD approach, by comparison with disturbed flow computed using the measured, subject-specific flow waveforms.

METHODS

Study Subjects and MRI Protocols

Data for this study belongs to a subset of the ongoing VALIDATE (Vascular Aging - The Link That Bridges Age to Atherosclerosis) study, which seeks to non-invasively characterize vascular age and atherosclerotic burden in participants with "successful" vs. premature vascular aging. Nine subjects (58±8 yrs) without known coronary, cerebral, or peripheral artery disease and without carotid artery stenosis were selected for the current study. Their carotid bifurcation geometries and inlet/outlet velocities were scanned on a 1.5 Tesla scanner (Intera; Philips Medical Systems, Eindhoven, The Netherlands) using contrast-enhanced MR angiography (CEMRA) and phase-contrast (PCMRI) acquisitions, respectively. Written informed consent was obtained from all participants and approval for VALIDATE was given by the institutional review board. Approval for the use of participants’ anonymized images in the current study was given by the VALIDATE study center.

The CEMRA images were obtained using a 3D acquisition having the following scan parameters: 1-mm coronal slice thickness with 0.5-mm overlap; 20–23 cm square field-of-view; 256×200 acquisition matrix zero padded to 512×512. Retrospectively-gated cine PCMRI images of the through-plane velocity component were acquired transverse to the nominal long axis of the right common carotid artery (CCA) at a distance 1.5 cm proximal to the flow divider; and a separate acquisition 0.5 cm distal to the flow divider, through the internal and external carotid arteries (ICA and ECA, respectively). Scan parameters included: 5 mm slice thickness; 13 cm square field of view; 256×128 acquisition matrix zero padded to 256×256; and 32 uniformly-spaced time points per cardiac cycle.

Lumen Geometry Extraction

For each subject, the right carotid bifurcation lumen geometry was reconstructed from the CEMRA images using a semi-automated level set segmentation technique implemented within the open-source Vascular Modeling ToolKit (VMTK) [7]. Subsequently, CCA, ICA and ECA centerlines were determined automatically from the 3D models. Simultaneously, the maximally-inscribed spheres in the vessel branches were used to define the distances along the vessel branches from the bifurcation origin in units of sphere radii [8]. Then, the cross-sectional area of the CCA at exactly 5 sphere radii (CCA5) along the CCA centerline starting from the CCA origin was computed. Similarly, the cross-sectional area of ICA at 10 sphere radii (ICA10) from the ICA origin was also computed. These were later used to calculate the assumed cycle-averaged flow rates required for scaling the characteristic young or older adult waveform shapes.

Flow Waveform Boundary Conditions

Flow waveforms for the CCA, ICA and ECA were extracted from the respective PCMRI data as described previously [4]. Owing to the effects of compliance, small branches or errors and uncertainties in the PCMRI measurements, it is possible for the instantaneous inflow (CCA) and outflow (ICA+ECA) rates not to match exactly [6]. To ensure instantaneous mass conservation for the rigid CFD models, we chose to reset the instantaneous ICA and ECA flow rates by scaling the instantaneous CCA flow rate by the instantaneous ICA:ECA flow division.

To investigate the effect of waveform shape on the hemodynamics, we considered four different waveform sets as boundary conditions for each bifurcation geometry (Table 1). The first set, denoted “Young”, represents the young and healthy adult flow waveform shape typically used for CFD simulations of the carotid bifurcation. For this waveform set, we adopted the flow waveform shapes proposed by Lee et al. [8]. The second set, denoted “Older”, represents a typical older, healthy adult [6]. For both Young and Older waveforms, the periods were set to 70 bpm and the cycle-averaged flow rates for the CCA and ICA were allometrically-scaled by the ratios of the CCA5 and ICA10 areas to the respective averages over the nine subjects, as described previously [8]. The characteristic and subject-specific CCA waveform are shown in Figure 1.

Table 1.

Details of waveform sets used as boundary conditions in CFD simulations

ID	Waveform Shape	Cycle-average Flow Rate	Heart Rate
Young	Young	Scaled	70 bpm
Older	Older	Scaled	70 bpm
Older+	Older	Measured	Measured
Truth	Measured	Measured	Measured

Figure 1.

Measured flow waveforms at the CCA for all nine subjects (dotted lines) compared to characteristic young adult (green/light solid line) and older adult (blue/dark solid line) waveforms. One potential outlier (Subject 4), exhibiting a highly damped waveform, is shown as a magenta dashed line.

To separate the influence of the assumed flow waveform shape from assumptions regarding the cycle-averaged flow rates, a third set of flow boundary conditions, denoted “Older+”, was prescribed by scaling the characteristic older adult flow waveform shape according to the period and cycle-averaged flow rate measured for that individual. The last set, denoted “Truth”, was the measured, subject-specific waveforms described above. These four different waveform boundary condition sets, summarized in Table 1, were used to impose velocity boundary conditions for the subsequent CFD simulations.

CFD Simulations

The CFD simulations were performed using previously validated in-house algorithms. Quadratic tetrahedral-element meshes were generated by ICEM-CFD (ANSYS Inc.; Canonsburg, PA, U.S.A) with node spacing of 0.1–0.2 mm, which was previously shown to successfully resolve wall shear stresses at normal carotid bifurcation geometries [9]. Fully developed, pulsatile velocity profile boundary conditions were imposed at the CCA inlet and ICA outlet, based on the respective waveforms; traction-free boundary conditions were imposed at the ECA outlet. Rigid walls and constant blood viscosity of 0.035 cm²/s were assumed for all models.

The CFD simulations were carried out using up to 4800 time steps per cardiac cycle, and at least 3 cycles were simulated to damp initial transients. For each CFD model, we then computed the surface distributions of time-averaged wall shear stress magnitude (WSS), oscillatory shear index (OSI) and relative residence time (RRT) [10]. WSS and RRT values were normalized by their nominal values at the CCA5 location.

Scalar Metrics of Disturbed Flow

As proposed by Lee et al. [8], for a given model the disturbed flow was quantified as its surface area (bounded by CCA3, ICA5 and ECA2) exposed to WSS ≤ 0.481, RRT ≥ 2.944, or OSI ≥ 0.145, these thresholds corresponding to the upper (for WSS, lower) quintiles based on 50 cases. Following Lee et al., we normalized the areas exposed to the disturbed flow quantities by the total surface of the respective model (also bounded by CCA3 and ICA5 and ECA2). In this way each case was assigned a scalar value, hereafter denoted SA_WSS, SA_RRT, or SA_OSI, representing the proportion of its surface exposed to disturbed flow.

RESULTS

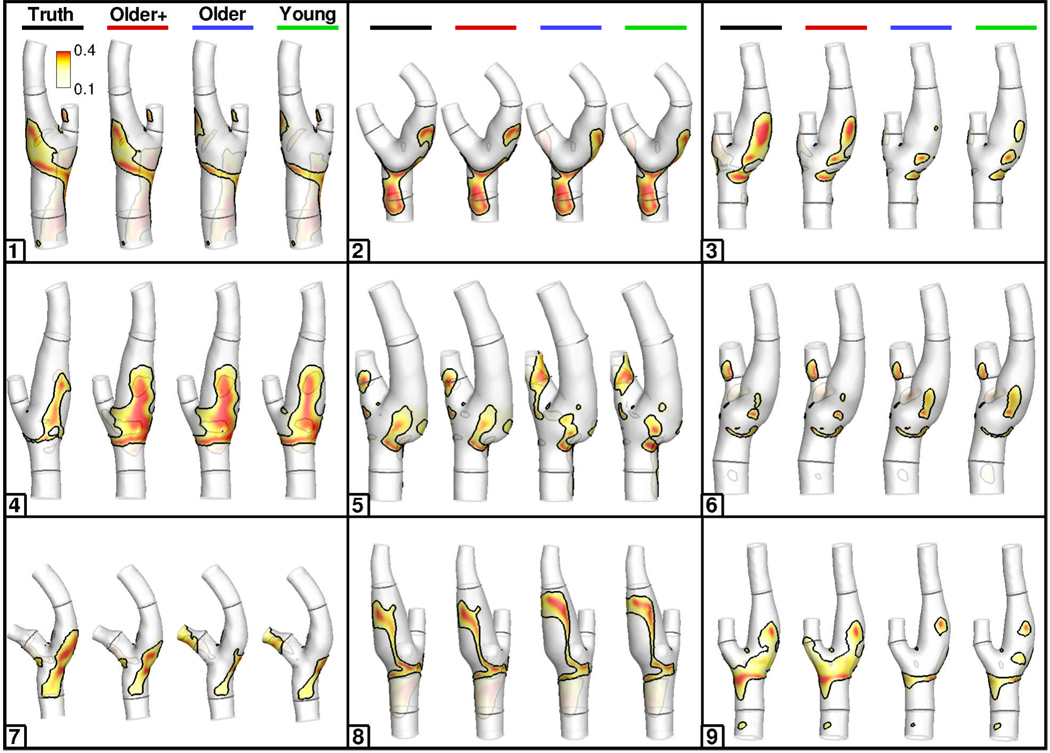
Cycle-averaged flow rates measured at the CCA, ICA and ECA were 6.91±1.23, 4.17±0.93 and 1.87±0.66 mL/s, respectively, for the N=9 subjects. After adjusting the ICA and ECA flow rates to ensure inlet-outlet mass conservation as described in the Methods, the root-mean-square errors (RMSE) between the adjusted-measured and allometrically-scaled cycle-averaged flow rates were 1.55, 1.96 and 0.63 mL/s, respectively. Despite such overall differences, Figure 2 shows that OSI distributions derived using the four different waveform sets were broadly similar within individual bifurcation models, at least in the context of differences between individuals. Compared to the models based on the subject-specific waveforms, the locations, if not always the extents, of disturbed flow were well preserved in the models based on the assumed flow waveform shapes. Overall, there appeared to be little difference between OSI distributions for corresponding Young vs. Older cases, and for Older+ vs. Truth cases. Similar trends were also observed for WSS and RRT distributions (not shown).

Figure 2.

Colour-coded distributions of OSI, for all nine subjects, for the various waveform boundary conditions indicated at the top row. Black contour lines on each surface identify the area exposed to OSI above its 80^th percentile value, as described in the Methods. Geometries are clipped at the CCA5, ICA10 and ECA5 locations used to scale the flow rates. CCA3, ICA5 and ECA2 locations, used to bound the surface for disturbed flow calculations, are shown in dark grey.

To quantify the effects of different waveform approximations on the computed disturbed flow quantities, we plotted linear regressions of SA_WSS, SA_RRT and SA_OSI derived from the assumed waveform conditions vs. those from the subject-specific (Truth) conditions (Figure 3). The slopes and correlation coefficients of these regressions are shown in Table 2. For SA_WSS and SA_RRT the correlation coefficients for all waveform approximations were strong. The slopes suggested a tendency for the assumed flow conditions to under-predict the actual disturbed flow exposure; however, none of these slopes was significantly different from unity, or significantly different among Young, Older and Older+ waveforms sets. In marked contrast, SA_OSI was found to be poorly predicted when using either the Young or Older waveform sets. For the Older+ case the correlation with the Truth data was weak, and the slope of 0.43, while not significantly different from unity, suggested a greater than 50% under-prediction of SA_OSI. For all disturbed flow metrics, there were negligible quantitative differences between corresponding SA exposures for the Young vs. Older waveform shapes, at least relative to differences due to the use of assumed vs. measured cycle-averaged flow rates (i.e., Older vs. Older+ cases).

Figure 3.

Surface area (SA) exposed to various disturbed flow indicators (WSS, RRT, OSI), derived from assumed-waveform models and compared against the corresponding SA from the subject-specific-waveform models. Coloured lines are linear regressions through the respectively-coloured data points. The black dotted line represents the line of unity.

Table 2.

Comparison of slopes and R² from linear regressions of different disturbed flow indicators based on assumed waveform sets vs. subject-specific (Truth) waveforms.

	R2			Slope
Truth vs.	WSS	RRT	OSI	WSS	RRT	OSI
Older+	0.76	0.98	0.21	0.67	0.96	0.43
Older	0.83	0.72	0.00	0.87	0.97	−0.02
Young	0.81	0.68	0.00	0.95	0.94	0.02

DISCUSSION

Summary and Implications of Findings

Our findings demonstrate that lumen surface exposure to disturbed flow in older carotid bifurcations can be captured, at least qualitatively, using allometrically-scaled characteristic flow waveforms as boundary conditions. Better quantitative agreement with the nominally true subject-specific hemodynamics can be achieved by scaling a characteristic waveform shape to measured cycle-averaged flow rates as CFD boundary conditions. When assuming cycle-averaged flow rates via a scaling law, there appears to be little benefit to using an “age-appropriate” characteristic waveform shape.

Among the three metrics of disturbed flow, RRT was most robust to the choice of flow rate boundary conditions, at least according to the linear regressions against the Truth case. On the other hand, those data suggest that exposure to elevated OSI cannot be reliably determined without using subject-specific flow rates and waveform shape. It is worth noting, however, that after excluding one of the cases (Subject 4) presenting with an unphysiologically damped flow waveform shape (possibly due to imaging complications), R² for the Older+ vs. Truth regression improved from 0.21 to 0.69, and slope from 0.43 to 0.73. Regressions for the Older and Young waveform cases vs. Truth did not improve significantly. Taken together, these observations would suggest that OSI is more sensitive to errors in the cycle-averaged flow rate rather than errors in the waveform shape itself.

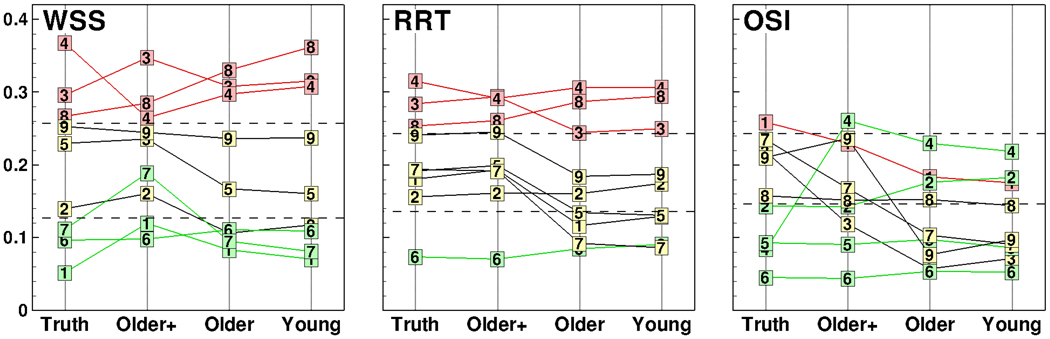
While use of assumed vs. measured flow boundary conditions may have non-negligible impact on predictions of disturbed flow for individual cases, Figure 2 suggests that, even for OSI, differences in the appearance of disturbed flow between individuals might be well preserved irrespective of the assumed flow conditions, which has important implications for large scale studies that are more interested in relative rather than absolute values of hemodynamics “risk”. To see whether this is indeed the case, in Figure 4, we show the bifurcation models ranked according to the various disturbed flow metrics computed from the different waveform sets, and sub-divided into categories of low, medium and high “risk” of disturbed flow exposure, where the low and high “risk” correspond, respectively, to the lower and upper tertiles derived from a larger sample of N=50 cases [8].

Figure 4.

Surface area (SA) exposed to various disturbed flow indicators (WSS, RRT, OSI), as a function of the waveform boundary condition used. The dashed lines separate SA (vertical axis) into lower, middle and upper tertiles according to the distributions of exposure levels found by Lee et al. [8]. Symbols denote the subject number, and green, yellow and red are used to highlight Truth cases falling into the lower, middle and upper tertiles, respectively

Comparing the “risk” ranking computed using the commonly adopted young adult waveform shape and the subject-specific waveforms (Truth), we found multiple crossovers among the two sets of models, indicating that the precise order of “risk” changed when different waveform shapes were used to compute the disturbed flow exposure. This was less evident in going from the young to older adult characteristic waveform, and most evident when going from Older to Older+ conditions, confirming the relative importance of cycle-averaged flow rates used to scale the waveforms, rather than the waveform shape itself. Nevertheless, the associated “risk” category of disturbed flow exposure in individual cases was largely unaffected by the choice of flow condition, for SA_WSS and SA_RRT at least. Reflecting earlier observations, the rankings for SA_OSI were more strongly affected, even after accounting for the outlier Subject 4. It is worth noting, however, that in our sample of nine subjects the mean SA_OSI was 0.16 for the Truth conditions, significantly less than the expected value of 0.2. On the other hand, the means of both SA_WSS (0.20) and SA_RRT (0.21) were not significantly different from the expected value, indicating that the sensitivity of OSI to assumed vs. measured flow conditions may have reflected, at least in part, the fact that these nine cases tended to have less OSI to begin with.

Putting all of this into a practical context, it seems reasonable to categorize nominal hemodynamic “risk” for large-scale studies of carotid bifurcations by adopting characteristic flow waveforms to compute the disturbed flow exposure, as was done by Lee et al. [8]. For hemodynamic investigations of individual cases, better agreement with subject-specific hemodynamics can be achieved by scaling the characteristic waveforms to the subject-specific cycle-averaged flow rates, which may be clinically accessible through non-invasive and relatively inexpensive measurement techniques such as Doppler ultrasound. However, the underlying assumption of fully-developed flow in converting Doppler velocities to flow rates might result in measurement errors approaching those from the use of allometric scaling [11, 12]. Having said this, bifurcation geometry is clearly the primary factor in determining disturbed flow exposure; cycle-averaged flow rate and then waveform shape are secondary factors.

To this end, previous findings from our laboratory suggested that the exposure of a young adult carotid bifurcation to disturbed flow could be predicted by a relatively simple geometrical relationship [8]: SA∝AR1-CxTortuosity, where AR1 is ratio of the total cross-sectional area at ICA1 and ECA1 to the cross-sectional area at CCA3, and C is a positive constant in the range of 19 to 27, depending on the disturbed flow indicator. In that study flow conditions were assumed to correspond to the Young case considered here. To investigate if these flow conditions might have biased the findings of [8], we fitted SA of different waveform sets to the computed AR1-CxTortuosity geometry factor by taking C=23 (i.e., average of 19 and 27) and tabulated their correlation coefficients in Table 3. Compared with the previous study that utilized young adult waveforms with N=50 young adult bifurcations, the correlation coefficients derived from our N=9 older subjects with the various flow conditions were broadly similar, especially considering the different sample sizes and ages of the subjects. A notable exception was R² = 0.031 for SA_OSI for the Truth waveform conditions; however, after excluding the one potential outlier case, R² = 0.292. These findings support the idea that surrogate geometric factors predicting disturbed flow may be investigated using assumed flow boundary conditions.

Table 3.

Comparison of R² from linear regressions of different disturbed flow indicators vs. a proposed geometric risk factor (AR – 23xTortuosity [8]).

AR-23xTortuosity vs.	Truth	Older+	Older	Young	Lee et al. [8]
SAWSS	0.358	0.266	0.476	0.446	0.343
SARRT	0.629	0.595	0.559	0.546	0.384
SAOSI	0.031	0.451	0.237	0.238	0.335

It has been reported that, for the older adult characteristic flow waveforms, the augmented second peak correlates positively with age and is significantly higher than in the young adult characteristic waveforms [6]. At the same time, older adult bifurcations also exhibit significantly greater interindividual geometric variations than the young adult bifurcations [13]. It is unclear if such age-dependent waveform dynamics and bifurcation geometries encourage vascular lesions in atherosclerosis-prone older bifurcations, such as perhaps amplifying or suppressing specific shear stress frequencies that associate with inflammatory response in the endothelium [14]. The negligible hemodynamic differences between Young and Older waveform cases suggest that, at least for the conventional disturbed flow indicators considered in the present study, age-related changes in waveform shape alone would do little to alter a vessel’s atherosusceptibility.

Potential Limitations

Although “disturbed flow” is suggested to play an important role in the initiation and progression of atherosclerotic diseases, it has not been clearly defined. The choice of using WSS, RRT and OSI to depict risk of disturbed flow exposure in current study was based on a previous comprehensive study of various indicators of disturbed flow at the normal carotid bifurcation [10]. Other possible hemodynamic parameters may have closer mechanistic links in individual biological responses to the disturbed flow are not examined in the current context. The influence of cycle-averaged flow rate and especially waveform shape may also be amplified at certain instants in time, such as late systolic deceleration; however, the physiological relevance of such instantaneous vs. temporally-integrated hemodynamics remains unclear.

In the current study, we corrected the measured outlet flow rates by scaling the CCA flow according to the instantaneous ICA:ECA flow to ensure mass conservation. This need to resolve instantaneous flow discrepancies was due to the assumption of rigid wall in our CFD simulations. It is, however, possible that the distensible arteries indeed produce instantaneous flow mismatches at the bifurcation. Such phenomena deserve further investigation. Moreover, our method of resolving the flow balance is one of many possible variations; other possibilities such as rescaling the CCA flow as the sum of the measured ICA and ECA flow can potentially be adopted as boundary conditions.

Differences between measured and allometrically-scaled cycle-averaged flow rates approached 40% in some cases. One of the main factors leading to such discrepancy could be the choice of the particular cross-sectional areas used in the current study, viz. CCA5, ICA10. Flow rates through long conductance arteries like the carotids are, if anything, reflected by the more uniform, distal dimensions of the branches [15]. Closer to the bifurcation the dimensions become more variable, and so a simple relationship between flow rates and the proximal vessel areas may be difficult to find. Nonetheless, bifurcation geometry remains the most influential factor in hemodynamics modeling and so, as discussed previously, the choice of scaling law may be of strict relevance only for studies of individual bifurcations.

Lastly, in addition to bifurcation geometry and flow waveform shapes, other factors such as the reconstruction errors/uncertainties [16, 17], inlet velocity profile [9, 18], Non-Newtonian blood properties [19, 20] and wall distensibility [21, 22] also impact the bifurcation hemodynamics, to a similar or perhaps greater degree to what the present study found for flow conditions.

CONCLUSIONS

When subject-specific flow conditions are unavailable, reasonable predictions of an individual carotid bifurcation’s exposure to low WSS or elevated RRT can be obtained in most cases by using a suitably-scaled characteristic waveform; however, the characteristics of OSI are more sensitive to errors in the prescribed flow rates. For large-scale studies of carotid bifurcation hemodynamics, where such flow measurements may be difficult or impossible to acquire, findings are likely to be insensitive to the choice of flow conditions given the primary importance of lumen geometry in determining the burden of disturbed flow. We therefore reiterate the recommendation of Moyle et al. [9] that, for image-based CFD studies of the carotid bifurcation, priority be given to more accurate and more precise geometric imaging and reconstruction.

Abbreviations

CCA

Common Carotid Artery

CFD

Computational Fluid Dynamics

ECA

External Carotid Artery

ICA

Internal Carotid Artery

OSI

Oscillatory Shear Index

RRT

Relative Residence Time

SA

Surface Area

3D

Three-dimensional

WSS

Cycle-averaged Wall Shear Stress Magnitude