Optimized Inversion Recovery Sequences for Quantitative T₁ and Magnetization Transfer Imaging

Abstract

Inversion recovery sequences that vary the inversion time (t_i) have been employed to determine T₁ and, more recently, quantitative magnetization transfer (qMT) parameters. Specifically, in previous work, the inversion recovery pulse sequences varied t_i only, while maintaining a constant delay (t_d) between repetitions. T₁ values were determined by fitting to an exponential function, and qMT parameters were then determined by fitting to a bi-exponential function with an approximate solution. In the current study, new protocols are employed, which vary both t_i and t_d and fit the data with minimal approximations. Cramer-Rao lower bounds (CRLB) are calculated to search for acquisition schemes that will maximize the precision efficiencies of T₁ and qMT parameters. This approach is supported by Monte Carlo simulations. Measurements on MnCl₂ samples verified the optimal T₁ schemes. The optimal qMT schemes are confirmed by measurements on a series of cross linked bovine serum albumin (BSA) phantoms of varying concentrations. The effects of varying the number of sampling data points are also explored, and a rapid acquisition scheme is demonstrated in vivo. These new optimized quantitative imaging methods provide an improved means for determining T₁ and MT parameter values compared to previous inversion recovery based methods.

Introduction

Magnetization Transfer (MT), or spin exchange between protons in different tissue pools, can serve as a contrast mechanism in biological systems. MT between free water and a broad, immobile pool of protons on macromolecules, was first demonstrated by Wolff and Balaban (1), who measured the equilibrium magnetization (M_s) of water protons after applying continuous irradiation. Subsequently, Henkelman et al. (2) developed a two-pool model and performed measurements on agar gels. By varying the RF offset frequency and amplitude; they determined the relaxation and exchange rates of the two proton pools. This determination of the underlying sample parameters is referred to as quantitative magnetization transfer (qMT).

Several qMT imaging methods have been developed. Sled and Pike (3,4) extended the technique of Henkelman et al. to pulsed-MT, in which off-resonance saturation pulses are interleaved with on-resonance excitation pulses. Ramani et al. (5) combined the method of Sled and Pike with an analysis similar to Henkelman et al. Gloor et al. (6) developed a qMT imaging method based on balanced steady state free precession (SSFP), while Ropele et al. (7) developed a method based on stimulated echoes. Gochberg et al. (8-10) developed a selective-inversion-recovery (SIR) technique, a qMT imaging method based on measuring the transient response to an RF pulse that selectively inverts the free water protons. MT induces bi-exponential recovery of longitudinal magnetization in most tissue types, including in vitro collagen (11,12), muscle (11), cartilage (13) and lung (14), and in vivo white matter (WM), grey matter (GM) and muscle (10). Prantner et al. (15) examined and dismissed non-MT explanations for this bi-exponential in brain matter. In the most recent version of the SIR method (10), a fast-spin-echo (FSE) readout is applied, which leaves both the liquid and solid proton pools saturated and therefore facilitates determination of qMT parameters using shorter repetition times.

The precision and accuracy of the estimates of the qMT parameters depend on several experimental factors, such as the MT pulse power (ω₁) and offset frequency (Δ) for pulsed-MT, and the inversion recovery time (t_i) and pre-delay time (t_d) values for SIR-FSE. In most published MT protocols, the set of sampling points is selected empirically. Cramer-Rao lower bounds (CRLB) (16) provide a general approach to assess this dependence on acquisition parameters, by setting a lower limit on the variance of any parameter estimate based on model fitting. This method has been used to optimize acquisition schemes for T₁ measurements with constrained scan time (17), T₂ measurements (18), diffusion coefficients (19), and echo spacing for multi-echo imaging (20). In Sled and Pike’s pulsed-MT work (4), they used only two values of ω₁, each with a range of Δ. Based on Ramani’s model (5), the pulsed-MT technique was optimized by Cercignani et al. (21) by calculating the CRLB to obtain optimal acquisition protocols.

For the SIR-FSE technique (10), Gochberg et al. used a constant t_d and varied t_i only. The experimental data were then fitted to a bi-exponential equation to determine first-order approximations of the qMT parameters. The current paper focuses on the optimization of this technique (10), introduces a new data analysis method as part of this optimization, and employs a new protocol that varies both t_i and t_d and fits the data with minimal approximations. CRLB are calculated to search for the variations in both t_i and t_d that will maximize the precision efficiency. The optimal schemes are supported by Monte Carlo simulations, and confirmed by measurements on BSA phantoms. It is further demonstrated that, in practice, only five sampling points are required to determine qMT parameters and is confirmed with in vivo rat brain measurements.

SIR-FSE is essentially an inversion recovery (IR) method with the assumption of bi-exponential recovery due to MT. Independently varying t_i and t_d also improves the precision efficiency of simple T₁ measurements, when assuming a single exponential recovery. While this method is often replaced by the more rapid single shot (22,23) and variable-flip-angle (VFA) methods (24-26), we include a variable t_i and t_d analysis of T₁ here for its inherent interest and as an introduction to the more complex qMT case.

Theory and Methods

IR Imaging Sequence

Conventionally, T₁ is determined by using an IR sequence (similar to Figure 1) with t_d ≥ 5 T₁, during which the magnetization returns to its equilibrium state before the next sequence repetition. Previous work has optimized T₁ measurement efficiency using constant t_d or constant repetition time (TR) (17). Here we will take a more general approach, by varying both t_i and t_d independently without constraint. For an IR with a spin-echo (SE) or fast-spin-echo (FSE) readout, the measured signal is:

$$S=M_0[S_f(1-e^{-t_d∕T_1})e^{-t_i∕T_1}+1-e^{-t_i∕T_1}]$$ [1]

where M₀ is the magnetization of the equilibrium state, and S_f (≈ −1) quantifies the effect of the inversion pulse.

Figure 1.

The SIR-FSE pulse sequence. The quantity t_d is the pre-delay time and t_i is the inversion recovery time. In this work, the first eight echoes are taken for data acquisition, and the next eight echoes were taken as dummy echoes to ensure the assumption of zero Mz magnetization of both pools after the last 180° pulse. A simulation of this sequence is presented in Ref. (10).

SIR-FSE qMT Imaging Sequence

The SIR-FSE pulse sequence (10) is illustrated in Figure 1. In order to model the signal when TR is short, an essential insight is that at the end of each repetition, both the macromolecular and free water pools have zero z-magnetization. The assumption has been discussed numerically and verified previously (10).

The qMT data analysis is based on a two-pool model. The coupling between the pools is modeled by adding coupling terms to the Bloch equations, as given in (9,10):

$$\begin{array}{c}\hfill \frac{d}{dt}\frac{M_f\left(t\right)}{M_{f\infty }}=-R_{1f}\left(\frac{M_f\left(t\right)}{M_{f\infty }}-1\right)-k_{fm}\left(\frac{M_f\left(t\right)}{M_{f\infty }}-\frac{M_m\left(t\right)}{M_{m\infty }}\right),\hfill \\ \hfill \frac{d}{dt}\frac{M_m\left(t\right)}{M_{m\infty }}=-R_{1m}\left(\frac{M_m\left(t\right)}{M_{m\infty }}-1\right)-k_{mf}\left(\frac{M_m\left(t\right)}{M_{m\infty }}-\frac{M_f\left(t\right)}{M_{f\infty }}\right)\hfill \end{array}$$ [2]

The subscripts f and m refer to the free and macromolecular proton pools. M_f(t) and M_m(t) are the longitudinal magnetizations at time t, whose equilibrium values are M_f∞ and M_m∞. R_1f and R_1m are the longitudinal relaxation rates of the free and macromolecular pools when there is no MT between them, and k_fm and k_mf are the rates of magnetization transfer between them. The pool size ratio (p_m/p_f) is defined by k_fm/k_mf. The recovery of the magnetization of the free pool is described by a bi-exponential decay function when there are no RF pulses:

$$\frac{M_f\left(t\right)}{M_{f\infty }}=b_f^{+}{e}^{-R_1^{+}t}+b_f^{-}{e}^{-R_1^{-}t}+1$$ [3]

where

$$\begin{array}{c}2R_1^{\pm }=R_{1f}+R_{1m}+k_{fm}+k_{mf}\pm \sqrt{(R_{1f}-R_{1m}+k_{fm}-k_{mf})+4k_{fm}{k}_{mf}}\hfill \\ b_f^{\pm }=\pm \frac{\left[\frac{M_f\left(0\right)}{M_{f\infty }}-1\right](R_{1f}-R_1^{\pm })+\left[\frac{M_f\left(0\right)}{M_{f\infty }}-\frac{M_m\left(0\right)}{M_{m\infty }}\right]k_{fm}}{R_1^{+}-R_1^{-}}\hfill \end{array}$$ [4]

where $R_1^{+}$ and $R_1^{-}$ are the fast and slow recovery rates, respectively. The magnetization of the macromolecular pool is described by a bi-exponential equation as well, by exchanging f and m subscripts in Eqs. [3] and [4].

Applying Eqs. [3] and [4] to each free evolution period gives the signal as function of the qMT parameters, allowing us to investigate the problem and fit the qMT parameters without taking the first-order approximations utilized previously (8-10). Specifically, both pools have zero z-magnetization at the end of the FSE train, their magnetization at the end of t_d is written as

$$\begin{array}{c}\frac{M_f\left(t_d^{-}\right)}{M_{f\infty }}=-\frac{R_{1f}-R_1^{-}}{R_1^{+}-R_1^{-}}{e}^{-R_1^{+}{t}_d}+\frac{R_{1f}-R_1^{+}}{R_1^{+}-R_1^{-}}{e}^{-R_1^{-}{t}_d}+1,\hfill \\ \frac{M_m\left(t_d^{-}\right)}{M_{m\infty }}=-\frac{R_{1m}-R_1^{-}}{R_1^{+}-R_1^{-}}{e}^{-R_1^{+}{t}_d}+\frac{R_{1m}-R_1^{+}}{R_1^{+}-R_1^{-}}{e}^{-R_1^{-}{t}_d}+1\hfill \end{array}$$ [5]

The effect of the inversion pulse is,

$$\begin{array}{c}\frac{M_f\left(t_d^{+}\right)}{M_{f\infty }}=S_f\frac{M_f\left(t_d^{-}\right)}{M_{f\infty }}\hfill \\ \frac{M_m\left(t_d^{+}\right)}{M_{m\infty }}=S_m\frac{M_m\left(t_d^{-}\right)}{M_{m\infty }}\hfill \end{array}$$ [6]

where S_f and S_m are the inversion coefficients of the free and macromolecular pools, and $t_d^{-}$ and $t_d^{+}$ are the time just before and after the inversion pulse, respectively.

The model discussed above contains seven parameters: R_1f, R_1m, p_m/p_f, k_mf (k_fm is equal to k_mf × p_m/p_f), S_f, S_m, and M_f∞. Among these parameters, the signal dependencies on S_m and R_1m are weak, as shown below. The weak dependence on R_1m is also the case in the pulsed saturation sequence (3-5,21). In this work, R_1m is set to be equal to R_1f for data analysis. Previous results (10) calculated an S_m of 0.83 ± 0.07 from numerical simulations, for a 1-ms hard inversion pulse on a solid pool with a Gaussian lineshape and a T₂ between 10 μs and 20 μs. There are then five remaining qMT parameters to fit: R_1f, p_m/p_f, k_mf, S_f and M_f∞. S_f is expected to be −1, but due to B₀ and B₁ inhomogeneities, it has to be fit from experimental data. Finally, combining Eqns. [3-6] for each time period gives a signal function, which we use to fit the qMT parameters directly without first-order approximations.

CRLB Theory

The optimization technique presented in this work is similar to that of Cercignani et al. (21), but is applied to a different pulse sequence and includes acquisition time effects when calculating parameter precisions. For a set of particular qMT parameters, the CRLB derived objective function is:

$$V=\left({\sum }_{j=1}^Q{\left[J^{-1}\right]}_{jj}{p}_j^{-2}\right)\times T_{\text{cost}}\left(\text{scheme}\right)$$ [7]

where Q is the number of fitted parameters, and p_j is the j^th parameter. T_cost(scheme) is given by:

$$T_{\text{cost}}\left(\text{scheme}\right)={\sum }_{n=1}^N(t_{i,n}+t_{d,n}+t_{fse})$$ [8]

where N is the number of sampling points, t_fse is the length of the FSE train, and t_i,n and t_d,n are the nth t_i and t_d values. The Fisher information matrix J is defined by its jk^th element

$$J_{jk}=\frac{1}{{\sigma }^2}\sum _{n=1}^N\left(\frac{\partial S(p_1,\cdots ,p_Q;x_n)}{\partial p_j}\frac{\partial S(p_1,\cdots ,p_Q;x_n)}{\partial p_k}\right)$$ [9]

where p_j is the j^th parameter, x are the (t_i, t_d) sampling points, and S are the signal function. The standard deviation (SD) of noise, σ is assumed to be independent of x. As pointed out in (21), the essence of the term ${\sum }_{j=1}^Q{\left[J^{-1}\right]}_{jj}{p}_j^{-2}$ in Eq. [7] is $\sum {\sigma }_j^2∕p_j^2$ where ${\sigma }_j^2$ is the variance of the parameter p_j. By including the time cost term in Eq. [7], the objective function becomes essentially the inverse of precision efficiency (precision-per-unit-time (27)). The optimization process yields the maximum precision efficiency, by searching for the minimum value of the objective function.

For optimization of heterogeneous samples, CRLB objective functions are constructed in a similar form as in (21):

$$V_{\max }=\underset{l}{\max }{\left\{{\sum }_{i=1}^Q{\left[J_l^{-1}\right]}_{ii}{p}_{il}^{-2}\right\}}^{\ast }{T}_{\text{cost}}\left(\text{scheme}\right)$$ [10]

Where l indexes parameter sets that characterize different tissues_. Minimizing V_max by varying the sample points x would maximize the precision efficiency for the worst combination of parameters.

Optimization Technique

The optimization process searches for the optimal acquisition schemes, x₁, …, x_N that minimize V and V_max defined in Eqs. [7] and [10]. A simulated annealing algorithm (28) was implemented in Matlab 2008b (The Mathworks, Natick, MA, USA) to search for the optimal acquisition schemes. It evaluates 500 objective functions at each temperature T by randomly varying x₁, …, x_N, i.e., all t_i and t_d values. The objective function is randomly perturbed by using a Metropolis algorithm (29), which allows uphill transitions and increases the possibility of reaching a global minimum. The temperature decreases according to the annealing schedule

$$T(n+1)=T\left(n\right)\times (1-\epsilon )$$ [11]

where 0 < ε << 1, until it reaches the final temperature. The initial and final temperatures are set as 100 and 0.001. To reduce the effects of local minima, the optimization is repeated from several random starting points. The scheme with a minimum objective function value is selected. The simulated annealing does not guarantee a global minimum, but we do not expect dramatic improvement in the objective function values.

By utilizing this technique, a series of optimization processes were performed. We optimized T₁ precision efficiency (using Eqs. [1, 7-10]) by varying all t_i and a single t_d values, and by varying all t_i and t_d values. A set of typical parameters values are: M_f = 1, T₁ = 1, and S_f = −1. The optimization of parameter ranges are: M₀ ∈ [0.5, 1.5], T₁ ∈ [0.5, 1.5], and S_f ∈ [−0.85, −1].

For qMT precision efficiency optimization, we searched for optimal acquisition schemes that have approximately the same total acquisition time as the original scheme given in (10), by repeating the optimization process while varying the number of sampling points and then selecting the scheme that most closely matches the total acquisition time of the original. A set of typical qMT parameters (roughly those of WM) are: R_1f = 0.5 Hz, p_m/p_f = 0.10, k_mf = 30 Hz, S_f = −0.95, and M_f∞ = 1.0, with R_1m = 0.5 Hz and S_m = 0.83. R_1f and R_1m values are smaller than the values presented in (9) because the measurements in this work are performed at higher magnetic field strengths. M_f∞ is simply set to 1.0 since it is only a scaling factor. The optimization of parameter ranges are: R_1f ∈ [0.4, 1.0], p_m/p_f ∈ [0.05, 0.20], k_mf ∈ [20, 40], S_f ∈ [−1.0, −0.9], and M_f∞ ∈ [0.6, 1.5]. This process takes more time because it has to calculate 33 parameter combination sets (2⁵ = 32 combinations of the listed parameter values plus one set of midpoint values). The lower limit of t_i and t_d are set as 4 ms and 10 ms, respectively. These parameter ranges encompass those of the (WM) and GM (10), so the optimal schemes are directly applicable to in vivo brain measurements.

Imaging methods

In the SIR-FSE sequence diagrammed in Figure 1, we applied 16 refocusing pulses with 10-ms spacing. We acquired data only during the first eight echoes, applying an additional eight pulses in order to ensure zero z-magnetization in both the free water and macromolecular pools at the end of the echo train. The initial inversion pulse is a 1-ms 180° hard pulse. The 90° and 180° refocusing pulses are 1-ms 5-lobe sinc pulses, with time bandwidth product (TBW) of 5.92 and 4.44, respectively. For each measurement, two dummy scans were applied and four or eight acquisitions were averaged, with phase cycling of the 90° and acquisition, but no cycling of the initial inversion pulse (in order to destroy residual transverse magnetization). Gradient spoilers were also applied after the inversion pulse.

T₁ measurements were made on a 9.4 T Varian system with a 38-mm litz coil. MnCl₂ samples of 0.058 mM and 0.116 mM were prepared. Images were acquired with a FOV of 28 × 28 mm², slice thickness of 2 mm, and data matrix of 32 × 32. A conventional scheme, with a long t_d of 6 s, and ten logarithmic-spaced t_i values varied between 1 and 6 s, was applied, with four acquisitions averaged. In addition, eight optimized schemes were developed and applied. Four of the schemes were optimized for M₀ = 1, T₁ = 1 s, and S_f = −1, and four for the parameter ranges M₀ ∈ [0.5, 1.5], T₁ ∈ [0.5, 1.5], and S_f ∈ [−0.85, −1]. Each set of four consisted of one optimization of t_i values with a single t_d of 1 s, and three optimizations where both t_i and t_d were allowed to vary amongst 10, 5, or 3 values. For ten-point optimal schemes, four acquisitions were averaged, while for five- and three-point schemes, eight acquisitions were averaged, to achieve roughly similar SNRs for a comparison.

A series of bovine serum albumin (BSA) samples served as test phantoms for the qMT measurements. The BSA samples have percent weights of 10, 15, 20, and 25, with corresponding BSA to water ratios of 0.11, 0.18, 0.25, and 0.33. An additional sample of 15% BSA with 0.05 mM MnCl₂ was measured as well in order to separate MT from relaxation effects. All samples were cross-linked using 25% glutaraldehyde. Measurements on these BSA samples were performed on a 4.7 T Varian system with a 63-mm quad coil. Images were acquired with FOV of 40 × 40 mm², slice thickness of 2 mm, and data matrix of 64 × 64. Two sets of experiments were performed on the BSA phantom: 1) a comparison of a previous method (10) with two optimized methods with the same acquisition time (~1 hour), and 2) a comparison of two optimized methods with 5 and 10 sampling points (and eight or four averages) with the same 16 minute acquisition time. All schemes were optimized for sample parameters that roughly match white matter, but are also a fairly good match for BSA. A measurement of R₂ was performed as well, by using a multiple spin echo imaging sequence (TR/TE = 15000/12 ms, 15 echoes, and 4 averages).

To demonstrate that the optimized schemes are applicable to brain tissues, in vivo rat brain measurements were acquired using a five-point scheme optimized for parameter ranges. The measurement was performed on a 7.0 T Varian animal system, with a 38-mm litz coil. The FOV was 38 × 38 mm², with a slice thickness of 1 mm and matrix of 128 × 128. To increase SNR, eight acquisitions were averaged, giving a total time of around 32 minutes.

Results

Optimal Schemes for determining T₁

For a typical parameter set of M₀ = 1, S_f = −1, and T₁ = 1, and a conventional acquisition scheme, which consists of a constant t_d of 6 s and a ten-point logarithmic spacing of t_i between 4 ms and t_d of 6 s. The objective function value of this scheme, calculated from Eqs. [1] and [7], is 286.1 s. A ten-point scheme, which optimizes for t_i and a single t_d (1s), has an objective function value of 62.4 s. The 1-s t_d value was found to be the optimal one by comparing objective function values of optimal schemes with different t_d values. Finally, for an optimal scheme with ten independently varied t_i and t_d values, the objective function value is 44.0 s. There is little variation in the objective function when there are 10 (44.0 s) or 3 (49.8 s) t_i and t_d values, we plot below a similar lack of dependence on sampling point numbers in the qMT optimization case, shown in Figure 2. Note that we have found that the minimum number of sampling points is three for T₁ determinations, with a total acquisition time of about 11s for one shot.

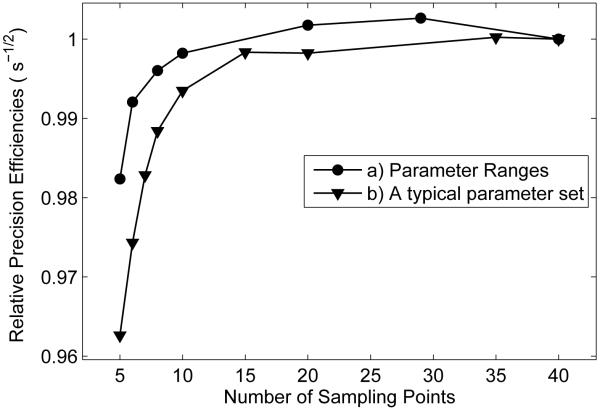
Figure 2.

Plots of relative precision efficiencies vs. sampling numbers after optimizing the acquisition parameters t_i and t_d. a) Optimizing for parameter ranges of : R_1f ∈ [0.4, 1.0] Hz, p_m/p_f ∈ [0.05, 0.20], k_mf ∈ [20, 40] Hz, S_f ∈ [−1.0, −0.9], and M_f∞ ∈ [0.6, 1.5], with precision efficiency defined by $1∕\sqrt{V_{\max }}$. b) Optimizing for a single typical parameter set: R_1f = 0.5 Hz, p_m/p_f = 0.10, k_mf = 30 Hz, S_f = −0.95, and M_f∞ = 1.0, with precision efficiency defined by $1∕\sqrt{V}$. The efficiencies are normalized to the last data point in the two curves, respectively.

Optimal schemes for determining qMT parameters

Table 1 lists three different schemes that have roughly equal acquisition times: the original scheme (Column 1), the optimal scheme for typical qMT parameters (Column 2) and the optimal scheme for qMT parameter ranges (Column 3). For scheme (1), its objective function values are V = 3.14 × 10⁴ s and V_max= 7.82 × 10⁵ s. For scheme (2), its objective function values are V = 1.39 × 10⁴ s and V_max = 3.35 × 10⁵ s. For scheme (3), its objective function values are V = 1.51 × 10⁴ s and V_max = 3.25 × 10⁵ s. Note that for scheme (2), the sampling points fall into seven groups, effectively making it a seven-point sequence with variation in the SNR of each point. As for the original scheme, the objective function does not reflect the additional errors that come from the first-order approximations previously employed (9,10).

Table 1.

Original and optimal schemes with roughly the same total acquisition time

1) Original Scheme(10): V = 3.14 × 104 s, Vmax = 7.82 × 105 s, Time cost= 105.54 s.	2) Optimized for a typical parameter set: V = 1.39 × 104 s, Vmax = 3.35 × 105 s, Time cost = 105.55 s.	3) Optimized for parameter ranges: V = 1.51 × 104 s, Vmax = 3.25 × 105 s, Time cost= 103.25s.
ti (s) td (s)	ti (s) td (s)	ti (s) td (s)
0.004 3.5	0.004 1.669	0.004 2.465
0.005 3.5	0.004 1.692	0.004 2.654
0.006 3.5	0.004 1.694	0.004 2.981
0.007 3.5	0.004 1.727	0.004 4.665
0.008 3.5	0.004 1.745	0.004 4.676
0.009 3.5	0.004 4.797	0.004 4.862
0.011 3.5	0.004 4.888	0.029 4.713
0.013 3.5	0.004 4.894	0.032 3.699
0.016 3.5	0.031 4.368	0.032 4.550
0.019 3.5	0.032 2.102	0.033 4.881
0.023 3.5	0.032 4.130	0.034 5.087
0.028 3.5	0.032 4.160	0.035 3.171
0.033 3.5	0.032 4.175	0.035 3.771
0.040 3.5	0.032 4.188	0.035 3.800
0.049 3.5	0.032 4.251	0.035 3.803
0.059 3.5	0.033 2.147	0.039 2.401
0.072 3.5	0.033 2.150	0.040 1.775
0.085 3.5	0.033 2.164	0.077 1.030
0.103 3.5	0.033 2.240	0.213 2.503
0.124 3.5	0.033 2.258	0.227 2.772
0.150 3.5	0.034 2.148	0.231 2.931
0.300 3.5	0.189 2.396	0.234 3.102
1.000 3.5	0.190 2.381	0.236 2.943
2.000 3.5	0.190 2.384	0.240 3.133
10.000 3.5	0.190 2.392	0.240 3.212
	0.190 2.428	0.240 3.292
	0.191 2.362	0.252 3.271
	0.191 2.388	1.514 0.010
	0.191 2.410	2.489 0.010
	0.191 2.443
	0.192 2.436
	0.193 2.437
	0.194 2.383
	1.635 0.010
	3.296 0.011

Investigation of number of sampling points for qMT measurements

As illustrated in scheme (2) in Table 1, we can determine qMT parameters with a much smaller number of sampling points. The optimization program was repeated while varying the number of sampling points, N. It is found that, for different N, the optimization processes yield similar objective function values, and only five sampling points are required to fit for five qMT parameters. In Figure 2, plots of calculated relative precision efficiencies vs. number of sampling points are shown, optimized for parameter ranges and the “typical” parameter set, respectively. Note that the precision efficiency is defined by the square root of the inverse of the CRLB objective function value, which is $1∕\sqrt{V}$. The precision efficiency decreases only slightly (2% drop for the parameter ranges and 4% drop for the typical parameter set) at small N, meaning that there is little penalty in the fitted parameter precision efficiencies when minimizing the acquisition time by decreasing the number of acquired images, assuming one employs the optimum t_i and t_d values at each N.

Monte Carlo Simulations

Monte Carlo simulations were performed at different noise levels to measure the uncertainties of fitted parameters for the optimal schemes. At each noise level, 10000 data sets were generated. Gaussian noise was introduced at each SNR level. Each data set was then fitted. The mean and standard deviation of the fits define the schemes’ systematic errors and uncertainties, respectively.

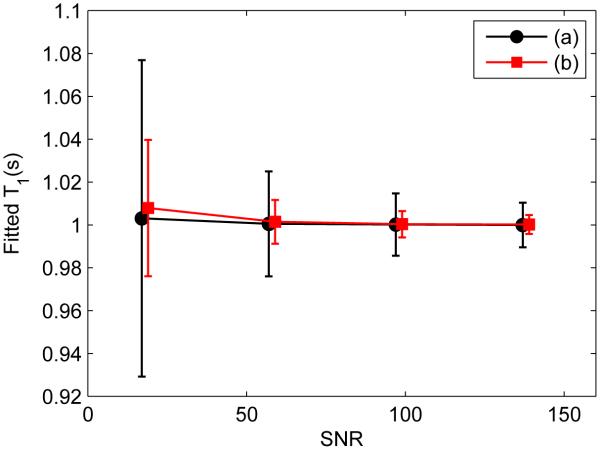
For T₁ simulations, the selected parameters are M₀ = 1, S_f = −1, and T₁ = 1. Figure 3 shows a comparison between a conventional scheme, with ten-point logarithmic spacing of t_i between 4 ms and 6 s, and t_d of 6 s, and a three-point optimal scheme, with both t_i and t_d varied. Only T₁ results are shown. The optimal scheme yields much less uncertainties in T₁ values than the conventional one, with uncertainties normalized to same total acquisition time.

Figure 3.

Monte Carlo simulation of T₁ fitting results vs. SNR using schemes: (a) a ten-point conventional scheme (black) with t_i logarithmically varied between 4 ms and 6 s, and t_d of 6 s; (b) a three-point scheme (red) optimized for parameter values of M₀ = 1, T₁ =1 s, and S_f = −1. Data points are slightly shifted to allow a clear comparison. The uncertainties are normalized for same total acquisition time.

For qMT simulations, the selected parameters used to generate the data are R_1f = 0.5, p_m/p_f = 0.1, k_mf = 30, S_f = −0.95, and M_f∞ = 1. The comparison of scheme (1) and (2) is shown in Figure 4. Scheme (3) has similar performances as scheme (2), as reflected in their objective function values, and its simulation result is not shown. M_f∞ is not shown either because both schemes produce similar results. The simulation data of the original scheme (1) were processed both with and without first-order approximations. It is obvious that for the original scheme, this approximation causes systematic errors in the fitted p_m/p_f, k_mf and S_f values, and that for k_mf and p_m/p_f, these errors have a fractional size on the order of the pool size ratio. Scheme (1) and (2) without approximations avoid these systematic errors. Scheme (2) also produces more precise values of p_m/p_f, k_mf than scheme (1), especially at low SNR. Additional simulations not shown here indicate that for the worst combination of parameter set, scheme (3) yield the least uncertainties, as reflected in its V_max value.

Figure 4.

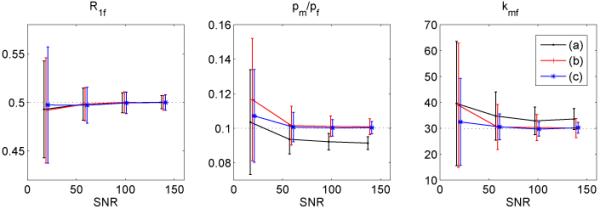
Monte Carlo Simulation of qMT fitting results vs. SNR: (a) scheme (1) (black) with first-order approximations, (b) scheme (1) (red) with direct fitting, and (c) scheme (2) (blue) with direct fitting. True values are indicated by dot lines. Data points are slightly shifted to allow a clear comparison. Note that the previously employed first-order approximations in scheme (1) lead to systematic deviations from the input value, and that scheme (2) has significantly smaller k_mf uncertainties than scheme (1), even when no first-order approximations are made.

Measurements

The measured T₁ values of MnCl₂ samples by using different acquisition schemes are plotted in Figure 5. The determined values and uncertainties are calculated from mean and standard deviation from pixels in the region of interest.

Figure 5.

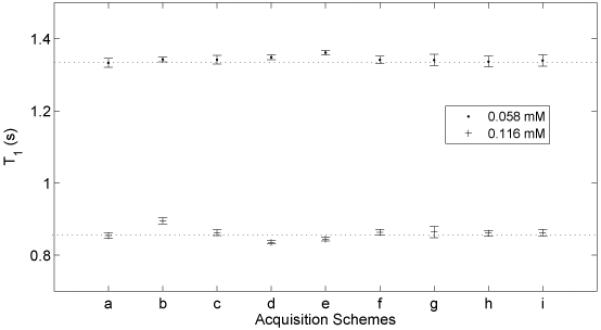
Measured T₁ values of MnCl₂ samples of 0.058 mM and 0.116 mM by using several different acquisition schemes. (a) a ten-point conventional scheme with t_i logarithmically varied between 4 ms and 6 s, and t_d of 6 s. Schemes (b) and (c) are optimized by varying t_i values with a constant optimal t_d of 1s. Scheme (b) is optimized for parameter values of M₀ = 1, T₁ =1, and S_f = −1. Scheme (c) is optimized for parameter range values of M₀ ∈ [0.5, 1.5], T₁ ∈ [0.5, 1.5], and S_f ∈ [−0.85, −1]. Schemes (d – i) are optimized by varying both t_i and t_d values. Schemes (d) (f) (h) are optimized for a single parameter set, as in (b), with numbers of sampling points of 10, 5, and 3, respectively. Schemes (e) (h) (i) are optimized for parameter range values as in (c), with numbers of sampling points of 10, 5, and 3, respectively. The determined values and uncertainties are calculated from the mean and standard deviation of the pixels in the region of interest.

Figure 6 shows corresponding plots of R_1f, p_m/p_f, k_mf, S_f and M_f∞. To show the effect of the new data processing technique, first-order approximations were employed to analyze the data acquired using scheme (1). The data from each pixel was fitted and qMT parameter values and uncertainties were set to the mean and standard deviation of the pixels in the regions of interest. The SNR of these measurements was around 270.

Figure 6.

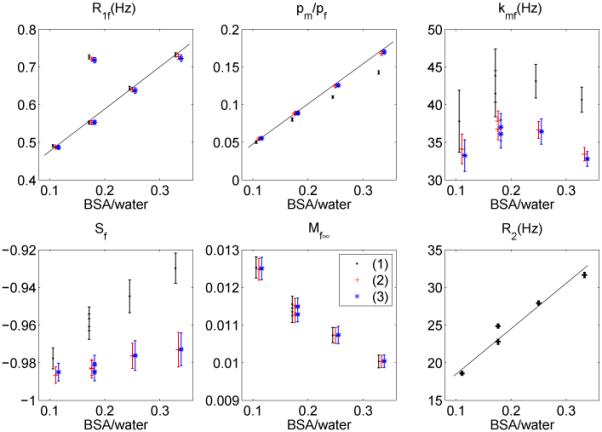
Measured R_1f, p_m/p_f, k_mf, S_f, M_f∞ and R₂ as a function of BSA weight vs. water weight ratio using acquisition schemes (1) (black), (2) (red) and (3) (blue), where M_f∞ is plotted in arbitrary units. Data points are shifted for a clear comparison. For scheme (1), first-order approximations were employed to process data. Note that the results from two 15% BSA samples are plotted, both with and without MnCl₂. The MnCl₂ changes R_1f and R₂ while having little effect on the fitted MT parameters, confirming that SIR-FSE is a true qMT sequence, and not just a function of the relaxation rates.

The comparison of measurement results using the five-point and ten-point optimal schemes is shown in Figure 7. It shows that both schemes produce similar qMT parameters within error ranges. Similar results are obtained for the five-point and ten-point schemes optimized for parameter ranges as well.

Figure 7.

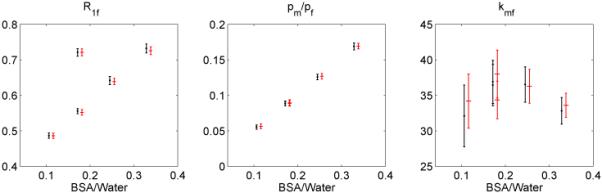
A comparison of results measuring the BSA samples by employing a five-point scheme (black) and a ten-point scheme (red) with roughly the same acquisition time. Data points are shifted for a clear comparison. While the 10 point scheme has slightly smaller parameter uncertainties, as expected from Figure 2, there are no systematic differences in the results using the two schemes, except that the five-point scheme yielded higher M_f values due to more averages (not shown).

The in vivo measurement results with the five-point scheme are show in Figure 8.The determined qMT parameters of WM and GM are listed in Table 2.

Figure 8.

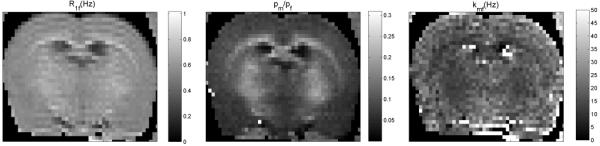
Measured qMT parameter maps of a live rat with a five-point scheme, optimized for qMT parameter ranges. Images were acquired with a FOV of 38 × 38 mm² and slice thickness of 1 mm. Eight acquisitions were taken for data fitting. Note the elevated pool size ratio values due to myelin in the corpus callosum, as expected.

Table 2.

Measured qMT parameters of WM and GM in a live rat brain

	R1f (Hz)	pm/pf	kmf (Hz)
WM	0.677 ± 0.076	0.173 ± 0.023	13.1 ± 2.9
GM	0.550 ± 0.046	0.080 ± 0.008	20.8 ± 6.5

Discussion

In this paper, we have shown how to optimize the SIR-FSE sequences for T₁ and qMT imaging using CRLB methods. The original qMT technique, presented in (9,10), used fixed t_d and varied t_i only and employed first-order approximations for data fitting. According to Monte Carlo simulations, as shown in Figure 4, first-order approximations will introduce systematic errors to p_m/p_f, k_mf and S_f. The p_m/p_f values, determined by the original technique will be lower than the true value, while k_mf will be larger. In the new method presented here, we varied both t_d and t_i and fitted the qMT parameters with minimal approximations. Both the precision and accuracy increase, as shown in simulations and experimental results.

T₁ measurement has also been optimized using the same approach. By varying t_i and t_d independently, global optimal acquisition schemes were obtained with precision efficiencies, which are much greater than previous inversion recovery methods. This optimization is confirmed by Monte Carlo simulations, as shown in Figure 3, by comparing a ten-point conventional scheme with a three-point optimal scheme with same total acquisition time. Figure 5 shows a comparison of measured T₁ values between the conventional scheme and a series of optimal schemes. It is shown that the optimal schemes yield consistent T₁ values across schemes, which validates the optimization technique. It is also verified that only three sampling points are required to determine T₁ value, as shown in schemes (h) and (i) in Figure 5. The three-point scheme optimized for parameter ranges of M₀ ∈ [0.5, 1.5], T₁ ∈ [0.5, 1.5], and S_f ∈ [−0.85, −1], is given in Table 3, which requires about 11s per acquisition, so, depending on SNR requirements, an 8 shot clinical scan would take 11s/shot × 8 shots × 2 averages = 3 minutes (Two averages allow phase cycling that destroys any transverse magnetization remaining after the gradient spoiling; Using a single average and fewer shots will proportionally lower the acquisition time).

Table 3.

An optimized three-point scheme for parameter ranges of M₀ ∈ [0.5, 1.5], T₁ ∈ [0.5, 1.5] s, and S_f ∈ [−0.85, −1]

ti (s)	0.004	0.898	4.781
td (s)	1.480	3.454	0.010

The qMT optimization results were confirmed by the experimental measurements of BSA samples, as shown in Figure 6. The optimal schemes have less uncertainty in the measured qMT parameters, most notably in k_mf, which, due to its greater fractional uncertainty tends to dominate the calculation in Eq. [7]. The performances of schemes (2) and (3) are similar, which is not surprising, given their similar V values in Table 1. Therefore, the optimal scheme for the set of typical parameters is applicable to a range of qMT parameters for BSA samples of different percent weights. In other words, if the qMT parameters do not cover a very wide range, we will be able to optimize for a single parameter inside this range and apply the optimized scheme for all measurements. In addition, as in (9), the R_1f, p_m/p_f values increase linearly with the BSA-to-water ratios. Note that the results from two 15% BSA samples are plotted, both with and without MnCl₂. The MnCl₂ changes R_1f and R₂ while having little effect on the fitted MT parameters, confirming that SIR-FSE is a true qMT sequence, and not just a function of the relaxation rates.

To further confirm the optimization technique, experimental precision efficiencies were calculated. Examples are given for qMT schemes (1), (2) and (3), as listed in Table 1. The CRLB theory predicts precision efficiency ratios of 1: 1.5: 1.45, from their V values. Monte Carlo simulations lead to precision efficiency ratios of 1: 1.56: 1.50, by extracting the simulation data at an SNR of 200. The experimental precision efficiency ratios of the qMT parameters of the 15% BSA are 1: 1.69: 1.35. These roughly similar ratios illustrate the advantage of the optimization technique. Consistent precision efficiency ratios were obtained for MnCl₂ samples T₁ measurements as well. A detailed comparison of relative precision efficiencies, derived from CRLB, Monte Carlo simulations and experimental results of T₁ and qMT results is given in Figure 9. The experimental precision efficiencies were calculated from the 0.058 mM MnCl₂ and 15% BSA samples, respectively. By varying t_i and t_d simultaneously, the precision efficiencies of T₁ and qMT measurements has increased roughly 150% and 50%, respectively, comparing with the conventional scheme and original technique.

Figure 9.

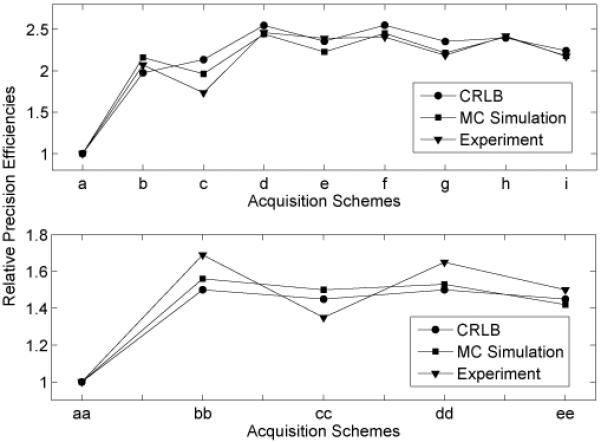
Plot of relative precision efficiencies of T₁ schemes and qMT schemes for the typical parameter values listed in Figure 2 and Figure 3. Schemes a-i are T₁ schemes, as given in Figure 5. Schemes aa, bb, and cc are schemes (1)-(3) in Table 1. Schemes dd and ee are the ten- and five-point schemes in Figure 7. As shown in these plots, we have obtained: (1) an increase in the T1 precision efficiencies when optimizing both t_i and t_d of roughly 250% over logarithmic spacing and 25% over optimizing t_i and only a single t_d; 2) an increase in the qMT precision efficiency when optimizing both t_i and t_d of roughly 50% over the previous logarithmic spacing; 3) only a small decrease in the precision efficiency when lowering the number of sampling points.

Figure 2 shows that the precision efficiency has only a weak dependence on the number of acquisitions, N. This indicates that we can take as few as five sampling points to determine the qMT parameters. This conclusion is confirmed by measurement of the BSA samples with five-point and ten-point schemes, as shown in Figure 7. It is further confirmed by in vivo measurements using the five-point scheme, as shown in Figure 8. The extracted qMT parameters of WM and GM are shown in Table 2. As shown in Monte Carlo simulations, the fitting process with first-order approximations leads to slightly larger k_mf but lower p_m/p_f values. This prediction is consistent with the differences between the qMT parameter values for WM in Table 2 and those in (10).

With the verification that only a five-point scheme is required to determine the five qMT parameters, this work provides more insight in rapid qMT acquisitions. For example, a five-point optimal scheme requires about 15s/acquisition, so, depending on SNR requirements, an 8 shot clinical scan would take 15s/shot × 8 shots × 2 averages = 4 minutes, making clinical application a possibility. A five-point scheme, proposed in this work for clinical applications, is shown in Table 4, which is optimized for above-mentioned parameter ranges.

Table 4.

An optimized five-point scheme proposed for clinical applications, for qMT parameters in ranges of: R_1f ∈ [0.4, 1.0] Hz, p_m/p_f ∈ [0.05, 0.20], k_mf ∈ [20, 40] Hz, S_f ∈[−1.0, −0.90], and M_f∞ ∈ [0.6, 1.5]

ti(s)	0.004	0.032	0.035	0.225	0.770
td(s)	3.502	4.603	1.507	3.273	0.011

A related issue for clinical application is the robustness of the standard FSE implementation on a given imaging system. Any ghosting or T₂ blurring will cause correlating effects in the SIR-FSE qMT imaging sequence. Also, given the significant MT effects from the off-resonance excitation and refocusing pulses (30,31), multi-slice acquisitions do not make sense for SIR-FSE. However, 3D acquisitions are viable, at least in a research setting, e.g. a 128×128×32 3D volume could be acquired in 2 averages x 15s / excitation × 128 × 32 phase encodes / 64 echoes = 32 minutes, not including benefits from partial k-space and parallel imaging effects. This acquisition time is comparable to pulsed saturation methods (32), but without the need for separate B₁, B₀, and T₁ maps. Pulsed saturation has, however, been more extensively tested in vivo.

In this work, we have given equal weights to all fitted parameter uncertainties in Eqs. [7] and [10]. Among the five qMT parameters, the pool size ratio (p_m/p_f) is often of most interest. An alternative would be to optimize for p_m/p_f only. Optimization results, which are not shown, indicate an increase in p_m/p_f precision about 30% from such optimization, but at the cost of large systematic errors in the other qMT parameters, making it an unappealing alternative.

Fitting qMT parameters necessitates assumption about R_1m and S_m. We performed Monte Carlo simulations to investigate the variances of fitted qMT parameters vs. different underlying R_1m and S_m values. We found that the fitted R_1f, k_mf, S_f, and M_f∞ values are almost independent of R_1m and S_m. The pool size ratios, p_m/p_f, has little dependence on R_1m but a relatively large dependence on S_m. The simulated data were generated with R_1f = 0.5, p_m/p_f = 0.1, k_mf = 30, S_f = −0.95, and M_f∞ = 1, by using scheme (2) in Table 1 at SNR of 100. For S_m = 0.76 and 0.9, the fitted p_m/p_f values are 0.104 ± 0.005 and 0.096 ± 0.005, respectively. With these variations, the maximum uncertainty of p_m/p_f is about 10%, which indicates that this technique is fairly robust to assumptions of R_1m and S_m.

Conclusion

In conclusion, we have shown how to optimize the SIR-FSE sequences by maximizing E the precision efficiency using an objective function, which includes CRLB and time cost. By varying both t_i and t_d, the precision efficiencies of both T₁ and qMT measurements are increased. Monte Carlo simulations support this approach by showing reduction in the uncertainties of fitted parameters. The optimization results are confirmed by measurements on MnCl₂ samples, BSA samples, and in vivo rat brain. Specifically, for qMT determinations, minimal approximations were applied to get rid of the systematic errors from first-order approximations in previous work (8-10). From the investigation of number of sampling data points, it is shown that five data points are enough to determine qMT parameters, and three data points are enough to determine T₁ parameters. This opens up the possibility of applying the SIR-FSE sequences to clinical 2D and preclinical 3D applications.