Manipulation of a fragile object

Abstract

We investigated strategies of adjustments in kinetic and kinematic patterns, and in multi-digit synergies during quick vertical transport of an instrumented handle that collapsed when the grasping force exceeded a certain magnitude (quantified with a fragility index). The collapse threshold of the object was set using a novel electromagnetic device. Moving a fragile object is viewed as a task with two constraints on the grip force defined by the slipping and crushing thresholds, respectively. When moving more fragile objects, subjects decreased object peak acceleration, increased movement time, showed a drop in the safety margin (extra force over the slipping threshold), and showed a tendency towards violating the minimum-jerk criterion. Linear regression analysis of grip force against load force has shown tight coupling between the two with a decline in the regression coefficient with increased fragility index. The safety margin was lower in bimanual tasks, compared to unimanual tasks, for both fragile and non-fragile objects. Two novel indices have been introduced and studied, the safety margin due to fragility and the drop-crush index. Both indices showed a decrease with increased object fragility. Changes in the drop-crush index showed that the subjects would rather crush the fragile objects as opposed to dropping them, possibly reflecting the particular experimental procedure. We did not find differences between the performance indices of the dominant and non-dominant hand thus failing to support the recently formulated dominance hypothesis. The synergies stabilizing grip force were quantified at two levels of an assumed two-level control hierarchy using co-variation indices between elemental variables across trials. There were strong synergies at the upper level of the hierarchy (the task is shared between the opposing groups of digits) that weakened with an increase in object fragility. At the lower level (action of an effector is shared among the four fingers), higher fragility led to higher synergy indices. Analysis of force variance showed that an increase in object fragility was accompanied by exploring a smaller range of equivalent combinations of elemental variables. The additional constraint imposed by high fragility facilitated synergies at the lower level of the hierarchy, while there was evidence for a trade-off between synergies at the two levels.

Introduction

Recent studies of multi-finger prehension have focused on the coordination of fingertip forces and moments of force during manipulation of rigid objects (Burstedt et al. 1997, 1999; Shim et al. 2003, 2005a,b; Zatsiorsky et al. 2003, 2005, 2006). While this is the case for some of the objects humans encounter in everyday life, they also manipulate objects that are fragile and deformable. Currently, it is not known how the human prehensile actions change during manipulation of fragile objects. The aim of the current study is to fill this gap.

It has been well established that, during quick movements of a hand-held object, grip force shows changes that correlate closely with the resultant force accelerating the object (load-bearing force; Flanagan and Wing 1993, 1995; Flanagan and Tresilian 1994; Wing et al. 1997). These phenomena have been discussed as evidence for anticipatory (feed-forward) control of grip force needed for the predicted changes in the load force and affected by the friction between the digits and the object (Flanagan and Johansson 2002, 2009; Johansson 2002). The main purpose of these adjustments is to keep grip force at a safely high level to ensure that the object does not slip out of the hand. When one has to move a fragile object quickly, a new constraint is imposed: The grip force cannot be higher than the crushing threshold. In such conditions, a large increase in the grip force may be dangerous.

Potentially, there are two strategies of making sure that a fragile object does not break during movement. First, one may slow down the movement resulting in smaller peak acceleration values that require proportionally smaller grip force adjustments. Second, one may alter the excessive grip force applied to the object but still keep the applied grip force above the slipping threshold, thereby decreasing the so-called safety margin (Johansson and Westling 1984; Burstedt et al. 1999; Pataky et al. 2004). We hypothesized that the subjects will use both strategies when transporting fragile objects. With respect to movement kinematics, we expected an increase in movement time and smaller magnitudes of object peak acceleration (Hypothesis 1). In addition to changes in movement time and peak object acceleration, the time profile of acceleration could also be adjusted. Slowing down is expected to lead to smaller integrated jerk values (the integral of the squared values of the third time derivative of the trajectory) because of straightforward mechanics. However, if the integrated jerk index is normalized by movement time (Hogan 1984; Flash and Hogan 1985; Teulings et al. 1997), the index allows comparison across movements at different speeds. A less efficient movement strategy may be revealed for movements with fragile objects resulting in higher indices of the normalized jerk (Hypothesis 2).

When one has to move a fragile object quickly, an increase in the grip force may lead to crushing the object. Therefore, we hypothesize that the mentioned close correlation between grip force and load force (Flanagan and Wing 1993, 1995; Flanagan and Tresilian 1994; Wing et al. 1997) will be violated during movements of fragile objects, which may involve both a drop in the regression coefficient (slope) and a drop in the correlation coefficient (Hypothesis 3). In a recent study, Winges et al. (2009) used a compliant contact surface for one of the fingers. These authors report similar grip force adjustments during the holding and lifting phases with only a difference in the amplitude of the force produced by the finger acting against the compliant surface. There was, however, a decoupling of the grip and load forces, which suggests that we could also expect a decoupling of these forces in the current experiment.

The second strategy mentioned in the previous paragraph is related to possible adjustments in safety margin. We hypothesized that the safety margin will decrease for more fragile objects (Hypothesis 4) as a result of avoiding high grip forces. It is not known, however, whether motion-related patterns of the safety margin change during the movement of fragile objects. This was an exploratory goal of this experiment. Note that the four mentioned Hypotheses are mutually non-exclusive; the first two are related to the transport component of the action, while the second two are related to the gripping component.

Studying fragile objects allows the introduction of two new indices related to safety of performance. The first we have termed “safety margin related to fragility, SM_FR”. It can be defined as the normalized difference between actual grip force applied to the object and the highest grip force that does not lead to crushing the object. The second index compares total grip force applied to the object to both crush and slip thresholds; we have termed this index the “drop-crush index (I_DC)”. It is defined as the amount of applied grip force above the slip threshold divided by the range of grip forces between the slip and crush thresholds. Since, to our knowledge, these indices have never been studied, we explored the behavior of these indices during changes in object fragility, at different time intervals during the movements, and for different effectors.

We also explored how people move fragile objects using the dominant hand, the non-dominant hand, and both hands together. Our earlier studies of static tasks with rigid objects have shown significant differences in a variety of indices between one-hand and two-hand conditions (Gorniak et al. 2009a, b). In particular, safety margin was the highest for the dominant hand. The recently formulated dominance hypothesis (Sainburg 2002, 2005; Wang and Sainburg 2007) suggests that the dominant hand has an advantage during dynamic tasks while the non-dominant hand may perform better in static tasks. Based on this hypothesis, we expected lower normalized jerk indices, higher accelerations, and lower safety margins for movements performed by the dominant hand (Hypothesis 5).

Manipulating a fragile object may have implications for synergies at the two levels of a control hierarchy involved in hand actions (Arbib et al. 1985). In this context, we define synergies as co-varied (across trials) adjustments of elemental variables at a selected level of analysis that stabilize a desired value (or a time profile) of a potentially important performance variable produced by that level (reviewed in Latash et al. 2002b, 2007). At the upper level, the hand action is shared between the thumb and an opposing effector, which is referred to as “virtual finger” (VF, an imaginary digit with the mechanical action equal to the combined action of the actual fingers). At the lower level, VF action is shared among the actual fingers. At each of the two levels, the system is mechanically redundant (Zatsiorsky and Latash 2008), that is, an infinite number of combinations of elemental variables can satisfy the task constraints. According to the principle of abundance (Gelfand and Latash 1998), this problem may be solved by facilitating families of solutions with the elemental variables co-varying to stabilize important action characteristics.

Several recent studies have documented a trade-off between synergies at two levels of a control hierarchy, strong synergies at the higher level are associated with weak or absent synergies at the lower level (Gorniak et al. 2007b, 2009b; Zhang et al. 2009). In particular, static prehension has been shown to be associated with strong synergies stabilizing total normal (grip) force at the higher hierarchical level (co-varied adjustments of the thumb and VF normal forces across trials) without synergies stabilizing VF normal force at the lower level by covaried adjustments of finger normal forces (Gorniak et al. 2009b). This trade-off is, however, not obligatory as shown, for example, by the emergence and strengthening of synergies at the lower level with practice, without negative effects on synergies at the upper level (Kang et al. 2004). We hypothesized that, while handling more fragile objects, the subjects would show stronger synergies stabilizing grip force at the lower level of the hierarchy because task constraints will imply accurate production not only of the resultant normal force (at close to zero level) but also of the VF normal force to avoid object collapse (Hypothesis 6). Further, we explored changes in two components of force variance that affected the synergy index to test a hypothesis that manipulation of fragile objects will be associated with using a smaller range of solutions (smaller range of finger force combinations) as compared to manipulation of non-fragile objects (Hypothesis 7). Using a smaller range of fingertip forces may reflect a more stereotypical task performance with the purpose to avoid finger force magnitudes that could potentially crush the object.

Methods

Participants

Seven male and seven female students served as subjects in this study. Average data for the males were (mean ± SD): 25 ± 1 years of age, 1.77 ± 0.04 m in height, 70.4 ± 3.1 kg in mass, 19.1 ± 0.9 cm for right hand length, 8.7 ± 0.5 cm for right hand width, 19.0 ± 0.9 cm for left hand length, and 8.4 ± 0.4 cm for left hand width. Average data for the females were: 21 ± 1 years of age, 1.65 ± 0.09 m in height, 62.5 ± 11.3 kg in mass, 17.8 ± 1.0 cm for right hand length, 8.0 ± 0.5 cm for right hand width, 18.1 ± 0.8 cm for left hand length, and 7.7 ± 0.6 cm for left hand width. Hand length was measured as the distance from the tip of the distal phalanx of digit three to the distal crease of the wrist with the hand in a neutral flexion/extension pose. Hand width was measured between the lateral aspects of the index and little finger metacarpophalangeal (MCP) joints. Handedness was assessed by the Edinburgh Inventory (Oldfield 1971), which ranges from a laterality quotient (LQ) of − 100 (which indicates strong left-handedness) to +100 (which indicates strong right-handedness). All subjects were strongly right-handed (LQ average = +89) and had no previous history of neuropathies or traumas to the upper limbs. None of the subjects had a history of long-term involvement in hand or finger professional activities such as typing or playing musical instruments. All subjects gave informed consent according to the procedures approved by the Office of Regulatory Compliance of the Pennsylvania State University.

Experimental Setup

Five six-component force-moment transducers (four Nano-17 and one Nano-25; ATI Industrial Automation, Garner, NC, USA) were mounted on a handle made of aluminum and high density polymer components. A hinge joint connected the aluminum and high density polymer components such that the location of the thumb along the Z-axis of the object could be altered, see Figure 1. The width of the object was maintained by a small solenoid attached at the bottom of the object, placed in opposition to the thumb. The electrical current through the solenoid was controlled by an external device, such that a range of levels of current flow corresponded to the total grip force of the digits that the setup could withstand just prior to collapse (small amplitude rotation in the hinge joint). Further information on the fragility settings used in this experiment can be found in the section titled “Object Fragility”.

Figure 1.

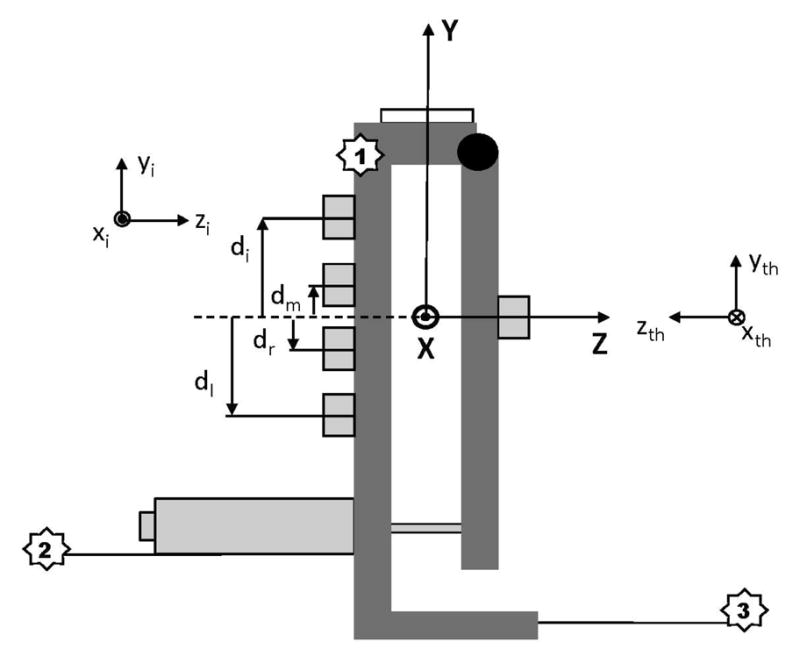
A schematic of the collapsible object. The Nano-17 and Nano-25 sensors (shown as light grey blocks) were attached to vertical aluminum and high density polyethylene bars. A circular bulls-eye (white block) was placed at the geometric center of the object. The global reference frame (X,Y,Z) of the handle is shown as well as the local axes of the thumb and index sensors (x_th,y_th,z_th and x_i,y_i,z_i; respectively). The solenoid that controlled object fragility can be found at the bottom virtual finger-side of the object; the body of the solenoid remained on the virtual finger side of the object at all times. A small metal plunger that moved if the object was collapsed was in contact with the thumb-side of the object. The hinge joint that allowed for object collapse is shown as the black circle on the thumb side of the object. Marker (3 passive markers) locations are denoted by numbered white stars.

The center points of two of the Nano-17 sensors were 0.03 m and 0.01 m above the midpoint of the object, respectively (X = 0, Y = 0.03 and 0.01 m; capital letters are used for coordinates in the handle-based reference frame, Figure 1). The center points of the remaining two Nano-17 sensors were 0.01 m and 0.03 m below the midpoint (X = 0, Y = −0.01 and −0.03 m) of the object, respectively. The Nano-25 sensor was located at the midpoint of the object (with respect to the X- and Y-axes; X, Y = 0). The point Z = 0 was set as the point halfway between the two sets of sensors, when the object was not in the collapsed state. The centers of all the sensors were within one plane referred to as the grasp plane. The grip width of the object (defined as the distance between the contact surface of the Nano-25 sensor and the contact surfaces of the Nano-17 sensors along the Z-axis of the handle) was set at 0.085 m when the object was not in the collapsed state. When the object had been collapsed, the width was 0.082 m.

A circular bulls-eye level with 2° tolerance was placed on the upper surface of the object (X, Z = 0). The mass of the object was 0.733 kg. Sandpaper (320-grit) was attached to the contact surfaces of each sensor to increase the friction between the digits and the transducers. The finger pad-sandpaper coefficient of static friction was approximately 0.96 (Savescu et al 2008). Transducer signals were amplified and multiplexed using a customized conditioning box (from ATI Industrial Automation) prior to being routed to a 12-bit analog to digital converter (PCI-6031, National Instruments, Austin, TX, USA). A customized Labview program (National Instruments, Austin, TZ, USA) was used for data acquisition and customized MATLAB (Mathworks Inc., Natick, MA, USA) programs were written for data processing. Signals were sampled at 480 Hz.

In addition, kinematics of object movement were recorded using passive reflective markers (2 cm in diameter) and a four camera ProReflex system (MCU240, Qualysis Inc., Gothenburg, Sweden) at 240 Hz, controlled by proprietary software (Qualysis Track Manager, Qualysis Inc., Gothenburg, Sweden). This software package was also used to digitize and reconstruct marker locations. Three passive markers were affixed to the object; one marker was located just below the bulls-eye level on the aspect of the object, to which the four Nano-17 sensors were attached; another marker was located 3 cm from the most lateral end of the solenoid on the same aspect of the object (attached to the object via a lightweight rigid attachment), and the third marker was located at the bottom aspect of the object, to which the Nano-25 sensor was attached, 5 cm from the most lateral aspect of the object (attached to the object via a lightweight rigid attachment). The locations of these markers can be found in Figure 1. The orientation and location of these markers on the object remained constant throughout the testing of all subjects. A three-dimensional accelerometer (Model 356B11, ICP Accelerometer; PCB Pizotronics, Depew, NY, USA) was affixed to the object oriented along the +Y axis, just below the circular bulls-eye level, to measure object acceleration along the object’s long axis aligned with the gravity vector, sampled at 480 Hz. The three data collection systems were synchronized via a rectangular electrical triggering pulse monitored by Labview.

Procedure

Subjects sat with an erect posture, arms unsupported, in a chair facing a small table. The height of the table was 0.725 m above the floor. Subjects were instructed to grasp the object using one of three different hand configurations: with the digits of the right hand (RIGHT); with the digits of the left hand (LEFT); and with the index, middle, ring, and little digits of the right hand in opposition to the index digit of the left hand (2-HAND). Four fragility settings were used in this experiment, see Table 1. The presentation of tested conditions was block randomized for each subject; hand configuration was used as the blocking factor. The presentation of blocks was randomized for each subject and factors within each block were also randomized per subject (i.e., each subject had a unique block design). For each of the four fragility settings, the trials were presented in blocks to allow the subject to adjust better to different fragility settings. A total of 12 experimental conditions were tested with 216 total trials (see below).

Table 1.

FR-indices tested with corresponding F^GRIP required for object collapse.

FR-index	FGRIP collapse (N)
0.45	16.7
0.37	20.2
0.24	30.8
0.15	50.2

At the onset of the task, the upper arm(s) of the subjects were abducted at approximately 45° in the frontal plane, flexed 45° in the sagittal plane, and internally rotated approximately 30°. Each of the hands was in a neutral supination-pronation position. The wrists were flexed approximately 30° during each task. In tasks involving only one hand, the non-involved hand was permitted to rest on the subject’s lap. In two-hand tasks, the two hands of the subject were not permitted to touch each other at any point during recording. At the beginning of each trial, the signals from each of the sensors were set to zero. Subjects were instructed to not touch the handle during the zeroing process. The object remained at rest, oriented vertically, prior to each trial. Prior to each of the tested conditions, subjects were required to grasp the object using the finger configuration of the current testing block and instructed to slowly squeeze and “crush” the object. This was done to orient the subject in regard to the fragility setting for each testing condition.

Once the object was grasped, subjects lifted the object to a height of 0.10 m above the surface of the table, indicated by a visual target. At that point, subjects were asked to maintain the orientation and location of the object without deviations from the vertical (Y) axis, using the bulls-eye level as a feedback device. When subjects indicated that they were ready to start a trial, data collection began. Subjects were instructed to move the object quickly and accurately 0.30 m vertically to the second visual target and remain there until the end of the trial. During data collection, signals from all three data collection systems were recorded for five seconds. On average, subjects deviated 5 ± 2° from the vertical y-axis across the duration of each trial. Subjects were given practice trials prior to testing each finger configuration and fragility setting. Three successful practice trials were required prior to the onset of data collection for each condition. A minimum of 15 successful trials were recorded for each experimental condition; a total minimum number of trials performed by each subject was 216 (180 recorded trials and 36 practice trials).

Object Fragility

Object fragility was controlled by altering the current flow to the solenoid maintaining object width. The current flow could only be regulated at pre-set levels, thus finer gradations of object fragility were not feasible in this experiment. The grip forces corresponding to the fragility indices (FR-indices) tested in this experiment can be found in Table 1. FR-index was calculated as the quotient of the minimum grip force required to maintain the object in static equilibrium (F^GRIP min = 7.5 N) divided by the grip force needed to collapse the object. As the object becomes more rigid, FR-index approaches zero.

Data Analysis

The data were processed off-line using customized MATLAB software (Mathworks Inc., Natick, MA, USA). The force data were low-pass filtered at 10 Hz using a 2^nd order, zero-lag Butterworth filter. The onset and termination of object movement were determined using data from the accelerometer, which were filtered using a low-pass 5 Hz, 2^nd order, zero-lag Butterworth filter. Movement onset was determined as the time of 3% maximal object acceleration; movement termination was determined as the time of 3% of the minimum object acceleration (in the negative direction). Movement time (MT) was defined as the period between movement onset and movement termination. All force and kinematic data were time normalized with respect to movement time (expressed as 0–100% of movement time) via cubic splines.

Local forces were computed within sensor-based reference frames for individual sensors referred to as x_j, y_j, and z_j (where j represents: th, i, m, r, and l refer to the thumb, index, middle, ring, and little fingers, respectively). Note that the x_th and z_th axes are in the opposite direction as compared to the axes of the finger sensors (x_j and z_j). Net force data are reported in the handle-based reference frame (X,Y,Z, see Figure 1).

Kinematic Analysis

Object acceleration recorded by the accelerometer was used to calculate mean squared jerk during object movement. Jerk is the time derivative of acceleration while mean squared jerk has been used as an index of movement smoothness over a given time period (Hogan 1984; Flash and Hogan 1985). Integrated squared jerk was calculated over movement time:

$$\mathit{MSJ}=\underset{0}{\overset{MT}{\int }}\frac{J^2}{2}dt$$ (1)

where MT is movement time and J is the time derivative of the recorded acceleration.

Orientation and location of the object during the experiment were recorded using infrared emitting cameras and a passive marker system consisting of three markers (see “Methods – Experimental Setup”). A customized three-dimensional model of the object was created via Qualysis software. The origin of the object was consistently defined at Marker-1; see Figure 1. The location and orientation of the object was calculated using standard 3D kinematic procedures, as described by Zatsiorsky (1998) and Hamill and Selbie (2004). The displacement of the object along the Z-axis was used to calculate the normalized mean squared jerk, a measure of movement smoothness that takes into account both movement time and object displacement (Teulings et al. 1997):

$$\mathit{NMSJ}=\sqrt{\frac{{MT}^5}{L^2}\underset{0}{\overset{MT}{\int }}\frac{J^2}{2}dt}$$ (2)

where MT is the duration of the movement, J is the derivative of the recorded acceleration, and L is the displacement of the object.

Kinetic Analysis

The equations of motion for the object of interest in this study are similar to the equations reported for static prehension in earlier publications (e.g. Gorniak et al. 2009a). For the sake of brevity, we present two equations (out of a total of nine equations) assuming vertical movement of the object without rotation.

The sum of the vertical tangential forces of the individual fingers and of the thumb (load bearing forces; along the Y-axis, see Figure 1) should be equal to the mass of the object multiplied by acceleration of the object plus its weight.

$$m{a}_Z+mg=F_{VF}^t+F_{TH}^t=F_{VF}^Y+F_{TH}^Y$$ (3)

$$F_{VF}^Y=F_i^y+F_m^y+F_r^y+F_l^y$$ (4)

where F represents force; g is acceleration due to gravity; a is the acceleration of the object; the subscripts VF, TH, i, m, r, and l refer to the virtual finger, thumb, index, middle, ring, and little fingers, respectively.

The safety margin (SM, the amount of grip force exerted beyond what is required to prevent object slip) has been defined in literature (Johansson and Westling, 1984; Burstedt et al. 1999; Pataky et al. 2004) as:

$$SM=\frac{(F^G-\mid F^L\mid /{\mu }_s)}{F^G}$$ (6)

where F^G is the grip force applied to the object, F^L is the load-bearing force applied to the object, and μ_s is the coefficient of static friction between the finger pad and sandpaper interface. Thus, the maximum value for SM is unity if no load-bearing force (F^L) is exerted on the object and the minimum value for SM is zero if just enough force is exerted on the object to prevent slipping. An example of the relationship between total grip force and the slip threshold for a typical subject can be found in Figure 2.

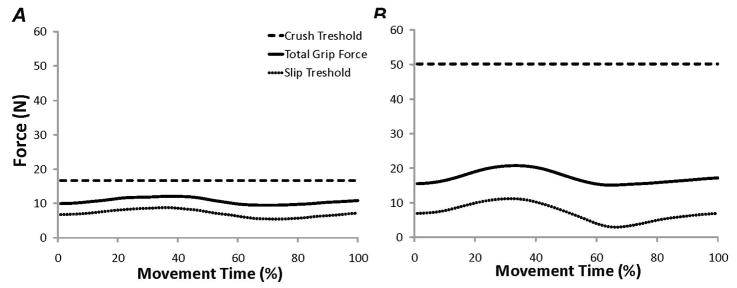
Figure 2.

A typical example of the average grip force applied to the object in comparison to the crush and slip thresholds for the most fragile (Panel A) and least fragile objects tested (Panel B). Data are shown from a typical subject. A: Force thresholds for the most fragile object (FR-index = 0.45). B: Force thresholds for the least fragile object (FR-index = 0.15).

While the traditional value for safety margin describes the amount of grip force applied to an object in comparison to the grip force required to prevent object slip, another type of safety margin can be calculated with respect to object fragility. The safety margin due to object fragility is defined as:

$${SM}_{FR}=\frac{F_{max}^G-F^G}{F_{max}^G}$$ (7)

where F^G_max is the maximal grip force the object can withstand prior to collapse and F^G is the total gripping force (F_TH=−F_VF) applied to the object. A schematic illustrating the relationship between total grip force and the crush threshold can be found in Figure 2.

An index comparing the amount of applied forces above the slip threshold to the range of grip forces between the slip and crush thresholds of the object was also computed. This index has been termed drop-crush index (I_DC) and defined as:

$$I_{DC}=\frac{(F^G-\mid F^L\mid /{\mu }_s)}{(F_{max}^G-\mid F^L\mid /{\mu }_s)}$$ (8)

where F^G is the grip force applied to the object, F^L is the load-bearing force applied to the object, μ_s is the coefficient of static friction between the finger pad and sandpaper interface, and F^G_max is the maximal grip force the object can withstand prior to collapse.

Analysis of Multi-Digit Synergies

Analysis of most measures of interest in this paper was performed at the task level (VF-TH). However, analysis of grip force variability was performed at two hierarchical levels: the VF-TH level and the IF level. At the VF-TH level, the outputs of the VF and an opposing effector are analyzed. At the IF level, the outputs of the fingers within the VF are analyzed (namely the right hand fingers, IMRL_R).

Variance Analysis

The purpose of this analysis was to compute indices of co-variation of elemental variables (forces and moments of force produced by individual digits) that reflect the stabilization of combined effector outputs across trials. At the VF-TH level, co-variation of elemental variables produced by the VF and the opposing effector (thumb of the same hand or the left index finger in the two-hand condition) was studied, while at the IF level, co-variation of elemental variables produced by individual fingers was studied. The index of co-variation ( Δ V) was computed for grip forces at both hierarchical levels using the equations presented in Gorniak et al. 2009b. Briefly, the index Δ V reflects the normalized difference between the total variance at the selected level of analysis and the variance of the combined output of the elements, both computed across trials.

The index Δ V is defined in such a way that positive values reflect predominantly negative co-variation among forces produced by the individual digits. We interpret such values as signs of a force stabilizing synergy (Gorniak et al. 2007a, b; Kang et al. 2004; Shim et al. 2005b). Large positive Δ V values correspond to larger amounts of negative co-variation, thus a stronger synergy. A result of Δ V = 0 implies independent variation of digit forces, and correspondingly the absence of a synergy, while Δ V < 0 may be interpreted as co-variation of elemental variables destabilizing their combined output. The normalization limits the value of Δ V by +1 for perfect force stabilizing synergies (the individual elemental variables vary across trials but variance of the performance variable equals zero).

The index of co-variation was computed across trials during three time intervals: 1–10% of movement time, 45–55% of movement time, and 91–100% of movement time. This was done to explore possible Δ V changes in different movement phases since several earlier studies showed non-monotonic Δ V changes during fast actions (Latash et al. 2002; Shim et al. 2005b). Subsequent analysis did not reveal significant differences between the 1–10% and 91–100% time intervals in the Δ V analysis. As a result, the data for these two intervals were averaged, resulting in one value representing behavior at the initial and final 10% of the movements, referred to as Interval Δ T_1–3.

In addition to the analysis of Δ V, the total variance (across trials) of all the elemental variables at that level (V^TOT) was computed at both hierarchical levels. The value of V^TOT may be viewed as the sum of two components, only one of which has an effect on performance (referred to as variance of task performance, V^P). Accurate performance (small V^P) may result from either small V^TOT in the absence of co-variation ( Δ V = 0) or larger V^TOT in the presence of co-variation ( Δ V > 0). To disambiguate changes in the index of co-variation (synergy index) with object fragility, we analyzed separately changes in V^TOT and V^P.

Statistics

The data are presented in the text and figures as means and standard errors. Mixed model analyses of variance (ANOVAs) were performed on the kinematic and kinetic data with the factors: FR-index (four levels; 0.45, 0.37, 0.24, and 0.15), Hand (three levels; Right, Left, and Two-Hand), and Interval (four possible levels; the first 10% of movement time ( Δ T₁), 45–55% of movement time ( Δ T₂), the last 10% of movement time ( Δ T₃), and the averaged value of the first and last 10% of movement time ( Δ T_1–3)). Note that Intervals Δ T₁ and Δ T₃ were used in analysis of kinetic data to explore possible effects of grip force increase after a quick action, while Intervals Δ T_1–3 and Δ T₂ were used in the analysis of synergy and variability indices to explore possible non-monotonic changes in those indices over the movement trajectory. Statistical analyses did not show significant differences between intervals Δ T₁ and Δ T₃ with respect to the kinetics data; hence, the kinetics data were averaged over these two intervals and presented as referring to a new interval, Δ T_1–3.

A random factor of Subject (14 levels; one for each subject) was also used in the statistical analyses; however significant effects of this factor are not necessarily interpretable and thus not presented in this paper. Post-hoc pair-wise comparisons were performed using Tukey’s tests. Bonferroni corrections were also used to analyze significant effects of ANOVAs with a controlled experiment-wise error rate for the multiple comparisons performed.

Safety margins, R² values from the regression analysis between grip and load forces, and Δ V data were subjected to Fisher z-transformation to mitigate the ceiling effects inherent to these variables. Non-transformed data are presented in the figures to avoid confusion. T-tests with Bonferroni corrections were performed to compare Δ V indices with zero.

Results

This section is organized in the following manner: the results for kinematic data, such as object acceleration, movement time, and (normalized) mean squared jerk, are presented in Part I. The results for kinetic data, normal (grip) force, safety margins, and the correlation between grip and load forces are presented in Part II. In Part III of this section, analyses of the Δ V indices for grip force [ Δ V(F^G)] are presented for the two hierarchical levels (VF-TH and IF levels).

Part I: Kinematics

Basic Movement Patterns

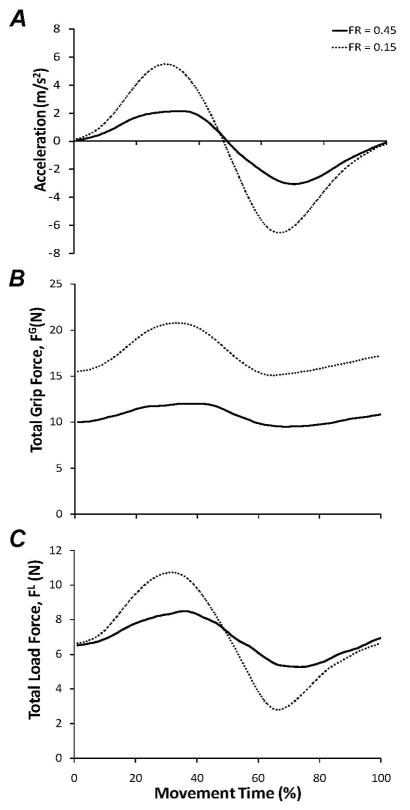
Typical movement trajectories were smooth, sigmoid, with bell-shaped velocity and double-peaked acceleration (positive and negative, or acceleration and deceleration, peaks) across all conditions tested in this experiment. An example of a typical acceleration profile can be found in Figure 3A for the most fragile and least fragile objects tested; FR = 0.45 and FR = 0.15, respectively. Object acceleration rapidly increased in the first 30% of total movement time then decreased rapidly to a minimum (negative maximum) around 60% of total movement time. Similar features in both total grip and load forces were also found across subjects and tested fragility indices. Examples of typical total grip and load force profiles for the most fragile and least fragile objects (FR = 0.45 and FR = 0.15, respectively) can be found in Figures 3B and 3C.

Figure 3.

Average object acceleration, total grip force, and total load-bearing force (the sum of VF and thumb tangential forces) profiles of a typical subject in trials with the most and least fragile objects (FR-indices of 0.45 and 0.15, respectively). A: Object acceleration. B: Total grip force. C: Total load-bearing force.

Object Acceleration

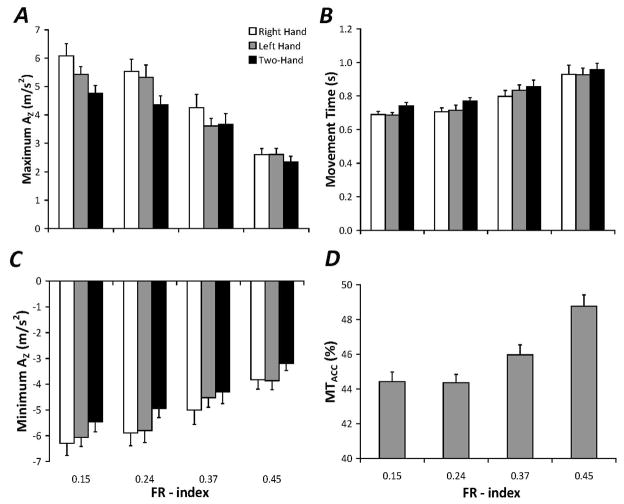
Analysis of object acceleration showed that peak acceleration (maximum A_Z) decreased by 50% as FR-index increased, shown in Figure 4A. Maximum A_Z was largest during movements performed by the right hand and lowest in movements performed by the two-hands (on average, by 17%). These differences were confirmed via mixed-effects ANOVA; main effects of FR-index (F_3,142 = 68.99, p < 0.001) and Hand (F_2,142 = 9.12, p < 0.001) were found with no interactions. Pairwise post-hoc Tukey testing indicated that maximum A_Z was significantly different among FR-indices in the following manner: A_Z (0.15), A_Z (0.24) > A_Z (0.37) > A_Z (0.45). In addition, post-hoc testing also confirmed that maximum A_Z was largest in right hand tasks and lowest in two-hand tasks.

Figure 4.

Mean and standard error of maximum object acceleration (A_Z), minimum object acceleration, total movement time (MT), and percent of movement time in which object was accelerated in the +Z direction (MT_ACC). Data are shown for the four different FR-indices for each of the hand conditions in Panels A–C. Data averaged across hand conditions is presented in Panel D. A: Maximum A_Z. B: Total movement time. C: Minimum A_Z. D: MT_ACC.

Similarly, the magnitude of peak deceleration (minimum A_Z) decreased by 39% as object fragility increased, as shown in Figure 4C. The magnitude of minimum A_Z was largest during movements performed by one-hand (by either the right or left hand separately) as compared to two-hand movements (on average, by 13%). These differences were confirmed via a mixed effects ANOVA; main effects of FR-index (F_3,142 = 35.52, p < 0.001) and Hand (F_2,142 = 7.32, p < 0.001) were found with no interactions. Pair-wise post-hoc testing indicated that the magnitude of minimum A_Z was significantly different among FR-indices in the same manner as maximum A_Z: A_Z (0.15), A_Z (0.24) > A_Z (0.37) > A_Z (0.45). In addition, post-hoc testing also confirmed that the magnitude of minimum A_Z was larger in one-hand tasks than in two-hand tasks.

Movement Time

Overall, MT was longest for the most fragile object, as shown in Figure 4B. These findings were confirmed with a mixed-effects ANOVA; main effects of FR-index (F_3,142 = 49.5, p < 0.001) and Hand (F_2,142 = 4.03, p < 0.05) were found with no interactions. Pairwise post-hoc testing indicated that MT was significantly different among FR-indices in the following manner: MT(0.15), MT(0.24) < MT(0.37) < MT(0.45). Post-hoc testing did not indicate any significant differences across the tested Hand conditions.

The subjects spent more time decelerating the object than accelerating it; this difference was pronounced for less fragile objects. The percent of movement time in which the object was accelerating in the +Z direction (MT_ACC) was significantly less than 50% of overall movement time (mean = 45.84 ± 4.05; t = −13.29, p < 0.001) across the tested conditions. Object fragility affected MT_ACC, such that an increase in the FR-index was associated with an increase in MT_ACC, as shown in Figure 4D. This was confirmed with a mixed-effects ANOVA; a main effect of FR-index (F_3,142 = 21.71, p < 0.001) was found. Post-hoc testing indicated that MT_ACC was largest for the most fragile object (FR-index = 0.45) compared to the remaining FR-indices; no other differences were found.

(Normalized) Mean Squared Jerk

The effect of object fragility on mean squared jerk (MSJ) and normalized mean squared jerk (NMSJ) is depicted in Figures 5A and 5B. As FR-index increased, MSJ decreased (on average, by 72%), and movements with the right hand exhibited about 38% higher MSJ as compared to two-hand movements. These effects were confirmed with a mixed-effects ANOVA; main effects of FR-index (F_3,142 = 25.32, p < 0.001) and Hand (F_2,142 = 8.77, p < 0.001) were found with no interactions. Pairwise post-hoc testing indicated that MSJ (FR = 0.15, 0.24) > MSJ(FR = 0.37, 0.45) . In addition, post-hoc testing indicated that movements with the right hand had significantly larger MSJ values as compared to movements with two-hands.

Figure 5.

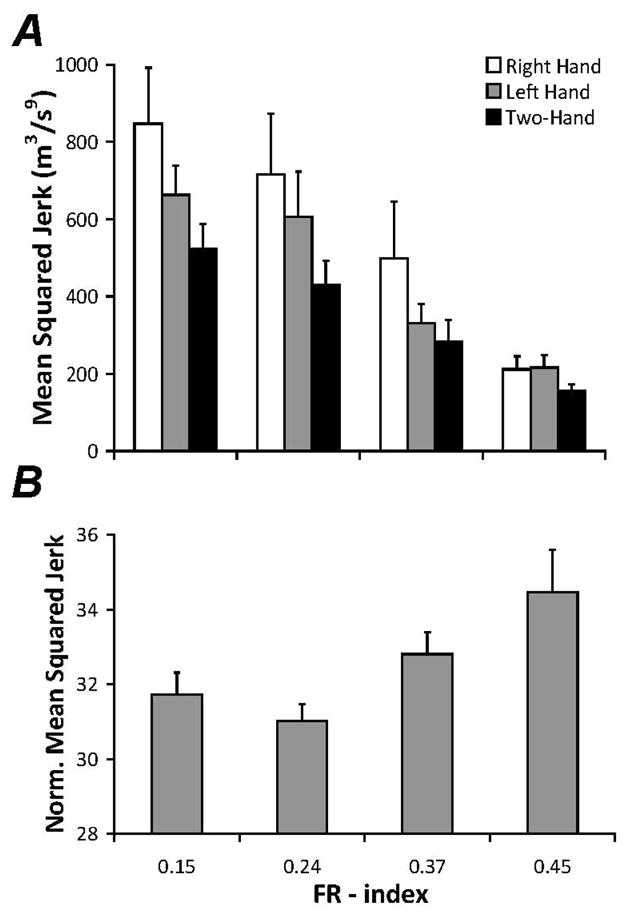
Mean and standard error of mean squared jerk (MSJ) and normalized mean squared jerk (NMSJ). Data are shown for the four different FR-indices for each of the hand conditions in Panel A, data averaged across hand conditions are presented in Panel B. A: Mean squared jerk. B: Normalized mean squared jerk.

Analysis of NMSJ only showed an effect of object fragility; NMSJ increased by about 9% as FR-index increased. This was confirmed with a main effect of FR-index (F_3,142 = 4.66, p < 0.01) with no effect of Hand and no interactions. Post-hoc analysis indicated that NMSJ (FR = 0.24) < NMSJ (FR = 0.45); no other significant effects were found.

Part II. Kinetics

In this section, data analysis is presented only for the VF-TH (task) level. Additionally, the data on correlation between the grip and load forces (at the VF-TH level) are included at the end of this section.

Grip Force (F^G)

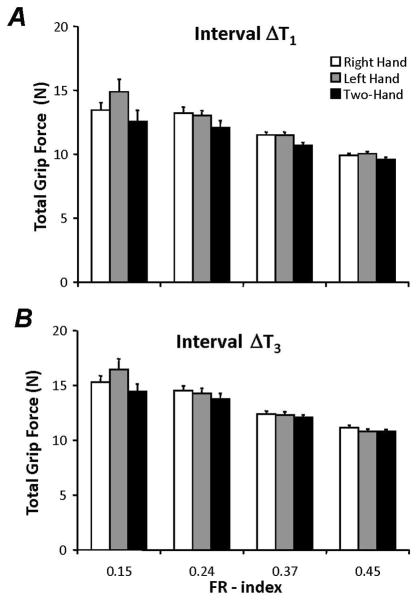
Overall, the average total grip force was 12.5 ± 0.1 N across all the tested conditions and intervals. The grip forces produced by the VF and opposing effector were nearly perfectly matched; on average, the VF force was 99.4% of the thumb force. Total grip force was lowest when two hands were used together, for the most fragile object, and at the onset of movement (in Figures 6A and 6B). These effects were confirmed using a mixed effects ANOVA; main effects of FR-index (F_3,297 = 108.77, p < 0.001), Hand (F_2,297 = 9.58, p < 0.001), Interval (F_1,297 = 57.78, p < 0.001), and the interaction Hand × FR-index (F_6,297 = 2.42, p < 0.05) were found. Pair-wise post-hoc testing confirmed that grip forces significantly decreased as FR-index increased; F^G (0.15) > F^G (0.24) > F^G (0.37) > F^G (0.45). Post-hoc testing also confirmed that grip force was significantly lower in two-hand tasks as compared to one-hand tasks and was lowest in the first 10% of movement time.

Figure 6.

Mean and standard error of total grip force produced at the VF-TH level. Data are shown for the four different FR-indices in Panels A and B for each of the hand conditions. A: Total grip force in Interval Δ T₁. B: Total grip force in Interval Δ T₃.

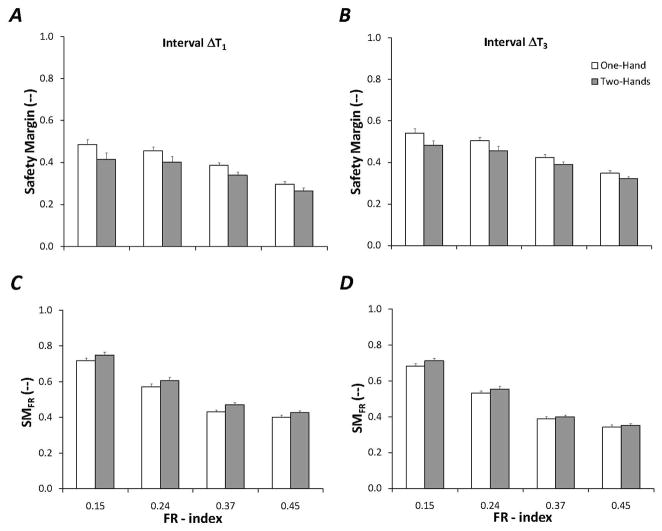
Safety Margin (SM)

Overall, safety margin dropped as FR-index increased, as shown in Figures 7A and 7B, from about 0.5 to about 0.3 (by 40%). Additionally, an effect of hand(s) used in the task was found, such that safety margin in one-hand tasks was larger than safety margin in two-hand tasks by about 10%. An effect of interval was also found, indicating that safety margin was larger at the end of movement by 12%. These effects were confirmed using a mixed effects ANOVA; main effects of FR-index (F_3,297 = 176.01, p < 0.001), Hand (F_2,297 = 28.43, p < 0.001), and Interval (F_1,297 = 76.49, p < 0.001) were found with no interactions. Pair-wise post- hoc testing indicated that SM(FR = 0.15) > SM(FR = 0.24) > SM(FR = 0.37) > SM(FR = 0.45). In addition, post-hoc testing also showed that safety margin was lowest in two-hand movements as compared to movements by the right and left hands separately.

Figure 7.

Mean and standard error of safety margin (SM) and safety margin due to object fragility (SM_FR). Data are shown for the four different FR-indices for one- and two-hand conditions. A: SM in Interval Δ T₁. B: SM in Interval Δ T₃. C: SM_FR in Interval Δ T₁. D: SM_FR in Interval Δ T₃.

Safety Margin due to Object Fragility (SM_FR)

Recall that SM_FR was computed as the difference between the force required to crush an object and the total grip force applied to the object; this quantity is subsequently normalized by the maximum allowable applied force to the object prior to collapse to allow for comparison across conditions. Analyses indicated that SM_FR decreased as object fragility increased, SM_FR was larger (by about 5%) for two-hand tasks as compared to one-hand tasks, and SM_FR was larger by 9% in the Δ T₁ time interval as compared to Δ T₃, as illustrated in Figures 7C and 7D.

These effects were confirmed using a mixed effects ANOVA; main effects of FR-index (F_3,297 = 978.16, p < 0.001), Hand (F_2,297 = 13.49, p < 0.001), and Interval (F_1,297 = 94.05, p < 0.001) with no interactions were found. Post-hoc testing confirmed that SM_FR dropped as FR-index increased in the following manner: SM_FR (0.15) > SMF_FR (0.24) > SM_FR (0.37), SM_FR (0.45). Also, SM_FR was found to be larger for two-hand movements as compared to movements made by either the right or left hand separately.

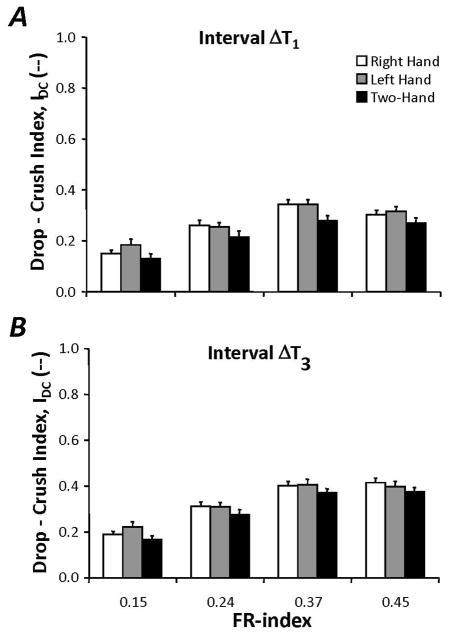
Drop – Crush Index (I_DC)

We also computed an index reflecting the combined effect of both the slip and crush thresholds on total grip force, the drop-crush index (I_DC). For this index, the numerator is the difference between the total applied grip force and the slip threshold of the object, and the denominator is the difference between the crush threshold and the slip threshold of the object. An illustration of the crush and drop thresholds with respect to the total applied grip force (averaged across trials) for a typical subject can be found in Figures 2A and 2B.

Overall, I_DC increased by about 99% as object fragility increased, I_DC was larger in one-hand tasks (on average, by 16%) as compared to two-hand tasks, and this index was largest in the final 10% of movement time, as shown in Figure 8A and 8B. These effects were confirmed using a mixed-effects ANOVA; main effects of FR-index (F_3,297 = 177.21, p < 0.001), Hand (F_2,297 = 17.59, p < 0.001), Interval (F_1,297 = 109.96, p < 0.001) and the interaction FR-index × Interval (F_3,297 = 4.18, p < 0.01) were found. Post-hoc tests confirmed that I_DC increased as FR-index increased in the following manner: I_DC (0.15) < I_DC (0.24) < I_DC (0.37) < I_DC (0.45) and that I_DC was larger for one-hand movements as compared to movements made by two hands together. Subsequent analysis of the FR-index × Index interaction showed that I_DC increased as object fragility increased; however, the values of I_DC for the FR-indices (0.45) and (0.37) were not significantly different from each other during interval Δ T₃.

Figure 8.

Mean and standard error of the drop-crush index (I_DC) for the four different FR- indices for each of the hand conditions. A: Drop-crush index (I_DC) in Interval Δ T₁. B: Drop-crush index (I_DC) in Interval Δ T₃.

Correlation Between Grip and Load Forces

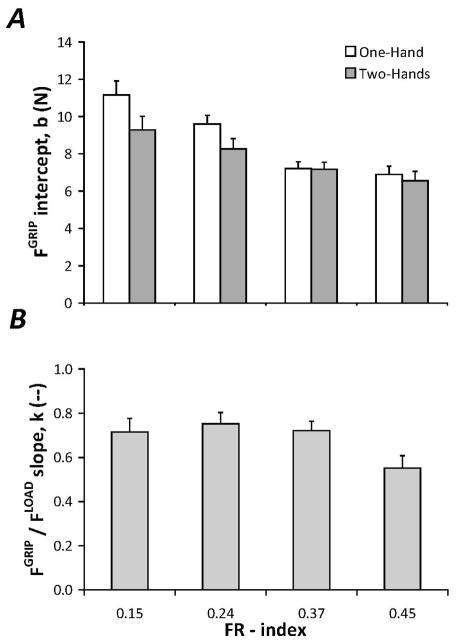
Overall, the total grip force correlated strongly with the load force during movement of the object (R² = 0.79, p < 0.001). As object fragility increased, the square of the correlation coefficient (R²) decreased and movements performed by one hand had overall higher R² as compared to two-hand movements. These effects were confirmed via a mixed-effects ANOVA on the Fisher-transformed R² values; main effects of FR-index (F_3,140 = 4.54, p < 0.01) and Hand (F_2,140 = 3.59, p < 0.05) were found with no interactions. Post-hoc testing indicated that the only significant difference in the R² values was between the two lowest FR-indices. No pair-wise post-hoc differences were detected for Hand.

Linear regression of total grip force on load force yielded results indicating that, given the equation F^G = b + k*F^L, both the force intercept (b) and the slope of the regression equation (k) decreased as object fragility increased, by 33% and 22% respectively (illustrated Figure 9A and 9B). The force intercept (b) was lower for two-hand movements compared to one-hand movements while the regression coefficient (k) was not affected by hand condition. Main effects on both the intercept and slope were confirmed via a mixed-effects ANOVAs, respectively; main effects of FR-index (b: F_3,140 = 38.37, p < 0.001; k: F_3,140 = 10.73, p < 0.001) and Hand (b: F_2,140 = 6.36, p < 0.005; k: no effect) were found with no interactions. Post-hoc testing for the force intercept (b) indicated that b(FR = 0.15) > b(FR = 0.24) > b(FR = 0.37), b(FR = 0.45); while the k(FR = 0.15), k(FR = 0.24), k(FR = 0.37) > k(FR = 0.45). Post-hoc testing indicated that the force intercept was lower for two-hand conditions compared to one-hand conditions.

Figure 9.

Mean and standard error of the force intercept (b, Panel A) and slope term (k, Panel B) from the linear regression of total grip force on total load force; data are shown for the four different FR-indices for one- and two-hand conditions in Panel A and across hand conditions in Panel B. A: Average grip force intercept (b). B: Average slope (grip force /load force; k).

Part III. Synergies

In this section, we investigate how the synergy index ( Δ V) for grip force and the two variance indices related to the synergy index (see Methods) change across the conditions. Analysis was performed for both levels of the proposed hierarchy (VF-TH and IF levels). Overall, it was found that Δ V decreased with increasing object fragility at the VF-TH level while it increased at the IF level. The amounts of variance affecting task performance (V^P) and total variance in the space of elemental variables (V^TOT) both decreased with increasing object fragility at both hierarchical levels, suggesting that the CNS used a smaller range of task solutions during transport of fragile objects. In addition, both V^P and V^TOT were lower during the first and last 10% of movement time as compared to the middle of the movement, and in tasks in which two hands were used together. The following subsections describe the statistical results of this analysis in detail.

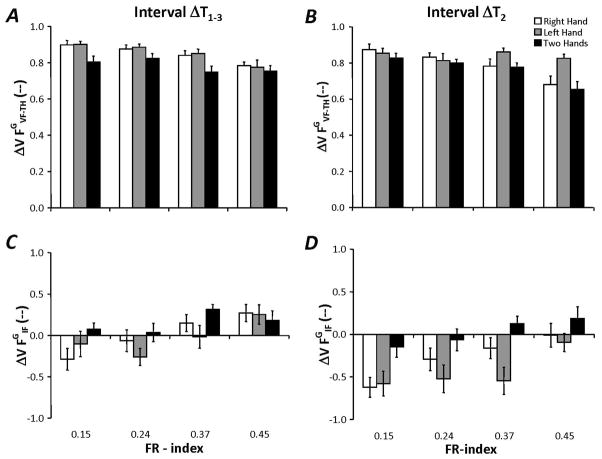
Synergy Index for Grip Force, Δ V(F^G)

In order to quantify grip force stabilizing synergies, indices of grip force co-variation, Δ V(F^G), were calculated at the VF-TH and IF levels. Overall, there were F^G stabilizing synergies ( Δ V > 0) only at the VF-TH level across all tested conditions. This finding was confirmed using individual t-tests with Bonferroni corrections [ Δ V(F^G)_VF-TH = 0.814 ± 0.006, t = 121.11, p < 0.001; Δ V(F^G)_IF = 0.092 ± 0.029, t = −3.23, p > 0.1]. It was found that as object fragility increased, Δ V decreased by about 13%, one-hand tasks resulted in stronger synergies as compared to two-hand tasks ( Δ V higher by 7%), and synergies were larger during the first and last 10% of movement time ( Δ T_1–3) as compared to Δ T₂ ( Δ V higher by 4%). These effects are illustrated in Figures 10A and 10B. They were confirmed using a mixed-effects ANOVA on the Fisher transformed Δ V(F^G)_VF-TH values; main effects of FR-index (F_3,297 = 23.54, p < 0.001), Hand (F_2,297 = 19.36, p < 0.001), and Interval (F_1,297 = 7.39, p < 0.01) were found with no interactions. Post-hoc analysis showed that Δ V(F^G)_VF-TH (0.15) > Δ V(F^G)_VF-TH (0.24), Δ V(F^G)_VF-TH (0.37) > Δ V(F^G)_VF-TH (0.45). Additionally, post-hoc testing also indicated that Δ V(F^G)_VF-TH was lowest in two-hand movements as compared to movements performed by the right and left hands separately. No difference between the right and left hands was found.

Figure 10.

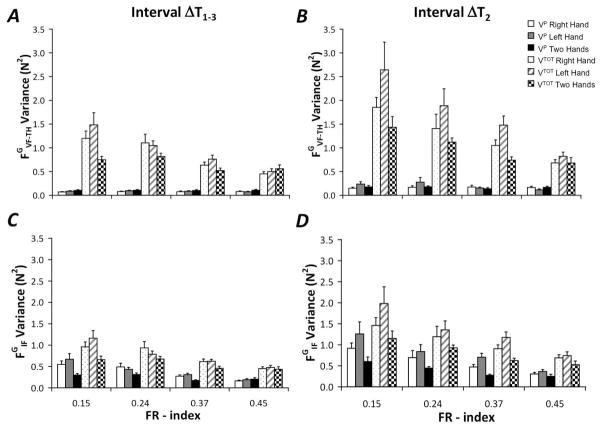
Mean and standard error of indices of co-variation of grip forces ( Δ V(F^G)) at the VF-TH and IF levels of the proposed synergy hierarchy [denoted by the subscripts, individual finger level (IF) and virtual finger – thumb level (VF-TH)]. Data are shown across the four tested FR-indices for each of the hand conditions. A: Δ V(F^G)_VF-TH in Interval Δ T_1–3. B: Δ V(F^G)_VF-TH in Interval Δ T₂. C: Δ V(F^G)_IF in Interval Δ T_1–3. D: Δ V(F^G)_IF in Interval Δ T₂.

Overall, Δ V(F^G)_IF indices became more positive as object fragility increased, the left hand tasks yielded lower Δ V(F^G)_IF as compared to two-hand tasks, and Δ V(F^G)_IF was largest in the first and last 10% of movement time, shown in Figures 10C and 10D. These effects were confirmed with a mixed-effect ANOVA; main effects of FR-index (F_3,297 = 8.78, p < 0.001), Hand (F_2,297 = 7.59, p < 0.001), Interval (F_1,297 = 22.61, p < 0.001), and the Hand × FR-Index interaction (F_6,297 = 2.44, p < 0.05) were found. Post-hoc testing indicated that Δ V(F^G)_IF was most positive for the most fragile object (FR = 0.45) as compared to more sturdy objects (FR = 0.24 and 0.15). Post-hoc testing also indicated that Δ V(F^G)_IF was largest for two-hand tasks as compared to left hand tasks; however, no significant pairwise differences with respect to the Hand × FR-Index interaction were found.

Analysis of Grip Force Variance

The analysis of V^TOT and V^P for the grip forces showed significant effects on both indices of the same factors (FR-index, Hands, and Interval) that showed significant effects in the analysis of Δ V. This was true at both the VF-TH and IF levels. Average values of the two variance indices at the two hierarchical levels were: V^TOT(F^G)_VF-TH = 0.9855 ± 0.0385 N²; V^P(F^G)_VF-TH = 0.1180 ± 0.0049 N²; V^TOT(F^G)_IF = 0.8114 ± 0.0283 N²; V^P(F^G)_IF = 0.4255 ± 0.0193 N².

Analysis of V^TOT and V^P at the VF-TH level indicated that V^TOT decreased by 59% as object fragility increased, it was lower by 61% in Δ T_1–3 as compared to Δ T₂, and it was lower for the two-hand tasks as compared to one-hand tasks (by 29%). V^P showed significant effects of only time interval, such that it was lower by 49% in Δ T_1–3 as compared to Δ T₂. These effects are illustrated in Figures 11A and 11B and were confirmed using mixed -effects ANOVAs on the values of V^TOT and V^P; main effects of FR-index (V^TOT: F_3,484 = 34.56, p < 0.001; V^P: no effect), Hand (V^TOT: F_2,484 = 15.09, p < 0.001; V^P: no effect), and Interval (V^TOT: F_1,484 = 53.84, p < 0.001; V^P: F_1,484 = 99.41, p < 0.001) were found with no interactions. Post-hoc analysis showed significant differences in V^TOT(VF-TH) across FR-indices such that: V^TOT(F^G)_VF-TH (0.15) > V^TOT(F^G)_VF-TH (0.24) > V^TOT(F^G)_VF-TH ^(0.37), V^TOT(F^G)_VF-TH (0.45). Additionally, post-hoc tests indicated that V^TOT(VF-TH) was lowest in two-hand tasks as compared to tasks performed by the right and left hands separately. No difference between the hands was found.

Figure 11.

Mean and standard error of grip force (F^G) variance measures V^TOT and V^P at the VF-TH and IF levels of the proposed synergy hierarchy, abbreviations are the same as in Figure 10. Data are shown across the four tested FR-indices for each of the hand conditions. A: F^G variance at the VF-TH level in Interval Δ T_1–3. B: F^G variance at the VF-TH level in Interval Δ T₂. C: F^G variance at the IF level in Interval Δ T_1–3. D: F^G variance at the IF level Interval Δ T₂.

Analysis at the IF level showed that both V^TOT and V^P decreased as object fragility increased (by 54% and 65%, between the lowest and highest FR-indices), were lower in Δ T_1–3 as compared to Δ T₂ (by 35% and 43%, respectively), and were lowest for the two-hand tasks (by 29% and 42%, respectively, as compared to data averaged across the one-hand tasks). These results are illustrated in Figures 11C and 11D. The effects were confirmed by mixed-effects ANOVAs on the values of V^TOT and V^P; main effects of FR-index (V^TOT: F_3,484 = 33.47, p < 0.001; V^P: F_3,484 = 33.91, p < 0.001), Hand (V^TOT: F_2,484 = 15.21, p < 0.001; V^P: F_2,484 = 18.42, p < 0.001), and Interval (V^TOT: F_1,484 = 58.36, p < 0.001; V^P: F_1,484 = 58.42, p < 0.001), and the interaction Hand x FR-index (V^TOT: no effect; V^P: F_6,484 = 2.97, p < 0.01) were found. Post-hoc analysis showed significant differences of both variance indices across FR-indices such that: FR-index (0.15) > FR-index (0.24) > FR-index (0.37), FR-index (0.45). Post-hoc analysis also indicated that both variance indices were lowest for the two-hand conditions as compared to one-hand tasks. Analysis of the Hand × FR-index interaction for V^P indicated that, as FR-index increased, V^P in two-hand tasks became significantly lower than V^P in one-hand tasks.

Discussion

In the Introduction, seven hypotheses were formulated; in summary, one of them has been falsified in this experiment while the other six have been at least partly supported. In particular the experiments have shown that moving fragile objects is associated with lower grip force, lower safety margin, an increase in movement time, a decrease in the magnitude of object peak acceleration, smaller integrated jerk index, and higher jerk index normalized by movement time. The coupling between grip and load forces was confirmed across all tested conditions, although a decrease in the correlation coefficient between the two was found during the transport of fragile objects. In addition, the two novel indices, safety margin due to object fragility and drop-crush index also showed decreases for more fragile objects. Synergies stabilizing grip force were found at the upper level of the assumed two-level hierarchy while synergies at the lower level were absent for sturdy object and emerged for fragile objects. A drop in the synergy index at the upper level was accompanied by a drop in the total amount of variance in the space of elemental variables at the upper level corresponding to a smaller range of solutions used to satisfy the task requirements when manipulating fragile objects.

The fifth hypothesis addressed the dynamic dominance theory of handedness (Sainburg 2005; Wang and Sainburg 2007). We expected movements produced by the right (dominant) hand to be associated with smaller normalized jerk and higher object accelerations as compared to the movements performed by the left hand. This hypothesis was falsified; in general, no significant differences were found between the right (dominant) and left (non-dominant) hands. In the following sub-sections of the Discussion, we address implications of the main results for handling fragile and non-fragile objects.

How to not crush a fragile object

When handling a fragile object, one obviously cannot apply forces above the crushing threshold. On the other hand, gripping force has to be sufficient to allow application of necessary forces to counteract the gravity and inertial forces. So, if one has to move a vertical fragile object in the vertical direction (as in our study), there are three mutually non-exclusive ways to ensure that the object neither collapses nor slips out of the hand during such a movement. First, one can decrease the safety margin at rest, that is the gripping force produced above the slipping threshold, and thus make more room for motion-related grip force adjustments. Second, one can try to decrease the peak inertial force by moving slower. Third, the subjects could change the scaling of gripping force with load-bearing force (Flanagan and Wing 1993, 1995; Flanagan and Tresilian 1994; Flanagan et al. 1993; Wing et al. 1997). Potentially, this could lead to violation of the established strong coupling between the grip and load forces (Winges et al. 2009). The data show that the subjects employed each of these three strategies. They decreased the safety margin at rest, achieved lower peak acceleration values, and attenuated the relationship between the grip and load forces.

The weaker coupling between the grip and load forces was found across all objects tested in this study. The parameters of this coupling changed with the fragility index of the object tested in this study: With an increase in the fragility index, the subjects showed both a drop in the grip force at steady-state and a decrease in the regression coefficient between grip and load forces. The force drop at steady-state suggests an important contribution of feedback loops from sensory receptors to grip force adjustment (Boudreau and Smith 2001; Johansson 1996, 1998). In contrast, adjustments of grip force to expected inertial forces are most commonly discussed as results of a feed-forward control process based on an estimation of inertial forces, in particular, because of the lack of a time delay between force and acceleration signals (Flanagan et al. 1993; Flanagan and Tresilian 1994; Flanagan and Wing 1993; Wing et al. 1997). The gain of this adjustment may be set in advance using sensory information, for example related to partial slip of the object (cf. Flanagan and Wing 1995) experienced during practice trials.

As far as changes in the trajectory time profile are concerned, the data showed that the subjects spent proportionally more time accelerating fragile objects as compared to non-fragile objects. This could be a consequence of slowing down that is known to lead to an increase in the acceleration time in proportion to total movement time (Jaric et al. 1993, 1998; Wiegner and Wierzbicka 1992). Changes in the jerk index normalized by movement time also suggest adjustments in the movement kinematic profile, namely performing movement less smoothly during the transport of fragile objects (cf. Flash and Hogan 1985; Teulings et al. 1997).

Is it better to risk crushing or dropping an object?

In handling an object in most everyday situations, there are two primary constraints to prehension: don’t drop the object and don’t crush it. Previous work in multi-finger prehension has focused on manipulation of rigid objects that were never at risk of collapsing (reviewed in Zatsiorsky and Latash 2008; Latash and Zatsiorsky 2009). The novel device designed for this study allowed us to introduce a new index, the drop-crush index (I_DC) reflecting how the CNS deals with the two competing prehension constraints. The data presented in this study consistently suggest that the applied grip forces decrease during prehension of more fragile objects. However, as object fragility increases, the amount of applied grip force gets closer to the crush threshold within the drop-crush range, suggesting that subjects would rather crush fragile objects as opposed to dropping them.

The tendency for people to apply relatively high forces at an increased risk of crushing an object as opposed to dropping it may stem from a combination of psychological and physiological factors. While it is not specifically known why subjects in this study preferred to risk crushing the object as opposed to dropping it, we suspect that this observation might be due to the formulation of the task. In particular, the subjects likely realized that the handle with sensors was a highly sensitive (and expensive!) device and that dropping it would probably mean the end of the study. On the other hand, the subjects were instructed to “crush” the object during practice, and they knew that crushing was safe. We can only speculate that, if subjects were given a task in which the consequences of crushing the object were more extreme, such as crushing an expensive and highly decorated egg, while there were a pillow under the object, then the results might have been different: The subjects might have shown values of I_DC reflecting a preference for dropping the object onto the soft surface.

Is it better to move objects with one hand or two?

A set of previous papers analyzing finger forces and moments of force in static prehensile tasks reported differences in both the mechanical output and synergy indices between one- and two-hand tasks (Gorniak et al. 2009a,b). In particular, in those earlier studies, the subjects applied higher grip forces (and higher safety margins) while holding statically an object with one hand as compared to holding the same object with two hands. While there were no significant differences found between performance variables during tasks performed by the dominant (right) and non-dominant (left) hands, one-hand tasks differed from two-hand tasks in this study as well. Specifically, one-hand tasks were associated with larger values of object acceleration, safety margin, and drop-crush index as compared to two-hand tasks. In the earlier study of static prehension tasks (Gorniak et al. 2009a), we suggested that the higher safety margin in one-hand tasks could be related to the mode of control that allows the use of a single referent variable (referent aperture, Pilon et al. 2007; Feldman and Levin 2009; Gorniak et al. 2009c) to control grip force. In two-hand tasks this mode of control may be unavailable, possibly because of the involvement of the two hemispheres, and the subjects have to define referent coordinates for each of the opposing effectors (cf. Smeets and Brenner 1999). Note that using a single referent aperture ensures that the resultant force in the horizontal direction is zero, i.e., that the object does not move in that direction. Controlling the two opposing effectors requires adjustments of the two referent coordinates to ensure that the two opposing normal forces are equal in magnitude and satisfy the constraints of statics.

Another factor that might have influenced the results is the fact that moving an object with one hand is a common everyday task, while moving a relatively small object with two hands in unusual (cf. Cesari and Newell 2000). The subjects could feel less confident in performing two-hand tasks, which resulted in slower movements and proportionally smaller grip force values. Note that force variability is known to scale with force magnitude (reviewed in Newell and Carlton 1988), so a decrease in force magnitude produced by each of the opposing effectors could be expected to lead to lower force variability indices and overall better chances to overcome consequences of a disadvantage associated with using two referent variables rather than one.

With respect to grip force synergies, the synergy index ( Δ V) at the higher hierarchical level was larger for unimanual tasks. However, synergies at the lower hierarchical level were stronger in bimanual tasks. This may be a direct consequence of the trade-off between synergies at the two hierarchical levels (Gorniak et al. 2007b; 2009b; Latash et al. 2008). Exploring a wider range of elemental variables that solve the task at the upper level of the hierarchy is associated with higher VF-TH synergy indices, while it also leads to larger variance in the VF force. This makes it harder for the controller to organize a synergy at the IF level. This hypothesis has been supported by our current findings. Indeed, at higher FR-index values, we observed an increase in the synergy indices at the IF level for the normal force and a drop in those indices at the VF-TH level.

The differences between the unimanual and bimanual prehension tasks may also be due to the over-practiced nature of the tested unimanual tasks in comparison to the relative novelty of the bimanual tasks tested in this and other similar experiments (Cesari and Newell 2000; Gorniak et al. 2009a,b; Kang et al. 2004). The task to move the object vertically required the resultant normal force to be zero at all times. This means that the normal forces applied by the thumb and VF had to co-vary negatively (confirmed by the study of Δ V indices at the VF-TH level). Note, however, that using higher force magnitudes is likely to be associated with proportionally higher variance (Newell and Carlton 1993; Slifkin and Newell 2000). So, in better practiced, unimanual tasks, where the controller could be expected to organize better force stabilizing synergies at the upper level, higher forces could be used.

No differences in synergy indices between conditions testing the right (dominant) and left (non-dominant) hands were found. This non-finding fails to support the dynamic dominance hypothesis (Sainburg 2002, 2005; Wang and Sainburg 2007) despite the fact that our subjects were all strongly right-handed, as in studies by the group of Sainburg.

Fragility as a constraint

Given the wide variety of tasks presented to us each day, many of the objects we manipulate are fragile in one sense of the word or another. The issue of manipulating fragile objects has been barely touched upon in studies of prehension. In particular, a recent study of Winges and colleagues (Winges et al. 2009) focused on the grip and load forces produced by digits in a three-digit grasp when one of the digits could act against a compliant surface. These authors report a decoupling between the grip and load forces for digits that acted against the compliant surface. This result is qualitatively similar to our observations of the correlation between the two forces, although in our study the two forces remained tightly coupled when moving fragile objects, and the changes in the R² magnitude were modest.

A method of studying grip and load force production while avoiding net moment of force production on the grasped object has been recently developed and applied to actions similar to picking a raspberry by healthy persons and patients with cerebellar disorders (Kutz et al. 2009). This constraint resulted in adjustments of the prehensile actions that could distinguish between the patients and healthy persons. We view fragility as a rather common constraint for everyday actions that is likely to affect both patterns of digit forces and their co-variation profiles, and may have clinical implications.

The analysis of the two variance indices, V^P (the component of variance that affected overall performance) and V^TOT (total variance of elemental variables) has shown that, at the higher hierarchical level, a decrease in the synergy index ( Δ V) was associated with a decrease in V^TOT while V^P remained nearly constant as object fragility increased. This result suggests that a smaller range of solutions was used to satisfy the task requirements when manipulating fragile objects. In contrast, at the lower hierarchical level, an increase in Δ V was associated with a decrease in both V^TOT and V^P when handling more fragile objects, suggesting two simultaneous adjustments: A decrease in the range of tasks solutions and higher accuracy of the output of that level. The latter may be seen as a direct reflection of the new constraint related to fragility. However, the former is a consequence of choice by the CNS not directly imposed by the fragility constraint. Our study is only the first step towards understanding how the CNS controls manipulation of fragile objects, and analysis of variance components has to be continued.

Time profiles of synergy indices

Several earlier studies with quick changes in a performance variable, such as the total force, reported a drop in synergy indices stabilizing that performance variable; this drop typically happened at high rates of change of that variable (Latash et al. 2002; Olafsdottir et al. 2007; Friedman et al. 2009). These effects have been interpreted as consequences of timing errors across trials (Goodman et al. 2005). For grip force, the synergy index at both hierarchical levels (VF-TH and IF) showed only minor differences between the time intervals. At the higher hierarchical level, indices were always positive and could show a trend towards lower or higher values in the middle of the movement. Indeed, if the object moved only vertically, its acceleration in other directions was expected to be very low. Consequently, the jerk values were also low, and timing errors had little effect on the synergy indices at the higher hierarchical level. Synergy indices at the lower hierarchical level were generally lower during the middle of movement time, potentially due to timing errors across trials during this highly dynamic portion of the task.