Characterizing Recurrent Positive Selection at Fast-Evolving Genes in Drosophila miranda and Drosophila pseudoobscura

Abstract

Characterizing the distribution of selection coefficients in natural populations remains a central challenge in evolutionary biology. We resequenced a subset of 19 fast-evolving protein-coding genes in the sister species Drosophila miranda and D. pseudoobscura and their flanking regions to characterize the spatial footprint left by recurrent and recent selection. Consistent with previous findings, fast-evolving genes and their flanking regions show reduced levels of neutral diversity compared with randomly chosen genes, as expected under recurrent selection models. Applying a variety of statistical tests designed for the detection of selection at different evolutionary timescales, we attempt to characterize parameters of adaptive evolution. In D. miranda, fast-evolving genes generally show evidence of increased rates of adaptive evolution relative to random genes, whereas this pattern is somewhat less pronounced in D. pseudoobscura. Our results suggest that fast-evolving genes are not characterized by significantly different selection coefficients but rather a shift in the distribution of the rate of fixation.

A central goal of evolutionary biology is to understand the process of adaptation. This pursuit has resulted in a great interest to detect genes, or genomic regions, that have been targeted by positive selection, and a variety of statistical methods have been proposed—ranging from the detection of individual adaptive fixations (see review by Jensen, Wong, and Aquadro 2007), to the identification of rapidly evolving genes (see review by Nielsen 2005), and to the quantification of genomic rates of adaptation (see review by Sella et al. 2009). These approaches utilize either only polymorphism data within species (polymorphism-based approaches) or jointly consider patterns of polymorphism and sequence divergence between species (divergence-based approaches) and are designed to detect adaptation on different evolutionary timescales. Polymorphism-based approaches require the action of relatively recent positive selection, as patterns of variation indicative of selection (such as patterns in the site frequency spectrum [SFS] or linkage disequilibrium [LD] between mutations) are quickly obscured by subsequent mutation and recombination events, as well as genetic drift (Kim and Stephan 2002; Przeworski 2002). Divergence-based approaches additionally rely on recurrent fixations of beneficial mutations to detect significantly elevated levels of divergence relative to background substitution patterns (Nielsen 2005).

Thus, considering polymorphism- and divergence-based approaches simultaneously is of considerable interest because it may allow for the detection of selection on different timescales. For example, do divergence-based and polymorphism-based approaches identify the same set of genes undergoing adaptive evolution? That is, is the rate of adaptation great enough that, on average, a recent adaptive fixation will have occurred in a gene undergoing recurrent adaptation? Or are the same genes that were evolving adaptively in the past currently under positive selection as well? Similarly, are rates of adaptation inferred from divergence-based approaches in line with rates estimated by polymorphism-based methods? Discrepancies between methods could either reflect differences in power or performance (i.e., approach could either over- or underestimate rates of selection) or reflect on real biological differences (i.e., rates of adaptation may have changed over time due to changes in ecology or other population parameters, such as population size). By evaluating polymorphism- and divergence-based approaches simultaneously and attempting to reconcile them with one another, it may be possible to answer some of these questions and to consider the process of adaptation across a very broad evolutionary timescale.

It has recently been shown that genes that undergo high rates of protein evolution in Drosophila (high amino acid divergence, K_a) show reduced levels of synonymous site diversity (i.e., low π_s; Andolfatto 2007; Macpherson et al. 2007; Bachtrog 2008). This pattern is consistent with the idea of high rates of protein adaptation resulting in reduced levels of diversity in fast-evolving genes owing to the effects of genetic hitchhiking (i.e., divergence-based and polymorphism-based approaches might indeed identify the same set of genes). To look for the spatial footprint left behind by recent selection, we resequenced a subset of the fastest evolving protein-coding genes and their flanking regions from a previous screen of randomly selected regions across the X chromosome of Drosophila miranda and D. pseudoobscura (Bachtrog et al. 2009). In particular, we generated polymorphism data for the 19 fastest evolving protein-coding genes (i.e., the gene fragments displaying the largest K_a between D. miranda and D. pseudoobscura from an initial set of 111 X-linked genes) and closely linked noncoding regions (four regions for each gene identified, roughly 5 and 10 kb away from the region initially studied) in both D. miranda as well as D. pseudoobscura.

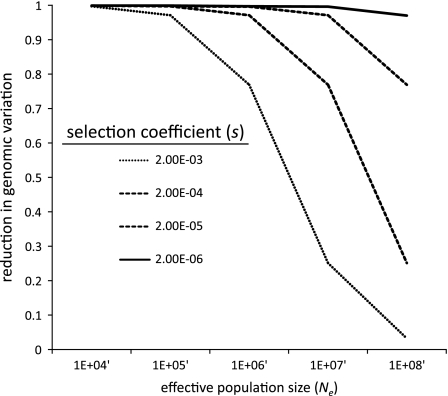
The comparison between these recently diverged species that differ in their effective population size (Loewe et al. 2006) is informative because patterns of adaptation may differ depending on underlying selection parameters. For example, the overall genomic effect of hitchhiking—that is, the average level of reduction in variation—is expected to differ in populations of different sizes. Assuming a fixed rate of mutation, recombination, and selection, figure 1 shows the expected reduction in diversity versus varying N_e for different values of s using the theoretical prediction of Wiehe and Stephan (1993). Selection is having a more pronounced effect as population size increases (fig. 1); thus, we a priori expect D. pseudoobscura to be impacted more by recurrent hitchhiking compared with D. miranda due to its larger effective population size.

FIG. 1.—

Plots of the expected reduction in variation due to recurrent hitchhiking based upon the theoretical prediction of Wiehe and Stephan (1993):

where θ = 4N_eμ (where N_e is the effective population size and μ is the mutation rate per site per generation), κ = 0.075 (a constant), λ = the rate of adaptive substitutions per site per generation, and γ = 2N_es (where s is the selection coefficient). By fixing μ, r, and λ, the effects of varying N_e on levels of polymorphisms are plotted for different values of s.

Patterns of Variation at Fast-Evolving Genes

Observed levels of variation at the 19 “fastest evolving” protein-coding genes varied greatly, with a mean synonymous diversity π_syn = 0.0034 in D. miranda and a mean π_syn = 0.0135 in D. pseudoobscura. Compared with randomly selected genes sampled in the same individuals (D. miranda mean π_syn = 0.0060; Bachtrog et al. 2009; D. pseudoobscura π_syn = 0.0171; Jensen JD, Bachtrog D, in preparation), levels of variation are significantly reduced in both species among our “fast-evolving” data set (Wilcoxon two-sample test, D. miranda, P < 7 × 10⁻⁴; D. pseudoobscura, P < 1 × 10⁻⁴). This observation is consistent with an increased rate of protein adaptation among the fast-evolving genes reducing linked neutral diversity owing to the effects of genetic hitchhiking (Wiehe and Stephan 1993). Also, Tajima's D is significantly more negative among the fast-evolving set of genes compared with random genes (mean D = −0.86 vs. D = −0.47 in D. miranda and D = −0.95 vs. D = −0.32 in D. pseudoobscura; Wilcoxon two-sample test, D. miranda, P < 2 × 10⁻⁴; D. pseudoobscura, P < 1 × 10⁻⁵). This indicates a greater excess of rare alleles within the fast-evolving class of genes in both species, an additional prediction consistent with models of frequent recurrent hitchhiking (Przeworski 2002).

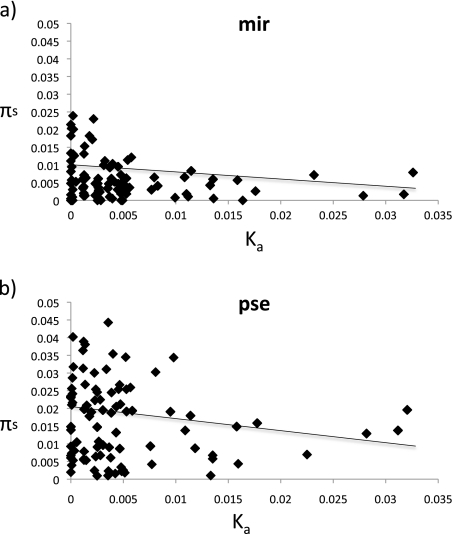
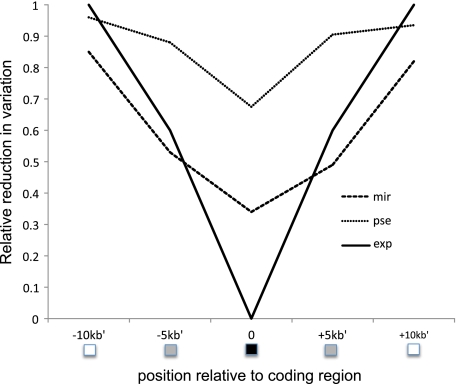
Consistent with previous observations in Drosophila (e.g., Andolfatto 2007), a significantly negative correlation is observed between K_a and π_s in both species (i.e., levels of synonymous site diversity are reduced in genes with rapid amino acid evolution; fig. 2). To investigate the spatial signature of selection acting on the fast-evolving genes, additional polymorphism data in flanking regions were obtained. Recent simulation studies have highlighted the utility of sequencing linked neutral regions to improve power and accuracy in estimating the parameters of selective events (Jensen, Thornton, and Aquadro 2008; Orengo and Aguade 2010). We generated 1 kb of sequence data both up- and downstream of the coding regions investigated at a distance of roughly 5 and 10 kb away for each gene (see schematic in fig. 3). Consistent with selection having recently acted directly at these protein-coding regions, average levels of polymorphism increase with distance from the identified fast-evolving exon (fig. 3). Note that our fast-evolving genes were not selected based on levels of diversity but solely based on showing elevated rates of protein evolution, thereby avoiding problems of ascertainment bias issues commonly encountered by genomic scans for selection (e.g., Thornton and Jensen 2007).

FIG. 2.—

Plot of synonymous diversity π_s versus amino acid divergence K_a. (a) Drosophila miranda: The pooled loci of both this study as well as the randomly selected genes of Bachtrog et al. (2009) are shown. (b) D. pseudoobscura: The pooled loci of homologous genes across the X chromosome. The solid line indicates the significant correlation between these measures of synonymous polymorphism and nonsynonymous divergence.

FIG. 3.—

A visual schematic of both the empirical and the simulation approaches taken here. On the x axis, the black box represents the coding region. In gray, a pair of regions are sequenced 5 kb up- and downstream. In white, another pair of regions are sequenced 10 kb up- and downstream. Table 2 compares the following three results: 1) black region only, 2) black + gray regions, and 3) black + gray + white regions. The solid line gives the expected levels of variation at these distances for a selective sweep occurring at position 0 (i.e., in the coding region)—where the length of the sequence = 1 kb, the beneficial mutation fixed at time (τ) = 0.0001 4N generations, θ = 0.01, ρ = 0.1, and α = 2Ns = 1000. Ten thousand replicates were simulated under each scenario. Overlaid are the observed relative reductions in variation among the 19 fast-evolving genes at each of the five regions for Drosophila miranda (dashed) and D. pseudoobscura (dotted).

Evidence for Recent Selective Sweeps in Fast-Evolving Protein-Coding Genes

In order to test for departures from neutrality in our fast-evolving gene set, a series of test statistics were employed. First, we utilized the composite likelihood ratio test (CLRT) of Kim and Stephan (2002), which detected 10 significant regions in D. miranda and 4 in D. pseudoobscura. The identical set of genes was identified as having undergone recent adaptive evolution utilizing the maximized composite likelihood surface (MCLS) method of Nielsen et al. (2005), which is based on a similar likelihood framework but instead utilizes the background SFS as the null model (table 1). Additionally, the CLRT procedure estimates the position of the selected site in the process of likelihood maximization, and, in all cases, the target prediction is within the coding region. However, previous studies have demonstrated that under a partial sampling scheme such as this, the performance of target estimation is extremely poor (Kim and Stephan 2002; Jensen, Thornton, and Aquadro 2008). Consistent with this result, confidence intervals (calculated via parametric bootstrapping) span nearly the entirety of the sampled regions.

Table 1.

Summary of Tests of Selection among 19 Fast-Evolving Genes in Drosophila miranda (D. pseudoobscura)

Gene Region	CLRT	GOF	MCLS	ω	MK	HKA
CG2841	0.02(0.02)	0.62(0.30)	0.01(0)
CG2984	0.01	0.34	0.02
CG6775						(0.01)
CG7051	(0.01)	(0.78)	(0.03)		0.02	0.02
CG7441
CG8128	0.01(0.01)	0.85(0.71)	0.02(0.01)	0.01(0.02)
CG8465
CG9007
CG9900
CG10107
CG10990						0.02
CG12737
CG12982	0.02	0.45	0.01			0.03
CG12983	0.01	0.33	0	0.02		0.01
CG14060	0	0.39	0
CG17150	0.02		0.01			0.01
CG17687	(0)		(0.02)
CG32210	0.02	0.57	0.02	0.02		(0.01)
CG32527	0.02	0.81	0.03		(0.01)	(0.03)

NOTE.—The presence of a value indicates significance of the test statistics. The coding region plus linked flanking regions are used to calculate the CLRT, GOF, MCLS, and ω statistics, whereas only the coding regions are used for the MK and HKA tests.

As the CLRT is sensitive to demographic perturbations, the goodness-of-fit (GOF) test of Jensen et al. (2005) was applied to loci rejecting the CLRT to assess their fit to a sweep model. Consistent with the more conservative nature of this statistic, eight regions are consistent with a hitchhiking model in D. miranda and three regions remain significant in D. pseudoobscura (table 1). If the same tests are applied to our random data set, three genes (out of 91) in D. miranda reject neutrality using the CLRT and one of those remain significant with the GOF test. The corresponding numbers for D. pseudoobscura are 17 loci rejecting neutrality by the CLRT and 6 by the GOF statistics. Thus, genes that evolve quickly at the protein level show increased rates of recent selective sweeps in D. miranda, whereas less difference in rates of adaptive evolution between fast-evolving and random genes are detected in D. pseudoobscura (Fisher's exact test P value = 0.0002 for D. miranda and P = 0.115 for D. pseudoobscura, comparing between the fast-evolving and random data set rejections).

In addition to SFS-based patterns, there are also specific spatial patterns of variation that are largely unique to hitchhiking models (e.g., Stephan et al. 2006). The ω_max statistic (Kim and Nielsen 2004) has specifically been shown to be robust to nonequilibrium models (Jensen, Thornton, et al. 2007). Consistent with previous results, this statistic appears more conservative than frequency spectrum–based approaches (Bachtrog et al. 2009), identifying three regions in D. miranda and a single region in D. pseudoobscura. Importantly, these regions comprise a subset of the genes identified jointly by the CLRT and GOF test (table 1). In the random data set, no genes are identified as having undergone adaptive evolution in D. miranda and three regions are identified in D. pseudoobscura. Consistent with the results of Jensen, Thornton, and Aquadro (2008), the addition of flanking sequence affords greater power to the CLRT/GOF/ω_max test statistics, owing to the sampling of additional segregating sites. This is particularly true for the ω_max statistic, in which it is crucial to sample enough flanking variation in order to estimate levels of LD (also, see simulation study below).

Interestingly, we observe an overlap in identified regions between species. Of the three regions that show strong support of recent selection in D. pseudoobscura (as assessed by the combined CLRT/GOF results), two are also identified as having undergone recent selection in D. miranda (table 1). This suggests that not only are these genes evolving rapidly on the very recent timescale detectable using polymorphism data but also the deeper timescale back to the D. miranda–D. pseudoobscura split. Overall, whereas the fast-evolving data set appears enriched for rapidly evolving genes in D. miranda, this pattern is less pronounced in D. pseudoobscura. However, consistent with N_e-based expectations, D. pseudoobscura appears to be generally experiencing a greater rate of adaptation at randomly selected loci.

In addition to identifying sweeps at individual loci, a variety of test statistics for identifying recurrent beneficial fixations exist. One of the most widely used approaches for inferring adaptive protein evolution by simultaneously considering polymorphism and divergence data is the McDonald–Kreitman (MK) test (see Materials and Methods). In D. miranda, one gene is significant in our fast-evolving data set, using a Fisher's test (CG7051), whereas CG32527 is significant in D. pseudoobscura. Consistent with the polymorphism analysis above, the random data set identifies more genes in D. pseudoobscura (no additional genes in D. miranda are significant, whereas 13 genes are significant in D. pseudoobscura). In order to test for selection at candidate loci considering multiple loci simultaneously, Wright and Charlesworth (2004) proposed a multilocus Hudson–Kreitman–Aguade (HKA) approach. By evaluating models of both neutrality and selection, it is possible to construct likelihood ratio tests consisting of 0 to n − 1 selected loci to determine the most likely number of loci under selection. When pooling our fast-evolving genes with the random data set, we reidentify many of the genes in our fast-evolving data set as undergoing recent selection. Using this approach, the maximum likelihood is achieved with five genes under selection in D. miranda (CG7051, CG12983, CH10990, CG12982, and CG17150) and three genes in D. pseudoobscura (CG6775, CG32210, and CG32527) (table 1).

Quantifying the Rate and Strength of Recurrent Positive Selection

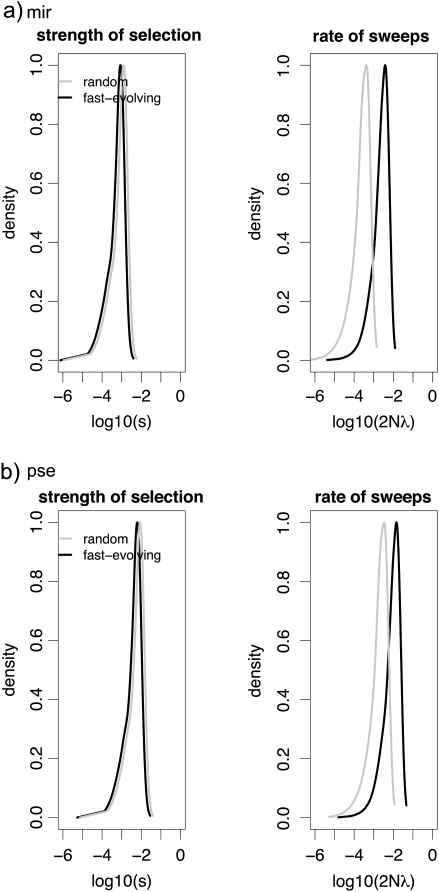
In addition to detecting adaptive evolution at specific loci or genomic regions, test statistics have recently been proposed for estimating parameters of recurrent hitchhiking models from multilocus polymorphism data. For example, the method of Jensen, Thornton, and Andolfatto (2008) has been demonstrated to result in accurate estimation of the mean rate (2Nλ) and strength (s) of positive selection for data sets of this size, and it allows for the modeling of these parameters to be given by distributions rather than representing fixed values. Applying this method to the 19 fast-evolving genes yields maximum a posteriori (MAP) estimates of the mean s = 9 × 10⁻⁴ and mean 2Nλ = 5 × 10⁻³ in D. miranda, and s = 2 × 10⁻³ and mean 2Nλ = 9 × 10⁻³ in D. pseudoobscura (fig. 4).

FIG. 4.—

Approximate Bayesian estimation of both the strength and the rate of recurrent positive selection among 19 fast-evolving genes, compared with randomly selected genes, in Drosophila miranda and D. pseudoobcura. Estimation is based on 10⁶ draws from the prior. Given are the marginal distributions, with fast-evolving genes in black and random genes in gray. Although there is no significant difference in the estimated strength of selection, there is over an order of magnitude increase in the estimated rate of selection among fast-evolving genes in D. miranda relative to random genes. Consistent with observed levels of reduction, frequency spectrum, and LD-based tests of selection, this hitchhiking pattern—though qualitatively similar—appears less pronounced in D. pseudoobscura among the fast-evolving data set.

Applying the same estimation procedure to our random data set, we infer MAP estimates of mean s = 9 × 10⁻⁴ and mean 2Nλ = 1 × 10⁻⁴ in D. miranda, and mean s = 5 × 10⁻³ and mean 2Nλ = 1 × 10⁻³ in D. pseudoobscura (fig. 4). Thus, although the mean selection coefficient does not appear to differ (i.e., the MAP estimate for the fast-evolving data set is contained within the 95% credibility intervals of the random data set), the rate of adaptation is estimated to be greatly augmented among the fast-evolving genes (i.e., the MAP estimate for the fast-evolving data sets are not contained within the 95% credibility intervals of the random data set). This suggests that genes are fast evolving because a larger fractions of mutations are beneficial (i.e., a larger 2Nλ) and not due to individual mutations having a higher fitness advantage (and thus having a higher probability of fixation; i.e., larger s). Again, the hitchhiking pattern among the fast-evolving D. miranda genes appears noticeably more pronounced than for D. pseudoobscura. This result suggests recurrent and recent adaptive evolution at fast-evolving genes, making them ideal candidate loci for future functional analysis. Interestingly, although rates of adaptation appear generally increased in D. pseudoobscura, in line with its larger effective population size, the differences in rates of adaptation between fast-evolving and random genes in this species are somewhat less pronounced.

Evaluating Sampling Schemes

In order to determine the relative benefit of sequencing closely linked regions, both experimental and computational approaches were taken. Considering the general empirical data structure (fig. 3), we compared the following scenarios: 1) sequence generated for the coding region only; 2) sequence generated for the coding region plus one pair of 1-kb regions residing 5 kb up- and downstream; and 3) sequence generated for the coding regions plus two pairs of 1-kb regions, one residing 5 kb up- and downstream and the other 10 kb up- and downstream. Our simulation results demonstrate a decisive advantage to generating linked data (table 2). Specifically, our sampling scheme improved power from 0.74 to 0.98 for the CLRT and 0.50 to 0.96 for ω, compared with sampling only coding regions (however, the ω statistic loses power much more quickly than the CLRT after fixation of an adaptive mutation; Jensen, Thornton, et al. 2007). In addition, there is a great improvement in the accuracy of the maximum likelihood estimate (MLE) of both the strength and target of selection (table 2). As is empirically observed and noted above, improvements are most notable in ω, as it relies upon capturing large haplotype blocks in regions flanking the target of selection. Interestingly, unlike the locus-by-locus tests of selection, no significant difference is observed in the estimation of recurrent hitchhiking parameters between models including short fragments of closely linked polymorphism data compared with simply sequencing coding regions—as assessed by comparing the relative mean square error between models (results not shown). As this estimation depends primarily upon the variance generated between unlinked regions of the genome (see Jensen, Thornton, and Andolfatto 2008), additional unlinked data are in this case more informative than linked data.

Table 2.

Simulation Study Examining the Impact of Sequencing Linked Variation

Statistic	Sampling Schemea	Pr(rej)b	Pr(MLE[X])c	Pr(MLE[α])d
	Coding	0.74	0.62	0.53
CLRT	Coding + 5 kb	0.95	0.78	0.74
	Coding + 5 + 10 kb	0.98	0.95	0.85
	Coding	0.50	0.52	N/A
ωmax	Coding + 5 kb	0.73	0.84	N/A
	Coding + 5 + 10 kb	0.96	0.93	N/A

N/A, not applicable.

^aSee figure 3 for a visual schematic.

^bThe probability of rejection of the test statistic.

^cThe probability of the predicted target of selection (X) being placed within 500 bp of the true target.

^dThe probability of the predicted strength of selection being within 10% of the true value.

Conclusion

By resequencing a fast-evolving subset of genes and linked regions from a previously published random screen, we have characterized parameters of recurrent selection and examined the concurrence of polymorphism- and divergence-based and single and recurrent hitchhiking-based methodologies to infer selection. We find that many historically fast-evolving genes in D. miranda and D. pseudoobscura continue to be evolving adaptively on a more recent timescale and are thus detectable in tests of selection using both patterns of polymorphism and LD. In comparisons with randomly chosen genes, we find that fast-evolving genes have increased rates of selective substitutions (i.e., a higher rate of beneficial mutations), although the strength of selection seems remarkably similar. Patterns of adaptation at fast versus randomly selected genes are more similar in D. pseudoobscura. Interestingly, analyses of randomly chosen genes clearly suggest both a greater average rate and strength of selection in D. pseudoobscura compared with D. miranda, consistent with expectations owing to its larger effective population size. Our study highlights the importance of considering and reconciling the wide array of traditionally separate approaches when conducting genomic analyses in order to gain a broad view of both recent and historical adaptive events in the genome.

Materials and Methods

Survey of Coding Regions

A total of 19 genes (and corresponding linked regions at distances of 5 and 10 kb both proximal and distal of the targeted gene) were surveyed in this study with a sample size of 13–16 alleles (mean sample size 15) in both D. miranda and D. pseudoobscura. Genes were selected for high K_a values based on the initial screen of 111 randomly chosen genes in D. miranda (Bachtrog et al. 2009). Additionally, the same “randomly chosen” data set was surveyed in the sister species D. pseudoobscura (Jensen JD and Bachtrog D, unpublished data). For the fast-evolving subset, both the genes and closely linked regions were sequenced for polymorphism data. All genes are located on the X chromosome of D. miranda and D. pseudoobscura both on chromosome arms X-L and X-R.

Standard polymerase chain reaction (PCR) procedures were used to amplify each region from genomic DNA from single male flies. PCR products were cleaned using Exonuclease I and Shrimp Alkaline Phosphatase and sequenced on both strands with the original PCR primers and internal sequencing primers if necessary using Big-Dye (Version 3, Applied Biosystems). Sequence reactions were cleaned with sephadex plates (Edge Biosystems) and run on an ABI 3730 capillary sequencer. Chromatograms were edited and assembled using Sequencher (Gene Codes) software, and multiple sequence alignments were generated using MUSCLE (http://www.drive5.com/muscle/) with protein alignment–assisted adjustments to preserve reading frames. Exon–intron boundaries were determined from the D. pseudoobscura genome sequence annotation (release 2.0). Sequences have been deposited in GenBank under accession numbers (FN252903–FN256223).

Polymorphism and Divergence Analysis

A library of Perl scripts were used to calculate the estimated number of synonymous sites, average pairwise diversity (π), and average pairwise divergence between D. miranda and D. pseudoobscura (K). A Jukes–Cantor correction was used to correct π and K for multiple hits. Insertion–deletion polymorphisms and polymorphic sites overlapping alignment gaps were excluded from the analysis. To compare polymorphism and divergence, we implemented the MK test (McDonald and Kreitman 1991). Briefly, this approach considers a 2 × 2 contingency table of polymorphic synonymous and nonsynonymous variation, with synonymous and nonsynonymous divergence. With the sequence polymorphism data for both D. miranda and D. pseudoobscura, it is possible to consider true fixed differences, avoiding issues of estimating divergence based on a single sample. P values are calculated using a Fisher's exact test.

Utilizing a screen of randomly selected genes in D. miranda (Bachtrog et al. 2009) and D. pseudoobscura (Jensen JD and Bachtrog D, unpublished data), we also make use of a recently proposed multilocus HKA (Hudson et al. 1987) approach (Wright and Charlesworth 2004). This approach conducts a maximum likelihood analysis of multilocus polymorphism and divergence data in order to test for the action of natural selection among candidate loci. Generating 1,000,000 cycles of the Markov chain (i.e., the chain length) assuming both neutral and selection models, it is possible to construct likelihood ratio tests in order to determine the number of selected loci with the greatest support—where twice the difference in log likelihood between the models is approximately chi-square distributed. The code and documentation are available for download at: http://www.yorku.ca/stephenw/Stephen_I._Wright/Programs.html.

Evaluating Single Hitchhiking Models

Several statistical tests to identify recent adaptive evolution were applied to genes from both species. The CLRT (Kim and Stephan 2002) uses the spatial distribution of mutation frequencies in a genomic region and levels of variability among a population sample of DNA sequences to test for evidence of a selective sweep. This method compares the ratio of the composite likelihood of the data under the standard neutral model of constant population size, neutral evolution, and random mating, L_N (Data), to the composite likelihood of the data under the model of a selective sweep, $L_{\text{S}}(\widehat{\alpha },\widehat{X}|\text{Data})$, where α is the MLE of 2Ns (where N is the effective population size and s the selection coefficient) and X is the MLE of the location of the beneficial mutation. The recombination rate ρ per site is set at 8.8 × 10⁻⁸ per site per generation (Bachtrog 2008). For each locus, 1,000 neutral replicates were simulated using locus-specific parameters in order to assess significance. A complete users manual, as well as all necessary code, can be found at: http://www.yuseobkim.net/YuseobPrograms.html. The neutral model is rejected at level γ (5% used here) when the observed ${\wedge }_{KS}$is greater than the 100(1 − γ) percentile of the null distribution.

The CLRT is sensitive to deviations from the assumptions of the standard neutral model, with population substructure and recent bottlenecks leading to a high false-positive rate (Jensen et al. 2005). As one approach to examining the potential effects of demography, we assess the fit of individual loci to a selective sweep model. This is accomplished through a GOF test that contrasts the null hypothesis, H₀, that the data are drawn from a selection model to the alternative hypothesis, H_A, that the data are not drawn from such a model (Jensen et al. 2005). The program is available for download at: http://www.yuseobkim.net/YuseobPrograms.html. We also applied the MCLS test of Nielsen et al. (2005)—which is an extension of the CLRT—to our data in which the randomly chosen set of genes is utilized to construct the background SFS to test for selection at individual regions. The program is available for download at: http://people.binf.ku.dk/rasmus/webpage/sf.html.

In addition to skewing the frequency spectrum, positive selection may also result in strong LD flanking the target of selection and reduced LD across the target (Kim and Nielsen 2004; Stephan et al. 2006; Jensen, Thornton, et al. 2007). We thus employ patterns of LD to test for selection at individual loci using the ω_max test (Kim and Nielsen 2004). Singletons were excluded prior to calculation. The null distribution of ω for each genomic region is obtained from simulation under the standard neutral model (using the program ms; Hudson 2002) with fixed θ and L. As above, we set ρ = 8.8 × 10⁻⁸ per site per generation. The program is available for download at: http://www.molpopgen.org/software/libsequence.html.

Simulation-Based Sampling Study

Using the sweep simulation machinery of Kim and Stephan (2002), data sets were generated in order to quantify the relative merits of generating sequence data at regions closely linked to the identified genes. Three scenarios are examined: 1) coding region, 2) coding regions plus flanking sequences 5 kb up- and downstream, and 3) coding regions plus flanking sequences 5 and 10 kb up- and downstream. In all cases, the length of the sequence = 1 kb and the target of selection (X) is located in the center of the coding region and fixed at time (τ) = 0.0001 4N generations. θ = 0.01, ρ = 0.1, and α = 2Ns = 1000. Ten thousand replicates were simulated under each scenario. The CLRT and ω test statistics were applied to each class of replicates.

Evaluating Recurrent Hitchhiking Models

To estimate selection parameters under a recurrent hitchhiking model, we use the approximate Bayesian approach of Jensen, Thornton, and Andolfatto (2008). The level of reduction in variation due to recurrent selection depends on the joint parameter 2Nsλ (Wiehe and Stephan 1993). Both the rate, 2Nλ, and the fitness effect, s, of recurrent selection are estimated based upon their relationship with the means and standard deviations of common polymorphism summary statistics (the mean average pairwise diversity (π), the number of segregating sites (S), θ_H, and ZnS; see Jensen, Thornton, and Andolfatto 2008). Calculating these summary statistics from the observed data and from simulated data with parameters drawn from uniform priors, we implement the regression approach of Beaumont et al. (2002), which fits a local linear regression of simulated parameter values to simulated summary statistics, and substitutes the observed statistics into a regression equation (see Thornton 2009). The prior distributions used were s ∼ Uniform (1.0 × 10⁻⁶, 1.0), 2N_eλ ∼ Uniform (1.0 × 10⁻⁷, 1.0 × 10⁻¹), and the tolerance, ε = 0.001. Estimation is based on 10⁶ draws from the prior using the recurrent selective sweep coalescent simulation machinery described in Jensen, Thornton, and Andolfatto (2008). We set ρ = 8.8 × 10⁻⁸ per site per generation and N_e = 5 × 10⁵ for D. miranda and 2.5 × 10⁶ for D. pseudoobscura (Loewe et al. 2006). For inferences on selection parameters, we assume exponential distributions of 2Nλ and s, such that each draw from the prior represents the mean of the distribution. A complete users manual, as well as all necessary code, can be found at: http://www.molpopgen.org/software/JensenThorntonAndolfatto2008/.