A TRACK-REPEATING ALGORITHM FOR FAST MONTE CARLO DOSE CALCULATIONS OF PROTON RADIOTHERAPY

Abstract

Monte Carlo codes are utilized for accurate dose calculations in proton radiation therapy research. While they are superior in accuracy to commonly used analytical dose calculations, they require significantly longer computation times. The aim of this work is to characterize a Monte Carlo track-repeating algorithm to increase computation speed without compromising dosimetric accuracy. The track-repeating approach reduced the CPU time required for a complete dose calculation in voxelized patient anatomy by more than two orders of magnitude, while on average reproducing the results from the traditional Monte Carlo approach within 4% dose difference and within 1-mm distance to agreement.

I. INTRODUCTION

The availability of proton radiotherapy as a treatment option for cancer has increased substantially in the last few years. Proton therapy offers an enhanced possibility of effective tumor control while minimizing treatment-related side effects. The calculation of proton dose in patients for clinical applications is usually performed with analytical methods. The analytical approach is fast and, in most cases, sufficiently accurate. However, for some challenging treatment sites, especially in the thorax, the analytical predictions may not be sufficiently accurate. For example, increased dosimetric accuracy may be essential in minimizing the incidence of pneumonitis in patients who receive radiotherapy for cancer of the lung. Also, the analytical algorithms do not predict stray and leakage radiation, that is, undesirable radiation produced when the proton beam interacts in the treatment unit or the patient. Stray and leakage radiation is important information for the avoidance of radiogenic second cancers, particularly for children with good prospects of long-term survival.¹ Stochastic dose algorithms have been used in place of analytical algorithms to overcome those limitations. In particular, several studies suggested that the Monte Carlo technique might eventually be feasible for routine use in patient care.^{2– 6} However, the length of the computation times remains the last major obstacle to translating the powerful Monte Carlo method into clinical applications.

At energies relevant to proton therapy, electromagnetic interaction with the atomic electrons in the target medium is the most frequent mechanism through which a proton loses energy. Low-energy electrons are produced in these interactions; however, typically, they do not travel far (<1 mm) away from the original proton track before they are absorbed. Secondary particles other than protons have been shown to contribute <1% to the in-field dose.⁷ Li et al.⁸ reported on a track-repeating algorithm for proton therapy based in GEANT3, which utilized three basic materials to describe patient anatomy. In the present work we extended the track-repeating approach to include 42 biological materials and several metals, which are important for patients with artificial implants⁹ and markers.¹⁰ In addition, the algorithm was developed with GEANT4 (Ref. ¹¹), a more up-to-date version of the GEANT toolkit.

The aim of this study is to develop a track-repeating algorithm with the advantages of stochastic approaches, which, at the same time, requires computational times that were previously achievable only with analytical methods. The fast dose calculator (FDC) track-repeating algorithm presented in this paper utilizes a precomputed database of proton trajectories in water to calculate the proton dose in a variety of materials. Dosimetric data in water are extrapolated to other materials by scaling methods. FDC simulates energy deposition and absorbed dose in a voxelized representation of patient anatomy and utilizes a proton track database that was generated with theGEANT4code toolkit.

II. METHODS

II.A. Database and Material Information

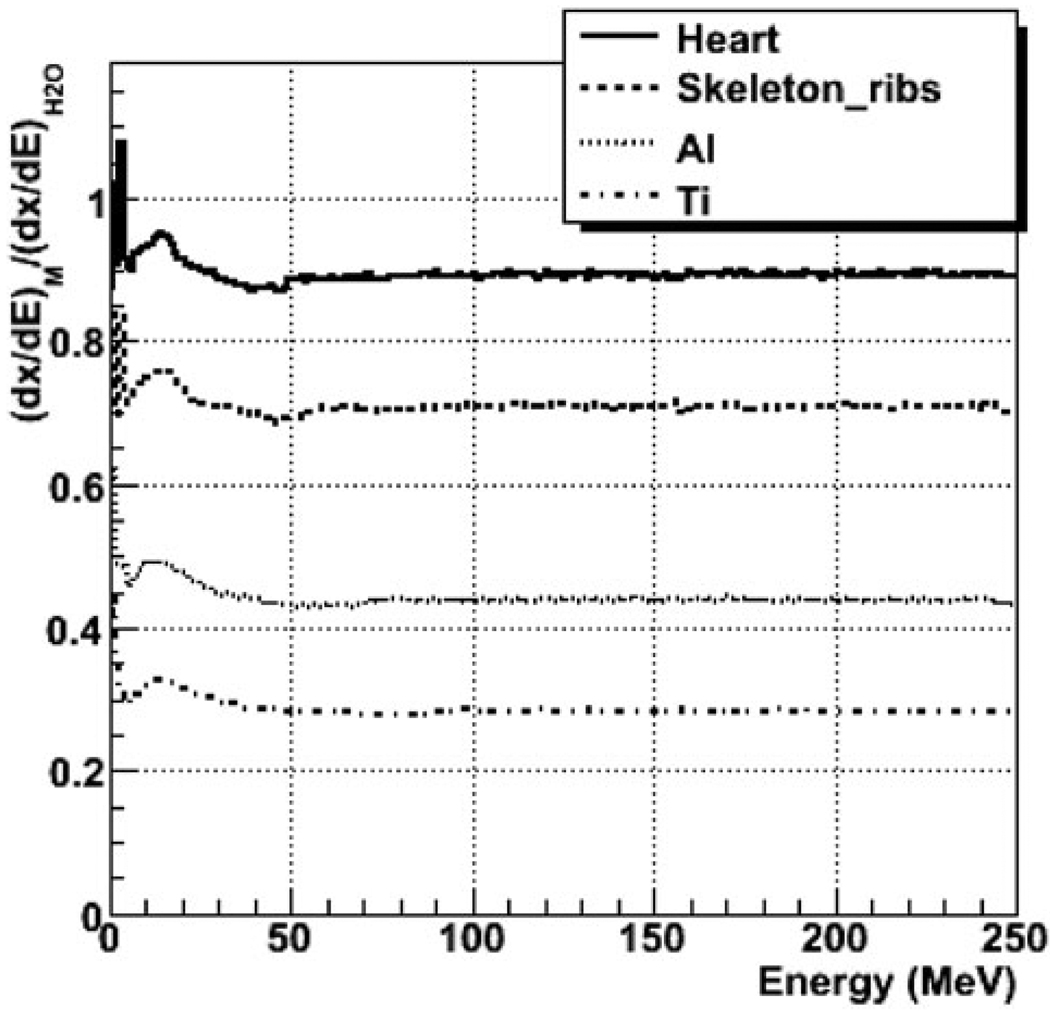
A database of trajectories of particles produced by 251-MeV protons impinging on a 660- × 660- × 750-mm³ water phantom was generated with GEANT4.Trajectories were discretized in steps of 1 mm or less. The path length, angles, energy loss, and energy deposited in water were stored for each step. The step length per deposited energy, dx/dE, was also recorded for each step in water. Similar simulations were also run with GEANT4 for phantoms of 42 biological materials and some relevant metals, including Al and Ti. Distributions of relative range, or R(E) = (dx/dE)_M / (dx/dE)_H2O, depending on the particle energy, were generated for each material M by recordingR(E) for each step in the Monte Carlo simulation.

II.B. Fast Dose Calculations

The FDC calculated the energy deposited in the various materials based on the database of particle trajectories in water. This is achieved by scaling the length of each step, and the angle between steps, according to the material and its mass density. The step length and angle were scaled according to the expressions: l_M = αl_H2O R(E) and Φ_M= βΦ_H2O, respectively, where α and β are energy-independent parameters adjusted for each material. The parameters α and β were optimized automatically by comparing one-dimensional projections of the distributions of energy deposited for 50-, 100-, 150-, 200-, and 250-MeV protons in the various materials calculated with GEANT4 and FDC.

II.C. Gamma Distribution

In order to evaluate the dosimetric accuracy of the FDC distributions, they were compared to distributions from GEANT4 using the gamma function¹² defined for three-dimensional distributions. The Γⁱ was calculated for each voxel as

$${\mathbf{\Gamma }}^i=\underset{j=1,N}{\text{min}}\sqrt{{\left(\frac{r_i-r_j}{\mathbf{\Delta }r}\right)}^2+{\left(\frac{D_i-D_j}{\mathbf{\Delta }D}\right)}^2},$$

where

• N = number of voxels in the distribution

• r_j = position of voxel j

• D_j = dose of voxel j

• Δr = 3 mm = maximum acceptable difference between two distributions in space

• ΔD =3%D_max = maximum acceptable difference between two distributions in absorbed dose.

The Γⁱ values were calculated using GEANT4 as the reference sample. This method of evaluating the distance to agreement and dose difference of the sample case versus the reference case is widely used in the analysis of dose distributions in radiotherapy. Two distributions are considered to be sufficiently close when an acceptable percentage of the values of Γⁱ are smaller than unity.

II.D. Voxelized Phantom and Treatment Technique

A voxelized phantom based on the computed tomography images of a patient, treated for prostate cancer at M. D. Anderson Cancer Center, was used to compare the results of the GEANT4, MCNPX, and FDC codes. The voxel size was 2.5 × 2.5 × 2.5 mm³. Prostate treatments usually consist of a two-field orientation; however, in this study only one lateral monoenergetic circular field of 200-MeV protons was calculated, because of the inherent symmetry of the patient anatomy and beam paths of both fields.

An initial run with a 2-cm-diam narrow beam was simulated withGEANT4,MCNPX(Ref. ¹³), and FDC. A similar number of proton histories, of the order of a million protons, were generated with each code. For the MCNPX simulations, the geometry-splitting technique was used to reduce variance in absorbed dose. The patient geometry was cropped to 53 244 voxels, thus eliminating many of the voxels outside of the beam path. A second field of 8-cm diameter was simulated with GEANT4 and FDC, in order to more closely simulate a lateral beam, used for prostate cancer treatments. Correspondingly, a larger cropping region in the lateral direction had to be used for the voxelized phantom in order to contain the larger beam. The expanded geometry contained 490 680 voxels.

III. RESULTS AND DISCUSSION

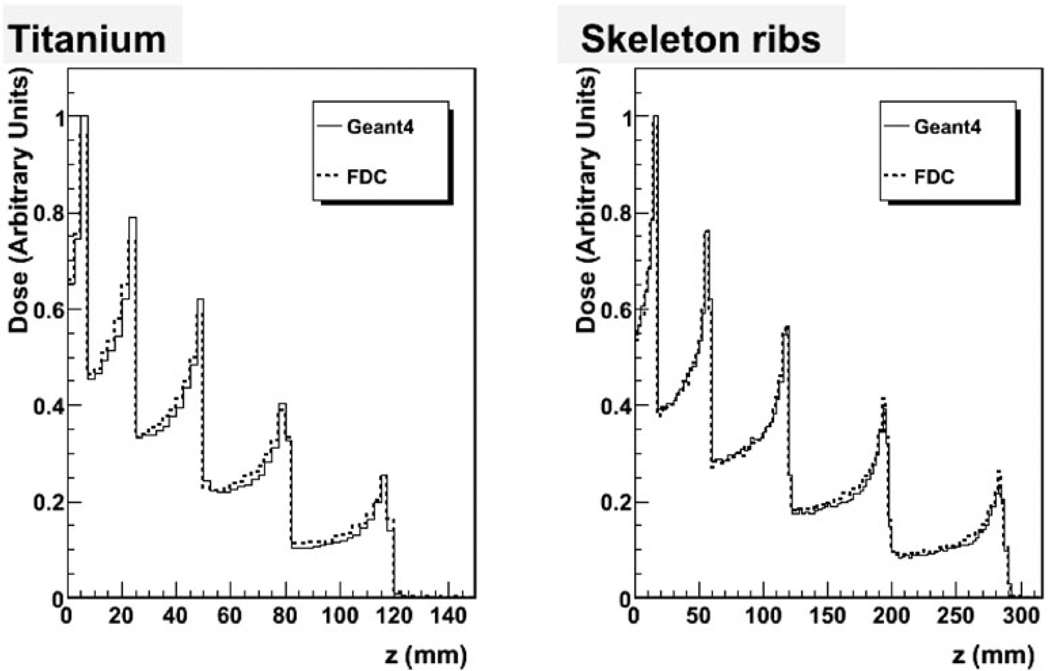
Figure 1 shows R(E) for soft tissue (heart), bone tissue (skeletal ribs), and metal (Al and Ti) as a function of proton energy as calculated with GEANT4. The ratios increase with decreasing energy below 10 MeV, they have a peak at ~20 MeV, and they are flat above 50 MeV. Figure 2 plots percent depth dose (PDD) for titanium and skeleton (rib) for a superposition of five protons beams of 50-, 100-, 150-, 200-, and 250-MeV, as calculated with GEANT4 and FDC extrapolated from trajectories in water. As shown in the plots in Fig. 2, good agreement was obtained between FDC and GEANT4, especially for the bone tissue.

Fig. 1.

The ratio dx/dE to that of water for various materials for protons, as a function energy. The dx/dE is the length traveled per unit of deposited energy calculated with the GEANT4 Monte Carlo code.

Fig. 2.

Comparison of the energy deposited along the beam between GEANT4 and FDC for metal (Ti) and bone (skeletal rib) for the superposition of 50-, 100-, 150-, 200-, and 250-MeV proton beams.

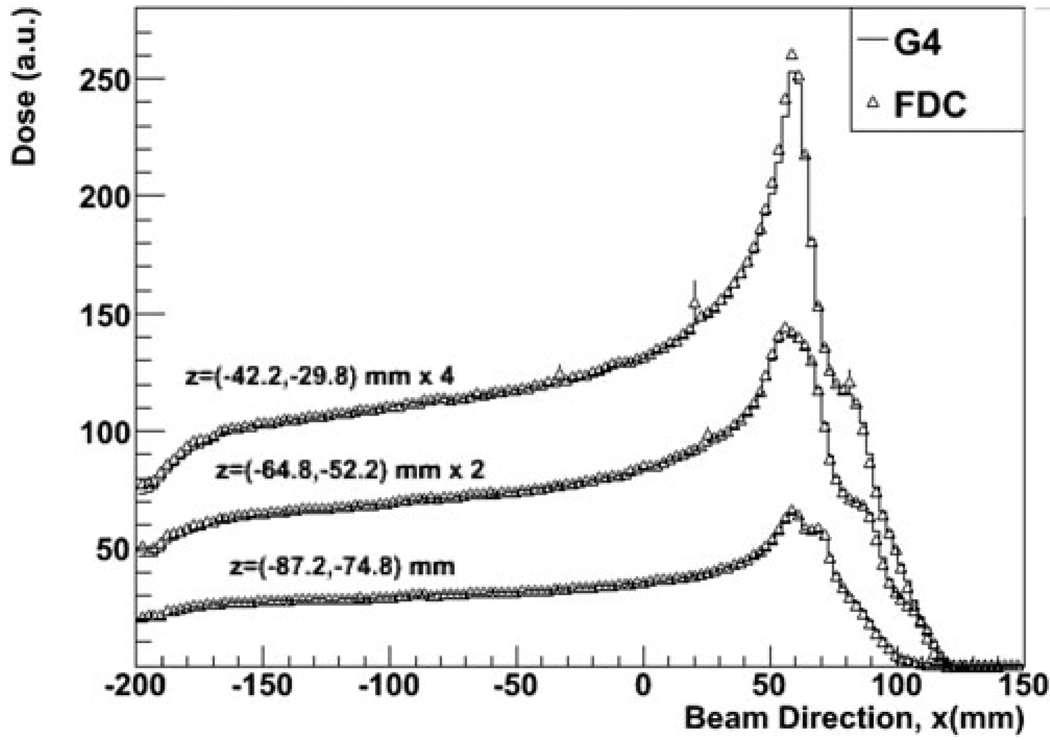
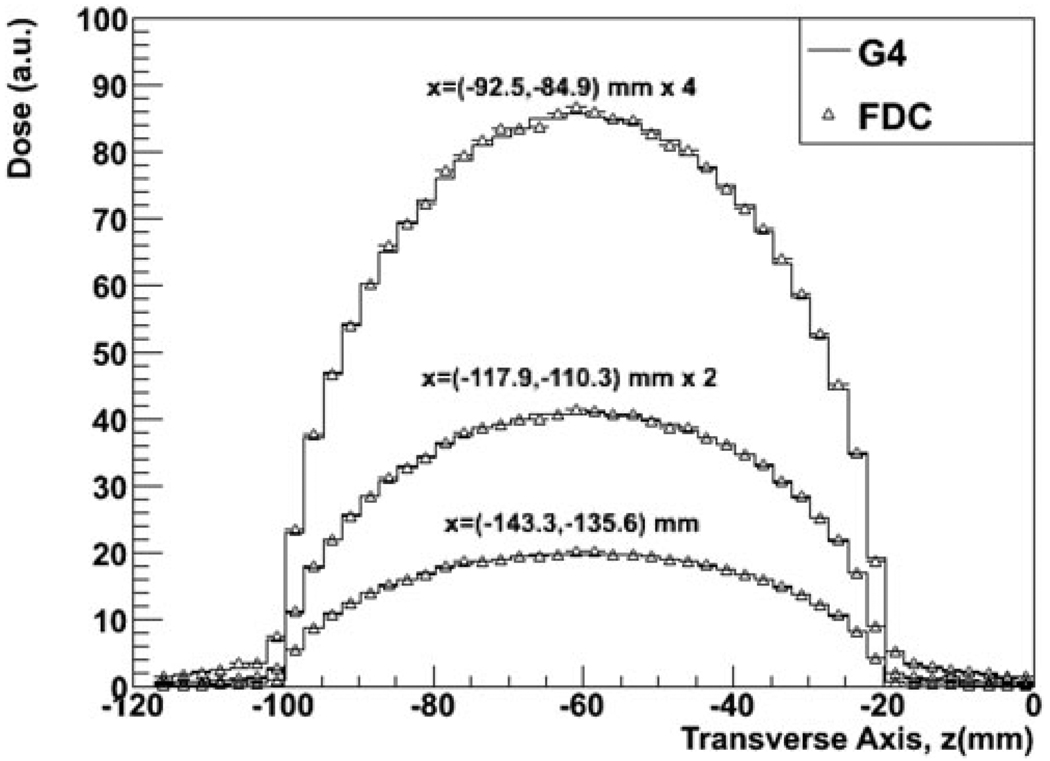
Figure 3 shows the PDD for the wider beam as calculated with GEANT4 and FDC at three depths along the z transverse plane. The cross-field distributions for three depths along the beam direction for the same simulations are shown in Fig. 4. As shown in Figs. 3 and ⁴, there is good agreement between GEANT4 and FDC.

Fig. 3.

The PDD at three depths along a transverse plane in a patient treated for prostate cancer calculated with GEANT4 and FDC.

Fig. 4.

Cross-field dose distributions at three depths along the beam axis in a patient treated for prostate cancer calculated with GEANT4 and FDC.

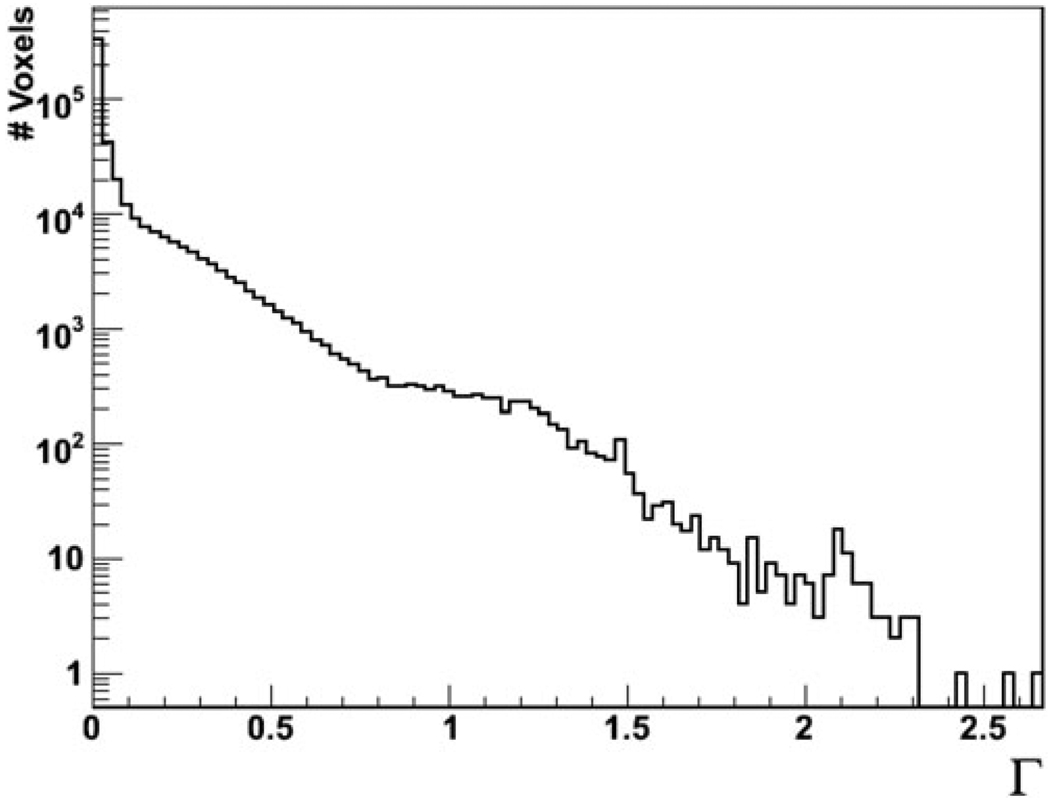
The values of the gamma function Γ were binned for each voxel, as shown in Fig. 5 in logarithmic scale. Of all the voxels describing the anatomy of the patient, 97.3% had values below 1 and 99.8% had values below 2. When comparing MCNPX and GEANT4, Γ < 1 for 97% and Γ < 2 for 99% of the nonair voxels. In other words, the gamma analyses revealed that the difference in accuracy between FDC and GEANT4 was less than the small dosimetric differences between GEANT4 and MCNPX, i.e., accurate Monte Carlo codes that have been previously used for proton therapy dose calculations.

Fig. 5.

The Γ function for each voxel comparing FDC and GEANT4 for the dose received by a patient treated for prostate cancer.

Table I shows the processing CPU time needed to simulate the proton trajectories and interactions through the patient geometry for the various programs. GEANT4 and FDC were run on 2.2-GHz AMD64 Opteron CPUs, while MCNPX was run on 2.6-GHz AMD64 Opteron CPUs. In both cases the amount of memory per processor was 2 gigabytes. Processing times have been scaled to the 2.2-GHz machine. FDC was two orders of magnitude faster than MCNPX, while MCNPX was significantly faster than GEANT4 for the setups used.

TABLE I.

Number of Voxels in the Patient Geometries and CPU Simulation Times per Incident Proton for the Various Simulation Programs^*

	Number of Voxels	MCNPX	GEANT	FDC
		Processing Time per Proton (s)
Narrow beam	53 244	0.2	0.45	2.9 × 10−3
Wide beam	491 680	0.58	5.0	2.9 × 10−3

^*Executed on AMD Opteron 2.2-GHz processors.

IV. CONCLUSIONS

An FDC track-repeating algorithm was implemented to speed up dose calculations for proton radiotherapy based on the GEANT4 Monte Carlo code. The FDC approach provided a substantial reduction in CPU time while preserving dosimetric accuracy. The approach is applicable to other Monte Carlo codes, such as MCNPX and FLUKA (Ref. ¹⁴).