Representativeness of the PROMIS Internet Panel

Abstract

Objective

To evaluate the Patient-Reported Outcomes Measurement Information System (PROMIS), which collected data from an Internet polling panel, and to compare PROMIS with national norms.

Study Design and Settings

We compared demographics and self-rated health of the PROMIS general Internet sample (N=11,796) and a sub-sample of it (n = 2,196) selected to approximate the joint distribution of demographics from the 2000 U.S. Census, with three national surveys and U.S. Census data. The comparisons were conducted using equivalence testing with weights created for PROMIS by raking.

Results

The weighted PROMIS population and sub-sample had similar demographics compared to the 2000 U.S. Census except that the sub-sample had a higher percentage of people with more education than high school. Equivalence testing shows similarity between PROMIS general population and national norms with regard to body mass index, EQ-5D health index, and self-rating of general health.

Conclusion

Self-rated health of the PROMIS general population is similar to that of existing samples from the general U.S. population. The weighted PROMIS general population is more comparable to national norms than the unweighted population with regard to subject characteristics. The findings suggest that representativeness of the Internet data is comparable to those from probability-based general population samples.

INTRODUCTION

There are many methods for collecting survey data, such as face-to-face or telephone interviews, mail, fax, e-mail, or web-based surveys.[1] The number of individuals who have access to the Internet is growing exponentially and the population of Internet users from which general surveys might sample is increasing.[2] As a result, the number of studies using Internet Data Collection (IDC) has increased, presenting new opportunities and challenges in data collection and analyses.

Limitations of traditional random digit dialing (RDD) with regard to obtaining representative samples have further stimulated IDC. These limitations have increased due to widespread screening of incoming calls and the increasing number of cell phone users without home phone “landlines”. Non-response associated with RDD sampling is higher than personal interviews, and it is possibly less appropriate for personal or sensitive questions, if there is no prior contact.[3] Compared with conventional data methods such as paper survey and face-to-face or phone interviews, there are several noteworthy advantages to IDC: it is cost-effective to study large and heterogeneous samples; it has the ability to recruit specialized samples (e.g., people with rare characteristics); and the standardization of data collection process makes studies easy to replicate. However, IDC also has disadvantages, such as difficulty ensuring the integrity, security, reliability and validity of data collected [2,4,5]; higher rates of loss of follow-up[6]; and biases in the population that often accesses the web, despite not being geographically restricted.[2]

A high response rate is commonly taken as an indicator of survey validity.[7] In addition, selection bias is an important consideration because of its impact on generalizability.[8] Some studies have shown that IDC led to a significantly lower response rate than traditional mailed surveys,[9] or found significant differences in the sample characteristics and overall costs between telephone and web surveys used to collect data on the corporate reputation of an international firm.[10] In contrast, other studies have found IDC to produce similar reliability and validity as traditional collection methods.[11-17] Schillewaert et al. [18] compared respondents recruited by postal mail, telephone, internet panels and pop-up internet surveys and found that online and offline methods yielded respondents with similar attitudes, interests and opinions after controlling for socio-demographics from census data.

Substantial data collection efficiency, low cost, and widespread availability of Internet access among diverse groups are stimulating increased usage of web-based surveys.[10] However, internet surveys may not be representative of a population of interest because the sub-population with access may be atypical. Weighting adjustments can be applied to surveys to compensate for non-response, non-coverage, unequal selection probability, and sampling fluctuation from known population values.

Different weighting methods have been developed, such as cell weighting and raking.[19] The purpose of weighting adjustments is to make the weighted sample distributions conform to distributions or estimates from an external source or a large high-quality survey. For each of the different weighting methods, two weighting approaches can be used: population weighting and sample weighting. When population weighting adjustments are used, the respondent sample is weighted so that the weighted sample distribution is the same as the distribution of the population across classes (such as population estimates by age and sex). Sample weighting adjustments weight respondents within classes so that the profile of respondents across classes is equivalent to the profile of the entire survey sample.[19,20]

The cell weighting method adjusts the sample weights so that the sample distributions or totals conform to the population distributions or totals on a cell-by-cell basis. The assumption underlying cell weighting adjustment for non-response is that the respondents within a given cell represent the non-respondents within that cell, which implies that data are missing at random.[21] A practical limitation of cell weighting is that as the number of stratification variables and number of cells increases, the number of subjects in each cell decreases, thus producing less stable aggregated estimates.

Raking matches cell counts to the marginal distributions of the grouping variables used in the weighting scheme.[19,21,22] Raking is an iterative proportion procedure, which performs cell-by-cell adjustments over the various univariate distributions to make the weighted sample cells match external values such as U.S. Census data. This process is repeated iteratively until there is convergence between the weighted sample and the external distributions.[23]

Propensity score adjustment can alleviate the confounding effects of the selection mechanism in observational studies by achieving a balance of covariates between comparisons.[24,25] Harris Interactive (http://www.harrisinteractive.com/) developed software for performing propensity score weighting (PSW) to correct for attitudinal and behavioral differences typically found in online respondents.[26] Propensity score matching,[24] on which PSW is based, has been used to ensure that comparison groups have similar characteristics when random assignment is not possible. Schonlau and Van Soest [27] found that the propensity adjustment to correct selection bias in internet surveys works well for many but not all variables investigated, and cautioned against the common practice of using only a few basic variables to correct for selectivity in convenience samples drawn over the Internet.

The Patient-Reported Outcomes Measurement Information System (PROMIS) project aims to develop highly reliable and valid item banks to measure patient-reported symptoms and other aspects of health-related quality of life for administration to persons with a wide range of chronic diseases and demographic characteristics. PROMIS collected data using a polling panel consisting of over one million members who had previously indicated a willingness to respond to online surveys. In this study, we evaluated the distributional characteristics obtained from those who accepted the invitation to complete a survey, created a weighting scheme to compensate for non-response and non-coverage to make weighted sample estimates conform to the U.S. population, and generated a sub-sample through disproportionate sampling to simulate the distribution of the U.S. general population demographics. We compared the PROMIS Internet samples with three U.S. national surveys, as well as general population with regard to participant demographics, general health, Body Mass Index (BMI), and EQ-5D health index score. Based on these comparisons, inferences were made about the quality and generalizability of the PROMIS Internet sample.

METHODS

PROMIS

PROMIS is a NIH Roadmap project that utilizes item response theory (IRT) and computer adaptive testing (CAT) to provide an accurate, efficient and publicly accessible system that can be used by medical researchers and health professionals to assess patient-reported outcomes across a number of measurement domains.[28] Five primary domains were selected for initial item-bank development: physical functioning, pain, fatigue, emotional distress, and social-role participation. For the initial wave 1 testing, PROMIS recruited an Internet general population sample of 11,796 individuals; data were collected from July 2006 to March 2007.[29]

The Internet polling vendor, Polimetrix (now “YouGov America”), maintains a panel of over one million respondents who have provided their names, physical addresses, email addresses, and other information, and who regularly participate in online surveys. Polimetrix differentially selected participants for PROMIS from among its panel to obtain a more representative sample, but this does not represent a random sample of the U.S. population. The sample matching methodology starts with a listing of all respondents in the desired or target population. Next, a random sample of the desired size is selected from the population listing (the “target sample”). Third, for each element of the target sample, the closest match is selected from the Polimetrix panel. For sub-populations with lower response rates, the target group invitation is “over-sampled”. For PROMIS, we specified targets in terms of gender (50% female), age (20% in each of 5 age groups: 18-29, 30-44, 45-59, 60-74, 75+), race/ethnicity (12.5% each for black and Hispanic), and education (10% less than high school graduate).

Respondents were paid $10 for completing 2 full banks of 56 items each or 14 blocks with 7 selected items per block. In addition to the PROMIS items and appropriate “legacy” items (items from widely used existing measures) completed by those administered full banks of items, participants were administered approximately 21 auxiliary items consisting of global health rating items and sociodemographic variables and a series of questions about the presence and degree of limitations related to 25 chronic medical conditions. Participants with high levels of missing data (e.g., completed less than half of the bank items), who completed items in less than 1 second/item, or who gave the same response to 10 consecutive items were excluded from analyses. A total of 725 respondents were excluded for one or more of these reasons. No difference in demographics was found between the analytical sample and the excluded sample except that the excluded sample was one and half years younger on average

Weighting Scheme

Using U.S. Census data as the standard, analytical weights were generated to compensate for non-response and non-coverage of PROMIS Internet sample so that the inferences based on PROMIS estimates can be applicable to the general population. The weights are a post-stratification adjustment that would allow the weights to sum to the target population (i.e., U.S. non-institutionalized persons 18 years of age or older). The weights were computed by the method of Iterative Proportional Fitting or raking which attempts to make the sample distributions of each variable match its known population distribution. Respondents who did not supply the demographic information necessary for raking were excluded from the raking procedure. The sample was weighted to have the same distribution of demographic variables (gender × age × race/ethnicity, education, marital status and income) as the U.S. Census. We paired each of the two gender groups (Male, Female) with each of the five age groups (18 to 29, 30 to 44, 45 to 59, 60 to 74, 75+) and each of the four race/ethnicity groups (African American, White, Hispanic, Other race), creating 40 categories. These 40 categories, together with education groups (Less than high school, High school diploma/GED, More than high school), marital status (Married, Widowed, Divorced/Separated, Never married/Living with partner) and income levels ($0 to $19,999, $20,000 to $49,999, $50,000 to $99,999, $100,000 and Over), were used as raking dimensions in the raking process.

Izrael et al. [30] introduced a SAS macro for raking (sometimes referred to as the IHB raking macro) that combines simplicity and versatility. Izrael et al. [31] enhanced the IHB raking macro to increase its utility and diagnostics. This macro requires input of the control totals and location of the sample data set. It filters through multiple iterations of the raking procedure to output weights for every observation in the data set. Weights were first adjusted to assure agreement on the first raking dimension, and then weights were adjusted for the second raking dimension, then for the third, etc. The process was repeated, again assuring agreement with each of the raking dimensions. The process continued to be repeated, with iterative controlling to each variable, until simultaneously close agreement for each variable was obtained.

Inordinately large weights tend to substantially increase sampling errors. By trimming weight values that are too large, one generally lowers sampling variability but may incur some bias. We used weight truncation and trimming to reduce the mean squared error (MSE) of the key outcome estimates. The MSE will be lower if the reduction in variance is large relative to the increase in bias arising from weight trimming. Two common indicators used in weight trimming are the median weight plus six times the interquartile range (IQR) of the weights, and five times the mean weight.[32] We used the median weight plus six times the IQR for weight trimming—that is, weights greater than the median weight plus six times IQR of the weights were reduced to this cutoff value. After trimming large weights, the raking process was then repeated so that survey estimates would still agree with the control total.

PROMIS general population sub-sample

Online surveys can also match demographic profiles with the target population through the use of disproportionate sampling. To ensure that the estimates indeed reflected the targeted general population of the PROMIS study, we identified a subset of the PROMIS Internet sample that approximated the joint distributions of selected key demographic variables (age, gender and race) in the 2000 U.S. Census. We refer to this sub-sample as the “general population sub-sample”. The algorithm of the re-sampling was as follows:

1. Obtain the marginal distribution of gender, age, and race/ethnicity of the PROMIS Internet general population

2. Create grids of cells: 2 (gender: Male, Female) × 5 (age: 18 to 29, 30 to 44, 45 to 59, 60 to 74, 75+) × 4 (race/ethnicity: African American, White, Hispanic, Other race) = 40 cells

3. Calculate the frequency of responses for each cell for the PROMIS sample: n_ijk with i = 1,2; j = 1,2,3,4,5; k = 1,2,3,4.

4. Calculate the corresponding percentage for each cell based on census data (SF4): c _ r_ijk with i = 1,2; j = 1,2,3,4,5; k = 1,2,3,4 with general U.S. population.

5. Compute the sample size for each cell for the sub-sample: $n{n}_{ijk}=c\_r_{ijk}\left\{\min \left(\frac{n_{ijk}}{c\_r_{ijk}}\right)\right\}$ where the minimum is over i, j and k.

6. Within each cell, draw nn_ijk random sample from n_ijk general population.

National Norms

To compare characteristics of the PROMIS Internet sample with the national population, we used as norms three large, publicly available datasets that include weights and other design features such as stratification and clustering necessary to generalize to the non-institutionalized general U.S. population: 2003 and 2004 Medical Expenditure Panel Survey (MEPS) Household Component Survey (HC),[33] 2005 Behavioral Risk Factor Surveillance System (BRFSS),[34] and 2001-2002 National Health and Nutrition Examination Survey (NHANES).[35]

MEPS is an ongoing nationally representative survey of health care utilization and expenditures for the U.S. non-institutionalized civilian population. The MEPS HC survey collected medical expenditure data at both the person and household levels for the calendar years 2003 and 2004. The sampling frame for the MEPS HC was drawn from respondents to the National Health Interview Survey. The MEPS HC sample design was a stratified multistage area probability design with disproportionate sampling to facilitate the selection of oversamples of subpopulations of interest such as Hispanics and Blacks. This analysis uses 2004 MEPS survey data except for the EQ-5D health status measures, which was collected in the 2003 MEPS, but not available in the 2004 MEPS.

BRFSS is a standardized, random telephone health survey, tracking health conditions and risk behaviors in the United States yearly since 1984. BRFSS provides state-specific information from adults relating to their health status, personal health habits, and use of preventive health services. Most states use the Disproportionate Stratified Sample Method.

NHANES is composed of a series of cross-sectional, nationally representative health and nutrition examination surveys of the U.S. civilian non-institutionalized population. The data are released every 2 years. The NHANES sample design is a stratified, multistage, national probability sample.

Statistical Methods

We assume that the PROMIS Internet sample and the general population sub-sample generated by simulating census demographic distributions are subsets of the U.S. general population. EQ-5D Health Index Score [36] was calculated by using the U.S. scoring algorithm derived by Shaw et al.[37] Since the focus of this paper is to find the equivalence between the PROMIS general population and sub-samples and national norms, we used equivalence testing methodology instead of difference tests. Difference testing has been widely used to answer questions about whether a disparity has been successfully addressed. A statistically significant difference between groups leads to rejecting the null hypothesis of no difference. With this approach, analysts focus on a difference, even though it may be too small to be meaningful. This, however, plagues large samples, in which differences too small to be of research concern are often statistically significant.[38] On the other hand, if the analysis does not reveal a statistically significant difference between groups, the null hypothesis cannot be rejected. However, failing to find difference is not proof of similarity because it may just indicate a sample size too small to detect a difference.

With equivalence testing, the null hypothesis states that the groups differ by more than a tolerably small amount Δ. The alternative hypothesis states that the groups differ by less than Δ—that is, they are similar. Thus, rejecting the null hypothesis is proof of similarity between the groups. Defining tolerable levels of difference is a necessary precursor to applying equivalence testing to assess equity.

Schuirmann [39] presented a two one-sided test (TOST) procedure or more commonly, the confidence interval approach to compare two groups. In this analysis, we Δ require that the population mean of the test groupμ_T be within some specified zone Δ around the population mean of the reference groupμ_R, i.e., |μ_T − μ_R|<Δ, which represents our equivalence hypothesis. The null hypothesis is |μ_T − μ_R| ≥ Δ, i.e., “a difference of Δ or more.” To test for equivalence, confidence intervals for the difference between two groups must be defined. In a TOST analysis, a (1– 2α)100 percent confidence interval is constructed. [40] In this analysis, we selectα = 0.05. Thus, we constructed 90 percent confidence intervals. Assuming sampling from normal distributions, we reject the null hypothesis that the groups differ by at least Δ and declare two groups similar at the α = 0.05 level, if the 90 percent confidence interval for the difference in coverage is completely contained in the interval with endpoints −Δ and +Δ. That is, the groups are similar if $({\widehat{\mu }}_T-{\widehat{\mu }}_R)\pm 1.645\times \mathit{SE}({\widehat{\mu }}_T-{\widehat{\mu }}_R)$ is completely contained in the interval with endpoints −Δ and +Δ, where ${\widehat{\mu }}_T$, ${\widehat{\mu }}_R$ are the point estimate of μ_T and μ_R, respectively; $\mathit{SE}({\widehat{\mu }}_T-{\widehat{\mu }}_R)$ is the standard error of ($({\widehat{\mu }}_T-{\widehat{\mu }}_R)$). Thus, α is the probability of concluding that the populations differ by less than Δ when the difference is actually Δ or larger. The critical choice of Δ should depend on research issues and will vary with the context. For example, in the pharmaceutical industry a standard for equivalence is that on agreed upon variables, the population mean of the test group μ_T must be within 20% of the mean of the reference groupμ_R [41]_. We can estimate μ_R with the sample mean since it is the best unbiased estimate of the population parameter.

For our equivalence testing analysis, we used Δ=0.1μ_R or Δ=0.05μ_R depending on outcome measures (see details in Discussion). Using SAS, version 9.1, we calculated point estimates and standard errors of outcome measures of PROMIS general population and sub-samples and national norms; these statistics formed the basis for equivalence testing for comparison between PROMIS and national norms.

RESULTS

Demographics of PROMIS general population along with U.S. Census data are shown in table 1. For U.S Census data, the mean age was 45 years (standard deviation [SD] = 18), and 48% were male. Most of the participants were White (74%) followed by Hispanic (11%), Black (11%) and Other Race (4%). Fifty-one percent had more than high school education, 29% had high school diploma or equivalent and the rest (20%) had less than high school education. Fifty-seven percent were married, 23% were never married or living with partner, 13% were divorced or separated and 7% were widowed. For income, 15% earned less than $20,000 yearly, 35% earned between $20k-$50k, 35% earned between $50k to $100k and 15% earned more than $100k yearly.

Table 1. Demographical Characteristics.

Characteristics	PROMIS [Unweighted] (N=11796)	PROMIS [Weighted] (N=2.18×108)	Census 2000 [SF4] (N=2.18×108)	PROMIS: sub-sample (N=2196)
Age
Mean (SD)	50 (18)	45 (17)	45 (18)	45 (17)
Age group, %
18-29	16.9	22.5	22.5	22.4
30-44	24.1	31.8	31.8	31.9
45-59	25.9	24.1	24.1	24.1
60-74	18.9	13.8	13.8	13.8
75+	14.3	7.7	7.7	7.6
Gender, %
Male	45.0	48.3	48.3	48.3
Female	55.0	51.7	51.7	51.7
Education, %
Less than high school	2.8	20.3	20.3	2.5
High school diploma/GED	18.7	28.6	28.6	18.6
More than high school	78.5	51.0	51.0	78.9
Race, %
White	74.8	74.2	74.2	74.3
Black	9.9	10.8	10.8	10.8
Hispanic	12.7	10.5	10.5	10.5
Other	2.6	4.4	4.4	4.4
Marital Status, %
Married	57.7	57.3	57.4	55.4
Widowed	6.1	7.0	7.0	4.5
Divorced/Separated	12.2	12.6	12.6	11.4
Never married/Living with partner	24.1	23.1	23.1	28.7
Annual Family Income, %
$0 to $19,999	10.3	15.1	15.1	11.0
$20,000 to $49,999	35.2	34.9	34.8	32.9
$50,000 to $99,999	37.5	34.8	34.8	39.3
$100,000 and Over	17.0	15.2	15.3	16.9
Height (Inches), mean (SD)	67 (4)	67 (4)	-	67 (4)
Weight (Pounds), mean (SD)	184 (48)	186 (51)	-	186 (48)

There were a total of 11,796 subjects in the PROMIS Internet population. The mean age was 50 years (SD = 18), and 45% were male. Most of the participants were White (75%) followed by Hispanic (13%), Black (10%) and Other Race (3%). Seventy-eight percent had more than a high school education, 19% had high school diploma or equivalent and the rest (3%) had less than high school education. Mismatch of target demographics versus the obtained sample was primarily due to over-sampling, and higher response rates among some of the sub-groups. This resulted in certain demographic groups having higher than predicted sample sizes, which in turn reduced the proportion (but not the original target sample size) of some of the lower frequency demographics. Compared to the 2000 U.S. Census, the weighted PROMIS general population had very similar distributions for age, gender, race, education, marital status, and annual family income. There were 2196 subjects in the PROMIS general population sub-sample and it had similar distributions to the U.S. Census for age, race, gender and income, but it had 27% more people having high school education.

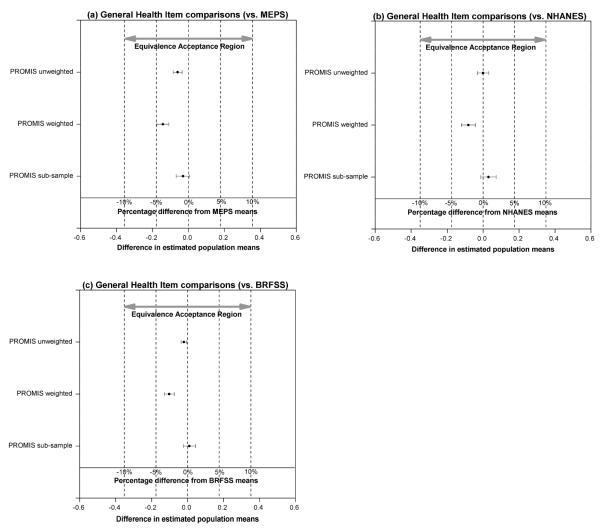
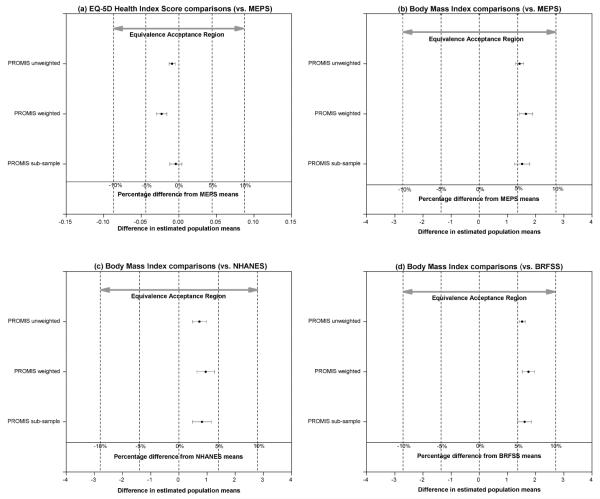
Table 2 displays the distribution of the general health item for national norms, PROMIS general population and sub-sample. For equivalence tests, boldface type in table 2 indicates similarity (the same for all other tables); that is, the null hypothesis of a difference greater than ±Δ is rejected. For general health items, confidence intervals for the difference are completely contained in the interval with endpoints −10% and +10% of the corresponding national norm means (see figure 1). Within this equivalence acceptance region Δ=0.1μ_R, where μ_R are the general health items means of comparison national norms, general health items of PROMIS general population (unweighted and weighted) and sub-sample are all equivalent to those of national norms MEPS, NHANES and BRFSS. Table 3 shows the matched comparisons based on the PROMIS age range (18-100 years old) to compare BMI between national norms and PROMIS general population and sub-sample. Within −10% and +10% of BMI means of comparison national norms, BMI’s of the PROMIS general population (unweighted and weighted) and sub-sample are equivalent to those of MEPS, NHANES and BRFSS (Figures 2b, 2c and 2d, respectively). Table 4 shows the matched comparisons based on the PROMIS age range (18-100 years old) to compare EQ-5D Health Index Score. Within Δ=0.05μ_R (See Discussion for reasoning choosing 0.05μ_R instead of 0.1μ_R), where μ_R are the EQ-5D means of MEPS, EQ-5D of PROMIS general population (unweighted and weighted) and sub-sample are equivalent to those of MEPS (Figure 2a).

Table 2. General Health Item Comparisons.

						90% confidence interval from equivalence testing
Variable	N	Mean	Std Error of Mean	95% CL for Mean		vs. MEPS	vs. NHANES	vs. BRFSS
General Health (5- Excellent, 4-Very Good, 3-Good, 2-Fair, 1-Poor)
2004 MEPS	20777	3.56	0.012	3.54	3.59
2001-2002 NHANES	6873	3.50	0.017	3.47	3.54
2005 BRFSS	352036	3.52	0.004	3.52	3.53
PROMIS: General population (Unweighted)	11794	3.50	0.009	3.48	3.52	−0.085, −0.035	−0.032, 0.032	−0.036, −0.004
PROMIS: General population (weighted)	218022053	3.42	0.016	3.39	3.45	−0.175, −0.108	−0.120, −0.043	−0.129, −0.074
PROMIS: General population sub-sample	2196	3.53	0.020	3.49	3.57	−0.068, 0.008	−0.013, 0.073	−0.024, 0.044

Note: equivalencies are printed in boldface type.

Figure 1. Equivalence testing for general health item comparisons between PROMIS samples and national norms (MEPS, NHANES, BRFSS).

note: The horizontal bars depict confidence intervals (CI). CI for equivalencies (90% CI) are contained in the interval with endpoints −10% and +10% of the corresponding national norm means.

Table 3. Matched Comparisons (by PROMIS age range 18-100) for Body Mass Index.

						90% confidence interval from equivalence testing
Variable	N	Mean	Std Error of Mean	95% CL for Mean		vs. MEPS	vs. NHANES	vs. BRFSS
2004 MEPS	22002	27.20	0.059	27.09	27.32
2001-2002 NHANES	10132	27.90	0.13	27.68	28.13
2005 BRFSS	335185	27.11	0.020	27.08	27.15
PROMIS: General population (Unweighted)	11730	28.63	0.062	28.51	28.76	1.29, 1.57	0.49, 0.97	1.41, 1.63
PROMIS: General population (weighted)	217451226	28.85	0.13	28.59	29.12	1.41, 1.89	0.64, 1.26	1.52, 1.97
PROMIS: general population sub-sample	2186	28.72	0.15	28.42	29.02	1.25, 1.79	0.49, 1.15	1.36, 1.86

Note: equivalencies are printed in boldface type.

Figure 2. Equivalence testing for comparisons of EQ-5D health index score and Body Mass Index (BMI) between PROMIS samples and national norms.

note: The horizontal bars depict confidence intervals (CI). CI for equivalencies (90% CI) are contained in the interval with endpoints −10% and +10% of the corresponding national norm means.

Table 4. Matched Comparisons (by PROMIS age range 18-100) for EQ-5D Health Index Score.

Variable	N	Mean	Std Error of Mean	95% CL for Mean		90% confidence interval from equivalence testing vs. MEPS
2003 MEPS	20428	0.8717	0.0018	0.8682	0.8751
PROMIS: General population (Unweighted)	5833	0.8631	0.0019	0.8594	0.8669	−0.013, −0.004
PROMIS: General population (weighted)	118528320	0.8487	0.0041	0.8406	0.8567	−0.030, −0.016
PROMIS: general population sub-sample	1073	0.8676	0.0045	0.8587	0.8765	−0.012, 0.004

Note: equivalencies are printed in boldface type.

DISCUSSION

With the rapid growth in the use of the Internet in the past decade, the number of studies using IDC has increased significantly. The traditional Random digit dialing (RDD) has limitations with regard to obtaining representative samples due to the increasing number of cell phone users without home phone landlines and widespread screening of incoming calls. Non-response rate associated with RDD sampling is higher than personal interviews.[3] To overcome these limitations, PROMIS collected health-related quality of life data using an Internet polling panel, a cost-effective method to recruit a large and heterogeneous sample using a standardized method. Polimetrix used a sample matching methodology to obtain a more representative sample. The resulting PROMIS unweighted general population, however, is still noticeably different from U.S. Census. Compared to the latter, the PROMIS unweighted general population was 5 years older, had a higher percentage of males, and had a higher percentage of having more than high school education.

In order to compensate for non-response and non-coverage of PROMIS Internet sample so that the inferences based on PROMIS estimates can be applicable to the general population, we used two methods to generate samples. First, we identified a subset of the PROMIS Internet sample that approximated the joint distributions of selected key demographic variables (age, gender and race) in the 2000 U.S. Census. The resulting PROMIS general population sub-sample was more similar to the U.S. Census data than the PROMIS unweighted general population for all demographic distributions except education (the sub-sample had a higher percentage of people who had more than high school education than U.S. census). This deviation is due to the exclusion of education from the sub-sample generating process, which resulted in some selection bias, affecting its generalizability across educational level.[7]

We used U.S. Census data as the standard for generating analytical weights by raking, a post-stratification adjustment that allows the distributions of selected subject characteristics to be similar to the target U.S. non-institutionalized population of persons 18 years of age or older. The resulting weighted PROMIS general population matches the U.S Census well for all demographic characteristics. Compared to the unweighted PROMIS sample, the weighted PROMIS general population is more comparable to national norms with regard to subject characteristics. Health measures such as BMI and EQ-5D also revealed similarities between weighted PROMIS general population and national norms.

We used equivalence testing to perform comparisons between the PROMIS population, the sub-sample, and national norms for BMI, EQ-5D health index score, and self-rated general health. With equivalence testing, researchers must specify an acceptable difference between groups, Δ. We cannot reject the null hypothesis of a difference greater than Δ unless the statistical evidence is strong. In order for results of equivalence testing to be useful in assessing representativeness of the PROMIS Internet sample, Δ must be carefully selected. All statistical analysis depends upon the specification of these bounds. On the other hand, the equivalence bounds provide a way to incorporate subject context directly into a statistical analysis, rather than using statistical analysis as a substitute for subject context. For example, the general health item of 2001-2002 NHANES is a 5-point polytomous response scale (see table 2), with 5-Excellent, 4-Very Good, 3-Good, 2-Fair, 1-Poor. The mean is 3.5, so −10% and +10% of the reference mean is 3.15 and 3.85, respectively. Therefore, differences from the reference mean are 0.35 or about one-third of a response unit, which is not important for this measure. For our equivalence testing analysis, we used −10% and +10% of reference mean for outcome measures (except EQ-5D) because ±10% of the reference mean was judged to be of little practical difference between these outcome measures of PROMIS and national norms by minimally importance difference and standardized effect size. [42, 43] For 10% of the reference mean, we calculated Cohen’s [42] standardized effect size, which is the mean difference divided by a standard deviation (SD). Cohen suggested that standardized effect sizes of 0.2–0.5 should be regarded as ‘small’, 0.5–0.8 as ‘moderate’ and those above 0.8 as ‘large’. The effect sizes of all outcome measures but EQ-5D ranged from 0.34 to 0.41, which are all considered small by Cohen’s standard [42, 43]. The effect size for EQ-5D using 10% of the reference mean ranged from 0.59 to 0.6, which is moderate by Cohen’s criterions. However, the actually observed difference of EQ-5D between PROMIS and national norm is quite small and the null hypothesis of the equivalence testing was rejected using 5% of the reference mean, which has a small effect size of 0.3. Thus, 5% of the reference mean was used in equivalence testing for EQ-5D.

Equivalence testing indicates that BMI, EQ-5D health index score, and self-rated general health of PROMIS general population (unweighted and weighted) are equivalent to those of national norms. Our results show that for most measures, the estimates were consistent with those produced by other national level surveys. The validity of internet-based survey methodology by using post-stratification weighting can be also seen in Knowledge Network’s Panel and Sampling method.[23]

There are a number of limitations with this analysis. First, self-reported information has potential problems such as recall bias and possible intentional misreporting of behaviors. As our analyses are solely based on self-reported information, there may be unidentifiable response bias. Secondly, Internet recruiting is still in its early stages, which suffers from known biases arising from the differences between the parts of the population who are online and those who are not. Moreover, unlike other available methods, Internet recruiting to general public surveys often depends on a volunteer panel, which could also influence differences. Finally, the limited availability of measures and formats provided in the census constrained the number of auxiliary measures we could use to generate the analytical weights, limiting our capacity to make the PROMIS general population more similar to the U.S. general population.

In summary, we compared PROMIS Internet samples with the U.S. general population. BMI, EQ-5D health index score, and self-rated general health of PROMIS general population (unweighted and weighted) are generally comparable to those of national norms including MEPS, NHANES and BRFSS. Compared to the unweighted PROMIS general population and sub-sample, the weighted PROMIS general population is more comparable to national norms with regard to subject characteristics. Our findings indicate that data collected via Internet polling panels--when weighted to account for differences in distributions on key demographic variables--may be representative of the general U.S. population.