Rank–rank hypergeometric overlap: identification of statistically significant overlap between gene-expression signatures

Abstract

Comparing independent high-throughput gene-expression experiments can generate hypotheses about which gene-expression programs are shared between particular biological processes. Current techniques to compare expression profiles typically involve choosing a fixed differential expression threshold to summarize results, potentially reducing sensitivity to small but concordant changes. We present a threshold-free algorithm called Rank–rank Hypergeometric Overlap (RRHO). This algorithm steps through two gene lists ranked by the degree of differential expression observed in two profiling experiments, successively measuring the statistical significance of the number of overlapping genes. The output is a graphical map that shows the strength, pattern and bounds of correlation between two expression profiles. To demonstrate RRHO sensitivity and dynamic range, we identified shared expression networks in cancer microarray profiles driving tumor progression, stem cell properties and response to targeted kinase inhibition. We demonstrate how RRHO can be used to determine which model system or drug treatment best reflects a particular biological or disease response. The threshold-free and graphical aspects of RRHO complement other rank-based approaches such as Gene Set Enrichment Analysis (GSEA), for which RRHO is a 2D analog. Rank–rank overlap analysis is a sensitive, robust and web-accessible method for detecting and visualizing overlap trends between two complete, continuous gene-expression profiles. A web-based implementation of RRHO can be accessed at http://systems.crump.ucla.edu/rankrank/.

INTRODUCTION

Technological advancements in molecular biology provide today’s scientist a wealth of tools to reproducibly measure the expression of a large number of genes in a variety of model systems and patient populations. Generating biological hypotheses from high-throughput expression profiling experiments can be aided by comparing multiple expression profiles to one another. For example, gene-expression changes conserved both in human tumors and mouse models of cancer can yield insight into underlying molecular mechanisms driving tumorigenesis (1). Comparing results from independently collected profiling experiments is often complicated by differences in a number of important variables—which and how many genes are measured and by which exact probes, which species, whether DNA, RNA or protein was measured, etc. Thus, algorithms that compare expression profiles should be as sensitive and robust as possible to detect overlap despite experimental and biological confounding factors.

Current methods that compare gene-expression profiles often test for correlation, overlap, or enrichment between multiple sets of genes (‘gene set versus gene set’ approaches) (2–4). Using thresholds for differential expression, many expression analysis approaches derive gene sets tens to hundreds of genes in size to represent the most significant results from what was originally a continuous range of thousands of gene-expression differences observed in a genome-wide experiment. These gene set expression signatures are then characterized using algorithms that measure statistical enrichment for genes in particular pathways, with particular functions or with particular structural characteristics attained from publicly available databases. The statistical significance of enrichment is typically determined using the hypergeometric distribution or equivalently the one-tailed version of Fisher’s exact test. Alternatively, approaches such as subclass mapping allow the comparison of clusters of genes that have similar expression patterns within subsets of samples in different profiling experiments (5). In both the gene set and gene cluster approaches, the size of the gene list and the number of overlapping genes calculated is dependent on the thresholds of differential expression used to create the representative gene sets (6). Consequently, a difficulty with using these types of approaches is that determining a representative gene set demands some statistical expertise in determining appropriate confidence thresholds. Furthermore, genes that have small but reproducible changes tend to be discarded when taking only the top changing genes as representatives for genome-wide expression profiles.

A notable improvement on these approaches is to treat the gene-expression data as a ranked continuum of differential expression changes rather than a truncated representative gene set. A ‘gene set versus ranked list’ approach was first introduced in expression analysis through the Gene Set Enrichment Analysis (GSEA) algorithm (7–9). This method searches for coordinated increased or decreased expression of biologically characterized gene sets in a microarray gene-expression experiment. Results of a gene-expression experiment in this case are represented as a continuous list of gene-expression changes ranked on (i) the degree of differential expression between two types of samples or (ii) correlation to a particular quantitative phenotype pattern across a range of samples. This gene set to ranked list approach has allowed for the detection of weaker signals that would be missed by previous approaches by allowing all genes in a gene-expression profile to contribute to overlap signal in proportion to their degree of differential expression, instead of using a fixed cutoff and equally weighting only those genes above threshold. In particular, GSEA facilitates the detection of small but concordant and statistically significant gene-expression changes. Thus, one can consider a full ranked list of differentially ranked genes as the profile signature for a certain biological attribute, rather than just considering the top n genes as an otherwise unweighted representative gene set. The use of ranked gene lists to represent gene-expression profiles has been demonstrated in the GSEA-based analysis of mouse models of cancer (1) and of the Connectivity Map (Cmap) drug response database (10).

The GSEA approach is often used with gene sets that are derived from continuous gene-expression profiles, such as results from a microarray experiment. In a recent example, a cross-species comparison was performed in which transcriptome microarrays were used to analyze global gene-expression profiles in a genetically engineered mouse model of lung cancer (1). A fixed size representative gene set from this mouse model profile was derived from the top differentially expressed genes using statistical tests designed to bound the false discovery rate (FDR). This mouse model gene set was then compared to a continuous human lung cancer gene-expression profile using GSEA. This allowed the authors to interrogate human lung tumor gene-expression profiles by applying the standard GSEA gene set (mouse signature) versus continuous ranked gene list (human signature) approach to compare what began as two continuous ranked gene lists.

By eliminating the need for applying thresholds in one gene-expression profile, GSEA can detect enrichment of groups of related genes that would be considered weakly differential or insignificant on their own. We reasoned that traversing the entire range of two expression profiles would even more sensitively detect overlap between the results of two genome-wide experiments and would be especially useful in cases of weak but statistically significant, biologically pertinent concordance. To this end, we have developed a threshold-free algorithm designed specifically for continuous ranked list versus ranked list genome-wide expression profile comparisons. Our Rank–rank Hypergeometric Overlap (RRHO) algorithm identifies and visualizes areas of significant overlap by determining the degree of statistical enrichment using the hypergeometric distribution while sliding across all possible thresholds through the two ranked lists. Whereas applications based on converting ranked lists to gene sets using carefully chosen thresholds remain useful, our approach complements these algorithms by providing more information about the strength and regions of overlap between two data sets without truncating gene-expression profiles. RRHO has been implemented to quickly and easily provide a graphical representation that reveals global characteristics of the relationship between two profiling experiments, such as whether upregulated or downregulated genes share more in common or whether there is greater evidence for anti-correlation than correlation. Eliminating the need to statistically determine thresholds for defining representative gene sets makes RRHO analysis simple to use and can identify overlap signal that would be missed using other approaches. The sensitivity and versatility of RRHO analysis aid in hypothesis generation by providing a statistical and graphical summary of shared gene-expression patterns between two continuous gene-expression profiles.

MATERIALS AND METHODS

RRHO approach

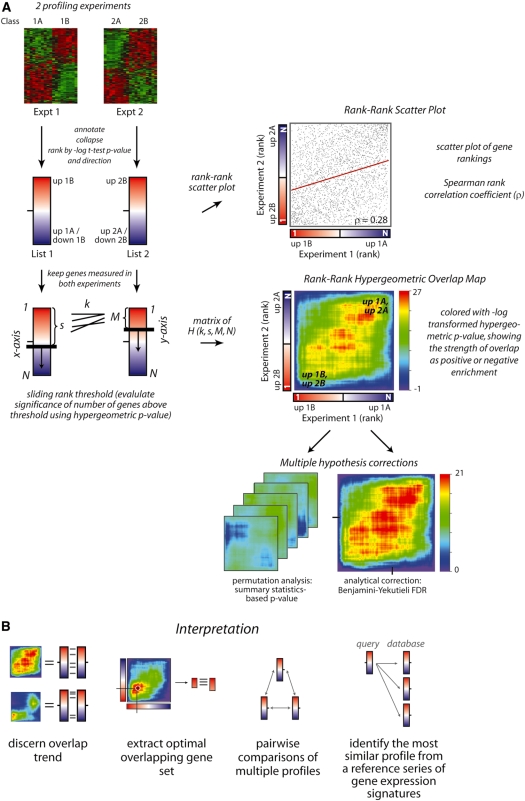
Our algorithm can be divided into several steps (schematically illustrated in Figure 1A). First, RRHO creates gene-expression profiles from the two data sets being compared by ranking the genes measured in each experiment according to their degree of differential expression. The genes can be ranked according to any measure of differential expression; this manuscript shows results using a signed log₁₀-transformed t-test P-value with the sign denoting the direction of change, positive for increasing in the second class of the experiment and negative for decreasing. Other common metrics are signal-to-noise ratios (highly related to the t-test P-value) and fold change. Sorting the genes by these metrics will place the significantly increasing genes at the top of a ranked list and the significantly decreasing genes at the bottom with all relatively unchanging genes in the middle. Using the rank of genes instead of the raw metric for graphing differential expression spreads the gene-expression changes more evenly across the range of the plot. Second, multiple probes that measure the same gene are collapsed to a single measurement by taking the most differentially expressed probe as a representative value. Data-driven supervised statistic-based collapsing has been demonstrated to improve biological discovery (11), but RRHO is robust to other collapsing techniques such as choosing the probe with greatest variation across samples. Third, genes not measured in both experiments are discarded. The gene rankings common to both experiments can be visualized using a rank-based scatter plot. When two gene-expression profiles are strongly and significantly overlapping throughout, enrichment can be observed along the diagonal of the rank–rank scatter plot and a simple correlation coefficient analysis can be used to quantify this enrichment. However, weaker but still statistically significant signal can not always be as clearly visualized using rank–rank scatter plots. Fourth, RRHO iterates through the entire ranked gene list from both datasets calculating if the amount of genes that are above the current thresholds in both sublists (overlapping genes) is significantly more or less than would be expected by random chance according to the hypergeometric distribution. This procedure results in a matrix of hypergeometric P-values whose dimensions are determined by the length of the ranked lists. A step parameter can be used to reduce the number of calculations and speed up the procedure. If a step size greater than one is used, the granularity of the graphical heatmap output provides feedback as to the adequacy of the resolution chosen. Fifth, this matrix is shown as a heat map colored by the direction-signed, log₁₀-transformed hypergeometric P-value (positive if the overlap is more than expected and negative if it is less). The point on the map that has the highest absolute log₁₀-transformed significance denotes the rank thresholds (and accordingly the metric thresholds) on the x- and y-axis (i.e. in both experiments) that would yield the most statistically significant set of overlapping differentially expressed genes or putatively co-regulated genes. This representation allows one to quickly observe whether there is significant overlap between the differentially expressed genes in both experiments and where the bounds of that overlap are located. Last, multiple hypothesis testing corrections are applied as described below. RRHO maps can be used in several ways to determine the nature of the overlap between gene-expression profiles, extract the optimal overlapping gene set, and determine relative overlap within a series of gene-expression profiles (Figure 1B).

Figure 1.

Schematic of the RRHO algorithm. (A) Preprocessing: gene-expression profiles are defined as continuous lists of genes ranked by their degree of differential expression. Here, we rank by the signed log₁₀-transformed t-test P-values between Class A and B, positive sign if the mean expression is higher in Class B and negative if lower. Microarray probes measuring the same gene are collapsed to a single value using the most differentially expressed probe and only genes measured in both experiments are retained. A scatter plot can be used to visualize gene ranking similarities, particularly when the degree of overlap is high. The regression fit (red line) and Spearman’s rank correlation coefficient (ρ) for this example are indicated. Creating the RRHO map: the hypergeometric P-value for enrichment of k overlapping genes is calculated for all possible threshold pairs for each experiment, creating a matrix where the indices are the current rank in each experiment (s, M). The direction-signed log₁₀-transformed hypergeometric P-values are plotted in a heatmap as indicated by an accompanying color scale, mapping the degree of statistically significant overlap between the two ranked lists from that point on the map (corresponding to a rank threshold pair) to either the bottom left (ranks 0,0) or top right corner (ranks N,N). Multiple hypothesis correction can be applied using either permutation analysis (when sample number is large) or a BY FDR correction. (B) Interpreting RRHO maps. (i) Different map patterns indicate different types of overlap, such as the full profiles being correlated or only genes increasing in both experiments overlapping. (ii) The highest intensity point on the map can be used to extract the most statistically significant overlapping gene set. RRHO analysis can be used (iii) to compare relative overlap pairwise within a set of profiles (e.g. Figures 3B and 4) or (iv) to compare an experimental profile to a series of reference signatures (e.g. Figure 5).

Hypergeometric probability distributions

The hypergeometric distribution (equivalent to Fisher’s one tailed exact test) describes the expected number of successes in a sequence of draws from a finite population without replacement. It is commonly used in the microarray analysis field to determine the degree of enrichment or overlap of particular subsets of genes (6,12–14). The hypergeometric probability distribution is defined as follows:

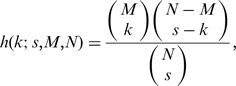where k is the number of successes in the sample (overlapping genes), s is the sample size, M is the number of successes in the population (s and M are the rank in each ranked list at the current rank step pair) and N is the population size (the total length of the input ranked lists), and the brackets indicate the binomial coefficient:

A P-value is obtained from the Cumulative Distribution Function (CDF) by integrating (summing) the probability distribution from one extremity of the distribution to the value of k:

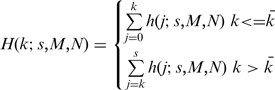where 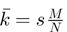is the expected value for the hypergeometric distribution. When k is more (or less) than expected, we calculate the probability of observing k or greater (or fewer) events. In our application, N is the total number of genes in the ranked lists, s and M are the rank thresholds and k is the number of overlapping genes (shown schematically in Figure 1A). The –log₁₀ P-value is calculated and direction-signed for each pixel in the RRHO map, with negative values indicating under enrichment:

In established pathway analysis approaches, s and M are the size of a gene set derived from gene-expression experiments or of a characterized gene set representing a particular signaling pathway or representing functionally related genes, k is the number of genes common to both gene sets and N is an estimate of the total number of genes from which the gene sets are chosen. Typically, k is tens to hundreds in size, s and M are hundreds to thousands and N is all genes measured on an expression microarray which is on the order of tens of thousands of transcripts. RRHO iterates through a full range of s and M sliding through rank thresholds in two experiments, calculating hypergeometric overlap P-values using the observed values of overlap (k).

Mathematical symmetries of the hypergeometric distribution

The hypergeometric CDF works well for our application because it is symmetric upon exchange of s and M (the two gene list rank thresholds), 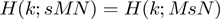. This symmetry makes the hypergeometric CDF more suitable for our situation, where both lists are continuous and treated in precisely the same fashion, than metrics such as the Kolmogorov–Smirnov statistic, which do not possess this same symmetry upon exchange of s and M as determined by which experiment is represented as a ranked list versus which is represented as a fixed-size gene set. An additional symmetry of the enrichment analysis and of the hypergeometric distribution ensures that enrichment at the top of two lists is equivalent to enrichment at the bottom of the two lists using the same rank threshold points, 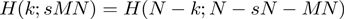, so the calculations only need to be performed once in a single direction. Additionally, the probability for over-enrichment between the top of list 1 and the top of list 2 is equal to the probability for the corresponding under-enrichment between the top of list 1 and the bottom of list 2, or 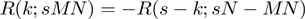due to our sign convention for over- or under-enrichment. These characteristics aid in the computational implementation and in the interpretation of the RRHO maps (see User’s Guide to interpreting RRHO heatmaps in the Supplementary Data).

Computational acceleration techniques

One difficulty that arises from calculating P-values from the hypergeometric distribution is the generation of numbers with high magnitude caused by factorials. For example, for a list of genes of moderate size, N = 5000, one would have to calculate 5000!, which is of the order of 10^{16 325}, a number that cannot be rendered with common representation for floating point numbers. Furthermore, processing these high magnitude numbers places high demands on processor time. We addressed both problems (speed and magnitude) by using a factorial acceleration technique (15) along with an effective implementation in the C programming language.

Factorial calculations

A factorial acceleration technique, based on work by Trong (15), was incorporated in our C implementation of the RRHO algorithm. The technique uses: (i) prime number factorization of factorials and cancellation of common factors between numerator and denominator and (ii) recursion formulas to calculate the CDF. With this technique, we can calculate the P-values for RRHO analysis without ever truly calculating any factorials.

For example, consider:

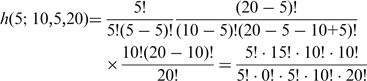This becomes, after prime number factorization of each factorial and cancellation of common factors:

We elected to use the IEEE extended double-precision format (16) to hold floating-point numbers because it allows for the largest exponent range (in this application, significant digits are of much less importance). The current implementation of that format on our computers provides: 1 sign bit, 15 bits for a signed exponent (−16 383 to 16 384), and 64 bits for the mantissa. Hence, the smallest and largest absolute numbers that can be represented are of the order of 2^{−16 383} and 2^{16 384}, respectively, corresponding to a range of approximately .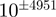

Since the largest number that can be expressed in extended double precision is on the order of 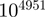(roughly 1760!), it is clear that additional actions are needed to be able to treat large factorials. For that purpose, we introduce an integer vector (dubbed the prime-exponent vector) used to represent factorials in which each element is the exponent of a prime number in the factorization. For a given hypergeometric calculation, the size of the vector corresponds to the number of prime numbers less than or equal to N. To actually perform a hypergeometric calculation, a running-sum prime-exponent vector is initialized with zeroes. Then each factorial in the calculation is in turn prime-factorized (in a vector) and added or subtracted to the running-sum vector depending on whether the factorial is located in the numerator or the denominator, respectively. The final result (probability) is obtained by carrying out this last multiplication one factor at a time and maintaining a running product. To avoid overflow or underflow during the procedure, factors are not considered in their given order. Rather, the running product is monitored and whenever its exponent becomes too close to one of the limits (viz. −16 383 or 16 384), only factors that bring the product away from the limit are applied. The process is repeated until all factors have been multiplied. The final result of the multiplication is kept in extended double precision representation. To reduce computations, the program uses a pre-calculated list of prime numbers along with their log₁₀ values.

Calculating the CDF

The calculation of the CDF involves summing over the probability distribution from one extremity to the value of k using recursion formulas. Recursion formulas and the prime factorization of factorials are well described (15). Due to the potentially large range in the magnitude of the numbers involved, the sum is carried over from larger numbers toward smaller numbers and stops as soon as the number to add to the running sum is so small that the result would only change less than the desired resolution.

Log-transformed (–log₁₀) P-values are used instead of actual P-values in the ultimate hypergeometric map visualization. The log of the resulting extended double-precision number had to be calculated with our own function since the standard C log function accepts only double precision arguments. The machine representation of a floating-point number x is:

where m is the mantissa (a fraction) and e is the base-2 exponent. In extended double precision, the 64-bit mantissa is stored as two 32-bits numbers (considered unsigned integers) called m0 (most significant digits) and m1 (least significant digits). Ignoring m₁, we can write:

Taking the log on both sides yields:

an expression that can be calculated with the standard C log function.

Multiple hypothesis corrections

In considering the biological implications of the hypergeometric overlap map results, it is important to consider multiple hypothesis correction. We have tested two methods for multiple hypothesis correction: sample permutation analysis and an analytical correction, a modified Benjamini multiple hypothesis correction factor.

Permutation-based correction

Generally, we recommend sample permutation analysis as a way of assessing the overall significance of a hypergeometric map. When permutations are performed by randomly reassigning the sample class labels and recalculating the ranked gene lists, gene–gene correlations within the data are preserved and thus this method provides a reliable estimate of how unlikely an overlap result could be attained by random chance (8). Note that shuffling gene labels instead of sample labels does not maintain these gene–gene correlations within each sample and thus simply recreates the hypergeometric distribution. Permutation-based correction requires relatively high computation time [O(N_permutations)] and a high enough number of samples in each class of the profiling experiments to allow for sufficient distinct permutations. We use summary statistics of the rank–rank overlap maps (described below) to screen through the permutated-sample maps and determine the frequency of permutation instances that had an optimal overlap more significant than in the true case to estimate the probability of observing the true amount of overlap by chance. For a comparison of gene lists of length 5000 and a rank threshold step size of 50, it takes ∼15 s to calculate the 10 000 [(5000/50)²] hypergeometric CDF results required to create one RRHO map using an Intel Xeon 3.2 GHz processor, thus requiring ∼4 h to create and analyze 1000 permutation maps on a single computational node.

We have designed summary statistics for rank–rank hypergeometric analysis based on our experience using gene-expression microarray data. The most straightforward summary statistic of a rank–rank hypergeometric map is the point with the maximum absolute log P-value, which represents the rank threshold pair that gives the most significant hypergeometric overlap in the experiments being compared. When genes are ranked using a direction-signed metric, there are often two distinct signals in the map: one corresponding to overlap in the tops of the lists (signal in the bottom left corner of the RRHO map, from genes upregulated in both experiments) and one corresponding to overlap in the bottoms of the lists (top right corner, co-downregulated genes) (see example in Figure 1B). This occurs when using lists with overlap at each end, but little rank correlation in the middle of the lists typically due to random ordering of the many genes that are not differentially expressed in the two individual experiments. In these cases, it can be helpful to use measures that summarize the top–top and bottom–bottom signals separately, namely the maximal absolute log P-value in these two regions of the map that correspond to genes changing in the same direction. We use these two maxima both individually and as a sum (see User-Guide Figure 2 in Supplementary Data and the application of this approach in Figures 4 and 5).

Figure 2.

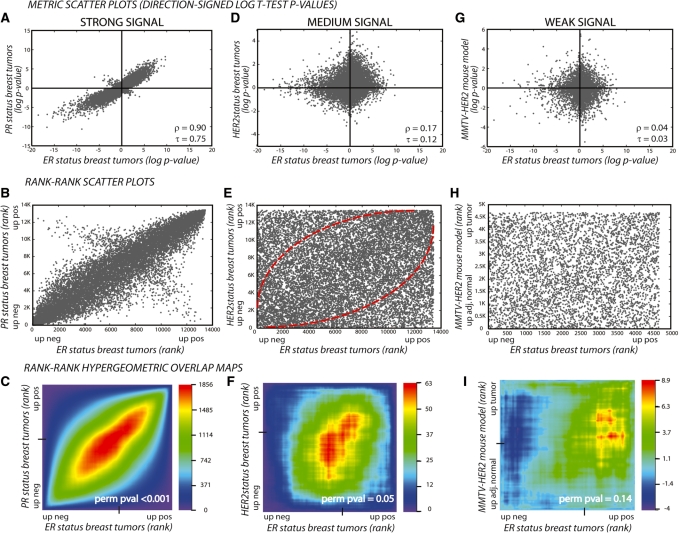
RRHO Maps are a sensitive method for detection and visualization of overlap in expression data. Three representations of overlapping published cancer-related gene-expression signatures: signatures with strong (A–C), medium (D–F) and weak (G–I) overlap represented as metric scatter plots (A, D and G), rank–rank scatter plots (B, E and H) and hypergeometric overlap maps (C, F and I). The first row of metric scatter plots show genes plotted by their direction-signed (up, positive; down, negative), log₁₀-transformed t-test P-values in each experiment; genes significantly changing in the same direction in both experiments are in Cartesian quadrants I and III and in opposite directions in quadrants II and IV. The Spearman’s ρ and Kendall’s τ rank correlation coefficients are indicated. The second row of rank–rank scatter plots show each gene plotted by its rank based on this metric. This representation spreads the genes more evenly across the plot and allows for assessment of overlap by increases in local density. The resulting plots show a higher density of genes along the diagonal in both the strong and medium overlap cases, especially at the bottom left and top right regions. The last row shows the rank–rank hypergeometric heatmap for each of these comparisons, where the overlap is represented statistically based on the hypergeometric distribution allowing visualization of any signal, even those that are relatively weak but significant. The log₁₀-transformed hypergeometric P-values are indicated in the color scale bar with negative values indicating under-enrichment. Sample permutation P-values based on the sum of the signal in the bottom left and top right regions are indicated (perm pval).

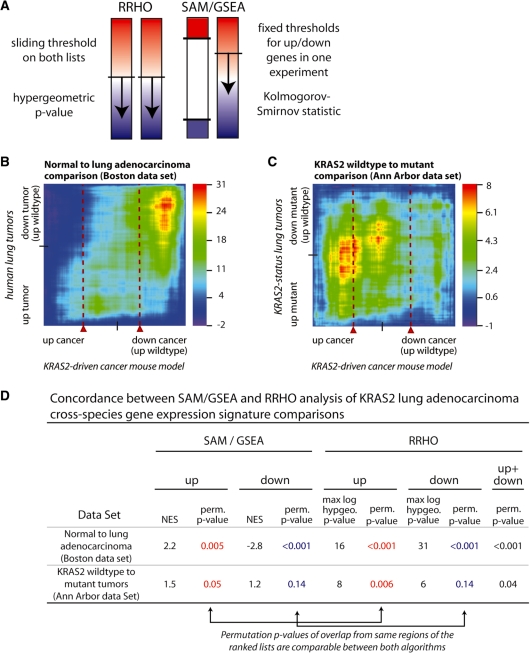
Figure 4.

RRHO yields comparable significance results to GSEA while adding a 2D perspective. (A) Schematic showing how RRHO and GSEA have been applied for comparing two continuous expression signatures. A previous application of GSEA used statistical methods (SAM algorithm) to choose an appropriate fixed threshold to define two ‘gene sets’ of up- and downregulated genes from their mouse model of lung cancer. These gene sets were then used in GSEA to search for overlap with the expression profile from human tumors treated as a continuous lists (SAM/GSEA approach) (1). RRHO treats both signatures as continuous by stepping through all possible threshold pairs in both ranked gene lists to create a hypergeometric overlap map. The two algorithms use different but highly related enrichment statistics, the hypergeometric distribution P-value for RRHO and the Kolmogorov–Smirnov statistic for GSEA (see ‘Materials and Methods’ section). Both approaches employ multiple hypothesis corrections through either permutations or analytical corrections, performing the sliding threshold(s) step in all permutations. (B and C) RRHO maps showing the overlap between a KRAS2-driven mouse model profile (x-axes) and two human lung cancer profiles (y-axes), one for lung tumorigenesis in general and one specific to KRAS2 status within tumor subgroups. Red dashed lines approximate the threshold chosen to represent the mouse model gene set in the published GSEA-based analysis and relate to the mountain plot output produced by GSEA. (D) Comparison of permutation P-values between the SAM/GSEA and RRHO approaches. Permutation P-values from our best recreation of Sweet-Cordero SAM/GSEA analysis mouse model defined up and down (dn) gene sets are listed juxtaposed to permutation P-values from summary statistic-based interpretations of the RRHO maps for the same data. Up results are from analysis of genes upregulated in both experiments, and likewise for down. Up+dn RRHO results simultaneously consider both directions by calculating the sum of the maximal absolute log P-value from both the up–up and down–down regions of the heatmap during the permutation analysis (see ‘Materials and Methods’ section).

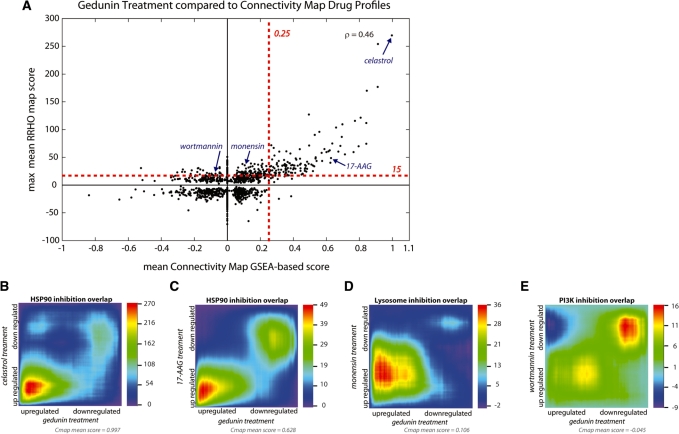
Figure 5.

Using RRHO to survey a compendium of gene-expression signatures. (A) We used both RRHO and a GSEA-based approach to compare the overlap of a gedunin treatment gene-expression profile with a panel of small molecule drug treatment signatures from the Cmap database. Mean Cmap scores are reported for multiple instances of a single drug (x-axis) using a gedunin signature of 50 up- and 50 downregulated genes. Benjamini-Yekutieli (BY)-corrected RRHO maps for multiple instances were created individually and combined into a composite map using a pixel-by-pixel mean; the maximum positive or minimum negative value (whichever has higher absolute value) is reported (y-axis). The Spearman rank correlation coefficient between the overlap measures of these two scoring techniques shows overall positive correlation (ρ = 0.46). Estimated significance thresholds for each algorithm are indicated with red dashed lines. (B–E) Mean BY-corrected RRHO maps showing gene-expression overlap of gedunin with the HSP90 inhibitors celastrol (B) and 17-AAG (C), the lysosome uptake inhibitor monensin (D), and the PI3 kinase inhibitor wortmannin (E). These drugs show statistically significant overlap by RRHO analysis, but varying degrees of overlap by Cmap analysis. Note that in the two cases where RRHO analysis detects signal while the GSEA-based approach does not (D and E), the maximal overlap is outside the top 50 genes used in the GSEA-based approach (i.e. the signal is further from the lower left or upper right corner than in the other cases).

Analytical correction: Benjamini and Yekutieli multiple hypothesis correction

In cases where a permutation-based correction is not feasible (when there are too few samples for permutation analysis), we have implemented an analytical approach to apply a correction factor to account for multiple hypothesis testing. As a multiple hypothesis correction estimate we use the Benjamini and Yekutieli (BY) method (17), which limits the FDR in the presence of an arbitrary dependency structure in the tests calculated. Our hypergeometric matrix calculates N² tests, where N represents the number of common genes between the two experiments being compared. But testing overlap in the top 50 genes in both experiments is not independent from testing overlap in the top 100 genes as the overlap information from the top 50 is shared between both tests. Given that the tests are not independent, a strong family-wise error rate correction (FWER) such as a Bonferroni correction would be predicted to be too stringent. We and others have observed that FWER correction is in fact too stringent for overlap and enrichment analysis techniques (8,18), for example in comparison to permutation-based probabilities (Supplementary Table S2). A FDR correction is more lenient and more appropriate when there are dependencies in the tests. BY proved that a conservative modification of the BY FDR correction would accommodate arbitrary dependencies in testing (18). We have implemented this BY correction, such that for a list of hypergeometric P-values in increasing order:

where H_N = 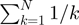is a harmonic number and j is the position of the P-value in the ordered list of P-values comprising the hypergeometric map. To speed up computations, we used the fact that H_n can be approximated through a limited asymptotic expansion: H_N ≈ γ + ln (N) where γ is the Euler–Mascheroni constant.

In practice we have found that the BY correction is not stringent enough in comparison to permutation-based correction (Supplementary Table S2). Nevertheless the BY correction provides a computationally quick first estimate prior to permutations, or when permutations are not feasible. For a direct comparison of all multiple hypothesis correction approaches and discussion about their appropriate use, please refer to the User’s Guide to interpreting RRHO heatmaps in the Supplementary Data.

Note that RRHO maps are most directly comparable when created using the same size ranked lists since the raw hypergeometric P-value is influenced by this parameter. The number of genes used in creating a RRHO map is based simply on the intersection of genes measured in both of the experiments. When two RRHO maps are made with two very different numbers of genes, we have developed a ‘list length correction’ method to scale RRHO map P-values before applying the BY analytical correction and subsequently comparing the maps to one another (see Supplementary Methods in Supplementary Data).

FDR for the overlapping gene list

Once the ranks corresponding to the most statistically significant overlap between the two lists are determined, the FDR of the observed set of overlapping genes (k) can be determined by calculating

where k_expected = 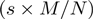, s and M are the optimal rank thresholds and N is the full gene list length. In cases where the overall signature overlap is statistically significant, the FDR of the overlapping gene list is not always small. Thus in applications where the genes on the overlapping list will be studied individually, the FDR should be calculated to help guide interpretation.

Data used in demonstration cases

The demonstration cases described below feature published microarray gene-expression data. They were converted to ranked lists by calculating t-test P-values between the relevant sample types (classes) for each probe, that were log₁₀-transformed and signed to indicate direction of change (positive for increased in Class B, negative for increased in Class A or decreased in Class B). Probes were annotated with current mouse or human UniGene identifiers and homologs were identified using HomoloGene; only the probe with the highest absolute signed t-test P-value within those with matching UniGene identifiers was kept in the collapsing step. Data downloaded from Gene-expression Omnibus (GEO) (19): MPAKT prostate cancer mouse model, GSE1413; breast tumors with ER, PR and HER2 status, GSE2603; MMTV-HER2/neu mouse model, GSE2528; BCR-ABL transfected cell line, GSE10912; mammary stem cell, GSE3711; KRAS2 overexpression cell line, GSE3151; lung tumors with KRAS2 status, GSE3141; imatinib treatment in leukemia patients, GSE2535; dasatinib treatment in cell lines, GSE9633 and GSE6569; castration and testosterone treatment in mice, GSE5901; gedunin treatment in prostate cancer cell line, GSE5506. Data downloaded from Array Express (20): imatinib treatment in leukemia patients, E-MEXP-433 (21). Data downloaded from an individual lab website: KRAS2 lung tumors and mouse model (1), Cmap database (10). Data communicated by collaborators: PTEN knockout prostate cancer mouse model, Dr Shunyou Wang, laboratory of Dr Hong Wu, UCLA (22).

RESULTS

Interpretation of RRHO graphical maps

The goal of RRHO is to identify trends in overlap between two biological signatures defined as ranked lists of differential gene expression in order to generate biological hypotheses. RRHO analysis will identify statistically significant overlap by stepping through genes ranked by their differential expression in two experiments, at each point using the hypergeometric distribution to assess the significance of the number of overlapping genes observed (Figure 1A). As shown in Figure 1B, RRHO analysis can be used in several ways to determine the overlap pattern and overlapping genes between two or more gene-expression profiles. (i) The overlap trend described by the overall map pattern reflects how the two gene-expression profiles are related: highly correlated throughout (positive signal along the diagonal), strongly differentially expressed genes overlapping (positive signal at the bottom left and top right corners), highly anticorrelated throughout (negative signal along the orthogonal diagonal, see User’s Guide) and other possibilities. (ii) The highest intensity point on the resulting overlap map corresponds to the pair of rank thresholds where the observed statistical overlap between the two gene-expression profiles is the strongest statistically. In other words, the highest intensity point represents the optimal overlap between the profiles in that this is the overlap that is least likely to occur by chance. The coordinates of the highest intensity point are the rank in each experiment above which are the most statistically significant set of overlapping genes. This overlapping gene set can be extracted from RRHO analysis to be validated or further analyzed. RRHO can be used (iii) in a pairwise fashion to determine which in a series of gene-expression profiles are most closely related to one another (e.g. Figures 3B and 4) or (iv) to compare an uncharacterized experimental profile to a series of characterized reference profiles (e.g. Figure 5). Statistically significant overlap can indicate that the biological samples or processes being compared have related underlying gene-expression programs, providing a biological lead that can be validated in follow-up experiments.

Figure 3.

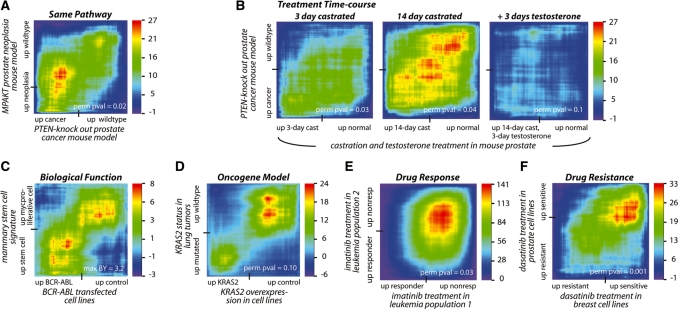
RRHO identifies statistically significant overlap between expression signatures supporting or generating biological hypotheses. (A) High overlap in gene-expression changes between mouse models of prostate neoplasia driven by PTEN and AKT, both in the PI3K signaling pathway, identifying genes consistently modulated by two different perturbations in the same pathway during tumorigenesis [hypergeometric P-value (HP) 10⁻²⁷] (22,26). (B) Increasing overlap of castration signature with PTEN-knockout-driven prostate cancer over time (minimum HP 10⁻²⁷) (22,27). Each map shows the overlap between non-cancerous prostate tissue following castration in a mouse (compared to prostate tissue from uncastrated mice) and a mouse model of prostate cancer driven by PTEN loss (compared to prostate tissue from wild-type littermates). The degree of overlap increases with time and is reversed when testosterone is given for 3 days. (C) Significant overlap between a stem cell signature from murine mammary glands and BCR-ABL fusion onco-protein signature (HP 10⁻⁸) (30,31). (D) High overlap between gene-expression changes driven by overexpression of KRAS2 oncogene in a cell line and by mutated KRAS2 in human lung tumors, identifying signaling events downstream of this oncogene that are potentially clinically relevant and can be studied in the cell line model (HP 10⁻²⁴) (35). (E) High overlap between treatment with the small-molecule inhibitor imatinib in two leukemia patient populations, identifying higher confidence markers for drug response (HP 10⁻¹⁴¹) (21,36). (F) Significant overlap between cell line-derived profiles from different tissue types based on sensitivity to the small-molecule inhibitor dasatinib, identifying possible adaptation mechanisms which can be targeted for higher drug efficacy (HP 10⁻³³) (38,39). The tick mark on each axis indicates the point in the ranked gene-expression signature list where the direction of differential expression switches. A permutation P-value based on the sum of the signal in bottom left and top right regions (perm pval) or when permutations are not possible the maximum of the BY-corrected RRHO map (max BY) is indicated.

The heatmap output of RRHO is colored by the direction-signed log₁₀-transformed hypergeometric P-values so high positive intensity areas indicate highly significant overlap of the ranked lists and high negative intensity indicates lower than expected overlap. Each pixel of the RRHO map represents the overlap in the top of the ranked lists, above the corresponding rank thresholds. High overlap throughout the entire ranked list of both experiments (increasing and decreasing genes) will produce a map where high intensity signal (red) will stretch down the diagonal between the bottom left corner and the top right corner, indicating that the best overlap with the top m genes in list 1 is typically with the top m genes in list 2. High overlap in only the tops of the lists (consistently increasing genes) will give a signal in only the bottom left region of the map and high overlap only in the bottoms of the lists (consistently decreasing genes) will produce signal in only the top right region. Since the hypergeometric calculation is applied from the tops of both lists or equivalently from the bottoms of both lists (see ‘Mathematical symmetries of the hypergeometric distribution’ in ‘Materials and Methods’ section), points on the maps should be read as indicating the degree of statistically significant overlap between the lists from that point on the map (corresponding to a rank threshold pair) to either the bottom left (rank 1, 1) or top right corner (rank N,N). Examples demonstrating this and other aspects are in the User’s Guide to interpreting RRHO heatmaps in the Supplementary Data.

Degree of overlap: RRHO analysis is sensitive to weak statistical signal

Gene expression similarities between biological experiments span a large range of possible strengths and patterns. We collected a series of published microarray experiments related to molecular characteristics of breast cancer that illustrates the wide range of overlap observed in true biological experimentation. As background to the breast cancer biology being studied, the similarity of gene-expression profiles of loss of ER (estrogen receptor), PR (progesterone receptor) and HER2 (ErbB receptor family, member 2) in breast cancer has been observed by many groups. Tumors that have loss of all of these markers (‘triple-negative’) are associated with the ‘basal-like’ gene expression-based subclass of breast tumors and with poor prognosis (23). The desire to understand the tumor cell biology downstream of these clinical markers has driven research groups to create genetically engineered mouse models with altered levels of these receptors in order to study the conserved expression changes that result. We used microarray experiments from two major human and mouse research studies to characterize the relationship between these molecular markers of breast cancer in terms of their gene-expression profiles.

Rank–rank overlap maps can be used to visualize the range of gene expression overlap between two signatures, shown in this series of breast cancer comparisons as strong, medium and weak correlation between molecular subtypes of human breast cancer and a related mouse model (Figure 2). Expression in both experiments is displayed using metric scatter plots, rank–rank scatter plots, or RRHO heatmaps. The x-axis on all representations shows the difference between ER positive to ER negative human breast tumors (24); the y-axis shows gene-expression profiles based on other mutations or other profiles relevant to human breast cancer. The first representation, metric scatter plot (Figure 2A, D and G), shows genes plotted by their direction-signed log₁₀-transformed P-values in Experiment 1 versus Experiment 2. In the case of a strong overlap signal (ER loss versus PR loss), more points are in top right and bottom left regions than in the opposite regions, clearly showing strong correlation in the two experiments. In this strong case, rank-based correlation coefficients show that these signatures are significantly similar to one another (Spearman coefficient ρ = 0.90 and Kendall coefficient τ = 0.75). In the case of a medium signal (ER loss versus HER2 receptor loss), there are many points in each of the regions, so it becomes harder to visualize how significant the number of correlated points are compared to the uncorrelated points. When the rank of each gene in Experiment 1 is plotted versus Experiment 2 (spreading the points more evenly across the plot in a rank–rank scatter plot, Figure 2E), an enrichment becomes visible along the diagonal, especially at the bottom left and top right regions. This enrichment is more clearly reflected as a positive signal in the rank–rank hypergeometric heatmap (Figure 2F). In the case of a weak signal, ER loss versus mouse model for HER2/Neu-driven mammary tumors (25), enrichment cannot be easily visualized by plotting the distribution of P-values or ranks, thus making it necessary to use an overlap statistic-based representation such as the hypergeometric map. In Figure 2I, the RRHO map shows that borderline significant overlap is present between the human breast cancer ER-positive signature and the HER2 mouse model of breast cancer. Weaker signal such as this requires additional or independent confirmation, but identification of this weak signal is important for generating hypotheses for future studies.

As these examples illustrate, the RRHO approach is able to discern weak overlap signals between expression profiles and is not saturated by high, near-perfect correlation. While rank-based correlation coefficients will identify overlap throughout the full ranked gene profiles, RRHO is sensitive to overlap occurring only in specific sub-regions of the profiles. Further analysis of the range of overlap detectable by RRHO analysis is shown in comparison to the Spearman rank correlation coefficient using synthetic differential gene expression data in the Supplementary Data (User-Guide Figure 1 and Supplementary Table S1). The range in degree of similarity demonstrated in Figure 2 is reflective of the range of trends in real biological data; strong signals are generally seen with related variables in the same biological system while weak signals are observed when a particular molecular or transcriptional aspect is shared between notably different biological systems.

Demonstration of RRHO maps in biological applications

To demonstrate the utility of RRHO maps, we analyzed several pairs of published microarray experiments relevant to cancer biology. These profiles were chosen because they address several important issues in oncology: characterizing oncogenic cell signaling in patients and using model systems, linking cell signaling networks with tumorigenic cellular processes and detailing molecular response to targeted therapies. The original experiments were executed completely independent of one another, but using RRHO we are able to sensitively compare the results in a straightforward manner.

The RRHO approach can be used to identify trends within and between signaling pathways and biological phenotypes. Beginning with a signaling pathway example, Figure 3A shows high overlap between mouse models of prostate neoplasia driven by loss of the tumor suppressor PTEN or expression of constitutively active AKT kinase. Both of these genetic changes lead to activation of the PI3K pathway and RRHO analysis identifies genes that are consistently modulated by these two different perturbations of the same pathway during tumorigenesis (22,26). Furthermore, this PTEN-loss prostate cancer model shares overlap with a castration phenotype signature (Figure 3B) (22,27). The degree of overlap increases with time and is reversed when exogenous testosterone is given for 3 days. This result confirms the notion that PTEN controlled signaling pathway intrinsically regulates androgen response (28,29) and PTEN loss may contribute to castration resistant prostate cancer development. Furthermore, this overlap suggests that PTEN knockout may lead to prostate cancer by initiating the same stem cell and growth properties required to rebuild the prostate after damage due to androgen ablation. These results are consistent with longer castration time course experiments in wild-type and PTEN-knockout mice (Dr Hong Wu, data not shown).

We identified another example of overlap between the stem cell phenotype and a signaling signature by comparing the gene-expression profile of mammary stem cells that can regenerate a murine mammary gland (versus myoepithelial cells that do not have this regenerative potential) to the gene-expression profile activated by the potent oncogenic kinase BCR-ABL (Figure 3C) (30,31). This result is consistent with recent studies linking stem cell function to transformation (31–34). The overlap between gene-expression changes driven by particular signaling mutations and those found in different cell states provides insight into the transcriptional and molecular mechanisms that link misregulated signaling pathways to the phenotypes that result in disease.

Expression profile overlap approaches can also be used to characterize gene-expression patterns in human cancer patients and the effect of targeted therapies used in the clinic. Here, we demonstrate how RRHO analysis of expression studies can be used to help assess (i) the relevance of a cancer model system, (ii) the degree of similarity between two independent clinical studies and (iii) the similarity between drug resistance mechanisms activated in different tumor tissue types. First, clinical research efforts can be advanced by designing model systems to study important molecular characteristics seen in patients in a reproducible, low cost, easily controlled manner. High overlap between gene-expression changes driven by mutated KRAS2 oncogene in human lung tumors and by overexpression of KRAS2 in a cell line identify signaling events downstream of this oncogene that have in vivo relevance that can be studied effectively in vitro (Figure 3D) (35).

Second, transcriptional responses conserved between multiple patient cohorts can be considered in higher regard when developing model organisms and testing hypotheses for underlying mechanisms. By comparing two published data sets, we found highly significant overlap between gene-expression profiles of two BCR-ABL-driven leukemia patient populations divided into those that did or did not respond to imatinib, a breakthrough small-molecule kinase inhibitor that targets the BCR-ABL onco-kinase (Figure 3E) (21,36). These patient samples were collected in different hospitals by different groups but our algorithm allows us to quickly and easily visualize that they share many expression characteristics that could be at the core of the mechanisms driving their illness and resistance to imatinib.

Third, the effects of new drugs that are being developed are often tested in established model systems in order to gain insight into their modes of action and potential mechanisms of resistance. Here, we compare experiments testing the effect of treatment with the second-generation small-molecule inhibitor dasatinib, which targets both ABL and SRC family kinases. Elevated SRC kinase activity has been implicated in contributing to many tumor types (37). We find that expression profiles that define dasatinib sensitivity versus resistance are conserved in two panels of cancer cell lines, one set isolated from breast tumors and the other from prostate tumors (Figure 3F) (38,39). The corresponding RRHO overlap map additionally shows that genes elevated in sensitive cell lines share more significant overlap than genes elevated in resistant cell lines. These results suggest that some mechanisms of dasatinib resistance are shared between different tumor tissue types. As shown in the three clinically relevant cases above, RRHO analysis can statistically and visually characterize the shared trends from gene-expression experiments that can build confidence in the relevance of model systems as well as characterize drug intervention at the patient level.

An advantage of RRHO maps is quick visualization of which parts of gene-expression profiles have significant overlap. In several examples in Figure 3, significant overlap signal is observed in the bottom left (increasing in both experiments) and top right (decreasing in both) regions showing overlap among genes highly differentially expressed in the same direction in both experiments, while genes that are not differentially expressed to as high an extent show little overlap signal (middle). In Figure 3D and F, while both the increasing and decreasing genes are significantly overlapping, the genes decreasing in both experiments show higher significance (greater overlap in top right corner) and thus might be of greater interest or hold greater potential for further characterization. Observing features of the RRHO map can allow the biologist to focus on particular groups of differentially expressed genes based on how significantly they overlap with other related profiling experiments. Further detail on applying and interpreting the visual patterns in RRHO maps can be found in the user’s guide in the Supplementary Data.

Comparing RRHO to other rank-based approaches for gene-expression analysis: GSEA

We next compared RRHO to another popular rank-based approach to demonstrate the unique aspects of our method. Sweet-Cordero et al. (1) describe their use of the popular rank-based algorithm called GSEA to identify a KRAS2 oncogenic kinase gene-expression signature in human lung tumors via comparison to a genetically engineered mouse model of lung cancer driven by KRAS2. As shown schematically in Figure 4A, GSEA compares a list of genes of defined size (called a gene set) to a ranked list representing the changes observed in all genes measured in a two-class microarray differential expression experiment. GSEA calculates the enrichment of a gene set in continuous ranked list using a Kolmogorov–Smirnov statistic, which in one dimension (one varying threshold) is highly related to the hypergeometric P-value. We have used the hypergeometric P-value because it is exact and symmetric in two dimensions (two thresholds). In the previously published work, in order to fit two ranked lists to a gene set versus ranked list approach, one ranked list was first converted to a gene set of top upregulated genes and a set of the top downregulated genes. The top upregulated and top downregulated genes from the KRAS2-driven mouse model were chosen by minimizing the FDR of differentially expressed genes within one experiment below a low, user-defined threshold using Significance Analysis of Microarrays (SAM) (40). Then the mouse model-defined gene sets were compared to the human cancer-defined continuous ranked list using standard GSEA. Using this adapted GSEA approach, the authors were able to identify statistically significant overlap that would likely have been missed by other techniques. Allowing one data set to be analyzed as a ranked list of all gene-expression changes added sensitivity to detect gene-expression overlap; RRHO allows the same threshold-free treatment for both of two gene-expression experiments to further improve sensitivity.

Applying RRHO to the human versus mouse KRAS gene-expression profile comparison we find similar and expanded results compared to the original publication. Figure 4B and C show the RRHO overlap maps for two human cancer populations used in the Sweet-Cordero publication, first comparing normal tissues to lung adenocarcinomas in mouse and human (B) and second comparing the KRAS2 mouse model to gene-expression changes between human tumors with wild-type versus mutant KRAS2 (C). Both overlap maps would allow you to conclude that there exists statistically significant overlap between this KRAS2-driven mouse model of lung cancer and human lung cancer patient profiles, just as was concluded with the adapted GSEA approach. To compare results, we also reproduced the originally reported SAM/GSEA analysis as closely as possible and performed sample permutation analysis as a means of multiple hypothesis correction. Comparing the permutation P-values from the SAM/GSEA approach to those from the RRHO approach demonstrates that both methods have equivalent sensitivity and are able to detect the weak but statistically significant cross-species signal (Figure 4D).

In the SAM/GSEA approach, the output is a permutation P-value and a Kolmogorov–Smirnov mountain plot illustrating the overlap between a subset of high-ranking genes chosen to represent the mouse model profile (a fixed gene set) and the range of differential gene expression in the human data set (a continuous ranked list) (1,8). The dotted lines in Figures 4B and C reflect these 1D mountain plot results. In contrast, the hypergeometric map shows 2D results over the entire range of differentially expressed genes in both the mouse and human data sets. The normal lung to lung adenocarcinoma comparison (Figure 4B) shows high overlap with the KRAS2 mouse model. Both SAM/GSEA and RRHO show more significant results in genes decreasing in both data sets (permutation P-value < 0.001) than in the increasing direction. In the second comparison, KRAS2 wild-type versus mutant tumors, the results show significant overlap of concordantly increasing genes using both RRHO and SAM/GSEA while concordantly decreasing genes have weaker overlap (Figure 4C and D). Thus, RRHO analysis offers similar sensitivity as the SAM/GSEA approach, but does not require the user to determine a threshold for one of the gene-expression signatures and provides a 2D map summarizing the regions and degree of overlap. These output maps aid in identifying the most significantly overlapping regions of two gene-expression profiles as thresholds chosen considering one data set alone may miss the overlap maximum in the 2D rank–rank space (e.g. compare the locations of the mountain plot dotted lines to the region of highest significance in Figure 4B).

Integrating RRHO with public gene-expression resources: Cmap

Another gene expression comparison application is the mining of compendiums of gene-expression signatures to identify biological perturbations that share related gene-expression programs (41). Such analysis can be used to determine which model system or drug treatment best reflects a biological response or disease process (8,35,42–46). An example resource for signature mining is the Cmap, a database of transcriptional responses to a panel of specific drug treatments (10). Mining of the Cmap database with the accompanying analysis tool involves entering significantly upregulated and downregulated genes from an expression profiling experiment as a query. Then, a GSEA-like Kolmogorov–Smirnov statistic-based procedure is used to search and score the query genes against a panel of small molecule inhibitor response rank-based signatures. In this analysis, the query expression signature is converted to a truncated gene set (algorithm guidelines recommend a query gene set between 10 and 500 genes in size) and the compendium signatures are ranked lists of genes—thus providing the two input types used in GSEA analysis.

Since both the query and compendium signatures can be represented as ranked lists, we investigated the use of RRHO for mining of the Cmap database. This removes the need for truncating one of the signatures using a fixed differential expression threshold and accordingly should reduce the chance of missing a weak but statistically significant and biologically pertinent overlap signal due to choosing a threshold that is either too stringent or lenient. The Cmap database is stored as ranked gene lists and thus represents a public resource that can easily be used with the rank-based RRHO algorithm.

We demonstrate the use of RRHO with the Cmap database using the query signature from a published profiling experiment on the effect of the small molecule drug gedunin in human prostate cancer cells (43). In this study, treatment with the phytochemical gedunin was queried against the Cmap database and shown to have high correlation to inhibitors of HSP90. The HSP90 chaperone protein is involved in the proper folding and degradation that regulates the abundance of many proteins, including several signaling- and cancer-associated proteins. We created a ranked gene list from the gedunin treatment microarray experiment and used RRHO analysis to compare it to each of the 6100 ranked gene lists in the Cmap database, representing multiple treatment conditions for 1309 different drugs. BY-corrected RRHO maps for multiple instances of a particular drug treatment were merged by taking the pixel-by-pixel mean to get an overall summary map for each drug. Similarly, mean Cmap scores were calculated for each drug using the top 50 genes that increased and decreased by gedunin treatment relative to controls—the exact same gedunin signature-based gene sets used in the original Cmap analysis (43).

Overall, we found correlation between drug signature overlap as determined by RRHO analysis and the GSEA-based Cmap analysis (Figure 5A). In particular, we validated the high overlap of gedunin with HSP90 inhibitors. The highest scoring overlap by both techniques was to celastrol, another natural compound shown to inhibit HSP90 function (Figure 5B) (43). Treatment with the HSP90 inhibitor 7-allylamino-17-demethoxygeldanamycin (17-AAG), highlighted in the original Cmap publication, also has strong overlap with gedunin treatment using either the RRHO or GSEA-based overlap analysis approach (Figure 5C).

Additionally, we found drug response signatures that had a low absolute mean Cmap GSEA-based score but had a high mean overlap signal by RRHO analysis (Figure 5A). One example shown in Figure 5D is the overlap of gedunin treatment to monensin treatment, a drug which binds to monovalent cations in the cell and prevents uptake of proteins into the lysosome for degradation. Monensin overlap is biologically intriguing as this drug has recently been shown to cause apoptosis synergistically with the HSP90 inhibitor 17-AAG in hepatic cells (47) and affects the release of heat shock proteins from blood cells (48). By RRHO analysis, monensin treatment showed comparable levels of overlap to gedunin treatment as did 17-AAG treatment. However, since the overlap involved some genes that were not as differentially expressed as the top 50 genes (and thus not part of the initial Cmap 50-gene query signature for gedunin), the mean Cmap score is quite low (0.106). The optimal overlap hypergeometric P-value by RRHO analysis occurs at rank position 3200 in the gedunin profile, thus the optimal overlap signal requires more genes than the standard recommendation for Cmap query signature size. Raising the number of upregulated genes toward the maximum allowable by the web-application (top 950 increasing genes, top 50 decreasing genes) does increase the Cmap score as expected (new score = 0.286). This result demonstrates the benefit of not using a pre-determined fixed cutoff threshold when mining compendium signature databases for biological leads.

Furthermore, we observed drug treatments that had lower but significant RRHO overlap scores and near-zero Cmap scores, such as the overlap between gedunin and wortmannin, an inhibitor of PI3 kinase (Figure 5E). This enrichment result provides an initial lead for further investigation since HSP90 inhibition has an anti-apoptotic effect on cardiomyocyte damage mediated by overactivation of the PI3K/AKT pathway (49), and HSP90 complexes with the downstream AKT kinase and is required for correct AKT protein folding and stability (50–52). Instances like this of weaker but statistically significant overlap that can be identified by RRHO analysis offer hypotheses related to the biological function of targeted drug treatments like gedunin in cancer cells.

Using RRHO maps in compendium signature mining reveals aspects of profile overlap that supplement those provided by GSEA-based scores: (i) an overall graphical view of the significance of overlap for genes throughout both ranked gene lists and (ii) the ranks in both lists that give the highest statistical overlap, thus ensuring that overlap signal is not missed due to choosing a query signature too stringently.

DISCUSSION

In this work, we have presented RRHO, a novel approach for comparing gene-expression profiles using the hypergeometric distribution. Our program efficiently traverses two full gene-expression profiling signatures to measure statistical significance of overlap with high dynamic range. Here, we have demonstrated results obtained via RRHO that characterize biologically and clinically relevant overlap signals between different species, different microarray platforms, different types of model systems and different types of molecular perturbations such as drug treatment and genetic variation. In particular, RRHO provides a straightforward and comprehensive method for overlap detection combined with a graphical output that summarizes the patterns and strengths of concordance between expression signatures that can aide in biological hypothesis generation.

We initially developed our rank–rank algorithm to detect weak but statistically significant signals between mouse models of cancer and human cancer patient samples. An early goal was to avoid defining signatures as sets of genes truncated by user-defined thresholds, but rather to make use of the whole continuum of differentially expressed genes. While the number of calculations required to traverse the entire range of genes in two genome-wide experiments is quite large (proportional to the number of genes measured in both experiments squared), RRHO features computational innovations to make this process fast and efficient. The continuum aspect of RRHO is particularly valuable in cases of weak overlap because it is possible to visualize where a weak signal is at a maximum level within the range of genes measured in both experiments and thus prevents potential mistaken conclusions that the overlap is insignificant based on thresholds determined in each experiment individually. General conclusions drawn from significant overlap patterns between two gene-expression profiles, or between a signature of interest and a large panel of previously defined signatures, can generate hypotheses that can be validated by follow-up cell biology or patient-level studies. In addition, once the rank thresholds corresponding to maximal overlap are identified, the resulting list of overlapping genes can be used for gene set functional and pathway-based enrichment analysis where the goal is to emphasize consistent results between the two experiments. In parallel work, we have applied RRHO analysis to the comparison of human cancer and mouse cancer model signaling pathway-specific signatures (K. Ellwood-Yen et al., manuscript in preparation) and to breast cancer signatures linked to glycolysis metabolism and fluorodeoxyglucose-positron emission tomography (FDG-PET) imaging (N. Palaskas et al., submitted for publication).

Gene-expression information from microarray data repositories such as Gene-expression Omnibus (19) and ArrayExpress (53) as well as from more specialized resources such as the drug response profile database Cmap (10) can be readily converted to ranked list inputs for our program. Thus, RRHO can be used to mine public gene-expression data for common trends and to aide in the biological interpretation of new microarray experiments. Using ranked lists as input for RRHO makes the algorithm versatile in that it can compare profiles generated with other technologies such as quantitative proteomics or perform cross-platform comparisons. We have created a web-accessible version of RRHO (http://systems.crump.ucla.edu/rankrank/) that generates a hypergeometric analysis and heatmap summary comparing two experiments, entered simply as the table of raw data with class labels. This implementation focuses on ease of use and interpretation by users from any field of biology.

The RRHO approach allows fast, sensitive, and quantitative determination of the degree of overlap between two genome-scale ranked gene lists. RRHO surveys the whole range of gene-expression changes and thus avoids missing the point of maximal overlap signal, as can occur when using fixed thresholds. In a single visualization and with minimal data pre-processing, the rank–rank hypergeometric output map indicates which of several possible overlap trends is present in expression signature comparisons and the strength of the observed trend.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

United States Department of Health and Human Services (USHHS) Ruth L. Kirschstein Institutional National Research Service Predoctoral Awards (T32 CA09056 to S.B.P., T32 GM008652 to S.B.P.); Alfred P. Sloan Foundation (Research Fellowship to T.G.G.). Funding for open access charge: Alfred P. Sloan Foundation.

Conflict of interest statement. None declared.