Abstract
Thermochemical data have been obtained from G3B3 quantum mechanical calculations for 18 prototypical organic molecules, which exhibit E/Z conformational equilibria. The results are fundamentally important for molecular design including evaluation of structures from protein-ligand docking. For the 18 E/Z pairs, relative energies, enthalpies, free energies, and dipole moments are reported; the E – Z free-energy differences at 298 K range from +8.2 kcal/mol for 1,3-dimethyl carbamate to −6.4 kcal/mol for acetone oxime. A combination of steric and electronic effects can rationalize the variations. Free energies of hydration were also estimated using the GB/SA continuum solvent model. These results indicate that differential hydration is unlikely to qualitatively change the preferred direction of the E/Z equilibria, though further study with free-energy methods using explicit solvent is desirable.
Introduction
Knowledge of the conformational energetics of small molecules is essential in many areas of chemistry including organic synthesis and molecular design.1 The conformational preferences for small molecules are well-known to carry over to macromolecular structures; e.g., the ca. 3 kcal/mol preference for the Z conformer of N-methylacetamide relative to the E alternative is primarily responsible for the rarity of cis-peptide bonds in proteins.2 The present study focuses on such molecules where rotation about a single bond leads to E and Z conformers that are energetically well-separated by an intervening potential-energy barrier. Besides amides, molecules in this category include other derivatives of carboxylic acids, aldehydes, or ketones such as esters, carbamates, carbonates, ureas, amidines, hydrazones, and oximes. The importance of these functional groups is enhanced by their common occurrence in combinatorial libraries, commercial screening collections, and in molecules of pharmacological interest.
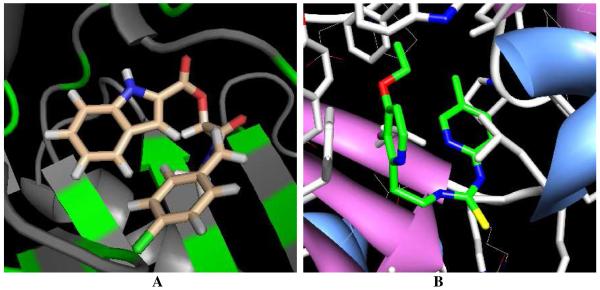
Furthermore, in seeking enzyme inhibitors through de novo design or virtual screening,3,4 questions often arise about the likelihood of E and Z conformers. For example, in docking studies, one is regularly confronted with computed structures for complexes, ‘poses’, such as in Figure 1a, where the ligand features an E or Z conformation. The scoring with docking software is still improving and such poses may score well,5 though the E-conformer for the ester in this case is unreasonable.1 Or, one may be confronted with a crystal structure, such as in Figure 1b, where the thiourea moiety is in an E, Z configuration.6 If one thought that there was an associated energetic penalty, alternative designs might be pursued to achieve enhanced potency. Given many such examples, we have pursued energetic clarification through reliable quantum mechanical calculations on prototypical molecules featuring E and Z conformers. The findings are also valuable as a basis for the improvement of scoring functions for docking software,7 the refinement of crystal structures, and development of molecular mechanics force fields for use in modeling organic and biomolecular systems.8,9
Figure 1.
(A) Structure of an ester-containing molecule docked into HIV-1 reverse transcriptase (RT), and (B) the 1dtt crystal structure of an analog of trovirdine bound to HIV-RT illustrating an E, Z conformer for a thiourea moiety.
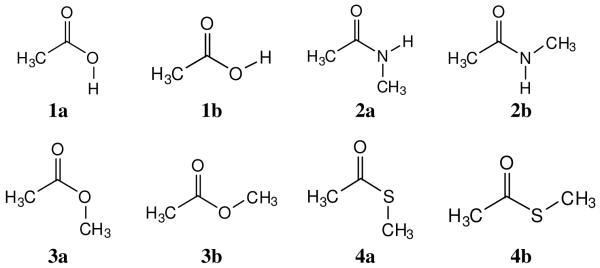
Though there have been prior computational studies of molecules featuring E/Z equilibria, most studies have focused on one or two functional groups using Hartree–Fock (HF), B3LYP-based density functional, or second-order Møller–Plesset (MP2) theory.10-30 Some classic studies include those of Wiberg and coworkers on formic acid, acetic acid, methyl formate, and methyl acetate.10 N-methylacetamide has also received much attention owing to its status as a model for the peptide bond.11,20,23,24,30 The need for quantum mechanical investigations in this area is enhanced by the fact that experimental studies of E/Z equilibria are often challenging owing to a very small population of the higher-energy conformer. For example, the first experimental observation of the E conformer of acetic acid was not made until 2003.31 Thus, for broader coverage of E/Z equilibria at a higher and consistent level of theory, the 18 pairs of conformers illustrated in Figures 2-4 have been examined here using composite ab initio methods.
Figure 2.
Molecules in the RCOX set.
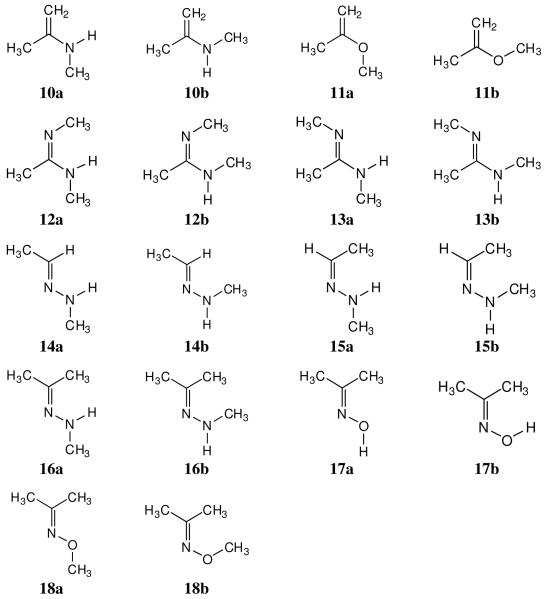
Figure 4.
Molecules in the C=C&N set.
Computational Details
All ab initio and DFT calculations were carried out using the Gaussian03 program.32 The G3 and G3B3 methods were applied to compute structures, dipole moments, vibrational frequencies, energies at 0 K, and enthalpies and free energies at 298 K.33,34 With the G3 method, the initial geometry optimization and vibrational frequency and zero-point energy calculations are performed at the 6-31G(d) level. The geometry is then refined including electron correlation at the MP2(full)/6-31G(d) level. A series of single-point energy calculations follows, using MP2/G3large (a basis set with core correlation), MP4/6-31G(d), and QCISD(T)/6-31G(d), with spin-orbit and other higher corrections. The G3B3 approach particularly improves the initial geometry, vibrational frequencies and zero-point energy by starting with a B3LYP/6-31G(d) geometry optimization. The increase in computer time for G3B3 over G3 for molecules of the present size is usually less than 50%.
Estimates of free energies of hydration were made for all conformers using the Generalized Born/Surface Area approach, as implemented in the BOSS program.35,36 Structures were optimized using the OPLS/CM1A force field,9 and the GB/SA calculations were performed with CM1A atomic charges scaled by 1.07.36
Results and Discussion
E/Z Conformers
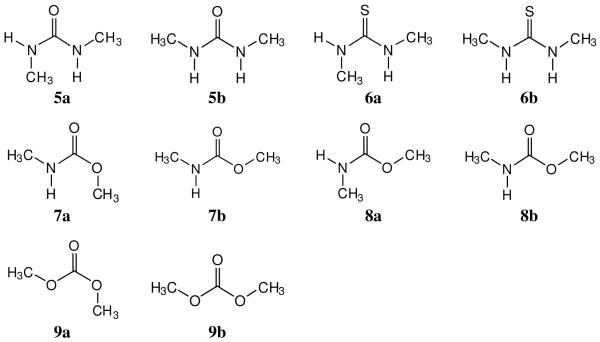
The 18 pairs of conformers that were investigated are shown in Figures 2-4. The RCOX set consists of a prototypical carboxylic acid, secondary amide, ester, and thioester. The RXCOYR set contains a urea, thiourea, carbamate (urethane), and carbonate, while the C=C&N set covers an enamine, an enol ether, amidines, hydrazones, and oximes. Conformer a is E and conformer b is Z for each pair. For amine derivatives, secondary cases RNHCH3 have been considered; E and Z are also well-defined for tertiary cases RNR’R”, but the E/Z preferences for them are generally well predicted by steric considerations. It should also be noted that conformers 7b and 8b are the same, which simplifies the presentation of results. For the RCOX set, both G3 and G3B3 calculations were performed, while the RXCOYR and C=C&N sets were investigated only using G3B3.
Results for the RCOX Set
For 1 – 4, the G3 and G3B3 results are given in Table 1. In all cases, the relative values are given for conformer a minus conformer b (E - Z). The G3 and G3B3 energetic results generally agree to within 0.1 kcal/mol. The thermal corrections to the vibrational energy are also almost the same for both conformers, so there is little difference between the results for ΔE (0 K) and ΔH (298 K). The computed entropy changes are also generally small, though there can be some sensitivity to the treatment of low-frequency vibrations.
Table 1.
Computed Differences in Energies (kcal/mol) and Dipole Moments (D) from G3 and G3B3 Calculations for the RCOX Set
| G3 | ||||
|---|---|---|---|---|
| Pair | ΔE (0 K) | ΔH (298 K) | ΔG (298 K) | Δ μ |
| 1 | 5.08 | 5.11 | 5.15 | 2.93 |
| 2 | 2.42 | 2.22 | 3.11 | 0.32 |
| 3 | 7.48 | 7.46 | 7.47 | 3.10 |
| 4 | 4.63 | 4.43 | 4.60 | 3.14 |
| G3B3 | ||||
|
| ||||
| 1 | 5.11 | 5.11 | 5.27 | 2.92 |
| 2 | 2.34 | 2.26 | 2.67 | 0.32 |
| 3 | 7.42 | 7.41 | 7.42 | 3.10 |
| 4 | 4.63 | 4.41 | 4.38 | 3.19 |
For acetic acid (1), the E conformer is found to be 5.1 kcal/mol higher in energy than the Z form from the G3 and G3B3 calculations. This is in accord with an MP4/cc-pVTZ result of 5.38 kcal/mol,25 while lower levels of ab initio theory generally give larger differences.10 An experimental result is not available for comparison, though the E conformer has been detected in an argon matrix at 8 K.31 The best estimate for the energy difference for formic acid is about 1 kcal/mol smaller at 4.21 kcal/mol.22 For N-methylacetamide (2), the present results concur with other high-level calculations and experiments that the enthalpy difference at 298 K is in the 2.1 - 2.5 kcal/mol range.11,20,23,24,30 The difference diminishes to 1.0 – 1.2 kcal/mol for N-methylformamide owing to reduced steric crowding in the E form.20,37
Similarly, the G3 and G3B3 results for methyl acetate are in-line with the energy difference of 7.72 kcal/mol from LMP2/cc-pVTZ(-f) calculations,20 while again older values are somewhat higher.10,15,16 For methyl formate, the LMP2 energy difference is reduced to 5.35 kcal/mol.20 Besides the steric effects favoring Z, the E conformer of carboxylic acids and esters is also destabilized by unfavorable dipole-dipole interactions or lone pair – lone pair repulsion between the oxygen atoms.10,11 As indicated in Table 1, the dipole moments for E acids and esters are ca. 3 D higher than for the Z forms. Overall, the population of E carboxylic esters is generally vanishingly low and drawing or invoking acyclic esters in this conformation is improper.38 The E – Z energy difference for the corresponding thioester (4) moderates to 4.6 kcal/mol owing in part to the longer C-S than C-O bonds, which diminishes the 1,4-CC steric penalty for the E conformer. Again, the difference is expected to be less for methyl thioformate, which is confirmed by NMR studies indicating a free energy difference of ca. 1.3 kcal/mol.37
Results for the RXCOYR and C=C&N Sets
The G3B3 results for the remaining pairs are given in Table 2. The results are largely understandable in terms of the strong preference for the Z conformers for 1 – 3 and additional steric and electronic effects, as presented below.
Table 2.
Computed Differences in Energies (kcal/mol) and Dipole Moments (D) from G3B3 Calculations for the RXCOYR and C=C&N Sets
| RXCOYR | ||||
|---|---|---|---|---|
| Pair | ΔE (0 K) | ΔH (298 K) | ΔG (298 K) | Δ μ |
| 5 | 1.06 | 1.03 | 1.09 | 0.50 |
| 6 | −0.17 | −0.09 | −0.55 | 0.80 |
| 7 | 7.47 | 7.30 | 8.18 | 3.05 |
| 8 | 1.24 | 1.15 | 1.75 | 0.34 |
| 9 | 3.03 | 2.99 | 3.09 | 3.60 |
| C=C&N | ||||
|
| ||||
| 10 | 2.67 | 2.65 | 2.60 | −0.13 |
| 11 | 4.47 | 4.61 | 4.01 | 1.27 |
| 12 | −4.06 | −4.05 | −3.95 | 0.31 |
| 13 | 3.13 | 3.00 | 3.44 | −0.04 |
| 14 | −0.16 | −0.03 | −0.35 | −0.01 |
| 15 | −3.30 | −3.21 | −3.28 | 0.37 |
| 16 | −2.54 | −2.43 | −2.69 | 0.54 |
| (17) a | −6.04 | −6.00 | −6.35 | −2.94 |
| (18) a | −19.07 | −18.34 | −20.40 | −2.66 |
The planar Z form b is a transition state.
Interestingly, in comparison to N-methylacetamide, the Z,Z over E,Z energetic preference for 1,3-dimethylurea (5) diminishes to 1.06 kcal/mol, and the E,Z conformer of 1,3-dimethylthiourea (6a) is actually favored by 0.17 kcal/mol. In prior work, MP2/aug-cc-pVDZ results favored the Z conformer of methylurea and methylthiourea by 1.25 and 0.70 kcal/mol,28,29 and MP2/6-31G(d) results preferred Z,Z over E,Z for 1,3-dimethylurea by 1.72 kcal/mol.19 The present result for 5 is expected to be more accurate and indicates that there would only be a small intrinsic penalty for incorporating an E,Z-urea substructure in a molecular design. Moreover, an E,Z-thiourea fragment as in Figure 1B is preferred over the Z,Z alternative. In fact, there have been extensive NMR studies of the conformational equilibria for 6 in multiple solvents with the conclusion that the E,Z conformer is lower by ca. 1 kcal/mol in free energy than the Z,Z conformer and that the E,E form is not populated.21 The electronic energy from MP2/cc-pVDZ calculations without zero-point or other corrections in that study appears to lead to the wrong qualitative conclusion by favoring the Z,Z conformer by 0.38 kcal/mol.21 In summary, the E,Z conformer for ureas is relatively more favorable than the E conformer of secondary amides, and the E,Z conformer for the prototypical 1,3-dialkylthiourea 6 is the lowest in energy. In view of the small differences in dipole moments for 5 and 6 in Table 2, the preferences are expected to not be strongly influenced by medium effects. A possible contributor to the increased favorability of the E,Z geometry in the ureas is π-electron donation (amide resonance +N=C-X−), which increases the partial negative charge on the oxygen or sulfur atom and improves the electrostatic interaction with the syn-hydrogen on nitrogen in the E substructure.
The results for 7 – 9 in Table 2 present an interesting contrast. For 1,3-dimethyl carbamate 7, rotation of the methoxy group to the E form is similarly unfavorable as for the ester 3, while rotation of the N-methyl group in going from 8b to 8a is about 1 kcal/mol less costly than for the amide 2. The relative G3B3 energies for the three conformers of the carbamate, Z,Z (7b), Z,E (7a), and E,Z (8a) are 0.0, 7.47, and 1.25 kcal/mol, respectively. Thus, as for the urea 5, the penalty for rotation of the N-methyl group in the carbamate to the E form is not large; however, an E geometry for the ester fragment remains too high in energy for significant population under normal conditions. The possibility for an E-ester substructure is significantly improved for dimethyl carbonate (9), for which the E,Z conformer is only 3.03 kcal/mol higher in energy than the Z,Z form. The 4-5 kcal/mol diminution relative to 3 or 7 likely stems from destabilization of the Z,Z conformer by repulsion between the lone pairs on the methoxy oxygen atoms. Previous MP2/6-31G(d) results for the relative electronic energies of the Z,Z, E,Z, and E,E conformers of 9 are 0.0, 3.36, and 26.73 kcal/mol.18
Turning to the molecules in Figure 4, 10 (N-methyl-2-aminopropene) and 11 (2-methoxypropene) are the olefinic analogs of 2 and 3. The energetic preference remains the same, significantly favoring the Z conformers by 2.67 (10) and 4.47 kcal/mol (11). Thus, the 1,4-CH3/CH3 interaction appears to continue to dominate, while the larger energy difference for the ester 3 than the enol ether 11 can be attributed to the addition of the lone-pair repulsion between the oxygens for the E conformer of the ester (3a). Based on the results mentioned above for formic acid vs acetic acid derivatives, the E – Z energy differences for the corresponding vinyl analogs of 10 and 11 should be reduced by ca. 1.0 and 2-3 kcal/mol, respectively. Indeed, MP3/6-31G results provide an E - Z energy difference of about 2.0 kcal/mol for methyl vinyl ether,39 and we find 1.74 kcal/mol for ΔE(0 K) using G3B3. It should be noted that the E conformers for 10 and 11 are not planar; the G3B3 results for the H3C-C-X-CH3 dihedral angles are 40.8° and 37.1° for 10a and 11a. Thus, these conformers may be described as skew. Amine nitrogens are also somewhat paramidalized in all structures, so, for example, the H3C-C-N-CH3 dihedral angle in 10b is 170.6°; however, the H3C-C-O-CH3 dihedral angle in 11b is 180°. The results for the corresponding dihedral angles for all conformers are listed in Table 3.
Table 3.
G3B3 Results for Key Dihedral Angles (deg.)
| Conf. | Angle | φ | Conf. | φ |
|---|---|---|---|---|
| 1a | CCOH | 0.0 | 1b | 180.0 |
| 2a | CCNC | 9.8 | 2b | 179.9 |
| 3a | CCOC | 0.3 | 3b | 179.9 |
| 4a | CCSC | 0.0 | 4b | 178.3 |
| 5a | NCNC | 20.4 | 5b | 169.4 |
| 6a | NCNC | 7.0 | 6b | 173.9 |
| 7a | NCOC | 5.6 | 7b | 179.9 |
| 8a | OCNC | 9.8 | 8b | 179.9 |
| 9a | OCOC | 0.0 | 9b | 180.0 |
| 10a | CCNC | 40.8 | 10b | 170.6 |
| 11a | CCOC | 37.1 | 11b | 180.0 |
| 12a | NCNC | 165.0 | 12b | 5.0 |
| 13a | NCNC | 148.5 | 13b | 9.0 |
| 14a | CNNC | 152.0 | 14b | 22.3 |
| 15a | CNNC | 159.7 | 15b | 69.2 |
| 16a | CNNC | 161.3 | 16b | 79.7 |
| 17a | CNOH | 179.9 | 17b a | 0.0 |
| 18a | CNOC | 180.0 | 18b a | 1.4 |
Transition state.
For 12 and 13 in Figure 4, the structures represent the four conformers for N,N’-dimethylacetamidine. The trans-(Z) conformer 13b can be argued to be the most analogous to (Z)-N-methylacetamide (2b) and it is the lowest in energy. The relative energies, ΔE(0 K), for the other conformers are 1.07, 3.13, and 5.13 kcal/mol for 12a, 13a, and 12b, respectively, at the G3B3 level. The E – Z energy difference in Table 2 for the 13 pair is also just a little greater than for 2, possibly reflecting diminished electrostatic attraction for N…HN in 13a than for O…HN in 2a. The 1,5-CH3-CH3 interaction in 12b is particularly destabilizing as it is similar to a syn-pentane interaction, so this conformer is not competitive. Overall, two low-energy conformers are apparent for the dimethylamidine, 13b and 12a.
Similarly, for 14 and 15 in Figure 4, the four structures are the conformers for the N-methyl hydrazone of acetaldehyde, while 16a and 16b are the E and Z possibilities for the N-methyl hydrazone of acetone. For 14 and 15, the lowest energy conformer is 14a and the relative energies, ΔE(0 K), are 0.16, 0.34, and 3.63 for 14b, 15a, and 15b. Thus, the first three conformers are very close in energy with only 15b being uncompetitive owing to the 1,5-CH3-CH3 interaction. It is also then easy to predict that Z conformer 16b is higher in energy than the E alternative 16a; the difference of 2.54 kcal/mol is a little smaller in magnitude than for the 15 pair. A message from this for molecular design is that the conformational diversity of hydrazones of ketones is much less than for hydrazones of aldehydes.
Finally, the oxime 17 and O-methyl oxime 18 of acetone were considered. In both cases, the planar Z form was found to be a transition state with the G3B3 calculations and only the E structures are energy minima. The Z transition states are 6.04 (17) and 19.07 (18) kcal/mol higher in energy than the E conformers. The Z structures are destabilized by electrostatic repulsion between the lone pair electrons on N and O and by the syn-pentane-like interaction in 18b. The status of the Z structure for acetoxime 17 is sensitive to the computational level. For example, we find with B3LYP/6-31G(d) energy minimizations and vibrational frequency calculations that the C=N-O-H planar Z structure is a shallow energy minimum; it is 6.16 kcal/mol above the E conformer, and it is separated from conversion to the E form by a barrier of 2.0 kcal/mol at a dihedral angle near 70°. The hydroxyl hydrogen is constrained between two of the hydrogens on the syn-methyl group, which stagger the C=N bond. However, the G3B3 results state that for both the oxime 17 and O-methyl oxime 18, only the E conformational energy well exists. Besides the common occurrence of oximes in screening collections, interest in them also continues as the substrates for Beckmann rearrangements. In this case, the dominance of the E conformers is relevant for proposed mechanistic schemes.40
Summary of E/Z Results
A summary of the E/Z free-energy differences for all conformer pairs is provided in Figure 5. A positive difference indicates that the Z conformer is favored, and a negative difference indicates that the E conformer is favored. Some general rules are evident.
For rotation about C-X (X = OR, SR, NHR) single bonds in O=C-X, N=C-X, and C=C-X substructures, Z conformers are normally preferred in the absence of significant steric effects that preferentially destabilize the Z conformer, especially syn-pentane-like interactions.
The Z-preference diminishes in the order X = OR > OH > SR > NHR. The Z-preference is also diminished for thione derivatives, S=C-X, and through additional conjugation as in ureas.
Rotation about the N-N and N-O bonds in hydrazones and oximes favors the E conformers, especially when reinforced by a syn-pentane-like interaction in the Z form.
Figure 5.
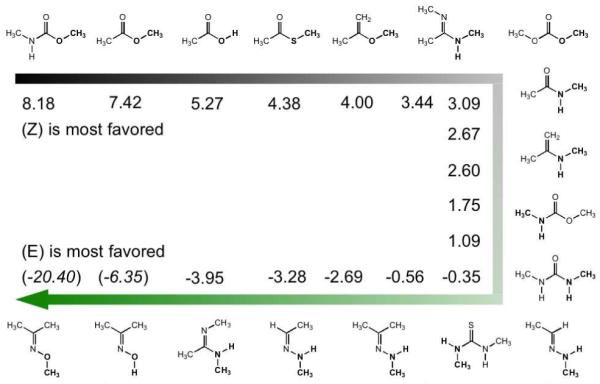
Summary of the G3B3 E/Z free-energy differences (kcal/mol). The preferred conformation is shown, and the fragment that is rotated is highlighted in bold.
Concerning dipole moments, there is a general correlation in Tables 1 and 2 such that the conformer with the larger dipole moment is normally higher in energy than the one with the smaller dipole moment. This is reasonable based on electrostatic considerations and contributes to the general preference for Z conformers. The largest differences in dipole moments (Δμ = μE − μZ) are 3-4 D and these correspond to cases where the E conformer is higher in energy by 3-8 kcal/mol. For the oximes, Δμ is ca. −3 D and consistently the E conformers are significantly favored. Of course, steric effects modulate the results such that, for example, Δμ is small for 12, 15 and 16, but the E conformers are strongly favored owing to the 1,5-CH3-CH3 interactions in the Z conformers.
GB/SA Results
The gas-phase results for the E/Z preferences can be shifted in different molecular environments, both relatively homogeneous as for a pure solvent and inhomogeneous as in a protein binding site. To gain some sense of magnitude for the former case, free energies of hydration were calculated for all conformers using the OPLS/CM1A force field and GB/SA continuum solvent model.9,36 The gas-phase G3B3 results, the GB/SA shifts ΔΔGhyd, and the net ΔGaq for the Z ↔ E equilibria in aqueous solution at 298 K are summarized in Table 4. A negativeΔΔGhyd indicates that the E conformer is predicted to be better hydrated. Based on calculations for 399 neutral organic molecules, the average absolute error for free energies of hydration from the GB/SA calculations is expected to be 1.0 kcal/mol.36 The errors for the differential hydration of conformers should be smaller, and results for several standard cases were shown to be in good accord with experimental data.36 However, E/Z conformers may be particularly challenging owing to the accompanying changes in solute-water hydrogen bonding as compared to simpler cases such as the gauche/anti equilibria for 1,2-dihaloethanes.36
Table 4.
Computed E – Z Free Energy Differences (kcal/mol) in the Gas Phase and in Aqueous Solution at 298 Ka
| Pair | Δ Ggas | Δ μ | Δ Δ Ghyd | Δ Gaq |
|---|---|---|---|---|
| 7 | 8.18 | 3.05 | −0.52 | 7.66 |
| 3 | 7.42 | 3.10 | −0.60 | 6.82 |
| 1 | 5.27 | 2.92 | −2.39 | 2.88 |
| 4 | 4.38 | 3.19 | −0.12 | 4.26 |
| 11 | 4.01 | 1.27 | −1.82 | 2.18 |
| 13 | 3.44 | −0.04 | 1.75 | 5.19 |
| 9 | 3.09 | 3.60 | 0.26 | 3.35 |
| 2 | 2.67 | 0.32 | 1.43 | 4.10 |
| 10 | 2.60 | −0.13 | 0.29 | 2.89 |
| 8 | 1.75 | 0.34 | 0.37 | 2.12 |
| 5 | 1.09 | 0.50 | 0.00 | 1.09 |
| 14 | −0.35 | −0.01 | −1.02 | −1.37 |
| 6 | −0.55 | 0.80 | 1.28 | 0.73 |
| 16 | −2.69 | 0.54 | −1.06 | −3.75 |
| 15 | −3.28 | 0.37 | −0.36 | −3.64 |
| 12 | −3.95 | 0.31 | 1.79 | −2.16 |
| (17) | −6.35 | −2.94 | −0.11 | −6.46 |
| (18) | −20.40 | −2.66 | −1.40 | −21.80 |
G3B3 results in the gas phase; hydration effect (ΔΔGhyd) from GB/SA calculations. Ordered by decreasing ΔGgas.
The computed ΔΔGhyd values in Table 4 fall in a relatively narrow range, ±2 kcal/mol, so the shifts are generally not enough to qualitatively change the direction of the E/Z equilibria. The possible exception is thiourea 6, for which ΔG appears to be 0 ± 1 kcal/mol in all media.21 The expectation from classical electrostatics is that, in the absence of steric effects, the conformer with the larger dipole moment should have a more negative free energy of hydration. Thus, for most cases in Tables 1 and 2, the E conformer is expected to be better hydrated than the Z conformer. In this regard, the results in Table 4 are mixed. For acetic acid (1) the E conformer has a 2.92-D larger dipole moment than the Z form and it is better hydrated by 2.39 kcal/mol. This value is significantly smaller in magnitude than estimates of ΔΔGhyd from a QM/MM study in TIP4P water (−4.8 kcal/mol)41 and from QM/RISM calculations (−5.2 kcal/mol).42 If these values are combined with the G3B3 gas-phase result, the prediction is that (E)- and (Z)-acetic acid are nearly equally populated in water at 298 K or, equivalently, that the Brønsted basicities of the syn and anti lone pairs for acetate ion in water are similar.43,44 It should be noted that in dilute aqueous solution at neutral pH, less than 1% of acetic acid is not ionized.
Furthermore, the ester 3 and carbamate 7 pairs also have changes of ca. 3 D in dipole moment, but the E conformer is predicted to be better hydrated by only ca. 0.6 kcal/mol. Previous results for 3 from free energy perturbation calculations in TIP4P water predicted preferential hydration of the E conformer by 3.0 kcal/mol.16 Most surprisingly, although the E,Z conformer of the carbonate 9 has a 3.60-D larger dipole moment than the Z,Z conformer, the Z,Z conformer is predicted to be better hydrated by 0.26 kcal/mol. The results for N-methylacetamide 2 also appear to be off-the-mark. There is general consensus that the E/Z equilibrium for 2 is affected little by hydration,11,30 while the GB/SA results favor hydration of the Z conformer by 1.43 kcal/mol. The differential hydration arises predominantly from differences in the GB term. The SA term varies by less than 0.1 kcal/mol for these E/Z equilibria.
The noted discrepancies do not reflect obvious problems with the 1.07*CM1A charges that are used in the GB/SA calculations. The computed dipole moments with these charges mimic the G3B3 results well. E.g., the 1.07*CM1A dipole moments for (E,Z)- and (Z,Z)-9 are 3.70 and 0.44 D, which are close to the G3B3 values of 3.97 vs 0.37 D. And, for (E)- and (Z)-N-methylacetamide, the 1.07*CM1A dipole moments are 4.00 and 3.44 D, while the G3B3 results are 4.54 and 4.22 D. Further examination of solvent effects on the E/Z equilibria is warranted using free-energy methods in simulations with explicit solvent. In view of the expected sensitivity of the results to details of solute-solvent hydrogen bonding, it is unclear if continuum models can accurately gauge solvent effects in such cases.
Conclusion
Changes in energy, enthalpy, free energy, and dipole moment were evaluated at the G3B3 level for 18 pairs of conformers exhibiting prototypical E/Z conformational equilibria for rotation about single bonds. The results are important for consideration in molecular design and in the evaluation of structures that arise from protein-ligand docking studies as well as from crystallography. For the systems studied, which included representatives of carboxylic acids, carboxylic esters, thioesters, secondary amides, ureas, carbamates, carbonates, enol ethers, enamines, and amidines, the preferred conformer is normally Z. Preference for the E conformer mostly arises from steric effects in hydrazones, amidines, and oximes that destabilize the Z conformer, especially via syn-1,5-CH3-CH3 interactions. A particularly interesting case is 1,3-dimethylthiourea, which is found to slightly favor the E,Z conformer over the Z,Z alternative in the gas phase. Free energies of hydration were also estimated for the conformers from GB/SA calculations. Accurate computation of the effects of hydration on E/Z equilibria is expected to be particularly challenging in view of the substantial, accompanying changes in solute-water hydrogen bonding. Though the differential effects from the GB/SA calculations were generally found to be insufficient to overcome the gas-phase preferences, the computed effects in several cases seem too small. Further investigation is warranted with free-energy methods in molecular dynamics or Monte Carlo simulations using explicit hydration to obtain more accurate results and to provide a basis for testing and improvement of continuum solvation methods.
Supplementary Material
Figure 3.
Molecules in the RXCOYR set.
Acknowledgments
Gratitude is expressed to the National Science Foundation and National Institutes of Health (GM32136) for support of this work.
Footnotes
Supporting Information Available: Tables of absolute and relative gas-phase energies, enthalpies, free energies, and dipole moments for 1 - 18 from the quantum mechanical calculations (3 pages). This information is available free of charge via the Internet at http://pubs.acs.org/.
References
- (1).Brameld KA, Kuhn B, Reuter DC, Stahl M. Small Molecule Conformational Preferences Derived from Crystal Structure Data. A Medicinal Chemistry Focused Analysis. J. Chem. Inf. Model. 2008;48:1–24. doi: 10.1021/ci7002494. [DOI] [PubMed] [Google Scholar]
- (2).Jabs A, Weiss MS, Hilgenfeld R. Non-proline Cis Peptide Bonds in Proteins. J. Mol. Biol. 1999;286:291–304. doi: 10.1006/jmbi.1998.2459. [DOI] [PubMed] [Google Scholar]
- (3).Klebe G. Virtual ligand screening: strategies, perspectives and limitations. Drug Disc. Today. 2006;11:580–594. doi: 10.1016/j.drudis.2006.05.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (4).Jorgensen WL. Efficient Drug Lead Discovery and Optimization. Acc. Chem. Res. 2009;42:724–733. doi: 10.1021/ar800236t. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (5).Nichols SE, Domaoal RA, Thakur VV, Bailey CM, Wang L, Tirado-Rives J, Anderson KS, Jorgensen WL. Discovery of Wild-type and Y181C Mutant Non-nucleoside HIV-1 Reverse Transcriptase Inhibitors Using Virtual Screening with Multiple Protein Structures. J. Chem. Inf. Model. 2009;49:1272–1279. doi: 10.1021/ci900068k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (6).Ren J, Diprose J, Warren J, Esnouf RM, Bird LE, Ikemizu S, Slater M, Milton J, Balzarini J, Stuart DI, Stammers DK. Phenylethylthiazolylthiourea (PETT) non-nucleoside inhibitors of HIV-1 and HIV-2 reverse transcriptases: Structural and biochemical analyses. J. Biol. Chem. 2000;275:5633–5639. doi: 10.1074/jbc.275.8.5633. [DOI] [PubMed] [Google Scholar]
- (7).Leach AR, Shoichet BK, Peishoff CE. Prediction of protein-ligand interactions. Docking and scoring: successes and gaps. J. Med. Chem. 2006;49:5851–5855. doi: 10.1021/jm060999m. [DOI] [PubMed] [Google Scholar]
- (8).Ponder JW, Case DA. Force Fields for Protein Simulations. Adv. Prot. Chem. 2003;66:27–85. doi: 10.1016/s0065-3233(03)66002-x. [DOI] [PubMed] [Google Scholar]
- (9).Jorgensen WL, Tirado-Rives J. Potential energy functions for atomic-level simulations of water and organic and biomolecular systems. Proc. Nat. Acad. Sci USA. 2005;102:6665–6670. doi: 10.1073/pnas.0408037102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (10).Wiberg KB, Laidig KE. Barriers to rotation adjacent to double bonds. The carbon-oxygen barrier in formic acid, methyl formate, acetic acid, and methyl acetate. The origin of ester and amide resonance. J. Am. Chem. Soc. 1987;109:5935–5943. [Google Scholar]
- (11).Jorgensen WL, Gao J. Cis - trans energy difference for the peptide bond in the gas phase and in aqueous solution. J. Am. Chem. Soc. 1988;110:4212–4216. [Google Scholar]
- (12).Remko M, Scheiner S. The geometry and internal rotational barrier of carbamic acid and several derivatives. J. Mol. Struct. THEOCHEM. 1988;180:175–188. [Google Scholar]
- (13).Glaser R, Streitwieser A. Configurational and conformational preferences in oximes and oxime carbanions: ab initio study of the syn effect in reactions of oxyimine enolate equivalents. J. Am. Chem. Soc. 1989;111:7340–7348. [Google Scholar]
- (14).Stang PJ, Kitamura T, Arif AM, Karni M, Apeloig Y. A single Crystal Structure Determination and Theoretical Calculations on Alkynyl Carboxylate Esters. J. Am. Chem. Soc. 1990;112:374–381. [Google Scholar]
- (15).Wiberg KB, Wong MW. Solvent Effects 4: Effect of solvent on the E/Z energy difference for methyl formate and methyl acetate. J. Am. Chem. Soc. 1993;115:1078–1084. [Google Scholar]
- (16).Evanseck JD, Houk KN, Briggs JM, Jorgensen WL. Quantification of Solvent Effects on the Acidities of Z and E Esters from Fluid Simulations. J. Am. Chem. Soc. 1994;116:10630–10638. [Google Scholar]
- (17).Deerfield DW, Pedersen LG. An ab initio quantum mechanical study of thioesters. J. Mol. Struct. THEOCHEM. 1995;358:99–106. [Google Scholar]
- (18).Sun H, Mumby SJ, Maple JR, Hagler AT. Ab initio calculations on small molecule analogues of polycarbonates. J. Phys. Chem. 1995;99:5873–5882. [Google Scholar]
- (19).Strassner T. Ab Initio and Molecular Mechanics Calculations of Various Substituted Ureas – Rotational Barriers and a New Parametrization for Urea. J. Mol. Model. 1996;2:217–226. [Google Scholar]
- (20).Murphy RB, Pollard WT, Friesner RA. Pseudospectral localized generalized Moller-Plesset methods with a generalized valence bond reference wave function: Theory and calculation of conformational energies. J. Chem. Phys. 1997;106:5073–5084. [Google Scholar]
- (21).Chambers CC, Archibong EF, Jabalameli A, Sullivan RH, Giesen DJ, Cramer CJ, Truhlar DG. Quantum mechanical and 13C dynamic NMR study of 1,3-dimethylthiourea conformational isomerizations. J. Mol. Struct. THEOCHEM. 1998;425:61–68. [Google Scholar]
- (22).Császár AG, Allen WD, Schaefer HF., III In pursuit of the ab initio limit for conformational energy prototypes. J. Chem. Phys. 1998;108:9751–9764. [Google Scholar]
- (23).Villani V, Alagona G, Ghio C. Ab initio studies on N-methylacetamide. Stationary point search and intrinsic reaction coordinate approach. Mol. Eng. 1999;8:135–153. [Google Scholar]
- (24).Kang YK. Ab initio MO and density functional studies on trans and cis conformers of N-methylacetamide. J. Mol. Struct. THEOCHEM. 2001;546:183–193. [Google Scholar]
- (25).Senent ML. Ab initio determination of the torsional spectra of acetic acid. Mol. Phys. 2001;99:1311–1321. [Google Scholar]
- (26).Kobychev VB, Larionova EY, Klyba NS. Ab initio study of the conformational and geometric isomerism in heteroallyl and heteropropenyl systems. J. Struct. Chem. 2003;44:748–756. [Google Scholar]
- (27).Zhong H, Stewart EL, Kontoyianni M, Bowen JP. Ab initio and DFT conformational studies of propanal, 2-butanone, and analogous imines and enamines. J. Chem. Theory Comput. 2005;1:230–238. doi: 10.1021/ct049890p. [DOI] [PubMed] [Google Scholar]
- (28).Bryantsev VS, Firman TK, Hay BP. Conformational Analysis and Rotational Barriers of Alkyl- and Phenyl-Substituted Urea Derivatives. J. Phys. Chem. A. 2005;109:832–842. doi: 10.1021/jp0457287. [DOI] [PubMed] [Google Scholar]
- (29).Bryantsev VS, Hay BP. Conformational preferences and internal rotation in alkyl-and phenyl-substituted thiourea derivatives. J. Phys. Chem. A. 2006;110:4678–4688. doi: 10.1021/jp056906e. [DOI] [PubMed] [Google Scholar]
- (30).Mantz YA, Branduardi D, Bussi G, Parrinello M. Ensemble of Transition State Structures for the Cis-Trans Isomerization of N-Methylacetamide. J. Phys. Chem. B. 2009;113:12521–12529. doi: 10.1021/jp8106556. [DOI] [PubMed] [Google Scholar]
- (31).Maçôas EMS, Khriachtchev L, Pettersson M, Fausto R, Räesänen M. Rotational Isomerism in Acetic Acid: The First Experimental Observation of the High-Energy Conformer. J. Am. Chem. Soc. 2003;125:16188–16189. doi: 10.1021/ja038341a. [DOI] [PubMed] [Google Scholar]
- (32).Frisch MJ, Trucks GW, Schlegel HB, Scuseria GE, Robb MA, Cheeseman JR, Montgomery JA, Jr., Vreven T, Kudin KN, Burant JC, Millam JM, Iyengar SS, Tomasi J, Barone V, Mennucci B, Cossi M, Scalmani G, Rega N, Petersson GA, Nakatsuji H, Hada M, Ehara M, Toyota K, Fukuda R, Hasegawa J, Ishida M, Nakajima T, Honda Y, Kitao O, Nakai H, Klene M, Li X, Knox JE, Hratchian HP, Cross JB, Bakken V, Adamo C, Jaramillo J, Gomperts R, Stratmann RE, Yazyev O, Austin AJ, Cammi R, Pomelli C, Ochterski JW, Ayala PY, Morokuma K, Voth GA, Salvador P, Dannenberg JJ, Zakrzewski VG, Dapprich S, Daniels AD, Strain MC, Farkas O, Malick DK, Rabuck AD, Raghavachari K, Foresman JB, Ortiz JV, Cui Q, Baboul AG, Clifford S, Cioslowski J, Stefanov BB, Liu G, Liashenko A, Piskorz P, Komaromi I, Martin RL, Fox DJ, Keith T, Al-Laham MA, Peng CY, Nanayakkara A, Challacombe M, Gill PMW, Johnson B, Chen W, Wong MW, Gonzalez C, Pople JA. Gaussian 03, Revision C.02. Gaussian, Inc.; Wallingford, CT: 2004. [Google Scholar]
- (33).Curtiss LA, Raghavachari K, Redfern PC, Rassolov V, Pople JA. Gaussian-3 (G3) theory for molecules containing first- and second-row atoms. J. Chem. Phys. 1998;109:7764–7774. [Google Scholar]
- (34).Baboul AG, Curtiss LA, Redfern PC, Raghavachari K. Gaussian-3 theory using density functional geometries and zero-point energies. J. Chem. Phys. 1999;110:7650–7657. [Google Scholar]
- (35).Jorgensen WL, Tirado-Rives J. Molecular modeling of organic and biomolecular systems using BOSS and MCPRO. J. Comput. Chem. 2005;26:1689–1700. doi: 10.1002/jcc.20297. [DOI] [PubMed] [Google Scholar]
- (36).Jorgensen WL, Ulmschneider JP, Tirado-Rives J. Free energies of hydration from a generalized Born model and an all-atom force field. J. Phys. Chem. B. 2004;108:16264–16270. [Google Scholar]
- (37).Pawar DM, Khalil AA, Hooks DR, Collins K, Elliott T, Stafford J, Smith L, Noe EA. E and Z Conformations of Esters, Thiol Esters, and Amides. J. Am. Chem. Soc. 1998;120:2108–2112. [Google Scholar]
- (38).(a) Huisgen R, Ott H. Medium-sized rings. XV. Configuration of the ester group and the singular properties of lactones. Tetrahedron. 1959;6:253–267. [Google Scholar]; (b) Schweizer WB, Dunitz JD. Structural Characteristics of the Carboxylic Ester Group. Helv. Chim. Acta. 1982;65:1547–1554. [Google Scholar]
- (39).Nobes RH, Radom L, Allinger NL. Equilibrium Conformations of Higher-Energy Rotationla Isomers of Vinyl Alcohol and Methyl Vinyl Ether. J. Mol. Struct. THEOCHEM. 1981;85:185–194. [Google Scholar]
- (40).Yamabe S, Tsuchida N, Yamazaki S. Is the Beckmann Rearrangement a Concerted or Stepwise Reaction? A Computational Study. J. Org. Chem. 2005;70:10638–10644. doi: 10.1021/jo0508346. [DOI] [PubMed] [Google Scholar]
- (41).Gao J, Pavelites JJ. Aqueous Basicity of the Carboxylate Lone Pairs and C-O Barrier in Acetic Acid: A Combined Quantum and Statistical Mechanical Study. J. Am. Chem. Soc. 1992;114:1912–1914. [Google Scholar]
- (42).Sato H, Hirata F. The syn-/anti-conformational equilibrium of acetic acid in water studied by the RISM-SCF/MCSCF method. J. Mol. Struct. THEOCHEM. 1999;461:113–120. [Google Scholar]
- (43).Li Y, Houk KN. Theoretical Assessments of the Basicity and Nucleophilicity of Carboxylate Syn and Anti Lone Pairs. J. Am. Chem. Soc. 1989;111:4505–4507. [Google Scholar]
- (44).Rebek J., Jr. Molecular Recognition with Model Systems. Angew. Chem Int. Ed. 1990;29:245–255. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.