Computational model of cell positioning: directed and collective migration in the intestinal crypt epithelium

Abstract

The epithelium of the intestinal crypt is a dynamic tissue undergoing constant regeneration through cell growth, cell division, cell differentiation and apoptosis. How the epithelial cells maintain correct positioning and how they migrate in a directed and collective fashion are still not well understood. In this paper, we developed a computational model to elucidate these processes. We show that differential adhesion between epithelial cells, caused by the differential activation of EphB receptors and ephrinB ligands along the crypt axis, is necessary to regulate cell positioning. Differential cell adhesion has been proposed previously to guide cell movement and cause cell sorting in biological tissues. The proliferative cells and the differentiated post-mitotic cells do not intermingle as long as differential adhesion is maintained. We also show that, without differential adhesion, Paneth cells are randomly distributed throughout the intestinal crypt. In addition, our model suggests that, with differential adhesion, cells migrate more rapidly as they approach the top of the intestinal crypt. Finally, by calculating the spatial correlation function of the cell velocities, we observe that differential adhesion results in the differentiated epithelial cells moving in a coordinated manner, where correlated velocities are maintained at large distances, suggesting that differential adhesion regulates coordinated migration of cells in tissues.

1. Introduction

Spatial arrangement of cells is critical for the formation of tissues by different types of cells. The process of cell sorting allows the segregation of cell populations and the maintenance of compartment boundaries between different types of cells. A connection between cell sorting and intercellular adhesion has been demonstrated in previous classic experiments with chicken (Moscona & Moscona 1952) and amphibian embryos (reviewed in Steinberg & Gilbert 2004). When different types of embryonic amphibian cells were mixed, the cells sorted into distinct homogeneous layers. Townes & Holtfreter (1955) proposed that tissue segregation is caused by differences in the degree of adhesiveness and chemotaxis. The differential adhesion hypothesis (DAH) proposed by Steinberg (1962) explains that the cell sorting behaviour is caused by cell motility combined with differences in intercellular adhesiveness. The hypothesis uses the formalism of equilibrium thermodynamics and assumes that the sorting process of cells with a certain affinity for each other is analogous to the motion of molecules in fluids.

Cell sorting, migration and polarity can be affected by cell adhesion arising from complex interactions between adhesion molecules. Major types of cell adhesion molecules, such as E-cadherin, mediate adhesion in regions of cell–cell contact, while other types such as integrins bind to different kinds of extracellular ligands (e.g. collagen, laminin and fibronectin) to regulate cell attachment with extracellular matrices. These adhesion molecules can be regulated by other signal transduction events. For example, cadherins, which are essential for the maintenance of cell–cell attachments at adherens junctions, can be regulated by small GTPases Cdc42, Rac and Rho (Kuroda et al. 1998; Braga et al. 1999; Wang et al. 2005). In addition to that, experiments performed in Xenopus embryos (Winning et al. 1996) indicate that activation of Eph receptors can result in the loss of cell–cell adhesion, which can be recovered through co-injection of RNA-encoding C-cadherin.

Erythropoietin-producing hepatoma-amplified sequence (Eph) receptors are transmembrane receptor tyrosine kinases (RTKs), which form the largest subfamily of RTKs. Their ligands are the ephrins. Although Eph receptors and ephrins are not adhesion molecules, previous experiments have shown that their interactions could trigger downstream signalling pathways that control cell–cell adhesion, cell–substrate adhesion and cytoskeletal organization (Kullander & Klein 2002). Eph receptors and ephrins have been found to play roles in processes such as the pathfinding of neural crest cells (Wilkinson 2001), axon guidance and the demarcation of tissue boundaries in vertebrate embryos (Xu et al. 2000). It has been shown that Eph/ephrins and N-cadherin mediate cell–cell adhesion, change the neural crest cell migration and cause alterations in the pattern of sympathetic ganglia (Kasemeier-Kulesa et al. 2006). Besides that, EphA2 and E-cadherin may play a critical role in colorectal tumour metastasis, as their expressions have been found to correlate closely with cancer progression (Saito et al. 2004). In addition to modulating cell–cell adhesion through cadherins, Eph receptor activation can also regulate integrin-mediated cell–matrix adhesion (Huynh-Do et al. 1999; Miao et al. 2000, 2005). EphB2 regulates integrins through the activity of R-Ras. Activated EphB2 phosphorylates R-Ras and this leads to a loss of cell–matrix adhesion, as phosphorylated R-Ras does not support integrin-mediated cell adhesion (Zou et al. 1999; Nakada et al. 2005).

To further understand the function of Eph/ephrin interactions in proliferating cells in adult tissues, experiments have been performed on intestinal epithelium, which is one of the fastest regenerating tissues. It was found that human small intestine and colon epithelium exhibit the presence of a broad spectrum of A- and B-class Eph receptors and ephrins, while the most abundantly expressed receptors and ligands are EphA2, EphB2, ephrinA1, ephrinB1 and ephrinB2 (Hafner et al. 2005). Interesting results obtained from experiments conducted by Batlle et al. (2002) showed that β-catenin and T cell factor (TCF) regulate the positioning and migration of epithelial cells in the intestinal crypt through interactions of EphB receptors and ephrinB. The β-catenin–TCF complex upregulates EphB receptors and downregulates their ligand ephrinB. EphB2 expression is highest at the bottom of the crypt, where the β-catenin–TCF complex is actively involved in transcriptional activity in the nuclei of proliferative cells. On the other hand, ephrinB1 and ephrinB2 expression is highest in differentiated cells at the top of the crypt (Batlle et al. 2002; Holmberg et al. 2006). Experiments using mice deficient for both EphB2 and EphB3 receptors showed that progenitor cells do not migrate in a uni-direction towards the lumen; instead, the proliferative cells and differentiated cells intermingle in these double-mutant mice (Batlle et al. 2002; Clevers & Batlle 2006). When EphB is knocked down, it has also been found that Paneth cells and progenitor cells are redistributed in the intestinal crypt.

As imaging of in vivo intestinal epithelial cell movement remains a challenge, computational models have been developed to study sorting and translocation of cells in the intestinal crypt epithelium. Loeffler et al. (1986) have presented a cellular automata model which used two-dimensional grids to study cell migration and proliferation in the intestinal crypt. Their model represents the crypt as rigid two-dimensional grids; all cells have equal size and are arranged in predefined rows and columns. The insertion of a newborn cell into a column of cells will cause the column of cells to shift upwards and thus the cells move in cell-sized spatial step (Loeffler et al. 1986); therefore, cell translocation in the model is connected explicitly to mitotic activity of cells. Instead of using discrete lattices, a two-dimensional lattice-free model using Voronoi tessellation has been developed by Meineke et al. (2001). This model allows the cells to move continuously. The model also assumed that mitotic pressure is the main driving force responsible for the cell movements. The above models allowed studies of the population growth, spatial arrangement and migration of epithelial cells in the intestinal crypt.

In addition to the spatial models mentioned above, stochastic models have been presented to study cell population dynamics and tumorigenesis in the colonic crypt. For example, a stochastic model was developed by Michor et al. (2004) to demonstrate the effects of mutations in different cell types and the importance of chromosomal instability. Johnston et al. (2007) used a compartmental approach to model the behaviour of populations of stem cells, differentiated cells and transit-amplifying cells in a crypt. They found that mutations in the parameters (e.g. renewal rate, apoptosis rate, differentiation rate) could affect the net growth rate and initiate tumorigenesis. However, all these models are not able to investigate cell behaviours caused by differences or changes in protein concentrations; for example, even though the spatial models allow investigations of processes such as cell growth, cell migration and cell differentiation, the models do not incorporate signalling pathways that account for changes in cell properties. On the other hand, the stochastic models outlined above were used to study the growth of cell populations and capture cell dynamics under both normal and aberrant growth rates without considering properties such as cell distributions, cell movements and cell morphology.

In this paper, we describe a computational model that couples EphB/ephrinB interactions with crypt cell dynamics using the cellular Potts model (CPM) developed by Glazier & Graner (1993). By assuming that EphB/ephrinB interactions regulate the cell adhesion properties, we want to determine whether differential cell adhesion can regulate cell positioning and cell translocation in the fast-regenerating intestinal crypt epithelium. The CPM, which generalizes the Ising model from statistical mechanics, could be used to study the effects of differential cell adhesion when multiple cell types were considered (Glazier & Graner 1993). Results from previous studies (Glazier & Graner 1993; Turner & Sherratt 2002) have shown that differential adhesion alone is sufficient to drive cell rearrangement and cell sorting. When cells of different adhesive properties are mixed, cells with weaker binding will tend to be displaced by those with stronger binding (Steinberg 1962). For example, if two types of cells, where one cell type has stronger adhesion than the other, are mixed, then the cells with stronger adhesion will cluster at the centre of the aggregate, while the cells with weaker adhesion will remain at the periphery of the aggregate. In previous studies, the CPM is a versatile model for describing the dynamics of biological phenomena like patterning in tissues (Savill & Sherratt 2003), cancer cell metastasis (Turner & Sherratt 2002) and vasculogenesis (Merks et al. 2006). Furthermore, chemotaxis could be incorporated into the model to investigate the role of chemotaxis in directional cell sorting (Käfer et al. 2006).

2. Theory and methods

2.1. Model description

Understanding how cell movement is controlled in rapidly proliferating tissues helps in the study of the maintenance of morphology and cell homeostasis in tissues. Thus, we use the intestine epithelium, which is a dynamic system that has a fast turnover rate, to study cell positioning and directed migration. The intestinal epithelium consists of a single layer of epithelial cells that form a barrier against the external environment and is constantly renewed every few days. In the small intestine, the epithelium can be divided into two spatially different compartments: finger-like projections called villi and invaginations called crypts of Lieberkühn. In the crypts of Lieberkühn, differentiated cells are found at the upper part of the crypts, while proliferating cells are confined to the lower two-thirds of the crypts (Wright & Alison 1984). The cells in the crypts then migrate upwards to the villi. In the mouse, intestinal stem cells are found at the bottom of the crypts. In experiments performed by Potten et al. (1997), long-term DNA-label retention suggested that intestinal stem cells were located at the +4 position immediately above the Paneth cells. More recent findings by Barker et al. (2007), however, showed that the Lgr5-positive crypt base columnar cell represents the stem cell of the small intestine and colon. Crypt base columnar cells are located at the bottom of the crypt; they are interspersed between Paneth cells. The Lgr5-positive crypt base columnar cells are able to generate all epithelial lineages over a 60 day period (Barker et al. 2007). There are four main intestinal epithelial lineages: enterocytes, goblet cells, enteroendocrine cells and Paneth cells (Sancho et al. 2003; Schonhoff et al. 2004). The position of a cell in the crypt is related to its age. Cell proliferation, differentiation, migration and apoptosis occur in a regulated manner along the crypt–villus axis (Radtke & Clevers 2005). As a result, how cells are positioned and sorted in the crypt epithelium is important in order to maintain the intestinal homeostasis.

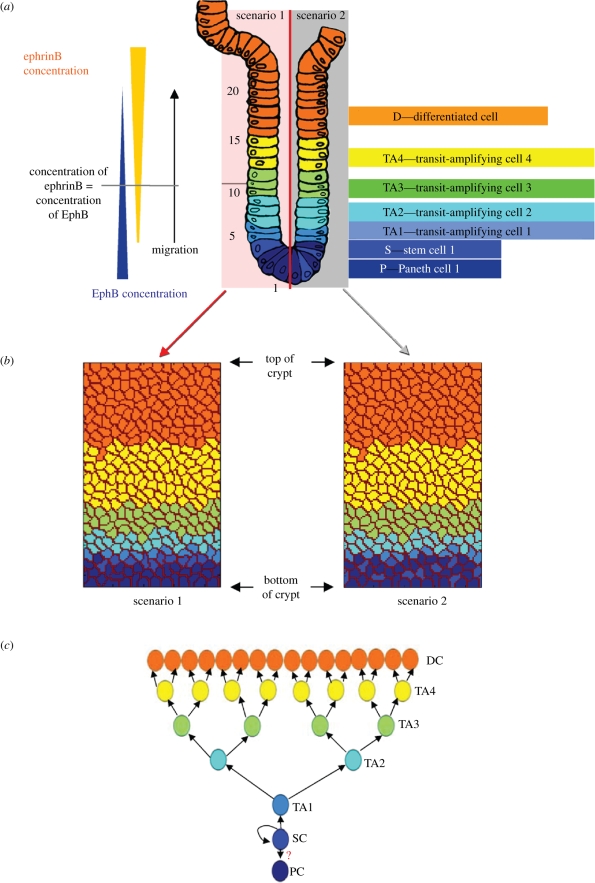
To quantitatively study cell positioning and movements that are regulated by differential cell adhesion caused by changes in adhesion at different positions, as well as cell morphological changes in the intestinal crypt epithelium, we use a two-dimensional lattice model based on the CPM to describe the dynamics of cells in a crypt of Lieberkühn. In the model, each cell is assigned a unique cell ID, σ(i, j), σ(i, j) {1, 2, 3, …, n}, where n is the number of cells in the system and (i, j) identifies a lattice site. Each cell is made up of several adjacent lattice sites that have the same cell ID σ. Cells in the model belong to different cell types, τ(σ). We assume that there are seven cell types in the intestinal crypt (figure 1a): Paneth cell (P), stem cell (S), four generations of transit-amplifying (TA) cells (TA1, TA2, TA3, TA4) and differentiated post-mitotic cell (D); τ(σ) = {P, S, TA1, TA2, TA3, TA4, D}. The positions of cells belonging to different cell types along the crypt in the model are as shown in figure 1b. Paneth cells and differentiated post-mitotic cells are differentiated cells that do not divide, whereas stem cells and the TA cells are proliferative cells that undergo cell division. The self-renewing stem cells give rise to the fast dividing progenitor cells (also referred to as TA cells). The TA cells migrate upwards from the crypt and differentiate. Differentiated cells (enterocytes, goblet cells and enteroendocrine cells) that are specialized in different functions then move towards the villus tip, where they are shed into the intestinal lumen. The fourth differentiated cell type, the Paneth cell, is the only lineage that migrates downward from the stem cell zone to the crypt bottom.

Figure 1.

Initial cell condition for the model. (a) Seven cell types defined and their positions in the crypt. (b) Initial cell configuration in the two-dimensional lattice model. (c) Transitions of cell types in model D.

Our model considers cell growth and cell division. The lineage of cell types is as shown in figure 1c. Every cell division produces two daughter cells. For example, when a stem cell located at the base of the crypt divides, it produces one daughter cell that keeps the cell ID of the parent cell and remains as a stem cell, while the other daughter cell becomes a TA1 cell and obtains a new cell ID. A TA1 cell produces two TA2 cells; a TA2 cell produces two TA3 cells; a TA3 cell produces two TA4 cells; and, finally, a TA4 cell divides into two D cells. The cell cycle time of stem cells is assumed to be 17 ± 1 h and the transit population has cycle times ranging from 12 to 14 h (Loeffler et al. 1986; Meineke et al. 2001). When the defined cell cycle is completed and the area a(σ) of a proliferative cell becomes twice the target area size, the cell divides. Division is at the middle of the cell and perpendicular to the longest cell axis (O'Connell & Wang 2000).

According to the differential adhesion hypothesis (Steinberg 1962; Steinberg & Takeichi 1994), in any population of motile cells with different adhesiveness, weaker cell bindings will tend to be displaced by stronger ones. This adhesion–maximization process will drive cell sorting until an ‘equilibrium configuration’ is reached. In the CPM, cell adhesion is represented through the surface energy at the cell interface. High surface energy corresponds to weak adhesion, and low surface energy indicates strong adhesion. A cell type-dependent surface energy, E_s, is defined to study the effects of cell adhesion. The cell type-dependent surface energy is zero between lattice sites within the same cell; it is only considered between neighbouring lattices of different cells to measure the adhesiveness between different cells at the boundary

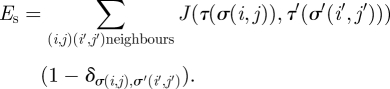2.1

Here, J(τ, τ′) is the surface energy per unit contact area. It is defined as a function of the cell types (τ and τ′) of the two surfaces in contact. The Kronecker delta term δ_{σ(i,j),σ(i′, j′)} is used so that the energy is zero within a cell, i.e. when σ(i, j) = σ(i′, j′). We assume that the surface of the cell is isotropic; therefore, the surface energy at the cell interface depends only on the type of cell. Cells belonging to the same cell type carry the same adhesion properties. As the position of a cell in the crypt is related to its age and thus can be related to the cell type in the model, by assigning different surface energies to cells of different types, we can simulate the changes in cell adhesion that may be caused by the gradients of proteins found in the intestinal crypt (e.g. EphB and ephrinB gradients (Batlle et al. 2002); see figure 1a). EphB2 expression decreases gradually towards the top of the crypt, while ephrinB1 and ephrinB2 expression decreases towards the bottom of the crypt. Activation of EphB receptors and ephrinB ligands regulates the function of cell adhesion molecules and results in changes in cell adhesion (Wilkinson 2003; Dravis et al. 2004) through endocytosis and regulation of the cytoskeleton (Marston et al. 2003; Zimmer et al. 2003). Thus, we assume that the interactions of EphB/ephrinB in vivo can also regulate adhesion between intestinal epithelial cells in our model. We account for this adhesion controlled by EphB/ephrinB interactions in our model through the cell type-dependent surface energy, E_s, considered between cells.

Two scenarios of stem cell distribution (scenario 1: stem cells at +4 position (Potten et al. 1997), and scenario 2: stem the cells located at the bottom of the crypt in between Paneth cells (Barker et al. 2007)) are also considered in this paper (see figure 1a). In our model, we introduce a position-dependent energy term (E_p) to simulate the distribution of stem cells in the two above scenarios. With this energy term, the stem cells will prefer to stay at their initial positions. A matrix M is used to record the position of stem cells in the initial cell configuration (figure 1b). In M, if entry (i, j) belongs to a stem cell, that is τ(σ(i, j)) = S, then M(i, j) = S. We have

2.2

where J_niche is the adhesion energy between the cell and the initial stem cell position.

Biological cells normally have a fixed range of sizes; therefore, cell size has to be maintained in the model. Glazier & Graner (1993) introduced an area constraint to fix cell sizes in a two-dimensional CPM. That is, each cell has an area-dependent energy term (E_a) to ensure that the cell maintains its area,

2.3

where τ(σ) is the cell type associated with the cell σ, a(σ) the current area of a cell σ and A_τ the target area for cells of type τ. All cells of a given type have the same target area.

Finally, the energy of the interactions between cells can be defined by the energy function,

2.4

where λ specifies the strength of the area constraint in the energy term.

We use the Metropolis Monte Carlo method to solve for the dynamics of our two-dimensional lattice model. At each step, a lattice site (i, j) is chosen randomly. Then, a neighbouring lattice site (i′, j′) is randomly selected from the eight neighbouring sites of (i, j). The value of σ(i, j) may be updated to the value of σ′(i′, j′) with the Monte Carlo probability, p,

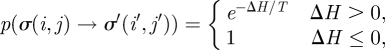2.5

where ΔH is the gain in energy after the change and T is the temperature that corresponds to the amplitude of the cell membrane fluctuations. Time is measured in Monte Carlo steps (MCSs) in the model. One MCS consists of x attempts to update lattices in the model, where x = 16 times the total number of lattice sites. In simulations, the cells rearrange themselves into a configuration that minimizes the energy resulting from cell–cell interactions.

2.2. Model parameters

Our model consists of approximately 280 cells. The height of the crypt in the model is about 21–23 cells and the width of the crypt is about 13 or 14 cells. Figure 1b depicts the initial configuration of cells in the model. Periodic boundary conditions are used at the left and right boundaries of the model. The simulations are performed on a 147 × 90 (row × column) two-dimensional lattice grid. Thus, each cell comprises approximately 40–50 adjacent lattice sites. We assume that the target area A_τ(σ) of a non-dividing cell is 40 lattice sites. However, for proliferative cells (S, TA1, TA2, TA3, TA4), the target area is set to be twice the original cell size, when the cell has gone through one cell cycle. Cells touching the upper boundary of the lattice have their areas reduced to zero to simulate cells leaving the system.

The matrix J(τ, τ′) in equation (2.1) describes the adhesion-free energy per unit contact area between cells. The individual matrix elements are shown in figure 2. These values are defined based on experimental results (Wilkinson 2003; Poliakov et al. 2004), which showed that a high level of Eph receptor activation by ephrin reduces cell adhesion. On the other hand, a low level of Eph receptor activation promotes cell adhesion.

Figure 2.

The values of the entries in the matrix J(τ, τ′) in equation (2.3).

In our computational model, only the relative magnitudes, not the absolute magnitudes, of cell adhesion strength are required to present differential adhesion for cells at different positions in the crypt. Therefore, the exact magnitude of the cell adhesion strength is not required.

By adjusting the adhesion energy in J, we take into account the signalling of EphB/ephrinB interactions between different cell types in our computational model. In the J matrix in figure 2, entries with smaller values denote stronger cell adhesion strength, i.e. strong adhesion strength indicates weak surface free energy. The surface free energy is minimal between cells of the same type. Thus, the diagonal elements of the J matrix have values (ranging from 2 to 15 similar to the surface energy values used in Glazier & Graner (1993)) whose magnitude in a particular row is smaller than the magnitudes of all the other non-diagonal entries in the row.

According to the experiments performed by Batlle et al. (2002), the expression of EphB2 was highest in cells located near the bottom of the crypts (at positions 4–6) and decreased as cells approached the top of the crypts. On the contrary, high levels of ephrinB1 and ephrinB2 were identified at the crypt–villus junctions and the expression decreased in a gradient towards the bottom of the crypts. In our model, we assume that cells belonging to the same cell type have identical EphB and ephrinB expression. As the expression level of ephrinB is lowest at the base of the crypt, we propose that the cell adhesion strength of cells at the base of the crypt is higher than those of the other cells; therefore, diagonal entries J(P,P) and J(S,S) have the lowest value 2. As ephrinB2 increases towards the top of the crypt, the cell adhesion strength becomes weaker (J(TA1, TA1), J(TA2, TA2), J(TA3, TA3), J(TA4, TA4), J(D, D) have values larger than J(P, P) and J(S, S)). The maximum EphB activation is assumed to occur in TA3 cells, where the concentration of EphB is assumed to be equal to the concentration of ephrinB (as shown in figure 1a); thus causing J(TA3, TA3) to have the highest value among the diagonal entries in matrix J. The adhesion strength of cells (TA4 and D cells) at the top of the crypt is stronger than those of TA3 cells, as the expression of EphB decreases towards the crypt–villus junction and the activation of EphB becomes lower.

Values of non-diagonal entries in the J matrix are also decided based on the difference in EphB and ephrinB expression in cells. We define that the surface energy between cell types increases as the difference in cell expression of EphB and ephrinB becomes larger. For example, stem cells located at the bottom of the crypt have a high concentration of EphB, while the expression of ephrinB is lowest; as the expression of ephrinB increases and the expression of EphB decreases towards the top of the crypt, differentiated cells at the upper part of the crypt have high concentration of ephrinB while the expression of EphB is lowest. Therefore, we have J(S, D) > J(S, TA4) > J(S, TA3) > J(S, TA2) > J(S, TA1) > J(S, P) > J(S, S).

The parameter λ in equation (2.4) is set to λ = 1. It is a Lagrange multiplier that constrains the cell area conservation. This value follows the λ value used in previous literature (Glazier & Graner 1993).

The parameter T in equation (2.5) is set to T = 10, which is identical to the value used in previous literature (Glazier & Graner 1993).

One MCS in the simulations is calibrated to be 0.1 h. This ensures that the time scale for cell growth and cell division (cells divide after they have completed one cell cycle) is set correctly.

Finally, sensitivity analyses of the parameters J, λ and T are also carried out and are discussed in the electronic supplementary material.

3. Results

3.1. Differential adhesion regulates positioning of cells in the intestinal crypt

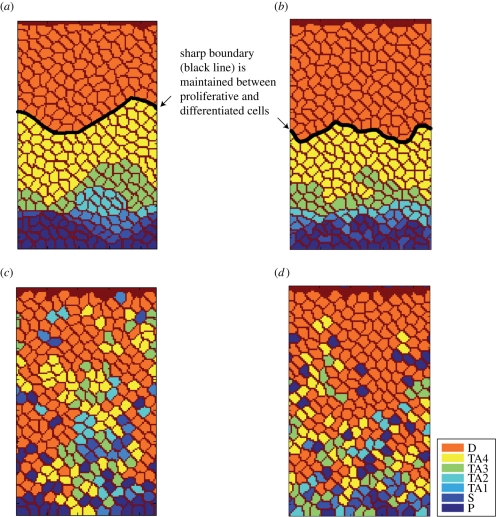
The simulation results demonstrate that, when differential adhesion is maintained, TA cells and differentiated cells translocate in a directed fashion towards the top of the crypt. This is similar to intestinal cell migration observed in vivo (Winton et al. 1988). A distinct boundary can be found to be maintained between the proliferative and the differentiated cells in both scenarios 1 and 2 (figure 3a,b). Paneth cells remain at the bottom of the crypt and do not migrate upwards while TA cells move in an orderly fashion to the top of the crypt as they divide and become differentiated. Differentiated cells are located only at the top of the crypt. The results in figure 3a,b also suggest that, even though stem cells are located at different positions in the two scenarios, cells in both scenarios are able to maintain ordered positioning when differential cell adhesion is considered.

Figure 3.

Cell distribution from the simulations. In the two-dimensional lattice model, when differential adhesion is maintained, proliferative cells and differentiated post-mitotic cells do not intermingle: (a) scenario 1, (b) scenario 2. The black line depicts the sharp boundary between the proliferative and differentiated areas. When differential adhesion is removed from the model, differentiated cells intermingle with proliferative cells: (c) scenario 1, (d) scenario 2.

We then modelled the removal of differential adhesion by setting the individual elements of the J matrix to have identical values (i.e. all the cells in the model have the same surface free energy). When differential adhesion between cells is removed, it is found that the differentiated cells intermingle with proliferative cells (figure 3c,d). In this case, TA cells no longer migrate in an orderly way to the top of the crypt. Consequently, the position of a cell no longer depends on its age. Furthermore, Paneth cells do not remain at the bottom of the crypt; instead, they are found distributed at different positions in the crypt. These behaviours of cells in our model are similar to movements of cells found in previous experimental studies (Batlle et al. 2002). The experiments using mice deficient for both EphB2 and EphB3 receptors showed that progenitor cells do not migrate in a uni-direction towards the lumen; instead, the proliferative cells and differentiated cells intermingle in these double-mutant mice (Batlle et al. 2002; Clevers & Batlle 2006).

In addition, our simulation results show that, as some of the proliferative cells move randomly towards the base of the crypt, dividing proliferative cells can be located at the positions originally occupied by Paneth cells. Increased proliferative activities are detected at the base of the crypt. The redistribution of proliferative cells in the simulations matches the observation found by Holmberg et al. (2006). Our model shows that differential adhesion regulates the positioning and directed migration of cells in a dynamic environment, where cells undergo cell growth and division.

3.2. Epithelial cells in the intestinal crypt move vertically upwards towards the top of the crypt

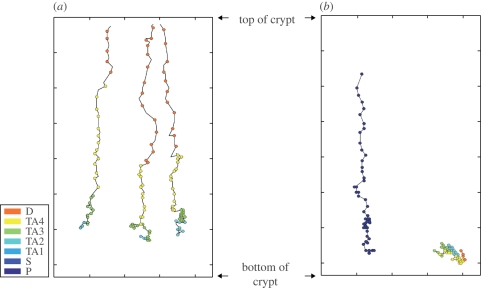
To study the translocation of a cell from the bottom to the top of the crypt, we followed the movements of a cell starting from its initial position at the base of the crypt. Figure 4a shows the migration trajectories of several cells in the model when differential adhesion is considered. From figure 4a, we can see that the cells move almost vertically upwards towards the top of the crypt. The cells in our model are not constrained to move in any particular direction, and can, in fact, move horizontally and downward. The results found show that their general trend is an upward migration towards the top of the crypt. This is reminiscent of the patterns shown by Winton et al. (1988). In the model, the cells take about 50 h to move from the base to the top of the crypt after proliferation from a stem cell. The dot-to-dot distance in figure 4a equals 1 h. The colour of the dot indicates the cell type at that time point. As a result, we can see that, as the cell moves, the cell differentiates and changes its type.

Figure 4.

Trajectories of cells. (a) The migration trajectories of cells moving from the bottom of the crypt to the top of the crypt when differential cell adhesion is maintained. (b) The trajectories of cells without differential cell adhesion show that, instead of staying at the bottom of the crypt, the Paneth cell (represented by dark blue dots) moves upwards when there is no differential adhesion. On the other hand, the proliferative cell in (b) stays at the bottom of the crypt and does not move upwards to the top of the crypt. The dot-to-dot distance equals 1 h. The colour of the dot corresponds to the cell type at that time point.

Figure 4b shows the migration trajectories of two cells in a scenario, where cell adhesion is the same for all cells in the model. A Paneth cell can be found moving vertically upwards from its initial position at the bottom of the crypt to the top of the crypt. Our model shows that, without differential adhesion, Paneth cells are not constrained to stay at the bottom of the crypts. The other cell, which is initially a TA cell in figure 4b, however, has a trajectory that is different from the path traversed by the Paneth cell in figure 4b. Instead of moving upwards, the cell migrates downwards to the base of the crypt.

Consequently, as the TA cell proliferates and becomes differentiated, the differentiated cell that normally stays at the top of the crypt can be found located at the base of the crypt.

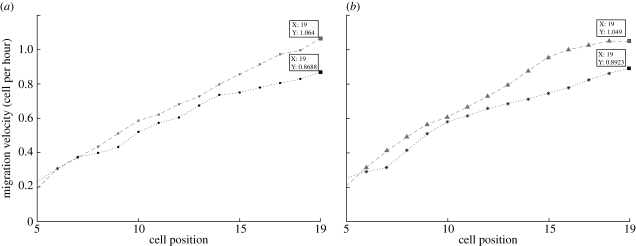
In previous experiments (Tsubouchi 1983), it was found that the speed of the directed migration towards the top of the crypt increased from 0.02 cell diameter per hour at cell position 1 (bottom of the crypt) to 1.05 cell diameter per hour at the top of the crypt. Our simulation results with differential adhesion also show this behaviour (figure 5a,b). The velocities calculated from our model match those of the experiments very well. This also means that differentiated cells at the top of the crypt have a faster velocity than proliferative cells located at the lower to the middle part of the crypt. On the other hand, when there is no differential adhesion, cell velocities are affected. As observed in figure 5, the results from the two-dimensional model indicate that cell velocities at the upper part of the crypt are smaller without differential adhesion. The differences in cell velocities demonstrate that, in addition to modulating cell positioning in the intestinal crypt, differential adhesion of cells plays a role in enhancing cell-directed movements.

Figure 5.

Mean migration velocity of cells at different positions in the crypt. The results found in (a) scenario 1 (squares with dashed line, results from the two-dimensional lattice model (with differential adhesion); filled circles with dotted line: results from the two-dimensional lattice model (without differential adhesion)) and (b) scenario 2 (triangles with dashed line: results from the two-dimensional lattice model (with differential adhesion); asterisks with dotted line, results from the two-dimensional lattice model (without differential adhesion)) show that, with differential cell adhesion, cell velocity is increased. The average is taken over cells from 20 datasets.

3.3. Movement of epithelial cells in the model is coordinated

Epithelial cells are found to move collectively as sheets in culture (Haga et al. 2005). To determine whether the movements of cells in our model are coordinated, we calculated the spatial correlation of the velocity C(r), given by (Haga et al. 2005)

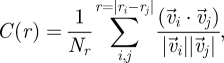3.1

where r is the distance between the two cell centroids, 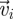the velocity of cell i at position r_i and N_r is the number of cell pairs with distance r. A large value of C(r) for 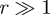indicates that the velocities of two cells at the distance r apart are highly correlated, whereas a decaying C(r) demonstrates that two cells begin to become uncorrelated when the distance between them increases.

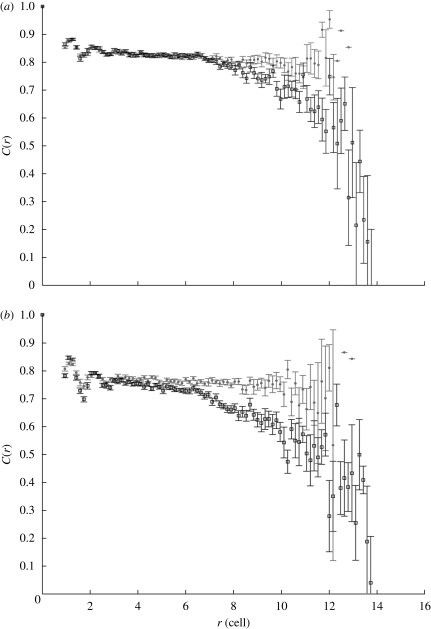
Figure 6a,b shows the correlation functions calculated from our simulations, when differential adhesion is maintained and when all the cells have identical adhesion strength. The velocities used are calculated at the time interval of 1 h (10 MCSs). We considered only differentiated cells (D cells) when calculating the spatial correlation of the cell velocity because differentiated cells form the largest cell population in the model and their velocities are less affected by cell division than other cell types.

Figure 6.

Spatial correlation of the cell velocity in cells with differential adhesion (circles) and cells without differential adhesion (squares). Comparison of cells with differential adhesion and without differential adhesion shows that the velocities of cells with differential adhesion are highly correlated; however, without differential adhesion, the spatial correlation of the velocity decreases when cell distance increases—(a) scenario 1; (b) scenario 2. Data are determined from cells in 20 datasets. The distance between cells, r, is normalized to the target cell diameter. Standard error (s.e.) bars are shown in the figure.

Data from figure 6a,b suggest that the differentiated cells in our simulations are quite highly correlated in their movements at all distances r shown when differential adhesion is maintained among the cells. We see that the spatial correlation for the cells without differential adhesion decreases and fluctuates more when the cell distance r increases.

Thus, the movements of cells without differential adhesion become more random for distant cells. This may be caused by the more random cell movement generated by the cell division of TA cells. As shown in figure 3b, without differential adhesion, the fast dividing progenitors are distributed among the differentiated cells; therefore, causing the translocation of differentiated cells to be affected by these neighbouring dividing cells. Consequently, we can conclude that, with differential adhesion, the differentiated cells preserve collective movement in the crypt. This demonstrates that differential adhesion contributes to correlated movement in the model.

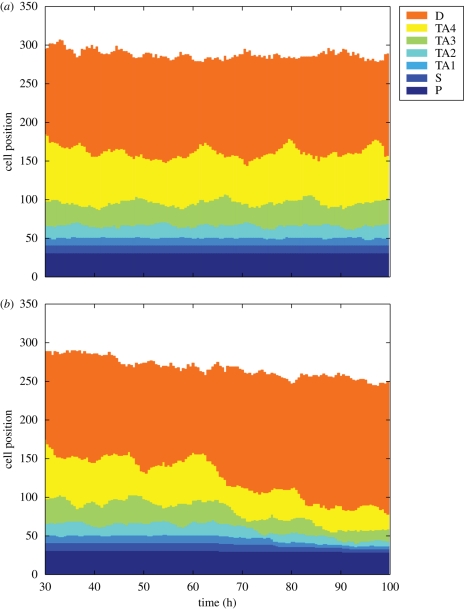
3.4. Intestinal epithelial cell homeostasis is maintained in the model

The crypts in the small intestine of mice contain about 150 proliferative cells each (Meineke et al. 2001). These proliferative cells are important to maintain intestinal epithelial cell homeostasis. The simulation results in figure 7a show that, when differential cell adhesion is considered in the model, the populations of different cell types (from 30 to 99 h after the initial state) are maintained and the fluctuations in cell populations are small. This is consistent with the previous experimental observations (Meineke et al. 2001). However, without differential cell adhesion, it is found that the cell populations in the crypt cannot be maintained in the model (figure 7b). The reduction in cell populations may be the result of proliferative cells leaving the system before they become differentiated.

Figure 7.

Cell populations maintained in the model. Preserving cell homeostasis is of critical importance in fast-regenerating tissue such as intestine. (a) Cell populations of different types are maintained throughout the two-dimensional lattice model simulation when differential cell adhesion is considered. (b) However, when no differential cell is maintained, the population of proliferative cells is reduced.

4. Discussion

In fast-regenerating tissues such as the intestinal epithelium, the maintenance of crypt architecture and cell distribution may be of critical importance to support the tissue functions and preserve tissue homeostasis. The positioning and translocation of proliferative progenitor cells, differentiated cells (including enterocytes, goblet cells and enteroendocrine cells) and Paneth cells is strictly ordered in the small intestinal crypt despite the fast turnover rate. Our two-dimensional lattice model based on the CPM can be used to analyse the spatial–temporal movements of epithelial cells in the intestinal crypt, while preserving dynamics in the tissue. In the two-dimensional model, cells move to minimize the surface free energy between cells. The cell movements are decided by the interactions of cells at the cell boundary. Therefore, unlike cell-centred methods, our two-dimensional lattice model can describe the changes in cell morphology triggered by cell movements. We do not artificially define the way (e.g. based on the age of neighbouring cells) a new cell should be inserted. Instead, the decision of cell division is based purely on the geometry of the cell.

We have shown that differential cell adhesion regulates cell positioning and enhances directed cell migration as well as collective cell movement in the intestinal crypt. Snapshots of cell distribution in our model demonstrate that cell positioning in the crypt epithelium depends on differential cell adhesion. By minimizing the surface free energy at cell boundaries with differential adhesion, random forces from processes such as cell growth and division can be resolved. Differential cell adhesion allows cells having identical properties (e.g. age, proliferative potential) to stay together and to be positioned in an ordered way, even though the proliferative cells have to go through several cell divisions before reaching a differentiated state. When calculating the spatial correlation of the cell velocity, the results found indicate that the movement of distant cells with differential adhesion is more highly correlated than distant cells without differential adhesion. This indicates that the differential cell adhesion helps to enhance collective movements of epithelial cells. The effects of cell positioning (especially for proliferative cells) in collective cell movement of epithelial cells may be further explored in computational models and experiments to help understand pattern formation or morphogenesis processes in biological systems.

Several mechanisms for the migration of epithelial cells have been previously proposed (Heath 1996; Meineke et al. 2001). They include mitotic pressure, active cell movement and basement membrane flow. Mitotic pressure is generated through the proliferation of cells. However, as epithelial cells are elastic, how the pressure can be passed to all the cells to trigger cell migration remains a question. In fact, it has been demonstrated previously that intestinal cell migration can take place in the complete absence of mitotic activity (Kaur & Potten 1986a). In the active cell movement mechanism, cells migrate by actively controlling their cytoskeletal structure to move in the desired direction. The monolayer of intestinal epithelial cells adheres to the basement membrane through binding of integrins to its ligands including collagen, laminin and fibronectin (Hynes 1992). However, the basal lamina is about 50–100 nm thick (Heath 1996) and previous experiments (Trier et al. 1990) have shown that the epithelial basement membrane of the small intestine does not migrate together with its overlying epithelium. These observations exclude basement membrane flow as the mechanism that drives cell migration in the intestine. On the other hand, Kaur & Potten (1986b) showed that the inhibition of smooth muscle contraction stopped the migration of villus cells but not the migration of crypt cells. Cell movement in the crypt was found to be inhibited only when the protein synthesis inhibitor puromycin was used (Kaur & Potten 1986b).

Results from our simulations suggest that the epithelial cells move faster as they move upwards to the top of the crypt. If mitotic pressure is the main driving force of crypt cell movements in the intestinal crypt, the velocities of cells close to the dividing proliferative cells should be larger than the velocities of cells further away, since, in biological cells, the effective forces (F) acting upon a cell can be described as F ∼ v, where v is the velocity. Our findings, however, show that differentiated cells at the top of the crypt move faster than proliferative TA cells at lower positions of the crypt. This agrees with the experimental results demonstrated by Kaur & Potten (1986a) and supports the conclusion that mitotic pressure is not the key factor responsible for the movements of cells in the intestinal crypt.

In addition, the trajectories of cells migrating from the bottom to the top of the crypt show that, without any directional information provided to the cells, the cells are still able to migrate persistently in a directed fashion for long distances. Newly born proliferative cells located at the base of the crypt move vertically upwards to the top of the crypt as they go through several cell divisions and finally become differentiated. However, when no differential adhesion is maintained, some of the proliferative cells are found moving randomly to the bottom of the crypt. Comparison of migration velocities of cells with and without differential adhesion also indicates that differential cell adhesion helps to increase cell migration velocity in the model. To know whether this change in cell velocities can affect crypt turnover time in vivo requires further experiments to be performed as crypt cell homeostasis can be modulated by many other factors such as cell proliferation rate, cell apoptosis, crypt size and crypt architecture.