Abstract
The controlled cortical impact (CCI) model has been extensively used to study region-specific patterns of neuronal injury and cell death after a focal traumatic brain injury. Although external parameters such as impact velocity and depth of penetration have been defined in this injury model, little is known about the intracranial mechanical responses within cortical and subcortical brain regions where neuronal loss is prevalent. At present, one of the best methods to determine the internal responses of the brain is finite element (FE) modeling. A previously developed and biomechanically validated detailed three-dimensional FE rat brain model, consisting of 255,700 hexahedral elements and representing all essential anatomical features of a rat brain, was used to study intracranial responses in a series of CCI experiments in which injury severity ranged from mild to severe. A linear relationship was found between the percentage of the neuronal loss observed in vivo and the FE model-predicted maximum principal strain (R2 = 0.602). Interestingly, the FE model also predicted some risk of injury in the cerebellum, located remote from the point of impact, with a 25% neuronal loss for the “severe” impact condition. More research is needed to examine other regions that do not have histological data for comparison with FE model predictions before this injury mechanism and the associated injury threshold can be fully established.
Key words: brain biomechanics, controlled cortical impact, finite element models, traumatic brain injury
Introduction
The controlled cortical impact (CCI) model, introduced in the late 1980s, is currently widely used to study the pathogenesis of traumatic brain injury (TBI) in the rodent (Dixon et al., 1991; Lighthall, 1988; Lighthall et al., 1989). The advantage of this model is that it uses a non-deformable constant size impactor, a controlled impact velocity, and a predefined dural compression depth and duration. However, although the external parameters are well controlled, the internal biomechanical responses that occur during impact have not been fully investigated. At present, numerical simulation is the best method to determine these internal responses, which are valuable for the interpretation of experimentally-observed region-specific damage resulting from injuries of varying magnitude. Further, such numerical models can be used to quantify and compare the injuries induced in these CCI animal studies by different laboratories using a variety of impact variables, such as impact location, depth, velocity, direction, and duration. For these reasons, biomechanical responses of the intracranial tissues may be a better parameter for use as a standardized basis for comparing brain trauma generated by different impact conditions (King et al., 2003; Pena et al., 2005).
Recently, three finite element (FE) rat brain models were developed to investigate intracranial tissue responses during CCI (Levchakov et al., 2006; Mao et al., 2006; Pena et al., 2005). Pena and colleagues (2005) first attempted to characterize displacement, mean stress, and shear stress using a two-dimensional (2D) FE brain model representing a single coronal section (Pena et al., 2005). Levchakov and associates (2006) developed a three-dimensional (3D) FE model of a rat brain using tetrahedral elements to predict intracranial strain and stress for both neonatal and mature rat brains in closed-head controlled impacts. Each of these two models assumed homogeneous material properties with no consideration given to the detailed anatomical organization of the brain. Mao and co-workers (2006) developed a 3D FE rat brain model representing all essential anatomical features of the rat brain, including the olfactory bulb, cortex, hippocampus, thalamus, hypothalamus, corpus callosum, brainstem (midbrain, pons, and medulla oblongata), cerebellum, lateral ventricle, third ventricle, fourth ventricle, internal capsule, external capsule, and part of the spinal cord, based on histological studies of a rat brain (Paxinos and Watson, 2005). The brain model consisted of 255,700 hexahedral elements with a typical spatial resolution of 200 microns. The use of such a detailed model enabled the prediction of internal responses at different anatomical sites. The FE model was then biomechanically validated against cortical tissue deformation as measured during dynamic cortical deformation experiments conducted by Shreiber and associates (1997). To the best of our knowledge, this was the only study in which cortical deformation was measured using high-precision instrumentation. In the experiments performed by Shreiber's group, a 5-mm-diameter craniotomy centered 3.0 mm posterior to the bregma and 2.5 mm lateral to the center line was performed. Negative pressures of 6.895, 13.790, and 20.684 kPa (2, 3, and 4 psi), with durations of 25, 50, and 100 msec, were applied to the exposed brain tissue while brain surface deformation was measured using an infrared laser displacement transducer with an accuracy of more than 0.016 mm. In the FE simulations, the same nine scenarios (three pressures and three durations) were applied to the exposed brain surface at the same craniotomy location as used in the experiments, and then nodal displacement time-histories were calculated by averaging the motion of 16 elements adjacent to the center of the craniotomy. The simulated cortical deformation fell within one standard deviation of the mean for all nine cases. Additionally, the cortical displacements increased as the suction pressure increased for all three durations (25, 50 and 100 msec) simulated.
In the study reported by Mao and colleagues (2006), the biomechanically-validated rat brain model simulated four different levels of CCI using unilateral craniotomy (Chen et al., 2003; Kochanek et al., 1995; Scheff et al., 1997; Sutton et al., 1993). In these studies, the impact velocities ranged from 2.25 to 4 m/sec, the maximum cortical deformation was 1, 2, or 3 mm, the impact angle ranged from 23° lateral to vertical, and impactor diameters were 2.5 or 5 mm. Contusion volumes were measured at 7, 8, or 14 days post-injury. Simulation results indicated that the peak maximum principal strain (MPS) with a threshold of 0.30 best correlated with experimentally-obtained contusion volumes when compared to intracranial pressure or shear strain.
Studies by Scheff and co-workers (1997), and Chen and colleagues (2003), also found neuronal losses in some anatomical regions, such as the hippocampus and thalamus. However, quantitative information related to the spatial locations of these neuronal losses was not provided. Consequently, the study reported by Mao and associates (2006) did not address neuronal cell losses in the hippocampus and thalamus. Recently, Igarashi and associates (2007) obtained data from histological sections after mild, moderate, or severe CCI injuries to the rodent brain, and published the percentages of neuronal cell loss, along with detailed spatial information in five regions. As might be expected, the percentage of neuronal cell loss was the highest for the “severe” injury group. Of interest was the fact that neuronal cell loss was also detected in the Purkinje cell layer of the vermis, a structure that is relatively remote from the site of the CCI injury. These experimental data are valuable for numerical study aimed at identifying the biomechanical injury threshold for neuronal cell loss. The purposes of the current study were to numerically investigate intracranial tissue strains for the same five brain regions due to mild, moderate, and severe CCI, and to correlate these FE model-predicted biomechanical responses with in vivo injury data to establish the relationship between tissue-level strains and cellular injuries.
Methods
The experimental study by Igarashi and associates
Details of the CCI injury, including the histological methods and assessments described by Igarashi and associates (2007) are briefly discussed. The authors used a 6-mm-diameter impactor with a convex tip to impact the exposed dural surface at a velocity of 4 m/sec. A total of 45 rats were assigned to four groups based on compression depth: 0 mm (sham controls, n = 4), 1.5 mm (mild injury, n = 10), 2.0 mm (moderate, n = 13), and 2.7 mm (severe, n = 18). Seven days after injury, the animal was sacrificed and its brain tissue was fixed before 40-μm-thick sections were prepared for histological evaluation at the superficial cortex, deep cortex, hippocampus CA2/CA3, laterodorsal thalamus, and cerebellar vermis on the ipsilateral side. The percentages of neuronal loss were quantified by means of markers. That used to detect neuronal loss in the forebrain was a mouse monoclonal antibody to vertebrate neuron-specific protein (NeuN; Chemicon, Temecula, CA). For Purkinje cell loss, rabbit anti-calbindin D-28 polyclonal antibody (calbindin; Chemicom), and anti-PEP-19, which is a rabbit polyclonal antibody recognizing a developmentally regulated-neuropeptide in Purkinje cells, were used. The extent of neuronal loss was quantified by calculating the ratio of dead cells over all cells counted using a Nikon microscope from three adjacent sections, consisting of the section with the maximal damage and one adjacent section on each side of it.
Finite element rat brain model by Mao and associates
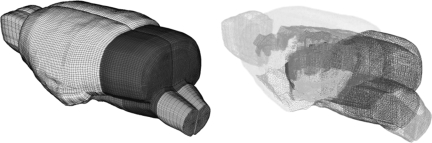
The same rat FE brain model developed by Mao and associates (2006) was used in the current study (Fig. 1). Brief descriptions of the model parameters and its previous applications are listed here for the sake of completeness. The brain was assumed to be a linear viscoelastic material (LS-DYNA Material Type 61) with a decay constant of 20 msec. For the cerebral gray matter, cerebellum, and brainstem, a short-term shear modulus of 1.72 kPa and a long-term shear modulus of 0.51 kPa were assumed. This assumption was based on combined in vitro and in situ indentation test results obtained from non-preconditioned adult rat brain as reported by Gefen and co-workers (2003). For the white matter, a short-term modulus of 1.2 kPa and a long-term modulus of 0.36 kPa were assumed. This assumption was based on measured material properties as reported by Prange and Margulies (2002). Additionally, the ventricles were assumed to have a short-term modulus of 1 kPa and a long-term modulus of 0.3 kPa, while the same parameters for the spinal cord were assumed to be 3.1 kPa and 0.92 kPa, respectively. For the pia-arachnoid membrane and dura mater, linear elastic material properties were assumed with a Young's modulus of 12.5 MPa (Jin et al., 2006) and 31.5 MPa (Galford and McElhaney, 1970), respectively.
FIG. 1.
The detailed finite element rat brain model developed by Mao and colleagues (2006).
Convergence study
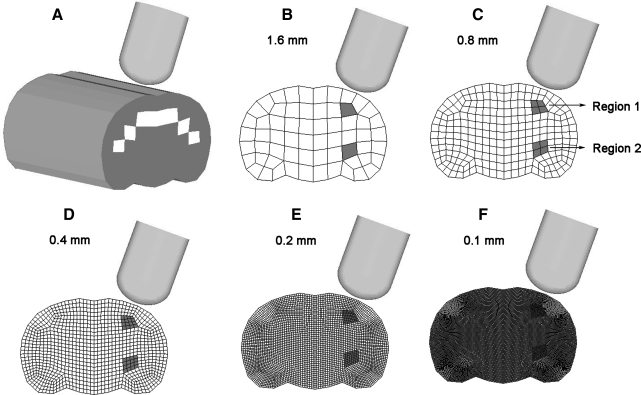
A mesh convergence study was conducted by extending a simplified 2D FE model, which represented the rat brain at 3.5 mm from the bregma, and 8 mm anteriorly and 8 mm posteriorly to form a simplified 3D FE model at a spatial resolution of 1.6 mm. At each mesh refinement step, every hexahedral element was subdivided into eight hexahedral elements. Altogether, five simplified 3D rat brain models with spatial resolution of 1.6, 0.8, 0.4, 0.2, and 0.1 mm were formed to determine the mesh density required to achieve reasonable convergence (Fig. 2). Material properties selected for these five models were the same as those of the gray and white matter used by Mao and colleagues (2006). The white color in Figure 2A shows the elements in which the white matter material properties were assigned. The exterior boundary of the brain was simulated using a layer of rigid shell elements to represent the dura mater and skull. The impactor used in the convergence study had the same shape and diameter as that used in the experimental study reported by Igarashi and associates (2007). The impact velocity was assumed to be 4.0 m/sec, with an impact depth of 2 mm, representing the moderate injury scenario as defined by Igarashi and colleagues (2007). The average MPS responses corresponding to the elements located in (1) Region 1 situated in the second mesh layer of the 1.6-mm-resolution model underneath the impactor (Fig. 2B), and (2) Region 2 located remote from the impactor, were selected to determine if convergence has been achieved based on these five FE models of different mesh densities.
FIG. 2.
Five simplified 3D controlled cortical impact models developed for the convergence study. The average finite element model-predicted maximum principal strain for the shaded elements was used to determine convergence. (A) Isometric view with white color indicating the white matter. (B–F) Coronal section meshes with spatial resolution of 1.6, 0.8, 0.4, 0.2, and 0.1 mm.
Finite element simulations and analysis
Three numerical simulations with an impact depth of 1.5, 2.0, and 2.7 mm, representing the mild, moderate, and severe impact conditions, respectively, were run. The material properties used for the rat brain were the same as those reported by Mao and colleagues (2006). The position and size of the craniotomy, along with the impactor size, impact velocity, direction, and distances were accurately defined according to the experimental settings in the cited publications (Fig. 3, left). The impactor tip was carefully meshed to represent the exact same convex shape as that used in the experiments (Fig. 3, right).
FIG. 3.
Isometric view (left) of the finite element simulation of controlled cortical impact, and a photo of the experimentally-used impactor (right).
Parametric studies
Four sets of parametric studies were conducted to determine the effect of different head size, decay constants for brain tissues, material properties of the white matter, and impact velocities. All simulations, except for cases with varying velocities in the parametric studies, were for a 7-mm-diameter craniotomy, a 2-mm impact depth, and an impact velocity of 4.0 m/sec. These parameters were used by Igarashi and associates (2007) to produce a moderate injury.
Head size
Ideally, a computational model should be developed to represent the exact size and shape of the animal head used in the experiments, to achieve more accurate prediction of internal tissue strains. However, the high costs associated with acquiring high-resolution CT and MR scans of each animal before the CCI, and of registering and segmenting these images to develop animal-specific FE models are prohibitive. The next best alternative would be to investigate the effect on intracranial responses of different head sizes. The rat brain model developed by Mao and colleagues (2006) represents an average adult rat with a weight of 290 g. According to Paxinos and Watson (2005), the head of a fully mature rat with a weight of 436 g is about 6–7% larger along the anterior-posterior and dorsal-ventral directions. Because the rats used in the cited experimental studies weighed between 340 and 400 g, it was reasonable to assume that a 7% increase in each of the three mutually perpendicular directions would be sufficient to cover the largest possible head size used in the experiments. Hypermesh software (Altair, Troy, MI) was used to geometrically morph the head in the Mao model into a new larger head model with a 7% increase in size in all three directions.
Decay constant
Four additional simulations were conducted to address the effect of different relaxation decay constants, which represented 25% (5 msec), 50% (10 msec), and 200% (40 msec) of the values used by Mao and associates, and a less viscous configuration of an 8-sec decay constant used by Levchakov and colleagues (2006), which was based on experimental data at an impact velocity of 1 mm/sec, with a hold time of 90–160 sec, as reported by Gefen and co-workers (2003).
White matter material property
The effect of relative stiffness of the gray and white matters was studied by assuming the shear modulus of the white matter to be 100% (homogeneous brain), and 125% of that of the gray matter. The selection of a stiffer white matter was based on the study by Arbogast and Margulies (1997) in which the porcine white and gray matters were tested and compared.
Impact velocity
To understand the effect of increasing impact velocity, two additional simulations at an impact velocity of 6 and 8 m/sec were conducted using the original Mao model. The moderate injury experimental set-up, including a 7-mm craniotomy and a 2-mm impact depth, was used.
Data analysis
All simulations were limited to 3 msec. At an impact velocity of 4 m/sec, the impactor tip reached its maximum depth of 2.7 mm (in the severe injury group) in 0.675 msec. Thus, a simulation time of 3 msec is sufficient to examine the peak strain values and subsequent viscous responses. All nodal displacements were calculated using LS-DYNA (LSTC, Livermore, CA) version 971, and output at a frequency of 10 kHz before the element strain tensor was calculated at each time step from the strain-displacement relationship. The MPS was selected as the principal response variable because previous investigations have shown that regions with higher MPS correlated well with experimentally measured contusion volumes (Mao et al., 2006). Furthermore, Mao (2009) showed that it was the peak MPS and not volumetric pressure or shear strain in the coronal section where histology was evaluated, that correlated with the location and shape of the contusion observed experimentally at 24 h post-injury, as reported by Elliott and associates (2008).
At each time step, the principal strain vector was calculated by rotating the element strain tensor until all shear strain components vanished. The MPS is the maximal value of the principal strain that corresponded to stretching of the tissue. MPS time histories for all elements within the five regions of interest (ROI) used in the cited experimental study (Fig. 4A–D) were output to an Excel (Microsoft Inc. Redmond, WA) file. Because rectangle-shaped elements do not always coincide with the boundaries of the ROI, it was decided that elements with 50% or more of their volume situated within the ROI should be included for MPS calculation. At each time step, the regional MPSs in all five ROI were obtained by averaging the MPSs for all elements within each ROI. Finally, the peak regional MPSs were calculated and used for correlation with the percentage of neuronal cell loss observed experimentally for all injured animals. The corresponding model-predicted regional tissue MPSs were then plotted against the percentage of neuronal loss, including the mean values and standard deviations. As an example, the MPSs predicted by the model for the superior cortex (SC) under moderate CCI were correlated against raw data of neuronal loss percentage in the SC region for all animals in the moderate injury group.
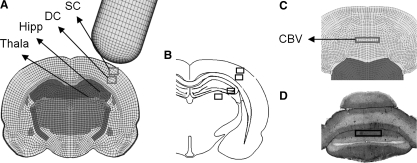
FIG. 4.
Five brain regions (SC, superior cortex; DC, deep cortex; Hipp, hippocampus CA2/CA3; Thala, laterodorsal thalamus; CBV, cerebellar vermis) were investigated for biomechanical response and neuronal loss. The regions investigated are the rectangular blocks shown in (A) and (C) for finite element simulations, and (B) and (D) for the experimental investigations.
Linear regression was performed between the experimentally-observed percentage of neuronal loss, and the model-predicted MPSs for all ROI. Additionally, cell losses for the cortex and hippocampus due to biaxial loading of the in vivo–like coronal brain sections reported by Cater and associates (2006), and Elkin and colleagues (2007), were compared with those found in the current study. In their studies, regressions were conducted to relate the cell loss to lagrangian strains. In order for the results from the current study to be directly comparable, MPS was converted to lagrangian strain according to Eq. 1, based on the 2D equi-axial loading scheme reported by Morrison and co-workers (2003). The cell loss percentage can then be calculated from lagrangian strain using the cell-loss-to-lagrangian-strain relationship proposed by Cater and associates (2006) and Elkin and colleagues (2007). The equations derived by Cater and associates (2006) and Elkin and co-workers (2007) at 4 days post-injury, the longest post-injury duration used in their in vivo–like experiments, were applied to calculate the percentage of cell loss.
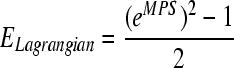 |
(1) |
Results
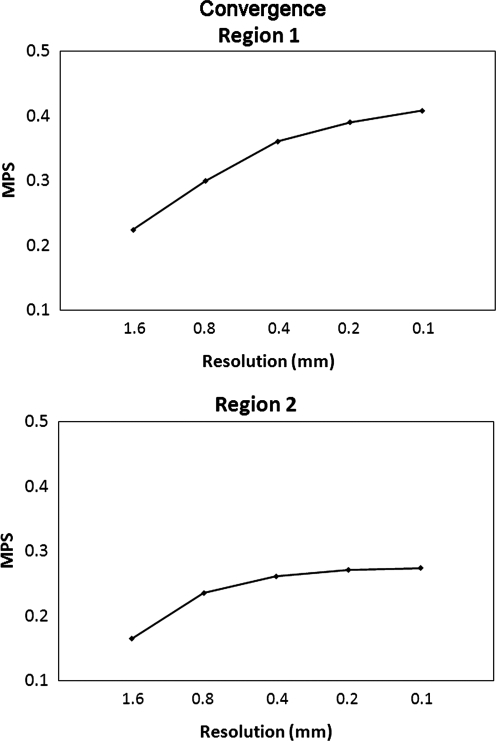
The run times were around 30 sec, 3 min, 39 min, 10 h, and 139 h for 3 msec of simulation time, using the 1.6, 0.8, 0.4, 0.2, and 0.1 mm mesh sizes, respectively, on a two AMD Opteron™ Processor 250 workstation with a clock speed of 2.4 GHz. The run time for simulations with the 3D rat brain FE model was around 40 h with same computational power. As expected, the average regional MPS increased as the mesh size decreased. However, the continued decrease in element size resulted in less and less variation in the average MPS value. For example, the difference between the 1.6-mm and 0.8-mm spatial resolution models was 33.9%, but the difference between the 0.2-mm and 0.1-mm resolution model was only 4.4% for Region 1 (Fig. 5). Similarly, the differences were 42.7% and 1.1% for the same levels of resolution for Region 2, respectively. These results indicated that a model with 200-μm spatial resolution reasonably balanced computational accuracy and efficiency. At this resolution, model-predicted results differed from the model with eight times the number of elements by less than 5% MPS in a region underneath the impactor, and by a much smaller amount in a region away from the impact, at a computational cost of only 7.2% of that for the 100-μm resolution model.
FIG. 5.
The average maximum principal strain (MPS) predicted by five simplified controlled cortical impact models at the region of interest as a function of finite element model spatial resolution.
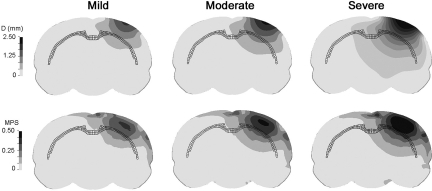
Resultant displacement and MPS contours, on a coronal plane beneath the center of the impactor at the time of maximum tip displacement, are shown in Figure 6 for all three injury severities. As expected, the area beneath the impactor center had the highest displacement, and it gradually dissipated in radial directions. The high-MPS region traveled from the cortical layer into deeper regions in an ellipsoidal shape. Most of the highest MPSs appeared in the cortical layers above the corpus callosum, which is highlighted by dark mesh in Figure 6. For all three injury severities simulated, most of the high MPSs were limited to the ipsilateral hemisphere.
FIG. 6.
Resultant displacement and maximum principal strain contours at the time of maximum compression. The corpus callosum is highlighted as dark mesh.
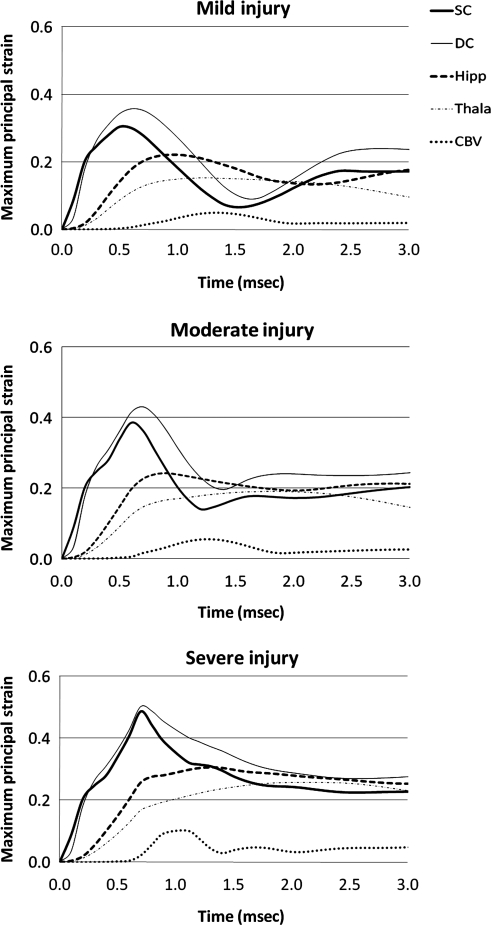
Examination of MPS time histories for all ROI revealed that the peak values occurred well within the 3-msec simulation time. For the cortical mantle, the deep cortex experienced higher MPSs than the superficial cortex by 17.4%, 11.8%, and 3.3%, for the simulation of mild, moderate, and severe injury, respectively (Fig. 7). The severe injury group had the least difference, probably because there was less space for the tissue to displace into. Brain tissues in the hippocampal region experienced higher peak MPSs than those in the thalamic region by 30.3 ± 13.2% for all three injury severities. As expected, the cerebellum region had the least MPS because it was farthest removed from the impact site (Fig. 7).
FIG. 7.
Time histories of the finite element model–predicted average maximum principal strains at the five selected regions of interest (SC, superior cortex; DC, deep cortex; Hipp, hippocampus CA2/CA3; Thala, laterodorsal thalamus; CBV, cerebellar vermis).
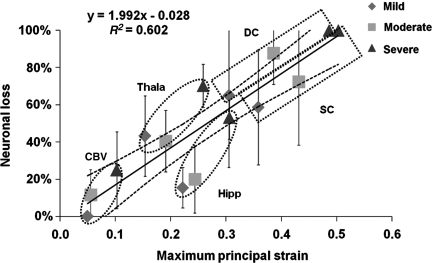
The experimentally-observed percentages of neuronal loss at 7-days post-injury for all five ROI were then plotted against model-predicted region-specific tissue MPSs (Fig. 8). Linear regression revealed an R2 value of 0.602. The slope of the regression line was significantly different from zero (p < 0.001).
FIG. 8.
Correlation between neuronal loss and maximum principal strain with standard deviations. Each data point represents the finite element (FE) model-predicted MPS, and the percentage of neuronal loss for a specific region, due to mild, moderate, or severe impact (SC, superior cortex; DC, deep cortex; Hipp, hippocampus CA2/CA3; Thala, laterodorsal thalamus; CBV, cerebellar vermis).
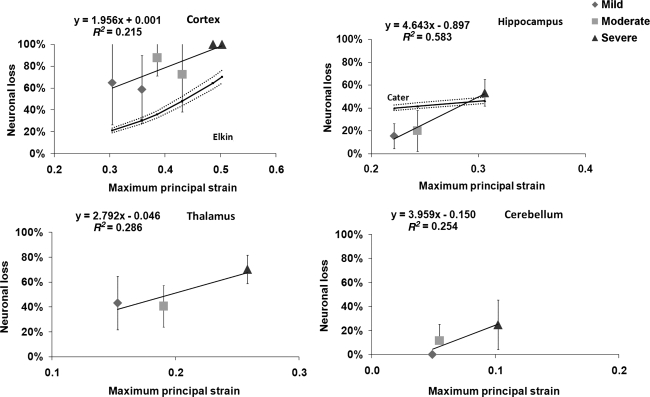
Linear regressions were also performed to calculate region-specific relationships between the percentage of cell loss and model-predicted MPSs (Fig. 9). None of these regression analyses had an R2 value greater than 0.6. The same figure also shows neuronal cell losses in the cortical region using the equation proposed by Elkin and associates (2007), and in the hippocampus region using the equation proposed by Cater and colleagues (2006). Strain rates for cortex elements were in the range of 1150–1450 sec–1. Note that these in vivo-like histological data were evaluated at 1-day intervals for up to a maximum of 4 days. It seemed that the injury tolerance calculated using the FE model for the cortex was lower than Elkin's data (i.e., more injuries were seen). The slope of the neuronal loss versus MPS curve found in this study for the hippocampal region was much steeper, but the range was comparable to that reported by Cater and co-workers (2006). Cell losses as a function of strain in the thalamus and cerebellum do not appear to have been reported in the literature.
FIG. 9.
Linear regression curves between neuronal loss and finite element model-predicted maximum principal strains for the cortex, hippocampus CA2/CA3, thalamus, and cerebellar vermis, are shown for all three injury severities. Error bars indicate the standard deviation in the experimental data reported by Igarashi and colleagues (2007). Calculated cell losses at the cortex reported by Elkin and associates (2007), and at the hippocampus reported by Cater and associates (2006) are also included in this figure.
Figure 10 shows strain contours at 1-mm intervals at the time point when the impactor just reached its maximum penetration. While there were no histological data available for comparison to the 3D strain maps calculated in this study, such data may be useful for comparison with detailed histological analyses or high-resolution magnetic resonance imaging in the future.
FIG. 10.
Strain contours at the time of maximum compression for the three injury severities.
Compared to results obtained from the average adult rat model, simulations of a fully mature rat brain resulted in a maximum reduction of less than 8%, and an average reduction of 4.1%, in the regional MPSs for all three impact severities (Table 1). However, the absolute difference in MPS never exceeded 0.025. The small difference found in this parametric study indicates that brain size is not a significant factor affecting FE model-predicted MPSs during CCI.
Table 1.
Regional Maximum Principal Strains Predicted by Finite Element Models of an Average Adult Rat and a Fully Mature Rat for All Three Impact Severities
| Impact depth (mm) | Average adult | Fully mature | |
|---|---|---|---|
| Superior cortex | 1.5 | 0.3049 | 0.2907 (−4.7%) |
| 2.0 | 0.3856 | 0.3702 (−4.0%) | |
| 2.7 | 0.4863 | 0.4615 (−5.1%) | |
| Deep cortex | 1.5 | 0.3580 | 0.3418 (−4.5%) |
| 2.0 | 0.4310 | 0.4190 (−2.8%) | |
| 2.7 | 0.5026 | 0.4969 (−1.1%) | |
| Hippocampus | 1.5 | 0.2213 | 0.2163 (−2.3%) |
| 2.0 | 0.2432 | 0.2389 (−1.8%) | |
| 2.7 | 0.3059 | 0.2387 (−7.3%) | |
| Thalamus | 1.5 | 0.1531 | 0.1505 (−1.7%) |
| 2.0 | 0.1903 | 0.1752 (−7.9%) | |
| 2.7 | 0.2582 | 0.2425 (−6.1%) | |
| Cerebellar vermis | 1.5 | 0.0491 | 0.0468 (−4.7%) |
| 2.0 | 0.0547 | 0.0535 (−2.3%) | |
| 2.7 | 0.1022 | 0.0970 (−5.1%) |
Data in parentheses are the percentage differences.
Compared to the peak MPSs predicted by the baseline FE model with a decay constant of 20 msec, peak MPSs predicted by the FE models with 5, 10, or 40 msec decay constants never exceeded a difference of 2% (Table 2). When the decay constant was increased to 8 sec, the model-predicted peak MPSs decreased between 8.7% and 16.0% for the five ROI. The shear modulus of brain material remained high (i.e., little or no decay) during the simulation period of 3 msec when using a long 8-sec decay constant. As a result, the MPSs were lower compared to the baseline model. The fast decay time of less than 100 msec was reported for brain material testing with shear displacement rates of up to 0.4 m/sec (Takhounts et al., 2003). Since the simulated impact speed was 4 m/sec, the slow decay observed by Gefen's group (2003), with a loading rate of 0.001 m/sec, may not be appropriate for the current study.
Table 2.
Peak Maximum Principal Strains Predicted by Finite Element Models with a Decay Constant of 20 msec (baseline model), and 5, 10, and 40 msec, and 8 sec
| Baseline (20 msec) | 5 msec | 10 msec | 40 msec | 8 sec | |
|---|---|---|---|---|---|
| Superior cortex | 0.3856 | 0.3856 (0.0%) | 0.3865 (0.2%) | 0.3856 (0.0%) | 0.3405 (−11.7%) |
| Deep cortex | 0.4310 | 0.4311 (0.0%) | 0.4318 (0.2%) | 0.4307 (−0.1%) | 0.3815 (−11.5%) |
| Hippocampus | 0.2432 | 0.2432 (0.0%) | 0.2433 (0.0%) | 0.2431 (−0.1%) | 0.2117 (−13.0%) |
| Thalamus | 0.1903 | 0.1875 (−1.5%) | 0.1895 (−0.4%) | 0.1912 (0.5%) | 0.1598 (−16.0%) |
| Cerebellum vermis | 0.0547 | 0.0546 (−0.2%) | 0.0547 (−0.0%) | 0.0547 (0.0%) | 0.0500 (−8.7%) |
Numbers in parentheses indicate the percentage differences compared to those of the baseline model.
Simulations with stiffer properties of the white matter demonstrated that MPSs were higher in the hippocampus and thalamus compared to the baseline model, but lower in the superior cortex, deep cortex, and cerebellum (Table 3). The differences among the more compliant baseline model, homogeneous model, and stiffer white matter model were below 4%.
Table 3.
Peak Maximum Principal Strains Predicted by the Baseline Model with a More Compliant White Matter (WM 0.7), a Homogeneous Model (WM 1.0), and a Stiffer White Matter Model (WM 1.25)
| Baseline (WM 0.70) | WM 1.0 | WM 1.25 | |
|---|---|---|---|
| Superior cortex | 0.3856 | 0.3853 (−0.1%) | 0.3858 (0.1%) |
| Deep cortex | 0.4310 | 0.4300 (−0.2%) | 0.4286 (−0.6%) |
| Hippocampus | 0.2432 | 0.2483 (2.1%) | 0.2517 (3.5%) |
| Thalamus | 0.1903 | 0.1919 (0.9%) | 0.1973 (3.7%) |
| Cerebellum vermis | 0.0547 | 0.0545 (−0.5%) | 0.0546 (−0.2%) |
Numbers in parentheses indicate the percentage differences when compared to those of the baseline model.
A 100% increase in impact velocity produced a 26.7% increase in the peak MPSs in the superior cortex, 19.5% in the deep cortex, and 20.2% in the hippocampus, but only a 9% increase in the thalamus (Table 4). A 50% increase of impact velocity produced much lower increases, with 13.7% in the superior cortex, 12.2% in the deep cortex, 8.5% in the hippocampus, and 1.2% in the thalamus. On the other hand, increasing the impact depth from 2 to 2.7 mm (a 35% increase) increased the MPSs in the superior cortex by 26.1%, the deep cortex by 16.6%, and the hippocampus by 25.8%, but the increase in MPSs for the thalamus was 35.7%. Percentage changes in the cerebellum are not discussed because the peak MPS predicted by the baseline model was so small that any variations would result in large percentage differences. These data also suggest that changing the impact depth is more effective than changing the impact velocity when trying to alter the CCI-induced intracranial responses.
Table 4.
Comparison of Maximum Principal Strains for the Simulations of the Mild Injury Group, the Severe Injury Group, and 6- and 8-m/sec Impact with 2-mm Impact Depth to the Baseline Model
| Baseline(2 mm, 4 m/sec) | Mild(1.5 mm, 4 m/sec) | Severe(2.7 mm, 4 m/sec) | New case 1(2 mm, 6 m/sec) | New case 2(2 mm, 8 m/sec) | |
|---|---|---|---|---|---|
| Superior cortex | 0.3856 | 0.3049 (−20.9%) | 0.4863 (26.1%) | 0.4383 (13.7%) | 0.4886 (26.7%) |
| Deep cortex | 0.4310 | 0.3580 (−16.9%) | 0.5026 (16.6%) | 0.4835 (12.2%) | 0.5149 (19.5%) |
| Hippocampus | 0.2432 | 0.2213 (−9.0%) | 0.3059 (25.8%) | 0.264 (8.5%) | 0.2923 (20.2%) |
| Thalamus | 0.1903 | 0.1531 (−19.5%) | 0.2582 (35.7%) | 0.1925 (1.2%) | 0.2074 (9.0%) |
| Cerebellum vermis | 0.0547 | 0.0491 (−10.2%) | 0.1022 (86.6%) | 0.0628 (14.8%) | 0.0758 (38.4%) |
Discussion
There is general agreement that CCI is a focal injury model with contusion concentrated in the region beneath the impactor (Dixon et al., 1991, Kochanek et al., 1995). On the other hand, some investigators have reported that CCI is more than a focal injury model (Hall et al., 2007). The experimental studies cited in the current study also revealed that the extent of neuronal cell loss varied greatly, depending on the region investigated. In other words, graded injuries within the same brain could be created under one CCI condition. The MPS contours shown in Figures 6 and 10 demonstrate that the ipsilateral cortical regions had the highest MPSs, but other regions also experienced elevated MPSs. The same finding of a graded strain pattern was also reported by Levchakov and associates (2006), based on numerical simulations of a closed-head impact. The much lower MPS responses seen in the contralateral hemisphere seem to qualitatively agree with experimental reports that most injuries were confined to the ipsilateral hemisphere in unilateral craniotomy CCI experiments (Kochanek et al., 1995; Sutton et al., 1993). High MPSs in the contralateral cortex were induced only under conditions in which bilateral craniotomies were performed (Mao et al., 2006). Results from these experimental and numerical investigations suggest that intracranial tissue responses are more critical than external impact parameters, because tissue responses are directly linked to site-specific brain injury. King and colleagues (2003) also demonstrated that external parameters (such as linear and angular acceleration) are less predictive of mild TBI than intracranial responses.
For the cerebellar region, which is remote from the impact site, the FE brain model also predicted an MPS of 10% for the “severe” impact scenario (Fig. 7). As speculated by Igarashi and co-workers (2007), the cerebellar damage seen was likely due to a primary mechanical injury, because there was no overt fiber degeneration associated with the cerebellum (Igarashi et al., 2007). However, it is possible that fiber degeneration did occur, but could not be detected at 7 days post-injury. Nevertheless, our model indicates a probable effect of cerebellar neuronal loss due to direct tissue stretch.
Based on results from the current study, it can be hypothesized that for every 1% increase in MPS there is an accompanying 2% increase in cell loss (Fig. 8). More experiments need to be conducted to test the validity of this hypothesis. Mao and associates (2006) found that an MPS threshold of 30% correlated well with the contusion volumes observed experimentally by four different laboratories. It seemed that 60% cell loss in the cortex was related to experimentally-observed contusion. However, readers should be aware that the current study utilized histological data collected at 7 days post-injury. In the experimental studies used to derive the contusion threshold, the contusion volumes were measured at 7–14 days post-injury, while neuronal cell loss data in the current study were collected at 7 days post-injury. Future studies should emphasize the effect of post-injury time on the progression of TBI. Another issue could be biological variations. As an example, the superior cortex in the mild injury case had neuronal loss varying from 25–100% as reported by Igarashi and colleagues (2007), thus making it difficult to derive an accurate relationship between the extent of cell loss and contusion.
Although FE models are the best means to study intracranial responses at present, this method has several significant limitations. First, there is a paucity of experimental data on the material properties of different anatomical structures within the brain, and even fewer biomechanical data for validating FE model predictions. The brain deformations measured by Bayly and associates (2006) using magnetic resonance imaging are not relevant, because both the spatial and temporal test parameters were too low for direct comparison with the current study. The FE model used in the current study was validated against experimentally-observed cortical deformation data by Schreiber and colleagues (1997), as no other brain deformation data were available. Hence, the biofidelity of the FE model is limited and may affect the accuracy of its predictions. Still, results from parametric studies suggest that the mesh employed converged within a reasonable limit. Additionally, using one set of FE geometry to represent the various sizes of rats used experimental studies, and the use a more compliant or stiffer white matter, did not significantly change the model-predicted MPSs. Zhou and colleagues (1994) found high shear stresses at the boundaries between the white and gray matter in their porcine heterogeneous brain model subjected to a pure rotational impact. Such stress concentrations were not present when a homogeneous brain model was used. The CCI studies simulated in the current investigation resulted in predominantly linear head accelerations. Therefore, the effect of assigning heterogeneous shear properties in this simulation of CCI could be different than that observed in rotational impact. Overall, the FE model used in the current study is deemed adequate for this investigation.
A second limitation is related to the unavailability of in vivo region-specific injury mechanism and its associated threshold. For this reason, in this study we assumed that the peak MPS is the injury mechanism that correlates with the percentage of neuronal cell loss. A linear relationship was found between these two parameters when we combined data from all five ROI, but it was not found in the regression for each intracranial region. This is in part because each FE simulation resulted in only a single MPS value for each ROI. Thus, only three data points, representing three injury severities, were generated by the FE model for regression analyses. More experimental impact severities should be conducted and the resulting injuries examined in more regions in order to refine the use of the FE brain model to predict regional risk of injuries. Nevertheless, the current work showed a lower injury tolerance for the cortex than the hippocampus, for example, a 30% MPS induced a loss of 59% cells in the cortex region, but a 50% loss in the hippocampus region (Fig. 9). This contradicted the results reported for in vivo-like cultured rat brain studies conducted by others ( Elkin and Morrison, 2007; Geddes et al., 2003; Morrison et al., 2003). Some possible explanations include: (1) strain rates were higher (100–1450 sec–1) in the CCI tests than in the in vivo-like studies (<150 sec–1), and the relationship between strain rate and tissue injury remains unclear [Cater and colleagues (2006) found that cell loss in the hippocampus was independent of strain rate, but Elkin and associates (2007) reported that the strain rate was important for predicting cell death in the cortex]; (2) the FE model calculated stretching of the brain tissue in planes that were perpendicular to the impact direction (Fig. 11), that is, out of the coronal plane [on the contrary, tissues from in vivo-like studies were stretched within the coronal plane, and further studies are needed to determine if cell death is directionally dependent]; and (3) cell death was evaluated on day 7 post-injury for the current study, and on the day 4 post-injury for the in vivo-like studies [more cell losses might occur if the brain slices could be kept viable for a longer period (Cater et al., 2006; Elkin and Morrison, 2007; Morrison et al., 2003).
FIG. 11.
Directions of principal strain in five elements in the cortex under the impactor. The first (maximum) principal strain and second principal strain are tensile; the third principal strain is compressive.
A third limitation is the fact that FE models can only be used to predict injuries that are directly related to mechanical loading, and not the result of excitotoxicity. The vulnerability of the hippocampus is at least partially attributable to three factors: (1) direct mechanical damage (Cater et al., 2006; Geddes et al., 2003; Morrison et al., 2003; Toth et al., 1997), (2) blood–brain barrier breakdown (Schmidt and Grady, 1993), and (3) excitotoxicity (Di et al., 1999; Lowenstein et al., 1992; Zanier et al., 2003). Since damage to the blood–brain barrier has been directly associated with tissue-level strains (Shreiber et al., 1997), excitotoxicity is the only mechanism that cannot be addressed by FE modeling. More studies are needed to determine if excitotoxicity-associated TBI can be studied by other means.
A fourth limitation is that the current FE model does not have sufficient resolution to study sub-regional injuries. In the hippocampus, the CA3 region was observed to have more injuries than the CA1 region, due to CCI (Anderson et al., 2005; Kim et al., 2001). However, Cater and colleagues (2006) reported that cell death tolerance for the CA1 and CA3 regions were similar. To study these contradictory effects, a much more refined FE model will be needed to accurately represent major sub-regions within the brain. It is estimated that a spatial resolution of 60 μm is needed, compared to the current resolution of 200 μm. This means that nearly 30 times the current number of elements will be needed if the same high mesh quality is maintained. Unfortunately, this refinement will require enormous computing power that is not practical at present, but it may become attainable as computational technology improves.
A fifth limitation is that the mesh convergence study was performed on models stretched from one 2D coronal section into 3D. This simplification was warranted because the effort needed for a more thorough convergence study, that includes the detailed complex 3D anatomy of a rat brain, would be enormous during the model development processes. The reason that Pena and associates (2005), Shreiber and colleagues (1997), and Levchakov and co-workers (2006), did not report convergence study may also be related to this limitation. Nevertheless, the model used in the current study consists of 255,700 hexahedral elements, which was approximately seven times more than the model reported by Shreiber and colleagues (1997), and more than eight times that of Levchakov's (2006) group, and represents the current state of the art. When more computational power becomes available, a convergence study using a complex 3D rat brain model with much finer resolution, such as 100 or 50 μm, will become possible.
Even with all aforementioned limitations, the results of the current study identified a critical area for future investigations: a smaller tissue stretch was found for the thalamus than for the hippocampus (Fig. 7). However, the experimentally-observed neuronal loss was greater for the thalamic region than for the hippocampus, for all injury scenarios (Fig. 8). One possible explanation is that neurons in the thalamus are more vulnerable to mechanical insult (i.e., they have a lower injury threshold). The other likely mechanism for increased thalamic injury is target deprivation (Conti et al., 1998). This means that thalamic neurons that project into the cortex may die because they lose their “target” in the cortex. Degeneration of thalamocortical axons, as the cortical lesion matures, may initiate neuronal loss (Igarashi et al., 2007). Further investigation of thalamic neuronal damage as a result of direct mechanical insult or axonal degeneration is warranted.
In summary, a detailed 3D FE rat brain model was successfully used to predict intracranial tissue strains on the brain for a graded CCI. The regional intracranial MPSs were found to correlate well with in vivo findings of neuronal cell death. More research is recommended to investigate other regions for which we have no injury data, to improve the correlation with FE model predictions. The advantage of FE modeling of the rat brain lies in its capability to predict internal tissue responses of the entire rat brain, not only for different severities of CCI, but also for other experimental brain injury models, such as weight drop, fluid percussion, or blast injury models. In the future, the application of the current FE brain model for investigating injury mechanisms, as well as quantitative descriptions of the extent of brain trauma, should be further explored.
Acknowledgment and Author Disclosure Statement
This study was supported in part by grants NS046389 and NS050159 from the National Institute of Neurological Disorders and Stroke.
References
- Anderson K.J. Miller K.M. Fugaccia I. Scheff S.W. Regional distribution of fluoro-jade b staining in the hippocampus following traumatic brain injury. Exp. Neurol. 2005;193:125–130. doi: 10.1016/j.expneurol.2004.11.025. [DOI] [PubMed] [Google Scholar]
- Arbogast K.B. Margulies S.S. Regional differences in mechanical properties of the porcine central nervous system. Proc 41 Stapp Car Crash Conference, SAE Paper No. 973336; Warrendale, PA: Society of Automotive Engineers; 1997. [Google Scholar]
- Bayly P.V. Black E.E. Pedersen R.C. Leister E.P. Genin G.M. In vivo imaging of rapid deformation and strain in an animal model of traumatic brain injury. J. Biomech. 2006;39:1086–1095. doi: 10.1016/j.jbiomech.2005.02.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cater H.L. Sundstrom L.E. Morrison B., 3rd Temporal development of hippocampal cell death is dependent on tissue strain but not strain rate. J. Biomech. 2006;39:2810–2818. doi: 10.1016/j.jbiomech.2005.09.023. [DOI] [PubMed] [Google Scholar]
- Chen S. Pickard J.D. Harris N.G. Time course of cellular pathology after controlled cortical impact injury. Exp. Neurol. 2003;182:87–102. doi: 10.1016/s0014-4886(03)00002-5. [DOI] [PubMed] [Google Scholar]
- Conti A.C. Raghupathi R. Trojanowski J.Q. McIntosh T.K. Experimental brain injury induces regionally distinct apoptosis during the acute and delayed post-traumatic period. J. Neurosci. 1998;18:5663–5672. doi: 10.1523/JNEUROSCI.18-15-05663.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Di X. Gordon J. Bullock R. Fluid percussion brain injury exacerbates glutamate-induced focal damage in the rat. J. Neurotrauma. 1999;16:195–201. doi: 10.1089/neu.1999.16.195. [DOI] [PubMed] [Google Scholar]
- Dixon C.E. Clifton G.L. Lighthall J.W. Yaghmai A.A. Hayes R.L. A controlled cortical impact model of traumatic brain injury in the rat. J. Neurosci. Methods. 1991;39:253–262. doi: 10.1016/0165-0270(91)90104-8. [DOI] [PubMed] [Google Scholar]
- Elkin B.S. Morrison B., 3rd Region-specific tolerance criteria for the living brain. Stapp Car Crash J. 2007;51:127–138. doi: 10.4271/2007-22-0005. [DOI] [PubMed] [Google Scholar]
- Elliott M.B. Jallo J.J. Tuma R.F. An investigation of cerebral edema and injury volume assessments for controlled cortical impact injury. J. Neurosci. Methods. 2008;168:320–324. doi: 10.1016/j.jneumeth.2007.10.019. [DOI] [PubMed] [Google Scholar]
- Galford J.E. McElhaney J.H. A viscoelastic study of scalp, brain, and dura. J. Biomech. 1970;3:211–221. doi: 10.1016/0021-9290(70)90007-2. [DOI] [PubMed] [Google Scholar]
- Geddes D.M. LaPlaca M.C. Cargill R.S., 2nd Susceptibility of hippocampal neurons to mechanically induced injury. Exp. Neurol. 2003;184:420–427. doi: 10.1016/s0014-4886(03)00254-1. [DOI] [PubMed] [Google Scholar]
- Gefen A. Gefen N. Zhu Q. Raghupathi R. Margulies S.S. Age-dependent changes in material properties of the brain and braincase of the rat. J Neurotrauma. 2003;20:1163–1177. doi: 10.1089/089771503770802853. [DOI] [PubMed] [Google Scholar]
- Igarashi T. Potts M.B. Noble-Haeusslein L.J. Injury severity determines Purkinje cell loss and microglial activation in the cerebellum after cortical contusion injury. Exp. Neurol. 2007;203:258–268. doi: 10.1016/j.expneurol.2006.08.030. [DOI] [PubMed] [Google Scholar]
- Jin X. Lee J.B. Leung L.Y. Zhang L. Yang K.H. King A.I. Biomechanical response of the bovine pia-arachnoid complex to tensile loading at varying strain-rates. Stapp Car Crash J. 2006;50:637–649. doi: 10.4271/2006-22-0025. [DOI] [PubMed] [Google Scholar]
- Kim B.T. Rao V.L. Sailor K.A. Bowen K.K. Dempsey R.J. Protective effects of glial cell line-derived neurotrophic factor on hippocampal neurons after traumatic brain injury in rats. J. Neurosurg. 2001;95:674–679. doi: 10.3171/jns.2001.95.4.0674. [DOI] [PubMed] [Google Scholar]
- King A.I. Yang K.H. Zhang L. Hardy W.N. Is head injury caused by linear or angular acceleration?. IRCOBI Conference; Lisbon, Portugal. 2003. [Google Scholar]
- Kochanek P.M. Marion D.W. Zhang W. Schiding J.K. White M. Palmer A.M. Clark R.S. O'Malley M.E. Styren S.D. Ho C. Dekosky S.T. Severe controlled cortical impact in rats: Assessment of cerebral edema, blood flow, and contusion volume. J. Neurotrauma. 1995;12:1015–1025. doi: 10.1089/neu.1995.12.1015. [DOI] [PubMed] [Google Scholar]
- Levchakov A. Linder-Ganz E. Raghupathi R. Margulies S.S. Gefen A. Computational studies of strain exposures in neonate and mature rat brains during closed head impact. J. Neurotrauma. 2006;23:1570–1580. doi: 10.1089/neu.2006.23.1570. [DOI] [PubMed] [Google Scholar]
- Lighthall J.W. Controlled cortical impact: A new experimental brain injury model. J. Neurotrauma. 1988;5:1–15. doi: 10.1089/neu.1988.5.1. [DOI] [PubMed] [Google Scholar]
- Lighthall J.W. Dixon C.E. Anderson T.E. Experimental models of brain injury. J. Neurotrauma. 1989;6:83–97. doi: 10.1089/neu.1989.6.83. [DOI] [PubMed] [Google Scholar]
- Lowenstein D.H. Thomas M.J. Smith D.H. McIntosh T.K. Selective vulnerability of dentate hilar neurons following traumatic brain injury: A potential mechanistic link between head trauma and disorders of the hippocampus. J. Neurosci. 1992;12:4846–4853. doi: 10.1523/JNEUROSCI.12-12-04846.1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mao H. Biomedical Engineering Department. Wayne State University; Detroit: 2009. Computational analysis of in vivo brain trauma. [Google Scholar]
- Mao H. Zhang L. Yang K.H. King A.I. Application of a finite element model of the brain to study traumatic brain injury mechanisms in the rat. Stapp Car Crash J. 2006;50:583–600. doi: 10.4271/2006-22-0022. [DOI] [PubMed] [Google Scholar]
- Morrison B., 3rd Cater H.L. Wang C.C. Thomas F.C. Hung C.T. Ateshian G.A. Sundstrom L.E. A tissue level tolerance criterion for living brain developed with an in vitro model of traumatic mechanical loading. Stapp Car Crash J. 2003;47:93–105. doi: 10.4271/2003-22-0006. [DOI] [PubMed] [Google Scholar]
- Paxinos G. Watson C. The Rat Brain in Stereotaxic Coordinates. Elsevier Academic Press; San Diego: 2005. [Google Scholar]
- Pena A. Pickard J.D. Stiller D. Harris N.G. Schuhmann M.U. Brain tissue biomechanics in cortical contusion injury: A finite element analysis. Acta Neurochir. Suppl. 2005;95:333–336. doi: 10.1007/3-211-32318-x_68. [DOI] [PubMed] [Google Scholar]
- Prange M.T. Margulies S.S. Regional, directional, and age-dependent properties of the brain undergoing large deformation. J Biomech Eng. 2002;124:244–252. doi: 10.1115/1.1449907. [DOI] [PubMed] [Google Scholar]
- Scheff S.W. Baldwin S.A. Brown R.W. Kraemer P.J. Morris water maze deficits in rats following traumatic brain injury: Lateral controlled cortical impact. J. Neurotrauma. 1997;14:615–627. doi: 10.1089/neu.1997.14.615. [DOI] [PubMed] [Google Scholar]
- Schmidt R.H. Grady M.S. Regional patterns of blood-brain barrier breakdown following central and lateral fluid percussion injury in rodents. J. Neurotrauma. 1993;10:415–430. doi: 10.1089/neu.1993.10.415. [DOI] [PubMed] [Google Scholar]
- Shreiber D.I. Bain A.C. Meaney D.F. In vivo thresholds for mechanical injury to the blood-brain barrier. Stapp Car Crash Conference, SAE Paper No. 973335; Warrendale, PA. 1997. [Google Scholar]
- Sutton R.L. Lescaudron L. Stein D.G. Unilateral cortical contusion injury in the rat: Vascular disruption and temporal development of cortical necrosis. J. Neurotrauma. 1993;10:135–149. doi: 10.1089/neu.1993.10.135. [DOI] [PubMed] [Google Scholar]
- Takhounts E.G. Crandall J.R. Darvish K. On the importance of nonlinearity of brain tissue under large deformations. Stapp Car Crash J. 2003;47:79–92. doi: 10.4271/2003-22-0005. [DOI] [PubMed] [Google Scholar]
- Toth Z. Hollrigel G.S. Gorcs T. Soltesz I. Instantaneous perturbation of dentate interneuronal networks by a pressure wave-transient delivered to the neocortex. J. Neurosci. 1997;17:8106–8117. doi: 10.1523/JNEUROSCI.17-21-08106.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zanier E.R. Lee S.M. Vespa P.M. Giza C.C. Hovda D.A. Increased hippocampal CA3 vulnerability to low-level kainic acid following lateral fluid percussion injury. J. Neurotrauma. 2003;20:409–420. doi: 10.1089/089771503765355496. [DOI] [PubMed] [Google Scholar]
- Zhou C. Khalil T.B. King A.I. Shear stress distribution in the porcine brain due to rotational impact. SAE 942214 1994 [Google Scholar]