Genomic biodiversity, phylogenetics, and coevolution in proteins

Abstract

Comprehensive sampling of genomic biodiversity is fast becoming a reality for some genomic regions and complete organelle genomes. Genomic biodiversity is defined as large genomic sequences from many species, and here some recent work is reviewed that demonstrates the potential benefits of genomic biodiversity for molecular evolutionary analysis and phylogenetic reconstruction. This work shows that using likelihood-based approaches, taxon addition can dramatically improve phylogenetic reconstruction. Features or dynamics of the evolutionary process are much more easily inferred with large numbers of taxa, and large numbers are essential for discriminating differences in evolutionary patterns between sites. Accurate prediction of site-specific patterns can improve phylogenetic reconstruction by an amount equivalent to quadrupling sequence length. Genomic biodiversity is particularly central to research relating patterns of evolution, adaptation and coevolution to structural and functional features of proteins. Research on detecting coevolution between amino acid residues in proteins demonstrates a clear need for much greater numbers of closely related taxa to better discriminate site-specific patterns of interaction, and to allow more detailed analysis of coevolutionary interactions between subunits in protein complexes. It is argued that parsing out coevolutionary and other context-dependent substitution probabilities is essential for discriminating between coevolution and adaptation, and for more realistically modelling the evolution of proteins. Also reviewed is research that argues for increasing the efficiency of acquiring genomic biodiversity, and suggests that this might be done by simultaneously shotgun cloning and sequencing genomic mixtures from many species. Increased efficiency is a prerequisite if genomic biodiversity levels are to rapidly increase by orders of magnitude, and thus lead to dramatically improved understanding of interactions between protein structure, function and sequence evolution.

Introduction

Dense sampling of genomic biodiversity will allow a dramatic and qualitative increase in our ability to understand evolutionary processes. The estimation of phylogenetic trees will also directly benefit from adding taxa and increasing sequence length, and will improve indirectly due to more biologically realistic models of evolution. The use of more realistic evolutionary models, particularly allowing different models among sites along a sequence, can dramatically increase the power of likelihood methods to accurately reconstruct phylogenetic relationships. Furthermore, accurate model estimation is known to decrease problems associated with long branch attraction, which can also confound phylogenetic estimation. When the evolutionary process varies among sites along a sequence, it is helpful to have large taxonomic samples to discriminate what process is operating at each site.

Variation in the evolutionary process reflects differences in structural and functional context, and therefore improved understanding of heterogeneity in the evolutionary process will undoubtedly improve our ability to understand the functional and structural causes of that heterogeneity, and the effect of changes in function (functional divergence) on the evolutionary process. An important component of changing structural context due to the evolutionary process is the changing amino acid composition among adjacent residues in the three dimensional structure. When substitution of one residue affects the evolution of other residues, the residues will, by definition, coevolve. Although coevolutionary processes in proteins are clearly quite complicated, their potential reflection of structural properties and of interactions between proteins makes understanding them extremely important. Ultimately, it is to be expected that analysis of the relationship between evolutionary dynamics and protein function will lead to improved utility of such analyses in predictions of protein function and protein interaction, ie functional genomics (Pellegrini et al 1999; Marcotte et al 1999a; Marcotte et al 1999b; Marcotte et al 2000).

Interactions between genomes and the environment can result in episodes of adaptation, coevolution among genes and altered rates of evolution. The timing and nature of such events can yield important clues to their cause, and to the nature of functional constraints and innovation. Deciphering the history of interactions between genomes and their environments, however, requires detailed analysis of extant genomes from a diversity of organisms over a range of divergence times. Here, we review a variety of studies by the author and others that detail some of the interactions between added taxonomic diversity and reconstructing phylogenies and complex evolutionary models. Higher-order model complexity involving interactions among sites is given particular attention, since this level of complexity is probably least explored and yet is critical to understanding protein evolutionary processes. Mitochondrial genomes are convenient densely-packed sets of functionally interacting coding sequences, and their value as a starting point for more detailed studies of adaptive coevolution and functional constraints is also considered.

What is genomic biodiversity?

The term ‘genomic biodiversity’ has been defined to describe a focus on analysing simultaneously genomes or genomic regions from large numbers of divergent taxa (Pollock et al 2000). Genomic diversity is a common description of studies that focus on intra-specific variation (usually in humans), and the word ‘biodiversity’ emphasises a concern for patterns of genome evolution well above the species level. Biodiversity is also a commonly used term in conservation biology, and its use is intended to convey the importance of the vast numbers of species that have not yet become extinct as an underutilised resource in genomic science. While biodiversity at deep levels is currently being explored by sequencing complete bacterial genomes, more closely related taxa are needed to evaluate important evolutionary processes that occur on shorter time scales. To understand human proteins, greater focus is needed on taxa closely related to humans, that is, on taxa that have a similar evolutionary environment.

Theoretical and computational studies reviewed below emphasise the importance of heavy sampling of genomic biodiversity to better understand evolutionary processes. Some results from these studies will of necessity be specific to the processes modelled. For example, the exact length of sequence required to obtain a specific probability of correct phylogenetic reconstruction will depend heavily on the phylogenetic structure of the tree and the exact details of how the sequences evolved. However, the qualitative conclusions are likely to be quite robust: denser taxonomic sampling is the best way to build more accurate and more complex evolutionary models, and since different processes occur at different rates, dense sampling should be obtained over a range of time scales. As dense taxonomic sampling is achieved in related groups, accurate comparative analysis of evolutionary processes will also become possible for complex models. It is reasonable to expect that each magnitude increase in the numbers of, for example, vertebrate mitochondrial genomes, will lead to dramatic changes in our perception of and ability to decipher evolution and coevolution in the proteins and RNA molecules encoded therein. There is strong motivation to rapidly increase the hundreds of genomes available today to thousands and tens of thousands or more, to realise the full potential of this kind of data.

Taxon addition and phylogenetics

An important and non-intuitive recent discovery in phylogenetics was the finding that adding taxa can be at least as important as increasing sequence length for improving phylogenetic accuracy (eg Hillis 1996; Hillis 1998). These studies indicated that datasets comprised of several thousand or tens of thousands of nucleotides (as opposed to hundreds of thousands) can be sufficient for accurate phylogenetic reconstruction of large numbers of taxa. Later studies have evaluated in detail the reasons why this is so (Graybeal 1998; Pollock and Bruno 2000; Pollock et al 2002; Zwickl et al 2002). To a computer scientist, it may appear that the problem is difficult because the number of possible phylogenies increases rapidly with the number of taxa. The difficulty of a perfect answer goes up superexponentially with more taxa, particularly with a constant length dataset and uniform rates among sites, mostly because the topological questions get harder. Every taxonomic addition also adds two new branches: one new branch leads to the new taxon, and another branch is split in two wherever the new taxon is attached to the old tree. This means that the number of possible trees also increases more rapidly than we would like, particularly considering that finding the optimal phylogenetic reconstruction is an NP complete problem (Garey and Johnson 1977; Graham and Foulds 1982; Day 1983; Day 1987).

These considerations are not the problem that they might at first appear to be. The success of many different phylogenetic methods in obtaining approximately correct answers is well known (Swofford et al 1996). Topological uncertainties are also generally local, meaning that not all phylogenetic possibilities need to be considered. Phylogenetic analyses find reasonable paths to approximately correct answers. In particular, recent developments in Bayesian and posterior predictive analysis allow incorporation of uncertainty in phylogenetic reconstruction without undue computational burden (Rannala and Yang 1996; Mau et al 1999; Larget 1999; Huelsenbeck 2000; Nielsen and Huelsenbeck 2002).

Another concern about the accuracy of phylogenetic reconstruction is that during speciation, different genes throughout the genome will acquire different phylogenetic histories due to sampling variation in the coalescent process (Hartl and Clark 1989). Thus, a single gene is but one instance of this process, and only an approximation to the species phylogeny. However, recent studies show that when phylogenies include a dense sampling of representative taxa, the correspondence between gene phylogenies can be quite high (Sheldon et al 2000; Murphy et al 2001; Madsen et al 2001), indicating that lack of resolution due to small datasets is currently a much greater constraint on predicting the species phylogeny than is variation among gene phylogenies.

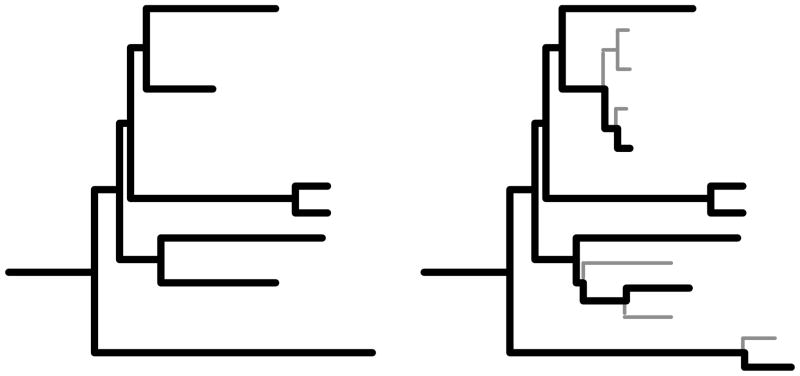
Consideration of the benefits of increased taxon sampling is confounded by the fact that branches on trees with more taxa are in principle more difficult to reconstruct, mostly because they are shorter (Figure 1). Every taxon added will split a branch on the existing tree. Thus, the more straightforward question to ask is how much an existing phylogeny can be improved through increased taxon sampling. This is done by determining how well the phylogeny for a set of species can be estimated using sequences from only those species, and comparing that to estimation in the presence of sequences from other species. In the latter case, a complete phylogeny is reconstructed for all the sequences, and then trimmed down to exclude those species outside the original set (Figure 1). In Pollock et al (2002), the difference in phylogenetic error between these two cases is taken as a proportion of the error in the existing phylogeny to obtain ΔE, the percent improvement due to taxon sampling. A convenient standard for comparison is often the improvement in reconstruction due to doubling the sequence length (eg Poe and Swofford 1999; Pollock and Bruno 2000; Pollock et al 2002).

Figure 1.

Graphic visualisation of taxon addition. In the tree on the right, the thin grey branches leading to the newly added tips tend to be shorter than the branches on the initial tree to the left. Branches on the initial tree that are split by the addition of new taxa are necessarily shorter. The effect of taxon addition is not confounded by the differences in branch lengths and placement if the accuracies of reconstructing the same initial tree (thick black) branches are considered in both trees.

If the evolutionary process is uncomplicated, the benefits of taxon addition can be viewed as largely due to an improvement in estimating the unknown states at internal nodes surrounding any branches in question. Changes must have occurred along that branch, they must be inferable after the passage of time, and they must be discriminated from apparent changes on competing incorrect topological arrangements. Thus, the precise benefits of taxon addition will depend on evolutionary rates, sequence length and details of the topology to be reconstructed. Benefits will vary depending on how added sequences are related to the initial sequences (Goldman 1998; Rannala et al 1998). The phenomenon of long-branch attraction (LBA), a bias towards preferential clustering of long versus short branches, can also lead to incorrect results in sparsely sampled trees (Felsenstein 1978; Hendy and Penny 1989), but the effects of LBA are greatly reduced by the use of maximum likelihood (ML) or Bayesian methods rather than parsimony (Bruno and Halpern 1999). It is also clear that parsimony is less efficient than ML at improving topology reconstruction with taxon addition (Pollock and Bruno 2000). This is particularly confounding since many early evaluations of the effect of taxon addition were made using parsimony because of its speed (Graybeal 1998; Hillis 1998; Kim 1996; Kim 1998; Poe and Swofford 1999; Rannala et al 1998; Yang 1998). Some aspects of results from these studies need to be reinterpreted in light of this new evidence.

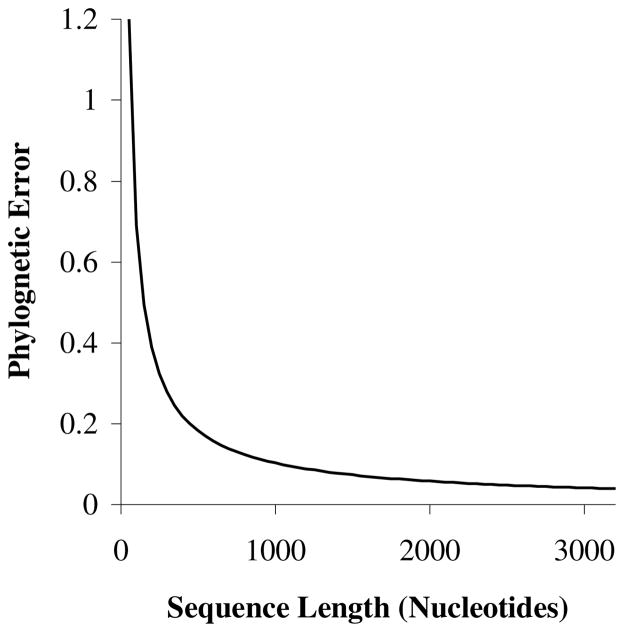
Despite this array of factors affecting taxon addition, some basic features are inferable. First, if sequences are shorter than about 500 bp, the benefits of increasing sequence length are large enough that they outweigh benefits of taxon addition (Pollock et al 2002). This is because the reduction in phylogenetic error with increasing sequence length follows a power curve (Figure 2) that decreases rapidly early on, and then is close to a constantly decreasing slope for larger sequence lengths (under one set of conditions, error was approximately 32 times the sequence length to the −0.826 power; r²=0.98; Figure 2). Second, if rates are extremely slow, such that multiple substitutions at sites are unlikely (ie below 0.7 substitutions per site), taxon addition can provide little benefit (Pollock et al 2002). Substitution rate also play a role in phylogenetic analyses if very fast-evolving sequences are selected (ie greater than 4.5 substitutions per site), but this effect is not nearly as large as for slow rates. For many realistic situations outside of these extremes, the benefits of taxon addition will be negligibly affected by substitution rate, and taxon addition will have an effect similar to increasing sequence length. For example, under the conditions analysed in Pollock et al (2002), doubling the number of randomly sampled taxa from 33 to 66 caused the same reduction in phylogenetic error as doubling the sequence length from 1000 to 2000 nucleotides. Assuming sequences that evolve at appropriate rates of evolution have been selected for analysis, researchers should focus on increasing sequence biodiversity as well as increasing sequence length (or other phylogenetically informative characters) to increase the accuracy of their phylogenetic estimate (Pollock et al 2002).

Figure 2.

Decreasing power curve relationship between phylogenetic error and sequence length. If sequence length is N, error is approximately proportional to 32 * N^−0.826. The slope is steep initially, but decreases rapidly. Between 1000 and 3000 nucleotides, the slope is relatively shallow, and the curve is nearly straight

Taxon addition and molecular evolution

The molecular evolutionary process is complex, and this complexity adds considerably to the benefits of sequence biodiversity. ML has been proven to be consistent given the correct model and unlimited data (Rogers 1997), and many studies have shown the benefits of ML when the model of evolution is known. Choosing a model and optimising its parameter estimates, however, is an important aspect of maximising the accuracy of estimated trees (eg see Cunningham et al 1998; Posada and Crandall 2001). The crucial question in molecular evolution is what to do in situations where the evolutionary process is unknown. Determining unknown models and their parameters are both increased more by taxon addition than by increasing sequence lengths (Pollock and Bruno 2000).

When the model varies among sites, a surprising and non-intuitive result is that the general nature of this variation can be determined and accurately taken into account using a gamma-distributed rates model (Yang 1996) without resulting in a noticeable improvement in phylogenetic reconstruction (Pollock and Bruno 2000). This compares unfavourably to a dramatic increase in accuracy (equivalent to quadrupling the sequence length) that is observed when the rate category of each site is accurately known (Pollock and Bruno 2000). Thus, although taxon addition primarily improves estimates of internal nodes surrounding uncertain branches when the model is simple, with model variation among sites there is a large potential for additional effects.

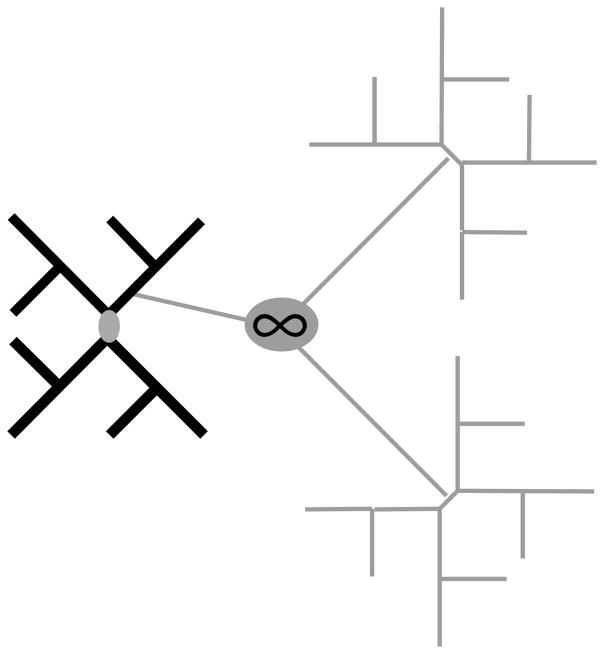
To evaluate these two effects of taxon addition separately, it is necessary to increase site-specific information without adding information concerning internal states. This can be accomplished using doppelgänger trees (Figure 3), which are exact doubles of the initial tree of interest, but evolve independently (Pollock and Bruno 2000). Operationally, multiple datasets are generated by simulation using the same tree structure, and then combined into a single alignment. Phylogenetic accuracy is determined for only the initial dataset. Sites in doppelgänger trees evolve at the same rates as sites in the initial tree, but the doppelgänger sequences are contributing no information towards estimating node states in the initial tree. This is equivalent to the sequences from the initial tree and the doppelgänger trees being related by branches of infinite length (Figure 3).

Figure 3.

Relationship of doppelgänger trees to focus tree of interest. The shadowy thin grey doppelgänger trees are identical in structure but evolve independently of the focus tree. This is equivalent to being connected to the focus tree by a branch with infinite length. In the bold black focus tree, only reconstruction of the short grey innermost branch was considered.

An initial result of the doppelgänger analysis is that likelihood methods tend to be at worst unaffected by addition of taxa outside the group of interest. This is in sharp contrast to parsimony methods, which show a dramatic decrease in reconstruction efficiency (Pollock and Bruno 2000). Thus, previous studies that have recommended avoidance of additional sequences outside the clade under consideration are likely a result of using parsimony rather than ML. It is recommended instead to avoid parsimony if outgroups are used (Pollock and Bruno 2000). It is worth noting that this effect is not the same as LBA, which is caused by attraction or repulsion of asymmetric branch lengths; in the doppelgänger studies, LBA was avoided by using symmetrical branch lengths.

The most striking result, however, is that the addition of doppelgänger trees has a dramatic effect on phylogenetic reconstruction accuracy under the gamma model. As the doppelgänger trees are added, the gamma model approaches the efficiency achieved when the rate category of each site is accurately known (Pollock and Bruno 2000). At the same time, the average posterior probability of each site being in the correct rate category approaches one. The conclusion is once again that adding taxa increases phylogenetic accuracy because it dramatically improves the ability to accurately assess the evolutionary model. The greatest portion of this improvement comes, however, not with accurate assessment of the global model, but rather with accurate assessment of the details of the model at individual sites. This increase in accuracy can be achieved only by adding taxa, not by increasing sequence length.

The studies cited above provide solid arguments for increasing genomic biodiversity to reduce phylogenetic error. Further support is provided by recent simulations by Zwickl and Hillis (2002). These results and conclusions support optimism for the potential of phylogenetic analysis of large data sets. A directed strategy of adding taxa to a phylogenetic analysis appears to be a quite profitable use of time and resources.

Adaptation, coevolution and changing evolutionary processes

The detection of adaptation, coevolution and other changes in the evolutionary processes will benefit from intense sampling of genomic biodiversity. Changes in process can come about through changes in functional constraints (Zhang and Gu 1998; Gu 1999), adaptation (eg Jollès et al 1989; Messier and Stewart 1997; Stewart et al 1987), or neutral changes in exchange rates due to changes in structural context or for unknown reasons (Felsenstein 2001; Galtier 2001; Gaucher et al 2001; Goldman et al 1996; Goldman et al 1998; Fitch 1976; Fitch and Ayala 1994; Miyamoto and Fitch 1995; Penny et al 2001; Thorne et al 1996; Thorne et al 1998; Thorne 2000; Tuffley and Steel 1998).

Prior to considering how to separately detect such changes, it is useful to first consider here what is meant by adaptation, since adaptation as a concept has long been controversial to define (Ridley 1997). It is often defined in terms of design optimisation or relative reproductive success, but neither of these can be easily measured retrospectively (although see work by SA Benner and colleagues for serious efforts in this direction). Here, in a statistical and retrospective context, we will use an operational definition of detectable adaptation that requires multiple substitutions, since individual adaptive substitutions will almost never be provable statistically. Thus, we mostly avoid what Gillespie calls ‘microadaptations’ involving one or a few amino acid changes (Gillespie 1991). It is also difficult to differentiate between the environment external to the organism and the internal cellular environment produced by interactions among the genes and the external environment. Adaptation will therefore be considered to be a detectable excess of multiple substitutions that occur in response to internal or external selective pressure.

Pairwise coevolution could itself be considered an example of microadaptation when substitution at one residue causes another residue to respond or ‘adapt’ to the first substitution. This seems trivial, and in speaking of adaptation in the context of coevolution, the interpretation will be that adaptation occurs when the pair of changes is together more fit than the starting point. In this context, it is similarly difficult to infer adaptation unless the coevolved pair is part of a larger series of adaptive substitutions.

A confounding factor in analysing coevolution is that selective processes leading to adaptation can potentially be confounded with coevolution even when the sites involved are not coevolving. Simultaneous evolution due to an outside influence may be indistinguishable from evolution due to pairwise interactions, and thus adaptation may obscure detection of non-adaptive pairwise coevolution. Phylogenetic means of detecting adaptive bursts by comparing substitution rates at neutral or independent sites to amino acid substitution rates in the protein of interest are much improved with large amounts of sequence data from closely related taxa. Large amounts of genomic biodiversity data will be necessary to fully separate effects of adaptation, coevolution and neutral rate changes.

As discussed in the previous section, increased genomic biodiversity is essential to analyse differences in evolutionary behaviour among sites. Accurate understanding of change in the evolutionary process among sites depends on better models of site-specific differences. Despite strong evidence for differences in the acceptability of different amino acids in addition to differences in rates, it has long been common practice to assume that all sites evolve in the same fashion. This may dramatically confound phylogenetic analyses, but progress has been made in analysing evolutionary behaviour at individual sites by limiting free parameters to the equilibrium amino acid frequencies (Bruno 1996), or by optimising functions of physicochemical properties (Koshi and Goldstein 1998; Koshi et al 1999; Yang 2000; Dimmic et al 2000). In Bruno’s work, amino acid frequencies are obtained for each site, although these estimates are influenced by other sites through the use of pseudocounts. Both Goldstein’s group and Yang clustered sites into groups according to natural tendencies arising from the data, and allowed for differences in substitution rates between amino acids in addition to frequency differences.

Fine structural details (such as position of catalytic or ligand-binding sites, secondary structure features or subunit interaction surfaces) have been linked to differences in evolutionary substitution patterns (Goldman et al 1996; Koshi and Goldstein 1996; Thompson and Goldstein 1996; Thorne et al 1996; Thompson and Goldstein 1997; Goldman et al 1998; Koshi et al 1999; Dean and Golding 2000), and the accuracy of predicting structural and functional features will also increase with increased taxonomic sampling. Attempts to experimentally verify the link between evolution and function have been increasingly successful (Malcolm et al 1990; Irwin and Wilson 1991; Goldman et al 1996; Karplus et al 1997; O’Brien et al 1997; Eisen 1998; Golding and Dean 1998; Clark 1999; Cort et al 1999; D’Onofrio et al 1999; Frishman et al 2000). Jermann et al (1995), for example, predicted ancestral sequences, determined catalytic properties of ancient ribonucleases, and found a large increase in activity associated with ruminant digestion. Ancestral reconstructions are inaccurate with small numbers of sequences (Yang et al 1995), and will be improved by more accurate predictions from a greater number of descendant sequences.

Genomic biodiversity and coevolution among protein residues

The detailed analysis of coevolution among protein residues provides particularly compelling motivation for dense sampling of genomic biodiversity. It has long been known that there are strong interactions between residues in protein structures; deleterious mutations causing serious dysfunction in a protein can sometimes be corrected by a second mutation at another residue (Altschuh et al 1987; Chothia et al 1987; Chothia and Lesk 1987). Thus, it is reasonable to conclude that substitutions should interact over the course of evolution – that is, they should coevolve. Coevolution among residues in proteins is important for what it may tell us about the interaction of protein structure and sequence evolution, and for its potential to confound analyses when it is ignored. Coevolution can have both positive and negative effects on phylogenetic analysis: it can potentially confound results by causing parallel or convergent changes, but can also lead to slower rates of substitution, thus providing unsaturated signal for deeper nodes. Furthermore, coevolution can be an important indicator of functional interactions between residues.

Despite its importance, it has proven difficult to detect coevolution (also termed correlated substitution, correlated mutation or covariation) between residues in proteins (Altschuh et al 1987; Korber et al 1993; Neher 1994; Shindyalov et al 1994; Taylor and Hatrick 1994; Chelvanayagam et al 1997; Pazos et al 1997; Pollock and Taylor 1997; Giraud et al 1998). Coevolution in proteins is complex, and does not necessarily occur in the form of strict pairwise relationships, as coevolution in RNA helices does (Higgs 2000; Pollock et al 1999; Savill et al 2001). Among the primary reasons that coevolution in proteins may be difficult to detect are that the strength and nature of interactions between residues may change over time, and that coevolutionary interactions may be spread over many residues, thus diluting the strength of detectable pairwise interactions. It is worth remembering that pairs with the strongest interactions are least likely to substitute over evolutionary time, since their intermediate single substitutions are by definition the most deleterious.

Detection of coevolution is also strongly influenced by phylogeny. It is essential to take phylogeny into account in the method of detecting coevolution (Pollock and Taylor 1997), and sampling density and topological relationships can affect the statistical power to detect coevolution from aligned sequences (Pollock and Taylor 1997; Pollock et al 1999). It is clearly preferable to have accurate phylogenies available, and if possible that the phylogenies should be estimated from sequences other than those being tested for coevolution. An important application is detecting coevolution between interacting proteins (Pazos et al 1997), and for this the phylogenetic sampling of the interacting proteins must match.

There are multiple approaches to detect coevolution among protein residues using phylogenetic tree structure. The most straightforward way is to identify changes on branches, and determine if two sites change on identical branches more often than expected, or whether particular kinds of changes are paired (Shindyalov et al 1994; Chelvanayagam et al 1997). This is conceptually simple, but relies on uncertain reconstruction of ancestral states and assumes that coevolution causes approximately simultaneous substitutions. If substitutions are not simultaneous, but rather an initial substitution at one site only quantitatively changes the probability of substitution at the other site, the probability of simultaneous substitution events on the same branch will decrease as the branches get shorter. Maddison (1990) developed a test for binary characters that also relies on ancestral reconstruction, and determines whether changes in a ‘dependent’ trait tend to occur in regions of the phylogenetic tree characterised by particular states of a ‘causal’ trait. I am not aware that this has been applied to proteins, nor is it clear how dependent and causal residues might be distinguished. A more general model-based alternative with good statistical properties, but computationally more intensive and only implemented for simple models, is to compare the likelihood that a pair of sites are evolving independently to the likelihood that they are coevolving (Pollock et al 1999). Another approach is to look for correlation or mutual information in the equilibrium amino acid frequencies at individual sites. This has been published using statistics derived directly from the alignment (Altschuh et al 1987; Korber et al 1993; Neher 1994; Taylor and Hatrick 1994; Chelvanayagam et al 1997; Pazos et al 1997a; Giraud et al 1998; Atchley et al 2000), and has been implemented but not yet published for tree-based statistics (Bruno 2000, pers comm). Another reasonable alternative, not yet implemented, is to use Bayesian methods to map substitutions onto the tree, and detect excess pairwise clustering of substitutions in the tree in the posterior predictive distributions (Nielsen and Huelsenbeck 2002).

It is worth considering the study of Pollock et al (1999) in greater detail to review the complexity of coevolutionary analysis and its interactions with phylogeny, and to illustrate the predictive utility of coevolutionary analysis. The ML method employed by Pollock et al (1999) was designed to take phylogenetic relationships into account and to be robust, statistically accurate and fast enough to make calculations rapidly for the thousands of comparisons in a typical protein. Still, coevolutionary analysis requires diverse sampling of at least 20 or so taxa, and preferably 50 or more, to obtain a reasonable sensitivity of detection (Pollock and Taylor 1997; Pollock et al 1999). To reduce model complexity, and to detect the strongest primary component of coevolution between any two sites, Pollock et al (1999) grouped the amino acids at every site into two states. They based their partitioning on either charge or size, but the approach can be used on any partition. Weaker and less detectable components of coevolution are ignored with this approach, but over-parameterisation of the model is avoided. Since the data for coevolutionary analysis come from only two sites at a time, over-parameterisation is a serious danger, and it is likely that much more taxonomically dense data sets will be required to safely increase the model complexity.

A consequence of the limited amount of data at each site is that asymptotic statistical assumptions (eg that twice the log of the likelihood ratio will be distributed ~ χ²) do not hold (Pollock et al 1999). It was shown that to obtain accurate distributions for coevolution statistics, it is necessary to employ parametric bootstrapping (Pollock et al 1999). Since there are a large number of pairwise comparisons in a single protein, it is useful to consider the posterior probability that a site has coevolved. If proper account is taken for multiple sampling (eg 11 175 pairwise comparisons for an alignment of 150 amino acids), it is extremely difficult to detect pairs that have coevolved with >95% probability. To avoid this conundrum, a predetermined cutoff for the coevolution statistic can be used (eg >95% probability of coevolution, ignoring multiple sampling effects). Taking into account the number of pairwise comparisons, it can then be determined how many pairs have coevolution statistics greater than the cutoff, and whether this number is greater than expected by chance alone. Using this approach, Pollock et al (1999) were able to show, for example, that close pairs in vertebrate myoglobin beyond a 5% cutoff had a 75% posterior probability of negative (compensatory) coevolution due to charge interactions. It was subsequently established that 75% of these pairs were stacked in adjacent positions in alpha helices, lending a structural confirmation to the purely statistical detection of these pairs. This independent verification by considering the structural context in this manner is important, since statistical proof, experimental verification, and prediction of coevolution in the absence of structural information are extremely challenging (Pollock and Taylor 1997).

Using this approach, good evidence was also found for broad trends in coevolutionary patterns that exhibited only weak pairwise relationships (Pollock et al 1999). For example, negative, or compensatory charge coevolution tends to occur between adjacent sites on the surface, but positive charge coevolution occurs between sites that are distant on the surface of the three dimensional structure. There is also a pronounced but weak bias towards positive size coevolution, and a 22% excess of size-segregated pairs beyond the 5% cutoff, with the excess distributed among pairs that are separated by 25 angstroms or less in the three dimensional structure. The pairwise interactions detected in such cases are probably weak due to the large number of sites that can structurally compensate for any given deleterious or slightly deleterious substitution.

Whether coevolutionary analysis results in deterministic prediction of pairwise interactions or trends in groups of sites, it is an excellent probabilistic tool that can be used to generate useful and testable hypotheses concerning the relationship of sequence variation and interaction to structure and function (Pollock et al 1999). Many studies have addressed the relationship between sequence and structure on a random basis (Sauer et al 1988; Lim and Sauer 1989; Lim and Sauer 1990; Lim et al 1992; Gu et al 1995; Riddle et al 1997; Scalley and Baker 1997; Shortle et al 1998; Gu et al 1999). It is, for example, common practice to perform alanine-scanning experiments, where every residue in a protein is replaced by alanine to get a rough estimate of its structural importance. Such random approaches become difficult, however, when considering interactions between sites. Including all possible amino acid combinations, a protein of 300 residues has around 18 million possible pairwise interactions to consider. This is clearly far too many to generate and evaluate using current mutagenesis technology. In contrast, a coevolutionary analysis might predict 100 pairs that are most likely to have significantly coevolved. Even if only 20%–30% of these have truly coevolved (the rest due to chance and multiple comparisons), the experimental problem of which interactions to test has been reduced to a tractable level. With increased sampling of genomic biodiversity, such predictions can dramatically improve.

Increased efficiency in obtaining genomic biodiversity

Progress in genomics research and associated development of strategies, techniques and tools for large-scale sequencing have begun to strongly influence molecular-based evolutionary studies (Murphy et al 2001; Madsen et al 2001). Still, datasets are needed from large genomic regions with much greater sampling of divergent taxa than are currently available. Research designs for molecular-based studies of evolution are changing from gene-based strategies, characterised by low throughput sequencing of one or a few short regions at a time, to more cost-efficient high-throughput approaches (Madsen et al 2001; Miya et al 2001; Murphy et al 2001; Pollock et al 2000).

Strong theoretical arguments indicate that there is room for improved throughput and efficiency by adapting genomic approaches to the constraint of simultaneously obtaining large genomic regions from many taxa, as opposed to an entire genome from a single taxon (Pollock et al 2000). A possible design for genomic biodiversity studies was proposed and evaluated using simulated sequence, cloning and assembly experiments (Pollock et al 2000), and experimental application of this approach is now underway to obtain complete vertebrate mitochondrial genomes.

In any genomic study, procedural steps should be optimised to minimise overall cost without sacrificing accuracy. Analogous to arguments for whole-genome shotgun sequencing (Fleischmann et al 1995; Venter et al 1996; Weber and Myers 1997; Venter et al 1998), it was proposed that DNA samples from different gene regions and diverse species be pooled and mixed prior to cloning, reducing cloning and management costs per taxon (Pollock et al 2000). Although breaking the direct association between sequences and samples is a counter-intuitive approach, these associations can be recreated using automated assembly programs (Bonfield et al 1995; Bonfield and Staden 1995; Sutton et al 1995; Staden 1996; Ewing and Green 1998; Ewing et al 1998) in combination with pre-existing sequence information used as an anchor similar to the anchor bacterial artificial chromosome (BAC) end sequencing approach used to complete the sequence of the human genome (Lander et al 2001).

There are several compelling reasons to sequence complete vertebrate mitochondrial genomes for initial genomic biodiversity studies. First, the mitochondrial genome is an extremely compact, obtainable and gene-rich segment of DNA, and well suited to cloning technologies. Second, in mitochondria recombination and differences in phylogenies between genes are rare or absent (for discussion see Arctander 1999; Awadalla et al 1999; Merriweather and Kaestle 1999; Awadalla et al 2000; Kivisild et al 2000), whereas this is not true for nuclear genes. Third, there is a quickly growing database of mitochondrial genomes that will allow analysis of varying evolutionary models across sites to be applied and compared across taxonomic groups. Mitochondrial genomic biodiversity analysis will allow simultaneous study of a suite of proteins that are functionally related (as members of the oxidative phosphorylation complex), with some subunits tightly linked both functionally and structurally. For example, the three cytochrome oxidase genes have interacting surfaces as subunits in the same protein complex, and are functionally linked with cytochrome b in the electron transport chain.

PCR amplification of 10–50 kb genomic regions has been well demonstrated (Chang et al 1994; Cheng et al 1994a; Cheng et al 1994b; Nelson et al 1996; Mindell et al 1999; Miya and Nishida 1999), and is a good choice for genomic biodiversity studies since it can be applied to tissues in a wide variety of preservation states. The cost of cloning in genome centres runs around 10% of the overall costs of cloning and sequencing once the DNA fragments are incorporated BACs. These BACs, though, are about 10 times the size of the average vertebrate mitochondrial genome. If a 16–17 kb mitochondrial genome is amplified in two to three fragments, each of which is cloned separately, cloning costs per ten genomes will be 20–30 times larger than for cloning a BAC, or about two to three times sequencing costs. Pooling all fragments from ten genomes would yield an aggregate sequence comparable to a BAC, with at least a 95% relative reduction in cloning costs (Pollock et al 2000). Small amounts of the original extractions should always be preserved for short PCR amplifications from the original samples.

The theoretical feasibility of this approach was demonstrated through extensive simulation of the protocol using existing mitochondrial genomes (Pollock et al 2000). As with the human genome project, potential assembly difficulties could arise through identical stretches of sequence, although with whole genomes these stretches are repeat segments, whereas with genomic biodiversity they arise from homologous regions in divergent taxa. Since these regions can lead to mis-assembling of contigs if they are too long, the distribution of identical length segments was evaluated for 8 taxon pairs ranging in divergence from the horse/donkey to the human/chicken pairs (Pollock et al 2000). Between human and chicken mitochondria, there are no identical segments longer than 35 bp in length, while between horse and donkey there are 5 segments longer than 100 bp, with the longest at 205 bp. The longest identical segments are less than half the length of the average sequence read, and are not long enough to cause difficulty in assembly. At any rate, there is no need to simultaneously clone genomes as closely related as the horse and the donkey.

To simulate the cloning process, ten existing mitochondrial genomes were randomly fragmented, mixed and sampled at seven-fold coverage with realistic variability incorporated for sequence read length, sample concentration and cloned insert size (Pollock et al 2000). Inserts had an average length of 2 kb, while sequence reads averaged a conservative 500 bp from both ends of the insert. Six genomes were assembled correctly with no gaps, while the other four had one gap each ranging from 56 to 118 bp. This result is in line with expectations from human genome and bacterial shotgun cloning, which require a small amount of finishing to close gaps. Experiments currently underway indicate in direct comparisons that, even in an academic setting, the shotgun cloning methods are more efficient and less labour-intensive than primer walking, particularly for genomes that lack well-dispersed conserved primers. As predicted, there is a need to pre-circularise the long PCR products before nebulisation to avoid bias towards the end (Pollock et al 2000), and some genomes also have a short difficult-to-clone and sequence segment of poly-G that need to be closed in the gap-filling stage.

Discussion

With the complete sequencing of the human genome, one of the most important problems of the coming century is to develop a complete understanding of how that sequence functions to carry out essential life processes. A major route to that understanding, and a serious challenge for bioinformatics, will be comparative analysis of sequence biodiversity. While a great deal of biodiversity is currently being explored at deep taxonomic levels with the sequencing of complete bacterial genomes, these taxa are generally too divergent to be useful in evaluating many important evolutionary processes that occur on a much shorter time scale. A greater focus on genomic biodiversity is needed among vertebrate taxa closely related to humans, that is, on the near human evolutionary environment. Currently, genomic biodiversity analyses are often data-limited, but this is expected to change rapidly. Bioinformatics and computational biology should move rapidly to address the challenges and reap the full benefits of such studies.