Dictionary Learning Algorithms for Sparse Representation

Abstract

Algorithms for data-driven learning of domain-specific overcomplete dictionaries are developed to obtain maximum likelihood and maximum a posteriori dictionary estimates based on the use of Bayesian models with concave/Schur-concave (CSC) negative log priors. Such priors are appropriate for obtaining sparse representations of environmental signals within an appropriately chosen (environmentally matched) dictionary. The elements of the dictionary can be interpreted as concepts, features, or words capable of succinct expression of events encountered in the environment (the source of the measured signals). This is a generalization of vector quantization in that one is interested in a description involving a few dictionary entries (the proverbial “25 words or less”), but not necessarily as succinct as one entry. To learn an environmentally adapted dictionary capable of concise expression of signals generated by the environment, we develop algorithms that iterate between a representative set of sparse representations found by variants of FOCUSS and an update of the dictionary using these sparse representations.

Experiments were performed using synthetic data and natural images. For complete dictionaries, we demonstrate that our algorithms have improved performance over other independent component analysis (ICA) methods, measured in terms of signal-to-noise ratios of separated sources. In the overcomplete case, we show that the true underlying dictionary and sparse sources can be accurately recovered. In tests with natural images, learned overcomplete dictionaries are shown to have higher coding efficiency than complete dictionaries; that is, images encoded with an over-complete dictionary have both higher compression (fewer bits per pixel) and higher accuracy (lower mean square error).

1 Introduction

FOCUSS, which stands for FOCal Underdetermined System Solver, is an algorithm designed to obtain suboptimally (and, at times, maximally) sparse solutions to the following m × n, underdetermined linear inverse problem¹ (Gorodnitsky, George, & Rao, 1995; Rao & Gorodnitsky, 1997; Gorodnitsky & Rao, 1997; Adler, Rao, & Kreutz-Delgado, 1996; Rao & Kreutz-Delgado, 1997; Rao, 1997, 1998),

$$y=Ax,$$ (1.1)

for known A. The sparsity of a vector is the number of zero-valued elements (Donoho, 1994), and is related to the diversity, the number of nonzero elements,

$$\begin{array}{l}\mathit{sparsity}=\#\{x[i]=0\}\\ \mathit{diversity}=\#\{x[i]\ne 0\}\\ \mathit{diversity}=n-\mathit{sparsity}.\end{array}$$

Since our initial investigations into the properties of FOCUSS as an algorithm for providing sparse solutions to linear inverse problems in relatively noise-free environments (Gorodnitsky et al., 1995; Rao, 1997; Rao & Gorodnitsky, 1997; Gorodnitsky & Rao, 1997; Adler et al., 1996; Rao & Kreutz-Delgado, 1997), we now better understand the behavior of FOCUSS in noisy environments (Rao & Kreutz-Delgado, 1998a, 1998b) and as an interior point-like optimization algorithm for optimizing concave functionals subject to linear constraints (Rao & Kreutz-Delgado, 1999; Kreutz-Delgado & Rao, 1997, 1998a, 1998b, 1998c, 1999; Kreutz-Delgado, Rao, Engan, Lee, & Sejnowski, 1999a; Engan, Rao, & Kreutz-Delgado, 2000; Rao, Engan, Cotter, & Kreutz-Delgado, 2002). In this article, we consider the use of the FOCUSS algorithm in the case where the matrix A is unknown and must be learned. Toward this end, we first briefly discuss how the use of concave (and Schur concave) functionals enforces sparse solutions to equation 1.1. We also discuss the choice of the matrix, A, in equation 1.1 and its relationship to the set of signal vectors y for which we hope to obtain sparse representations. Finally, we present algorithms capable of learning an environmentally adapted dictionary, A, given a sufficiently large and statistically representative sample of signal vectors, y, building on ideas originally presented in Kreutz-Delgado, Rao, Engan, Lee, and Sejnowski (1999b), Kreutz-Delgado, Rao, and Engan (1999), and Engan, Rao, and Kreutz-Delgado (1999).

We refer to the columns of the full row-rank m × n matrix A,

$$A=[a_1,\dots ,a_n]\in {\mathbb{R}}^{m\times n},n\gg m,$$ (1.2)

as a dictionary, and they are assumed to be a set of vectors capable of providing a highly succinct representation for most (and, ideally, all) statistically representative signal vectors y ∈ ℝ^m. Note that with the assumption that rank(A) = m, every vector y has a representation; the question at hand is whether this representation is likely to be sparse. We call the statistical generating mechanism for signals, y, the environment and a dictionary, A, within which such signals can be sparsely represented an environmentally adapted dictionary.

Environmentally generated signals typically have significant statistical structure and can be represented by a set of basis vectors spanning a lower-dimensional submanifold of meaningful signals (Field, 1994; Ruderman, 1994). These environmentally meaningful representation vectors can be obtained by maximizing the mutual information between the set of these vectors (the dictionary) and the signals generated by the environment (Comon, 1994; Bell & Sejnowski, 1995; Deco & Obradovic, 1996; Olshausen & Field, 1996; Zhu, Wu, & Mumford, 1997; Wang, Lee, & Juang, 1997). This procedure can be viewed as a natural generalization of independent component analysis (ICA) (Comon, 1994; Deco & Obradovic, 1996). As initially developed, this procedure usually results in obtaining a minimal spanning set of linearly independent vectors (i.e., a true basis). More recently, the desirability of obtaining “overcomplete” sets of vectors (or “dictionaries”) has been noted (Olshausen & Field, 1996; Lewicki & Sejnowski, 2000; Coifman & Wickerhauser, 1992; Mallat & Zhang, 1993; Donoho, 1994; Rao & Kreutz-Delgado, 1997). For example, projecting measured noisy signals onto the signal submanifold spanned by a set of dictionary vectors results in noise reduction and data compression (Donoho, 1994, 1995). These dictionaries can be structured as a set of bases from which a single basis is to be selected to represent the measured signal(s) of interest (Coifman & Wickerhauser, 1992) or as a single, overcomplete set of individual vectors from within which a vector, y, is to be sparsely represented (Mallat & Zhang, 1993; Olshausen & Field, 1996; Lewicki & Sejnowski, 2000; Rao & Kreutz-Delgado, 1997).

The problem of determining a representation from a full row-rank over-complete dictionary, A = [a₁, …, a_n], n ≫ m, for a specific signal measurement, y, is equivalent to solving an underdetermined inverse problem, Ax = y, which is nonuniquely solvable for any y. The standard least-squares solution to this problem has the (at times) undesirable feature of involving all the dictionary vectors in the solution² (the “spurious artifact” problem) and does not generally allow for the extraction of a categorically or physically meaningful solution. That is, it is not generally the case that a least-squares solution yields a concise representation allowing for a precise semantic meaning.³ If the dictionary is large and rich enough in representational power, a measured signal can be matched to a very few (perhaps even just one) dictionary words. In this manner, we can obtain concise semantic content about objects or situations encountered in natural environments (Field, 1994). Thus, there has been significant interest in finding sparse solutions, x (solutions having a minimum number of nonzero elements), to the signal representation problem. Interestingly, matching a specific signal to a sparse set of dictionary words or vectors can be related to entropy minimization as a means of elucidating statistical structure (Watanabe, 1981). Finding a sparse representation (based on the use of a “few” code or dictionary words) can also be viewed as a generalization of vector quantization where a match to a single “code vector” (word) is always sought (taking “code book” = “dictionary”).⁴ Indeed, we can refer to a sparse solution, x, as a sparse coding of the signal instantiation, y.

1.1 Stochastic Models

It is well known (Basilevsky, 1994) that the stochastic generative model

$$y=Ax=\nu ,$$ (1.3)

can be used to develop algorithms enabling coding of y ∈ ℝ^m via solving the inverse problem for a sparse solution x ∈ ℝⁿ for the undercomplete (n < m) and complete (n = m) cases. In recent years, there has been a great deal of interest in obtaining sparse codings of y with this procedure for the overcomplete (n > m) case (Mallat & Zhang, 1993; Field, 1994). In our earlier work, we have shown that given an overcomplete dictionary, A (with the columns of A comprising the dictionary vectors), a maximum a posteriori (MAP) estimate of the source vector, x, will yield a sparse coding of y in the low-noise limit if the negative log prior, −log(P(x)), is concave/Schur-concave (CSC) (Rao, 1998; Kreutz-Delgado & Rao, 1999), as discussed below. For P(x) factorizable into a product of marginal probabilities, the resulting code is also known to provide an independent component analysis (ICA) representation of y. More generally, a CSC prior results in a sparse representation even in the nonfactorizable case (with x then forming a dependent component analysis, or DCA, representation).

Given independently and identically distributed (i.i.d.) data, Y = Y^N = (y₁, …, y_N), assumed to be generated by the model 1.3, a maximum likelihood estimate, Â_ML, of the unknown (but nonrandom) dictionary A can be determined as (Olshausen & Field, 1996; Lewicki & Sejnowski, 2000)

$${\widehat{A}}_{\text{ML}}=arg\underset{A}{max}P(Y;A).$$

This requires integrating out the unobservable i.i.d. source vectors, X = X^N = (x₁, …, x_N), in order to compute P(Y; A) from the (assumed) known probabilities P(x) and P(ν). In essence, X is formally treated as a set of nuisance parameters that in principle can be removed by integration. However, because the prior P(x) is generally taken to be supergaussian, this integration is intractable or computationally unreasonable. Thus, approximations to this integration are performed that result in an approximation to P(Y; A), which is then maximized with respect to Y. A new, better approximation to the integration can then be made, and this process is iterated until the estimate of the dictionary A has (hopefully) converged (Olshausen & Field, 1996). We refer to the resulting estimate as an approximate maximum likelihood (AML) estimate of the dictionary A (denoted here by Â_AML). No formal proof of the convergence of this algorithm to the true maximum likelihood estimate, Â_ML, has been given in the prior literature, but it appears to perform well in various test cases (Olshausen & Field, 1996). Below, we discuss the problem of dictionary learning within the framework of our recently developed log-prior model-based sparse source vector learning approach that for a known overcomplete dictionary can be used to obtain sparse codes (Rao, 1998; Kreutz-Delgado & Rao, 1997, 1998b, 1998c, 1999; Rao & Kreutz-Delgado, 1999). Such sparse codes can be found using FOCUSS, an affine scaling transformation (AST)–like iterative algorithm that finds a sparse locally optimal MAP estimate of the source vector x for an observation y. Using these results, we can develop dictionary learning algorithms within the AML framework and for obtaining a MAP-like estimate, Â_MAP, of the (now assumed random) dictionary, A, assuming in the latter case that the dictionary belongs to a compact submanifold corresponding to unit Frobenius norm. Under certain conditions, convergence to a local minimum of a MAP-loss function that combines functions of the discrepancy e = (y − Ax) and the degree of sparsity in x can be rigorously proved.

1.2 Related Work

Previous work includes efforts to solve equation 1.3 in the overcomplete case within the maximum likelihood (ML) framework. An algorithm for finding sparse codes was developed in Olshausen and Field (1997) and tested on small patches of natural images, resulting in Gabor-like receptive fields. In Lewicki and Sejnowski (2000) another ML algorithm is presented, which uses the Laplacian prior to enforce sparsity. The values of the elements of x are found with a modified conjugate gradient optimization (which has a rather complicated implementation) as opposed to the standard ICA (square mixing matrix) case where the coefficients are found by inverting the A matrix. The difficulty that arises when using ML is that finding the estimate of the dictionary A requires integrating over all possible values of the joint density P(y, x; A) as a function of x. In Olshausen and Field (1997), this is handled by assuming the prior density of x is a delta function, while in Lewicki and Sejnowski (2000), it is approximated by a gaussian. The fixed-point FastICA (Hyvärinen, Cristescu, & Oja, 1999) has also been extended to generate overcomplete representations. The FastICA algorithm can find the basis functions (columns of the dictionary A) one at a time by imposing a quasi-orthogonality condition and can be thought of as a “greedy” algorithm. It also can be run in parallel, meaning that all columns of A are updated together.

Other methods to solve equation 1.3 in the overcomplete case have been developed using a combination of the expectation-maximization (EM) algorithm and variational approximation techniques. Independent factor analysis (Attias, 1999) uses a mixture of gaussians to approximate the prior density of the sources, which avoids the difficulty of integrating out the parameters X and allows different sources to have different densities. In another method (Girolami, 2001), the source priors are assumed to be supergaussian (heavy-tailed), and a variational lower bound is developed that is used in the EM estimation of the parameters A and X. It is noted in Girolami (2001) that the mixtures used in independent factor analysis are more general than may be needed for the sparse overcomplete case, and they can be computationally expensive as the dimension of the data vector and number of mixtures increases.

In Zibulevsky and Pearlmutter (2001), the blind source separation problem is formulated in terms of a sparse source underlying each unmixed signal. These sparse sources are expanded into the unmixed signal with a predefined wavelet dictionary, which may be overcomplete. The unmixed signals are linearly combined by a different mixing matrix to create the observed sensor signals. The method is shown to give better separation performance than ICA techniques. The use of learned dictionaries (instead of being chosen a priori) is suggested.

2 FOCUSS: Sparse Solutions for Known Dictionaries

2.1 Known Dictionary Model

A Bayesian interpretation is obtained from the generative signal model, equation 1.3, by assuming that x has the parameterized (generally nongaussian) probability density function (pdf),

$$P_p(x)=Z_p^{-1}{e}^{-{\gamma }_p{d}_p(x)},Z_p=\int e^{-{\gamma }_p{d}_p(x)}dx,$$ (2.1)

with parameter vector p. Similarly, the noise ν is assumed to have a parameterized (possibly nongaussian) density P_q(ν) of the same form as equation 2.1 with parameter vector q. It is assumed that x and ν have zero means and that their densities obey the property d(x) = d(|x|), for | · | defined component-wise. This is equivalent to assuming that the densities are symmetric with respect to sign changes in the components x, x[i] ← −x[i] and therefore that the skews of these densities are zero. We also assume that d(0) = 0. With a slight abuse of notation, we allow the differing subscripts q and p to indicate that d_q and d_p may be functionally different as well as parametrically different. We refer to densities like equation 2.1 for suitable additional constraints on d_p(x), as hypergeneralized gaussian distributions (Kreutz-Delgado & Rao, 1999; Kreutz-Delgado et al., 1999).

If we treat A, p, and q as known parameters, then x and y are jointly distributed as

$$P(x,y)=P(x,y;p,q,A).$$

Bayes’ rule yields

$$P(x\mid y;p,A)=\frac{1}{\beta }P(y\mid x;p,A)·P(x;p,A)=\frac{1}{\beta }{P}_q(y-Ax)·P_p(x)$$ (2.2)

$$\beta =P(y)=P(y;p,q,A)=\int P(y\mid x)·P_p(x)dx.$$ (2.3)

Usually the dependence on p and q is notationally suppressed, for example, β = P(y; A). Given an observation, y, maximizing equation 2.2 with respect to x yields a MAP estimate x̂. This ideally results in a sparse coding of the observation, a requirement that places functional constraints on the pdfs, and particularly on d_p. Note that β is independent of x and can be ignored when optimizing equation 2.2 with respect to the unknown source vector x.

The MAP estimate equivalently is obtained from minimizing the negative logarithm of P(x | y), which is

$$\widehat{x}=arg\underset{x}{min}{d}_q(y-Ax)+\lambda d_p(x),$$ (2.4)

where λ = γ_p/γ_q and d_q(y−Ax) = d_q(Ax−y) by our assumption of symmetry. The quantity $\frac{1}{\lambda }$ is interpretable as a signal-to-noise ratio (SNR). Furthermore, assuming that both d_q and d_p are concave/Schur–concave (CSC) as defined in section 2.4, then the term d_q(y − Ax) in equation 2.4 will encourage sparse residuals, e = y − Ax̂, while the term d_p(x) encourages sparse source vector estimates, x̂. A given value of λ then determines a trade-off between residual and source vector sparseness.

This most general formulation will not be used here. Although we are interested in obtaining sparse source vector estimates, we will not enforce sparsity on the residuals but instead, to simplify the development, will assume the q = 2 i.i.d. gaussian measurement noise case (ν gaussian with known covariance σ² · I), which corresponds to taking,

$${\gamma }_q{d}_q(y-\widehat{A}\widehat{x})=\frac{1}{2{\sigma }^2}{\left|\right|y-\widehat{A}\widehat{x}\left|\right|}^2.$$ (2.5)

In this case, problem 2.4 becomes

$$\widehat{x}=arg\underset{x}{min}\frac{1}{2}{\left|\right|y-Ax\left|\right|}^2+\lambda d_p(x).$$ (2.6)

In either case, we note that λ → 0 as γ_p → 0 which (consistent with the generative model, 1.3) we refer to as the low noise limit. Because the mapping A is assumed to be onto, in the low-noise limit, the optimization, equation 2.4, is equivalent to the linearly constrained problem,

$$\widehat{x}=argmin{d}_p(x)\text{subject}\text{to}Ax=y.$$ (2.7)

In the low-noise limit, no sparseness constraint need be placed on the residuals, e = y − Ax̂, which are assumed to be zero. It is evident that the structure of d_p(·) is critical for obtaining a sparse coding, x̂, of the observation y (Kreutz-Delgado & Rao, 1997; Rao & Kreutz-Delgado, 1999). Throughtout this article, the quantity d_p(x) is always assumed to be CSC (enforcing sparse solutions to the inverse problem 1.3). As noted, and as will be evident during the development of dictionary learning algorithms below, we do not impose a sparsity constraint on the residuals; instead, the measurement noise ν will be assumed to be gaussian (q = 2).

2.2 Independent Component Analysis and Sparsity Inducing Priors

An important class of densities is given by the generalized gaussians for which

$$d_p(x)={\left|\right|x\left|\right|}_p^p=\sum _{k=1}^n{\mid x[k]\mid }^p,$$ (2.8)

for p > 0 (Kassam, 1982). This is a special case of the larger ℓ_p class (the p-class) of functions, which allows p to be negative in value (Rao & Kreutz-Delgado, 1999; Kreutz-Delgado & Rao, 1997). Note that this function has the special property of separability,

$$d_p(x)=\sum _{k=1}^n{d}_p(x[k]),$$

which corresponds to factorizability of the density P_p(x),

$$P_p(x)=\prod _{k=1}^n{P}_p(x[k]),$$

and hence to independence of the components of x. The assumption of independent components allows the problem of solving the generative model, equation 1.3, for x to be interpreted as an ICA problem (Comon, 1994; Pham, 1996; Olshausen & Field, 1996; Roberts, 1998). It is of interest, then, to consider the development of a large class of parameterizable separable functions d_p(x) consistent with the ICA assumption (Rao & Kreutz-Delgado, 1999; Kreutz-Delgado & Rao, 1997). Given such a class, it is natural to examine the issue of finding a best fit within this class to the “true” underlying prior density of x. This is a problem of parametric density estimation of the true prior, where one attempts to find an optimal choice of the model density P_p(x) by an optimization over the parameters p that define the choice of a prior from within the class. This is, in general, a difficult problem, which may require the use of Monte Carlo, evolutionary programming, or stochastic search techniques.

Can the belief that supergaussian priors, P_p(x), are appropriate for finding sparse solutions to equation 1.3 (Field, 1994; Olshausen & Field, 1996) be clarified or made rigorous? It is well known that the generalized gaussian distribution arising from the use of equation 2.8 yields supergaussian distributions (positive kurtosis) for p < 2 and subgaussian (negative kurtosis) for p > 2. However, one can argue (see section 2.5 below) that the condition for obtaining sparse solutions in the low-noise limit is the stronger requirement that p ≤ 1, in which case the separable function d_p(x) is CSC. This indicates that supergaussianness (positive kurtosis) alone is necessary but not sufficient for inducing sparse solutions. Rather, sufficiency is given by the requirement that −log P_p(x) ≈ d_p(x) be CSC.

We have seen that the function d_p(x) has an interpretation as a (negative logarithm of) a Bayesian prior or as a penalty function enforcing sparsity in equation 2.4, where d_p(x) should serve as a “relaxed counting function” on the nonzero elements of x. Our perspective emphasizes that d_p(x) serves both of these goals simultaneously. Thus, good regularizing functions, d_p(x), should be flexibly parameterizable so that P_p(x) can be optimized over the parameter vector p to provide a good parametric fit to the underlying environmental pdf, and the functions should also have analytical properties consistent with the goal of enforcing sparse solutions. Such properties are discussed in the next section.

2.3 Majorization and Schur-Concavity

In this section, we discuss functions that are both concave and Schur-concave (CSC functions; Marshall & Olkin, 1979). We will call functions, d_p(·), which are CSC, diversity functions, anticoncentration functions or antisparsity functions. The larger the value of the CSC function d_p(x), the more diverse (i.e., the less concentrated or sparse) the elements of the vector x are. Thus, minimizing d_p(x) with respect to x results in less diverse (more concentrated or sparse) vectors x.

2.3.1 Schur-Concave Functions

A measure of the sparsity of the elements of a solution vector x (or the lack thereof, which we refer to as the diversity of x) is given by a partial ordering on vectors known as the Lorentz order. For any vector in the positive orthant, $x\in R_{+}^n$, define the decreasing rearrangement

$$x\doteq (x_{\lfloor 1\rfloor },\dots ,x_{\lfloor n\rfloor }),x_{\lfloor 1\rfloor }\ge \cdots \ge x_{\lfloor n\rfloor }\ge 0$$

and the partial sums (Marshall & Olkin, 1979; Wickerhauser, 1994),

$$S_x[k]=\sum _{i=1}^k{x}_{\lfloor n\rfloor },k=1,\dots ,n.$$

We say that y majorizes x, y > x, iff for k = 1, …, n,

$$S_y[k]\ge S_x[k];S_y[n]=S_x[n],$$

and the vector y is said to be more concentrated, or less diverse, than x. This partial order defined by majorization then defines the Lorentz order.

We are interested in scalar-valued functions of x that are consistent with majorization. Such functions are known as Schur-concave functions, $d(·):R_{+}^n\to R$. They are defined to be precisely the class of functions consistent with the Lorentz order,

$$y\succ x\Rightarrow d(y)<d(x).$$

In words, if y is less diverse than x (according to the Lorentz order) then d(y) is less than d(x) for d(·) Schur-concave. We assume that Schur-concavity is a necessary condition for d(·) to be a good measure of diversity (antisparsity).

2.3.2 Concavity Yields Sparse Solutions

Recall that a function d(·) is concave on the positive orthant $R_{+}^n$ iff (Rockafellar, 1970)

$$d((1-\gamma )x+\gamma y)\ge (1-\gamma )d(x)+\gamma d(y),$$

∀x, $y\in R_{+}^n$, ∀γ, 0 ≤ γ ≤ 1. In addition, a scalar function is said to be permutation invariant if its value is independent of rearrangements of its components. An important fact is that for permutation invariant functions, concavity is a sufficient condition for Schur-concavity:

$$\text{Concavity}+\text{permutation}\text{invariance}\Rightarrow \text{Schur}-\text{concavity}.$$

Now consider the low-noise sparse inverse problem, 2.7. It is well known that subject to linear constraints, a concave function on $R_{+}^n$ takes its minima on the boundary of $R_{+}^n$ (Rockafellar, 1970), and as a consequence these minima are therefore sparse. We take concavity to be a sufficient condition for a permutation invariant d(·) to be a measure of diversity and obtain sparsity as constrained minima of d(·). More generally, a diversity measure should be somewhere between Schur-concave and concave. In this spirit, one can define almost concave functions (Kreutz-Delgado & Rao, 1997), which are Schur-concave and (locally) concave in all n directions but one, which also are good measures of diversity.

2.3.3 Separability, Schur-Concavity, and ICA

The simplest way to ensure that d(x) be permutation invariant (a necessary condition for Schur-concavity) is to use functions that are separable. Recall that separability of d_p(x) corresponds to factorizability of P_p(x). Thus, separability of d(x) corresponds to the assumption of independent components of x under the model 1.3. We see that from a Bayesian perspective, separability of d(x) corresponds to a generative model for y that assumes a source, x, with independent components. With this assumption, we are working within the framework of ICA (Nadal & Parga, 1994; Pham, 1996; Roberts, 1998). We have developed effective algorithms for solving the optimization problem 2.7 for sparse solutions when d_p(x) is separable and concave (Kreutz-Delgado & Rao, 1997; Rao & Kreutz-Delgado, 1999).

It is now evident that relaxing the restriction of separability generalizes the generative model to the case where the source vector, x, has dependent components. We can reasonably call an approach based on a nonseparable diversity measure d(x) a dependent component analysis (DCA). Unless care is taken, this relaxation can significantly complicate the analysis and development of optimization algorithms. However, one can solve the low-noise DCA problem, at least in principle, provided appropriate choices of nonseparable diversity functions are made.

2.4 Supergaussian Priors and Sparse Coding

The P-class of diversity measures for 0 < p ≤ 1 result in sparse solutions to the low-noise coding problem, 2.7. These separable and concave (and thus Schur-concave) diversity measures correspond to supergaussian priors, consistent with the folk theorem that supergaussian priors are sparsity-enforcing priors. However, taking 1 ≤ p < 2 results in supergaussian priors that are not sparsity enforcing. Taking p to be between 1 and 2 yields a d_p(x) that is convex and therefore not concave. This is consistent with the well-known fact that for this range of p, the pth-root of d_p(x) is a norm. Minimizing d_p(x) in this case drives x toward the origin, favoring concentrated rather than sparse solutions. We see that if a sparse coding is to be found based on obtaining a MAP estimate to the low-noise generative model, 1.3, then, in a sense, supergaussianness is a necessary but not sufficient condition for a prior to be sparsity enforcing. A sufficient condition for obtaining a sparse MAP coding is that the negative log prior be CSC.

2.5 The FOCUSS Algorithm

Locally optimal solutions to the known-dictionary sparse inverse problems in gaussian noise, equations 2.6 and 2.7, are given by the FOCUSS algorithm. This is an affine-scaling transformation (AST)-like (interior point) algorithm originally proposed for the low-noise case 2.7 in Rao and Kreutz-Delgado (1997, 1999) and Kreutz-Delgado and Rao (1997); and extended by regularization to the nontrivial noise case, equation 2.6, in Rao and Kreutz-Delgado (1998a), Engan et al. (2000), and Rao et al. (2002). In these references, it is shown that the FOCUSS algorithm has excellent behavior for concave functions (which includes the the CSC concentration functions) d_p(·). For such functions, FOCUSS quickly converges to a local minimum, yielding a sparse solution to problems 2.7 and 2.6.

One can quickly motivate the development of the FOCUSS algorithm appropriate for solving the optimization problem 2.6 by considering the problem of obtaining the stationary points of the objective function. These are given as solutions, x^*, to

$$A^T({Ax}^{\ast }-y)+\lambda {\nabla }_x{d}_p(x^{\ast })=0.$$ (2.9)

In general, equation 2.9 is nonlinear and cannot be explicitly solved for a solution x^*. However, we proceed by assuming the existence of a gradient factorization,

$${\nabla }_x{d}_p(x)=\alpha (x)\mathrm{\Pi }(x)x,$$ (2.10)

where α(x) is a positive scalar function and Π(x) is symmetric, positive-definite, and diagonal. As discussed in Kreutz-Delgado and Rao (1997, 1998c) and Rao and Kreutz-Delgado (1999), this assumption is generally true for CSC sparsity functions d_p(·) and is key to understanding FOCUSS as a sparsity-inducing interior-point (AST-like) optimization algorithm.⁵

With the gradient factorization 2.10, the stationary points of equation 2.9 are readily shown to be solutions to the (equally nonlinear and implicit) system,

$$x^{\ast }={(A^{T}A+\beta (x^{\ast })\mathrm{\Pi }(x^{\ast }))}^{-1}{A}^{T}y$$ (2.11)

$$={\mathrm{\Pi }}^{-1}(x^{\ast })A^T{(\beta (x^{\ast })I+A{\mathrm{\Pi }}^{-1}(x^{\ast })A^T)}^{-1}y,$$ (2.12)

where β(x) = λα(x) and the second equation follows from identity A.18. Although equation 2.12 is also not generally solvable in closed form, it does suggest the following relaxation algorithm,

$$\widehat{x}\leftarrow {\mathrm{\Pi }}^{-1}(\widehat{x})A^T{(\beta (\widehat{x})I+A{\mathrm{\Pi }}^{-1}(\widehat{x})A^T)}^{-1}y,$$ (2.13)

which is to be repeatedly reiterated until convergence.

Taking β ≡ 0 in equation 2.13 yields the FOCUSS algorithm proved in Kreutz-Delgado and Rao (1997, 1998c) and Rao and Kreutz-Delgado (1999) to converge to a sparse solution of equation 2.7 for CSC sparsity functions d_p(·). The case β ≠ 0 yields the regularized FOCUSS algorithm that will converge to a sparse solution of equation 2.6 (Rao, 1998; Engan et al., 2000; Rao et al., 2002). More computationally robust variants of equation 2.13 are discussed elsewhere (Gorodnitsky & Rao, 1997; Rao & Kreutz-Delgado, 1998a).

Note that for the general regularized FOCUSS algorithm, 2.13, we have β(x̂) = λα(x̂), where λ is the regularization parameter in equation 2.4. The function β(x) is usually generalized to be a function of x̂, y and the iteration number. Methods for choosing λ include the quality-of-fit criteria, the sparsity critera, and the L-curve (Engan, 2000; Engan et al., 2000; Rao et al., 2002). The quality-of-fit criterion attempts to minimize the residual error y − Ax (Rao, 1997), which can be shown to converge to a sparse solution (Rao & Kreutz-Delgado, 1999). The sparsity criterion requires that a certain number of elements of each x_k be nonzero.

The L-curve method adjusts λ to optimize the trade-off between the residual and sparsity of x. The plot of d_p(x) versus d_q(y − Ax) has an L shape, the corner of which provides the best trade-off. The corner of the L-curve is the point of maximum curvature and can be found by a one-dimensional maximization of the curvature function (Hansen & O’Leary, 1993).

A hybrid approach known as the modified L-curve method combines the L-curve method on a linear scale and the quality-of-fit criterion, which is used to place limits on the range of λ that can be chosen by the L-curve (Engan, 2000). The modified L-curve method was shown to have good performance, but it requires a one-dimensional numerical optimization step for each x_k at each iteration, which can be computationally expensive for large vectors.

3 Dictionary Learning

3.1 Unknown, Nonrandom Dictionaries

The MLE framework treats parameters to be estimated as unknown but deterministic (nonrandom). In this spirit, we take the dictionary, A, to be the set of unknown but deterministic parameters to be estimated from the observation set Y = Y^N. In particular, given Y^N, the maximum likelihood estimate Â_ML is found from maximizing the likelihood function L(A | Y^N) = P(Y^N; A). Under the assumption that the observations are i.i.d., this corresponds to the optimization

$${\widehat{A}}_{\text{ML}}=arg\underset{A}{max}\prod _{k=1}^{N}P(y_k;A),$$ (3.1)

$$\begin{array}{l}P(y_k;A)=\int P(y_k,x;A)dx=\int P(y_k\mid x;A)·P_p(x)dx\\ =\int P_q(y_k-Ax)·P_p(x)dx.\end{array}$$ (3.2)

Defining the sample average of a function f (y) over the sample set Y^N = (y₁, …, y_N) by

$${\langle f(y)\rangle }_N=\frac{1}{N}\sum _{k=1}^{N}f(y_k),$$

the optimization 3.1 can be equivalently written as

$${\widehat{A}}_{\text{ML}}=arg\underset{A}{min}-{\langle log(P(y;A))\rangle }_N.$$ (3.3)

Note that P(y_k; A) is equal to the normalization factor β already encountered, but now with the dependence of β on A and the particular sample, y_k, made explicit. The integration in equation 3.2 in general is intractable, and various approximations have been proposed to obtain an approximate maximum likelihood estimate, Â_AML (Olshausen & Field, 1996; Lewicki & Sejnowski, 2000).

In particular, the following approximation has been proposed (Olshausen & Field, 1996),

$$P_p(x)\approx \delta (x-{\widehat{x}}_k(\widehat{A})),$$ (3.4)

where

$${\widehat{x}}_k(\widehat{A})=arg\underset{x}{max}P(y_k,x;\widehat{A}),$$ (3.5)

for k = 1, …, N, assuming a current estimate, Â, for A. This approximation corresponds to assuming that the source vector x_k for which y_k = Ax_k is known and equal to x̂_k(Â). With this approximation, the optimization 3.3 becomes

$${\widehat{A}}_{\text{AML}}=arg\underset{A}{min}\langle d_q{(y-A\widehat{x})}_N,$$ (3.6)

which is an optimization over the sample average 〈 · 〉_N of the functional 2.4 encountered earlier. Updating our estimate for the dictionary,

$$\widehat{A}\leftarrow {\widehat{A}}_{\text{AML}},$$ (3.7)

we can iterate the procedure (3.5)–(3.6) until Â_AML has converged, hopefully (at least in the limit of large N) to Â_ML = Â_ML(Y^N) as the maximum likelihood estimate Â_ML(Y^N) has well-known desirable asymptotic properties in the limit N → ∞.

Performing the optimization in equation 3.6 for the q = 2 i.i.d. gaussian measurement noise case (ν gaussian with known covariance σ² · I) corresponds to taking

$$d_q(y-\widehat{A}\widehat{x})=\frac{1}{2{\sigma }^2}{\left|\right|y-\widehat{A}\widehat{x}\left|\right|}^2,$$ (3.8)

in equation 3.6. In appendix A, it is shown that we can readily obtain the unique batch solution,

$${\widehat{A}}_{\text{AML}}={\mathrm{\sum }}_{y\widehat{x}}{\mathrm{\sum }}_{\widehat{x}\widehat{x}}^{-1},$$ (3.9)

$${\mathrm{\sum }}_{y\widehat{x}}=\frac{1}{N}\sum _{k=1}^N{y}_k{\widehat{x}}_k^T,{\mathrm{\sum }}_{\widehat{x}\widehat{x}}=\frac{1}{N}\sum _{k=1}^N{\widehat{x}}_k{\widehat{x}}_k^T.$$ (3.10)

Appendix A derives the maximum likelihood estimate of A for the ideal case of known source vectors X = (x₁, …, x_N),

$$\text{Known}\text{source}\text{vector}\text{case}:A_{\text{ML}}={\mathrm{\sum }}_{yx}{\mathrm{\sum }}_{xx}^{-1},$$

which is, of course, actually not computable since the actual source vectors are assumed to be hidden.

As an alternative to using the explicit solution 3.9, which requires an often prohibitive n × n inversion, we can obtain A_AML iteratively by gradient descent on equations 3.6 and 3.8,

$$\begin{array}{l}{\widehat{A}}_{\text{AML}}\leftarrow {\widehat{A}}_{\text{AML}}-\mu \frac{1}{N}\sum _{k=1}^N{e}_k{\widehat{x}}_k^T,\\ e_k={\widehat{A}}_{\text{AML}}{\widehat{x}}_k-y_k,k=1,\dots ,N,\end{array}$$ (3.11)

for an appropriate choice of the (possibly adaptive) positive step-size parameter μ. The iteration 3.11 can be initialized as Â_AML = Â.

A general iterative dictionary learning procedure is obtained by nesting the iteration 3.11 entirely within the iteration defined by repeatedly solving equation 3.5 every time a new estimate, Â_AML, of the dictionary becomes available. However, performing the optimization required in equation 3.5 is generally nontrivial (Olshausen & Field, 1996; Lewicki & Sejnowski, 2000). Recently, we have shown how the use of the FOCUSS algorithm results in an effective algorithm for performing the optimization required in equation 3.5 for the case when ν is gaussian (Rao & Kreutz-Delgado, 1998a; Engan et al., 1999). This approach solves equation 3.5 using the affine-scaling transformation (AST)-like algorithms recently proposed for the low-noise case (Rao & Kreutz-Delgado, 1997, 1999; Kreutz-Delgado & Rao, 1997) and extended by regularization to the nontrivial noise case (Rao & Kreutz-Delgado, 1998a; Engan et al., 1999). As discussed in section 2.5, for the current dictionary estimate, Â, a solution to the optimization problem, 3.5, is provided by the repeated iteration,

$${\widehat{x}}_k\leftarrow {\mathrm{\Pi }}^{-1}({\widehat{x}}_k){\widehat{A}}^T{(\beta ({\widehat{x}}_k)I+\widehat{A}{\mathrm{\Pi }}^{-1}({\widehat{x}}_k){\widehat{A}}^T)}^{-1}{y}_k,$$ (3.12)

k = 1, …, N, with Π(x) defined as in equation 3.18, given below. This is the regularized FOCUSS algorithm (Rao, 1998; Engan et al., 1999), which has an interpretation as an AST-like concave function minimization algorithm. The proposed dictionary learning algorithm alternates between iteration 3.12 and iteration 3.11 (or the direct batch solution given by equation 3.9 if the inversion is tractable). Extensive simulations show the ability of the AST-based algorithm to recover an unknown 20 × 30 dictionary matrix A completely (Engan et al., 1999).

3.2 Unknown, Random Dictionaries

We now generalize to the case where the dictionary A and the source vector set X = X^N = (x₁, …, x_N) are jointly random and unknown. We add the requirement that the dictionary is known to obey the constraint

$$A\in \mathcal{A}=\text{compact}\text{submanifold}\text{of}{\mathbb{R}}^{m\times n}.$$

A compact submanifold of ℝ^m×n is necessarily closed and bounded. On the constraint submanifold, the dictionary A has the prior probability density function P(A), which in the sequel we assume has the simple (uniform on 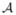) form,

$$P(A)=c\mathcal{X}(A\in \mathcal{A}),$$ (3.13)

where (·) is the indicator function and c is a positive constant chosen to ensure that

$$P(\mathcal{A})={\int }_{\mathcal{A}}P(A)dA=1.$$

The dictionary A and the elements of the set X are also all assumed to be mutually independent,

$$P(A,X)=P(A)P(X)=P(A)P_p(x_1),\dots ,P_p(x_N).$$

With the set of i.i.d. noise vectors, (ν₁, …, ν_N) also taken to be jointly random with, and independent of, A and X, the observation set Y = Y^N = (y₁, …, y_N) is assumed to be generated by the model 1.3. With these assumptions, we have

$$\begin{array}{l}P(A,X\mid Y)=P(Y\mid A,X)P(A,X)/P(Y)\\ =c\mathcal{X}(A\in \mathcal{A})P(Y\mid A,X)P(X)/P(Y)\\ =\frac{c\mathcal{X}(A\in \mathcal{A})}{P(Y)}\prod _{k=1}^{N}P(y_k\mid A,x_k)P_p(x_k)\\ =\frac{c\mathcal{X}(A\in \mathcal{A})}{P(Y)}\prod _{k=1}^N{P}_q(y-{Ax}_k)P_p(x_k),\end{array}$$ (3.14)

using the facts that the observations are conditionally independent and P(y_k | A, X) = P(y_k | A, x_k).

The jointly MAP estimates

$$({\widehat{A}}_{\text{MAP}},{\widehat{X}}_{\text{MAP}})=({\widehat{A}}_{\text{MAP}},{\widehat{x}}_{1,\text{MAP}},\dots ,{\widehat{x}}_{N,\text{MAP}})$$

are found by maximizing a posteriori probability density P(A, X | Y) simultaneously with respect to A ∈ and X. This is equivalent to minimizing the negative logarithm of P(A, X | Y), yielding the optimization problem,

$$({\widehat{A}}_{\text{MAP}},{\widehat{X}}_{\text{MAP}})=arg\underset{A\in \mathcal{A},X}{min}{\langle d_q(y-Ax)+\lambda d_p(x)\rangle }_N.$$ (3.15)

Note that this is a joint minimization of the sample average of the functional 2.4, and as such is a natural generalization of the single (with respect to the set of source vectors) optimization previously encountered in equation 3.6. By finding joint MAP estimates of A and X, we obtain a problem that is much more tractable than the one of finding the single MAP estimate of A (which involves maximizing the marginal posterior density P(A | Y)).

The requirement that A ∈ , where is a compact and hence bounded subset of ℝ^m×n, is sufficient for the optimization problem 3.15 to avoid the degenerate solution,⁶

$$\text{for}k=1,\dots ,N,y_k={Ax}_k,\text{with}\left|\right|A\left|\right|\to \infty \text{and}\left|\right|x_k\left|\right|\to 0.$$ (3.16)

This solution is possible for unbounded A because y = Ax is almost always solvable for x since learned overcomplete A’s are (generically) onto, and for any solution pair (A, x) the pair ( $\frac{1}{\alpha }A$, αx) is also a solution. This fact shows that the inverse problem of finding a solution pair (A, x) is generally ill posed unless A is constrained to be bounded (as we have explicitly done here) or the cost functional is chosen to ensure that bounded A’s are learned (e.g., by adding a term monotonic in the matrix norm ||A|| to the cost function in equation 3.15).

A variety of choices for the compact set are available. Obviously, since different choices of correspond to different a priori assumptions on the set of admissible matrices, A, the choice of this set can be expected to affect the performance of the resulting dictionary learning algorithm. We will consider two relatively simple forms for .

3.3 Unit Frobenius–Norm Dictionary Prior

For the i.i.d. q = 2 gaussian measurement noise case of equation 3.8, algorithms that provably converge (in the low step-size limit) to a local minimum of equation 3.15 can be readily developed for the very simple choice,

$${\mathcal{A}}_{\text{F}}=\{A\mid {\left|\right|A\left|\right|}_F=1\}\subset {\mathbb{R}}^{m\times n},$$ (3.17)

where ||A||_F denotes the Frobenius norm of the matrix A,

$${\left|\right|A\left|\right|}_F^2=\text{tr}(A^{T}A)\triangleq \text{trace}(A^{T}A),$$

and it is assumed that the prior P(A) is uniformly distributed on as per condition 3.13. As discussed in appendix A, is simply connected, and there exists a path in between any two matrices in .

Following the gradient factorization procedure (Kreutz-Delgado & Rao, 1997; Rao & Kreutz-Delgado, 1999), we factor the gradient of d(x) as

$$\nabla d(x)=\alpha (x)\mathrm{\Pi }(x)x,\alpha (x)>0,$$ (3.18)

where it is assumed that Π(x)is diagonal and positive definite for all nonzero x. For example, in the case where $d(x)={\left|\right|x\left|\right|}_p^p$,

$${\mathrm{\Pi }}^{-1}(x)=\text{diag}({\mid x[i]\mid }^{2-p}).$$ (3.19)

Factorizations for other diversity measures d(x) are given in Kreutz-Delgado and Rao (1997). We also define β(x) = λα(x). As derived and proved in appendix A, a learning law that provably converges to a minimum of equation 3.15 on the manifold 3.17 is then given by

$$\begin{array}{l}\frac{d}{dt}{\widehat{x}}_k=-{\mathrm{\Omega }}_k\{({\widehat{A}}^T\widehat{A}+\beta ({\widehat{x}}_k)\mathrm{\Pi }({\widehat{x}}_k)){\widehat{x}}_k-{\widehat{A}}^T{y}_k\},\\ \frac{d}{dt}\widehat{A}=-\mu (\delta \widehat{A}-\text{tr}({\widehat{A}}^T\delta \widehat{A})\widehat{A}),\mu >0,\end{array}$$ (3.20)

for k = 1, …, N, where  is initialized to ||Â||_F = 1, Ω_k are n × n positive definite matrices, and the “error” δÂis

$$\delta \widehat{A}={\langle e(\widehat{x}){\widehat{x}}^T\rangle }_N=\frac{1}{N}\sum _{k=1}^{N}e({\widehat{x}}_k){\widehat{x}}_k^T,e({\widehat{x}}_k)=\widehat{A}{\widehat{x}}_k-y_k,$$ (3.21)

which can be rewritten in the perhaps a more illuminating form (cf. equations 3.9 and 3.10),

$$\delta \widehat{A}=\widehat{A}{\mathrm{\sum }}_{\widehat{x}\widehat{x}}-{\mathrm{\sum }}_{y\widehat{x}}.$$ (3.22)

A formal convergence proof of equation 3.20 is given in appendix A, where it is also shown that the right-hand side of the second equation in 3.20 corresponds to projecting the error term δ onto the tangent space of , thereby ensuring that the derivative of  lies in the tangent space. Convergence of the algorithm to a local optimum of equation 3.15 is formally proved by interpreting the loss functional as a Lyapunov function whose time derivative along the trajectories of the adapted parameters (Â, X̂) is guaranteed to be negative definite by the choice of parameter time derivatives shown in equation 3.20. As a consequence of the La Salle invariance principle, the loss functional will decrease in value, and the parameters will converge to the largest invariant set for which the time derivative of the loss functional is identically zero (Khalil, 1996).

Equation 3.20 is a set of coupled (between  and the vectors x̂_k) nonlinear differential equations that correspond to simultaneous, parallel updating of the estimates  and x̂_k. This should be compared to the alternated separate (nonparallel) update rules 3.11 and 3.12 used in the AML algorithm described in section 3.1. Note also that (except for the trace term) the right-hand side of the dictionary learning update in equation 3.20 is of the same form as for the AML update law given in equation 3.11 (see also the discretized version of equation 3.20 given in equation 3.28 below). The key difference is the additional trace term in equation 3.20. This difference corresponds to a projection of the update onto the tangent space of the manifold 3.17, thereby ensuring a unit Frobenius norm (and hence boundedness) of the dictionary estimate at all times and avoiding the ill-posedness problem indicated in equation 3.16. It is also of interest to note that choosing Ω_k to be the positive-definite matrix,

$${\mathrm{\Omega }}_k={\eta }_k{({\widehat{A}}^T\widehat{A}+\beta ({\widehat{x}}_k)\mathrm{\Pi }({\widehat{x}}_k))}^{-1},{\eta }_k>0,$$ (3.23)

in equation 3.20, followed by some matrix manipulations (see equation A.18 in appendix A), yields the alternative algorithm,

$$\frac{d}{dt}{\widehat{x}}_k=-{\eta }_k\{{\widehat{x}}_k-{\mathrm{\Pi }}^{-1}({\widehat{x}}_k){\widehat{A}}^T{(\beta ({\widehat{x}}_k)I+\widehat{A}{\mathrm{\Pi }}^{-1}({\widehat{x}}_k){\widehat{A}}^T)}^{-1}{y}_k\}$$ (3.24)

with η_k > 0. In any event (regardless of the specific choice of the positive definite matrices Ω_k as shown in appendix A), the proposed algorithm out-lined here converges to a solution (x̂_k, Â), which satisfies the implicit and nonlinear relationships,

$$\begin{array}{l}{\widehat{x}}_k={\mathrm{\Pi }}^{-1}({\widehat{x}}_k){\widehat{A}}^T{(\beta ({\widehat{x}}_k)I+\widehat{A}{\mathrm{\Pi }}^{-1}({\widehat{x}}_k){\widehat{A}}^T)}^{-1}y,\\ \widehat{A}={\mathrm{\sum }}_{y\widehat{x}}^T{({\mathrm{\sum }}_{\widehat{x}\widehat{x}}-cI)}^{-1}\in {\mathcal{A}}_{\text{F}},\end{array}$$ (3.25)

for scalar c = tr(Â^TδÂ).

To implement the algorithm 3.20 (or the variant using equation 3.24) in discrete time, a first-order forward difference approximation at time t = t_l can be used,

$$\begin{array}{l}\frac{d}{dt}{\widehat{x}}_k(t_l)\approx \frac{{\widehat{x}}_k(t_{l+1})-{\widehat{x}}_k(t_l)}{t_{l+1}-t_l}\\ \triangleq \frac{{\widehat{x}}_k[l+1]-{\widehat{x}}_k[l]}{{\mathrm{\Delta }}_l}.\end{array}$$ (3.26)

Applied to equation 3.24, this yields

$$\begin{array}{l}{\widehat{x}}_k[l+1]=(1-{\mu }_l){\widehat{x}}_k[l]+{\mu }_l{\widehat{x}}_k^{\text{FOCUSS}}[l]\\ {\widehat{x}}_k^{\text{FOCUSS}}[l]={\mathrm{\Pi }}^{-1}({\widehat{x}}_k){\widehat{A}}^T{(\beta ({\widehat{x}}_k)I+\widehat{A}{\mathrm{\Pi }}^{-1}({\widehat{x}}_k){\widehat{A}}^T)}^{-1}{y}_k\\ {\mu }_l={\eta }_k{\mathrm{\Delta }}_l\ge 0.\end{array}$$ (3.27)

Similarly, discretizing the Â-update equation yields the A-learning rule, equation 3.28, given below. More generally, taking μ_l to have a value between zero and one, 0 ≤ μ_l ≤ 1 yields an updated value x̂_k[l + 1], which is a linear interpolation between the previous value x̂_k[l] and ${\widehat{x}}_k^{\text{FOCUSS}}[l]$.

When implemented in discrete time, and setting μ_l = 1, the resulting Bayesian learning algorithm has the form of a combined iteration where we loop over the operations,

$$\begin{array}{l}{\widehat{x}}_k\leftarrow {\mathrm{\Pi }}^{-1}({\widehat{x}}_k){\widehat{A}}^T{(\beta ({\widehat{x}}_k)I+\widehat{A}{\mathrm{\Pi }}^{-1}({\widehat{x}}_k){\widehat{A}}^T)}^{-1}{y}_k,\\ k=1,\dots ,N\text{and}\\ \widehat{A}\leftarrow \widehat{A}-\gamma (\delta \widehat{A}-\text{tr}({\widehat{A}}^T\delta \widehat{A})\widehat{A})\gamma >0.\end{array}$$ (3.28)

We call this FOCUSS-based, Frobenius-normalized dictionary-learning algorithm the FOCUSS-FDL algorithm. Again, this merged procedure should be compared to the separate iterations involved in the maximum likelihood approach given in equations 3.11 and 3.12. Equation 3.28, with δ given by equation 3.21, corresponds to performing a finite step-size gradient descent on the manifold . This projection in equation 3.28 of the dictionary update onto the tangent plane of (see the discussion in appendix A) ensures the well-behavedness of the MAP algorithm.⁷ The specific step-size choice μ_l = 1, which results in the first equation in equation 3.28, is discussed at length for the low-noise case in Rao and Kreutz-Delgado (1999).

3.4 Column-Normalized Dictionary Prior

Although mathematically very tractable, the unit-Frobenius norm prior, equation 3.17, appears to be somewhat too loose, judging from simulation results given below. In simulations with the Frobenius norm constraint , some columns of A can tend toward zero, a phenomenon that occurs more often in highly overcomplete A. This problem can be understood by remembering that we are using the d_p(x), p ≠ 0 diversity measure, which penalizes columns associated with terms in x with large magnitudes. If a column a_i has a small relative magnitude, the weight of its coefficient x[i] can be large, and it will be penalized more than a column with a larger norm. This leads to certain columns being underused, which is especially problematic in the overcomplete case.

An alternative, and more restrictive, form of the constraint set is obtained by enforcing the requirement that the columns a_i of A each be normalized (with respect to the Euclidean 2-norm) to the same constant value (Murray & Kreutz-Delgado, 2001). This constraint can be justified by noting that Ax can be written as the nonunique weighted sum of the columns a_i,

$$\begin{array}{l}Ax=\sum _{i=1}^n{a}_{i}x[i]=\sum _{i=1}^n\left(\frac{a_i}{{\alpha }_i}\right)({\alpha }_{i}x[i])=A^{\prime }{x}^{\prime },\\ \text{for}\text{any}{\alpha }_i>0,i=1,\dots ,n,\end{array}$$

showing that there is a column-wise ambiguity that remains even after the overall unit-Frobenius norm normalization has occurred, as one can now Frobenius-normalize the new matrix A′.

Therefore, consider the set of matrices on which has been imposed the column-wise constraint that

$${\mathcal{A}}_{\text{C}}=\left\{A\mid {\left|\right|a_i\left|\right|}^2=a_i^T{a}_i=\frac{1}{n},i=1,\dots ,n\right\}.$$ (3.29)

The set is an mn − n = n(m−1)–dimensional submanifold of ℝ^m×n. Note that every column of a matrix in has been normalized to the value $\frac{1}{\sqrt{n}}$. In fact, any constant value for the column normalization can be used (including the unit normalization), but, as shown in appendix B, the particular normalization of $\frac{1}{\sqrt{n}}$ results in being a proper submanifold of the mn − 1 dimensional unit Frobenius manifold ,

$${\mathcal{A}}_{\text{C}}\subset {\mathcal{A}}_{\text{F}},$$

indicating that a tighter constraint on the matrix A is being imposed. Again, it is assumed that the prior P(A) is uniformly distributed on in the manner of equation 3.13. As shown in appendix B, is simply connected.

A learning algorithm is derived for the constraint in appendix B, following much the same approach as in appendix A. Because the derivation of the x̂_k update to find sparse solutions does not depend on the form of the constraint , only the  update in algorithm 3.28 needs to be modified. Each column a_i is now updated independently (see equation B.17),

$$\begin{array}{l}{a}_i\leftarrow a_i-\gamma (I-{\widehat{a}}_i{\widehat{a}}_i^T)\delta a_i\\ i=1,\dots ,n,\end{array}$$ (3.30)

where δa_i is the ith column of δ in equation 3.21. We call the resulting column-normalized dictionary-learning algorithm the FOCUSS-CNDL algorithm. The implementation details of the FOCUSS-CNDL algorithm are presented in section 4.2.

4 Algorithm Implementation

The dictionary learning algorithms derived above are an extension of the FOCUSS algorithm used for obtaining sparse solutions to the linear inverse problem y = Ax to the case where dictionary learning is now required. We refer to these algorithms generally as FOCUSS-DL algorithms, with the unit Frobenius-norm prior-based algorithm denoted by FOCUSS-FDL and the column-normalized prior-base algorithm by FOCUSS-CNDL. In this section, the algorithms are stated in the forms implemented in the experimental tests, where it is shown that the column normalization-based algorithm achieves higher performance in the overcomplete dictionary case.

4.1 Unit Frobenius-Norm Dictionary Learning Algorithm

We now summarize the FOCUSS-FDL algorithm derived in section 3.3. For each of the data vectors y_k, we update the sparse source vectors x_k using the FOCUSS algorithm:

$$\begin{array}{l}{\mathrm{\Pi }}^{-1}({\widehat{x}}_k)=\text{diag}({\mid {\widehat{x}}_k[i]\mid }^{2-p})\\ {\widehat{x}}_k\leftarrow {\mathrm{\Pi }}^{-1}({\widehat{x}}_k){\widehat{A}}^T{({\lambda }_{k}I+\widehat{A}{\mathrm{\Pi }}^{-1}({\widehat{x}}_k){\widehat{A}}^T)}^{-1}{y}_k(\text{FOCUSS}),\end{array}$$ (4.1)

where λ_k = β(x̂_k) is the regularization parameter. After updating the N source vectors x_k, k = 1, …, n, the dictionary  is reestimated,

$$\begin{array}{l}{\mathrm{\sum }}_{y\widehat{x}}=\frac{1}{N}\sum _{k=1}^N{y}_k{\widehat{x}}_k^T\\ {\mathrm{\sum }}_{\widehat{x}\widehat{x}}=\frac{1}{N}\sum _{k=1}^N{\widehat{x}}_k{\widehat{x}}_k^T\\ \delta \widehat{A}=\widehat{A}{\mathrm{\sum }}_{\widehat{x}\widehat{x}}-{\mathrm{\sum }}_{y\widehat{x}}\\ \widehat{A}\leftarrow \widehat{A}-\gamma (\delta \widehat{A}-\text{tr}({\widehat{A}}^T\delta \widehat{A})\widehat{A}),\gamma >0,\end{array}$$ (4.2)

where γ controls the learning rate. For the experiments in section 5, the data block size is N = 100. During each iteration all training vectors are updated using equation 4.1, with a corresponding number of dictionary updates using equation 4.2. After each update of the dictionary Â, it is renormalized to have unit Frobenius norm, ||Â||_F = 1.

The learning algorithm is a combined iteration, meaning that the FOCUSS algorithm is allowed to run for only one iteration (not until full convergence) before the A update step. This means that during early iterations, the x̂_k are in general not sparse. To facilitate learning A, the covariances Σ_yx̂ and Σ_x̂x̂ are calculated with sparsified x̂_k that have all but the r̃ largest elements set to zero. The value of r̃ is usually set to the largest desired number of nonzero elements, but this choice does not appear to be critical.

The regularization parameter λ_k is taken to be a monotonically increasing function of the iteration number,

$${\lambda }_k={\lambda }_{max}tanh({10}^{-3}·(\mathit{iter}-1500))+1).$$ (4.3)

While this choice of λ_k does not have the optimality properties of the modified L-curve method (see section 2.5), it does not require a one-dimensional optimization for each x̂_k and so is much less computationally expensive. This is further discussed below.

4.2 Column Normalized Dictionary Learning Algorithm

The improved version of the algorithm called FOCUSS-CNDL, which provides increased accuracy especially in the overcomplete case, was proposed in Murray and Kreutz-Delgado (2001). The three key improvements are column normalization that restricts the learned Â, an efficient way of adjusting the regularization parameter λ_k, and reinitialization to escape from local optima.

The column-normalized learning algorithm discussed in section 3.4 and derived in appendix B is used. Because the x̂_k update does not depend on the constraint set , the FOCUSS algorithm in equation 4.1 is used to update N vectors, as discussed in section 4.1. After every N source vectors are updated, each column of the dictionary is then updated as

$$\begin{array}{l}{a}_i\leftarrow a_i-\gamma (I-{\widehat{a}}_i{\widehat{a}}_i^T)\delta a_i\\ i=1,\dots ,n,\end{array}$$ (4.4)

where δa_i are the columns of δÂ, which is found using equation 4.2. After updating each a_i, it is renormalized to ||a_i||² = 1/n by

$$a_i\leftarrow \frac{a_i}{\sqrt{n}\left|\right|a_i\left|\right|},$$ (4.5)

which also ensures that ||Â||_F = 1 as shown in section B.1.

The regularization parameter λ_k may be set independently for each vector in the training set, and a number of methods have been suggested, including quality of fit (which requires a certain level of reconstruction accuracy), sparsity (requiring a certain number of nonzero elements), and the L-curve which attempts to find an optimal trade-off (Engan, 2000). The L-curve method works well, but it requires solving a one-dimensional optimization for each λ_k, which becomes computationally expensive for large problems. Alternatively, we use a heuristic method that allows the trade-off between error and sparsity to be tuned for each application, while letting each training vector y_k have its own regularization parameter λ_k to improve the quality of the solution,

$${\lambda }_k={\lambda }_{max}\left(1-\frac{\left|\right|y_k-\widehat{A}{\widehat{x}}_k\left|\right|}{\left|\right|y_k\left|\right|}\right),{\lambda }_k,{\lambda }_{max}>0.$$ (4.6)

For data vectors that are represented accurately, λ_k will be large, driving the algorithm to find sparser solutions. If the SNR can be estimated, we can set λ_max = (SNR)⁻¹.

The optimization problem, 3.15, is concave when p ≤ 1, so there will be multiple local minima. The FOCUSS algorithm is guaranteed to converge only to one of these local minima, but in some cases, it is possible to determine when that has happened by noticing if the sparsity is too low. Periodically (after a large number of iterations), the sparsity of the solutions x̂_k is checked, and if found too low, x̂_k is reinitialized randomly. The algorithm is also sensitive to initial conditions, and prior information may be incorporated into the initialization to help convergence to the global solution.

5 Experimental Results

Experiments were performed using complete dictionaries (n = m) and over-complete dictionaries (n > m) on both synthetically generated data and natural images. Performance was measured in a number of ways. With synthetic data, performance measures include the SNR of the recovered sources x_k compared to the true generating source and comparing the learned dictionary with the true dictionary. For images of natural scenes, the true underlying sources are not known, so the accuracy and efficiency of the image coding are found.

5.1 Complete Dictionaries: Comparison with ICA

To test the FOCUSS-FDL and FOCUSS-CNDL algorithms, simulated data were created following the method of Engan et al. (1999) and Engan (2000). The dictionary A of size 20×20 was created by drawing each element a_ij from a normal distribution with μ = 0, σ² = 1 (written as 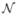(0, 1)) followed by a normalization to ensure that ||A||_F = 1. Sparse source vectors x_k, k = 1, …, 1000 were created with r = 4 nonzero elements, where the r nonzero locations are selected at random (uniformly) from the 20 possible locations. The magnitudes of each nonzero element were also drawn from 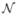(0, 1) and limited so that |x_kl| > 0.1. The input data y_k were generated using y = Ax (no noise was added).

For the first iteration of the algorithm, the columns of the initialization estimate, Â_init, were taken to be the first n = 20 training vectors y_k. The initial x_k estimates were then set to the pseudoinverse solution ${\widehat{x}}_k={\widehat{A}}_{\mathit{init}}^T{({\widehat{A}}_{\mathit{init}}{\widehat{A}}_{\mathit{init}}^T)}^{-1}{y}_k$. The constant parameters of the algorithm were set as follows: p = 1.0, γ = 1.0, and λ_max = 2 × 10⁻³ (low noise, assumed SNR ≈ 27 dB). The algorithms were run for 200 iterations through the entire data set, and during each iteration, Â was updated after updating 100 data vectors x̂_k.

To measure performance, the SNR between the recovered sources x̂_k and the the true sources x_k were calculated. Each element x_k[i] for fixed i was considered as a time-series vector with 1000 elements, and SNR_i for each was found using

$${\text{SNR}}_i=10{log}_{10}\left(\frac{{\left|\right|x_k[i]\left|\right|}^2}{{\left|\right|x_k[i]-{\widehat{x}}_k[i]\left|\right|}^2}\right).$$ (5.1)

The final SNR is found by averaging SNR_i over the i = 1, …, 20 vectors and 20 trials of the algorithms. Because the dictionary A is learned only to within a scaling factor and column permutations, the learned sources must be matched with corresponding true sources and scaled to unit norm before the SNR calculation is done.

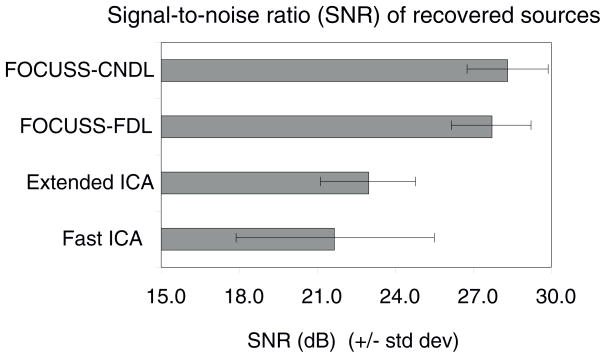
The FOCUSS-FDL and FOCUSS-CNDL algorithms were compared with extended ICA (Lee, Girolami, & Sejnowski, 1999) and Fastica⁸ (Hyvärinen et al., 1999). Figure 1 shows the SNR for the tested algorithms. The SNR for FOCUSS-FDL is 27.7 dB, which is a 4.7 dB improvement over extended ICA, and for FOCUSS-CNDL, the SNR is 28.3 dB. The average run time for FOCUSS-FDL/CNDL was 4.3 minutes, for FastICA 0.10 minute, and for extended ICA 0.19 minute on a 1.0 GHz Pentium III Xeon computer.

Figure 1.

Comparison between FOCUSS-FDL, FOCUSS-CNDL, extended ICA, and FastICA on synthetically generated data with a complete dictionary A, size 20 × 20. The SNR was computed between the recovered sources x̂_k and the true sources x_k. The mean SNR and standard deviation were computed over 20 trials.

5.2 Overcomplete Dictionaries

To test the ability to recover the true A and x_k solutions in the overcomplete case, dictionaries of size 20 × 30 and 64 × 128 were generated. Diversity r was set to fixed values (4 and 7) and uniformly randomly (5–10 and 10–15). The elements of A and the sources x_k were created as in section 5.1.

The parameters were set as follows: p = 1.0, γ = 1.0, λ_max = 2 × 10⁻³. The algorithms were run for 500 iterations through the entire data set, and during each iteration, Â was updated after updating 100 data vectors x̂_k.

As a measure of performance, we find the number of columns of A that were matched during learning. Because A can be learned only to within column permutations and sign and scale changes, the columns are normalized so that ||â_i|| = ||a_j|| = 1, and  is rearranged columnwise so that â_j is given the index of the closest match in A (in the minimum two-norm sense). A match is counted if

$$1-\mid a_i^T{\widehat{a}}_i\mid <\mathrm{0.01.}$$ (5.2)

Similarly, the number of matching x̂_k are counted (after rearranging the elements in accordance with the indices of the rearranged Â),

$$1-\mid x_i^T{\widehat{x}}_i\mid <\mathrm{0.05.}$$ (5.3)

If the data are generated by an A that is not column normalized, other measures of performance need to be used to compare x_k and x̂_k.

The performance is summarized in Table 1, which compares the FOCUSS-FDL with the column-normalized algorithm (FOCUSS-CNDL). For the 20 × 30 dictionary, 1000 training vectors were used, and for the 64×128 dictionary 10,000 were used. Results are averaged over four or more trials. For the 64 × 128 matrix and r = 10–15, FOCUSS-CNDL is able to recover 99.5% (127.4/128) of the columns of A and 94.6% (9463/10,000) of the solutions x_k to within the tolerance given above. This shows a clear improvement over FOCUSS-FDL, which learns only 80.3% of the A columns and 40.1% of the solutions x_k.

Table 1.

Synthetic Data Results.

Algorithm	Size of A	Diversity, r	Learned A Columns			Learned x
			Average	SD	%	Average	SD	%
FOCUSS-FDL	20 × 30	7	25.3	3.4	84.2	675.9	141.0	67.6
FOCUSS-CNDL	20 × 30	7	28.9	1.6	96.2	846.8	97.6	84.7
FOCUSS-CNDL	64 × 128	7	125.3	2.1	97.9	9414.0	406.5	94.1
FOCUSS-CNDL	64 × 128	5–10	126.3	1.3	98.6	9505.5	263.8	95.1
FOCUSS-FDL	64 × 128	10–15	102.8	4.5	80.3	4009.6	499.6	40.1
FOCUSS-CNDL	64 × 128	10–15	127.4	1.3	99.5	9463.4	330.3	94.6

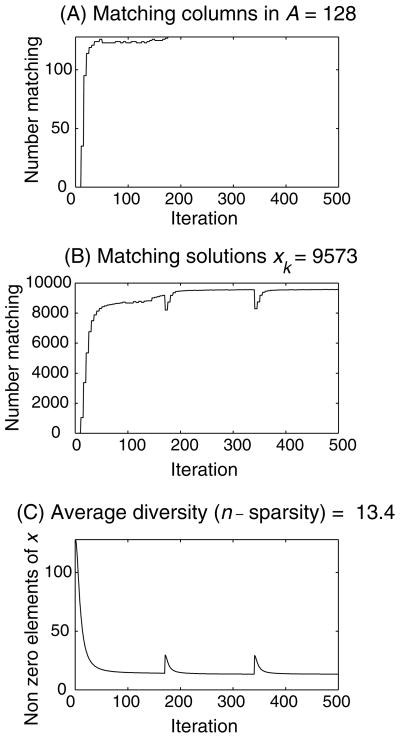
Learning curves for one of the trials of this experiment (see Figure 2) show that most of the columns of A are learned quickly within the first 100 iterations, and that the diversity of the solutions drops to the desired level. Figure 2b shows that it takes somewhat longer to learn the x_k correctly and that reinitialization of the low sparsity solutions (at iterations 175 and 350) helps to learn additional solutions. Figure 2c shows the diversity at each iteration, measured as the average number of elements of each x̂_k that are larger than 1 × 10⁻⁴.

Figure 2.

Performance of the FOCUSS-CNDL algorithm with overcomplete dictionary A, size 64 × 128. (a) Number of correctly learned columns of A at each iteration. (b) Number of sources x_k learned. (c) Average diversity (n-sparsity) of the x_k. The spikes in b and c indicate where some solutions x̂_k were reinitialized because they were not sparse enough.

5.3 Image Data Experiments

Previous work has shown that learned basis functions can be used to code data more efficiently than traditional Fourier or wavelet bases (Lewicki & Olshausen, 1999). The algorithm for finding overcomplete bases in Lewicki and Olshausen (1999) is also designed to solve problem 1.1 but differs from our method in a number of ways, including using only the Laplacian prior (p = 1), and using conjugate gradient optimization for finding sparse solutions (whereas we use the FOCUSS algorithm). It is widely believed that overcomplete representations are more efficient than complete bases, but in Lewicki and Olshausen (1999), the overcomplete code was less efficient for image data (measured in bits per pixel entropy), and it was suggested that different priors could be used to improve the efficiency. Here, we show that our algorithm is able to learn more efficient overcomplete codes for priors with p < 1.

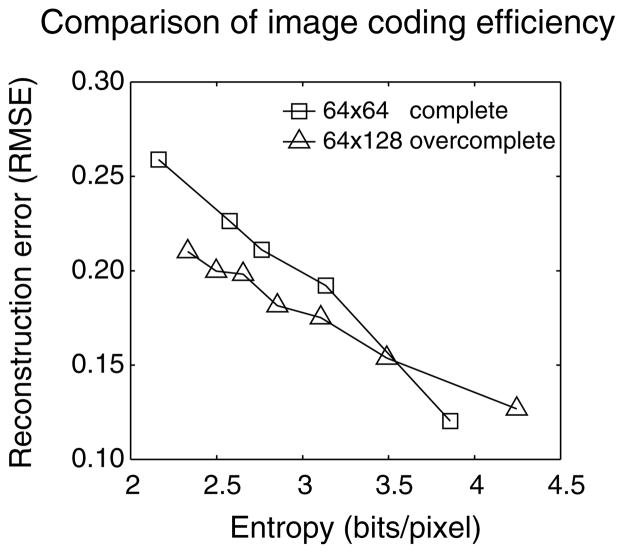
The training data consisted of 10,000 8 × 8 image patches drawn at random from black and white images of natural scenes. The parameter p was varied from 0.5–1.0, and the FOCUSS-CNDL algorithm was trained for 150 iterations. The complete dictionary (64 × 64) was compared with the 2× overcomplete dictionary (64 × 128). Other parameters were set: γ = 0.01, λ_max = 2 × 10⁻³. The coding efficiency was measured using the entropy (bits per pixel) method described in Lewicki and Olshausen (1999). Figure 3 plots the entropy versus reconstruction error (root mean square error, RMSE) and shows that when p < 0.9, the entropy is less for the overcomplete representation at the same RMSE.

Figure 3.

Comparing the coding efficiency of complete and 2× overcomplete representations on 8×8 pixel patches drawn from natural images. The points on the curve are the results from different values of p, at the bottom right, p = 1.0, and at the top left, p = 0.5. For smaller p, the overcomplete case is more efficient at the same level of reconstruction error (RMSE).

An example of coding an entire image is shown in Figure 4. The original test image (see Figure 4a) of size 256 × 256 was encoded using the learned dictionaries. Patches from the test image were not used during training. Table 2 gives results for low- and high-compression cases. In both cases, coding with the overcomplete dictionary (64×128) gives higher compression (lower bits per pixel) and lower error (RMSE). For the high-compression case (see Figures 4b and 4c), the 64 × 128 overcomplete dictionary gives compression of 0.777 bits per pixel at error 0.328, compared to the 64 × 64 complete dictionary at 0.826 bits per pixel at error 0.329. The amount of compression was selected by adjusting λ_max (the upper limit of the regularization parameter). For high compression, λ_max = 0.02, and for low compression, λ_max = 0.002.

Figure 4.

Image compression using complete and overcomplete dictionaries. Coding with an overcomplete dictionary is more efficient (fewer bits per pixel) and more accurate (lower RMSE). (a) Original image of size 256 × 256 pixels. (b) Compressed with 64×64 complete dictionary to 0.826 bits per pixel at RMSE = 0.329. (c) Compressed with 64 × 128 overcomplete dictionary to 0.777 bits per pixel at RMSE = 0.328.

Table 2.

Image Compression Results.

Dictionary Size	p	Compression (bits/pixel)	RMSE	Average Diversity
64 × 64	0.5	2.450	0.148	17.3
64 × 128	0.6	2.410	0.141	15.4
64 × 64	0.5	0.826	0.329	4.5
64 × 128	0.6	0.777	0.328	4.0

6 Discussion and Conclusions

We have applied a variety of tools and perspectives (including ideas drawn from Bayesian estimation theory, nonlinear regularized optimization, and the theory of majorization and convex analysis) to the problem of developing algorithms capable of simultaneously learning overcomplete dictionaries and solving sparse source-vector inverse problems.

The test experiment described in section 5.2 is a difficult problem designed to determine if the proposed learning algorithm can solve for the known true solutions for A and the spare source vectors x_k to the underdetermined inverse problem y_k = Ax_k. Such testing, which does not appear to be regularly done in the literature, shows how well an algorithm can extract stable and categorically meaningful solutions from synthetic data. The ability to perform well on such test inverse problems would appear to be at least a necessary condition for an algorithm to be trustworthy in domains where a physically or biologically meaningful sparse solution is sought, such as occurs in biomedical imaging, geophysical seismic sounding, and multitarget tracking.

The experimental results presented in section 5.2 show that the FOCUSS-DL algorithms can recover the dictionary and the sparse sources vectors. This is particularly gratifying when one considers that little or no optimization of the algorithm parameters has been done. Furthermore, the convergence proofs given in the appendixes show convergence only to local optima, whereas one expects that there will be many local optima in the cost function because of the concave prior and the generally multimodal form of the cost function.

One should note that algorithm 3.28 was constructed precisely with the goal of solving inverse problems of the type considered here, and therefore one must be careful when comparing the results given here with other algorithms reported in the literature. For instance, the mixture-of-gaussians prior used in Attias (1999) does not necessarily enforce sparsity. While other algorithms in the literature might perform well on this test experiment, to the best of our knowledge, possible comparably performing algorithms such as Attias (1999), Girolami (2001), Hyvärinen et al. (1999), and Lewicki and Olshausen (1999) have not been tested on large, overcomplete matrices to determine their accuracy in recovering A, and so any comparison along these lines would be premature. In section 5.1, the FOCUSS-DL algorithms were compared to the well-known extended ICA and FastICA algorithms in a more conventional test with complete dictionaries. Performance was measured in terms of the accuracy (SNR) of the recovered sources x_k, and both FOCUSS-DL algorithms were found to have significantly better performance (albeit with longer run times).

We have also shown that the FOCUSS-CNDL algorithm can learn an over-complete representation, which can encode natural images more efficiently than complete bases learned from data (which in turn are more efficient than standard nonadaptive bases, such as Fourier or wavelet bases; Lewicki & Olshausen, 1999). Studies of the human visual cortex have shown a higher degree of overrepresentation of the fovea compared to the other mammals, which suggests an interesting connection between overcomplete representations and visual acuity and recognition abilities (Popovic & Sjöstrand, 2001).

Because the coupled dictionary learning and sparse-inverse solving algorithms are merged and run in parallel, it should be possible to run the algorithms in real time to track dictionary evolution in quasistationary environments once the algorithm has essentially converged. One way to do this would be to constantly present randomly encountered new signals, y_k, to the algorithm at each iteration instead of the original training set. One also has to ensure that the dictionary learning algorithm is sensitive to the new data so that dictionary tracking can occur. This would be done by an appropriate adaptive filtering of the current dictionary estimate driven by the new-data derived corrections, similar to techniques used in the adaptive filtering literature (Kalouptsidis & Theodoridis, 1993).

Appendix A: The Frobenius-Normalized Prior Learning Algorithm

Here we provide a derivation of the algorithm 3.20–3.21 and prove that it converges to a local minimum of equation 3.15 on the manifold = {A | ||A||_F = 1} ⊂ ℝ^m×n defined in equation 3.17. Although we focus on the development of the learning algorithm on , the derivations in sections A.2 and A.3, and the beginning of subsection are done for a general constraint manifold .

A.1 Admissible Matrix Derivatives

A.1.1 The Constraint Manifold

In order to determine the structural form of admissible derivatives, $\stackrel{.}{A}=\frac{d}{dt}A$ for matrices belonging to ,⁹ it is useful to view as embedded in the finite-dimensional Hilbert space of matrices, ℝ^m×n, with inner product

$$\langle A,B\rangle =\text{tr}(A^{T}B)=\text{tr}(B^{T}A)=\text{tr}({AB}^T)=\text{tr}({BA}^T).$$

The corresponding matrix norm is the Frobenius norm,

$$\left|\right|A\left|\right|={\left|\right|A\left|\right|}_F=\sqrt{\text{tr}{A}^{T}A}=\sqrt{\text{tr}{AA}^T}.$$

We will call this space the Frobenius space and the associated inner product the Frobenius inner product. It is useful to note the isometry,

$$A\in {\mathbb{R}}^{m\times n}\iff \mathbf{A}=\text{vec}(A)\in {\mathbb{R}}^{mn},$$

where A is the mn-vector formed by stacking the columns of A. Henceforth, bold type represents the stacked version of a matrix (e.g., B = vec(B)). The stacked vector A belongs to the standard Hilbert space ℝ^mn, which we shall henceforth refer to as the stacked space. This space has the standard Euclidean inner product and norm,

$$\langle \mathbf{A},\mathbf{B}\rangle ={\mathbf{A}}^T\mathbf{B},\left|\right|\mathbf{A}\left|\right|=\sqrt{{\mathbf{A}}^T\mathbf{A}}.$$

It is straightforward to show that

$$\langle A,B\rangle =\langle \mathbf{A},\mathbf{B}\rangle \text{and}\left|\right|A\left|\right|=\left|\right|\mathbf{A}\left|\right|.$$

In particular, we have

$$A\in {\mathcal{A}}_{\text{F}}\iff \left|\right|A\left|\right|=\left|\right|\mathbf{A}\left|\right|=1.$$

Thus, the manifold in equation 3.17 corresponds to the (mn−1)–dimensional unit sphere in the stacked space, ℝ^mn (which, with a slight abuse of notation, we will continue to denote by ). It is evident that is simply connected so that a path exists between any two elements of and, in particular, a path exists between any initial value for a dictionary, A_init ∈ , used to initialize a learning algorithm, and a desired target value, A_final ∈ .¹⁰

A.1.2 Derivatives on : The Tangent Space T

Determining the form of admissible derivatives on equation 3.17 is equivalent to determining the form of admissible derivatives on the unit ℝ^mn–sphere. On the unit sphere, we have the well-known fact that

$$\mathbf{A}\in {\mathcal{A}}_{\text{F}}\Rightarrow \frac{d}{dt}{\left|\right|\mathbf{A}\left|\right|}^2=2{\mathbf{A}}^T\stackrel{.}{\mathbf{A}}=0\Rightarrow \stackrel{.}{\mathbf{A}}\perp \mathbf{A}.$$

This shows that the general form of Ȧ is Ȧ = ΛQ, where Q is arbitrary and

$$\mathbf{\Lambda }=\left(\mathbf{I}-\frac{\mathbf{A}{\mathbf{A}}^T}{{\left|\right|\mathbf{A}\left|\right|}^2}\right)=(\mathbf{I}-\mathbf{A}{\mathbf{A}}^T)$$ (A.1)

is the stacked space projection operator onto the tangent space of the unit ℝ^mn–sphere at the point A (note that we used the fact that ||A|| = 1). The projection operator Λ is necessarily idempotent, Λ = Λ². Λ is also self-adjoint, Λ = Λ^*, where the adjoint operator Λ^* is defined by the requirement that

$$\langle {\mathbf{\Lambda }}^{\ast }{\mathbf{Q}}_1,{\mathbf{Q}}_2\rangle =\langle {\mathbf{Q}}_1,\mathbf{\Lambda }{\mathbf{Q}}_2\rangle ,\text{for}\text{all}{\mathbf{Q}}_{\mathbf{1}},{\mathbf{Q}}_2\in {\mathbb{R}}^{mn},$$

showing that Λ is an orthogonal projection operator. In this case, Λ^* = Λ^T, so that self-adjointness corresponds to Λ being symmetric. One can readily show that an idempotent, self-adjoint operator is nonnegative, which in this case corresponds to the symmetric, idempotent operator Λ being a positive semidefinite matrix.

This projection can be easily rewritten in the Frobenius space,

$$\begin{array}{l}\stackrel{.}{\mathbf{A}}=\mathbf{\Lambda }\mathbf{Q}=\mathbf{Q}-\langle \mathbf{A},\mathbf{Q}\rangle \mathbf{A}\iff \stackrel{.}{A}=\mathrm{\Lambda }Q=Q-\langle A,Q\rangle A\\ =Q-\text{tr}(A^{T}Q)A.\end{array}$$ (A.2)

Of course, this result can be derived directly in the Frobenius space using the fact that

$$A\in {\mathcal{A}}_{\text{F}}\Rightarrow \frac{d}{dt}{\left|\right|A\left|\right|}^2=2\langle A,\stackrel{.}{A}\rangle =2\text{tr}(A^T\stackrel{.}{A})=0,$$

from which it is directly evident that

$$\stackrel{.}{A}\in T{\mathcal{A}}_{\text{F}}\text{at}A\in {\mathcal{A}}_{\text{F}}\iff \langle A,\stackrel{.}{A}\rangle =\text{tr}{A}^T\stackrel{.}{A}=0,$$ (A.3)

and therefore Ȧ must be of the form¹¹

$$\stackrel{.}{A}=\mathrm{\Lambda }Q=Q-\frac{\text{tr}(A^{T}Q)}{\text{tr}(A^{T}A)}A=Q-\text{tr}(A^{T}Q)A.$$ (A.4)

One can verify that Λ is idempotent and self-adjoint and is therefore a nonnegative, orthogonal projection operator. It is the orthogonal projection operator from ℝ^m×n onto the tangent space T.

In the stacked space (with some additional abuse of notation), we represent the quadratic form for positive semidefinite symmetric matrices W as

$${\left|\right|\mathbf{A}\left|\right|}_{\mathbf{W}}^2={\mathbf{A}}^T\mathbf{WA}.$$

Note that this defines a weighted norm if, and only if, W is positive definite, which might not be the case by definition. In particular, when W = Λ, the quadratic form ${\left|\right|\mathbf{A}\left|\right|}_{\mathbf{\Lambda }}^2$ is only positive semidefinite. Finally, note from equation A.4 that ∀A ∈ ,

$$\mathrm{\Lambda }Q=0\iff Q=cA,\text{with}c=\text{tr}(A^{T}Q).$$ (A.5)

A.2 Minimizing the Loss Function over a General Manifold

Consider the Lyapunov function,

$$V_N(X,A)={\langle d_q(y-Ax)+\lambda d_p(x)\rangle }_N,A\in \mathcal{A},$$ (A.6)

where is some arbitrary but otherwise appropriately defined constraint manifold associated with the prior, equation 3.13. Note that this is precisely the loss function to be minimized in equation 3.15. If we can determine smooth parameter trajectories (i.e., a parameter-vector adaptation rule) (Ẋ, Ȧ) such that along these trajectories V̇(X, A) ≤ 0, then as a consequence of the La Salle invariance principle (Khalil, 1996), the parameter values will converge to the largest invariant set (of the adaptation rule viewed as a nonlinear dynamical system) contained in the set

$$\mathrm{\Gamma }=\{(X,A)\mid {\stackrel{.}{V}}_N(X,A)\equiv 0\text{and}A\in \mathcal{A}\}.$$ (A.7)

The set Γ contains the local minima of V_N. With some additional technical assumptions (generally dependent on the choice of adaptation rule), the elements of Γ will contain only local minima of V_N.

Assuming the i.i.d. q = 2 gaussian measurement noise case of equation 3.8,¹² the loss (Lyapunov) function to be minimized is then

$$V_N(X,A)={\langle \frac{1}{2}{\left|\right|Ax-y\left|\right|}^2+\lambda d_p(x)\rangle }_N,A\in \mathcal{A},$$ (A.8)

which is essentially the loss function to be minimized in equation 3.15.¹³

Suppose for the moment, as in equations 3.4 through 3.9, that X is assumed to be known, and note that then (ignoring constant terms depending on X and Y) V_N can be rewritten as

$$\begin{array}{l}{V}_N(A)={\langle \text{tr}(Ax-y){(Ax-y)}^T\rangle }_N\\ ={\langle \text{tr}({\mathit{Axx}}^T{A}^T)-2\text{tr}({\mathit{Axy}}^T)+\text{tr}({yy}^T)\rangle }_N\\ =\text{tr}A{\mathrm{\sum }}_{xx}{A}^T-2\text{tr}A{\mathrm{\sum }}_{xy}\\ V_N(A)=\text{tr}\{A{\mathrm{\sum }}_{xx}{A}^T-2A{\mathrm{\sum }}_{xy}\},\end{array}$$

for Σ_xx and ${\mathrm{\sum }}_{xy}={\mathrm{\sum }}_{yx}^T$ defined as in equation 3.10. Using standard results from matrix calculus (Dhrymes, 1984), we can show that V_N(A) is minimized by the solution 3.9. This is done by setting

$$\frac{\partial }{\partial A}{V}_N(\widehat{A})=0,$$

and using the identities (valid for W symmetric)

$$\frac{\partial }{\partial A}\text{tr}{\mathit{AWA}}^T=2AW\text{and}\frac{\partial }{\partial A}\text{tr}AB=B^T.$$

This yields (assuming that Σ_xx is invertible),

$$\begin{array}{c}\frac{\partial }{\partial A}{V}_N(\widehat{A})=2\widehat{A}{\mathrm{\sum }}_{xx}-2{\mathrm{\sum }}_{xy}^T=2(\widehat{A}{\mathrm{\sum }}_{xx}-{\mathrm{\sum }}_{yx})=0,\\ \Rightarrow \widehat{A}={\mathrm{\sum }}_{y\widehat{x}}{\mathrm{\sum }}_{\widehat{x}\widehat{x}}^{-1},\end{array}$$

which is equation 3.9, as claimed. For Σ_xx nonsingular, the solution is unique and globally optimal. This is, of course, a well-known result.

Now return to the general case, equation A.8, where both X and A are unknown. For the data indexed by k = 1, …, N, define the quantities

$$d_k=d_p(x_k),e(x)=Ax-y,\text{and}{e}_k={Ax}_k-y_k.$$

The loss function and its time derivative can be written,

$$\begin{array}{l}{V}_N(X,A)={\langle \frac{1}{2}{e}^T(x)e(x)+\lambda d_p(x)\rangle }_N\\ {\stackrel{.}{V}}_N(X,A)={\langle e^T(x)\stackrel{.}{e}(x)+\lambda {\nabla }^T{d}_p(x)\stackrel{.}{x}\rangle }_N\\ ={\langle e^T(x)(A\stackrel{.}{x}+\stackrel{.}{A}x)+\lambda {\nabla }^T{d}_p(x)\stackrel{.}{x}\rangle }_N.\end{array}$$

Then, to determine an appropriate adaptation rule, note that

$${\stackrel{.}{V}}_N=T_1+T_2,$$ (A.9)

where

$$T_1={\langle (e^T(x)A+\lambda {\nabla }^T{d}_p(x))\stackrel{.}{x}\rangle }_N=\frac{1}{N}\sum _{k=1}^N(e_k^{T}A+\lambda {\nabla }^T{d}_k){\stackrel{.}{x}}_k$$ (A.10)

and

$$T_2={\langle e^T(x)\stackrel{.}{A}x\rangle }_N=\frac{1}{N}\sum _{k=1}^N{e}_k^T\stackrel{.}{A}{x}_k.$$ (A.11)

Enforcing the separate conditions

$$T_1\le 0\text{and}{T}_2\le 0,$$ (A.12)

(as well as the additional condition that A ∈ ) will be sufficient to ensure that V̇_N ≤ 0 on . In this case, the solution-containing set Γ of equation A.7 is given by

$$\mathrm{\Gamma }=\{(X,A)\mid T_1(X,A)\equiv 0,T_2(X,A)\equiv 0\text{and}A\in \mathcal{A}\}.$$ (A.13)

Note that if A is known and fixed, then T₂ ≡ 0, and only the first condition of equation A.12 (which enforces learning of the source vectors, x_k) is of concern. Contrawise, if source vectors x_k, which ensure that e(x_k) = 0 are fixed and known, then T₁ ≡ 0, and the second condition of equation A.12 (which enforces learning of the dictionary matrix, A) is at issue.

A.3 Obtaining the x_k Solutions with the FOCUSS Algorithm

We now develop the gradient factorization-based derivation of the FOCUSS algorithm, which provides estimates of x_k while satisfying the first convergence condition of equation A.12. The constraint manifold is still assumed to be arbitrary. To enforce the condition T₁ ≤ 0 and derive the first adaptation rule given in equation 3.20, we note that we can factor ∇d_k = ∇d(x_k) as (Kreutz-Delgado & Rao, 1997; Rao & Kreutz-Delgado, 1999)

$$\nabla d_k={\alpha }_k{\mathrm{\Pi }}_k{x}_k$$

with α_k = α_xk > 0 and Π_xk = Π_k positive definite and diagonal for all nonzero x_k. Then, defining β_k = λα_k > 0 and selecting an arbitrary set of (adaptable) symmetric positive-definite matrices Ω_k, we choose the learning rule

$$\begin{array}{l}{\stackrel{.}{x}}_k=-{\mathrm{\Omega }}_k\{A^T{e}_k+\lambda \nabla d_k\}=-{\mathrm{\Omega }}_k\{(A^{T}A+{\beta }_k{\mathrm{\Pi }}_k)x_k-A^T{y}_k\},\\ k=1,\dots ,N,\end{array}$$ (A.14)

which is the adaptation rule for the state estimates x_k = x̂_k given in the first line of equation 3.20. With this choice, we obtain

$$\begin{array}{l}{T}_1=-{\langle {\left|\right|A^{T}e(x)+\lambda \nabla d(x)\left|\right|}_{\mathrm{\Omega }}^2\rangle }_N\\ =-\frac{1}{N}\sum _{k=1}^N{\left|\right|A^T{e}_k+\lambda \nabla d_k\left|\right|}_{{\mathrm{\Omega }}_k}^2\\ =-\frac{1}{N}\sum _{k=1}^N{\left|\right|(A^{T}A+{\beta }_k{\mathrm{\Pi }}_k)x_k-A^T{y}_k\left|\right|}_{{\mathrm{\Omega }}_k}^2\le 0,\end{array}$$ (A.15)

as desired. Assuming convergence to the set A.13 (which will be seen to be the case after we show below how to ensure that we also have T₂ ≤ 0), we will asymptotically obtain (reintroducing the “hat” notation to now denote converged parameter estimates)

$${\left|\right|({\widehat{A}}^T\widehat{A}+{\beta }_k{\mathrm{\Pi }}_k){\widehat{x}}_k-{\widehat{A}}^T{y}_k\left|\right|}_{{\mathrm{\Omega }}_k}^2\equiv 0,k=1,\dots ,N,$$

which is equivalent to

$${\widehat{x}}_k={({\widehat{A}}^T\widehat{A}+{\beta }_k{\mathrm{\Pi }}_k)}^{-1}{\widehat{A}}^T{y}_k,k=1,\dots ,N,$$ (A.16)

at convergence. This is also equivalent to the condition given in the first line of equation 3.25, as shown below.

Exploiting the fact that Ω_k in equation A.14 are arbitrary (subject to the symmetry and positive-definiteness constraint), let us make the specific choice shown in equation 3.23,

$${\mathrm{\Omega }}_k={\eta }_k{(A^{T}A+{\beta }_k{\mathrm{\Pi }}_k)}^{-1},{\eta }_k>0,k=1,\dots ,N.$$ (A.17)

Also note the (trivial) identity,

$$(A^{T}A+\beta \mathrm{\Pi }){\mathrm{\Pi }}^{-1}{A}^T=A^T(A{\mathrm{\Pi }}^{-1}{A}^T+\beta I),$$

which can be recast nontrivially as

$${(A^{T}A+\beta \mathrm{\Pi })}^{-1}{A}^T={\mathrm{\Pi }}^{-1}{A}^T{(\beta I+A{\mathrm{\Pi }}^{-1}{A}^T)}^{-1}.$$ (A.18)

With equations A.17 and A.18, the learning rule, A.14, can be recast as

$${\stackrel{.}{x}}_k=-{\eta }_k\{x_k-{\mathrm{\Pi }}_k^{-1}{A}^T{({\beta }_{k}I+A{\mathrm{\Pi }}_k^{-1}{A}^T)}^{-1}{y}_k\},k=1,\dots ,N,$$ (A.19)

which is the alternative learning algorithm, 3.24. At convergence (when T₁ ≡ 0) we have the condition shown in the first line of equation 3.25,

$${\widehat{x}}_k={\mathrm{\Pi }}^{-1}{\widehat{A}}^T{({\beta }_{k}I+\widehat{A}{\mathrm{\Pi }}^{-1}{\widehat{A}}^T)}^{-1}{y}_k.$$ (A.20)

This also follows from the convergence condition A.16 and the identity A.18, showing that the result, A.20, is independent of the specific choice of Ω_k > 0. Note from equations A.14 and A.15 that T₁ ≡ 0 also results in ẋ_k ≡ 0 for k = 1, …, N, so that we will have converged to constant values, x̂_k, which satisfy equation A.20.

For the case of known, fixed A, the learning rule derived here will converge to sparse solutions, x_k, and when discretized as in section 3.3, yields equation 3.27, which is the known dictionary FOCUSS algorithm (Rao & Kreutz-Delgado, 1998a, 1999).

Note that the derivation of the sparse source-vector learning algorithm here, which enforces the condition T₁ ≤ 0, is entirely independent of any constraints placed on A (such as, for example, the unit Frobenius-norm and column-norm constraints considered in this article) or of the form of the A-learning rule. Thus alternative choices of constraints placed on A, as considered in Murray and Kreutz-Delgado (2001) and described in appendix B, will not change the form of the x_k-learning rule derived here. Of course, because the x_k learning rule is strongly coupled to the A-learning rule, algorithmic performance and speed of convergence may well be highly sensitive to conditions placed on A and the specific A learning algorithm used.

A.4 Learning the Dictionary A

A.4.1 General Results

We now turn to the enforcement of the second convergence condition, T₂ ≤ 0 and the development of the dictionary adaptation rule shown in equation 3.20. First, as in equation 3.21, we define the error term δA as

$$\delta A={\langle e(x)x^T\rangle }_N=\frac{1}{N}\sum _{k=1}^{N}e(x_k)x_k^T=A{\mathrm{\sum }}_{xx}-{\mathrm{\sum }}_{yx},$$ (A.21)

using the fact that e(x) = Ax − y. Then, from equation A.11, we have

$$\begin{array}{l}{T}_2={\langle e^T(x)\stackrel{.}{A}x\rangle }_N={\langle \text{tr}({xe}^T(x)\stackrel{.}{A})\rangle }_N=\text{tr}({\langle {xe}^T(x)\rangle }_N\stackrel{.}{A})\\ =\text{tr}(\delta A^T\stackrel{.}{A})=\delta {\mathbf{A}}^T\stackrel{.}{\mathbf{A}}.\end{array}$$ (A.22)

So far, these steps are independent of any specific constraints that may be placed on A, other than that the manifold be smooth and compact. With A constrained to lie on a specified smooth, compact manifold, to ensure correct learning behavior, it is sufficient to impose the constraint that Ȧ lies in the tangent space to the manifold and the condition that T₂ ≤ 0.

A.4.2 Learning on the Unit Frobenius Sphere,

To ensure that T₂ ≤ 0 and that Ȧ is in the tangent space of the unit sphere in the Frobenius space ℝ^mn, we take

$$\stackrel{.}{\mathbf{A}}=-\mu \mathbf{\Lambda }\delta \mathbf{A}\iff \stackrel{.}{A}=-\mu \mathrm{\Lambda }\delta A=-\mu (\delta A-\text{tr}(A^T\delta A)A),\mu >0,$$ (A.23)

which is the adaptation rule given in equation 3.20. With this choice, and using the positive semidefiniteness of Λ, we have

$$T_2=-\mu {\left|\right|\delta \mathbf{A}\left|\right|}_{\mathbf{\Lambda }}^2\le 0,$$

as required. Note that at convergence, the condition T₂ ≡ 0, yields Ȧ ≡ 0, so that we will have converged to constant values for the dictionary elements, and

$$0=\mathrm{\Lambda }\delta \widehat{A}=\mathrm{\Lambda }(\widehat{A}{\mathrm{\sum }}_{\widehat{x}\widehat{x}}-{\mathrm{\sum }}_{y\widehat{x}})\Rightarrow \delta \widehat{A}=(\widehat{A}{\mathrm{\sum }}_{\widehat{x}\widehat{x}}-{\mathrm{\sum }}_{y\widehat{x}})=c\widehat{A},$$ (A.24)

from equation A.5, where c = tr(Â^TδÂ). Thus, the steady-state solution is

$$\widehat{A}={\mathrm{\sum }}_{y,\widehat{x}}{({\mathrm{\sum }}_{\widehat{x}\widehat{x}}-cI)}^{-1}\in {\mathcal{A}}_{\text{F}}.$$ (A.25)

Note that equations A.20 and A.25 are the steady-state values given earlier in equation 3.25.

Appendix B: Convergence of the Column–Normalized Learning Algorithm

The derivation and proof of convergence of the column-normalized learning algorithm, applicable to learning members of , is accomplished by appropriately modifying key steps of the development given in appendix A. As in appendix A, the standard Euclidean norm and inner product apply to column vectors, while the Frobenius norm and inner product apply to m × n matrix elements of ℝ^m×n.

B.1 Admissible Matrix Derivatives

B.1.1 The Constraint Manifold

Let e_i = (0 · · · 0 1 0 · · ·0)^T ∈ ℝⁿ be the canonical unit vector whose components are all zero except for the value 1 in the ith location. Then

$$I=\sum _{i=1}^n{e}_i{e}_i^T\text{and}{a}_i={Ae}_i.$$

Note that

$${\left|\right|a_i\left|\right|}^2=a_i^T{a}_i={({Ae}_i)}^T{Ae}_i=e_i^T{A}^T{Ae}_i=\text{tr}{e}_i{e}_i^T{A}^{T}A=\text{tr}{M}_i^{T}A=\langle M_i,A\rangle ,$$

where

$$M_i\triangleq {Ae}_i{e}_i^T=a_i{e}_i^T=[00\cdots 0a_{i}0\cdots 0]\in {\mathbb{R}}^{m\times n}.$$ (B.1)

Note that only the ith column of M_i is nonzero and is equal to a_i = ith column of A. We therefore have that

$$A=\sum _{i=1}^n{M}_i.$$ (B.2)

Also, for i, j = 1, …, n,

$$\langle M_i,M_j\rangle =\text{tr}{M}_i^T{M}_j=\text{tr}{e}_i{e}_i^T{A}^T{Ae}_j{e}_j^T=\text{tr}{e}_i^T{A}^T{Ae}_j{e}_j^T{e}_i={\left|\right|a_i\left|\right|}^2{\delta }_{i,j},$$ (B.3)

where δ_i,j is the Kronecker delta. Note, in particular, that ||a_i|| = ||M_i||.

Let A ∈ , where is the set of column-normalized matrices, as defined by equation 3.29. is an mn − n = n(m−1)–dimensional submanifold of the Frobenius space ℝ^m×n as each of the n columns of A is normalized as

$${\left|\right|a_i\left|\right|}^2={\left|\right|M_i\left|\right|}^2\equiv \frac{1}{n},$$

and

$${\left|\right|A\left|\right|}^2=\text{tr}{A}^{T}A=\text{tr}\sum _{i=1}^n{M}_i^T\sum _{j=1}^n{M}_j=\sum _{i=1}^n{\left|\right|a_i\left|\right|}^2=\frac{n}{n}=1,$$

using linearity of the trace function and property, B.3. It is evident, therefore, that

$${\mathcal{A}}_{\text{C}}\subset {\mathcal{A}}_{\text{F}},$$

for defined by equation 3.17.

We can readily show that is simply connected, so that a continuous path exists between any matrix A = A_init ∈ to any other column-normalized matrix A′ = A_Final ∈ . Indeed, let A and A′ be such that

$$\begin{array}{l}A=[a_1,\dots ,a_n],A^{\prime }=[a_1^{\prime },\dots ,a_n^{\prime }],\\ \left|\right|a_i\left|\right|=\left|\right|a_j^{\prime }\left|\right|=1/\sqrt{n},\forall i,j=1,\dots ,n.\end{array}$$

There is obviously a continuous path entirely in from A ∈ to the intermediate matrix $[a_1^{\prime },a_2,\dots ,a_n]\in {\mathcal{A}}_{\text{C}}$. Similarly, there is a continuous path entirely in from [ $a_1^{\prime },a_2,\dots ,a_n$] to [ $a_1^{\prime },a_2^{\prime },\dots ,a_n$], and so on to $[a_1^{\prime },\dots ,a_n^{\prime }]=A^{\prime }$. To summarize, is a simply connected (nm − n)–dimensional submanifold of the simply connected (nm − 1)–dimensional manifold and they are both submanifolds of the (nm)–dimensional Frobenius space ℝ^m×n.

B.1.2 Derivatives on : The Tangent Space T

For convenience, for i = 1, …, n define

$${\widehat{a}}_i=\frac{a_i}{\left|\right|a_i\left|\right|}=\sqrt{n}{a}_i,\left|\right|{\widehat{a}}_i\left|\right|=1,$$

and

$${\widehat{M}}_i=\frac{M_i}{\left|\right|M_i\left|\right|}=\sqrt{n}{M}_i={\widehat{a}}_i{e}_i^T,\left|\right|{\widehat{M}}_i\left|\right|=1.$$

Note that equation B.3 yields

$$\langle {\widehat{M}}_i,{\widehat{M}}_j\rangle =\text{tr}{\widehat{M}}_i^T{\widehat{M}}_j={\delta }_{i,j}.$$ (B.4)

For any A ∈ we have for each i = 1, …, n,

$$\begin{array}{l}0=\frac{d}{dt}{\left|\right|a_i\left|\right|}^2=\frac{d}{dt}{a}_i^T{a}_i=\frac{d}{dt}{e}_i^T{A}^T{Ae}_i=2e_i^T{A}^T\stackrel{.}{A}{e}_i\\ =2\text{tr}{e}_i{e}_i^T{A}^T\stackrel{.}{A}=2\text{tr}{M}_i^T\stackrel{.}{A},\end{array}$$

or

$$A\in {\mathcal{A}}_{\text{C}}\Rightarrow \langle M_i,\stackrel{.}{A}\rangle =\text{tr}{M}_i^T\stackrel{.}{A}=0\text{for}i=1,\dots ,n.$$ (B.5)

In fact,

$$\begin{array}{l}\stackrel{.}{A}\in {\mathcal{A}}_{\text{C}}\text{at}A\in {\mathcal{A}}_{\text{C}}\iff \langle {\widehat{M}}_i,\stackrel{.}{A}\rangle =\text{tr}{\widehat{M}}_i^T\stackrel{.}{A}=0\\ \text{for}i=1,\dots ,n.\end{array}$$ (B.6)

Note from equations B.2 and B.5 that

$$\langle A,\stackrel{.}{A}\rangle =\langle \sum _{i=1}^n{M}_i,\stackrel{.}{A}\rangle =0,$$

showing that (see equation A.3) T ⊂ T , as expected from the fact that ⊂ .

An important and readily proven fact is that for each i = 1, …, n,

$$\text{tr}{\widehat{M}}_i^T\stackrel{.}{A}=0\iff \stackrel{.}{A}=P_i{Q}_i$$ (B.7)

for some matrix Q_i and projection operator, P_i, defined by

$$P_{i}Q\triangleq Q-{\widehat{M}}_i\langle {\widehat{M}}_i,Q\rangle =Q-{\widehat{M}}_i\text{tr}{\widehat{M}}_i^{T}Q.$$ (B.8)

From equation B.4, it can be shown that the projection operators commute,

$$P_i{P}_j=P_j{P}_i,i\ne j,i,j=1,\dots ,n,$$ (B.9)

and are idempotent,

$$P_i^2=P_i,i=1,\dots ,n.$$ (B.10)

Indeed, it is straightforward to show from equation B.4 that for all Q,

$$P_i{P}_{j}Q=P_j{P}_{i}Q=Q-{\widehat{M}}_i\langle {\widehat{M}}_i,Q\rangle -{\widehat{M}}_j\langle {\widehat{M}}_j,Q\rangle ,\text{for}\text{all}i\ne j,$$ (B.11)

and

$$P_i^{2}Q=Q-{\widehat{M}}_i\langle {\widehat{M}}_i,Q\rangle =P_{i}Q,i=1,\dots ,n.$$ (B.12)

It can also be shown that

$$\langle P_i{Q}_1,Q_2\rangle =\langle Q_1,P_i{Q}_2\rangle ,$$

showing that P_i is self–adjoint, $P_i=P_i^{\ast }$.

Define the operator,

$$P=P_1,\dots ,P_n.$$ (B.13)

Note that because of the commutativity of the P_i, the order of multiplication on the right-hand side of equation B.11 is immaterial, and it is easily determined that P is idempotent,

$$P^2=P.$$

By induction on equation B.11, it is readily shown that

$$PQ=Q-{\widehat{M}}_1\langle {\widehat{M}}_1,Q\rangle -\cdots -{\widehat{M}}_n\langle {\widehat{M}}_n,Q\rangle =Q-\sum _{i=1}^n{\widehat{M}}_i\langle {\widehat{M}}_i,Q\rangle .$$ (B.14)

Either from the self-adjointness and idempotency of each P_i, or directly from equation B.14, it can be shown that P itself is self–adjoint, P = P^*,

$$\langle {PQ}_1,Q_2\rangle =\langle Q_1,{PQ}_2\rangle .$$

Thus, P is the orthogonal projection operator from ℝ^m×n onto T .

As a consequence, we have the key result that

$$\stackrel{.}{A}\in T{\mathcal{A}}_{\text{C}}\text{at}A\iff \stackrel{.}{A}=PQ,$$ (B.15)

for some matrix Q ∈ ℝ^m×n. This follows from the fact that given Q, then the right-hand side of equation B.6 is true for Ȧ = PQ. On the other hand, if the right-hand side of equation B.6 is true for Ȧ, we can take Q = Ȧ in equation B.15. Note that for the T –projection operator Λ given by equation A.2, we have that

$$P=\mathrm{\Lambda }P=P\mathrm{\Lambda },$$

consistent with the fact that T ⊂ T .

Let q_i, i = 1, …, n be the columns of Q = [q₁, …, q_n]. The operation Q′ = P_jQ, corresponds to

$$q_i^{\prime }=q_i,i\ne j,\text{and}{q}_j^{\prime }=(I-{\widehat{a}}_j{\widehat{a}}_j^T)q_j,$$

while the operation Q′= PQ, corresponds to

$$q_i^{\prime }=(I-{\widehat{a}}_i{\widehat{a}}_i^T)q_i,i=1,\dots ,n.$$

B.2 Learning on the Manifold

The development of equations A.6 through A.22 is independent of the precise nature of the constraint manifold and can be applied here to the specific case of = . To ensure that T₂ ≤ 0 in equation A.22 and that Ȧ ∈ T , we can use the learning rule,

$$\stackrel{.}{A}=-\mu P\delta A=-\mu \left(\delta A-\sum _{i=1}^n{\widehat{M}}_i\text{tr}{\widehat{M}}_i\delta A\right),$$ (B.16)

for μ > 0 and δA given by equation A.21. With the ith column of δA denoted by δa_i, this corresponds to the learning rule,

$${\stackrel{.}{a}}_i=-\mu (I-{\widehat{a}}_i{\widehat{a}}_i^T)\delta a_i,i=1,\dots ,n.$$ (B.17)

With rule B.16, we have

$$\begin{array}{l}{T}_2=\langle \delta A,\stackrel{.}{A}\rangle =-\mu \langle \delta A,P\delta A\rangle =-\mu \langle \delta A,P^2\delta A\rangle \\ =-\mu \langle P\delta A,P\delta A\rangle =-\mu {\left|\right|P\delta A\left|\right|}^2\le 0,\end{array}$$

where we have explicitly shown that the idempotency and self-adjointness of P correspond to its being a nonnegative operator. Thus, we will have convergence to the largest invariant set for which Ȧ ≡ 0, which from equation B.16 is equivalent to the set for which

$$P\delta A=\delta A-\sum _{i=1}^n{\widehat{M}}_i\langle {\widehat{M}}_i,\delta A\rangle \equiv 0.$$ (B.18)

This, in turn, is equivalent to

$$\delta A=\sum _{i=1}^n{\widehat{M}}_i\langle {\widehat{M}}_i,\delta A\rangle =\sum _{i=1}^n{nM}_i\langle M_i,\delta A\rangle =\sum _{i=1}^n{c}_i{M}_i,$$

with

$$c_i\triangleq n\langle M_i,\delta A\rangle ={na}_i^T\delta a_i,i=1,\dots ,n.$$

An equivalent statement to equation B.19 is

$$\delta a_i=c_i{a}_i,i=1,\dots ,n.$$

Defining the diagonal matrix

$$C=\text{diag}[c_i,\dots ,c_n]$$

and recalling the definitions A.21 and B.1, we obtain from equation B.19 that

$$A{\mathrm{\sum }}_{xx}-{\mathrm{\sum }}_{yx}=\delta A=AC,$$

which can be solved as

$$A={\mathrm{\sum }}_{yx}{({\mathrm{\sum }}_{xx}-C)}^{-1}.$$ (B.20)

This is the general form of the solution found by the –learning algorithm.